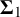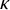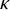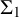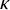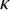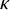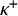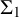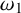1 Introduction
Mathematical objects whose existence are usually proved with the axiom of choice are often referred to as pathological sets. Important examples of such objects are Hamel bases of the vector space of real numbers over the field of rational numbers, nonprincipal ultrafilters on infinite sets and bistationary, that is, stationary and costationary) subsets of uncountable regular cardinals. For many types of pathological sets of real numbers, it is possible to use results from descriptive set theory to show that these objects cannot be defined by simple formulas in second-order arithmetic. Moreover, many canonical extensions of the axioms of
![]() ${\mathrm {ZFC}}$
prove that these objects are not definable in second-order arithmetic at all and this implication is often viewed as a desirable feature of such extensions because it allows us to clearly separate pathological sets of real numbers from the explicitly constructed sets of reals.
${\mathrm {ZFC}}$
prove that these objects are not definable in second-order arithmetic at all and this implication is often viewed as a desirable feature of such extensions because it allows us to clearly separate pathological sets of real numbers from the explicitly constructed sets of reals.
In this paper, we study the set-theoretic definability of pathological sets of higher cardinalities. More specifically, we aim to generalize classical nondefinability results for sets of real numbers to subsets of the power set
![]() ${\mathcal {P}}({\kappa })$
of an uncountable cardinal
${\mathcal {P}}({\kappa })$
of an uncountable cardinal
![]() $\kappa $
that are definable by
$\kappa $
that are definable by
![]() $\Sigma _1$
-formulasFootnote 1 with parameters in
$\Sigma _1$
-formulasFootnote 1 with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. This bound on the complexity of the used formulas is motivated by the observation that the assumption
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. This bound on the complexity of the used formulas is motivated by the observation that the assumption
![]() ${\mathrm {V}}={\mathrm {HOD}}$
implies the
${\mathrm {V}}={\mathrm {HOD}}$
implies the
![]() $\Sigma _2$
-definability of various pathological sets (see [Reference Lücke34, Proposition 3.9]), and this assumption is compatible with many canonical extensions of
$\Sigma _2$
-definability of various pathological sets (see [Reference Lücke34, Proposition 3.9]), and this assumption is compatible with many canonical extensions of
![]() ${\mathrm {ZFC}}$
. The restriction of the set of parameters is motivated by the existence of highly potent coding forcings at uncountable regular cardinals
${\mathrm {ZFC}}$
. The restriction of the set of parameters is motivated by the existence of highly potent coding forcings at uncountable regular cardinals
![]() $\kappa $
that can be used to make highly pathological subsets of
$\kappa $
that can be used to make highly pathological subsets of
![]() ${\mathcal {P}}({\kappa })$
definable by a
${\mathcal {P}}({\kappa })$
definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa ^+)$
. For example, the results of [Reference Lücke33, Section 3] show that, if
${\mathrm {H}}(\kappa ^+)$
. For example, the results of [Reference Lücke33, Section 3] show that, if
![]() $\kappa $
is an uncountable cardinal satisfying
$\kappa $
is an uncountable cardinal satisfying
![]() $\kappa =\kappa ^{{<}\kappa }$
and A is a subset
$\kappa =\kappa ^{{<}\kappa }$
and A is a subset
![]() ${\mathcal {P}}({\kappa })$
, then, in some cofinality-preserving forcing extension
${\mathcal {P}}({\kappa })$
, then, in some cofinality-preserving forcing extension
![]() ${\mathrm {V}}[G]$
of the ground model
${\mathrm {V}}[G]$
of the ground model
![]() ${\mathrm {V}}$
, the sets A and
${\mathrm {V}}$
, the sets A and
![]() ${\mathcal {P}}({\kappa })^{{\mathrm {V}}[G]}\setminus A$
are definable by
${\mathcal {P}}({\kappa })^{{\mathrm {V}}[G]}\setminus A$
are definable by
![]() $\Sigma _1$
-formulas with parameters in
$\Sigma _1$
-formulas with parameters in
![]() ${\mathrm {H}}(\kappa ^+)$
. Moreover, the main result of [Reference Holy and Lücke22] shows that for every cardinal
${\mathrm {H}}(\kappa ^+)$
. Moreover, the main result of [Reference Holy and Lücke22] shows that for every cardinal
![]() $\kappa $
with these properties, there is a cofinality-preserving forcing extension in which a well-ordering of
$\kappa $
with these properties, there is a cofinality-preserving forcing extension in which a well-ordering of
![]() ${\mathcal {P}}({\kappa })$
is definable by a
${\mathcal {P}}({\kappa })$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa ^+)$
, and the results of [Reference Friedman, Holy and Lücke13] show that various large cardinal properties of
${\mathrm {H}}(\kappa ^+)$
, and the results of [Reference Friedman, Holy and Lücke13] show that various large cardinal properties of
![]() $\kappa $
can be preserved by such coding forcings. Finally, results of Caicedo and Veličković in [Reference Caicedo and Veličković5] show that the bounded proper forcing axiom
$\kappa $
can be preserved by such coding forcings. Finally, results of Caicedo and Veličković in [Reference Caicedo and Veličković5] show that the bounded proper forcing axiom
![]() ${\mathrm {BPFA}}$
outright implies the existence of a well-ordering of
${\mathrm {BPFA}}$
outright implies the existence of a well-ordering of
![]() ${\mathcal {P}}({\omega _1})$
that is definable by a
${\mathcal {P}}({\omega _1})$
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\omega _2)$
(see the proof of Proposition 10.6 below).
${\mathrm {H}}(\omega _2)$
(see the proof of Proposition 10.6 below).
Previous work in this direction (see [Reference Lücke34], [Reference Lücke, Schindler and Schlicht37] and [Reference Welch51]) has already provided important examples that show that we can achieve the above aim when we work in one of the following scenarios:
-
○ The cardinal
 $\kappa $
is a limit of cardinals possessing certain large cardinal properties, like measurability.
$\kappa $
is a limit of cardinals possessing certain large cardinal properties, like measurability. -
○ The cardinal
 $\kappa $
is the first uncountable cardinal
$\kappa $
is the first uncountable cardinal
 $\omega _1$
and either certain large cardinals exist above
$\omega _1$
and either certain large cardinals exist above
 $\kappa $
or strong forcing axioms hold.
$\kappa $
or strong forcing axioms hold.
In the following, we will derive structural results for simply definable sets that will allow us to prove the nondefinability of several types of pathological sets in the above settings. These implications can again be seen as desirable features of the corresponding axiom systems. Moreover, for most of our results about singular limits of large cardinals, we prove that the used large cardinal assumption is optimal for the corresponding nondefinability statement at singular cardinals.
The starting point of our work is a perfect set theorem for
![]() $\Sigma _1$
-definable sets at limits of measurable cardinals. In order to formulate this result, we generalize some basic topological concepts to higher function spaces and power sets. Given a cardinal
$\Sigma _1$
-definable sets at limits of measurable cardinals. In order to formulate this result, we generalize some basic topological concepts to higher function spaces and power sets. Given a cardinal
![]() $\kappa>0$
and an infinite cardinal
$\kappa>0$
and an infinite cardinal
![]() $\mu $
, we equip the set
$\mu $
, we equip the set
![]() ${}^\mu \kappa $
of all functions from
${}^\mu \kappa $
of all functions from
![]() $\mu $
to
$\mu $
to
![]() $\kappa $
with the topology whose basic open sets consists of all functions that extend a given function
$\kappa $
with the topology whose basic open sets consists of all functions that extend a given function
![]() ${s}:{\xi }\longrightarrow {\kappa }$
with
${s}:{\xi }\longrightarrow {\kappa }$
with
![]() $\xi <\mu $
. In the same way, we equip the power set
$\xi <\mu $
. In the same way, we equip the power set
![]() ${\mathcal {P}}({\nu })$
of an infinite cardinal
${\mathcal {P}}({\nu })$
of an infinite cardinal
![]() $\nu $
with the topology whose basic open sets consists of all subsets of
$\nu $
with the topology whose basic open sets consists of all subsets of
![]() $\nu $
whose intersection with a given ordinal
$\nu $
whose intersection with a given ordinal
![]() $\eta <\nu $
is equal to a fixed subset of
$\eta <\nu $
is equal to a fixed subset of
![]() $\eta $
. We then say that an injection
$\eta $
. We then say that an injection
![]() ${\iota }:{{}^\mu \kappa }\longrightarrow {{\mathcal {P}}({\nu })}$
is a perfect embedding if it induces a homeomorphism between
${\iota }:{{}^\mu \kappa }\longrightarrow {{\mathcal {P}}({\nu })}$
is a perfect embedding if it induces a homeomorphism between
![]() ${}^\mu \kappa $
and the subspace
${}^\mu \kappa $
and the subspace
![]() ${{\mathrm {ran}}(\iota )}$
of
${{\mathrm {ran}}(\iota )}$
of
![]() ${\mathcal {P}}({\nu })$
. The following result now shows that, analogously to the perfect set property of analytic sets of reals, simply definable thin sets of subsets of limits of measurable cardinals have small cardinality.
${\mathcal {P}}({\nu })$
. The following result now shows that, analogously to the perfect set property of analytic sets of reals, simply definable thin sets of subsets of limits of measurable cardinals have small cardinality.
Theorem 1.1. Let
![]() $\kappa $
be a limit of measurable cardinals, and let D be a subset of
$\kappa $
be a limit of measurable cardinals, and let D be a subset of
![]() ${\mathcal {P}}({\kappa })$
that is definable by a
${\mathcal {P}}({\kappa })$
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. If D has cardinality greater than
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. If D has cardinality greater than
![]() $\kappa $
, then there is a perfect embedding
$\kappa $
, then there is a perfect embedding
![]() ${\iota }:{{}^{{{\mathrm {cof}}(\kappa )}}\kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
${\iota }:{{}^{{{\mathrm {cof}}(\kappa )}}\kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
![]() ${{\mathrm {ran}}(\iota )}\subseteq D$
.
${{\mathrm {ran}}(\iota )}\subseteq D$
.
In the case of singular limits of measurable cardinals, we will use core model theory developed in [Reference Koepke31] and, for example, in [Reference Zeman53] to show that the consistency strength of the assumption of this theorem is optimal for its conclusion.
Theorem 1.2. Let
![]() $\kappa $
be a singular strong limit cardinal with the property that, for every subset D of
$\kappa $
be a singular strong limit cardinal with the property that, for every subset D of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, there is a perfect embedding
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, there is a perfect embedding
![]() ${\iota }:{{}^{{{\mathrm {cof}}(\kappa )}}\kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
${\iota }:{{}^{{{\mathrm {cof}}(\kappa )}}\kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
![]() ${{\mathrm {ran}}(\iota )}\subseteq D$
. Then there is an inner model with a sequence of measurable cardinals of length
${{\mathrm {ran}}(\iota )}\subseteq D$
. Then there is an inner model with a sequence of measurable cardinals of length
![]() ${{\mathrm {cof}}(\kappa )}$
.
${{\mathrm {cof}}(\kappa )}$
.
The next type of pathological sets that we will study in this paper are almost disjoint families of large cardinalities. Given an infinite cardinal
![]() $\kappa $
, a set A of unbounded subsets of
$\kappa $
, a set A of unbounded subsets of
![]() $\kappa $
is an almost disjoint family in
$\kappa $
is an almost disjoint family in
![]() ${\mathcal {P}}({\kappa })$
if
${\mathcal {P}}({\kappa })$
if
![]() $x\cap y$
is bounded in
$x\cap y$
is bounded in
![]() $\kappa $
for all distinct
$\kappa $
for all distinct
![]() $x,y\in A$
. In addition, we say that such a family A is maximal if for every unbounded subset x of
$x,y\in A$
. In addition, we say that such a family A is maximal if for every unbounded subset x of
![]() $\kappa $
, there exists
$\kappa $
, there exists
![]() $y\in A$
with the property that
$y\in A$
with the property that
![]() $x\cap y$
is unbounded in
$x\cap y$
is unbounded in
![]() $\kappa $
. Motivated by a classical result of Mathias in [Reference Mathias39] that shows that all analytic maximal almost disjoint families in
$\kappa $
. Motivated by a classical result of Mathias in [Reference Mathias39] that shows that all analytic maximal almost disjoint families in
![]() ${\mathcal {P}}({\omega })$
are finite and many additional influential results on maximal almost disjoint families by Mathias, A. Miller, Törnquist, Horowitz and Shelah, Neeman and Norwood, Bakke-Haga, Fischer, Schrittesser, Weinert, and others (see [Reference Bakke Haga, Schrittesser and Törnquist3, Reference Fischer, Schrittesser and Weinert12, Reference Horowitz and Shelah23, Reference Mathias39, Reference Miller40, Reference Neeman and Norwood42, Reference Schrittesser and Törnquist45, Reference Törnquist50]), we will use the techniques developed in the proof of Theorem 1.1 to prove that, if a cardinal
${\mathcal {P}}({\omega })$
are finite and many additional influential results on maximal almost disjoint families by Mathias, A. Miller, Törnquist, Horowitz and Shelah, Neeman and Norwood, Bakke-Haga, Fischer, Schrittesser, Weinert, and others (see [Reference Bakke Haga, Schrittesser and Törnquist3, Reference Fischer, Schrittesser and Weinert12, Reference Horowitz and Shelah23, Reference Mathias39, Reference Miller40, Reference Neeman and Norwood42, Reference Schrittesser and Törnquist45, Reference Törnquist50]), we will use the techniques developed in the proof of Theorem 1.1 to prove that, if a cardinal
![]() $\kappa $
possesses sufficiently strong large cardinal properties, then every simply definable almost disjoint family in
$\kappa $
possesses sufficiently strong large cardinal properties, then every simply definable almost disjoint family in
![]() ${\mathcal {P}}({\kappa })$
has cardinality at most
${\mathcal {P}}({\kappa })$
has cardinality at most
![]() $\kappa $
. In particular, by a simple diagonalization argument, all simply definable maximal almost disjoint families in
$\kappa $
. In particular, by a simple diagonalization argument, all simply definable maximal almost disjoint families in
![]() ${\mathcal {P}}({\kappa })$
have cardinality less than
${\mathcal {P}}({\kappa })$
have cardinality less than
![]() $\kappa $
in this case.
$\kappa $
in this case.
In order to reduce the large cardinal assumptions used in our arguments, we recall the notion of iterable cardinals, introduced by Sharpe and Welch in [Reference Sharpe and Welch46] and studied extensively in [Reference Gitman and Welch17]. An uncountable cardinal
![]() $\kappa $
is iterable if for every subset x of
$\kappa $
is iterable if for every subset x of
![]() $\kappa $
, there exists a transitive model M of
$\kappa $
, there exists a transitive model M of
![]() ${\mathrm {ZFC}}^-$
of cardinality
${\mathrm {ZFC}}^-$
of cardinality
![]() $\kappa $
with
$\kappa $
with
![]() $\kappa ,x\in M$
and a weakly amenable M-ultrafilter U on
$\kappa ,x\in M$
and a weakly amenable M-ultrafilter U on
![]() $\kappa $
such that the structure
$\kappa $
such that the structure
![]() $\langle M,U\rangle $
is iterable. Note that all iterable cardinals are weakly compact and all Ramsey cardinals are iterable (see, for example, [Reference Gitman16, Theorem 1.3]). In particular, all measurable limits of measurable cardinals satisfy the assumptions of the following result.
$\langle M,U\rangle $
is iterable. Note that all iterable cardinals are weakly compact and all Ramsey cardinals are iterable (see, for example, [Reference Gitman16, Theorem 1.3]). In particular, all measurable limits of measurable cardinals satisfy the assumptions of the following result.
Theorem 1.3. Let
![]() $\kappa $
be an iterable cardinal that is a limit of measurable cardinals, and let A be a subset of
$\kappa $
be an iterable cardinal that is a limit of measurable cardinals, and let A be a subset of
![]() ${\mathcal {P}}({\kappa })$
that is definable by a
${\mathcal {P}}({\kappa })$
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. If A has cardinality greater than
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. If A has cardinality greater than
![]() $\kappa $
, then there exist distinct
$\kappa $
, then there exist distinct
![]() $x,y\in A$
with the property that
$x,y\in A$
with the property that
![]() $x\cap y$
is unbounded in
$x\cap y$
is unbounded in
![]() $\kappa $
.
$\kappa $
.
The third type of pathological sets studied in this paper are long well-orders, that is, well-orderings of subsets of the power set
![]() ${\mathcal {P}}({\kappa })$
of an infinite cardinal
${\mathcal {P}}({\kappa })$
of an infinite cardinal
![]() $\kappa $
of order-type at least
$\kappa $
of order-type at least
![]() $\kappa ^+$
. The study of the definability of these objects is motivated by the classical fact that projective determinacy implies that all well-orderings definable in second-order arithmetic have countable length. In the case of limits of measurable cardinals
$\kappa ^+$
. The study of the definability of these objects is motivated by the classical fact that projective determinacy implies that all well-orderings definable in second-order arithmetic have countable length. In the case of limits of measurable cardinals
![]() $\kappa $
, it is possible to use arguments contained in the proof of [Reference Lücke and Schlicht38, Lemma 1.3] to show that for every well-ordering of
$\kappa $
, it is possible to use arguments contained in the proof of [Reference Lücke and Schlicht38, Lemma 1.3] to show that for every well-ordering of
![]() $\kappa $
, the collection of proper initial segments of the given order is not definable by a
$\kappa $
, the collection of proper initial segments of the given order is not definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. In Section 7 below, we will show that it is possible to use classical results of Dehornoy in [Reference Dehornoy11] to show that for all such limits
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. In Section 7 below, we will show that it is possible to use classical results of Dehornoy in [Reference Dehornoy11] to show that for all such limits
![]() $\kappa $
, no well-ordering of
$\kappa $
, no well-ordering of
![]() ${\mathcal {P}}({\kappa })$
is definable in the above way (see Corollary 7.4). We will then proceed by using ideas from the proof of Theorem 1.1 to prove results about well-orderings whose domain is a large proper subset of
${\mathcal {P}}({\kappa })$
is definable in the above way (see Corollary 7.4). We will then proceed by using ideas from the proof of Theorem 1.1 to prove results about well-orderings whose domain is a large proper subset of
![]() ${\mathcal {P}}({\kappa })$
. The following theorem provides a scenario in which such orders have no simple definition.
${\mathcal {P}}({\kappa })$
. The following theorem provides a scenario in which such orders have no simple definition.
Theorem 1.4. Let
![]() $\kappa $
be a cardinal of countable cofinality that is a limit of measurable cardinals. If there exists a well-ordering of a subset of
$\kappa $
be a cardinal of countable cofinality that is a limit of measurable cardinals. If there exists a well-ordering of a subset of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
, then there is a
$\kappa $
, then there is a
![]() $\mathbf {\Sigma }^1_3$
-well-ordering of the reals.
$\mathbf {\Sigma }^1_3$
-well-ordering of the reals.
In addition, the theory developed in this paper allow us to determine the exact consistency strength of the nonexistence of
![]() $\Sigma _1$
-definable long well-orderings of subsets of a singular strong limit cardinal of countable cofinality. The following theorem is proven by combining our techniques with results about short core models from [Reference Koepke31] in one direction and diagonal Prikry forcing in the other direction.
$\Sigma _1$
-definable long well-orderings of subsets of a singular strong limit cardinal of countable cofinality. The following theorem is proven by combining our techniques with results about short core models from [Reference Koepke31] in one direction and diagonal Prikry forcing in the other direction.
Theorem 1.5. The following statements are equiconsistent over
![]() ${\mathrm {ZFC}}$
:
${\mathrm {ZFC}}$
:
-
(i) There exist infinitely many measurable cardinals.
-
(ii) There exists a singular cardinal
 $\kappa $
with the property that no well-ordering of a subset of
$\kappa $
with the property that no well-ordering of a subset of
 ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
 $\kappa $
is definable by a
$\kappa $
is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
We now continue by considering analogues of the above results for pathological sets consisting of subsets of the first uncountable cardinal
![]() $\omega _1$
. Using results of Woodin in [Reference Woodin52], a perfect subset theorem for subsets of
$\omega _1$
. Using results of Woodin in [Reference Woodin52], a perfect subset theorem for subsets of
![]() ${\mathcal {P}}({\omega _1})$
definable by a
${\mathcal {P}}({\omega _1})$
definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
is provided by [Reference Lücke, Schindler and Schlicht37, Theorem 4.9] that shows that if the nonstationary ideal on
${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
is provided by [Reference Lücke, Schindler and Schlicht37, Theorem 4.9] that shows that if the nonstationary ideal on
![]() $\omega _1$
is saturated and there is a measurable cardinal, then every such subset either contains a continuous image of
$\omega _1$
is saturated and there is a measurable cardinal, then every such subset either contains a continuous image of
![]() ${}^{\omega _1}\omega _1$
or is a subset of
${}^{\omega _1}\omega _1$
or is a subset of
![]() ${\mathrm {L}}({\mathbb {R}})$
. As observed in [Reference Lücke, Schindler and Schlicht37], it is, in general, not possible to strengthen the second alternative to state that the given set has cardinality at most
${\mathrm {L}}({\mathbb {R}})$
. As observed in [Reference Lücke, Schindler and Schlicht37], it is, in general, not possible to strengthen the second alternative to state that the given set has cardinality at most
![]() $\aleph _1$
, because the failure of
$\aleph _1$
, because the failure of
![]() ${\mathrm {CH}}$
implies that
${\mathrm {CH}}$
implies that
![]() $\{{x\in {}^{\omega _1}\omega _1}~\vert ~{\forall \alpha <\omega _1 ~ x(\omega +\alpha )=0}\}$
is a subset of
$\{{x\in {}^{\omega _1}\omega _1}~\vert ~{\forall \alpha <\omega _1 ~ x(\omega +\alpha )=0}\}$
is a subset of
![]() ${}^{\omega _1}\omega _1$
of cardinality greater than
${}^{\omega _1}\omega _1$
of cardinality greater than
![]() $\aleph _1$
that is definable by a
$\aleph _1$
that is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\omega _1$
and does not contain a perfect subset. The following result now shows that analogs of Theorems 1.3 and 1.4 for
$\omega _1$
and does not contain a perfect subset. The following result now shows that analogs of Theorems 1.3 and 1.4 for
![]() $\omega _1$
follow both from strong large cardinal assumptions and the validity of strong forcing axioms.
$\omega _1$
follow both from strong large cardinal assumptions and the validity of strong forcing axioms.
Theorem 1.6. Assume that either there is a measurable cardinal above infinitely many Woodin cardinals or Woodin’s axiom
![]() $(*)$
holds.
$(*)$
holds.
-
(i) No well-ordering of a subset of
 ${\mathcal {P}}({\omega _1})$
of cardinality greater than
${\mathcal {P}}({\omega _1})$
of cardinality greater than
 $\aleph _1$
is definable by a
$\aleph _1$
is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 ${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
.
${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
. -
(ii) If A is a set of cardinality greater than
 $\aleph _1$
that consists of unbounded subsets of
$\aleph _1$
that consists of unbounded subsets of
 $\omega _1$
and is definable by a
$\omega _1$
and is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 ${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
, then there exist distinct
${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
, then there exist distinct
 $x,y\in A$
with the property that
$x,y\in A$
with the property that
 $x\cap y$
is unbounded in
$x\cap y$
is unbounded in
 $\omega _1$
.
$\omega _1$
.
We will end this paper by observing that the above results cannot be generalized from
![]() $\omega _1$
to
$\omega _1$
to
![]() $\omega _2$
. More specifically, we will show that all large cardinal assumptions are compatible with the existence of an almost disjoint family of cardinality
$\omega _2$
. More specifically, we will show that all large cardinal assumptions are compatible with the existence of an almost disjoint family of cardinality
![]() $2^{\aleph _2}$
in
$2^{\aleph _2}$
in
![]() ${\mathcal {P}}({\omega _2})$
that is definable by a
${\mathcal {P}}({\omega _2})$
that is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\omega _2$
(see Proposition 10.6 below).
$\omega _2$
(see Proposition 10.6 below).
2 A perfect subset theorem for limits of measurable cardinals
In this section, we prove Theorem 1.1 with the help of iterated ultrapowers. Throughout this paper, we will use two types of iterated ultrapower constructions for transitive
![]() ${\mathrm {ZFC}}^-$
-models M: iterated ultrapowers of M constructed using a single weakly amenable M-ultrafilter (as defined in [Reference Kanamori28, Section 19]) and iterated ultrapowers of M constructed using a set of normal measures in M (as defined in [Reference Steel49, Section 3]). In order to establish notation, we now discuss some details of the second type of construction. Given a transitive model M of
${\mathrm {ZFC}}^-$
-models M: iterated ultrapowers of M constructed using a single weakly amenable M-ultrafilter (as defined in [Reference Kanamori28, Section 19]) and iterated ultrapowers of M constructed using a set of normal measures in M (as defined in [Reference Steel49, Section 3]). In order to establish notation, we now discuss some details of the second type of construction. Given a transitive model M of
![]() ${\mathrm {ZFC}}^-$
and
${\mathrm {ZFC}}^-$
and
![]() $\mathcal {E}\in M$
with
$\mathcal {E}\in M$
with
a linear iteration of
![]() $\langle M,\mathcal {E}\rangle $
is a sequence
$\langle M,\mathcal {E}\rangle $
is a sequence
![]() $I=\langle {U_\alpha }~\vert ~{\alpha <\lambda }\rangle $
with
$I=\langle {U_\alpha }~\vert ~{\alpha <\lambda }\rangle $
with
![]() $\lambda>0$
and the property that there exists a directed system
$\lambda>0$
and the property that there exists a directed system
of transitive
![]() ${\mathrm {ZFC}}^-$
-models and elementary embeddings such that the following statements hold:
${\mathrm {ZFC}}^-$
-models and elementary embeddings such that the following statements hold:
-
(i)
 $M_0=M$
.
$M_0=M$
. -
(ii)
 $U_\alpha \in i_{0,\alpha }(\mathcal {E})$
for all
$U_\alpha \in i_{0,\alpha }(\mathcal {E})$
for all
 $\alpha <\lambda $
.
$\alpha <\lambda $
. -
(iii) If
 $\alpha $
is an ordinal with
$\alpha $
is an ordinal with
 $\alpha +1<\lambda $
, then
$\alpha +1<\lambda $
, then
 $M_{\alpha +1}$
is the (transitive collapse) of the ultrapower of
$M_{\alpha +1}$
is the (transitive collapse) of the ultrapower of
 $M_\alpha $
constructed using
$M_\alpha $
constructed using
 $U_\alpha $
and
$U_\alpha $
and
 $i_{\alpha ,\alpha +1}$
is the corresponding ultrapower embedding.
$i_{\alpha ,\alpha +1}$
is the corresponding ultrapower embedding. -
(iv) If
 $\eta <\lambda $
is a limit ordinal, then
$\eta <\lambda $
is a limit ordinal, then
 $\langle M_\eta ,\langle {i_{\alpha ,\eta }}~\vert ~{\alpha <\eta }\rangle \rangle $
is a direct limit of the directed system
$\langle M_\eta ,\langle {i_{\alpha ,\eta }}~\vert ~{\alpha <\eta }\rangle \rangle $
is a direct limit of the directed system
 $\langle \langle {M_\alpha }~\vert ~{\alpha <\eta }\rangle ,\langle {{i_{\alpha ,\beta }}:{M_\alpha }\longrightarrow {M_\beta }}~\vert ~{\alpha \leq \beta <\eta }\rangle \rangle $
.
$\langle \langle {M_\alpha }~\vert ~{\alpha <\eta }\rangle ,\langle {{i_{\alpha ,\beta }}:{M_\alpha }\longrightarrow {M_\beta }}~\vert ~{\alpha \leq \beta <\eta }\rangle \rangle $
.
The ordinal
![]() $\lambda $
is then called the length of I, and we use
$\lambda $
is then called the length of I, and we use
![]() ${\mathrm {lh}}({I})$
to refer to this ordinal.
${\mathrm {lh}}({I})$
to refer to this ordinal.
It is easy to see that the above system is uniquely determined by the sequence I, and therefore we write
![]() $U^I_\alpha =U_\alpha $
,
$U^I_\alpha =U_\alpha $
,
![]() $M^I_\alpha =M_\alpha $
and
$M^I_\alpha =M_\alpha $
and
![]() $i^I_{\alpha ,\beta }=i_{\alpha ,\beta }$
for all
$i^I_{\alpha ,\beta }=i_{\alpha ,\beta }$
for all
![]() $\alpha \leq \beta <{\mathrm {lh}}({I})$
. We then let
$\alpha \leq \beta <{\mathrm {lh}}({I})$
. We then let
![]() $\langle M^I_\infty ,\langle {{i^I_{\alpha ,\infty }}:{M^I_\alpha }\longrightarrow {M^I_\infty }}~\vert ~{\alpha <{\mathrm {lh}}({I})}\rangle \rangle $
denote the direct limit of the above system and, if the model
$\langle M^I_\infty ,\langle {{i^I_{\alpha ,\infty }}:{M^I_\alpha }\longrightarrow {M^I_\infty }}~\vert ~{\alpha <{\mathrm {lh}}({I})}\rangle \rangle $
denote the direct limit of the above system and, if the model
![]() $M^I_\infty $
is well-founded, then we identify it with its transitive collapse. Finally, the pair
$M^I_\infty $
is well-founded, then we identify it with its transitive collapse. Finally, the pair
![]() $\langle M,\mathcal {E}\rangle $
is called linearly iterable if the model
$\langle M,\mathcal {E}\rangle $
is called linearly iterable if the model
![]() $M^I_\infty $
is well-founded for every linear iteration I of
$M^I_\infty $
is well-founded for every linear iteration I of
![]() $\langle M,\mathcal {E}\rangle $
. Note that [Reference Steel49, Theorem 3.3] shows that, if every element of
$\langle M,\mathcal {E}\rangle $
. Note that [Reference Steel49, Theorem 3.3] shows that, if every element of
![]() $\mathcal {E}$
is
$\mathcal {E}$
is
![]() $\sigma $
-complete in
$\sigma $
-complete in
![]() ${\mathrm {V}}$
, then the pair is
${\mathrm {V}}$
, then the pair is
![]() $\langle M,\mathcal {E}\rangle $
is linearly iterable. In particular, the pair
$\langle M,\mathcal {E}\rangle $
is linearly iterable. In particular, the pair
![]() $\langle {\mathrm {V}},\mathcal {E}\rangle $
is linearly iterable for every set
$\langle {\mathrm {V}},\mathcal {E}\rangle $
is linearly iterable for every set
![]() $\mathcal {E}$
of normal ultrafilters.
$\mathcal {E}$
of normal ultrafilters.
Given a transitive
![]() $ZFC^-$
-model M and
$ZFC^-$
-model M and
![]() $U\in M$
with
$U\in M$
with
the set U is a weakly amenable M-ultrafilter and the pair
![]() $\langle M,U\rangle $
is iterable (in the sense of [Reference Kanamori28, Section 19]) if and only if the pair
$\langle M,U\rangle $
is iterable (in the sense of [Reference Kanamori28, Section 19]) if and only if the pair
![]() $\langle M,\{U\}\rangle $
is linearly iterable (in the above sense). Moreover, if
$\langle M,\{U\}\rangle $
is linearly iterable (in the above sense). Moreover, if
![]() $\langle M,U\rangle $
is iterable,
$\langle M,U\rangle $
is iterable,
denotes the iteration of
![]() $\langle M,U\rangle $
(as defined in [Reference Kanamori28, Section 19]) and
$\langle M,U\rangle $
(as defined in [Reference Kanamori28, Section 19]) and
![]() $\lambda>0$
is an ordinal, then
$\lambda>0$
is an ordinal, then
![]() $\langle {j_{0,\alpha }(U)}~\vert ~{\alpha <\lambda }\rangle $
is the unique linear iteration
$\langle {j_{0,\alpha }(U)}~\vert ~{\alpha <\lambda }\rangle $
is the unique linear iteration
![]() $I(U,\lambda )$
of
$I(U,\lambda )$
of
![]() $\langle M,\{U\}\rangle $
of length
$\langle M,\{U\}\rangle $
of length
![]() $\lambda $
and we have
$\lambda $
and we have
![]() $M^{I(U,\lambda )}_\alpha =M_\alpha $
and
$M^{I(U,\lambda )}_\alpha =M_\alpha $
and
![]() $i^{I(U,\lambda )}_{\alpha ,\beta }=j_{\alpha ,\beta }$
for all
$i^{I(U,\lambda )}_{\alpha ,\beta }=j_{\alpha ,\beta }$
for all
![]() $\alpha \leq \beta <\lambda $
.
$\alpha \leq \beta <\lambda $
.
The following technical lemma about the existence of certain systems of linear iterations is the starting point of the proofs of most of the results about limits of measurable cardinals stated in the introduction:
Lemma 2.1. Let
![]() $\mu $
be an infinite regular cardinal, let
$\mu $
be an infinite regular cardinal, let
![]() $\kappa $
be a limit of measurable cardinals with
$\kappa $
be a limit of measurable cardinals with
![]() ${{\mathrm {cof}}(\kappa )}=\mu $
and let
${{\mathrm {cof}}(\kappa )}=\mu $
and let
![]() $\mathcal {E}$
denote the collection of all normal ultrafilters on cardinals smaller than
$\mathcal {E}$
denote the collection of all normal ultrafilters on cardinals smaller than
![]() $\kappa $
. Given an element z of
$\kappa $
. Given an element z of
![]() ${\mathrm {H}}(\kappa )$
and a subset D of
${\mathrm {H}}(\kappa )$
and a subset D of
![]() ${\mathcal {P}}({\kappa })$
of cardinality
${\mathcal {P}}({\kappa })$
of cardinality
![]() $\kappa ^+$
, there exists
$\kappa ^+$
, there exists
-
○ an element x of D,
-
○ a system
 $\langle {\nu _s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
of inaccessible cardinals smaller than
$\langle {\nu _s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
of inaccessible cardinals smaller than
 $\kappa $
,
$\kappa $
, -
○ a system
 $\langle {\kappa _s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
of measurable cardinals smaller than
$\langle {\kappa _s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
of measurable cardinals smaller than
 $\kappa $
,
$\kappa $
, -
○ a system
 $\langle {U_s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
of elements of
$\langle {U_s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
of elements of
 $\mathcal {E}$
, and
$\mathcal {E}$
, and -
○ a system
 $\langle {I_s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
of linear iterations of
$\langle {I_s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
of linear iterations of
 $\langle {\mathrm {V}},\mathcal {E}\rangle $
of length less than
$\langle {\mathrm {V}},\mathcal {E}\rangle $
of length less than
 $\kappa $
$\kappa $
such that the following statements hold for all
![]() $s,t\in {}^{{<}\mu }\kappa $
:
$s,t\in {}^{{<}\mu }\kappa $
:
-
(i)
 $z\in {\mathrm {H}}(\nu _\emptyset )$
and
$z\in {\mathrm {H}}(\nu _\emptyset )$
and
 $\mu <\kappa $
implies that
$\mu <\kappa $
implies that
 $\mu <\nu _\emptyset $
.
$\mu <\nu _\emptyset $
. -
(ii)
 $U_s$
is an ultrafilter on
$U_s$
is an ultrafilter on
 $\kappa _s$
.
$\kappa _s$
. -
(iii)
 $I_s$
is a linear iteration of
$I_s$
is a linear iteration of
 $\langle {\mathrm {V}},\{{U_{s\restriction \xi }}~\vert ~{\xi \in {{\mathrm {dom}}(s)}}\}\rangle $
.
$\langle {\mathrm {V}},\{{U_{s\restriction \xi }}~\vert ~{\xi \in {{\mathrm {dom}}(s)}}\}\rangle $
. -
(iv) The sequence
 $\langle {\min \{{\kappa _s}~\vert ~{s\in {}^\xi \kappa }\}}~\vert ~{\xi <\mu }\rangle $
is cofinal in
$\langle {\min \{{\kappa _s}~\vert ~{s\in {}^\xi \kappa }\}}~\vert ~{\xi <\mu }\rangle $
is cofinal in
 $\kappa $
.
$\kappa $
. -
(v) If
 $I_s$
is nontrivial, then
$I_s$
is nontrivial, then
 ${\mathrm {lh}}({I_s})\in {\mathrm {Lim}}$
.
${\mathrm {lh}}({I_s})\in {\mathrm {Lim}}$
. -
(vi) If
 $s\subsetneq t$
, then
$s\subsetneq t$
, then
 ${\mathrm {lh}}({I_s}){}<\nu _s<\kappa _s<\nu _t$
.
${\mathrm {lh}}({I_s}){}<\nu _s<\kappa _s<\nu _t$
. -
(vii)
 $i^{I_s}_{0,\infty }(\nu _s)=\nu _s$
and
$i^{I_s}_{0,\infty }(\nu _s)=\nu _s$
and
 $i^{I_s}_{0,\infty }(\kappa _s)=\kappa _s$
.
$i^{I_s}_{0,\infty }(\kappa _s)=\kappa _s$
. -
(viii)
 $i^{I_s}_{0,\infty }(\mu )=\mu $
,
$i^{I_s}_{0,\infty }(\mu )=\mu $
,
 $i^{I_s}_{0,\infty }(\kappa )=\kappa $
and
$i^{I_s}_{0,\infty }(\kappa )=\kappa $
and
 $i^{I_s}_{0,\infty }(z)=z$
.
$i^{I_s}_{0,\infty }(z)=z$
. -
(ix) If
 $s\subseteq t$
, then
$s\subseteq t$
, then
 ${\mathrm {lh}}({I_s}){}\leq {\mathrm {lh}}({I_t}){}$
and
${\mathrm {lh}}({I_s}){}\leq {\mathrm {lh}}({I_t}){}$
and
 $U^{I_s}_\alpha =U^{I_t}_\alpha $
for all
$U^{I_s}_\alpha =U^{I_t}_\alpha $
for all
 $\alpha <{\mathrm {lh}}({I_s}){}$
.Footnote 2
$\alpha <{\mathrm {lh}}({I_s}){}$
.Footnote 2 -
(x) If
 $s\subseteq t$
with
$s\subseteq t$
with
 ${\mathrm {lh}}({I_s}){}<{\mathrm {lh}}({I_t}){}$
, then
${\mathrm {lh}}({I_s}){}<{\mathrm {lh}}({I_t}){}$
, then
 ${\mathrm {H}}(\kappa _s)^{M^{I_s}_\infty }={\mathrm {H}}(\kappa _s)^{M^{I_t}_\infty }$
and
${\mathrm {H}}(\kappa _s)^{M^{I_s}_\infty }={\mathrm {H}}(\kappa _s)^{M^{I_t}_\infty }$
and  $$ \begin{align*}i^{I_t}_{{\mathrm{lh}}({I_s}){},\infty}\restriction{\mathrm{H}}(\kappa_s)^{M^{I_s}_\infty} ~ = ~ {\mathrm{id}}_{{\mathrm{H}}(\kappa_s)^{M^{I_s}_\infty}}.\end{align*} $$
$$ \begin{align*}i^{I_t}_{{\mathrm{lh}}({I_s}){},\infty}\restriction{\mathrm{H}}(\kappa_s)^{M^{I_s}_\infty} ~ = ~ {\mathrm{id}}_{{\mathrm{H}}(\kappa_s)^{M^{I_s}_\infty}}.\end{align*} $$
-
(xi) If
 $\xi \in {{\mathrm {dom}}(s)}\cap {{\mathrm {dom}}(t)}$
satisfying
$\xi \in {{\mathrm {dom}}(s)}\cap {{\mathrm {dom}}(t)}$
satisfying
 $s\restriction \xi =t\restriction \xi $
and
$s\restriction \xi =t\restriction \xi $
and
 $s(\xi )< t(\xi )$
, then
$s(\xi )< t(\xi )$
, then
 $\nu _{s\restriction (\xi +1)}\leq \nu _{t\restriction (\xi +1)}$
and
$\nu _{s\restriction (\xi +1)}\leq \nu _{t\restriction (\xi +1)}$
and  $$ \begin{align*}i^{I_s}_{0,\infty}(x)\cap \nu_{s\restriction(\xi+1)} ~ \neq ~ i^{I_t}_{0,\infty}(x)\cap\nu_{s\restriction(\xi+1)}.\end{align*} $$
$$ \begin{align*}i^{I_s}_{0,\infty}(x)\cap \nu_{s\restriction(\xi+1)} ~ \neq ~ i^{I_t}_{0,\infty}(x)\cap\nu_{s\restriction(\xi+1)}.\end{align*} $$
Proof. Pick a strictly increasing, cofinal sequence
![]() $\langle {\kappa _\xi }~\vert ~{\xi <\mu }\rangle $
of measurable cardinals in
$\langle {\kappa _\xi }~\vert ~{\xi <\mu }\rangle $
of measurable cardinals in
![]() $\kappa $
with the property that
$\kappa $
with the property that
![]() $\mu <\kappa $
implies that
$\mu <\kappa $
implies that
![]() $\mu <\kappa _0$
. Given
$\mu <\kappa _0$
. Given
![]() $\xi <\mu $
, fix a normal ultrafilter
$\xi <\mu $
, fix a normal ultrafilter
![]() $U_\xi $
on
$U_\xi $
on
![]() $\kappa _\xi $
and let
$\kappa _\xi $
and let
denote the iteration of
![]() $\langle {\mathrm {V}},U_\xi \rangle $
. Given
$\langle {\mathrm {V}},U_\xi \rangle $
. Given
![]() $\xi <\mu $
, we then have
$\xi <\mu $
, we then have
![]() $j^\xi _{0,\kappa }(\kappa _\xi )=\kappa $
and
$j^\xi _{0,\kappa }(\kappa _\xi )=\kappa $
and
![]() $j^\xi _{0,\alpha }(\kappa )=\kappa $
for all
$j^\xi _{0,\alpha }(\kappa )=\kappa $
for all
![]() $\alpha <\kappa $
. In particular, we know that
$\alpha <\kappa $
. In particular, we know that
![]() $\vert {{\mathcal {P}}({\kappa })^{N^\xi _\kappa }}\vert =\kappa $
holds for all
$\vert {{\mathcal {P}}({\kappa })^{N^\xi _\kappa }}\vert =\kappa $
holds for all
![]() $\xi <\mu $
. Therefore, we can find
$\xi <\mu $
. Therefore, we can find
![]() $x\in D$
with
$x\in D$
with
![]() $x\notin N^\xi _\kappa $
for all
$x\notin N^\xi _\kappa $
for all
![]() $\xi <\mu $
. Given
$\xi <\mu $
. Given
![]() $\xi <\mu $
, we then have
$\xi <\mu $
, we then have
![]() $x\neq j^\xi _{0,\kappa }(x)\cap \kappa $
and hence we know that
$x\neq j^\xi _{0,\kappa }(x)\cap \kappa $
and hence we know that
holds for all sufficiently large
![]() $\lambda <\kappa $
.
$\lambda <\kappa $
.
By earlier remarks, the pair
![]() $\langle {\mathrm {V}},\mathcal {E}\rangle $
is linearly iterable. In the following, we inductively construct systems with the properties listed above while also ensuring that for every
$\langle {\mathrm {V}},\mathcal {E}\rangle $
is linearly iterable. In the following, we inductively construct systems with the properties listed above while also ensuring that for every
![]() $s\in {}^{{<}\mu }\kappa $
, there exists
$s\in {}^{{<}\mu }\kappa $
, there exists
![]() ${{\mathrm {dom}}(s)}\leq \xi <\mu $
with
${{\mathrm {dom}}(s)}\leq \xi <\mu $
with
![]() $\kappa _s=\kappa _\xi $
and
$\kappa _s=\kappa _\xi $
and
![]() $U_s=U_\xi $
. Note that this additional property will directly ensure that (iv) holds in the end.
$U_s=U_\xi $
. Note that this additional property will directly ensure that (iv) holds in the end.
First, we define
![]() $I_\emptyset $
to be the trivial linear iteration of
$I_\emptyset $
to be the trivial linear iteration of
![]() $\langle {\mathrm {V}},\mathcal {E}\rangle $
. Moreover, we pick some inaccessible cardinal
$\langle {\mathrm {V}},\mathcal {E}\rangle $
. Moreover, we pick some inaccessible cardinal
![]() $\nu _\emptyset <\kappa $
such that
$\nu _\emptyset <\kappa $
such that
![]() $z\in {\mathrm {H}}(\nu _\emptyset )$
and
$z\in {\mathrm {H}}(\nu _\emptyset )$
and
![]() $\mu <\kappa $
implies
$\mu <\kappa $
implies
![]() $\mu <\nu _\emptyset $
.
$\mu <\nu _\emptyset $
.
Next, assume that
![]() $\zeta \in {\mathrm {Lim}}\cap \mu $
and the objects
$\zeta \in {\mathrm {Lim}}\cap \mu $
and the objects
![]() $\nu _t$
,
$\nu _t$
,
![]() $\kappa _t$
,
$\kappa _t$
,
![]() $U_t$
and
$U_t$
and
![]() $I_t$
are defined for all
$I_t$
are defined for all
![]() $t\in {}^{{<}\zeta }\kappa $
. Fix
$t\in {}^{{<}\zeta }\kappa $
. Fix
![]() $s\in {}^\zeta \kappa $
, and define
$s\in {}^\zeta \kappa $
, and define
![]() $I_s$
to be the unique linear iteration of
$I_s$
to be the unique linear iteration of
![]() $\langle {\mathrm {V}},\{{U_{s\restriction \eta }}~\vert ~{\eta <\zeta }\}\rangle $
of length
$\langle {\mathrm {V}},\{{U_{s\restriction \eta }}~\vert ~{\eta <\zeta }\}\rangle $
of length
![]() $\sup _{\eta <\zeta }{\mathrm {lh}}({I_{s\restriction \eta }}){}<\kappa $
with the property that
$\sup _{\eta <\zeta }{\mathrm {lh}}({I_{s\restriction \eta }}){}<\kappa $
with the property that
![]() $U^{I_s}_\alpha =U^{I_{s\restriction \eta }}_\alpha $
holds for all
$U^{I_s}_\alpha =U^{I_{s\restriction \eta }}_\alpha $
holds for all
![]() $\eta <\zeta $
and
$\eta <\zeta $
and
![]() $\alpha <{\mathrm {lh}}({I_{s\restriction \eta }}){}$
. In addition, define
$\alpha <{\mathrm {lh}}({I_{s\restriction \eta }}){}$
. In addition, define
![]() $\nu _s$
to be an inaccessible cardinal smaller than
$\nu _s$
to be an inaccessible cardinal smaller than
![]() $\kappa $
and bigger than both
$\kappa $
and bigger than both
![]() $\sup _{\eta <\zeta }\kappa _{s\restriction \eta }$
and
$\sup _{\eta <\zeta }\kappa _{s\restriction \eta }$
and
![]() ${\mathrm {lh}}({I_s}){}$
. This setup ensures that
${\mathrm {lh}}({I_s}){}$
. This setup ensures that
![]() ${\mathrm {lh}}({I_s})>1$
implies that
${\mathrm {lh}}({I_s})>1$
implies that
![]() ${\mathrm {lh}}({I_s})\in {\mathrm {Lim}}$
, and therefore we know that (v) holds. Moreover, these definitions directly ensure that the relevant parts of (vi) and (vii) hold in this case. In addition, since
${\mathrm {lh}}({I_s})\in {\mathrm {Lim}}$
, and therefore we know that (v) holds. Moreover, these definitions directly ensure that the relevant parts of (vi) and (vii) hold in this case. In addition, since
![]() ${\mathrm {lh}}({I_s})<\nu _s$
and
${\mathrm {lh}}({I_s})<\nu _s$
and
![]() $I_s$
only makes use of ultrafilter on cardinals contained in the interval
$I_s$
only makes use of ultrafilter on cardinals contained in the interval
![]() $(\nu _\emptyset ,\nu _s)$
, the fact that the cofinality of
$(\nu _\emptyset ,\nu _s)$
, the fact that the cofinality of
![]() $\kappa $
is not contained in this interval allows us to conclude that (viii) holds in this case. Next, notice that our construction directly ensures that (ix) holds in this case. Moreover, if
$\kappa $
is not contained in this interval allows us to conclude that (viii) holds in this case. Next, notice that our construction directly ensures that (ix) holds in this case. Moreover, if
![]() $\eta <\zeta $
with
$\eta <\zeta $
with
![]() ${\mathrm {lh}}({I_{s\restriction \eta }}){}<{\mathrm {lh}}({I_s}){}$
, then the fact that (v) and (x) hold for all
${\mathrm {lh}}({I_{s\restriction \eta }}){}<{\mathrm {lh}}({I_s}){}$
, then the fact that (v) and (x) hold for all
![]() $\eta <\rho <\zeta $
ensures that
$\eta <\rho <\zeta $
ensures that
and
By the definition of
![]() $I_s$
, this shows that (x) also holds in this case. Finally, pick
$I_s$
, this shows that (x) also holds in this case. Finally, pick
![]() $t\in {}^{{<}\mu }\kappa $
with
$t\in {}^{{<}\mu }\kappa $
with
![]() ${{\mathrm {dom}}(t)}\leq \zeta $
and
${{\mathrm {dom}}(t)}\leq \zeta $
and
![]() $\xi \in {{\mathrm {dom}}(t)}$
with
$\xi \in {{\mathrm {dom}}(t)}$
with
![]() $s\restriction \xi =t\restriction \xi $
and
$s\restriction \xi =t\restriction \xi $
and
![]() $s(\xi )\neq t(\xi )$
. Set
$s(\xi )\neq t(\xi )$
. Set
![]() $\rho =\min (\nu _{s\restriction (\xi +1)},\nu _{t\restriction (\xi +1)})$
. Since we know that
$\rho =\min (\nu _{s\restriction (\xi +1)},\nu _{t\restriction (\xi +1)})$
. Since we know that
![]() $\rho <\min (\kappa _{s\restriction (\xi +1)},\kappa _{t\restriction (\xi +1)})$
, we can use (x) and (xi) to show that
$\rho <\min (\kappa _{s\restriction (\xi +1)},\kappa _{t\restriction (\xi +1)})$
, we can use (x) and (xi) to show that
By the properties of
![]() $\nu _{s\restriction (\xi +1)}$
ensured by our induction hypothesis, these computations show that (xi) also holds in this case.
$\nu _{s\restriction (\xi +1)}$
ensured by our induction hypothesis, these computations show that (xi) also holds in this case.
Now, assume that
![]() $\zeta <\mu $
and the objects
$\zeta <\mu $
and the objects
![]() $\nu _t$
,
$\nu _t$
,
![]() $\kappa _u$
,
$\kappa _u$
,
![]() $U_u$
and
$U_u$
and
![]() $I_t$
are defined for all
$I_t$
are defined for all
![]() $t,u\in {}^{{<}\mu }\kappa $
with
$t,u\in {}^{{<}\mu }\kappa $
with
![]() ${{\mathrm {dom}}(t)}\leq \zeta $
and
${{\mathrm {dom}}(t)}\leq \zeta $
and
![]() ${{\mathrm {dom}}(u)}<\zeta $
. Fix
${{\mathrm {dom}}(u)}<\zeta $
. Fix
![]() $s\in {}^\zeta \kappa $
, and pick
$s\in {}^\zeta \kappa $
, and pick
![]() $\zeta \leq \xi <\mu $
with
$\zeta \leq \xi <\mu $
with
![]() $\kappa _\xi>\nu _s$
. Set
$\kappa _\xi>\nu _s$
. Set
![]() $\kappa _s=\kappa _\xi $
and
$\kappa _s=\kappa _\xi $
and
![]() $U_s=U_\xi $
. By Equation (1), there exists a limit ordinal
$U_s=U_\xi $
. By Equation (1), there exists a limit ordinal
![]() $\kappa _s<\lambda <\kappa $
with the property that
$\kappa _s<\lambda <\kappa $
with the property that
Let
![]() $\langle {\lambda _\beta }~\vert ~{\beta <\kappa }\rangle $
denote the unique continuous sequence of ordinals with
$\langle {\lambda _\beta }~\vert ~{\beta <\kappa }\rangle $
denote the unique continuous sequence of ordinals with
![]() $\lambda _0=0$
and
$\lambda _0=0$
and
![]() $\lambda _{\beta +1}=\lambda _\beta +j^\xi _{0,\lambda _\beta }(\lambda )$
for all
$\lambda _{\beta +1}=\lambda _\beta +j^\xi _{0,\lambda _\beta }(\lambda )$
for all
![]() $\beta <\lambda $
. Since
$\beta <\lambda $
. Since
![]() $\kappa $
is a limit of inaccessible cardinals, we know that
$\kappa $
is a limit of inaccessible cardinals, we know that
![]() $\lambda _\beta <\kappa $
holds for all
$\lambda _\beta <\kappa $
holds for all
![]() $\beta <\kappa $
. Given
$\beta <\kappa $
. Given
![]() $\beta <\kappa $
, define
$\beta <\kappa $
, define
![]() $I_{s^\frown \langle \beta \rangle }$
to be the unique linear iteration of
$I_{s^\frown \langle \beta \rangle }$
to be the unique linear iteration of
![]() $\langle {\mathrm {V}},\mathcal {E}\rangle $
of length
$\langle {\mathrm {V}},\mathcal {E}\rangle $
of length
![]() ${\mathrm {lh}}({I_s})+i^{I_s}_{0,\infty }(\lambda _\beta )$
with
${\mathrm {lh}}({I_s})+i^{I_s}_{0,\infty }(\lambda _\beta )$
with
![]() $U^{I_{s^\frown \langle \beta \rangle }}_\alpha =U^{I_s}_\alpha $
for all
$U^{I_{s^\frown \langle \beta \rangle }}_\alpha =U^{I_s}_\alpha $
for all
![]() $\alpha <{\mathrm {lh}}({I_s}){}$
and
$\alpha <{\mathrm {lh}}({I_s}){}$
and
![]() $U^{I_{s^\frown \langle \beta \rangle }}_\alpha =i^{I_{s^\frown \langle \beta \rangle }}_{0,\alpha }(U_s)$
for all
$U^{I_{s^\frown \langle \beta \rangle }}_\alpha =i^{I_{s^\frown \langle \beta \rangle }}_{0,\alpha }(U_s)$
for all
![]() ${\mathrm {lh}}({I_s}){}\leq \alpha <{\mathrm {lh}}({I_{s^\frown \langle \beta \rangle }}){}$
. That means we linearly iterate
${\mathrm {lh}}({I_s}){}\leq \alpha <{\mathrm {lh}}({I_{s^\frown \langle \beta \rangle }}){}$
. That means we linearly iterate
![]() $U_s$
on top of what we already have to obtain
$U_s$
on top of what we already have to obtain
![]() $I_{s^\frown \langle \beta \rangle }$
. Moreover, for every
$I_{s^\frown \langle \beta \rangle }$
. Moreover, for every
![]() $\beta <\kappa $
, we define
$\beta <\kappa $
, we define
![]() $\nu _{s^\frown \langle \beta \rangle }$
to be the least inaccessible cardinal greater than
$\nu _{s^\frown \langle \beta \rangle }$
to be the least inaccessible cardinal greater than
![]() ${\mathrm {lh}}({I_{s^\frown \langle \beta +1\rangle }}){}$
. These definitions then directly ensure that (v) and (ix) hold. In addition, for all
${\mathrm {lh}}({I_{s^\frown \langle \beta +1\rangle }}){}$
. These definitions then directly ensure that (v) and (ix) hold. In addition, for all
![]() $\beta <\kappa $
, we have
$\beta <\kappa $
, we have
and this can be used to conclude that
![]() $i^{I_s}_{0,\infty }(\kappa _s)=\kappa _s$
and
$i^{I_s}_{0,\infty }(\kappa _s)=\kappa _s$
and
![]() $i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(\nu _{s^\frown \langle \beta \rangle })=\nu _{s^\frown \langle \beta \rangle }$
. This shows that the relevant instances of (vi) and (vii) hold in this case. Moreover, the fact that all linear iterations of the form
$i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(\nu _{s^\frown \langle \beta \rangle })=\nu _{s^\frown \langle \beta \rangle }$
. This shows that the relevant instances of (vi) and (vii) hold in this case. Moreover, the fact that all linear iterations of the form
![]() $I_{s^\frown \langle \beta \rangle }$
with
$I_{s^\frown \langle \beta \rangle }$
with
![]() $\beta <\kappa $
have length less than
$\beta <\kappa $
have length less than
![]() $\kappa $
and only make use of ultrafilters on cardinals contained in the interval
$\kappa $
and only make use of ultrafilters on cardinals contained in the interval
![]() $[\kappa _0,\kappa )$
directly implies that (viii) holds in this case as
$[\kappa _0,\kappa )$
directly implies that (viii) holds in this case as
![]() $\mu < \kappa _0$
in case
$\mu < \kappa _0$
in case
![]() $\mu < \kappa $
. Next, notice that, if
$\mu < \kappa $
. Next, notice that, if
![]() $0<\beta <\kappa $
and
$0<\beta <\kappa $
and
![]() ${\mathrm {lh}}({I_s}){}\leq \alpha <{\mathrm {lh}}({I_{s^\frown \langle \beta \rangle }}){}$
, then our construction ensures that
${\mathrm {lh}}({I_s}){}\leq \alpha <{\mathrm {lh}}({I_{s^\frown \langle \beta \rangle }}){}$
, then our construction ensures that
and
This directly implies that (x) holds in this case. Finally, fix
![]() $\beta <\gamma <\kappa $
. Then
$\beta <\gamma <\kappa $
. Then
![]() ${\mathrm {lh}}({I_{s^\frown \langle \beta +1\rangle }}){}<{\mathrm {lh}}({I_{s^\frown \langle \gamma +1\rangle }}){}$
, and hence we know that
${\mathrm {lh}}({I_{s^\frown \langle \beta +1\rangle }}){}<{\mathrm {lh}}({I_{s^\frown \langle \gamma +1\rangle }}){}$
, and hence we know that
![]() $\nu _{s^\frown \langle \beta \rangle }\leq \nu _{s^\frown \langle \gamma \rangle }$
.
$\nu _{s^\frown \langle \beta \rangle }\leq \nu _{s^\frown \langle \gamma \rangle }$
.
Claim.
![]() $i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(x)\cap \nu _{s^\frown \langle \beta \rangle } ~ \neq ~ i^{I_{s^\frown \langle \gamma \rangle }}_{0,\infty }(x)\cap \nu _{s\frown \langle \beta \rangle }$
.
$i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(x)\cap \nu _{s^\frown \langle \beta \rangle } ~ \neq ~ i^{I_{s^\frown \langle \gamma \rangle }}_{0,\infty }(x)\cap \nu _{s\frown \langle \beta \rangle }$
.
Proof of the claim
Let
denote the iteration of
![]() $\langle M^{I_s}_\infty ,i^{I_s}_{0,\infty }(U_s)\rangle $
. Given
$\langle M^{I_s}_\infty ,i^{I_s}_{0,\infty }(U_s)\rangle $
. Given
![]() $\delta <\kappa $
and
$\delta <\kappa $
and
![]() $\alpha <i^{I_s}_{0,\infty }(\lambda _\delta )$
, the definition of
$\alpha <i^{I_s}_{0,\infty }(\lambda _\delta )$
, the definition of
![]() $I_{s^\frown \langle \delta \rangle }$
ensures that the following statements hold:
$I_{s^\frown \langle \delta \rangle }$
ensures that the following statements hold:
-
○
 $M^{I_{s^\frown \langle \delta \rangle }}_{{\mathrm {lh}}({I_s})+\alpha }=N_\alpha $
and
$M^{I_{s^\frown \langle \delta \rangle }}_{{\mathrm {lh}}({I_s})+\alpha }=N_\alpha $
and
 $M^{I_{s^\frown \langle \delta \rangle }}_\infty =N_{i^{I_s}_\infty (\lambda _\delta )}$
.
$M^{I_{s^\frown \langle \delta \rangle }}_\infty =N_{i^{I_s}_\infty (\lambda _\delta )}$
. -
○
 $i^{I_{s^\frown \langle \delta \rangle }}_{0,{\mathrm {lh}}({I_s})+\alpha }=j_{0,\alpha }\circ i^{I_s}_{0,\infty }$
and
$i^{I_{s^\frown \langle \delta \rangle }}_{0,{\mathrm {lh}}({I_s})+\alpha }=j_{0,\alpha }\circ i^{I_s}_{0,\infty }$
and
 $i^{I_{s^\frown \langle \delta \rangle }}_{0,\infty }=j_{0,i^{I_s}_{0,\infty }(\lambda _\delta )}\circ i^{I_s}_{0,\infty }$
.
$i^{I_{s^\frown \langle \delta \rangle }}_{0,\infty }=j_{0,i^{I_s}_{0,\infty }(\lambda _\delta )}\circ i^{I_s}_{0,\infty }$
.
Now, set
![]() $M_*=M^{I_{s^\frown \langle \beta \rangle }}_\infty $
,
$M_*=M^{I_{s^\frown \langle \beta \rangle }}_\infty $
,
![]() $x_*=i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(x)$
,
$x_*=i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(x)$
,
![]() $\kappa _*=i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(\kappa _s)$
,
$\kappa _*=i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(\kappa _s)$
,
![]() $\lambda _*=i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(\lambda )$
and
$\lambda _*=i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(\lambda )$
and
![]() $U_*=i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(U_s)$
. Note that elementarity ensures that
$U_*=i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }(U_s)$
. Note that elementarity ensures that
and this allows us to conclude that
In particular, we know that
Now, define
to be the iteration of
![]() $\langle M_*,U_*\rangle $
. Given ordinals
$\langle M_*,U_*\rangle $
. Given ordinals
![]() $\alpha _0\leq \alpha _1$
, we then have
$\alpha _0\leq \alpha _1$
, we then have
![]() $N^*_{\alpha _0}=N_{i^{I_s}_\infty (\lambda _\beta )+\alpha _0}$
and
$N^*_{\alpha _0}=N_{i^{I_s}_\infty (\lambda _\beta )+\alpha _0}$
and
![]() $j^*_{\alpha _0,\alpha _1}=j_{i^{I_s}_\infty (\lambda _\beta )+\alpha _0,i^{I_s}_\infty (\lambda _\beta )+\alpha _1}$
. In particular, we can use Equation (3) to find an ordinal
$j^*_{\alpha _0,\alpha _1}=j_{i^{I_s}_\infty (\lambda _\beta )+\alpha _0,i^{I_s}_\infty (\lambda _\beta )+\alpha _1}$
. In particular, we can use Equation (3) to find an ordinal
![]() $\alpha \geq \lambda _*$
with
$\alpha \geq \lambda _*$
with
![]() $M^{I_{s^\frown \langle \gamma \rangle }}_\infty =N^*_\alpha $
and
$M^{I_{s^\frown \langle \gamma \rangle }}_\infty =N^*_\alpha $
and
![]() $i^{I_{s^\frown \langle \gamma \rangle }}_{0,\infty }=j^*_{0,\alpha }\circ i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }$
.
$i^{I_{s^\frown \langle \gamma \rangle }}_{0,\infty }=j^*_{0,\alpha }\circ i^{I_{s^\frown \langle \beta \rangle }}_{0,\infty }$
.
By elementarity, the inequality (2) implies that
Moreover, our setup ensures that
and
Since for
![]() $\alpha \geq \lambda _*$
as above
$\alpha \geq \lambda _*$
as above
and
we know that
 $$ \begin{align*} \begin{aligned} i^{I_{s^\frown\langle\gamma\rangle}}_{0,\infty}(x)\cap j^*_{0,\lambda_*}(\kappa_*) ~ & = ~ j^*_{0,\lambda_*}(x_*)\cap j^*_{0,\lambda_*}(\kappa_*) ~ = ~ j^*_{0,\lambda_*}(x_*\cap\kappa_*) \\ & \neq ~ x_*\cap j^*_{0,\lambda_*}(\kappa_*) ~ = ~ i^{I_{s^\frown\langle\beta\rangle}}_{0,\infty}(x)\cap j^*_{0,\lambda_*}(\kappa_*) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} i^{I_{s^\frown\langle\gamma\rangle}}_{0,\infty}(x)\cap j^*_{0,\lambda_*}(\kappa_*) ~ & = ~ j^*_{0,\lambda_*}(x_*)\cap j^*_{0,\lambda_*}(\kappa_*) ~ = ~ j^*_{0,\lambda_*}(x_*\cap\kappa_*) \\ & \neq ~ x_*\cap j^*_{0,\lambda_*}(\kappa_*) ~ = ~ i^{I_{s^\frown\langle\beta\rangle}}_{0,\infty}(x)\cap j^*_{0,\lambda_*}(\kappa_*) \end{aligned} \end{align*} $$
and the fact that
![]() $\nu _{s^\frown \langle \beta \rangle }> j^*_{0,\lambda _*}(\kappa _*)$
then yields the statement of the claim.
$\nu _{s^\frown \langle \beta \rangle }> j^*_{0,\lambda _*}(\kappa _*)$
then yields the statement of the claim.
The above claim now shows that (xi) also holds in this case. This completes the proof of the lemma.
We now extend the above construction to obtain linear iterations indexed by sequences of length equal to the cofinality of the given limit of measurable cardinals. In addition, we also allow these sequences to exist in small forcing extensions of the ground model.
Lemma 2.2. In the situation of Lemma 2.1, let
![]() $\lambda \leq \mu $
be a limit ordinal, let
$\lambda \leq \mu $
be a limit ordinal, let
![]() ${\mathbb {P}}$
be a partial orderFootnote 3 and let G be
${\mathbb {P}}$
be a partial orderFootnote 3 and let G be
![]() ${\mathbb {P}}$
-generic over
${\mathbb {P}}$
-generic over
![]() ${\mathrm {V}}$
. Given a function
${\mathrm {V}}$
. Given a function
![]() $c\in ({}^\lambda \kappa )^{{\mathrm {V}}[G]}$
with the property that all of its proper initial segments are contained in
$c\in ({}^\lambda \kappa )^{{\mathrm {V}}[G]}$
with the property that all of its proper initial segments are contained in
![]() ${\mathrm {V}}$
, we let
${\mathrm {V}}$
, we let
![]() $I_c$
denote the unique linear iteration of
$I_c$
denote the unique linear iteration of
![]() $\langle {\mathrm {V}},\{{U_{c\restriction \xi }}~\vert ~{\xi <\lambda }\}\rangle $
of length
$\langle {\mathrm {V}},\{{U_{c\restriction \xi }}~\vert ~{\xi <\lambda }\}\rangle $
of length
![]() $\sup _{\xi <\lambda }{\mathrm {lh}}({I_{c\restriction \xi }}){}$
in
$\sup _{\xi <\lambda }{\mathrm {lh}}({I_{c\restriction \xi }}){}$
in
![]() ${\mathrm {V}}[G]$
with
${\mathrm {V}}[G]$
with
![]() $U^{I_c}_\alpha =U^{I_{c\restriction \xi }}_\alpha $
for all
$U^{I_c}_\alpha =U^{I_{c\restriction \xi }}_\alpha $
for all
![]() $\xi <\lambda $
and
$\xi <\lambda $
and
![]() $\alpha <{\mathrm {lh}}({I_{c\restriction \xi }}){}$
.
$\alpha <{\mathrm {lh}}({I_{c\restriction \xi }}){}$
.
If either
![]() ${\mathbb {P}}$
is an element of
${\mathbb {P}}$
is an element of
![]() ${\mathrm {H}}(\kappa _\emptyset )$
or forcing with
${\mathrm {H}}(\kappa _\emptyset )$
or forcing with
![]() ${\mathbb {P}}$
does not add bounded subsets of
${\mathbb {P}}$
does not add bounded subsets of
![]() $\kappa $
, then the following statements hold in
$\kappa $
, then the following statements hold in
![]() ${\mathrm {V}}[G]$
for all functions
${\mathrm {V}}[G]$
for all functions
![]() $c,d\in {}^\lambda \kappa $
with the property that all of their proper initial segments are contained in
$c,d\in {}^\lambda \kappa $
with the property that all of their proper initial segments are contained in
![]() ${\mathrm {V}}$
:
${\mathrm {V}}$
:
-
(i)
 $M^{I_c}_\infty $
is well-founded.
$M^{I_c}_\infty $
is well-founded. -
(ii)
 $i^{I_c}_{0,\infty }(\mu )=\mu $
,
$i^{I_c}_{0,\infty }(\mu )=\mu $
,
 $i^{I_c}_{0,\infty }(\kappa )=\kappa $
and
$i^{I_c}_{0,\infty }(\kappa )=\kappa $
and
 $i^{I_c}_{0,\infty }(z)=z$
.
$i^{I_c}_{0,\infty }(z)=z$
. -
(iii) If
 $\xi <\lambda $
with
$\xi <\lambda $
with
 $c\restriction \xi =d\restriction \xi $
and
$c\restriction \xi =d\restriction \xi $
and
 $c(\xi )\neq d(\xi )$
, then and there is
$c(\xi )\neq d(\xi )$
, then and there is $$ \begin{align*}i^{I_c}_{0,\infty}(x)\cap\kappa_{c\restriction\xi} ~ = ~ i^{I_d}_{0,\infty}(x)\cap\kappa_{c\restriction\xi}\end{align*} $$
$$ \begin{align*}i^{I_c}_{0,\infty}(x)\cap\kappa_{c\restriction\xi} ~ = ~ i^{I_d}_{0,\infty}(x)\cap\kappa_{c\restriction\xi}\end{align*} $$
 $\rho <\min (\kappa _{c\restriction (\xi +1)},\kappa _{d\restriction (\xi +1)})$
with (4)
$\rho <\min (\kappa _{c\restriction (\xi +1)},\kappa _{d\restriction (\xi +1)})$
with (4) $$ \begin{align} i^{I_c}_{0,\infty}(x)\cap\rho ~ \neq ~ i^{I_d}_{0,\infty}(x)\cap\rho. \end{align} $$
$$ \begin{align} i^{I_c}_{0,\infty}(x)\cap\rho ~ \neq ~ i^{I_d}_{0,\infty}(x)\cap\rho. \end{align} $$
Proof. Work in
![]() ${\mathrm {V}}[G]$
, pick a function
${\mathrm {V}}[G]$
, pick a function
![]() $c\in {}^\lambda \kappa $
with the desired properties and define
$c\in {}^\lambda \kappa $
with the desired properties and define
![]() $I_c$
as above. If
$I_c$
as above. If
![]() ${\mathbb {P}}$
is contained in
${\mathbb {P}}$
is contained in
![]() ${\mathrm {H}}(\kappa _\emptyset )$
, then we can use the Lévy–Solovay theorem to show that for all
${\mathrm {H}}(\kappa _\emptyset )$
, then we can use the Lévy–Solovay theorem to show that for all
![]() $\xi <\lambda $
, the set
$\xi <\lambda $
, the set
![]() $\{{B\in {\mathcal {P}}({\kappa _\xi })}~\vert ~{\exists A\in U_{c\restriction \xi } ~ A\subseteq B}\}$
is a normal ultrafilter on
$\{{B\in {\mathcal {P}}({\kappa _\xi })}~\vert ~{\exists A\in U_{c\restriction \xi } ~ A\subseteq B}\}$
is a normal ultrafilter on
![]() $\kappa _\xi $
, and therefore we know that
$\kappa _\xi $
, and therefore we know that
![]() $U_{c\restriction \xi }$
itself is a
$U_{c\restriction \xi }$
itself is a
![]() $\sigma $
-complete
$\sigma $
-complete
![]() ${\mathrm {V}}$
-ultrafilter. Since the same conclusion obviously holds true if forcing with
${\mathrm {V}}$
-ultrafilter. Since the same conclusion obviously holds true if forcing with
![]() ${\mathbb {P}}$
does not add bounded subsets of
${\mathbb {P}}$
does not add bounded subsets of
![]() $\kappa $
, we can apply [Reference Steel49, Theorem 3.3] to conclude that the pair
$\kappa $
, we can apply [Reference Steel49, Theorem 3.3] to conclude that the pair
![]() $\langle {\mathrm {V}},\{{U_{c\restriction \xi }}~\vert ~{\xi <\lambda }\}\rangle $
is linearly iterable, and therefore we know that
$\langle {\mathrm {V}},\{{U_{c\restriction \xi }}~\vert ~{\xi <\lambda }\}\rangle $
is linearly iterable, and therefore we know that
![]() $M^{I_c}_\infty $
is well-founded.
$M^{I_c}_\infty $
is well-founded.
Next, since (x) of Lemma 2.1 ensures that
and
 $$ \begin{align*}i^{I_c}_{{\mathrm{lh}}({I_{c\restriction\xi}}){},{\mathrm{lh}}({I_{c\restriction\zeta}}){}}\restriction{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty} ~ = ~ i^{I_{c\restriction\zeta}}_{{\mathrm{lh}}({I_{c\restriction\xi}}){},\infty}\restriction{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty} ~ = ~ {\mathrm{id}}_{{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty}}\end{align*} $$
$$ \begin{align*}i^{I_c}_{{\mathrm{lh}}({I_{c\restriction\xi}}){},{\mathrm{lh}}({I_{c\restriction\zeta}}){}}\restriction{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty} ~ = ~ i^{I_{c\restriction\zeta}}_{{\mathrm{lh}}({I_{c\restriction\xi}}){},\infty}\restriction{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty} ~ = ~ {\mathrm{id}}_{{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty}}\end{align*} $$
hold for all
![]() $\xi <\zeta <\lambda $
with
$\xi <\zeta <\lambda $
with
![]() ${\mathrm {lh}}({I_{c\restriction \xi }}){}<{\mathrm {lh}}({I_{c\restriction \zeta }}){}<{\mathrm {lh}}({I_c}){}$
, we know that
${\mathrm {lh}}({I_{c\restriction \xi }}){}<{\mathrm {lh}}({I_{c\restriction \zeta }}){}<{\mathrm {lh}}({I_c}){}$
, we know that
and
 $$ \begin{align} i^{I_c}_{{\mathrm{lh}}({I_{c\restriction\xi}}){},\infty}\restriction{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty} ~ = ~ {\mathrm{id}}_{{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty}} \end{align} $$
$$ \begin{align} i^{I_c}_{{\mathrm{lh}}({I_{c\restriction\xi}}){},\infty}\restriction{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty} ~ = ~ {\mathrm{id}}_{{\mathrm{H}}(\kappa_{c\restriction\xi})^{M^{I_{c\restriction\xi}}_\infty}} \end{align} $$
hold for all
![]() $\xi <\lambda $
with
$\xi <\lambda $
with
![]() ${\mathrm {lh}}({I_{c\restriction \xi }}){}<{\mathrm {lh}}({I_c}){}$
. In particular, it follows that
${\mathrm {lh}}({I_{c\restriction \xi }}){}<{\mathrm {lh}}({I_c}){}$
. In particular, it follows that
![]() $i^{I_c}_{0,\infty }(z)=z$
and, if
$i^{I_c}_{0,\infty }(z)=z$
and, if
![]() $\mu <\kappa $
, then
$\mu <\kappa $
, then
![]() $i^{I_c}_{0,\infty }(\mu )=\mu $
. In addition, for all
$i^{I_c}_{0,\infty }(\mu )=\mu $
. In addition, for all
![]() $\xi <\lambda $
with the property that
$\xi <\lambda $
with the property that
![]() ${\mathrm {lh}}({I_{c\restriction \xi }}){}<{\mathrm {lh}}({I_c}){}$
, we have
${\mathrm {lh}}({I_{c\restriction \xi }}){}<{\mathrm {lh}}({I_c}){}$
, we have
![]() $i^{I_c}_{0,{\mathrm {lh}}({I_{c\restriction \xi }}){}}=i^{I_{c\restriction \xi }}_{0,\infty }$
and therefore
$i^{I_c}_{0,{\mathrm {lh}}({I_{c\restriction \xi }}){}}=i^{I_{c\restriction \xi }}_{0,\infty }$
and therefore
for all
![]() $\alpha <\kappa _{c\restriction \xi }$
. In particular, a combination of Equations (5) and (6) allows us to conclude that
$\alpha <\kappa _{c\restriction \xi }$
. In particular, a combination of Equations (5) and (6) allows us to conclude that
![]() $i^{I_c}_{0,\infty }[\kappa _{c\restriction \xi }]\subseteq \kappa _{c\restriction \xi }$
holds for all
$i^{I_c}_{0,\infty }[\kappa _{c\restriction \xi }]\subseteq \kappa _{c\restriction \xi }$
holds for all
![]() $\xi <\lambda $
. If the sequence
$\xi <\lambda $
. If the sequence
![]() $\langle {\kappa _{c\restriction \xi }}~\vert ~{\xi <\lambda }\rangle $
is cofinal in
$\langle {\kappa _{c\restriction \xi }}~\vert ~{\xi <\lambda }\rangle $
is cofinal in
![]() $\kappa $
, then this observation directly implies that
$\kappa $
, then this observation directly implies that
![]() $i^{I_c}_{0,\infty }(\kappa )=\kappa $
. In the other case, if the above sequence is bounded by
$i^{I_c}_{0,\infty }(\kappa )=\kappa $
. In the other case, if the above sequence is bounded by
![]() $\rho <\kappa $
, then
$\rho <\kappa $
, then
![]() $I_c$
is a linear iteration of length less than
$I_c$
is a linear iteration of length less than
![]() $\kappa $
that only uses ultrafilters on measurable cardinals in the interval
$\kappa $
that only uses ultrafilters on measurable cardinals in the interval
![]() $[\kappa _\emptyset ,\rho ]$
and, since
$[\kappa _\emptyset ,\rho ]$
and, since
![]() $\kappa $
is a limit of inaccessible cardinals whose cofinality is not contained in this interval, we also know that
$\kappa $
is a limit of inaccessible cardinals whose cofinality is not contained in this interval, we also know that
![]() $i^{I_c}_{0,\infty }(\kappa )=\kappa $
holds in this case.
$i^{I_c}_{0,\infty }(\kappa )=\kappa $
holds in this case.
Finally, pick functions
![]() $c,d\in {}^\lambda \kappa $
whose proper initial segments are all contained in
$c,d\in {}^\lambda \kappa $
whose proper initial segments are all contained in
![]() ${\mathrm {V}}$
and
${\mathrm {V}}$
and
![]() $\xi <\lambda $
with
$\xi <\lambda $
with
![]() $c\restriction \xi =d\restriction \xi $
and
$c\restriction \xi =d\restriction \xi $
and
![]() $c(\xi )\neq d(\xi )$
. Then Equation (5) implies that
$c(\xi )\neq d(\xi )$
. Then Equation (5) implies that
If we now define
then statement (xi) of Lemma 2.1 directly implies that Equation (4) holds.
We now use the above constructions to derive the desired perfect subset result for
![]() $\Sigma _1$
-definable subsets of power sets of limits of measurable cardinals.
$\Sigma _1$
-definable subsets of power sets of limits of measurable cardinals.
Proof of Theorem 1.1
Let
![]() $\mu $
be an infinite regular cardinal, let
$\mu $
be an infinite regular cardinal, let
![]() $\kappa $
be a limit of measurable cardinals with
$\kappa $
be a limit of measurable cardinals with
![]() ${{\mathrm {cof}}(\kappa )}=\mu $
, let z be an element of
${{\mathrm {cof}}(\kappa )}=\mu $
, let z be an element of
![]() ${\mathrm {H}}(\kappa )$
and let D be a subset of
${\mathrm {H}}(\kappa )$
and let D be a subset of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\kappa $
and z. An application of Lemma 2.2 with the trivial partial order now yields
$\kappa $
and z. An application of Lemma 2.2 with the trivial partial order now yields
![]() $x\in D$
and systems
$x\in D$
and systems
![]() $\langle {\kappa _s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
,
$\langle {\kappa _s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
,
![]() $\langle {U_s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
and
$\langle {U_s}~\vert ~{s\in {}^{{<}\mu }\kappa }\rangle $
and
![]() $\langle {I_c}~\vert ~{c\in {}^\mu \kappa }\rangle $
such that the following statements hold for all
$\langle {I_c}~\vert ~{c\in {}^\mu \kappa }\rangle $
such that the following statements hold for all
![]() $s,t\in {}^{{<}\mu }\kappa $
and all
$s,t\in {}^{{<}\mu }\kappa $
and all
![]() $c,d\in {}^\mu \kappa $
:
$c,d\in {}^\mu \kappa $
:
-
○
 $\kappa _s$
is a measurable cardinal smaller than
$\kappa _s$
is a measurable cardinal smaller than
 $\kappa $
.
$\kappa $
. -
○
 $U_s$
is a normal ultrafilter on
$U_s$
is a normal ultrafilter on
 $\kappa _s$
.
$\kappa _s$
. -
○
 $I_c$
is a linear iteration of
$I_c$
is a linear iteration of
 $\langle {\mathrm {V}},\{{U_{c\restriction \xi }}~\vert ~{\xi <\mu }\}\rangle $
with
$\langle {\mathrm {V}},\{{U_{c\restriction \xi }}~\vert ~{\xi <\mu }\}\rangle $
with
 $M^{I_c}_\infty $
well-founded.
$M^{I_c}_\infty $
well-founded. -
○ The sequence
 $\langle {\kappa _{c\restriction \xi }}~\vert ~{\xi <\mu }\rangle $
is cofinal in
$\langle {\kappa _{c\restriction \xi }}~\vert ~{\xi <\mu }\rangle $
is cofinal in
 $\kappa $
.
$\kappa $
. -
○
 $i^{I_c}_{0,\infty }(\mu )=\mu $
,
$i^{I_c}_{0,\infty }(\mu )=\mu $
,
 $i^{I_c}_{0,\infty }(\kappa )=\kappa $
and
$i^{I_c}_{0,\infty }(\kappa )=\kappa $
and
 $i^{I_c}_{0,\infty }(z)=z$
.
$i^{I_c}_{0,\infty }(z)=z$
. -
○ If
 $\xi <\mu $
with
$\xi <\mu $
with
 $c\restriction \xi =d\restriction \xi $
and
$c\restriction \xi =d\restriction \xi $
and
 $c(\xi )\neq d(\xi )$
, then and
$c(\xi )\neq d(\xi )$
, then and $$ \begin{align*}i^{I_c}_{0,\infty}(x)\cap\kappa_{c\restriction\xi} ~ = ~ i^{I_d}_{0,\infty}(x)\cap\kappa_{c\restriction\xi}\end{align*} $$
where
$$ \begin{align*}i^{I_c}_{0,\infty}(x)\cap\kappa_{c\restriction\xi} ~ = ~ i^{I_d}_{0,\infty}(x)\cap\kappa_{c\restriction\xi}\end{align*} $$
where $$ \begin{align*}i^{I_c}_{0,\infty}(x)\cap\rho ~ \neq ~ i^{I_d}_{0,\infty}(x)\cap\rho,\end{align*} $$
$$ \begin{align*}i^{I_c}_{0,\infty}(x)\cap\rho ~ \neq ~ i^{I_d}_{0,\infty}(x)\cap\rho,\end{align*} $$
 $\rho =\min (\kappa _{c\restriction (\xi +1)},\kappa _{d\restriction (\xi +1)})$
.
$\rho =\min (\kappa _{c\restriction (\xi +1)},\kappa _{d\restriction (\xi +1)})$
.
We now define
Then
![]() $\iota $
is an injection.
$\iota $
is an injection.
Claim. The map
![]() $\iota $
is a perfect embedding.
$\iota $
is a perfect embedding.
Proof of the claim
Fix
![]() $c\in {}^\mu \kappa $
. Given
$c\in {}^\mu \kappa $
. Given
![]() $\alpha <\kappa $
, there is
$\alpha <\kappa $
, there is
![]() $\xi <\mu $
with
$\xi <\mu $
with
![]() $\kappa _{c\restriction \xi }\geq \alpha $
and, if
$\kappa _{c\restriction \xi }\geq \alpha $
and, if
![]() $d\in {}^\mu \kappa $
with
$d\in {}^\mu \kappa $
with
![]() $c\restriction \xi =d\restriction \xi $
, then
$c\restriction \xi =d\restriction \xi $
, then
![]() $\iota (c)\cap \kappa _{c\restriction \xi }=\iota (d)\cap \kappa _{c\restriction \xi }$
. In the other direction, fix
$\iota (c)\cap \kappa _{c\restriction \xi }=\iota (d)\cap \kappa _{c\restriction \xi }$
. In the other direction, fix
![]() $\xi <\nu $
and
$\xi <\nu $
and
![]() $d\in {}^\mu \kappa $
with
$d\in {}^\mu \kappa $
with
![]() $\iota (c)\cap \kappa _{c\restriction \xi }=\iota (d)\cap \kappa _{c\restriction \xi }$
. Assume, towards a contradiction, that
$\iota (c)\cap \kappa _{c\restriction \xi }=\iota (d)\cap \kappa _{c\restriction \xi }$
. Assume, towards a contradiction, that
![]() $c\restriction \xi \neq d\restriction \xi $
. Then there is
$c\restriction \xi \neq d\restriction \xi $
. Then there is
![]() $\eta <\xi $
with
$\eta <\xi $
with
![]() $c\restriction \eta =d\restriction \eta $
and
$c\restriction \eta =d\restriction \eta $
and
![]() $c(\eta )\neq d(\eta )$
. Our construction then ensures that
$c(\eta )\neq d(\eta )$
. Our construction then ensures that
![]() $\iota (c)\cap \kappa _{c\restriction (\eta +1)}\neq \iota (d)\cap \kappa _{c\restriction (\eta +1)}$
and therefore
$\iota (c)\cap \kappa _{c\restriction (\eta +1)}\neq \iota (d)\cap \kappa _{c\restriction (\eta +1)}$
and therefore
![]() $\iota (c)\cap \kappa _{c\restriction \xi }\neq \iota (c)\cap \kappa _{c\restriction \xi }$
, a contradiction. This proves the statement of the claim.
$\iota (c)\cap \kappa _{c\restriction \xi }\neq \iota (c)\cap \kappa _{c\restriction \xi }$
, a contradiction. This proves the statement of the claim.
Claim.
![]() ${{\mathrm {ran}}(\iota )}\subseteq D$
.
${{\mathrm {ran}}(\iota )}\subseteq D$
.
Proof of the claim
Fix
![]() $c\in {}^\mu \kappa $
. Pick a
$c\in {}^\mu \kappa $
. Pick a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
such that
$\varphi (v_0,v_1,v_2)$
such that
As
![]() $x \in D$
,
$x \in D$
,
![]() $\varphi (\kappa ,x,z)$
holds in V and hence the properties listed above ensure that
$\varphi (\kappa ,x,z)$
holds in V and hence the properties listed above ensure that
![]() $\varphi (\kappa ,\iota (c),z)$
holds in
$\varphi (\kappa ,\iota (c),z)$
holds in
![]() $M^{I_c}_\infty $
. Since the upwards absoluteness of
$M^{I_c}_\infty $
. Since the upwards absoluteness of
![]() $\Sigma _1$
-statements directly implies that
$\Sigma _1$
-statements directly implies that
![]() $\varphi (\kappa ,\iota (c),z)$
holds in
$\varphi (\kappa ,\iota (c),z)$
holds in
![]() ${\mathrm {V}}$
, we can conclude that
${\mathrm {V}}$
, we can conclude that
![]() $\iota (c)$
is an element of D.
$\iota (c)$
is an element of D.
This completes the proof of the theorem.
Note that, in general, the conclusion of Theorem 1.1 cannot be extended to
![]() $\Sigma _1$
-formulas using arbitrary subsets of the cardinal
$\Sigma _1$
-formulas using arbitrary subsets of the cardinal
![]() $\kappa $
as parameters. For example, if
$\kappa $
as parameters. For example, if
![]() $\kappa $
is a regular limit of measurable cardinals, then, in a generic extension by some
$\kappa $
is a regular limit of measurable cardinals, then, in a generic extension by some
![]() ${<}\kappa $
-closed forcing, there exists a subset of
${<}\kappa $
-closed forcing, there exists a subset of
![]() ${\mathcal {P}}({\kappa })$
that does not contain the range of a perfect embedding and is definable by a
${\mathcal {P}}({\kappa })$
that does not contain the range of a perfect embedding and is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathcal {P}}({\kappa })$
(see [Reference Lücke33, Corollary 7.9]).
${\mathcal {P}}({\kappa })$
(see [Reference Lücke33, Corollary 7.9]).
3 Local complexity of canonical inner models
As a first application of the results of Section 2, we prove a result that shows that canonical inner models with infinitely many measurable cardinals are not locally
![]() $\Sigma _1$
-definable. Note that Gödel’s constructible universe
$\Sigma _1$
-definable. Note that Gödel’s constructible universe
![]() ${\mathrm {L}}$
, the Dodd–Jensen core model and Kunen’s model
${\mathrm {L}}$
, the Dodd–Jensen core model and Kunen’s model
![]() ${\mathrm {L}}[U]$
all possess the property that for every uncountable cardinal
${\mathrm {L}}[U]$
all possess the property that for every uncountable cardinal
![]() $\kappa $
, the
$\kappa $
, the
![]() ${\mathrm {H}}(\kappa ^+)^M$
of the corresponding inner model M is definable by a
${\mathrm {H}}(\kappa ^+)^M$
of the corresponding inner model M is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\kappa +1$
(see, for example, the proof of [Reference Lücke34, Lemma 4.13]). In particular, these models satisfy the assumptions of the next theorem.
$\kappa +1$
(see, for example, the proof of [Reference Lücke34, Lemma 4.13]). In particular, these models satisfy the assumptions of the next theorem.
Theorem 3.1. Assume that M is a class term with the property that
![]() ${\mathrm {ZFC}}$
proves the following statements:Footnote 4
${\mathrm {ZFC}}$
proves the following statements:Footnote 4
-
(i) The class M is a transitive model of
 ${\mathrm {ZFC}}+{{\mathrm {V}}=M}$
that contains all ordinals.
${\mathrm {ZFC}}+{{\mathrm {V}}=M}$
that contains all ordinals. -
(ii) M is forcing invariant under Cohen forcing
 ${\mathrm {Add}}({\omega },{1})$
.
${\mathrm {Add}}({\omega },{1})$
. -
(iii) If
 $\kappa $
is a limit of measurable cardinals with
$\kappa $
is a limit of measurable cardinals with
 ${{\mathrm {cof}}(\kappa )}=\omega $
and
${{\mathrm {cof}}(\kappa )}=\omega $
and
 $(\kappa ^+)^M=\kappa ^+$
, then there is a subset of
$(\kappa ^+)^M=\kappa ^+$
, then there is a subset of
 $M\cap {\mathcal {P}}({\kappa })$
of cardinality greater than
$M\cap {\mathcal {P}}({\kappa })$
of cardinality greater than
 $\kappa $
that is definable by a
$\kappa $
that is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 ${\mathrm {H}}(\kappa )^M\cup \{\kappa \}$
.
${\mathrm {H}}(\kappa )^M\cup \{\kappa \}$
.
Then
![]() ${\mathrm {ZFC}}$
proves that M contains only finitely many measurable cardinals.
${\mathrm {ZFC}}$
proves that M contains only finitely many measurable cardinals.
Proof. Assume, towards a contradiction, that the above conclusion fails. Then we may work in a model
![]() ${\mathrm {V}}$
of
${\mathrm {V}}$
of
![]() ${\mathrm {ZFC}}+{{\mathrm {V}}=M}$
that contains infinitely many measurable cardinals. Let
${\mathrm {ZFC}}+{{\mathrm {V}}=M}$
that contains infinitely many measurable cardinals. Let
![]() $\kappa $
be the least limit of measurable cardinals, and let G be
$\kappa $
be the least limit of measurable cardinals, and let G be
![]() ${\mathrm {Add}}({\omega },{1})$
-generic over
${\mathrm {Add}}({\omega },{1})$
-generic over
![]() ${\mathrm {V}}$
. An application of (ii) and (iii) in
${\mathrm {V}}$
. An application of (ii) and (iii) in
![]() ${\mathrm {V}}[G]$
now yields
${\mathrm {V}}[G]$
now yields
![]() $z\in {\mathrm {H}}(\kappa )^{\mathrm {V}}$
and a
$z\in {\mathrm {H}}(\kappa )^{\mathrm {V}}$
and a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
with the property that the set
$\varphi (v_0,v_1,v_2)$
with the property that the set
![]() $\{{y\in {\mathrm {V}}[G]}~\vert ~{{\mathrm {V}}[G]\models \varphi (\kappa ,y,z)}\}$
is a subset of
$\{{y\in {\mathrm {V}}[G]}~\vert ~{{\mathrm {V}}[G]\models \varphi (\kappa ,y,z)}\}$
is a subset of
![]() ${\mathcal {P}}({\kappa })^{\mathrm {V}}$
that has cardinality greater than
${\mathcal {P}}({\kappa })^{\mathrm {V}}$
that has cardinality greater than
![]() $\kappa $
in
$\kappa $
in
![]() ${\mathrm {V}}[G]$
. In this situation, the homogeneity of
${\mathrm {V}}[G]$
. In this situation, the homogeneity of
![]() ${\mathrm {Add}}({\omega },{1})$
in
${\mathrm {Add}}({\omega },{1})$
in
![]() ${\mathrm {V}}$
ensures that these statements about the class defined by the formula
${\mathrm {V}}$
ensures that these statements about the class defined by the formula
![]() $\varphi $
and the parameters
$\varphi $
and the parameters
![]() $\kappa $
and z hold in every
$\kappa $
and z hold in every
![]() ${\mathrm {Add}}({\omega },{1})$
-generic extension of
${\mathrm {Add}}({\omega },{1})$
-generic extension of
![]() ${\mathrm {V}}$
.
${\mathrm {V}}$
.
Now, let
![]() $G_0\times G_1$
be
$G_0\times G_1$
be
![]() $({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-generic over
$({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-generic over
![]() ${\mathrm {V}}$
. Then the above observations show that
${\mathrm {V}}$
. Then the above observations show that
is a subset of
![]() ${\mathcal {P}}({\kappa })^{\mathrm {V}}$
that has cardinality greater than
${\mathcal {P}}({\kappa })^{\mathrm {V}}$
that has cardinality greater than
![]() $\kappa $
in
$\kappa $
in
![]() ${\mathrm {V}}[G_0]$
. An application of Lemma 2.1 in
${\mathrm {V}}[G_0]$
. An application of Lemma 2.1 in
![]() ${\mathrm {V}}[G_0]$
then yields
${\mathrm {V}}[G_0]$
then yields
![]() $x\in D$
and systems
$x\in D$
and systems
![]() $\langle {\nu _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
$\langle {\nu _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
![]() $\langle {\kappa _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
$\langle {\kappa _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
![]() $\langle {U_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
and
$\langle {U_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
and
![]() $\langle {I_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
satisfying the statements listed in the lemma with respect to z and some subset of D of cardinality
$\langle {I_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
satisfying the statements listed in the lemma with respect to z and some subset of D of cardinality
![]() $\kappa ^+$
. Define
$\kappa ^+$
. Define
and let I denote the unique linear iteration of
![]() $\langle {\mathrm {V}}[G_0],\{{U_{c\restriction n}}~\vert ~{n<\omega }\}\rangle $
of length
$\langle {\mathrm {V}}[G_0],\{{U_{c\restriction n}}~\vert ~{n<\omega }\}\rangle $
of length
![]() $\sup _{n<\omega }{\mathrm {lh}}({I_{c\restriction n}}){}$
in
$\sup _{n<\omega }{\mathrm {lh}}({I_{c\restriction n}}){}$
in
![]() ${\mathrm {V}}[G_0,G_1]$
with
${\mathrm {V}}[G_0,G_1]$
with
![]() $U^I_\alpha =U^{I_{c\restriction n}}_\alpha $
for all
$U^I_\alpha =U^{I_{c\restriction n}}_\alpha $
for all
![]() $n<\omega $
and
$n<\omega $
and
![]() $\alpha <{\mathrm {lh}}({I_{c\restriction n}}){}$
. Then Lemma 2.2 shows that
$\alpha <{\mathrm {lh}}({I_{c\restriction n}}){}$
. Then Lemma 2.2 shows that
![]() $M^I_\infty $
is well-founded. Set
$M^I_\infty $
is well-founded. Set
![]() $x_*=i^I_{0,\infty }(x)$
. Since Lemma 2.2 ensures that
$x_*=i^I_{0,\infty }(x)$
. Since Lemma 2.2 ensures that
![]() $i^I_{0,\infty }(\kappa )=\kappa $
and
$i^I_{0,\infty }(\kappa )=\kappa $
and
![]() $i^I_{0,\infty }(z)=z$
, we can use the elementarity of
$i^I_{0,\infty }(z)=z$
, we can use the elementarity of
![]() $i^I_{0,\infty }$
and
$i^I_{0,\infty }$
and
![]() $\Sigma _1$
-upwards absoluteness to conclude that
$\Sigma _1$
-upwards absoluteness to conclude that
![]() $\varphi (\kappa ,x_*,z)$
holds in
$\varphi (\kappa ,x_*,z)$
holds in
![]() ${\mathrm {V}}[G_0,G_1]$
. Since
${\mathrm {V}}[G_0,G_1]$
. Since
![]() ${\mathrm {V}}[G_0,G_1]$
is an
${\mathrm {V}}[G_0,G_1]$
is an
![]() ${\mathrm {Add}}({\omega },{1})$
-generic extension of
${\mathrm {Add}}({\omega },{1})$
-generic extension of
![]() ${\mathrm {V}}$
, our earlier observations allow us to conclude that
${\mathrm {V}}$
, our earlier observations allow us to conclude that
![]() $x_*$
is an element of
$x_*$
is an element of
![]() ${\mathcal {P}}({\kappa })^{\mathrm {V}}$
. If we now pick
${\mathcal {P}}({\kappa })^{\mathrm {V}}$
. If we now pick
![]() $n<\omega $
and set
$n<\omega $
and set
![]() $\rho =\min (\kappa _{(c\restriction n)^\frown \langle 0\rangle },\kappa _{(c\restriction n)^\frown \langle 1\rangle })$
, then clause (iii) of Lemma 2.2 shows that
$\rho =\min (\kappa _{(c\restriction n)^\frown \langle 0\rangle },\kappa _{(c\restriction n)^\frown \langle 1\rangle })$
, then clause (iii) of Lemma 2.2 shows that
![]() $c(n)$
is the unique
$c(n)$
is the unique
![]() $i<2$
with
$i<2$
with
This conclusion implies that c is an element of
![]() ${\mathrm {V}}[G_0]$
, a contradiction.
${\mathrm {V}}[G_0]$
, a contradiction.
The above result can easily be shown to be optimal, in the sense that there exists a class term M satisfying the above three properties that can consistently contain any finite number of measurable cardinals. Ideas from the proof of Theorem 1.2 for singular cardinals of countable cofinality will allow us to prove the following result in Section 4.
Proposition 3.2. There exists a class term M with the following properties:
-
(i) There is a
 $\Sigma _1$
-formula
$\Sigma _1$
-formula
 $\varphi (v_0,v_1,v_2)$
with the property that
$\varphi (v_0,v_1,v_2)$
with the property that
 ${\mathrm {ZFC}}$
proves the following statements:
${\mathrm {ZFC}}$
proves the following statements:-
(a) The class M is a transitive model of
 ${\mathrm {ZFC}}+{{\mathrm {V}}=M}$
that contains all ordinals.
${\mathrm {ZFC}}+{{\mathrm {V}}=M}$
that contains all ordinals. -
(b) M is forcing invariant.
-
(c) If
 $\kappa $
is an uncountable cardinal, then there exists
$\kappa $
is an uncountable cardinal, then there exists
 $z\in {\mathrm {H}}(\kappa )^M$
with
$z\in {\mathrm {H}}(\kappa )^M$
with
 ${\mathrm {H}}(\kappa ^+)^M=\{{y}~\vert ~{\varphi (\kappa ,y,z)}\}$
.
${\mathrm {H}}(\kappa ^+)^M=\{{y}~\vert ~{\varphi (\kappa ,y,z)}\}$
.
-
-
(ii) Given a natural number n, if the theory
is consistent, then so is the theory $$ \begin{align*}{\mathrm{ZFC}} ~ + ~ {\text{"}\hspace{0.3ex}{\textit{There exist}\ n\ \textit{measurable cardinals}}\hspace{0.3ex}\text{"}} \end{align*} $$
$$ \begin{align*}{\mathrm{ZFC}} ~ + ~ {\text{"}\hspace{0.3ex}{\textit{There exist}\ n\ \textit{measurable cardinals}}\hspace{0.3ex}\text{"}} \end{align*} $$
 $$ \begin{align*}{\mathrm{ZFC}} ~ + ~ {\mathrm{V}}=M ~ + ~ {\text{"}\hspace{0.3ex}{\textit{There exist}\ n\ \textit{measurable cardinals}.}\hspace{0.3ex}\text{"}} \end{align*} $$
$$ \begin{align*}{\mathrm{ZFC}} ~ + ~ {\mathrm{V}}=M ~ + ~ {\text{"}\hspace{0.3ex}{\textit{There exist}\ n\ \textit{measurable cardinals}.}\hspace{0.3ex}\text{"}} \end{align*} $$
4 The lower bound for singular cardinals of countable cofinality
In this section, we will prove the following result that covers the case of singular strong limit cardinals of countable cofinality in the statement of Theorem 1.2:
Theorem 4.1. Assume that there is no inner model with infinitely many measurable cardinals, and let
![]() $\kappa $
be a singular strong limit cardinal of countable cofinality. Then there is a subset D of
$\kappa $
be a singular strong limit cardinal of countable cofinality. Then there is a subset D of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
such that there is no continuous injection
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
such that there is no continuous injection
![]() ${\iota }:{{}^\omega \kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
${\iota }:{{}^\omega \kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
![]() ${{\mathrm {ran}}(\iota )}\subseteq D$
.
${{\mathrm {ran}}(\iota )}\subseteq D$
.
The proof of the above theorem relies on the theory of short core models developed by Koepke in [Reference Koepke31] and generalizations of basic concepts from classical descriptive set theory to simply definable collections of subsets of singular cardinals of countable cofinality. In the following, we will briefly introduce these generalized notions.
Definition 4.2. Let
![]() $\kappa $
be a limit cardinal of countable cofinality, and let
$\kappa $
be a limit cardinal of countable cofinality, and let
![]() $0<n<\omega $
be a natural number.
$0<n<\omega $
be a natural number.
-
(i) A subset T of
 $({}^{{<}\omega }\kappa )^n$
is a subtree of
$({}^{{<}\omega }\kappa )^n$
is a subtree of
 $({}^{{<}\omega }\kappa )^n$
if the following statements hold for all
$({}^{{<}\omega }\kappa )^n$
if the following statements hold for all
 ${\langle t_0,\ldots ,t_{n-1}\rangle \in T}$
:
${\langle t_0,\ldots ,t_{n-1}\rangle \in T}$
:-
(a)
 ${\mathrm {lh}}({t_0}) = \ldots = {\mathrm {lh}}({t_{n-1}})$
.
${\mathrm {lh}}({t_0}) = \ldots = {\mathrm {lh}}({t_{n-1}})$
. -
(b) If
 $m<{\mathrm {lh}}({t_0})$
, then
$m<{\mathrm {lh}}({t_0})$
, then
 $\langle t_0\restriction m,\ldots ,t_{n-1}\restriction m\rangle ~ \in ~ T$
.
$\langle t_0\restriction m,\ldots ,t_{n-1}\restriction m\rangle ~ \in ~ T$
.
-
-
(ii) If T is a subtree of
 $({}^{{<}\omega }\kappa )^n$
, then we define
$({}^{{<}\omega }\kappa )^n$
, then we define
 $[T]$
to be the set of all elements
$[T]$
to be the set of all elements
 $\langle x_0,\ldots ,x_{n-1}\rangle $
of
$\langle x_0,\ldots ,x_{n-1}\rangle $
of
 $({}^\omega \kappa )^n$
with the property that
$({}^\omega \kappa )^n$
with the property that
 $\langle x_0\restriction m,\ldots ,x_{n-1}\restriction m\rangle \in T$
holds for all
$\langle x_0\restriction m,\ldots ,x_{n-1}\restriction m\rangle \in T$
holds for all
 $m<\omega $
.
$m<\omega $
. -
(iii) A subset X of
 $({}^\omega \kappa )^n$
is a
$({}^\omega \kappa )^n$
is a
 $\mathbf {\Sigma }^1_1$
-subset if there exists a subtree T of
$\mathbf {\Sigma }^1_1$
-subset if there exists a subtree T of
 $({}^{{<}\omega }\kappa )^{n+1}$
with
$({}^{{<}\omega }\kappa )^{n+1}$
with  $$ \begin{align*}X ~ = ~ p[T] ~ = ~ \{{\langle x_0,\ldots,x_{n-1}\rangle\in({}^\omega\kappa)^n}~\vert~{\exists y ~ \langle x_0,\ldots,x_{n-1},y\rangle\in[T]}\}.\end{align*} $$
$$ \begin{align*}X ~ = ~ p[T] ~ = ~ \{{\langle x_0,\ldots,x_{n-1}\rangle\in({}^\omega\kappa)^n}~\vert~{\exists y ~ \langle x_0,\ldots,x_{n-1},y\rangle\in[T]}\}.\end{align*} $$
-
(iv) A subset of
 $({}^\omega \kappa )^n$
is a
$({}^\omega \kappa )^n$
is a
 $\mathbf {\Pi }^1_1$
-subset if its complement in
$\mathbf {\Pi }^1_1$
-subset if its complement in
 $({}^\omega \kappa )^n$
is a
$({}^\omega \kappa )^n$
is a
 $\mathbf {\Sigma }^1_1$
-subset.
$\mathbf {\Sigma }^1_1$
-subset.
As in the classical case, we can use universal sets to show that the classes of
![]() $\mathbf {\Sigma }^1_1$
- and
$\mathbf {\Sigma }^1_1$
- and
![]() $\mathbf {\Pi }^1_1$
-subsets do not coincide at singular strong limits of countable cofinality.
$\mathbf {\Pi }^1_1$
-subsets do not coincide at singular strong limits of countable cofinality.
Proposition 4.3. If
![]() $\kappa $
is a singular strong limit cardinal of countable cofinality, then there exists a
$\kappa $
is a singular strong limit cardinal of countable cofinality, then there exists a
![]() $\mathbf {\Sigma }^1_1$
-subset of
$\mathbf {\Sigma }^1_1$
-subset of
![]() ${}^\omega \kappa $
that is not a
${}^\omega \kappa $
that is not a
![]() $\mathbf {\Pi }^1_1$
-subset.
$\mathbf {\Pi }^1_1$
-subset.
Proof. Pick a strictly increasing sequence
![]() $\langle {\kappa _m}~\vert ~{m<\omega }\rangle $
of infinite cardinals that is cofinal in
$\langle {\kappa _m}~\vert ~{m<\omega }\rangle $
of infinite cardinals that is cofinal in
![]() $\kappa $
. In addition, fix an enumeration
$\kappa $
. In addition, fix an enumeration
![]() $\langle {a_\alpha }~\vert ~{\alpha <\kappa }\rangle $
of
$\langle {a_\alpha }~\vert ~{\alpha <\kappa }\rangle $
of
![]() ${\mathrm {H}}(\kappa )$
. Define U to be the set of all pairs
${\mathrm {H}}(\kappa )$
. Define U to be the set of all pairs
![]() $\langle s,t\rangle $
in
$\langle s,t\rangle $
in
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with the property that
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with the property that
![]() ${\mathrm {lh}}({s})={\mathrm {lh}}({t})$
and
${\mathrm {lh}}({s})={\mathrm {lh}}({t})$
and
![]() $\langle s\restriction l,t\restriction l\rangle \in a_{s(m)}$
for all
$\langle s\restriction l,t\restriction l\rangle \in a_{s(m)}$
for all
![]() $l\leq m<{\mathrm {lh}}({s})$
with
$l\leq m<{\mathrm {lh}}({s})$
with
![]() $s[l]\cup t[l]\subseteq \kappa _m$
. Then it is easy to see that U is a subtree of
$s[l]\cup t[l]\subseteq \kappa _m$
. Then it is easy to see that U is a subtree of
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
. Assume, towards a contradiction, that there exists a subtree T of
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
. Assume, towards a contradiction, that there exists a subtree T of
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with
![]() $p[T]={}^\omega \kappa \setminus p[U]$
. Pick a function
$p[T]={}^\omega \kappa \setminus p[U]$
. Pick a function
![]() $x\in {}^\omega \kappa $
with the property that
$x\in {}^\omega \kappa $
with the property that
![]() $a_{x(m)}={\mathrm {H}}(\kappa _m)\cap T$
holds for all
$a_{x(m)}={\mathrm {H}}(\kappa _m)\cap T$
holds for all
![]() $m<\omega $
.
$m<\omega $
.
Now, assume that there is
![]() $y\in {}^\omega \kappa $
with
$y\in {}^\omega \kappa $
with
![]() $\langle x,y\rangle \in [T]$
. Then
$\langle x,y\rangle \in [T]$
. Then
![]() $\langle x,y\rangle \notin [U]$
and there exists
$\langle x,y\rangle \notin [U]$
and there exists
![]() $l<\omega $
with
$l<\omega $
with
![]() $\langle x\restriction l,y\restriction l\rangle \notin U$
. Then there exists
$\langle x\restriction l,y\restriction l\rangle \notin U$
. Then there exists
![]() $l\leq m<\omega $
with
$l\leq m<\omega $
with
![]() $x[l]\cup y[l]\subseteq \kappa _m$
and
$x[l]\cup y[l]\subseteq \kappa _m$
and
![]() $\langle x\restriction l,y\restriction l\rangle \notin a_{x(m)}={\mathrm {H}}(\kappa _m)\cap T$
. But, this yields a contradiction because
$\langle x\restriction l,y\restriction l\rangle \notin a_{x(m)}={\mathrm {H}}(\kappa _m)\cap T$
. But, this yields a contradiction because
![]() $\langle x\restriction l,y\restriction l\rangle $
is an element of T. This shows that there is
$\langle x\restriction l,y\restriction l\rangle $
is an element of T. This shows that there is
![]() $y\in {}^\omega \kappa $
with
$y\in {}^\omega \kappa $
with
![]() $\langle x,y\rangle \in [U]$
. Then
$\langle x,y\rangle \in [U]$
. Then
![]() $\langle x,y\rangle \notin [T]$
and there is
$\langle x,y\rangle \notin [T]$
and there is
![]() $l<\omega $
with
$l<\omega $
with
![]() $\langle x\restriction l,y\restriction l\rangle \notin T$
. Pick
$\langle x\restriction l,y\restriction l\rangle \notin T$
. Pick
![]() $l\leq m<\omega $
with
$l\leq m<\omega $
with
![]() $x[l]\cup y[l]\subseteq \kappa _m$
. Then the fact that
$x[l]\cup y[l]\subseteq \kappa _m$
. Then the fact that
![]() $\langle x,y\rangle \in [U]$
implies that
$\langle x,y\rangle \in [U]$
implies that
![]() $\langle x\restriction l,y\restriction l\rangle \in a_{x(m)}\subseteq T$
, a contradiction.
$\langle x\restriction l,y\restriction l\rangle \in a_{x(m)}\subseteq T$
, a contradiction.
The proof of Theorem 4.1 relies on a generalization of the Boundedness Lemma to singular cardinals of countable cofinality. Below, we introduce the definitions needed in the formulation of this result.
Definition 4.4. Let
![]() $\kappa $
be an infinite cardinal, let
$\kappa $
be an infinite cardinal, let
![]() $\vec {\kappa }=\langle {\kappa _\xi }~\vert ~{\xi <{{\mathrm {cof}}(\kappa )}}\rangle $
be a strictly increasing sequence of ordinals that is cofinal in
$\vec {\kappa }=\langle {\kappa _\xi }~\vert ~{\xi <{{\mathrm {cof}}(\kappa )}}\rangle $
be a strictly increasing sequence of ordinals that is cofinal in
![]() $\kappa $
and let
$\kappa $
and let
![]() $\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\kappa }\rangle $
be a sequence of elements of
$\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\kappa }\rangle $
be a sequence of elements of
![]() ${\mathrm {H}}(\kappa )$
.
${\mathrm {H}}(\kappa )$
.
-
(i) Given
 $z\subseteq \kappa $
, we define
$z\subseteq \kappa $
, we define
 $\lhd _z$
to be the unique binary relation on
$\lhd _z$
to be the unique binary relation on
 $\kappa $
with the property that holds for all
$\kappa $
with the property that holds for all $$ \begin{align*}\alpha\lhd_z\beta ~ \Longleftrightarrow ~ {\prec}{\alpha},{\beta}{\succ}\in z\end{align*} $$
$$ \begin{align*}\alpha\lhd_z\beta ~ \Longleftrightarrow ~ {\prec}{\alpha},{\beta}{\succ}\in z\end{align*} $$
 $\alpha ,\beta <\kappa $
.Footnote 5
$\alpha ,\beta <\kappa $
.Footnote 5
-
(ii) We define
 $\mathcal {W}\mathcal {O}_\kappa $
to be the set of all
$\mathcal {W}\mathcal {O}_\kappa $
to be the set of all
 $z\in {\mathcal {P}}({\kappa })$
with the property that
$z\in {\mathcal {P}}({\kappa })$
with the property that
 $\lhd _z$
is a well-ordering of
$\lhd _z$
is a well-ordering of
 $\kappa $
.
$\kappa $
. -
(iii) We let
 $\mathsf {WO}(\vec {\kappa },\vec {a})$
denote the set of all
$\mathsf {WO}(\vec {\kappa },\vec {a})$
denote the set of all
 $x\in {}^{{{\mathrm {cof}}(\kappa )}}\kappa $
with the property that there exists
$x\in {}^{{{\mathrm {cof}}(\kappa )}}\kappa $
with the property that there exists
 $y\in \mathcal {W}\mathcal {O}_\kappa $
such that
$y\in \mathcal {W}\mathcal {O}_\kappa $
such that
 $y\cap \kappa _\xi =a_{x(\xi )}$
holds for all
$y\cap \kappa _\xi =a_{x(\xi )}$
holds for all
 $\xi <{{\mathrm {cof}}(\kappa )}$
.
$\xi <{{\mathrm {cof}}(\kappa )}$
. -
(iv) Given an element x of
 $\mathsf {WO}(\vec {\kappa },\vec {a})$
, we let
$\mathsf {WO}(\vec {\kappa },\vec {a})$
, we let
 $\|x\|_{\vec {a}}$
denote the order-type of the resulting well-order
$\|x\|_{\vec {a}}$
denote the order-type of the resulting well-order
 $\langle \kappa ,\lhd _{\hspace {0.9pt}\bigcup \{{a_{x(\xi )}}~\vert ~{\xi <{{\mathrm {cof}}(\kappa )}}\}}\rangle $
.
$\langle \kappa ,\lhd _{\hspace {0.9pt}\bigcup \{{a_{x(\xi )}}~\vert ~{\xi <{{\mathrm {cof}}(\kappa )}}\}}\rangle $
.
Lemma 4.5. Let
![]() $\kappa $
be a singular strong limit cardinal of countable cofinality, let
$\kappa $
be a singular strong limit cardinal of countable cofinality, let
![]() $\vec {\kappa }=\langle {\kappa _m}~\vert ~{m<\omega }\rangle $
be a strictly increasing sequence of cardinals that is cofinal in
$\vec {\kappa }=\langle {\kappa _m}~\vert ~{m<\omega }\rangle $
be a strictly increasing sequence of cardinals that is cofinal in
![]() $\kappa $
and let
$\kappa $
and let
![]() $\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\kappa }\rangle $
be an enumeration of
$\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\kappa }\rangle $
be an enumeration of
![]() ${\mathrm {H}}(\kappa )$
. If B is a
${\mathrm {H}}(\kappa )$
. If B is a
![]() $\mathbf {\Sigma }^1_1$
-subset of
$\mathbf {\Sigma }^1_1$
-subset of
![]() ${}^\omega \kappa $
with
${}^\omega \kappa $
with
![]() $B\subseteq \mathsf {WO}(\vec {\kappa },\vec {a})$
, then there exists an ordinal
$B\subseteq \mathsf {WO}(\vec {\kappa },\vec {a})$
, then there exists an ordinal
![]() $\gamma <\kappa ^+$
with
$\gamma <\kappa ^+$
with
![]() $\|y\|_{\vec {a}}<\gamma $
for all
$\|y\|_{\vec {a}}<\gamma $
for all
![]() $y\in B$
.
$y\in B$
.
Proof. Assume, towards a contradiction, that the set
![]() $\{{\|y\|_{\vec {a}}}~\vert ~{y\in B}\}$
is unbounded in
$\{{\|y\|_{\vec {a}}}~\vert ~{y\in B}\}$
is unbounded in
![]() $\kappa ^+$
. Pick a subtree S of
$\kappa ^+$
. Pick a subtree S of
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with
![]() $p[S]=B$
. By Proposition 4.3, there exists a subtree T of
$p[S]=B$
. By Proposition 4.3, there exists a subtree T of
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with the property that the set
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with the property that the set
![]() $A={}^\omega \kappa \setminus p[T]$
is not a
$A={}^\omega \kappa \setminus p[T]$
is not a
![]() $\mathbf {\Sigma }^1_1$
-subset of
$\mathbf {\Sigma }^1_1$
-subset of
![]() ${}^\omega \kappa $
. Given
${}^\omega \kappa $
. Given
![]() $x\in {}^\omega \kappa $
, set
$x\in {}^\omega \kappa $
, set
Then
![]() $T_x$
is a subtree of
$T_x$
is a subtree of
![]() ${}^{{<}\omega }\kappa $
for all
${}^{{<}\omega }\kappa $
for all
![]() $x\in {}^\omega \kappa $
and
$x\in {}^\omega \kappa $
and
![]() $A=\{{x\in {}^\omega \kappa }~\vert ~{[T_x]=\emptyset }\}$
. By standard arguments (see [Reference Kechris30, Section 2.E]), we now know that a function
$A=\{{x\in {}^\omega \kappa }~\vert ~{[T_x]=\emptyset }\}$
. By standard arguments (see [Reference Kechris30, Section 2.E]), we now know that a function
![]() $x\in {}^\omega \kappa $
is contained in A if and only if there exists an ordinal
$x\in {}^\omega \kappa $
is contained in A if and only if there exists an ordinal
![]() $\gamma <\kappa ^+$
and a function
$\gamma <\kappa ^+$
and a function
![]() ${r}:{T_x}\longrightarrow {\gamma }$
with
${r}:{T_x}\longrightarrow {\gamma }$
with
![]() $r(s)>r(t)$
for all
$r(s)>r(t)$
for all
![]() $s,t\in T_x$
with
$s,t\in T_x$
with
![]() $s\subsetneq t$
. Since our assumption implies that for every
$s\subsetneq t$
. Since our assumption implies that for every
![]() $\gamma <\kappa ^+$
, there is
$\gamma <\kappa ^+$
, there is
![]() $y\in B$
with the property that there exists an order-preserving embedding of
$y\in B$
with the property that there exists an order-preserving embedding of
![]() $\langle \gamma ,<\rangle $
into
$\langle \gamma ,<\rangle $
into
![]() $\langle \kappa ,\lhd _{\hspace {0.9pt}\bigcup \{{a_{y(\xi )}}~\vert ~{\xi <{{\mathrm {cof}}(\kappa )}}\}}\rangle $
, we know that A consists of all
$\langle \kappa ,\lhd _{\hspace {0.9pt}\bigcup \{{a_{y(\xi )}}~\vert ~{\xi <{{\mathrm {cof}}(\kappa )}}\}}\rangle $
, we know that A consists of all
![]() $x\in {}^\omega \kappa $
with the property that there exists
$x\in {}^\omega \kappa $
with the property that there exists
![]() $y\in B$
and a function
$y\in B$
and a function
![]() ${f}:{T_x}\longrightarrow {\kappa }$
such that for all
${f}:{T_x}\longrightarrow {\kappa }$
such that for all
![]() $s,t\in T_x$
with
$s,t\in T_x$
with
![]() $s\subsetneq t$
and all
$s\subsetneq t$
and all
![]() $m<\omega $
with
$m<\omega $
with
![]() $f(s),f(t)<\kappa _m$
, we have
$f(s),f(t)<\kappa _m$
, we have
![]() ${\prec }{f(t)},{f(s)}{\succ }\in a_{y(m)}$
.
${\prec }{f(t)},{f(s)}{\succ }\in a_{y(m)}$
.
Below, we aim to derive a contradiction from the above assumption by constructing a subtree U of
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with the property that a pair
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
with the property that a pair
![]() $\langle x,y\rangle $
in
$\langle x,y\rangle $
in
![]() ${}^\omega \kappa \times {}^\omega \kappa $
is an element of
${}^\omega \kappa \times {}^\omega \kappa $
is an element of
![]() $[U]$
if and only if y codes (in some fixed canonical way) functions
$[U]$
if and only if y codes (in some fixed canonical way) functions
![]() ${c}:{T_x}\longrightarrow {\omega }$
,
${c}:{T_x}\longrightarrow {\omega }$
,
![]() ${f}:{T_x}\longrightarrow {\kappa }$
and
${f}:{T_x}\longrightarrow {\kappa }$
and
![]() ${u,v}:{\omega }\longrightarrow {\kappa }$
such that
${u,v}:{\omega }\longrightarrow {\kappa }$
such that
![]() $f(p)<\kappa _{c(p)}$
for all
$f(p)<\kappa _{c(p)}$
for all
![]() $p\in T_x$
, the pair
$p\in T_x$
, the pair
![]() $\langle u,v\rangle $
is an element of
$\langle u,v\rangle $
is an element of
![]() $[S]$
and
$[S]$
and
![]() ${\prec }{f(q)},{f(p)}{\succ }\in a_{u(\max (c(p),c(q)))}$
holds for all
${\prec }{f(q)},{f(p)}{\succ }\in a_{u(\max (c(p),c(q)))}$
holds for all
![]() $p,q\in T_x$
with
$p,q\in T_x$
with
![]() $p\subsetneq q$
. Note that if U is a tree with these properties,
$p\subsetneq q$
. Note that if U is a tree with these properties,
![]() $\langle x,y\rangle $
is an element of U and c, f, u and v are the functions coded by y, then u is an element of B and the functions f and u witness that x is an element of A. But this means that, if we succeed in constructing such a tree U, then we derive a contradiction because the properties of U ensure that
$\langle x,y\rangle $
is an element of U and c, f, u and v are the functions coded by y, then u is an element of B and the functions f and u witness that x is an element of A. But this means that, if we succeed in constructing such a tree U, then we derive a contradiction because the properties of U ensure that
![]() $p[U]=A$
and hence such a tree U witnesses that A is a
$p[U]=A$
and hence such a tree U witnesses that A is a
![]() $\mathbf {\Sigma }^1_1$
-subset of
$\mathbf {\Sigma }^1_1$
-subset of
![]() ${}^\omega \kappa $
.
${}^\omega \kappa $
.
We now show that our assumptions allow us to construct a tree U with the properties described above. For every
![]() $s\in {}^{{<}\omega }\kappa $
, we set
$s\in {}^{{<}\omega }\kappa $
, we set
Define U to be the subset of
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
consisting of pairs
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
consisting of pairs
![]() $\langle s,t\rangle $
with
$\langle s,t\rangle $
with
![]() ${\mathrm {lh}}({s})={\mathrm {lh}}({t})$
and the property that for all
${\mathrm {lh}}({s})={\mathrm {lh}}({t})$
and the property that for all
![]() $m<{\mathrm {lh}}({s})$
, there exist
$m<{\mathrm {lh}}({s})$
, there exist
![]() $c_m,f_m,u_m,v_m\in {\mathrm {H}}(\kappa )$
such that
$c_m,f_m,u_m,v_m\in {\mathrm {H}}(\kappa )$
such that
![]() $a_{t(m)}=\langle c_m,f_m,u_m,v_m\rangle $
and the following statements hold for all
$a_{t(m)}=\langle c_m,f_m,u_m,v_m\rangle $
and the following statements hold for all
![]() $l\leq m$
:
$l\leq m$
:
-
○
 $\langle u_l,v_l\rangle ,\langle u_m,v_m\rangle \in S$
,
$\langle u_l,v_l\rangle ,\langle u_m,v_m\rangle \in S$
,
 ${\mathrm {lh}}({u_m})=m+1$
,
${\mathrm {lh}}({u_m})=m+1$
,
 $u_l=u_m\restriction (l+1)$
and
$u_l=u_m\restriction (l+1)$
and
 $v_l=v_m\restriction (l+1)$
.
$v_l=v_m\restriction (l+1)$
. -
○
 ${c_m}:{{\mathrm {H}}(\kappa _m)\cap T_{s\restriction m}}\longrightarrow {\omega }$
with
${c_m}:{{\mathrm {H}}(\kappa _m)\cap T_{s\restriction m}}\longrightarrow {\omega }$
with
 $c_m\restriction {{\mathrm {dom}}(c_l)}=c_l$
.
$c_m\restriction {{\mathrm {dom}}(c_l)}=c_l$
. -
○
 ${f_m}:{\{{w\in {\mathrm {H}}(\kappa _m)\cap T_{s\restriction m}}~\vert ~{c_m(w)\leq m}\}}\longrightarrow {\kappa _m}$
with
${f_m}:{\{{w\in {\mathrm {H}}(\kappa _m)\cap T_{s\restriction m}}~\vert ~{c_m(w)\leq m}\}}\longrightarrow {\kappa _m}$
with
 $f_m\restriction {{\mathrm {dom}}(f_l)}=f_l$
and
$f_m\restriction {{\mathrm {dom}}(f_l)}=f_l$
and
 ${\prec }{f_m(q)},{f_m(p)}{\succ }\in a_{u_m(m)}$
for all
${\prec }{f_m(q)},{f_m(p)}{\succ }\in a_{u_m(m)}$
for all
 $p,q\in {{\mathrm {dom}}(f_m)}$
with
$p,q\in {{\mathrm {dom}}(f_m)}$
with
 $p\subsetneq q$
.
$p\subsetneq q$
.
Then U is a subtree of
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
.
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
.
Claim.
![]() $p[U] = A$
.
$p[U] = A$
.
Proof of the Claim
First, fix
![]() $\langle x,y\rangle \in [U]$
. Then there are
$\langle x,y\rangle \in [U]$
. Then there are
![]() ${c}:{T_x}\longrightarrow {\omega }$
,
${c}:{T_x}\longrightarrow {\omega }$
,
![]() ${f}:{T_x}\longrightarrow {\kappa }$
and
${f}:{T_x}\longrightarrow {\kappa }$
and
![]() $\langle u,v\rangle \in [S]$
with the property that for all
$\langle u,v\rangle \in [S]$
with the property that for all
![]() $m<\omega $
, the set
$m<\omega $
, the set
![]() $a_{y(m)}$
is equal to the quadruple
$a_{y(m)}$
is equal to the quadruple
Then
![]() $u\in B$
and
$u\in B$
and
![]() ${\prec }{f(q)},{f(p)}{\succ }\in a_{u(m)}$
holds for all
${\prec }{f(q)},{f(p)}{\succ }\in a_{u(m)}$
holds for all
![]() $p,q\in T_x$
with
$p,q\in T_x$
with
![]() $p\subsetneq q$
and all
$p\subsetneq q$
and all
![]() $m<\omega $
with
$m<\omega $
with
![]() $f(p),f(q)<\kappa _m$
. By earlier observations, this shows that
$f(p),f(q)<\kappa _m$
. By earlier observations, this shows that
![]() $x\in A$
.
$x\in A$
.
Now, pick
![]() $x\in A$
. Then we can find
$x\in A$
. Then we can find
![]() $\langle u,v\rangle \in S$
and a function
$\langle u,v\rangle \in S$
and a function
![]() ${f}:{T_x}\longrightarrow {\kappa }$
such that for all
${f}:{T_x}\longrightarrow {\kappa }$
such that for all
![]() $p,q\in T_x$
with
$p,q\in T_x$
with
![]() $p\subsetneq q$
and all
$p\subsetneq q$
and all
![]() $m<\omega $
with
$m<\omega $
with
![]() $f(p),f(q)<\kappa _m$
, we have
$f(p),f(q)<\kappa _m$
, we have
![]() ${\prec }{f(q)},{f(p)}{\succ }\in a_{u(m)}$
. Let
${\prec }{f(q)},{f(p)}{\succ }\in a_{u(m)}$
. Let
![]() ${c}:{T_x}\longrightarrow {\omega }$
denote the unique function with
${c}:{T_x}\longrightarrow {\omega }$
denote the unique function with
![]() $c(p)=\min \{{m<\omega }~\vert ~{f(p)<\kappa _m}\}$
. If we then pick
$c(p)=\min \{{m<\omega }~\vert ~{f(p)<\kappa _m}\}$
. If we then pick
![]() $y\in {}^\omega \kappa $
such that the set
$y\in {}^\omega \kappa $
such that the set
![]() $a_{y(m)}$
is equal to the quadruple
$a_{y(m)}$
is equal to the quadruple
for all
![]() $m<\omega $
, then we can conclude that
$m<\omega $
, then we can conclude that
![]() $\langle x,y\rangle \in [U]$
.
$\langle x,y\rangle \in [U]$
.
The above computations allow us to conclude that
![]() $A=p[U]$
, contradicting the fact that A is not a
$A=p[U]$
, contradicting the fact that A is not a
![]() $\mathbf {\Sigma }^1_1$
-subset of
$\mathbf {\Sigma }^1_1$
-subset of
![]() ${}^\omega \kappa $
.
${}^\omega \kappa $
.
We are now ready to prove the main result of this section.
Proof of Theorem 4.1
Assume that there is no inner model with infinitely many measurable cardinals. Then [Reference Koepke31, Theorem 2.14] implies that
![]() $0^{\text {long}}$
(as defined in [Reference Koepke31, Definition 2.13]) does not exist. Let
$0^{\text {long}}$
(as defined in [Reference Koepke31, Definition 2.13]) does not exist. Let
![]() $U_{\text {can}}$
denote the canonical sequence of measures, and let
$U_{\text {can}}$
denote the canonical sequence of measures, and let
![]() ${\mathrm {K}}[U_{\text {can}}]$
denote the canonical core model (as defined in [Reference Koepke31, Definition 3.15]). Then our assumption implies that
${\mathrm {K}}[U_{\text {can}}]$
denote the canonical core model (as defined in [Reference Koepke31, Definition 3.15]). Then our assumption implies that
![]() ${{\mathrm {dom}}(U_{\text {can}})}$
is finite and [Reference Koepke31, Theorem 3.23] shows that there is a generic extension
${{\mathrm {dom}}(U_{\text {can}})}$
is finite and [Reference Koepke31, Theorem 3.23] shows that there is a generic extension
![]() ${\mathrm {K}}[U_{\text {can}},G]$
of
${\mathrm {K}}[U_{\text {can}},G]$
of
![]() ${\mathrm {K}}[U_{\text {can}}]$
by finitely many Prikry forcings with the property that for every ordinal
${\mathrm {K}}[U_{\text {can}}]$
by finitely many Prikry forcings with the property that for every ordinal
![]() $\tau \geq \omega _2$
and every
$\tau \geq \omega _2$
and every
![]() $X\subseteq \tau $
such that
$X\subseteq \tau $
such that
![]() $\vert {X}\vert $
is a regular cardinal smaller than
$\vert {X}\vert $
is a regular cardinal smaller than
![]() $\vert {\tau }\vert $
, there exists
$\vert {\tau }\vert $
, there exists
![]() $Z\in {\mathcal {P}}({\tau })^{{\mathrm {K}}[U_{\text {can}},G]}$
with
$Z\in {\mathcal {P}}({\tau })^{{\mathrm {K}}[U_{\text {can}},G]}$
with
![]() $X\subseteq Z$
and
$X\subseteq Z$
and
![]() $\vert {Z}\vert ^{{\mathrm {K}}[U_{\text {can}},G]}<\tau $
.
$\vert {Z}\vert ^{{\mathrm {K}}[U_{\text {can}},G]}<\tau $
.
Now, let
![]() $\kappa $
be a singular strong limit cardinal of countable cofinality. Then
$\kappa $
be a singular strong limit cardinal of countable cofinality. Then
![]() $\kappa $
is singular in
$\kappa $
is singular in
![]() ${\mathrm {K}}[U_{\text {can}},G]$
and
${\mathrm {K}}[U_{\text {can}},G]$
and
![]() $\kappa ^+=(\kappa ^+)^{{\mathrm {K}}[U_{\text {can}},G]}$
. Moreover, since forcing with a finite iteration of Prikry forcings preserves all cardinals, we also know that
$\kappa ^+=(\kappa ^+)^{{\mathrm {K}}[U_{\text {can}},G]}$
. Moreover, since forcing with a finite iteration of Prikry forcings preserves all cardinals, we also know that
![]() $\kappa ^+=(\kappa ^+)^{{\mathrm {K}}[U_{\text {can}}]}$
. Set
$\kappa ^+=(\kappa ^+)^{{\mathrm {K}}[U_{\text {can}}]}$
. Set
![]() $U={U_{\text {can}}}\restriction {\kappa }$
and
$U={U_{\text {can}}}\restriction {\kappa }$
and
![]() ${\mathrm {K}}={\mathrm {K}}[U]$
(see [Reference Koepke31, Definition 3.1]). Then [Reference Koepke31, Theorem 3.2] shows that
${\mathrm {K}}={\mathrm {K}}[U]$
(see [Reference Koepke31, Definition 3.1]). Then [Reference Koepke31, Theorem 3.2] shows that
![]() ${\mathrm {K}}$
is an inner model of
${\mathrm {K}}$
is an inner model of
![]() ${\mathrm {ZFC}}$
. Moreover, we can use [Reference Koepke31, Theorem 3.9.(iii)] to conclude that
${\mathrm {ZFC}}$
. Moreover, we can use [Reference Koepke31, Theorem 3.9.(iii)] to conclude that
![]() ${\mathcal {P}}({\kappa })^{{\mathrm {K}}[U_{\text {can}}]}\subseteq {\mathrm {K}}$
and therefore we know that
${\mathcal {P}}({\kappa })^{{\mathrm {K}}[U_{\text {can}}]}\subseteq {\mathrm {K}}$
and therefore we know that
![]() $\kappa ^+=(\kappa ^+)^{\mathrm {K}}$
.
$\kappa ^+=(\kappa ^+)^{\mathrm {K}}$
.
Next, let
![]() $<_{\mathrm {K}}$
denote the canonical well-ordering of
$<_{\mathrm {K}}$
denote the canonical well-ordering of
![]() ${\mathrm {K}}$
given by [Reference Koepke31, Theorem 3.4]). For every
${\mathrm {K}}$
given by [Reference Koepke31, Theorem 3.4]). For every
![]() $\kappa \leq \gamma <\kappa ^+$
, let
$\kappa \leq \gamma <\kappa ^+$
, let
![]() ${b_\gamma }:{\kappa }\longrightarrow {\gamma }$
denote the
${b_\gamma }:{\kappa }\longrightarrow {\gamma }$
denote the
![]() $<_{\mathrm {K}}$
-least bijection between
$<_{\mathrm {K}}$
-least bijection between
![]() $\kappa $
and
$\kappa $
and
![]() $\gamma $
, and set
$\gamma $
, and set
![]() $y_\gamma =\{{{\prec }{\alpha },{\beta }{\succ }}~\vert ~{\alpha ,\beta <\kappa , ~ b_\gamma (\alpha )<b_\gamma (\beta )}\}$
. Finally, we define
$y_\gamma =\{{{\prec }{\alpha },{\beta }{\succ }}~\vert ~{\alpha ,\beta <\kappa , ~ b_\gamma (\alpha )<b_\gamma (\beta )}\}$
. Finally, we define
![]() $D=\{{y_\gamma }~\vert ~{\kappa \leq \gamma <\kappa ^+}\}$
. Then D is a subset of
$D=\{{y_\gamma }~\vert ~{\kappa \leq \gamma <\kappa ^+}\}$
. Then D is a subset of
![]() $\mathcal {W}\mathcal {O}_\kappa $
of cardinality
$\mathcal {W}\mathcal {O}_\kappa $
of cardinality
![]() $\kappa ^+$
.
$\kappa ^+$
.
Claim. The set D is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
Proof of the claim
First, note that our assumption implies that U is an element of
![]() ${\mathrm {H}}(\kappa )^{\mathrm {K}}$
. By arguing as in the proof of [Reference Lücke and Schlicht38, Lemma 2.3], we can combine [Reference Koepke31, Theorem 2.7] with [Reference Koepke31, Theorem 2.10] to conclude that the collection of all initial segments of the restriction of
${\mathrm {H}}(\kappa )^{\mathrm {K}}$
. By arguing as in the proof of [Reference Lücke and Schlicht38, Lemma 2.3], we can combine [Reference Koepke31, Theorem 2.7] with [Reference Koepke31, Theorem 2.10] to conclude that the collection of all initial segments of the restriction of
![]() $<_{\mathrm {K}}$
to
$<_{\mathrm {K}}$
to
![]() ${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
is definable by a
${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\kappa $
and U. This conclusion directly implies the statement of the claim.
$\kappa $
and U. This conclusion directly implies the statement of the claim.
In the following, assume, towards a contradiction, that there is a continuous injection
![]() ${\iota }:{{}^\omega \kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
${\iota }:{{}^\omega \kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
![]() ${{\mathrm {ran}}(\iota )}\subseteq D$
. Fix a strictly increasing sequence
${{\mathrm {ran}}(\iota )}\subseteq D$
. Fix a strictly increasing sequence
![]() $\vec {\kappa }=\langle {\kappa _m}~\vert ~{m<\omega }\rangle $
of cardinals that is cofinal in
$\vec {\kappa }=\langle {\kappa _m}~\vert ~{m<\omega }\rangle $
of cardinals that is cofinal in
![]() $\kappa $
and an enumeration
$\kappa $
and an enumeration
![]() $\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\kappa }\rangle $
of
$\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\kappa }\rangle $
of
![]() ${\mathrm {H}}(\kappa )$
. Define T to be the set of all pairs
${\mathrm {H}}(\kappa )$
. Define T to be the set of all pairs
![]() $\langle s,t\rangle $
in
$\langle s,t\rangle $
in
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
such that
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
such that
![]() ${\mathrm {lh}}({s})={\mathrm {lh}}({t})$
, and the following statements hold for all
${\mathrm {lh}}({s})={\mathrm {lh}}({t})$
, and the following statements hold for all
![]() $l\leq m<{\mathrm {lh}}({s})$
:
$l\leq m<{\mathrm {lh}}({s})$
:
-
○
 $a_{s(m)}\subseteq \kappa _m$
and
$a_{s(m)}\subseteq \kappa _m$
and
 $a_{s(l)}=a_{s(m)}\cap \kappa _l$
.
$a_{s(l)}=a_{s(m)}\cap \kappa _l$
. -
○
 $a_{t(l)},a_{t(m)}\in {}^{{<}\omega }\kappa $
with
$a_{t(l)},a_{t(m)}\in {}^{{<}\omega }\kappa $
with
 $l\leq {\mathrm {lh}}({a_{t(l)}})\leq {\mathrm {lh}}({a_{t(m)}})$
,
$l\leq {\mathrm {lh}}({a_{t(l)}})\leq {\mathrm {lh}}({a_{t(m)}})$
,
 $a_{t(l)}=a_{t(m)}\restriction {\mathrm {lh}}({a_{t(l)}})$
and
$a_{t(l)}=a_{t(m)}\restriction {\mathrm {lh}}({a_{t(l)}})$
and
 $\iota (u)\cap \kappa _m=a_{s(m)}$
for all
$\iota (u)\cap \kappa _m=a_{s(m)}$
for all
 $u\in {}^\omega \kappa $
with
$u\in {}^\omega \kappa $
with
 $a_{t(m)}\subseteq u$
.
$a_{t(m)}\subseteq u$
.
This definition directly ensures that T is a subtree of
![]() ${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
. Pick
${}^{{<}\omega }\kappa \times {}^{{<}\omega }\kappa $
. Pick
![]() $\langle x,y\rangle \in [T]$
. Set
$\langle x,y\rangle \in [T]$
. Set
![]() $u=\bigcup \{{a_{y(m)}}~\vert ~{m<\omega }\}\in {}^\omega \kappa $
and
$u=\bigcup \{{a_{y(m)}}~\vert ~{m<\omega }\}\in {}^\omega \kappa $
and
![]() $v=\bigcup \{{a_{x(m)}}~\vert ~{m<\omega }\}\subseteq \kappa $
. By the definition of T, we then have
$v=\bigcup \{{a_{x(m)}}~\vert ~{m<\omega }\}\subseteq \kappa $
. By the definition of T, we then have
![]() $\iota (u)=v\in D\subseteq \mathcal {W}\mathcal {O}_\kappa $
and this shows that x is an element of
$\iota (u)=v\in D\subseteq \mathcal {W}\mathcal {O}_\kappa $
and this shows that x is an element of
![]() $\mathsf {WO}(\vec {\kappa },\vec {a})$
. This shows that
$\mathsf {WO}(\vec {\kappa },\vec {a})$
. This shows that
![]() $p[T]\subseteq \mathsf {WO}(\vec {\kappa },\vec {a})$
, and therefore Lemma 4.5 yields an ordinal
$p[T]\subseteq \mathsf {WO}(\vec {\kappa },\vec {a})$
, and therefore Lemma 4.5 yields an ordinal
![]() $\gamma <\kappa ^+$
with
$\gamma <\kappa ^+$
with
![]() $\|x\|_{\vec {a}} < \gamma $
for all
$\|x\|_{\vec {a}} < \gamma $
for all
![]() $x\in p[T]$
.
$x\in p[T]$
.
Since, for every ordinal
![]() $\kappa \leq \delta <\kappa ^+$
, there is a unique element y of D with
$\kappa \leq \delta <\kappa ^+$
, there is a unique element y of D with
![]() ${{\mathrm {otp}}\left (\kappa ,\lhd _y\right )}=\delta $
, we know that the map
${{\mathrm {otp}}\left (\kappa ,\lhd _y\right )}=\delta $
, we know that the map
is an injection and we can find
![]() $u\in {}^\omega \kappa $
with
$u\in {}^\omega \kappa $
with
![]() ${{\mathrm {otp}}\left (\kappa ,\lhd _{\iota (u)}\right )}>\gamma $
. Pick
${{\mathrm {otp}}\left (\kappa ,\lhd _{\iota (u)}\right )}>\gamma $
. Pick
![]() $x\in {}^\omega \kappa $
with
$x\in {}^\omega \kappa $
with
![]() $a_{x(m)}=\iota (u)\cap \kappa _m$
for all
$a_{x(m)}=\iota (u)\cap \kappa _m$
for all
![]() $m<\omega $
. In addition, pick
$m<\omega $
. In addition, pick
![]() $y\in {}^\omega \kappa $
with the property that for all
$y\in {}^\omega \kappa $
with the property that for all
![]() $l\leq m<\omega $
, we have
$l\leq m<\omega $
, we have
![]() $a_{y(l)},a_{y(m)}\in {}^{{<}\omega }\kappa $
,
$a_{y(l)},a_{y(m)}\in {}^{{<}\omega }\kappa $
,
![]() $l\leq {\mathrm {lh}}({a_{y(l)}})\leq {\mathrm {lh}}({a_{y(m)}})$
,
$l\leq {\mathrm {lh}}({a_{y(l)}})\leq {\mathrm {lh}}({a_{y(m)}})$
,
![]() $a_{y(l)}\subseteq a_{y(m)}=u\restriction {\mathrm {lh}}({a_{y(m)}})$
and
$a_{y(l)}\subseteq a_{y(m)}=u\restriction {\mathrm {lh}}({a_{y(m)}})$
and
![]() $\iota (w)\cap \kappa _m=\iota (u)\cap \kappa _m$
for all
$\iota (w)\cap \kappa _m=\iota (u)\cap \kappa _m$
for all
![]() $w\in {}^\omega \kappa $
with
$w\in {}^\omega \kappa $
with
![]() $u\restriction {\mathrm {lh}}({a_{y(m)}})\subseteq w$
. Note that this is possible as
$u\restriction {\mathrm {lh}}({a_{y(m)}})\subseteq w$
. Note that this is possible as
![]() $\iota $
is a continuous injection. Then
$\iota $
is a continuous injection. Then
![]() $\langle x,y\rangle \in [T]$
and
$\langle x,y\rangle \in [T]$
and
![]() $x\in p[T]\subseteq \mathsf {WO}(\vec {\kappa },\vec {a})$
with
$x\in p[T]\subseteq \mathsf {WO}(\vec {\kappa },\vec {a})$
with
![]() $\|x\|_{\vec {a}}={{\mathrm {otp}}\left (\kappa ,\lhd _{\iota (u)}\right )}>\gamma $
, a contradiction.
$\|x\|_{\vec {a}}={{\mathrm {otp}}\left (\kappa ,\lhd _{\iota (u)}\right )}>\gamma $
, a contradiction.
We close this section by using ideas from the above proof to show that the assumptions of Theorem 3.1 are optimal. These arguments make use of the following observation that can be seen as a special case of the generic absoluteness of the core model as, for example, in [Reference Schimmerling43, Theorem 3.4], [Reference Jensen and Steel26] or [Reference Steel47].
Lemma 4.6. Assume that
![]() $0^{\text {long}}$
does not exist. If
$0^{\text {long}}$
does not exist. If
![]() ${\mathrm {V}}[G]$
is a generic extension of the ground model
${\mathrm {V}}[G]$
is a generic extension of the ground model
![]() ${\mathrm {V}}$
, then
${\mathrm {V}}$
, then
![]() ${\mathrm {K}}[U_{can}]^{\mathrm {V}}={\mathrm {K}}[U_{can}]^{{\mathrm {V}}[G]}$
.
${\mathrm {K}}[U_{can}]^{\mathrm {V}}={\mathrm {K}}[U_{can}]^{{\mathrm {V}}[G]}$
.
Proof. The statement of the lemma will be a direct consequence of the following two claims:
Claim. If
![]() ${\mathrm {V}}[G]$
is a generic extension of the ground model
${\mathrm {V}}[G]$
is a generic extension of the ground model
![]() ${\mathrm {V}}$
, then
${\mathrm {V}}$
, then
![]() ${\mathrm {K}}[U_{can}]^{\mathrm {V}}={\mathrm {K}}[U_{can}^{\mathrm {V}}]^{{\mathrm {V}}[G]}$
.
${\mathrm {K}}[U_{can}]^{\mathrm {V}}={\mathrm {K}}[U_{can}^{\mathrm {V}}]^{{\mathrm {V}}[G]}$
.
Proof of the claim
Since the property of being a U-mouse is upwards absolute between transitive models of
![]() ${\mathrm {ZFC}}$
with the same ordinals, we know that
${\mathrm {ZFC}}$
with the same ordinals, we know that
![]() ${\mathrm {K}}[U_{can}]^{\mathrm {V}}\subseteq {\mathrm {K}}[U_{can}^{\mathrm {V}}]^{{\mathrm {V}}[G]}$
. Next, observe that the fact that
${\mathrm {K}}[U_{can}]^{\mathrm {V}}\subseteq {\mathrm {K}}[U_{can}^{\mathrm {V}}]^{{\mathrm {V}}[G]}$
. Next, observe that the fact that
![]() ${\mathrm {V}}[G]$
is a set forcing extension of
${\mathrm {V}}[G]$
is a set forcing extension of
![]() ${\mathrm {V}}$
implies that all sufficiently large singular cardinals in
${\mathrm {V}}$
implies that all sufficiently large singular cardinals in
![]() ${\mathrm {V}}[G]$
are singular in
${\mathrm {V}}[G]$
are singular in
![]() ${\mathrm {V}}$
. Moreover, an application of [Reference Koepke31, Theorem 3.23] shows that all sufficiently large singular cardinals in
${\mathrm {V}}$
. Moreover, an application of [Reference Koepke31, Theorem 3.23] shows that all sufficiently large singular cardinals in
![]() ${\mathrm {V}}$
are singular in
${\mathrm {V}}$
are singular in
![]() ${\mathrm {K}}[U_{can}]^{\mathrm {V}}$
. In combination, this shows that for all sufficiently large singular cardinals
${\mathrm {K}}[U_{can}]^{\mathrm {V}}$
. In combination, this shows that for all sufficiently large singular cardinals
![]() $\lambda $
of uncountable cofinality in
$\lambda $
of uncountable cofinality in
![]() ${\mathrm {V}}[G]$
, every closed unbounded subset of
${\mathrm {V}}[G]$
, every closed unbounded subset of
![]() $\lambda $
in
$\lambda $
in
![]() ${\mathrm {V}}[G]$
contains an element that is singular in
${\mathrm {V}}[G]$
contains an element that is singular in
![]() ${\mathrm {K}}[U_{can}]^{\mathrm {V}}$
. This observation allows us to use [Reference Koepke31, Theorem 3.24(ii)] to conclude that
${\mathrm {K}}[U_{can}]^{\mathrm {V}}$
. This observation allows us to use [Reference Koepke31, Theorem 3.24(ii)] to conclude that
![]() ${\mathrm {K}}[U_{can}^{\mathrm {V}}]^{{\mathrm {V}}[G]}\subseteq {\mathrm {K}}[U_{can}]^{\mathrm {V}}$
.
${\mathrm {K}}[U_{can}^{\mathrm {V}}]^{{\mathrm {V}}[G]}\subseteq {\mathrm {K}}[U_{can}]^{\mathrm {V}}$
.
Claim. Let
![]() ${\mathbb {P}}$
be a weakly homogeneous partial order. If G is
${\mathbb {P}}$
be a weakly homogeneous partial order. If G is
![]() ${\mathbb {P}}$
-generic over
${\mathbb {P}}$
-generic over
![]() ${\mathrm {V}}$
, then
${\mathrm {V}}$
, then
![]() ${\mathrm {K}}[U_{can}]^{\mathrm {V}}={\mathrm {K}}[U_{can}]^{{\mathrm {V}}[G]}$
.
${\mathrm {K}}[U_{can}]^{\mathrm {V}}={\mathrm {K}}[U_{can}]^{{\mathrm {V}}[G]}$
.
Proof of the claim
First, the weak homogeneity of
![]() ${\mathbb {P}}$
in
${\mathbb {P}}$
in
![]() ${\mathrm {V}}$
ensures that
${\mathrm {V}}$
ensures that
In particular, we know that the set
![]() $U_{can}^{{\mathrm {V}}[G]}(\kappa )\cap {\mathcal {P}}({\kappa })^{\mathrm {V}}$
is an element of
$U_{can}^{{\mathrm {V}}[G]}(\kappa )\cap {\mathcal {P}}({\kappa })^{\mathrm {V}}$
is an element of
![]() ${\mathrm {V}}$
for every
${\mathrm {V}}$
for every
![]() $\kappa \in {{\mathrm {dom}}(U_{can}^{{\mathrm {V}}[G]})}$
. In this situation, we can now use the first claim to inductively show that the definition of the canonical measure sequence ensures that
$\kappa \in {{\mathrm {dom}}(U_{can}^{{\mathrm {V}}[G]})}$
. In this situation, we can now use the first claim to inductively show that the definition of the canonical measure sequence ensures that
![]() $U_{\text {can}}^{\mathrm {V}}\restriction \xi =U_{can}^{{\mathrm {V}}[G]}\restriction \xi $
holds for all
$U_{\text {can}}^{\mathrm {V}}\restriction \xi =U_{can}^{{\mathrm {V}}[G]}\restriction \xi $
holds for all
![]() $\xi \in {\mathrm {On}}$
.
$\xi \in {\mathrm {On}}$
.
Now, let
![]() ${\mathbb {P}}$
be a partial order, and let G be
${\mathbb {P}}$
be a partial order, and let G be
![]() ${\mathbb {P}}$
-generic over
${\mathbb {P}}$
-generic over
![]() ${\mathrm {V}}$
. Pick a sufficiently large cardinal
${\mathrm {V}}$
. Pick a sufficiently large cardinal
![]() $\delta $
such that
$\delta $
such that
![]() ${\mathbb {P}}\times {\mathrm {Col}}({\omega },{\delta })$
densely embeds into
${\mathbb {P}}\times {\mathrm {Col}}({\omega },{\delta })$
densely embeds into
![]() ${\mathrm {Col}}({\omega },{\delta })$
, and let H be
${\mathrm {Col}}({\omega },{\delta })$
, and let H be
![]() ${\mathrm {Col}}({\omega },{\delta })$
-generic over
${\mathrm {Col}}({\omega },{\delta })$
-generic over
![]() ${\mathrm {V}}[G]$
. Since
${\mathrm {V}}[G]$
. Since
![]() ${\mathrm {Col}}({\omega },{\delta })$
is weakly homogeneous in both
${\mathrm {Col}}({\omega },{\delta })$
is weakly homogeneous in both
![]() ${\mathrm {V}}$
and
${\mathrm {V}}$
and
![]() ${\mathrm {V}}[G]$
, we can now use the above claim twice to conclude that
${\mathrm {V}}[G]$
, we can now use the above claim twice to conclude that
![]() ${\mathrm {K}}[U_{can}]^{\mathrm {V}}={\mathrm {K}}[U_{can}]^{{\mathrm {V}}[G,H]}={\mathrm {K}}[U_{can}]^{{\mathrm {V}}[G]}$
.
${\mathrm {K}}[U_{can}]^{\mathrm {V}}={\mathrm {K}}[U_{can}]^{{\mathrm {V}}[G,H]}={\mathrm {K}}[U_{can}]^{{\mathrm {V}}[G]}$
.
Proof of Proposition 3.2
Let M denote the class term with the property that
![]() ${\mathrm {ZFC}}$
proves the following statements:
${\mathrm {ZFC}}$
proves the following statements:
-
○ If either
 $0^{\text {long}}$
exists or
$0^{\text {long}}$
exists or
 $0^{\text {long}}$
does not exist and the model
$0^{\text {long}}$
does not exist and the model
 ${\mathrm {K}}[U_{can}]$
contains infinitely many measurable cardinals, then M is equal to the constructible universe
${\mathrm {K}}[U_{can}]$
contains infinitely many measurable cardinals, then M is equal to the constructible universe
 ${\mathrm {L}}$
.
${\mathrm {L}}$
. -
○ Otherwise, M is equal to
 ${\mathrm {K}}[U_{can}]$
.
${\mathrm {K}}[U_{can}]$
.
Then the standard results about
![]() ${\mathrm {L}}$
together with [Reference Koepke31, Theorem 3.2] show that
${\mathrm {L}}$
together with [Reference Koepke31, Theorem 3.2] show that
![]() ${\mathrm {ZFC}}$
proves that M is a transitive model of
${\mathrm {ZFC}}$
proves that M is a transitive model of
![]() ${\mathrm {ZFC}}+{{\mathrm {V}}=M}$
that contains all ordinals. Moreover, Lemma 4.6 together with the fact that
${\mathrm {ZFC}}+{{\mathrm {V}}=M}$
that contains all ordinals. Moreover, Lemma 4.6 together with the fact that
![]() $0^{\text {long}}$
cannot be added by forcing show that M is forcing invariant.
$0^{\text {long}}$
cannot be added by forcing show that M is forcing invariant.
Claim. Assume that
![]() $0^{\text {long}}$
does not exist and
$0^{\text {long}}$
does not exist and
![]() ${\mathrm {K}}[U_{can}]$
contains only finitely many measurable cardinals. If
${\mathrm {K}}[U_{can}]$
contains only finitely many measurable cardinals. If
![]() $\kappa $
is an uncountable cardinal, then
$\kappa $
is an uncountable cardinal, then
![]() ${\mathrm {H}}(\kappa ^+)^{{\mathrm {K}}[U_{can}]}$
is definable by a
${\mathrm {H}}(\kappa ^+)^{{\mathrm {K}}[U_{can}]}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
Proof of the claim
Set
![]() $U=U_{can}\restriction \kappa $
and
$U=U_{can}\restriction \kappa $
and
![]() ${\mathrm {K}}={\mathrm {K}}[U]$
. Then [Reference Koepke31, Theorem 3.9] shows that
${\mathrm {K}}={\mathrm {K}}[U]$
. Then [Reference Koepke31, Theorem 3.9] shows that
![]() ${\mathrm {H}}(\kappa ^+)^{{\mathrm {K}}[U_{can}]}={\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
. Moreover, if
${\mathrm {H}}(\kappa ^+)^{{\mathrm {K}}[U_{can}]}={\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
. Moreover, if
![]() $\kappa $
is not the successor of an element of
$\kappa $
is not the successor of an element of
![]() ${{\mathrm {dom}}(U)}$
in
${{\mathrm {dom}}(U)}$
in
![]() ${\mathrm {K}}$
, then U is an element of
${\mathrm {K}}$
, then U is an element of
![]() ${\mathrm {H}}(\kappa )$
and we can repeat arguments from the proof of Theorem 4.1 to show that the class of all U-mice M (see [Reference Koepke31, Definition 2.9]) that contain
${\mathrm {H}}(\kappa )$
and we can repeat arguments from the proof of Theorem 4.1 to show that the class of all U-mice M (see [Reference Koepke31, Definition 2.9]) that contain
![]() $\kappa $
in their lower part
$\kappa $
in their lower part
![]() $lp(M)$
(see [Reference Koepke31, Definition 2.1]) is definable by a
$lp(M)$
(see [Reference Koepke31, Definition 2.1]) is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\kappa $
and U. Since every element of
$\kappa $
and U. Since every element of
![]() ${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
is contained in such a lower part, the statement of the claim follows in this case.
${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
is contained in such a lower part, the statement of the claim follows in this case.
In the following, assume that there is
![]() $\delta \in {{\mathrm {dom}}(U)}$
with
$\delta \in {{\mathrm {dom}}(U)}$
with
![]() $\kappa =(\delta ^+)^{\mathrm {K}}$
. Let F be a simple predicate with
$\kappa =(\delta ^+)^{\mathrm {K}}$
. Let F be a simple predicate with
![]() ${{\mathrm {dom}}(F)}={{\mathrm {dom}}(U)}$
, and let M be an F-mouse such that
${{\mathrm {dom}}(F)}={{\mathrm {dom}}(U)}$
, and let M be an F-mouse such that
![]() $\kappa ,F\in lp(M)$
,
$\kappa ,F\in lp(M)$
,
![]() $\kappa =(\delta ^+)^M$
and
$\kappa =(\delta ^+)^M$
and
![]() $F(\mu )$
is an ultrafilter in M for every
$F(\mu )$
is an ultrafilter in M for every
![]() $\mu \in {{\mathrm {dom}}(F)}$
. Since every subset of
$\mu \in {{\mathrm {dom}}(F)}$
. Since every subset of
![]() $\delta $
in
$\delta $
in
![]() ${\mathrm {K}}[F]$
is contained in an F-mouse of cardinality less than
${\mathrm {K}}[F]$
is contained in an F-mouse of cardinality less than
![]() $\kappa $
, we can now apply [Reference Koepke31, Theorem 2.10] to conclude that
$\kappa $
, we can now apply [Reference Koepke31, Theorem 2.10] to conclude that
![]() $F(\mu )$
is an ultrafilter in
$F(\mu )$
is an ultrafilter in
![]() ${\mathrm {K}}[F]$
for every
${\mathrm {K}}[F]$
for every
![]() $\mu \in {{\mathrm {dom}}(F)}$
. This shows that
$\mu \in {{\mathrm {dom}}(F)}$
. This shows that
![]() ${\mathrm {K}}[F]$
is a core model (in the sense of [Reference Koepke31, Definition 3.6]) and therefore [Reference Koepke31, Theorem 3.14] shows that
${\mathrm {K}}[F]$
is a core model (in the sense of [Reference Koepke31, Definition 3.6]) and therefore [Reference Koepke31, Theorem 3.14] shows that
![]() ${\mathrm {K}}={\mathrm {K}}[F]$
holds. Since every element of
${\mathrm {K}}={\mathrm {K}}[F]$
holds. Since every element of
![]() ${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
is contained in the lower part of a U-mouse M with
${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
is contained in the lower part of a U-mouse M with
![]() $\kappa ,U\in lp(M)$
and
$\kappa ,U\in lp(M)$
and
![]() $\kappa =(\delta ^+)^M$
, we now know that
$\kappa =(\delta ^+)^M$
, we now know that
![]() ${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
consists of all sets x with the property that there exists a simple predicate F and an F-mouse M such that
${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
consists of all sets x with the property that there exists a simple predicate F and an F-mouse M such that
![]() ${{\mathrm {dom}}(F)}={{\mathrm {dom}}(U)}$
,
${{\mathrm {dom}}(F)}={{\mathrm {dom}}(U)}$
,
![]() $F(\mu )$
is an ultrafilter in M for every
$F(\mu )$
is an ultrafilter in M for every
![]() $\mu \in {{\mathrm {dom}}(F)}$
,
$\mu \in {{\mathrm {dom}}(F)}$
,
![]() $\kappa =(\delta ^+)^M$
and
$\kappa =(\delta ^+)^M$
and
![]() $\kappa ,F,x\in lp(M)$
. This allows us to conclude that the set
$\kappa ,F,x\in lp(M)$
. This allows us to conclude that the set
![]() ${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
is definable by a
${\mathrm {H}}(\kappa ^+)^{\mathrm {K}}$
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\delta $
,
$\delta $
,
![]() $\kappa $
and
$\kappa $
and
![]() ${{\mathrm {dom}}(U)}$
in this case.
${{\mathrm {dom}}(U)}$
in this case.
The above claim now allows us to find a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
with the property that for every uncountable cardinal
$\varphi (v_0,v_1,v_2)$
with the property that for every uncountable cardinal
![]() $\kappa $
, we have
$\kappa $
, we have
![]() ${\mathrm {L}}_{\kappa ^+}=\{{x}~\vert ~{\varphi (\kappa ,\kappa ,x)}\}$
and, if
${\mathrm {L}}_{\kappa ^+}=\{{x}~\vert ~{\varphi (\kappa ,\kappa ,x)}\}$
and, if
![]() $0^{\text {long}}$
does not exist and
$0^{\text {long}}$
does not exist and
![]() ${\mathrm {K}}[U_{can}]$
contains only finitely many measurable cardinals, then there exists
${\mathrm {K}}[U_{can}]$
contains only finitely many measurable cardinals, then there exists
![]() $z\in {\mathrm {H}}(\kappa )$
with
$z\in {\mathrm {H}}(\kappa )$
with
![]() ${\mathrm {H}}(\kappa ^+)^{{\mathrm {K}}[U_{can}]}=\{{x}~\vert ~{\varphi (\kappa ,x,z)}\}$
. Finally, if the existence of n measurable cardinals is consistent with the axioms of
${\mathrm {H}}(\kappa ^+)^{{\mathrm {K}}[U_{can}]}=\{{x}~\vert ~{\varphi (\kappa ,x,z)}\}$
. Finally, if the existence of n measurable cardinals is consistent with the axioms of
![]() ${\mathrm {ZFC}}$
for some natural number n, then the existence of exactly n measurable cardinals in
${\mathrm {ZFC}}$
for some natural number n, then the existence of exactly n measurable cardinals in
![]() ${\mathrm {K}}[U_{can}]$
is consistent with
${\mathrm {K}}[U_{can}]$
is consistent with
![]() ${\mathrm {ZFC}}$
.
${\mathrm {ZFC}}$
.
5 The lower bound for singular cardinals of uncountable cofinality
We now use ideas from [Reference Hayut and Müller21] to complete the proof of Theorem 1.2.
Proof of Theorem 1.2
Let
![]() $\kappa $
be a singular strong limit cardinal with the property that for every subset D of
$\kappa $
be a singular strong limit cardinal with the property that for every subset D of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, there exists a perfect embedding
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, there exists a perfect embedding
![]() ${\iota }:{{}^{{{\mathrm {cof}}(\kappa )}}\kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
${\iota }:{{}^{{{\mathrm {cof}}(\kappa )}}\kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
![]() ${{\mathrm {ran}}(\iota )}\subseteq D$
. Assume, towards a contradiction, that there is no inner model with a sequence of measurable cardinals of length
${{\mathrm {ran}}(\iota )}\subseteq D$
. Assume, towards a contradiction, that there is no inner model with a sequence of measurable cardinals of length
![]() ${{\mathrm {cof}}(\kappa )}$
. Then Theorem 4.1 implies that the cofinality of
${{\mathrm {cof}}(\kappa )}$
. Then Theorem 4.1 implies that the cofinality of
![]() $\kappa $
is uncountable. Moreover, we know that there is no inner model with a measurable cardinal of Mitchell order
$\kappa $
is uncountable. Moreover, we know that there is no inner model with a measurable cardinal of Mitchell order
![]() $1$
and therefore we can construct the canonical core model
$1$
and therefore we can construct the canonical core model
![]() ${\mathrm {K}}$
as in [Reference Zeman53] (which is Steel’s core model [Reference Steel47] in this easier setting). Note that our hypothesis implies that, in
${\mathrm {K}}$
as in [Reference Zeman53] (which is Steel’s core model [Reference Steel47] in this easier setting). Note that our hypothesis implies that, in
![]() ${\mathrm {K}}$
, the sequence of measurable cardinals below
${\mathrm {K}}$
, the sequence of measurable cardinals below
![]() $\kappa $
is bounded below
$\kappa $
is bounded below
![]() $\kappa $
. In addition, as
$\kappa $
. In addition, as
![]() $\kappa $
is singular in
$\kappa $
is singular in
![]() ${\mathrm {V}}$
, weak covering (see [Reference Zeman53, Theorem 7.5.1]) holds for
${\mathrm {V}}$
, weak covering (see [Reference Zeman53, Theorem 7.5.1]) holds for
![]() ${\mathrm {K}}$
at
${\mathrm {K}}$
at
![]() $\kappa $
, that is, we have
$\kappa $
, that is, we have
![]() $ (\kappa ^+)^{\mathrm {K}} = \kappa ^+$
. Finally, we know that
$ (\kappa ^+)^{\mathrm {K}} = \kappa ^+$
. Finally, we know that
![]() $\kappa $
is singular in
$\kappa $
is singular in
![]() ${\mathrm {K}}$
, because otherwise the fact that
${\mathrm {K}}$
, because otherwise the fact that
![]() $\kappa $
is a singular cardinal of uncountable cofinality would allow us to apply the second part of [Reference Cox10, Theorem 1] to find an inner model in which
$\kappa $
is a singular cardinal of uncountable cofinality would allow us to apply the second part of [Reference Cox10, Theorem 1] to find an inner model in which
![]() $\kappa $
has Mitchell order greater than
$\kappa $
has Mitchell order greater than
![]() $0$
.
$0$
.
We will now construct a tree of height
![]() ${{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
that is an element of
${{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
that is an element of
![]() ${\mathrm {K}}$
and then argue that this tree does not have a perfect subtree in
${\mathrm {K}}$
and then argue that this tree does not have a perfect subtree in
![]() ${\mathrm {V}}$
. These arguments use ideas from [Reference Hayut and Müller21] that ultimately go back to Solovay’s argument for the consistency strength of the Kurepa hypothesis (see [Reference Jech24, Section 4]). Our tree consists of hulls of initial segments of
${\mathrm {V}}$
. These arguments use ideas from [Reference Hayut and Müller21] that ultimately go back to Solovay’s argument for the consistency strength of the Kurepa hypothesis (see [Reference Jech24, Section 4]). Our tree consists of hulls of initial segments of
![]() ${\mathrm {K}}$
of size
${\mathrm {K}}$
of size
![]() $\kappa $
, and we will argue that we can obtain such initial segments in a
$\kappa $
, and we will argue that we can obtain such initial segments in a
![]() $\Sigma _1$
-definable way with parameters in
$\Sigma _1$
-definable way with parameters in
![]() ${\mathrm {H}}(\kappa ) \cup \{ \kappa \}$
.
${\mathrm {H}}(\kappa ) \cup \{ \kappa \}$
.
In the following, we say a premouse N (in the sense of [Reference Zeman53, Section 4.1]) is good if the following statements hold:
-
○ N is iterable (in the sense of [Reference Zeman53, Section 4.2]).
-
○
 $\kappa +1 \subseteq N$
and
$\kappa +1 \subseteq N$
and
 $\vert {N}\vert = \kappa $
.
$\vert {N}\vert = \kappa $
. -
○
 ${{\mathrm {cof}}(\kappa )}^N={{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
.
${{\mathrm {cof}}(\kappa )}^N={{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
. -
○
 $\kappa $
is the largest cardinal in N.
$\kappa $
is the largest cardinal in N. -
○ If
 $\gamma < \kappa $
is the supremum of the measurable cardinals below
$\gamma < \kappa $
is the supremum of the measurable cardinals below
 $\kappa $
in
$\kappa $
in
 ${\mathrm {K}}$
, then In particular, K and N have the same measurable cardinals and the same total measures below
${\mathrm {K}}$
, then In particular, K and N have the same measurable cardinals and the same total measures below $$\begin{align*}N \vert \gamma^{++} ~ = ~ {\mathrm{K}} \vert \gamma^{++}. \end{align*}$$
$$\begin{align*}N \vert \gamma^{++} ~ = ~ {\mathrm{K}} \vert \gamma^{++}. \end{align*}$$
 $\kappa $
.
$\kappa $
.
Claim. Let N be a good premouse. Then
![]() $N \lhd {\mathrm {K}}$
.
$N \lhd {\mathrm {K}}$
.
Proof of the Claim
Compare N and
![]() ${\mathrm {K}}$
, and suppose, towards a contradiction, that the comparison is not trivial. Consider the first measure that is used. As
${\mathrm {K}}$
, and suppose, towards a contradiction, that the comparison is not trivial. Consider the first measure that is used. As
![]() $N \vert \gamma ^{++} = {\mathrm {K}} \vert \gamma ^{++},$
where
$N \vert \gamma ^{++} = {\mathrm {K}} \vert \gamma ^{++},$
where
![]() $\gamma < \kappa $
is the supremum of the measurable cardinals below
$\gamma < \kappa $
is the supremum of the measurable cardinals below
![]() $\kappa $
in N and
$\kappa $
in N and
![]() ${\mathrm {K}}$
, the first measure that is used in the comparison has to be a partial measure above
${\mathrm {K}}$
, the first measure that is used in the comparison has to be a partial measure above
![]() $\gamma $
. Say this is a partial measure
$\gamma $
. Say this is a partial measure
![]() $\mu $
with critical point
$\mu $
with critical point
![]() $\nu $
on the
$\nu $
on the
![]() ${\mathrm {K}}$
-side of the comparison. Then, in order to use this partial measure, we need to truncate
${\mathrm {K}}$
-side of the comparison. Then, in order to use this partial measure, we need to truncate
![]() ${\mathrm {K}}$
as
${\mathrm {K}}$
as
![]() $\mu $
does not measure all subsets of
$\mu $
does not measure all subsets of
![]() $\nu $
in
$\nu $
in
![]() ${\mathrm {K}}$
. By the comparison lemma (see, for example, [Reference Zeman53, Lemma 4.4.2] or [Reference Steel48, Theorem 3.11]), we obtain iterates
${\mathrm {K}}$
. By the comparison lemma (see, for example, [Reference Zeman53, Lemma 4.4.2] or [Reference Steel48, Theorem 3.11]), we obtain iterates
![]() $N^*$
of N and
$N^*$
of N and
![]() ${\mathrm {K}}^*$
of
${\mathrm {K}}^*$
of
![]() ${\mathrm {K}}$
(or, in fact, of a truncation
${\mathrm {K}}$
(or, in fact, of a truncation
![]() ${\mathrm {K}}\vert \xi $
of
${\mathrm {K}}\vert \xi $
of
![]() ${\mathrm {K}}$
) such that
${\mathrm {K}}$
) such that
![]() $N^* \unlhd {{\mathrm {K}}^*}$
. Note that truncations can only appear on one side of the comparison, and this side has to come out longer in the end. In particular, the iteration from N to
$N^* \unlhd {{\mathrm {K}}^*}$
. Note that truncations can only appear on one side of the comparison, and this side has to come out longer in the end. In particular, the iteration from N to
![]() $N^*$
can only use total measures with critical point above
$N^*$
can only use total measures with critical point above
![]() $\nu> \gamma $
and is therefore trivial, that is, we have
$\nu> \gamma $
and is therefore trivial, that is, we have
![]() $N = N^*$
.
$N = N^*$
.
Suppose that
![]() $\nu> \kappa $
. Note that
$\nu> \kappa $
. Note that
![]() $\nu $
is a cardinal in
$\nu $
is a cardinal in
![]() ${\mathrm {K}}^*$
. As
${\mathrm {K}}^*$
. As
![]() $\nu < N \cap {\mathrm {On}}$
and
$\nu < N \cap {\mathrm {On}}$
and
![]() $N \unlhd {\mathrm {K}}^*$
, this implies that there are cardinals above
$N \unlhd {\mathrm {K}}^*$
, this implies that there are cardinals above
![]() $\kappa $
in N, contradicting the assumption that
$\kappa $
in N, contradicting the assumption that
![]() $\kappa $
is the largest cardinal in N.
$\kappa $
is the largest cardinal in N.
Now, suppose that
![]() $\nu < \kappa $
. The iteration from
$\nu < \kappa $
. The iteration from
![]() ${\mathrm {K}}|\xi $
to
${\mathrm {K}}|\xi $
to
![]() ${\mathrm {K}}^*$
cannot leave any total measures below
${\mathrm {K}}^*$
cannot leave any total measures below
![]() $\kappa $
behind as
$\kappa $
behind as
![]() $N \unlhd {\mathrm {K}}^*$
does not have any total measures between
$N \unlhd {\mathrm {K}}^*$
does not have any total measures between
![]() $\gamma $
and
$\gamma $
and
![]() $\kappa $
. As we suppose that there is no inner model with a sequence of measurable cardinals of length
$\kappa $
. As we suppose that there is no inner model with a sequence of measurable cardinals of length
![]() ${{\mathrm {cof}}(\kappa )}$
, this implies that the iteration from
${{\mathrm {cof}}(\kappa )}$
, this implies that the iteration from
![]() ${\mathrm {K}}|\xi $
to
${\mathrm {K}}|\xi $
to
![]() ${\mathrm {K}}^*$
is a linear iteration of
${\mathrm {K}}^*$
is a linear iteration of
![]() $\mu $
and its images. Again, as
$\mu $
and its images. Again, as
![]() $N \unlhd {\mathrm {K}}^*$
does not have any total measures between
$N \unlhd {\mathrm {K}}^*$
does not have any total measures between
![]() $\gamma $
and
$\gamma $
and
![]() $\kappa $
and
$\kappa $
and
![]() $N \cap {\mathrm {On}} \geq \kappa $
, this iteration needs to last at least
$N \cap {\mathrm {On}} \geq \kappa $
, this iteration needs to last at least
![]() $\kappa $
-many steps by [Reference Kanamori28, Corollary 19.7.(b)] since
$\kappa $
-many steps by [Reference Kanamori28, Corollary 19.7.(b)] since
![]() $\kappa $
is a cardinal in
$\kappa $
is a cardinal in
![]() ${\mathrm {V}}$
. Moreover, [Reference Kanamori28, Corollary 19.7.(b)] shows that
${\mathrm {V}}$
. Moreover, [Reference Kanamori28, Corollary 19.7.(b)] shows that
![]() $\kappa $
is inaccessible in
$\kappa $
is inaccessible in
![]() ${\mathrm {K}}^*$
. As
${\mathrm {K}}^*$
. As
![]() $N \unlhd {\mathrm {K}}^*$
, this contradicts the fact that
$N \unlhd {\mathrm {K}}^*$
, this contradicts the fact that
![]() $\kappa $
is singular in N. Therefore,
$\kappa $
is singular in N. Therefore,
![]() $\mu $
is not used on the
$\mu $
is not used on the
![]() ${\mathrm {K}}$
-side of the comparison.
${\mathrm {K}}$
-side of the comparison.
Similarly, we can argue that no partial measure on N gets used in the comparison and hence we can conclude that
![]() $N \lhd {\mathrm {K}}$
.
$N \lhd {\mathrm {K}}$
.
Claim. For every
![]() $x \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^{\mathrm {K}}$
, there is a good premouse N with
$x \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^{\mathrm {K}}$
, there is a good premouse N with
![]() $x \in N$
.
$x \in N$
.
Proof of the Claim
As
![]() ${\mathrm {K}}$
satisfies the
${\mathrm {K}}$
satisfies the
![]() ${\mathrm {GCH}}$
, there is some
${\mathrm {GCH}}$
, there is some
![]() $\xi < (\kappa ^+)^{\mathrm {K}}=\kappa ^+$
such that
$\xi < (\kappa ^+)^{\mathrm {K}}=\kappa ^+$
such that
![]() $x \in {\mathrm {K}}|\xi $
and
$x \in {\mathrm {K}}|\xi $
and
![]() ${\mathrm {K}}|\xi $
is a good premouse.
${\mathrm {K}}|\xi $
is a good premouse.
Following [Reference Hayut and Müller21], we say a pair
![]() $\langle M, \bar {x}\rangle $
is an active node at
$\langle M, \bar {x}\rangle $
is an active node at
![]() $\rho $
for some
$\rho $
for some
![]() $\rho < {{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
if there is a good premouse N and some
$\rho < {{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
if there is a good premouse N and some
![]() $x \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^N$
with
$x \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^N$
with
![]() ${{\mathrm {ran}}(x)} \subseteq \mathrm {Reg}^N$
, the regular cardinals in N, such that the following statements hold:
${{\mathrm {ran}}(x)} \subseteq \mathrm {Reg}^N$
, the regular cardinals in N, such that the following statements hold:
-
○ x is strictly increasing and cofinal in
 $\kappa $
.
$\kappa $
. -
○ M is equal to the transitive collapse of
 ${{\mathrm {Hull}}}^{N}(x(\rho ) \cup \{x\})$
and
${{\mathrm {Hull}}}^{N}(x(\rho ) \cup \{x\})$
and
 $\bar {x} \in M$
is the image of x under the transitive collapse.
$\bar {x} \in M$
is the image of x under the transitive collapse. -
○ If
 ${\pi }:{M}\longrightarrow {N}$
is the corresponding uncollapsing map, then
${\pi }:{M}\longrightarrow {N}$
is the corresponding uncollapsing map, then
 ${{\mathrm {crit}}\left ({\pi }\right )} = \bar {x}(\rho )$
.
${{\mathrm {crit}}\left ({\pi }\right )} = \bar {x}(\rho )$
.
In addition, we say a pair
![]() $\langle M, \bar {x}\rangle $
is an active node if there is some ordinal
$\langle M, \bar {x}\rangle $
is an active node if there is some ordinal
![]() $\rho <{{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
such that
$\rho <{{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
such that
![]() $\langle M, \bar {x}\rangle $
is an active node at
$\langle M, \bar {x}\rangle $
is an active node at
![]() $\rho $
.
$\rho $
.
We now let T denote the unique partial order defined by the following clauses:
-
(i) The elements of T are triples of the form
 $\langle M, \bar {x}, s\rangle $
satisfying the following properties:
$\langle M, \bar {x}, s\rangle $
satisfying the following properties:-
(a) The pair
 $\langle M, \bar {x}\rangle $
is either an active node or equal to the pair
$\langle M, \bar {x}\rangle $
is either an active node or equal to the pair
 $\langle \emptyset , \emptyset \rangle $
.
$\langle \emptyset , \emptyset \rangle $
. -
(b) s is an element of
 $({}^{{<}{{\mathrm {cof}}(\kappa )}}\kappa )^{\mathrm {K}}$
with the property that the set is finite.
$({}^{{<}{{\mathrm {cof}}(\kappa )}}\kappa )^{\mathrm {K}}$
with the property that the set is finite. $$ \begin{align*}\bigcup_{0 < \alpha < \kappa} s^{{-}1}(\{\alpha\})\end{align*} $$
$$ \begin{align*}\bigcup_{0 < \alpha < \kappa} s^{{-}1}(\{\alpha\})\end{align*} $$
-
(c) If
 $\langle M, \bar {x}\rangle $
is an active node at
$\langle M, \bar {x}\rangle $
is an active node at
 $\rho $
, then
$\rho $
, then
 ${{\mathrm {dom}}(s)} \geq \rho $
.
${{\mathrm {dom}}(s)} \geq \rho $
.
-
-
(ii) The order of T is defined by
if and only if the following statements hold: $$ \begin{align*}\langle M_0, x_0, s_0\rangle ~ \leq_{T} ~ \langle M_1, x_1, s_1\rangle\end{align*} $$
$$ \begin{align*}\langle M_0, x_0, s_0\rangle ~ \leq_{T} ~ \langle M_1, x_1, s_1\rangle\end{align*} $$
-
(a)
 $M_0$
is the transitive collapse of
$M_0$
is the transitive collapse of
 ${{\mathrm {Hull}}}^{M_1}(x_1(\rho ) \cup \{x_1\})$
for some ordinal
${{\mathrm {Hull}}}^{M_1}(x_1(\rho ) \cup \{x_1\})$
for some ordinal
 $\rho $
and
$\rho $
and
 $x_0$
is the image of
$x_0$
is the image of
 $x_1$
under the transitive collapse, or
$x_1$
under the transitive collapse, or
 $M_0 = x_0 = \emptyset $
. In the following, write
$M_0 = x_0 = \emptyset $
. In the following, write
 $\rho $
for the minimal such ordinal and
$\rho $
for the minimal such ordinal and
 $\rho = -1$
if
$\rho = -1$
if
 $M_0 = x_0 = \emptyset $
.
$M_0 = x_0 = \emptyset $
. -
(b)
 $s_0$
is an initial segment of
$s_0$
is an initial segment of
 $s_1$
.
$s_1$
. -
(c) There is no ordinal
 $\rho '$
between
$\rho '$
between
 $\rho $
and
$\rho $
and
 ${{\mathrm {dom}}(s_0)}$
with the property that
${{\mathrm {dom}}(s_0)}$
with the property that
 $\langle {{\mathrm {Hull}}}^{M_1}(x_1(\rho ') \cup \{x_1\}), x_1\rangle $
transitively collapses to an active node which, in case
$\langle {{\mathrm {Hull}}}^{M_1}(x_1(\rho ') \cup \{x_1\}), x_1\rangle $
transitively collapses to an active node which, in case
 $\rho \neq -1$
, is not
$\rho \neq -1$
, is not
 $\langle M_0, x_0\rangle $
.
$\langle M_0, x_0\rangle $
.
-
It is now easy to see that T is a tree of height
![]() ${{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
that is contained in
${{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
that is contained in
![]() ${\mathrm {K}}$
and has the property that each node is splitting into
${\mathrm {K}}$
and has the property that each node is splitting into
![]() $\kappa $
-many successors. Moreover, each
$\kappa $
-many successors. Moreover, each
![]() $x \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^{\mathrm {K}}$
that is strictly increasing and cofinal in
$x \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^{\mathrm {K}}$
that is strictly increasing and cofinal in
![]() $\kappa $
with range contained in
$\kappa $
with range contained in
![]() $\mathrm {Reg}^N$
naturally gives rise to a cofinal branch
$\mathrm {Reg}^N$
naturally gives rise to a cofinal branch
![]() $b_x$
through T and two different such elements
$b_x$
through T and two different such elements
![]() $x,y \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^{\mathrm {K}}$
give rise to different branches
$x,y \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^{\mathrm {K}}$
give rise to different branches
![]() $b_x$
and
$b_x$
and
![]() $b_y$
. Hence, the fact that the
$b_y$
. Hence, the fact that the
![]() ${\mathrm {GCH}}$
holds in
${\mathrm {GCH}}$
holds in
![]() ${\mathrm {K}}$
implies that the set of cofinal branches through T has cardinality at least
${\mathrm {K}}$
implies that the set of cofinal branches through T has cardinality at least
Claim. Let b be a cofinal branch through T, and let
![]() $\langle \mathcal {R}_b, x_b \rangle $
denote the direct limit of models along b. Then
$\langle \mathcal {R}_b, x_b \rangle $
denote the direct limit of models along b. Then
![]() $\mathcal {R}_b$
is well-founded and we can identify it with its transitive collapse. Moreover,
$\mathcal {R}_b$
is well-founded and we can identify it with its transitive collapse. Moreover,
![]() $\mathcal {R}_b \lhd K$
.
$\mathcal {R}_b \lhd K$
.
Proof of the claim
As the proof of the well-foundedness of
![]() $\mathcal {R}_b$
is easier, we focus on the argument that
$\mathcal {R}_b$
is easier, we focus on the argument that
![]() $\mathcal {R}_b \lhd K$
. By our first claim, it suffices to show that
$\mathcal {R}_b \lhd K$
. By our first claim, it suffices to show that
![]() $\mathcal {R}_b$
is a good premouse. We obtain iterability for
$\mathcal {R}_b$
is a good premouse. We obtain iterability for
![]() $\mathcal {R}_b$
by reflecting countable elementary substructures of
$\mathcal {R}_b$
by reflecting countable elementary substructures of
![]() $\mathcal {R}_b$
into models in the tree T, as in [Reference Hayut and Müller21], using the fact that
$\mathcal {R}_b$
into models in the tree T, as in [Reference Hayut and Müller21], using the fact that
(see [Reference Jech25, Lemma 3.7(ii)]). In the following, write
![]() $\langle {M_\rho }~\vert ~{\rho < {{\mathrm {cof}}(\kappa )}^{\mathrm {K}}}\rangle $
for the sequence of models appearing in active nodes at
$\langle {M_\rho }~\vert ~{\rho < {{\mathrm {cof}}(\kappa )}^{\mathrm {K}}}\rangle $
for the sequence of models appearing in active nodes at
![]() $\rho $
along the branch b. Then the definition of T ensures that for every
$\rho $
along the branch b. Then the definition of T ensures that for every
![]() $\xi < \kappa $
, there is some
$\xi < \kappa $
, there is some
![]() $\rho < {{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
such that if
$\rho < {{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
such that if
![]() $M_\rho $
is the transitive collapse of
$M_\rho $
is the transitive collapse of
![]() ${{\mathrm {Hull}}}^{N_\rho }(x_\rho (\rho ) \cup \{x_\rho \})$
for some good premouse
${{\mathrm {Hull}}}^{N_\rho }(x_\rho (\rho ) \cup \{x_\rho \})$
for some good premouse
![]() $N_\rho $
and some
$N_\rho $
and some
![]() $x_\rho \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^{N_\rho }$
, then
$x_\rho \in \left ({}^{{{\mathrm {cof}}(\kappa )}} \kappa \right )^{N_\rho }$
, then
![]() $x_\rho (\rho )> \xi $
. Therefore, we know that
$x_\rho (\rho )> \xi $
. Therefore, we know that
![]() $\kappa \subseteq \mathcal {R}_b$
and elementarity implies that
$\kappa \subseteq \mathcal {R}_b$
and elementarity implies that
![]() $\kappa +1 \subseteq \mathcal {R}_b$
. Our setup also directly ensures that
$\kappa +1 \subseteq \mathcal {R}_b$
. Our setup also directly ensures that
![]() $\vert {\mathcal {R}_b}\vert = \kappa $
. As
$\vert {\mathcal {R}_b}\vert = \kappa $
. As
![]() $N_\rho \lhd K$
and the critical point of the inverse of the collapse embedding
$N_\rho \lhd K$
and the critical point of the inverse of the collapse embedding
![]() $\pi _\rho \colon M_\rho \rightarrow N_\rho $
is at least
$\pi _\rho \colon M_\rho \rightarrow N_\rho $
is at least
![]() $x_\rho (\rho )$
, this also shows that
$x_\rho (\rho )$
, this also shows that
![]() $N_\rho | \gamma ^{++} = K | \gamma ^{++}$
, where
$N_\rho | \gamma ^{++} = K | \gamma ^{++}$
, where
![]() $\gamma < \kappa $
is the supremum of the measurable cardinals below
$\gamma < \kappa $
is the supremum of the measurable cardinals below
![]() $\kappa $
in
$\kappa $
in
![]() ${\mathrm {K}}$
and
${\mathrm {K}}$
and
![]() $N_\rho $
. Moreover, we know that
$N_\rho $
. Moreover, we know that
![]() $\kappa $
has cofinality
$\kappa $
has cofinality
![]() ${{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
in
${{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
in
![]() $\mathcal {R}_b$
, as witnessed by
$\mathcal {R}_b$
, as witnessed by
![]() $x_b$
. Finally,
$x_b$
. Finally,
![]() $\kappa $
is the largest cardinal in
$\kappa $
is the largest cardinal in
![]() $\mathcal {R}_b$
by elementarity as
$\mathcal {R}_b$
by elementarity as
![]() $\kappa = \sup ({{\mathrm {ran}}(x_\rho )})$
is the largest cardinal in
$\kappa = \sup ({{\mathrm {ran}}(x_\rho )})$
is the largest cardinal in
![]() $N_\rho $
for all
$N_\rho $
for all
![]() $\rho < {{\mathrm {cof}}(\kappa )}$
.
$\rho < {{\mathrm {cof}}(\kappa )}$
.
Claim. The set T is
![]() $\Sigma _1$
-definable with parameters in
$\Sigma _1$
-definable with parameters in
![]() ${\mathrm {H}}(\kappa ) \cup \{\kappa \}$
.
${\mathrm {H}}(\kappa ) \cup \{\kappa \}$
.
Proof of the claim
It clearly suffices to show that the set of all good mice N is definable in the above way. As there is no inner model with
![]() ${{\mathrm {cof}}(\kappa )}$
-many measurable cardinals, the mice we consider are simple and therefore iterability for N is
${{\mathrm {cof}}(\kappa )}$
-many measurable cardinals, the mice we consider are simple and therefore iterability for N is
![]() $\Sigma _1$
-definable from the parameter
$\Sigma _1$
-definable from the parameter
![]() $\omega _1$
, using [Reference Zeman53, Theorem 4.5.5]. All other conditions can obviously be stated by
$\omega _1$
, using [Reference Zeman53, Theorem 4.5.5]. All other conditions can obviously be stated by
![]() $\Sigma _1$
-formulas using the parameters
$\Sigma _1$
-formulas using the parameters
![]() $\kappa $
and
$\kappa $
and
![]() $K\vert \gamma ^{++} \in {\mathrm {H}}(\kappa )$
.
$K\vert \gamma ^{++} \in {\mathrm {H}}(\kappa )$
.
Claim. There is an injection
![]() ${i}:{T}\longrightarrow {{\mathrm {H}}(\kappa )\cap {\mathcal {P}}({\kappa })}$
that is definable by a
${i}:{T}\longrightarrow {{\mathrm {H}}(\kappa )\cap {\mathcal {P}}({\kappa })}$
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
Proof of the claim
It clearly suffices to construct an injection from the set of all active nodes to
![]() ${\mathrm {H}}(\kappa )\cap {\mathcal {P}}({\kappa })$
. Let
${\mathrm {H}}(\kappa )\cap {\mathcal {P}}({\kappa })$
. Let
![]() $\langle M,\bar {x}\rangle $
be an active node at some
$\langle M,\bar {x}\rangle $
be an active node at some
![]() $\rho <{{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
. Since M is the transitive collapse of an elementary submodel of some good premouse
$\rho <{{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
. Since M is the transitive collapse of an elementary submodel of some good premouse
![]() $N=\langle \mathrm {J}^{\vec E}_{\alpha },\vec E\rangle $
, we know that M is of the form
$N=\langle \mathrm {J}^{\vec E}_{\alpha },\vec E\rangle $
, we know that M is of the form
![]() $\langle \mathrm {J}^A_\epsilon ,A\rangle $
and there is a well-ordering
$\langle \mathrm {J}^A_\epsilon ,A\rangle $
and there is a well-ordering
![]() $\lhd $
of M that is definable in M. Let
$\lhd $
of M that is definable in M. Let
![]() ${\tau }:{\langle M,\lhd \rangle }\longrightarrow {\langle \lambda ,<\rangle }$
denote the corresponding transitive collapse and associate
${\tau }:{\langle M,\lhd \rangle }\longrightarrow {\langle \lambda ,<\rangle }$
denote the corresponding transitive collapse and associate
![]() $\langle M,\bar {x}\rangle $
with the element
$\langle M,\bar {x}\rangle $
with the element
 $$ \begin{align*} \begin{aligned} & \{{{\prec}{0},{{\prec}{\alpha},{\beta}{\succ}}{\succ}}~\vert~{\alpha,\beta<\lambda, ~ \tau^{{-}1}(\alpha)\in\tau^{{-}1}(\beta)}\} \\ & \cup ~ \{{{\prec}{1},{\alpha}{\succ}}~\vert~{\alpha<\lambda, ~ \tau^{{-}1}(\alpha)\in A}\} \\ & ~ \cup ~ \{{{\prec}{2},{\alpha}{\succ}}~\vert~{\alpha<\lambda, ~ \tau^{{-}1}(\alpha)\in\bar{x}}\} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \{{{\prec}{0},{{\prec}{\alpha},{\beta}{\succ}}{\succ}}~\vert~{\alpha,\beta<\lambda, ~ \tau^{{-}1}(\alpha)\in\tau^{{-}1}(\beta)}\} \\ & \cup ~ \{{{\prec}{1},{\alpha}{\succ}}~\vert~{\alpha<\lambda, ~ \tau^{{-}1}(\alpha)\in A}\} \\ & ~ \cup ~ \{{{\prec}{2},{\alpha}{\succ}}~\vert~{\alpha<\lambda, ~ \tau^{{-}1}(\alpha)\in\bar{x}}\} \end{aligned} \end{align*} $$
of
![]() ${\mathrm {H}}(\kappa )\cap {\mathcal {P}}({\kappa })$
. It is now easy to see that the resulting injection is definable in the desired way.
${\mathrm {H}}(\kappa )\cap {\mathcal {P}}({\kappa })$
. It is now easy to see that the resulting injection is definable in the desired way.
Claim. No countably closed forcing adds a cofinal branch through T.
Proof of the claim
Let
![]() ${\mathbb {P}}$
be a countably closed forcing notion, and let G be
${\mathbb {P}}$
be a countably closed forcing notion, and let G be
![]() ${\mathbb {P}}$
-generic over
${\mathbb {P}}$
-generic over
![]() ${\mathrm {V}}$
. Suppose, towards a contradiction, that there is a cofinal branch b through T in
${\mathrm {V}}$
. Suppose, towards a contradiction, that there is a cofinal branch b through T in
![]() ${\mathrm {V}}[G]$
that is not contained in
${\mathrm {V}}[G]$
that is not contained in
![]() ${\mathrm {V}}$
. By considering the direct limit of the active nodes along b and using the fact that
${\mathrm {V}}$
. By considering the direct limit of the active nodes along b and using the fact that
![]() ${{\mathrm {cof}}(\kappa )}^{\mathrm {V}}$
has uncountable cofinality in
${{\mathrm {cof}}(\kappa )}^{\mathrm {V}}$
has uncountable cofinality in
![]() ${\mathrm {V}}[G]$
, we obtain a pair
${\mathrm {V}}[G]$
, we obtain a pair
![]() $\langle \mathcal {R}_b, x_b\rangle $
such that b (modulo some choice of an almost zero sequence s) can be recovered from
$\langle \mathcal {R}_b, x_b\rangle $
such that b (modulo some choice of an almost zero sequence s) can be recovered from
![]() $\mathcal {R}_b$
and
$\mathcal {R}_b$
and
![]() $x_b$
via the transitive collapses of models of the form
$x_b$
via the transitive collapses of models of the form
for
![]() $\rho < {{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
. As
$\rho < {{\mathrm {cof}}(\kappa )}^{\mathrm {K}}$
. As
![]() ${{\mathrm {cof}}(\kappa )}^{\mathrm {V}}$
has uncountable cofinality in
${{\mathrm {cof}}(\kappa )}^{\mathrm {V}}$
has uncountable cofinality in
![]() ${\mathrm {V}}[G]$
, the argument in one of our previous claims then shows that
${\mathrm {V}}[G]$
, the argument in one of our previous claims then shows that
![]() $\mathcal {R}_b \lhd {\mathrm {K}}^{V[G]}$
holds in
$\mathcal {R}_b \lhd {\mathrm {K}}^{V[G]}$
holds in
![]() $V[G]$
. By [Reference Zeman53, Theorem 7.4.11], the core model
$V[G]$
. By [Reference Zeman53, Theorem 7.4.11], the core model
![]() ${\mathrm {K}}$
is forcing absolute, that is, we have
${\mathrm {K}}$
is forcing absolute, that is, we have
![]() ${\mathrm {K}}^{\mathrm {V}} = {\mathrm {K}}^{{\mathrm {V}}[G]}$
. Therefore, we know that
${\mathrm {K}}^{\mathrm {V}} = {\mathrm {K}}^{{\mathrm {V}}[G]}$
. Therefore, we know that
![]() $\mathcal {R}_b$
and hence b is already an element of
$\mathcal {R}_b$
and hence b is already an element of
![]() ${\mathrm {V}}$
, a contradiction.
${\mathrm {V}}$
, a contradiction.
Fix a strictly increasing, cofinal function
![]() ${c}:{{{\mathrm {cof}}(\kappa )}}\longrightarrow {{{\mathrm {cof}}(\kappa )}^{\mathrm {K}}}$
, and let
${c}:{{{\mathrm {cof}}(\kappa )}}\longrightarrow {{{\mathrm {cof}}(\kappa )}^{\mathrm {K}}}$
, and let
![]() $T_*$
denote the unique partial order defined by the following clauses:
$T_*$
denote the unique partial order defined by the following clauses:
-
(i) The elements of
 $T_*$
are functions t such that
$T_*$
are functions t such that
 ${{\mathrm {dom}}(t)}\in {{\mathrm {cof}}(\kappa )}$
and the following statements hold:
${{\mathrm {dom}}(t)}\in {{\mathrm {cof}}(\kappa )}$
and the following statements hold:-
(a) If
 $\alpha \in {{\mathrm {dom}}(t)}$
, then
$\alpha \in {{\mathrm {dom}}(t)}$
, then
 $t(\alpha )$
is a branch through T of order-type
$t(\alpha )$
is a branch through T of order-type
 $c(\alpha )$
.
$c(\alpha )$
. -
(b) If
 $\alpha <\beta \in {{\mathrm {dom}}(t)}$
, then
$\alpha <\beta \in {{\mathrm {dom}}(t)}$
, then
 $t(\alpha )$
is an initial segment of
$t(\alpha )$
is an initial segment of
 $t(\beta )$
.
$t(\beta )$
.
-
-
(ii) The ordering of
 $T_*$
is given by inclusion.
$T_*$
is given by inclusion.
It then follows that
![]() $T_*$
is a tree of height
$T_*$
is a tree of height
![]() ${{\mathrm {cof}}(\kappa )}$
with the property that every node has
${{\mathrm {cof}}(\kappa )}$
with the property that every node has
![]() $\kappa $
-many successors. Since the tree T has at least
$\kappa $
-many successors. Since the tree T has at least
![]() $\kappa ^+$
-many branches, it follows that
$\kappa ^+$
-many branches, it follows that
![]() $T_*$
also has at least
$T_*$
also has at least
![]() $\kappa ^+$
-many branches. Moreover, by using the injection i, it is possible to construct an injection
$\kappa ^+$
-many branches. Moreover, by using the injection i, it is possible to construct an injection
![]() ${i_*}:{T_*}\longrightarrow {{\mathrm {H}}(\kappa )\cap {\mathcal {P}}({\kappa })}$
with
${i_*}:{T_*}\longrightarrow {{\mathrm {H}}(\kappa )\cap {\mathcal {P}}({\kappa })}$
with
![]() $\emptyset \notin {{\mathrm {ran}}(i_*)}$
that is definable by a
$\emptyset \notin {{\mathrm {ran}}(i_*)}$
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. Finally, the above computations also imply that forcing with a countably closed partial order does not add a new cofinal branch to
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. Finally, the above computations also imply that forcing with a countably closed partial order does not add a new cofinal branch to
![]() $T_*$
.
$T_*$
.
Define D to be the set of all subsets of
![]() $\kappa $
of the form
$\kappa $
of the form
for some function b with domain
![]() ${{\mathrm {cof}}(\kappa )}$
and the property that
${{\mathrm {cof}}(\kappa )}$
and the property that
![]() $b\restriction \alpha \in T_*$
for all
$b\restriction \alpha \in T_*$
for all
![]() $\alpha <{{\mathrm {cof}}(\kappa )}$
. Since the fact that the tree
$\alpha <{{\mathrm {cof}}(\kappa )}$
. Since the fact that the tree
![]() $T_*$
has at least
$T_*$
has at least
![]() $\kappa ^+$
-many cofinal branches implies that D has cardinality greater than
$\kappa ^+$
-many cofinal branches implies that D has cardinality greater than
![]() $\kappa $
and the above computations show that D is definable by a
$\kappa $
and the above computations show that D is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, our assumption yields a perfect embedding
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, our assumption yields a perfect embedding
![]() ${\iota }:{{}^{{{\mathrm {cof}}(\kappa )}}\kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
${\iota }:{{}^{{{\mathrm {cof}}(\kappa )}}\kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
![]() ${{\mathrm {ran}}(\iota )}\subseteq D$
. Using the fact that
${{\mathrm {ran}}(\iota )}\subseteq D$
. Using the fact that
![]() ${{\mathrm {cof}}(\kappa )}$
is uncountable, a routine construction now allows us to find
${{\mathrm {cof}}(\kappa )}$
is uncountable, a routine construction now allows us to find
-
○ a system
 $\langle {u_s}~\vert ~{s\in {}^{{<}{{\mathrm {cof}}(\kappa )}}2}\rangle $
of elements of
$\langle {u_s}~\vert ~{s\in {}^{{<}{{\mathrm {cof}}(\kappa )}}2}\rangle $
of elements of
 ${}^{{<}{{\mathrm {cof}}(\kappa )}}2$
,
${}^{{<}{{\mathrm {cof}}(\kappa )}}2$
, -
○ a strictly increasing sequence
 $\langle {\kappa _\alpha }~\vert ~{\alpha <{{\mathrm {cof}}(\kappa )}}\rangle $
that is cofinal in
$\langle {\kappa _\alpha }~\vert ~{\alpha <{{\mathrm {cof}}(\kappa )}}\rangle $
that is cofinal in
 $\kappa $
, and
$\kappa $
, and -
○ a system
 $\langle {a_s}~\vert ~{s\in {}^{{<}{{\mathrm {cof}}(\kappa )}}2}\rangle $
of bounded subsets of
$\langle {a_s}~\vert ~{s\in {}^{{<}{{\mathrm {cof}}(\kappa )}}2}\rangle $
of bounded subsets of
 $\kappa $
$\kappa $
such that the following statements hold for all
![]() $s,t\in {}^{{<}{{\mathrm {cof}}(\kappa )}}2$
:
$s,t\in {}^{{<}{{\mathrm {cof}}(\kappa )}}2$
:
-
(i) If
 ${\mathrm {lh}}({s}){}={\mathrm {lh}}({t}){}$
, then
${\mathrm {lh}}({s}){}={\mathrm {lh}}({t}){}$
, then
 ${\mathrm {lh}}({u_s}){}={\mathrm {lh}}({u_t}){}$
.
${\mathrm {lh}}({u_s}){}={\mathrm {lh}}({u_t}){}$
. -
(ii)
 $a_s$
is a subset of
$a_s$
is a subset of
 $\kappa _{{\mathrm {lh}}({s}){}}$
.
$\kappa _{{\mathrm {lh}}({s}){}}$
. -
(iii) If
 $s\subseteq t$
, then
$s\subseteq t$
, then
 $a_s=a_t\cap \kappa _{{\mathrm {lh}}({s}){}}$
and
$a_s=a_t\cap \kappa _{{\mathrm {lh}}({s}){}}$
and
 $u_s\subseteq u_t$
.
$u_s\subseteq u_t$
. -
(iv)
 $a_{s^\frown \langle 0\rangle }\neq a_{s^\frown \langle 1\rangle }$
and
$a_{s^\frown \langle 0\rangle }\neq a_{s^\frown \langle 1\rangle }$
and
 $u_{s^\frown \langle 0\rangle }\neq u_{s^\frown \langle 1\rangle }$
.
$u_{s^\frown \langle 0\rangle }\neq u_{s^\frown \langle 1\rangle }$
. -
(v)
 $\iota [\{{x\in {}^{{\mathrm {cof}}(\kappa )}2}~\vert ~{x\restriction {\mathrm {lh}}({s}){}= s}\}]=\{{y\in {{\mathrm {ran}}(\iota )}}~\vert ~{y\cap \kappa _{{\mathrm {lh}}({s}){}}=a_s}\}$
.
$\iota [\{{x\in {}^{{\mathrm {cof}}(\kappa )}2}~\vert ~{x\restriction {\mathrm {lh}}({s}){}= s}\}]=\{{y\in {{\mathrm {ran}}(\iota )}}~\vert ~{y\cap \kappa _{{\mathrm {lh}}({s}){}}=a_s}\}$
. -
(vi) If
 $\alpha <{\mathrm {lh}}({s}){}$
, then there are
$\alpha <{\mathrm {lh}}({s}){}$
, then there are
 $\gamma \leq \delta <\kappa _{{\mathrm {lh}}({s}){}}$
with
$\gamma \leq \delta <\kappa _{{\mathrm {lh}}({s}){}}$
with
 ${\prec }{\alpha },{{\prec }{\gamma },{\delta }{\succ }}{\succ }\in a_s$
.
${\prec }{\alpha },{{\prec }{\gamma },{\delta }{\succ }}{\succ }\in a_s$
.
Now, let G be
![]() ${\mathrm {Add}}({{{\mathrm {cof}}(\kappa )}},{1})$
-generic over
${\mathrm {Add}}({{{\mathrm {cof}}(\kappa )}},{1})$
-generic over
![]() ${\mathrm {V}}$
. Set
${\mathrm {V}}$
. Set
![]() $x_G=\bigcup G\in ({}^{{\mathrm {cof}}(\kappa )}2)^{{\mathrm {V}}[G]}$
and
$x_G=\bigcup G\in ({}^{{\mathrm {cof}}(\kappa )}2)^{{\mathrm {V}}[G]}$
and
In this situation, our construction ensures that there is a function
![]() $b_G$
in
$b_G$
in
![]() ${\mathrm {V}}[G]$
such that
${\mathrm {V}}[G]$
such that
![]() ${{\mathrm {dom}}(b_G)}={{\mathrm {cof}}(\kappa )}$
,
${{\mathrm {dom}}(b_G)}={{\mathrm {cof}}(\kappa )}$
,
![]() $b_G\restriction \alpha \in T_*$
for all
$b_G\restriction \alpha \in T_*$
for all
![]() $\alpha <{{\mathrm {cof}}(\kappa )}$
and
$\alpha <{{\mathrm {cof}}(\kappa )}$
and
![]() $y_G=y_{b_G}$
. By our earlier observations, the cofinal branch through
$y_G=y_{b_G}$
. By our earlier observations, the cofinal branch through
![]() $T_*$
induced by
$T_*$
induced by
![]() $b_G$
is contained in
$b_G$
is contained in
![]() ${\mathrm {V}}$
and hence
${\mathrm {V}}$
and hence
![]() $b_G$
is an element of
$b_G$
is an element of
![]() ${\mathrm {V}}$
. But this implies that
${\mathrm {V}}$
. But this implies that
![]() $y_G$
is also contained in the ground model
$y_G$
is also contained in the ground model
![]() ${\mathrm {V}}$
. Since
${\mathrm {V}}$
. Since
![]() $x_G$
is the unique element x of
$x_G$
is the unique element x of
![]() $({}^{{{\mathrm {cof}}(\kappa )}}2)^{{\mathrm {V}}[G]}$
with the property that
$({}^{{{\mathrm {cof}}(\kappa )}}2)^{{\mathrm {V}}[G]}$
with the property that
![]() $y_G\cap \kappa _\alpha =a_{x\restriction \alpha }$
holds for all
$y_G\cap \kappa _\alpha =a_{x\restriction \alpha }$
holds for all
![]() $\alpha <{{\mathrm {cof}}(\kappa )}$
, we can now conclude that
$\alpha <{{\mathrm {cof}}(\kappa )}$
, we can now conclude that
![]() $x_G$
is contained in
$x_G$
is contained in
![]() ${\mathrm {V}}$
, a contradiction.
${\mathrm {V}}$
, a contradiction.
6 Almost disjoint families at limits of measurable cardinals
We now proceed by using the techniques developed in Section 2 to show that large almost disjoint families at cardinals with sufficiently strong large cardinal properties are not simply definable.
Proof of Theorem 1.3
Let
![]() $\kappa $
be an iterable cardinal that is a limit of measurable cardinals, let z be an element of
$\kappa $
be an iterable cardinal that is a limit of measurable cardinals, let z be an element of
![]() ${\mathrm {H}}(\kappa )$
and let A be a subset of
${\mathrm {H}}(\kappa )$
and let A be a subset of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
with the property that there exists a
$\kappa $
with the property that there exists a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
with
$\varphi (v_0,v_1,v_2)$
with
![]() $A=\{{y\subseteq \kappa }~\vert ~{\varphi (\kappa ,y,z)}\}$
. Assume, towards a contradiction, that A is an almost disjoint family in
$A=\{{y\subseteq \kappa }~\vert ~{\varphi (\kappa ,y,z)}\}$
. Assume, towards a contradiction, that A is an almost disjoint family in
![]() ${\mathcal {P}}({\kappa })$
. Since
${\mathcal {P}}({\kappa })$
. Since
![]() $\kappa $
is an inaccessible cardinal and the collection of all bounded subsets of
$\kappa $
is an inaccessible cardinal and the collection of all bounded subsets of
![]() $\kappa $
is definable by a
$\kappa $
is definable by a
![]() $\Sigma _0$
-formula with parameter
$\Sigma _0$
-formula with parameter
![]() $\kappa $
, we may then also assume that A consists of unbounded subsets of
$\kappa $
, we may then also assume that A consists of unbounded subsets of
![]() $\kappa $
. Fix an inaccessible cardinal
$\kappa $
. Fix an inaccessible cardinal
![]() $\lambda <\kappa $
with
$\lambda <\kappa $
with
![]() $z\in {\mathrm {H}}(\lambda )$
, and use Lemma 2.1 to obtain
$z\in {\mathrm {H}}(\lambda )$
, and use Lemma 2.1 to obtain
![]() $x\in A$
and systems
$x\in A$
and systems
![]() $\langle {\nu _s}~\vert ~{s\in {}^{{<}\kappa }\kappa }\rangle $
,
$\langle {\nu _s}~\vert ~{s\in {}^{{<}\kappa }\kappa }\rangle $
,
![]() $\langle {\kappa _s}~\vert ~{s\in {}^{{<}\kappa }\kappa }\rangle $
,
$\langle {\kappa _s}~\vert ~{s\in {}^{{<}\kappa }\kappa }\rangle $
,
![]() $\langle {U_s}~\vert ~{s\in {}^{{<}\kappa }\kappa }\rangle $
and
$\langle {U_s}~\vert ~{s\in {}^{{<}\kappa }\kappa }\rangle $
and
![]() $\langle {I_s}~\vert ~{s\in {}^{{<}\kappa }\kappa }\rangle $
with
$\langle {I_s}~\vert ~{s\in {}^{{<}\kappa }\kappa }\rangle $
with
![]() $\lambda <\kappa _\emptyset $
and the properties listed in the lemma. Then there exists an
$\lambda <\kappa _\emptyset $
and the properties listed in the lemma. Then there exists an
![]() ${\mathrm {Add}}({\lambda },{1})$
-nice name
${\mathrm {Add}}({\lambda },{1})$
-nice name
![]() $\dot {x}$
for an unbounded subset of
$\dot {x}$
for an unbounded subset of
![]() $\kappa $
with the property that
$\kappa $
with the property that
![]() $\dot {x}^G=i^{I_{c_G}}_{0,\infty }(x)$
holds whenever G is
$\dot {x}^G=i^{I_{c_G}}_{0,\infty }(x)$
holds whenever G is
![]() ${\mathrm {Add}}({\lambda },{1})$
-generic over
${\mathrm {Add}}({\lambda },{1})$
-generic over
![]() ${\mathrm {V}}$
,
${\mathrm {V}}$
,
![]() $c_G=\bigcup G\in ({}^\lambda 2)^{{\mathrm {V}}[G]}$
and
$c_G=\bigcup G\in ({}^\lambda 2)^{{\mathrm {V}}[G]}$
and
![]() $I_{c_G}$
is the unique linear iteration of
$I_{c_G}$
is the unique linear iteration of
![]() $\langle {\mathrm {V}},\{{U_{c_G\restriction \xi }}~\vert ~{\xi <\lambda }\}\rangle $
of length
$\langle {\mathrm {V}},\{{U_{c_G\restriction \xi }}~\vert ~{\xi <\lambda }\}\rangle $
of length
![]() $\sup _{\xi <\lambda }{\mathrm {lh}}({I_{c_G\restriction \xi }}){}$
in
$\sup _{\xi <\lambda }{\mathrm {lh}}({I_{c_G\restriction \xi }}){}$
in
![]() ${\mathrm {V}}[G]$
with
${\mathrm {V}}[G]$
with
![]() $U^{I_G}_\alpha =U^{I_{c_G\restriction \xi }}_\alpha $
for all
$U^{I_G}_\alpha =U^{I_{c_G\restriction \xi }}_\alpha $
for all
![]() $\xi <\lambda $
and
$\xi <\lambda $
and
![]() $\alpha <{\mathrm {lh}}({I_{c_G\restriction \xi }}){}$
. Note that, by Lemma 2.2, the elementarity of
$\alpha <{\mathrm {lh}}({I_{c_G\restriction \xi }}){}$
. Note that, by Lemma 2.2, the elementarity of
![]() $i^{I_{c_G}}_{0,\infty }$
and the upwards absoluteness of
$i^{I_{c_G}}_{0,\infty }$
and the upwards absoluteness of
![]() $\Sigma _1$
-statements between
$\Sigma _1$
-statements between
![]() $M^{I_{c_G}}_\infty $
and
$M^{I_{c_G}}_\infty $
and
![]() ${\mathrm {V}}[G]$
ensures that
${\mathrm {V}}[G]$
ensures that
holds in
![]() ${\mathrm {V}}$
.
${\mathrm {V}}$
.
Claim. If
![]() $G_0\times G_1$
is
$G_0\times G_1$
is
![]() $({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over
$({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over
![]() ${\mathrm {V}}$
, then
${\mathrm {V}}$
, then
![]() $\dot {x}^{G_0}\neq \dot {x}^{G_1}$
.
$\dot {x}^{G_0}\neq \dot {x}^{G_1}$
.
Proof of the claim
Given
![]() $i<2$
, the absoluteness of the iterated ultrapower construction ensures that
$i<2$
, the absoluteness of the iterated ultrapower construction ensures that
![]() $(I_{c_{G_i}})^{{\mathrm {V}}[G_i]}=(I_{c_{G_i}})^{{\mathrm {V}}[G_0,G_1]}$
holds, and this implies that
$(I_{c_{G_i}})^{{\mathrm {V}}[G_i]}=(I_{c_{G_i}})^{{\mathrm {V}}[G_0,G_1]}$
holds, and this implies that
Since mutual genericity implies that
![]() $c_{G_0}\neq c_{G_1}$
, the desired inequality now directly follows from an application of statement (iii) of Lemma 2.2 in
$c_{G_0}\neq c_{G_1}$
, the desired inequality now directly follows from an application of statement (iii) of Lemma 2.2 in
![]() ${\mathrm {V}}[G_0,G_1]$
.
${\mathrm {V}}[G_0,G_1]$
.
Pick an elementary submodel
![]() $M_0$
of
$M_0$
of
![]() ${\mathrm {H}}(\kappa ^+)$
of cardinality
${\mathrm {H}}(\kappa ^+)$
of cardinality
![]() $\kappa $
with
$\kappa $
with
![]() ${}^{{<}\kappa }M_0\subseteq M_0$
that contains
${}^{{<}\kappa }M_0\subseteq M_0$
that contains
![]() ${\mathrm {H}}(\kappa )$
and all objects listed above. Since iterable cardinals are weakly compact, we can find a transitive set
${\mathrm {H}}(\kappa )$
and all objects listed above. Since iterable cardinals are weakly compact, we can find a transitive set
![]() $M_1$
of cardinality
$M_1$
of cardinality
![]() $\kappa $
and an elementary embedding
$\kappa $
and an elementary embedding
![]() ${j}:{M_0}\longrightarrow {M_1}$
with
${j}:{M_0}\longrightarrow {M_1}$
with
![]() ${{\mathrm {crit}}\left ({j}\right )}=\kappa $
(see [Reference Hauser20, Theorem 1.3]). Then
${{\mathrm {crit}}\left ({j}\right )}=\kappa $
(see [Reference Hauser20, Theorem 1.3]). Then
![]() $j(\dot {x})$
is an
$j(\dot {x})$
is an
![]() ${\mathrm {Add}}({\lambda },{1})$
-name for an unbounded subset of
${\mathrm {Add}}({\lambda },{1})$
-name for an unbounded subset of
![]() $j(\kappa )$
and there is a canonical
$j(\kappa )$
and there is a canonical
![]() ${\mathrm {Add}}({\lambda },{1})$
-name
${\mathrm {Add}}({\lambda },{1})$
-name
![]() $\dot {\gamma }$
for an ordinal in the interval
$\dot {\gamma }$
for an ordinal in the interval
![]() $[\kappa ,j(\kappa ))$
with the property that
$[\kappa ,j(\kappa ))$
with the property that
holds whenever G is
![]() ${\mathrm {Add}}({\lambda },{1})$
-generic over
${\mathrm {Add}}({\lambda },{1})$
-generic over
![]() ${\mathrm {V}}$
.
${\mathrm {V}}$
.
Claim. If
![]() $G_0\times G_1$
is
$G_0\times G_1$
is
![]() $({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over
$({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over
![]() ${\mathrm {V}}$
, then
${\mathrm {V}}$
, then
![]() $\dot {\gamma }^{G_0}\neq \dot {\gamma }^{G_1}$
.
$\dot {\gamma }^{G_0}\neq \dot {\gamma }^{G_1}$
.
Proof of the claim
Given an
![]() ${\mathrm {Add}}({\lambda },{1})$
-name
${\mathrm {Add}}({\lambda },{1})$
-name
![]() $\dot {a}$
, let
$\dot {a}$
, let
![]() $\dot {a}_l$
and
$\dot {a}_l$
and
![]() $\dot {a}_r$
denote the canonical
$\dot {a}_r$
denote the canonical
![]() $({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-names such that
$({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-names such that
![]() $\dot {a}_l^{G_0\times G_1}=\dot {a}^{G_0}$
and
$\dot {a}_l^{G_0\times G_1}=\dot {a}^{G_0}$
and
![]() $\dot {a}_r^{G_0\times G_1}=\dot {a}^{G_1}$
holds whenever
$\dot {a}_r^{G_0\times G_1}=\dot {a}^{G_1}$
holds whenever
![]() $G_0\times G_1$
is
$G_0\times G_1$
is
![]() $({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over
$({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over
![]() ${\mathrm {V}}$
. Given an
${\mathrm {V}}$
. Given an
![]() ${\mathrm {Add}}({\lambda },{1})$
-name
${\mathrm {Add}}({\lambda },{1})$
-name
![]() $\dot {a}$
in
$\dot {a}$
in
![]() $M_0$
, we then have
$M_0$
, we then have
![]() $j(\dot {a}_l)=j(\dot {a})_l$
and
$j(\dot {a}_l)=j(\dot {a})_l$
and
![]() $j(\dot {a}_r)=j(\dot {a})_r$
.
$j(\dot {a}_r)=j(\dot {a})_r$
.
Assume, towards a contradiction, that
holds for some condition
![]() $\langle p,q\rangle $
in
$\langle p,q\rangle $
in
![]() $({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
.
$({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
.
Subclaim.
![]() $\langle p,q\rangle \Vdash _{{\mathrm {Add}}({\lambda },{1}) \times {\mathrm {Add}}({\lambda },{1})}{\text {"}\hspace {0.3ex}{\dot {x}_l\cap \dot {x}_r \textit {is unbounded in } \check {\kappa }}\hspace {0.3ex}\text {"}}.$
$\langle p,q\rangle \Vdash _{{\mathrm {Add}}({\lambda },{1}) \times {\mathrm {Add}}({\lambda },{1})}{\text {"}\hspace {0.3ex}{\dot {x}_l\cap \dot {x}_r \textit {is unbounded in } \check {\kappa }}\hspace {0.3ex}\text {"}}.$
Proof of the subclaim
Let
![]() $G_0\times G_1$
be
$G_0\times G_1$
be
![]() $({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over
$({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over
![]() ${\mathrm {V}}$
with
${\mathrm {V}}$
with
![]() $\langle p,q\rangle \in G_0\times G_1$
. By standard arguments, there exists an elementary embedding
$\langle p,q\rangle \in G_0\times G_1$
. By standard arguments, there exists an elementary embedding
with
![]() $j_*(\dot {b}^{G_0\times G_1})=j(\dot {b})^{G_0\times G_1}$
for every
$j_*(\dot {b}^{G_0\times G_1})=j(\dot {b})^{G_0\times G_1}$
for every
![]() $({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-name
$({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-name
![]() $\dot {b}$
in
$\dot {b}$
in
![]() $M_0$
. Then our assumptions ensure that
$M_0$
. Then our assumptions ensure that
 $$ \begin{align*} \begin{aligned} \dot{\gamma}^{G_0} ~ = ~ \dot{\gamma}^{G_1} ~ \in ~ & ~ j(\dot{x})^{G_0} ~ \cap ~ j(\dot{x})^{G_1} ~ \cap ~ [\kappa,j(\kappa)) \\ & = ~ j_*(\dot{x}_l^{G_0\times G_1}) ~ \cap ~ j_*(\dot{x}_r^{G_0\times G_1}) ~ \cap ~ [\kappa,j_*(\kappa)) ~ \neq ~ \emptyset. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \dot{\gamma}^{G_0} ~ = ~ \dot{\gamma}^{G_1} ~ \in ~ & ~ j(\dot{x})^{G_0} ~ \cap ~ j(\dot{x})^{G_1} ~ \cap ~ [\kappa,j(\kappa)) \\ & = ~ j_*(\dot{x}_l^{G_0\times G_1}) ~ \cap ~ j_*(\dot{x}_r^{G_0\times G_1}) ~ \cap ~ [\kappa,j_*(\kappa)) ~ \neq ~ \emptyset. \end{aligned} \end{align*} $$
In particular, if
![]() $\alpha <\kappa $
, then the elementarity of
$\alpha <\kappa $
, then the elementarity of
![]() $j_*$
and the fact that
$j_*$
and the fact that
![]() $j_*(\alpha )=\alpha $
directly imply that
$j_*(\alpha )=\alpha $
directly imply that
This proves the statement of the subclaim.
We now use the fact that
![]() $\kappa $
is an iterable cardinal to find a transitive model M of
$\kappa $
is an iterable cardinal to find a transitive model M of
![]() ${\mathrm {ZFC}}^-$
of cardinality
${\mathrm {ZFC}}^-$
of cardinality
![]() $\kappa $
with
$\kappa $
with
![]() $M_0\in M$
and a weakly amenable M-ultrafilter F on
$M_0\in M$
and a weakly amenable M-ultrafilter F on
![]() $\kappa $
such that
$\kappa $
such that
![]() $\langle M,F\rangle $
is iterable. Pick an elementary submodel
$\langle M,F\rangle $
is iterable. Pick an elementary submodel
![]() $\langle X,\in ,\bar {F}\rangle $
of
$\langle X,\in ,\bar {F}\rangle $
of
![]() $\langle M,\in ,F\rangle $
of cardinality
$\langle M,\in ,F\rangle $
of cardinality
![]() $\lambda $
with
$\lambda $
with
![]() ${}^{{<}\lambda }X\subseteq X$
that contains
${}^{{<}\lambda }X\subseteq X$
that contains
![]() ${\mathrm {H}}(\lambda )$
,
${\mathrm {H}}(\lambda )$
,
![]() $M_0$
and all other relevant objects. Let
$M_0$
and all other relevant objects. Let
![]() ${\pi }:{X}\longrightarrow {N_0}$
denote the corresponding transitive collapse and set
${\pi }:{X}\longrightarrow {N_0}$
denote the corresponding transitive collapse and set
![]() $F_0=\pi [\bar {F}]$
. By [Reference Kanamori28, Theorem 19.15], we know that
$F_0=\pi [\bar {F}]$
. By [Reference Kanamori28, Theorem 19.15], we know that
![]() $\langle N_0,F_0\rangle $
is iterable. Let
$\langle N_0,F_0\rangle $
is iterable. Let
![]() $\langle N_1,F_1\rangle $
denote the
$\langle N_1,F_1\rangle $
denote the
![]() $\kappa $
-th iterate of
$\kappa $
-th iterate of
![]() $\langle N_0,F_0\rangle $
and let
$\langle N_0,F_0\rangle $
and let
![]() ${i}:{N_0}\longrightarrow {N_1}$
denote the corresponding elementary embedding. Then
${i}:{N_0}\longrightarrow {N_1}$
denote the corresponding elementary embedding. Then
![]() $(i\circ \pi )(\kappa )=\kappa $
,
$(i\circ \pi )(\kappa )=\kappa $
,
![]() $(i\circ \pi )(z)=z$
,
$(i\circ \pi )(z)=z$
,
![]() $(i\circ \pi )(\langle p,q\rangle )=\langle p,q\rangle $
and
$(i\circ \pi )(\langle p,q\rangle )=\langle p,q\rangle $
and
![]() ${\mathrm {H}}(\pi (\kappa ))^{N_0}={\mathrm {H}}(\pi (\kappa ))^{N_1}$
. Since
${\mathrm {H}}(\pi (\kappa ))^{N_0}={\mathrm {H}}(\pi (\kappa ))^{N_1}$
. Since
![]() ${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
is
${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
is
![]() ${<}\lambda $
-closed and a subset of
${<}\lambda $
-closed and a subset of
![]() $N_0$
, we know that
$N_0$
, we know that
![]() $N_0$
contains all sequences of conditions in
$N_0$
contains all sequences of conditions in
![]() ${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
of length less than
${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
of length less than
![]() $\lambda $
and therefore the fact that
$\lambda $
and therefore the fact that
![]() $\vert {N_0}\vert =\lambda $
allows us to find a filter
$\vert {N_0}\vert =\lambda $
allows us to find a filter
![]() $H_0\times H_1$
on
$H_0\times H_1$
on
![]() ${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
that contains
${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
that contains
![]() $\langle p,q\rangle $
and is generic over
$\langle p,q\rangle $
and is generic over
![]() $N_0$
by constructing a descending sequence of conditions in
$N_0$
by constructing a descending sequence of conditions in
![]() ${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
below
${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
below
![]() $\langle p,q\rangle $
that has length
$\langle p,q\rangle $
that has length
![]() $\lambda $
and intersects all dense subsets of
$\lambda $
and intersects all dense subsets of
![]() ${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
contained in
${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
contained in
![]() $N_0$
. Moreover, since
$N_0$
. Moreover, since
![]() ${\mathrm {H}}(\lambda ^+)^{N_1}\subseteq N_0$
, we know that the filter
${\mathrm {H}}(\lambda ^+)^{N_1}\subseteq N_0$
, we know that the filter
![]() $H_0\times H_1$
is also generic over
$H_0\times H_1$
is also generic over
![]() $N_1$
.
$N_1$
.
Given
![]() $i<2$
, we now define
$i<2$
, we now define
![]() $x_i=(i\circ \pi )(\dot {x})^{H_i}$
. Set
$x_i=(i\circ \pi )(\dot {x})^{H_i}$
. Set
![]() $N=(i\circ \pi )(M_0)$
. Then
$N=(i\circ \pi )(M_0)$
. Then
![]() ${\mathrm {Add}}({\lambda },{1})\subseteq N$
,
${\mathrm {Add}}({\lambda },{1})\subseteq N$
,
![]() $(i\circ \pi )(\dot {x})\in N$
and
$(i\circ \pi )(\dot {x})\in N$
and
![]() $H_0\times H_1$
is
$H_0\times H_1$
is
![]() $({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over N. Since our first claim and the above subclaim show that
$({\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1}))$
-generic over N. Since our first claim and the above subclaim show that
holds in
![]() $M_0$
, elementarity implies that
$M_0$
, elementarity implies that
![]() $x_0$
and
$x_0$
and
![]() $x_1$
are distinct subsets of
$x_1$
are distinct subsets of
![]() $\kappa $
and
$\kappa $
and
![]() $x_0\cap x_1$
is unbounded in
$x_0\cap x_1$
is unbounded in
![]() $\kappa $
. Moreover, using Equation (7),
$\kappa $
. Moreover, using Equation (7),
![]() $\Sigma _1$
-upwards absoluteness and the fact that
$\Sigma _1$
-upwards absoluteness and the fact that
![]() $\Sigma _1$
-statements in the forcing language can be expressed by
$\Sigma _1$
-statements in the forcing language can be expressed by
![]() $\Sigma _1$
-formulas, we know that
$\Sigma _1$
-formulas, we know that
holds in
![]() $M_0$
and therefore elementarity allows us to conclude that
$M_0$
and therefore elementarity allows us to conclude that
![]() $\varphi (\kappa ,x_i,z)$
holds in
$\varphi (\kappa ,x_i,z)$
holds in
![]() $N[H_0,H_1]$
for all
$N[H_0,H_1]$
for all
![]() $i<2$
. By
$i<2$
. By
![]() $\Sigma _1$
-upwards absoluteness, this implies that
$\Sigma _1$
-upwards absoluteness, this implies that
![]() $x_0$
and
$x_0$
and
![]() $x_1$
are distinct elements of A, contradicting the fact that A is an almost disjoint family.
$x_1$
are distinct elements of A, contradicting the fact that A is an almost disjoint family.
Now, let G be
![]() ${\mathrm {Add}}({\lambda },{\kappa ^+})$
-generic over
${\mathrm {Add}}({\lambda },{\kappa ^+})$
-generic over
![]() ${\mathrm {V}}$
. Since
${\mathrm {V}}$
. Since
![]() $\lambda $
is inaccessible, the model
$\lambda $
is inaccessible, the model
![]() ${\mathrm {V}}[G]$
has the same cardinals as
${\mathrm {V}}[G]$
has the same cardinals as
![]() ${\mathrm {V}}$
. Let
${\mathrm {V}}$
. Let
![]() $\langle {G_\delta }~\vert ~{\delta <\kappa ^+}\rangle $
denote the induced sequence of filters on
$\langle {G_\delta }~\vert ~{\delta <\kappa ^+}\rangle $
denote the induced sequence of filters on
![]() ${\mathrm {Add}}({\lambda },{1})$
. Given
${\mathrm {Add}}({\lambda },{1})$
. Given
![]() $\delta <\varepsilon <\kappa ^+$
, the filter
$\delta <\varepsilon <\kappa ^+$
, the filter
![]() $G_\delta \times G_\varepsilon $
on
$G_\delta \times G_\varepsilon $
on
![]() ${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
is generic over
${\mathrm {Add}}({\lambda },{1})\times {\mathrm {Add}}({\lambda },{1})$
is generic over
![]() ${\mathrm {V}}$
and therefore the previous claim implies that
${\mathrm {V}}$
and therefore the previous claim implies that
![]() $\dot {\gamma }^{G_\delta }\neq \dot {\gamma }^{G_\varepsilon }$
. In particular, the map
$\dot {\gamma }^{G_\delta }\neq \dot {\gamma }^{G_\varepsilon }$
. In particular, the map
is an injection. Since
![]() $j(\kappa )<\kappa ^+$
, this yields a contradiction.
$j(\kappa )<\kappa ^+$
, this yields a contradiction.
The conclusion of Theorem 1.3 provably does not generalize to
![]() $\Sigma _1$
-definitions using arbitrary subsets of
$\Sigma _1$
-definitions using arbitrary subsets of
![]() $\kappa $
as parameters. If
$\kappa $
as parameters. If
![]() $\kappa $
is an infinite cardinal and
$\kappa $
is an infinite cardinal and
![]() $z\subseteq \kappa $
codes an injective sequence
$z\subseteq \kappa $
codes an injective sequence
![]() $\langle {s_\beta }~\vert ~{\beta <\kappa }\rangle $
of elements of
$\langle {s_\beta }~\vert ~{\beta <\kappa }\rangle $
of elements of
![]() ${}^{{<}\kappa }2$
with the property that the set
${}^{{<}\kappa }2$
with the property that the set
has cardinality greater than
![]() $\kappa $
, then the collection
$\kappa $
, then the collection
![]() $\{{\{{\beta <\kappa }~\vert ~{s_\beta \subseteq x}\}}~\vert ~{x\in I}\}$
is an almost disjoint family of cardinality greater than
$\{{\{{\beta <\kappa }~\vert ~{s_\beta \subseteq x}\}}~\vert ~{x\in I}\}$
is an almost disjoint family of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameter z. Note that such sequences exist for every strong limit cardinal
$\Sigma _1$
-formula with parameter z. Note that such sequences exist for every strong limit cardinal
![]() $\kappa $
, or, more generally, for every cardinal
$\kappa $
, or, more generally, for every cardinal
![]() $\kappa $
that is a strong limit cardinal in an inner model M satisfying
$\kappa $
that is a strong limit cardinal in an inner model M satisfying
![]() $(2^\kappa )^M\geq \kappa ^+$
.
$(2^\kappa )^M\geq \kappa ^+$
.
7 Long well-orders at limits of measurable cardinals
In order to motivate the statement of Theorem 1.4, we first show how classical results of Dehornoy can easily be used to show that, if
![]() $\kappa $
is a limit of measurable cardinals, then no well-ordering of
$\kappa $
is a limit of measurable cardinals, then no well-ordering of
![]() ${\mathcal {P}}({\kappa })$
is definable by a
${\mathcal {P}}({\kappa })$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. Moreover, if
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
. Moreover, if
![]() $\kappa $
has uncountable cofinality, then we can also easily show that no injection from
$\kappa $
has uncountable cofinality, then we can also easily show that no injection from
![]() $\kappa ^+$
into
$\kappa ^+$
into
![]() ${\mathcal {P}}({\kappa })$
is definable in this way. This nondefinability result will be a direct consequence of the following theorem.
${\mathcal {P}}({\kappa })$
is definable in this way. This nondefinability result will be a direct consequence of the following theorem.
Theorem 7.1. If
![]() $\delta $
is a measurable cardinal,
$\delta $
is a measurable cardinal,
![]() $z\in {\mathrm {H}}(\delta )$
and
$z\in {\mathrm {H}}(\delta )$
and
![]() $\nu $
is a cardinal with
$\nu $
is a cardinal with
![]() ${{\mathrm {cof}}(\nu )}\neq \delta $
and
${{\mathrm {cof}}(\nu )}\neq \delta $
and
![]() $\mu ^\delta <\nu $
for all
$\mu ^\delta <\nu $
for all
![]() $\mu <\nu $
, then the following statements hold for
$\mu <\nu $
, then the following statements hold for
![]() $\kappa \in \{\nu ,\nu ^+\}$
:
$\kappa \in \{\nu ,\nu ^+\}$
:
-
(i) No well-ordering of
 ${\mathcal {P}}({\kappa })$
is definable by a
${\mathcal {P}}({\kappa })$
is definable by a
 $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
 $\nu $
,
$\nu $
,
 $\nu ^+$
and z.
$\nu ^+$
and z. -
(ii) If
 ${{\mathrm {cof}}(\kappa )}>\omega $
, then no injection from
${{\mathrm {cof}}(\kappa )}>\omega $
, then no injection from
 $\kappa ^+$
into
$\kappa ^+$
into
 ${\mathcal {P}}({\kappa })$
is definable by a
${\mathcal {P}}({\kappa })$
is definable by a
 $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
 $\kappa $
and z.
$\kappa $
and z.
The proof of the above theorem is based on two standard results about measurable cardinals. A proof of the first of these lemmas is contained in the proof of [Reference Lücke and Schlicht38, Lemma 1.3]:
Lemma 7.2. Let U be a normal ultrafilter on a measurable cardinal
![]() $\delta $
, and let
$\delta $
, and let
![]() $\nu>\delta $
be a cardinal with
$\nu>\delta $
be a cardinal with
![]() ${{\mathrm {cof}}(\nu )}\neq \delta $
and
${{\mathrm {cof}}(\nu )}\neq \delta $
and
![]() $\mu ^\delta <\nu $
for all
$\mu ^\delta <\nu $
for all
![]() $\mu <\nu $
. If
$\mu <\nu $
. If
![]() ${j}:{{\mathrm {V}}}\longrightarrow {{\mathrm {Ult}}({{\mathrm {V}}},{U})}$
is the induced ultrapower embedding, than
${j}:{{\mathrm {V}}}\longrightarrow {{\mathrm {Ult}}({{\mathrm {V}}},{U})}$
is the induced ultrapower embedding, than
![]() $j(\nu )=\nu $
and
$j(\nu )=\nu $
and
![]() $j(\nu ^+)=\nu ^+$
.
$j(\nu ^+)=\nu ^+$
.
![]() $\Box $
$\Box $
Lemma 7.3. Let U be a normal ultrafilter on a measurable cardinal
![]() $\delta $
, and let
$\delta $
, and let
denote the system of iterated ultrapowers of
![]() $\langle {\mathrm {V}},\in ,U\rangle $
. If
$\langle {\mathrm {V}},\in ,U\rangle $
. If
![]() $\nu $
is a cardinal with
$\nu $
is a cardinal with
![]() ${{\mathrm {cof}}(\nu )}\neq \delta $
and
${{\mathrm {cof}}(\nu )}\neq \delta $
and
![]() $\mu ^\delta <\nu $
for all
$\mu ^\delta <\nu $
for all
![]() $\mu <\nu $
, then
$\mu <\nu $
, then
![]() $j_{0,\alpha }(\kappa )=\kappa $
holds for
$j_{0,\alpha }(\kappa )=\kappa $
holds for
![]() $\kappa \in \{\nu ,\nu ^+\}$
and all
$\kappa \in \{\nu ,\nu ^+\}$
and all
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
Proof. We start by using induction to show that
![]() $j_{0,\alpha }(\nu )=\nu $
holds for all
$j_{0,\alpha }(\nu )=\nu $
holds for all
![]() $\alpha <\nu $
. In the successor case, the desired conclusion follows directly from the induction hypothesis and an application of Lemma 7.2 in
$\alpha <\nu $
. In the successor case, the desired conclusion follows directly from the induction hypothesis and an application of Lemma 7.2 in
![]() $N_\alpha $
. Hence, we may assume that
$N_\alpha $
. Hence, we may assume that
![]() $\alpha $
is a limit ordinal. Pick
$\alpha $
is a limit ordinal. Pick
![]() $\bar {\alpha }<\alpha $
and
$\bar {\alpha }<\alpha $
and
![]() $\xi <\nu $
. Then elementarity allows us to apply [Reference Kanamori28, Corollary 19.7. (a)] in
$\xi <\nu $
. Then elementarity allows us to apply [Reference Kanamori28, Corollary 19.7. (a)] in
![]() $N_{\bar {\alpha }}$
to conclude that
$N_{\bar {\alpha }}$
to conclude that
![]() $j_{\bar {\alpha },\alpha }(\xi )<\nu $
. Since every element of
$j_{\bar {\alpha },\alpha }(\xi )<\nu $
. Since every element of
![]() $j_{0,\alpha }(\nu )\geq \nu $
is of the form
$j_{0,\alpha }(\nu )\geq \nu $
is of the form
![]() $j_{\bar {\alpha },\alpha }(\xi )$
for some
$j_{\bar {\alpha },\alpha }(\xi )$
for some
![]() $\bar {\alpha }<\alpha $
and
$\bar {\alpha }<\alpha $
and
![]() $\xi <j_{0,\bar {\alpha }}(\nu )=\nu $
, these computations show that
$\xi <j_{0,\bar {\alpha }}(\nu )=\nu $
, these computations show that
![]() $j_{0,\alpha }(\nu )=\nu $
holds.
$j_{0,\alpha }(\nu )=\nu $
holds.
Next, we inductively show that
![]() $j_{0,\alpha }(\nu )<\nu ^+$
holds for all
$j_{0,\alpha }(\nu )<\nu ^+$
holds for all
![]() $\alpha <\nu ^+$
, where the successor step is again a direct consequence of the induction hypothesis and Lemma 7.2. In the other case, if
$\alpha <\nu ^+$
, where the successor step is again a direct consequence of the induction hypothesis and Lemma 7.2. In the other case, if
![]() $\alpha \in \nu ^+\cap {\mathrm {Lim}}$
and
$\alpha \in \nu ^+\cap {\mathrm {Lim}}$
and
![]() $j_{0,\bar {\alpha }}(\nu )<\nu ^+$
holds for all
$j_{0,\bar {\alpha }}(\nu )<\nu ^+$
holds for all
![]() $\bar {\alpha }<\alpha $
, then every element of
$\bar {\alpha }<\alpha $
, then every element of
![]() $j_{0,\alpha }(\nu )$
is of the form
$j_{0,\alpha }(\nu )$
is of the form
![]() $j_{\bar {\alpha },\alpha }(\xi )$
with
$j_{\bar {\alpha },\alpha }(\xi )$
with
![]() $\bar {\alpha }<\alpha $
and
$\bar {\alpha }<\alpha $
and
![]() $\xi <j_{0,\bar {\alpha }}(\nu )$
and this shows that
$\xi <j_{0,\bar {\alpha }}(\nu )$
and this shows that
![]() $\vert {j_{0,\alpha }(\nu )}\vert \leq \nu \cdot \vert {\alpha }\vert <\nu ^+$
.
$\vert {j_{0,\alpha }(\nu )}\vert \leq \nu \cdot \vert {\alpha }\vert <\nu ^+$
.
Finally, we have
![]() $\nu ^+\leq j_{0,\alpha }(\nu ^+)\leq \vert {j_{0,\alpha }(\nu )}\vert ^+$
for all
$\nu ^+\leq j_{0,\alpha }(\nu ^+)\leq \vert {j_{0,\alpha }(\nu )}\vert ^+$
for all
![]() $\alpha <\nu ^+$
. Since the above computations show that
$\alpha <\nu ^+$
. Since the above computations show that
![]() $\vert {j_{0,\alpha }(\nu )}\vert =\nu $
holds for all
$\vert {j_{0,\alpha }(\nu )}\vert =\nu $
holds for all
![]() $\alpha <\nu ^+$
, this shows that
$\alpha <\nu ^+$
, this shows that
![]() $j_{0,\alpha }(\nu ^+)=\nu ^+$
holds for all
$j_{0,\alpha }(\nu ^+)=\nu ^+$
holds for all
![]() $\alpha <\nu ^+$
.
$\alpha <\nu ^+$
.
Proof of Theorem 7.1
Let U be a normal ultrafilter on a measurable cardinal
![]() $\delta $
, and let
$\delta $
, and let
denote the system of iterated ultrapowers of
![]() $\langle {\mathrm {V}},\in ,U\rangle $
. Moreover, for every
$\langle {\mathrm {V}},\in ,U\rangle $
. Moreover, for every
![]() $\alpha \in {\mathrm {Lim}}$
, we define
$\alpha \in {\mathrm {Lim}}$
, we define
![]() ${M_\alpha =\bigcap \{{N_\xi }~\vert ~{\xi <\alpha }\}}$
. Then [Reference Dehornoy11, Proposition 1.6.1] shows that each
${M_\alpha =\bigcap \{{N_\xi }~\vert ~{\xi <\alpha }\}}$
. Then [Reference Dehornoy11, Proposition 1.6.1] shows that each
![]() $M_\alpha $
is an inner model of
$M_\alpha $
is an inner model of
![]() ${\mathrm {ZF}}$
.
${\mathrm {ZF}}$
.
(i) Assume, towards a contradiction, that there is a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_4)$
with the property that
$\varphi (v_0,\ldots ,v_4)$
with the property that
is a well-ordering of
![]() ${\mathcal {P}}({\kappa })$
. For all
${\mathcal {P}}({\kappa })$
. For all
![]() $\alpha \in {\mathrm {On}}$
, we define
$\alpha \in {\mathrm {On}}$
, we define
![]() $\lhd _\alpha =j_{0,\alpha }({\lhd })$
. Given
$\lhd _\alpha =j_{0,\alpha }({\lhd })$
. Given
![]() $\alpha <\omega ^2$
, Lemma 7.3 implies that
$\alpha <\omega ^2$
, Lemma 7.3 implies that
![]() $j_{0,\alpha }(\nu )=\nu $
and
$j_{0,\alpha }(\nu )=\nu $
and
![]() $j_{0,\alpha }(\nu ^+)=\nu ^+$
. In particular, elementarity implies that
$j_{0,\alpha }(\nu ^+)=\nu ^+$
. In particular, elementarity implies that
![]() $\lhd _\alpha $
is a well-ordering of
$\lhd _\alpha $
is a well-ordering of
![]() ${\mathcal {P}}({\kappa })^{N_\alpha }$
and the sequence
${\mathcal {P}}({\kappa })^{N_\alpha }$
and the sequence
![]() $\langle {\lhd _{\alpha +\beta }}~\vert ~{\beta <\omega ^2}\rangle $
is an element of
$\langle {\lhd _{\alpha +\beta }}~\vert ~{\beta <\omega ^2}\rangle $
is an element of
![]() $N_\alpha $
. By our assumptions, elementarity and
$N_\alpha $
. By our assumptions, elementarity and
![]() $\Sigma _1$
-upwards absoluteness imply that
$\Sigma _1$
-upwards absoluteness imply that
![]() ${\lhd _\beta }\subseteq {\lhd _\alpha }\subseteq {\lhd }$
for all
${\lhd _\beta }\subseteq {\lhd _\alpha }\subseteq {\lhd }$
for all
![]() $\alpha \leq \beta <\omega ^2$
. Define
$\alpha \leq \beta <\omega ^2$
. Define
![]() ${\blacktriangleleft }=\bigcap \{{\lhd _\alpha }~\vert ~{\alpha <\omega ^2}\}$
. If
${\blacktriangleleft }=\bigcap \{{\lhd _\alpha }~\vert ~{\alpha <\omega ^2}\}$
. If
![]() $\alpha <\omega ^2$
, then
$\alpha <\omega ^2$
, then
![]() ${\blacktriangleleft }=\bigcap \{{\lhd _{\alpha +\beta }}~\vert ~{\beta <\omega ^2}\}$
and therefore
${\blacktriangleleft }=\bigcap \{{\lhd _{\alpha +\beta }}~\vert ~{\beta <\omega ^2}\}$
and therefore
![]() ${\blacktriangleleft }\in N_\alpha $
. This shows that
${\blacktriangleleft }\in N_\alpha $
. This shows that
![]() ${\blacktriangleleft }$
is an element of
${\blacktriangleleft }$
is an element of
![]() $M_{\omega ^2}$
, and it follows that
$M_{\omega ^2}$
, and it follows that
![]() ${\blacktriangleleft }$
is a well-ordering of
${\blacktriangleleft }$
is a well-ordering of
![]() ${\mathcal {P}}({\kappa })^{M_{\omega ^2}}$
. But this yields a contradiction because [Reference Dehornoy11, Theorem 5.3.4] shows that
${\mathcal {P}}({\kappa })^{M_{\omega ^2}}$
. But this yields a contradiction because [Reference Dehornoy11, Theorem 5.3.4] shows that
![]() $M_{\omega ^2}$
contains a subset
$M_{\omega ^2}$
contains a subset
![]() $\mathcal {G}_{\omega ^2}$
of
$\mathcal {G}_{\omega ^2}$
of
![]() ${\mathcal {P}}({j_{0,\omega ^2}(\delta )})$
with the property that
${\mathcal {P}}({j_{0,\omega ^2}(\delta )})$
with the property that
![]() $M_{\omega ^2}$
does not contain a well-ordering of the set
$M_{\omega ^2}$
does not contain a well-ordering of the set
![]() $\mathcal {G}_{\omega ^2}$
.
$\mathcal {G}_{\omega ^2}$
.
(ii) Assume, towards a contradiction, that
![]() ${{\mathrm {cof}}(\kappa )}>\omega $
and there is an injection
${{\mathrm {cof}}(\kappa )}>\omega $
and there is an injection
![]() ${\iota }:{\kappa ^+}\longrightarrow {{\mathcal {P}}({\kappa })}$
that is definable by a
${\iota }:{\kappa ^+}\longrightarrow {{\mathcal {P}}({\kappa })}$
that is definable by a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_3)$
and the parameters
$\varphi (v_0,\ldots ,v_3)$
and the parameters
![]() $\kappa $
and z.
$\kappa $
and z.
Claim. If
![]() $\alpha <\kappa $
, then
$\alpha <\kappa $
, then
![]() $j_{0,\alpha }(\iota )=\iota $
.
$j_{0,\alpha }(\iota )=\iota $
.
Proof of the claim
Since Lemma 7.3 shows that
![]() $j_{0,\alpha }(\kappa )=\kappa $
, we also know that
$j_{0,\alpha }(\kappa )=\kappa $
, we also know that
![]() $j_{0,\alpha }(\kappa ^+)=\kappa ^+$
and therefore elementarity implies that
$j_{0,\alpha }(\kappa ^+)=\kappa ^+$
and therefore elementarity implies that
![]() $j_{0,\alpha }(\iota )$
is an injection from
$j_{0,\alpha }(\iota )$
is an injection from
![]() $\kappa ^+$
into
$\kappa ^+$
into
![]() ${\mathcal {P}}({\kappa })$
that is definable in
${\mathcal {P}}({\kappa })$
that is definable in
![]() $N_\alpha $
by the formula
$N_\alpha $
by the formula
![]() $\varphi $
and the parameters
$\varphi $
and the parameters
![]() $\kappa $
and z. But then
$\kappa $
and z. But then
![]() $\Sigma _1$
-upwards absoluteness implies that
$\Sigma _1$
-upwards absoluteness implies that
![]() $j_{0,\alpha }(\iota )\subseteq \iota $
and this allows us to conclude that
$j_{0,\alpha }(\iota )\subseteq \iota $
and this allows us to conclude that
![]() $j_{0,\alpha }(\iota )=\iota $
.
$j_{0,\alpha }(\iota )=\iota $
.
The above claim directly implies that the injection
![]() $\iota $
is an element of
$\iota $
is an element of
![]() $ M_\kappa $
. By [Reference Dehornoy11, Theorem B. (i)], the fact that
$ M_\kappa $
. By [Reference Dehornoy11, Theorem B. (i)], the fact that
![]() ${{\mathrm {cof}}(\kappa )}>\omega $
implies that
${{\mathrm {cof}}(\kappa )}>\omega $
implies that
![]() $N_\kappa = M_\kappa =\bigcap _{\alpha <\kappa }N_\alpha $
and hence
$N_\kappa = M_\kappa =\bigcap _{\alpha <\kappa }N_\alpha $
and hence
![]() $\vert {{\mathcal {P}}({\kappa })^{N_\kappa }}\vert \geq \kappa ^+$
. Since
$\vert {{\mathcal {P}}({\kappa })^{N_\kappa }}\vert \geq \kappa ^+$
. Since
![]() $N_\kappa $
is a direct limit and
$N_\kappa $
is a direct limit and
![]() $j_{0,\kappa }(\delta )=\kappa $
, we also know that
$j_{0,\kappa }(\delta )=\kappa $
, we also know that
But our assumptions imply that
![]() $2^\delta <\kappa $
and therefore
$2^\delta <\kappa $
and therefore
holds for all
![]() $\alpha <\kappa $
. We can now conclude that
$\alpha <\kappa $
. We can now conclude that
![]() $\vert {{\mathcal {P}}({\kappa })^{N_\kappa }}\vert =\kappa $
, a contradiction.
$\vert {{\mathcal {P}}({\kappa })^{N_\kappa }}\vert =\kappa $
, a contradiction.
Corollary 7.4. Let
![]() $\kappa $
be a limit of measurable cardinals.
$\kappa $
be a limit of measurable cardinals.
-
(i) No well-ordering of
 ${\mathcal {P}}({\kappa })$
is definable by a
${\mathcal {P}}({\kappa })$
is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 ${\mathrm {H}}(\kappa )\cup \{\kappa ,\kappa ^+\}$
.
${\mathrm {H}}(\kappa )\cup \{\kappa ,\kappa ^+\}$
. -
(ii) If
 ${{\mathrm {cof}}(\kappa )}>\omega $
, then no injection from
${{\mathrm {cof}}(\kappa )}>\omega $
, then no injection from
 $\kappa ^+$
into
$\kappa ^+$
into
 ${\mathcal {P}}({\kappa })$
is definable by a
${\mathcal {P}}({\kappa })$
is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
 $\Box $
$\Box $
We now proceed by proving our result on the nonexistence of long
![]() $\Sigma _1$
-well-orders.
$\Sigma _1$
-well-orders.
Proof of Theorem 1.4
Let
![]() $\kappa $
be a limit of measurable cardinals with
$\kappa $
be a limit of measurable cardinals with
![]() ${{\mathrm {cof}}(\kappa )}=\omega $
, let D be a subset of
${{\mathrm {cof}}(\kappa )}=\omega $
, let D be a subset of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
and let
$\kappa $
and let
![]() $\lhd $
be a well-ordering of D that is definable by a
$\lhd $
be a well-ordering of D that is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
. Then D is definable in the same way and we can pick
$\kappa $
. Then D is definable in the same way and we can pick
![]() $\Sigma _1$
-formulas
$\Sigma _1$
-formulas
![]() $\varphi (v_0,v_1)$
and
$\varphi (v_0,v_1)$
and
![]() $\psi (v_0,v_1,v_2)$
with
$\psi (v_0,v_1,v_2)$
with
![]() $D=\{{x}~\vert ~{\varphi (x,\kappa )}\}$
and
$D=\{{x}~\vert ~{\varphi (x,\kappa )}\}$
and
![]() $\lhd = \{{\langle x,y\rangle }~\vert ~{\psi (x,y,\kappa )}\}$
. Now, use Lemma 2.1 to find
$\lhd = \{{\langle x,y\rangle }~\vert ~{\psi (x,y,\kappa )}\}$
. Now, use Lemma 2.1 to find
![]() $x\in D$
and systems
$x\in D$
and systems
![]() $\langle {\nu _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
$\langle {\nu _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
![]() $\langle {\kappa _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
$\langle {\kappa _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
![]() $\langle {U_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
and
$\langle {U_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
and
![]() $\langle {I_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
with the listed properties. Pick an
$\langle {I_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
with the listed properties. Pick an
![]() ${\mathrm {Add}}({\omega },{1})$
-nice name
${\mathrm {Add}}({\omega },{1})$
-nice name
![]() $\dot {x}$
for a subset of
$\dot {x}$
for a subset of
![]() $\kappa $
such that
$\kappa $
such that
![]() $\dot {x}^G=i^{I_{c_G}}_{0,\infty }(x)$
holds whenever G is
$\dot {x}^G=i^{I_{c_G}}_{0,\infty }(x)$
holds whenever G is
![]() ${\mathrm {Add}}({\omega },{1})$
-generic over
${\mathrm {Add}}({\omega },{1})$
-generic over
![]() ${\mathrm {V}}$
,
${\mathrm {V}}$
,
![]() $c_G=\bigcup G\in ({}^\omega 2)^{{\mathrm {V}}[G]}$
and
$c_G=\bigcup G\in ({}^\omega 2)^{{\mathrm {V}}[G]}$
and
![]() $I_{c_G}$
is the unique linear iteration of
$I_{c_G}$
is the unique linear iteration of
![]() $\langle {\mathrm {V}},\{{U_{c_G\restriction n}}~\vert ~{n<\omega }\}\rangle $
of length
$\langle {\mathrm {V}},\{{U_{c_G\restriction n}}~\vert ~{n<\omega }\}\rangle $
of length
![]() $\sup _{n<\omega }{\mathrm {lh}}({I_{c_G\restriction n}}){}$
in
$\sup _{n<\omega }{\mathrm {lh}}({I_{c_G\restriction n}}){}$
in
![]() ${\mathrm {V}}[G]$
with
${\mathrm {V}}[G]$
with
![]() $U^{I_G}_\alpha =U^{I_{c_G\restriction n}}_\alpha $
for all
$U^{I_G}_\alpha =U^{I_{c_G\restriction n}}_\alpha $
for all
![]() $n<\omega $
and
$n<\omega $
and
![]() $\alpha <{\mathrm {lh}}({I_{c_G\restriction n}}){}$
. The elementarity of
$\alpha <{\mathrm {lh}}({I_{c_G\restriction n}}){}$
. The elementarity of
![]() $i^{I_{c_G}}_{0,\infty }$
and
$i^{I_{c_G}}_{0,\infty }$
and
![]() $\Sigma _1$
-upwards absoluteness between
$\Sigma _1$
-upwards absoluteness between
![]() $M^{I_{c_G}}_\infty $
and
$M^{I_{c_G}}_\infty $
and
![]() ${\mathrm {V}}[G]$
then imply that
${\mathrm {V}}[G]$
then imply that
holds in
![]() ${\mathrm {V}}$
. Finally, let
${\mathrm {V}}$
. Finally, let
![]() ${z}:{\omega }\longrightarrow {2}$
denote the constant function with value
${z}:{\omega }\longrightarrow {2}$
denote the constant function with value
![]() $0$
and for each
$0$
and for each
![]() $n<\omega $
, set
$n<\omega $
, set
![]() $\kappa _n=\kappa _{z\restriction n}$
and
$\kappa _n=\kappa _{z\restriction n}$
and
![]() $U_n=U_{z\restriction n}$
. Then the sequence
$U_n=U_{z\restriction n}$
. Then the sequence
![]() $\langle {\kappa _n}~\vert ~{n<\omega }\rangle $
is strictly increasing and cofinal in
$\langle {\kappa _n}~\vert ~{n<\omega }\rangle $
is strictly increasing and cofinal in
![]() $\kappa $
.
$\kappa $
.
Pick a sufficiently large regular cardinal
![]() $\theta $
and a countable elementary submodel X of
$\theta $
and a countable elementary submodel X of
![]() ${\mathrm {H}}(\theta )$
containing
${\mathrm {H}}(\theta )$
containing
![]() $\kappa $
,
$\kappa $
,
![]() $\dot {x}$
,
$\dot {x}$
,
![]() $\langle {\kappa _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
$\langle {\kappa _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
,
![]() $\langle {U_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
and
$\langle {U_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
and
![]() $\langle {I_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
. Let
$\langle {I_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
. Let
![]() ${\pi }:{X}\longrightarrow {M}$
denote the corresponding transitive collapse. Define
${\pi }:{X}\longrightarrow {M}$
denote the corresponding transitive collapse. Define
![]() $\bar {\kappa }=\pi (\kappa )$
and, given
$\bar {\kappa }=\pi (\kappa )$
and, given
![]() $n<\omega $
, set
$n<\omega $
, set
![]() $\bar {\kappa }_n=\pi (\kappa _n)$
and
$\bar {\kappa }_n=\pi (\kappa _n)$
and
![]() $\bar {U}_n=\pi (U_n)$
. Then [Reference Steel49, Lemma 3.5] shows that the pair
$\bar {U}_n=\pi (U_n)$
. Then [Reference Steel49, Lemma 3.5] shows that the pair
![]() $\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
is linearly iterable. Let
$\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
is linearly iterable. Let
![]() $\bar {I}$
denote the unique linear iteration of
$\bar {I}$
denote the unique linear iteration of
![]() $\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
of length
$\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
of length
![]() $\kappa $
with the property that
$\kappa $
with the property that
holds for all
![]() $\alpha <\kappa $
. Set
$\alpha <\kappa $
. Set
![]() $N=M^{\bar {I}}_{0,\infty }$
and
$N=M^{\bar {I}}_{0,\infty }$
and
![]() ${j=i^{\bar {I}}_{0,\infty }}:{M}\longrightarrow {N}$
. Then it is easy to see that
${j=i^{\bar {I}}_{0,\infty }}:{M}\longrightarrow {N}$
. Then it is easy to see that
![]() $j(\bar {\kappa }_n)=\kappa _n$
for all
$j(\bar {\kappa }_n)=\kappa _n$
for all
![]() $n<\omega $
and this implies that
$n<\omega $
and this implies that
![]() $j(\bar {\kappa })=\kappa $
.
$j(\bar {\kappa })=\kappa $
.
Now, pick
![]() $c\in {}^\omega 2$
with the property that
$c\in {}^\omega 2$
with the property that
![]() $G_c=\{{c\restriction n}~\vert ~{n<\omega }\}$
is
$G_c=\{{c\restriction n}~\vert ~{n<\omega }\}$
is
![]() ${\mathrm {Add}}({\omega },{1})$
-generic over M. Then
${\mathrm {Add}}({\omega },{1})$
-generic over M. Then
![]() $G_c$
is also
$G_c$
is also
![]() ${\mathrm {Add}}({\omega },{1})$
-generic over N and we define
${\mathrm {Add}}({\omega },{1})$
-generic over N and we define
Claim. If
![]() $c\in {}^\omega 2$
has the property that
$c\in {}^\omega 2$
has the property that
![]() $G_c$
is
$G_c$
is
![]() ${\mathrm {Add}}({\omega },{1})$
-generic over M, then
${\mathrm {Add}}({\omega },{1})$
-generic over M, then
![]() $x_c\in D$
.
$x_c\in D$
.
Proof of the claim
By
![]() $\Sigma _1$
-absoluteness, we know that Equation (8) implies that the given forcing statement also holds in
$\Sigma _1$
-absoluteness, we know that Equation (8) implies that the given forcing statement also holds in
![]() ${\mathrm {H}}(\theta )$
. This shows that
${\mathrm {H}}(\theta )$
. This shows that
holds in N. But this allows us to conclude that
![]() $\varphi (x_c,\kappa )$
holds in
$\varphi (x_c,\kappa )$
holds in
![]() $N[G_c]$
and
$N[G_c]$
and
![]() $\Sigma _1$
-upwards absoluteness implies that this statement also holds in
$\Sigma _1$
-upwards absoluteness implies that this statement also holds in
![]() ${\mathrm {V}}$
.
${\mathrm {V}}$
.
Let E denote the set of all pairs
![]() $\langle c,d\rangle $
in
$\langle c,d\rangle $
in
![]() ${}^\omega 2\times {}^\omega 2$
with the property that
${}^\omega 2\times {}^\omega 2$
with the property that
![]() $G_c\times G_d$
is
$G_c\times G_d$
is
![]() $({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-generic over M. Then E is a comeager subset of
$({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-generic over M. Then E is a comeager subset of
![]() ${}^\omega 2\times {}^\omega 2$
and a classical result of Mycielski (see [Reference Kechris30, Theorem 19.1]) yields a continuous injection
${}^\omega 2\times {}^\omega 2$
and a classical result of Mycielski (see [Reference Kechris30, Theorem 19.1]) yields a continuous injection
![]() ${p}:{{}^\omega 2}\longrightarrow {{}^\omega 2}$
with
${p}:{{}^\omega 2}\longrightarrow {{}^\omega 2}$
with
![]() $\langle p(a),p(b)\rangle \in E$
for all distinct
$\langle p(a),p(b)\rangle \in E$
for all distinct
![]() $a,b\in {}^\omega 2$
.
$a,b\in {}^\omega 2$
.
Claim. The map
is an injection.
Proof of the claim
Given an
![]() ${\mathrm {Add}}({\omega },{1})$
-name
${\mathrm {Add}}({\omega },{1})$
-name
![]() $\dot {y}$
, let
$\dot {y}$
, let
![]() $\dot {y}_l$
and
$\dot {y}_l$
and
![]() $\dot {y}_r$
denote the canonical
$\dot {y}_r$
denote the canonical
![]() $({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-names such that
$({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-names such that
![]() $\dot {y}_l^{G_0\times G_1}=\dot {y}^{G_0}$
and
$\dot {y}_l^{G_0\times G_1}=\dot {y}^{G_0}$
and
![]() $\dot {y}_r^{G_0\times G_1}=\dot {y}^{G_1}$
holds whenever
$\dot {y}_r^{G_0\times G_1}=\dot {y}^{G_1}$
holds whenever
![]() $G_0\times G_1$
is
$G_0\times G_1$
is
![]() $({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-generic over
$({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-generic over
![]() ${\mathrm {V}}$
. If
${\mathrm {V}}$
. If
![]() $G_0\times G_1$
is
$G_0\times G_1$
is
![]() $({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-generic over
$({\mathrm {Add}}({\omega },{1})\times {\mathrm {Add}}({\omega },{1}))$
-generic over
![]() ${\mathrm {V}}$
and
${\mathrm {V}}$
and
![]() $i<2$
, then
$i<2$
, then
![]() $(I_{c_{G_i}})^{{\mathrm {V}}[G_i]}=(I_{c_{G_i}})^{{\mathrm {V}}[G_0,G_1]}$
and this shows that
$(I_{c_{G_i}})^{{\mathrm {V}}[G_i]}=(I_{c_{G_i}})^{{\mathrm {V}}[G_0,G_1]}$
and this shows that
holds for the
![]() ${\mathrm {Add}}({\omega },{1})$
-name
${\mathrm {Add}}({\omega },{1})$
-name
![]() $\dot {x}$
fixed at the beginning of the proof of Theorem 1.3. Therefore, we can apply Lemma 2.2 to see that
$\dot {x}$
fixed at the beginning of the proof of Theorem 1.3. Therefore, we can apply Lemma 2.2 to see that
holds in
![]() ${\mathrm {V}}$
and, by
${\mathrm {V}}$
and, by
![]() $\Sigma _1$
-absoluteness, this statement also holds in
$\Sigma _1$
-absoluteness, this statement also holds in
![]() ${\mathrm {H}}(\theta )$
.
${\mathrm {H}}(\theta )$
.
Now, given
![]() $a,b\in {}^\omega 2$
with
$a,b\in {}^\omega 2$
with
![]() $a\neq b$
, we have
$a\neq b$
, we have
 $$ \begin{align*} \begin{aligned} \iota(a) ~ = & ~ x_{p(a)} ~ = ~ j(\pi(\dot{x}))^{G_{p(a)}} ~ = ~ j(\pi(\dot{x}_l))^{G_{p(a)}\times G_{p(b)}} \\ & \neq ~ j(\pi(\dot{x}_r))^{G_{p(a)}\times G_{p(b)}} ~ = ~ j(\pi(\dot{x}))^{G_{p(b)}} ~ = ~ x_{p(b)} ~ = ~ \iota(b).\\[-33pt] \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \iota(a) ~ = & ~ x_{p(a)} ~ = ~ j(\pi(\dot{x}))^{G_{p(a)}} ~ = ~ j(\pi(\dot{x}_l))^{G_{p(a)}\times G_{p(b)}} \\ & \neq ~ j(\pi(\dot{x}_r))^{G_{p(a)}\times G_{p(b)}} ~ = ~ j(\pi(\dot{x}))^{G_{p(b)}} ~ = ~ x_{p(b)} ~ = ~ \iota(b).\\[-33pt] \end{aligned} \end{align*} $$
In the following, let
![]() $\blacktriangleleft $
denote the unique binary relation on
$\blacktriangleleft $
denote the unique binary relation on
![]() ${}^\omega 2$
with
${}^\omega 2$
with
for all
![]() $a,b\in {}^\omega 2$
. Then the above claim implies that
$a,b\in {}^\omega 2$
. Then the above claim implies that
![]() $\blacktriangleleft $
is a well-ordering of
$\blacktriangleleft $
is a well-ordering of
![]() ${}^\omega 2$
.
${}^\omega 2$
.
Claim. The following statements are equivalent for all
![]() $a,b\in {}^\omega 2$
:
$a,b\in {}^\omega 2$
:
-
(i)
 $a\blacktriangleleft b$
.
$a\blacktriangleleft b$
. -
(ii) There exists a countable transitive model W of
 ${\mathrm {ZFC}}^-$
and elements
${\mathrm {ZFC}}^-$
and elements
 $\delta $
,
$\delta $
,
 $\vec {\delta }$
,
$\vec {\delta }$
,
 $\vec {F}$
and I of W such that the following statements hold:
$\vec {F}$
and I of W such that the following statements hold:-
○ W contains M,
 $p(a)$
,
$p(a)$
,
 $p(b)$
and a surjection from
$p(b)$
and a surjection from
 $\omega $
onto M.
$\omega $
onto M. -
○
 $\vec {\delta }=\langle {\delta _n}~\vert ~{n<\omega }\rangle $
is a strictly increasing sequence of cardinals in W with
$\vec {\delta }=\langle {\delta _n}~\vert ~{n<\omega }\rangle $
is a strictly increasing sequence of cardinals in W with
 $\delta =\sup _{n<\omega }\delta _n$
.
$\delta =\sup _{n<\omega }\delta _n$
. -
○
 $\vec {F}=\langle {F_n}~\vert ~{n<\omega }\rangle $
is a sequence with the property that
$\vec {F}=\langle {F_n}~\vert ~{n<\omega }\rangle $
is a sequence with the property that
 $F_n$
is a normal ultrafilter on
$F_n$
is a normal ultrafilter on
 $\delta _n$
in W for all
$\delta _n$
in W for all
 $n<\omega $
.
$n<\omega $
. -
○ If
 ${k}:{\bar {W}}\longrightarrow {W}$
is an elementary embedding of a transitive model
${k}:{\bar {W}}\longrightarrow {W}$
is an elementary embedding of a transitive model
 $\bar {W}$
into W and
$\bar {W}$
into W and
 $\mathcal {E}\in \bar {W}$
satisfies
$\mathcal {E}\in \bar {W}$
satisfies
 $k(\mathcal {E})=\{{F_n}~\vert ~{n<\omega }\}$
, then the pair
$k(\mathcal {E})=\{{F_n}~\vert ~{n<\omega }\}$
, then the pair
 $\langle \bar {W},\mathcal {E}\rangle $
is
$\langle \bar {W},\mathcal {E}\rangle $
is
 $\alpha $
-iterable (see [Reference Steel49, p. 131]) for all
$\alpha $
-iterable (see [Reference Steel49, p. 131]) for all
 $\alpha <\omega _1$
.
$\alpha <\omega _1$
. -
○ I is the unique linear iteration of
 $\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
of length
$\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
of length
 $\delta $
with the property that holds for all
$\delta $
with the property that holds for all $$ \begin{align*}U^I_\alpha ~ = ~ i^I_{0,\alpha}(\bar{U}_{\min\{n<\omega\vert\alpha<\delta_n\}})\end{align*} $$
$$ \begin{align*}U^I_\alpha ~ = ~ i^I_{0,\alpha}(\bar{U}_{\min\{n<\omega\vert\alpha<\delta_n\}})\end{align*} $$
 $\alpha <\delta $
.
$\alpha <\delta $
.
-
○ The statement
holds in W. $$ \begin{align*}\psi(i^I_{0,\infty}(\pi(\dot{x}))^{G_{p(a)}},i^I_{0,\infty}(\pi(\dot{x}))^{G_{p(b)}},\delta)\end{align*} $$
$$ \begin{align*}\psi(i^I_{0,\infty}(\pi(\dot{x}))^{G_{p(a)}},i^I_{0,\infty}(\pi(\dot{x}))^{G_{p(b)}},\delta)\end{align*} $$
-
Proof of the claim
First, assume that (i) holds. Pick a sufficiently large regular cardinal
![]() $\vartheta>\theta $
and a countable elementary submodel Y of
$\vartheta>\theta $
and a countable elementary submodel Y of
![]() ${\mathrm {H}}(\vartheta )$
containing
${\mathrm {H}}(\vartheta )$
containing
![]() $\theta $
,
$\theta $
,
![]() $p(a)$
,
$p(a)$
,
![]() $p(b)$
,
$p(b)$
,
![]() $\langle {U_n}~\vert ~{n<\omega }\rangle $
, X and
$\langle {U_n}~\vert ~{n<\omega }\rangle $
, X and
![]() $\bar {I}$
. Let
$\bar {I}$
. Let
![]() ${\tau }:{Y}\longrightarrow {W}$
denote the the corresponding transitive collapse. Given
${\tau }:{Y}\longrightarrow {W}$
denote the the corresponding transitive collapse. Given
![]() $n<\omega $
, set
$n<\omega $
, set
![]() $\delta _n=\tau (\kappa _n)$
and
$\delta _n=\tau (\kappa _n)$
and
![]() $F_n=\tau (U_n)$
. Moreover, define
$F_n=\tau (U_n)$
. Moreover, define
![]() $\delta =\tau (\kappa )$
and
$\delta =\tau (\kappa )$
and
![]() $I=\tau (\bar {I})$
. In this situation, [Reference Steel49, Lemma 3.5] shows that the pair
$I=\tau (\bar {I})$
. In this situation, [Reference Steel49, Lemma 3.5] shows that the pair
![]() $\langle W,\{{F_n}~\vert ~{n<\omega }\}\rangle $
is linearly iterable. Another application of [Reference Steel49, Lemma 3.5] allows us to also conclude that
$\langle W,\{{F_n}~\vert ~{n<\omega }\}\rangle $
is linearly iterable. Another application of [Reference Steel49, Lemma 3.5] allows us to also conclude that
![]() $\langle \bar {W},\mathcal {E}\rangle $
is
$\langle \bar {W},\mathcal {E}\rangle $
is
![]() $\alpha $
-iterable, whenever
$\alpha $
-iterable, whenever
![]() $\alpha $
is a countable ordinal,
$\alpha $
is a countable ordinal,
![]() $\bar {W}$
is a transitive set,
$\bar {W}$
is a transitive set,
![]() ${k}:{\bar {W}}\longrightarrow {W}$
is an elementary embedding and
${k}:{\bar {W}}\longrightarrow {W}$
is an elementary embedding and
![]() $\mathcal {E}\in \bar {W}$
with
$\mathcal {E}\in \bar {W}$
with
![]() $k(\mathcal {E})=\{{F_n}~\vert ~{n<\omega }\}$
. Next, since we have
$k(\mathcal {E})=\{{F_n}~\vert ~{n<\omega }\}$
. Next, since we have
![]() $\delta =\sup _{n<\omega }\delta _n$
and
$\delta =\sup _{n<\omega }\delta _n$
and
![]() $\tau \restriction (M\cup \{M\})={\mathrm {id}}_{M\cup \{M\}}$
, elementarity directly implies that I is the unique linear iteration of
$\tau \restriction (M\cup \{M\})={\mathrm {id}}_{M\cup \{M\}}$
, elementarity directly implies that I is the unique linear iteration of
![]() $\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
of length
$\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
of length
![]() $\delta $
with the property that
$\delta $
with the property that
holds for all
![]() $\alpha <\delta $
. Finally, since (i) implies that
$\alpha <\delta $
. Finally, since (i) implies that
holds in
![]() ${\mathrm {H}}(\vartheta )$
, elementarity directly implies that
${\mathrm {H}}(\vartheta )$
, elementarity directly implies that
holds in W. In combination, these observations show that W,
![]() $\delta $
,
$\delta $
,
![]() $\langle {\delta _n}~\vert ~{n<\omega }\rangle $
,
$\langle {\delta _n}~\vert ~{n<\omega }\rangle $
,
![]() $\langle {F_n}~\vert ~{n<\omega }\rangle $
and I witness that (ii) holds.
$\langle {F_n}~\vert ~{n<\omega }\rangle $
and I witness that (ii) holds.
Now, assume that W,
![]() $\delta $
,
$\delta $
,
![]() $\langle {\delta _n}~\vert ~{n<\omega }\rangle $
,
$\langle {\delta _n}~\vert ~{n<\omega }\rangle $
,
![]() $\langle {F_n}~\vert ~{n<\omega }\rangle $
and I witness that (ii) holds. By [Reference Steel49, Lemma 3.6], our assumptions ensure that the pair
$\langle {F_n}~\vert ~{n<\omega }\rangle $
and I witness that (ii) holds. By [Reference Steel49, Lemma 3.6], our assumptions ensure that the pair
![]() $\langle W,\{{F_n}~\vert ~{n<\omega }\}\rangle $
is linearly iterable. Let
$\langle W,\{{F_n}~\vert ~{n<\omega }\}\rangle $
is linearly iterable. Let
![]() $I_*$
denote the unique linear iteration of
$I_*$
denote the unique linear iteration of
![]() $\langle W,\{{F_n}~\vert ~{n<\omega }\}\rangle $
of length
$\langle W,\{{F_n}~\vert ~{n<\omega }\}\rangle $
of length
![]() $\kappa $
with the property that
$\kappa $
with the property that
holds for all
![]() $\alpha <\kappa $
. Then we have
$\alpha <\kappa $
. Then we have
![]() $i^{I_*}_{0,\infty }(\delta _n)=\kappa _n$
for all
$i^{I_*}_{0,\infty }(\delta _n)=\kappa _n$
for all
![]() $n<\omega $
and
$n<\omega $
and
![]() $i^{I_*}_{0,\infty }(\delta )=\kappa $
. Moreover, we know that
$i^{I_*}_{0,\infty }(\delta )=\kappa $
. Moreover, we know that
This shows that
![]() $i^{I_*}_{0,\infty }(I)$
is a linear iteration of
$i^{I_*}_{0,\infty }(I)$
is a linear iteration of
![]() $\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
of length
$\langle M,\{{\bar {U}_n}~\vert ~{n<\omega }\}\rangle $
of length
![]() $\kappa $
with the property that
$\kappa $
with the property that
holds for all
![]() $\alpha <\kappa $
, and this implies that
$\alpha <\kappa $
, and this implies that
![]() $i^{I_*}_{0,\infty }(I)=\bar {I}$
holds. In particular, it follows that
$i^{I_*}_{0,\infty }(I)=\bar {I}$
holds. In particular, it follows that
holds for all
![]() $y\in M$
. By our assumptions and the above observations, this shows that
$y\in M$
. By our assumptions and the above observations, this shows that
holds in
![]() $M^{I_*}_{0,\infty }$
. Using
$M^{I_*}_{0,\infty }$
. Using
![]() $\Sigma _1$
-upwards absoluteness, we know that
$\Sigma _1$
-upwards absoluteness, we know that
![]() $\psi (x_{p(a)},x_{p(b)},\kappa )$
holds in
$\psi (x_{p(a)},x_{p(b)},\kappa )$
holds in
![]() ${\mathrm {V}}$
and this shows that (i) holds in this case.
${\mathrm {V}}$
and this shows that (i) holds in this case.
Since the above claim shows that the relation
![]() $\blacktriangleleft $
is definable over
$\blacktriangleleft $
is definable over
![]() ${\mathrm {H}}(\aleph _1)$
by a
${\mathrm {H}}(\aleph _1)$
by a
![]() $\Sigma _2$
-formula with parameters, we can conclude that
$\Sigma _2$
-formula with parameters, we can conclude that
![]() $\blacktriangleleft $
is a
$\blacktriangleleft $
is a
![]() $\mathbf {\Sigma }^1_3$
-subset of
$\mathbf {\Sigma }^1_3$
-subset of
![]() ${}^\omega 2\times {}^\omega 2$
(see [Reference Jech25, Lemma 25.25]). This completes the proof of the theorem.
${}^\omega 2\times {}^\omega 2$
(see [Reference Jech25, Lemma 25.25]). This completes the proof of the theorem.
We end this section by proving the equiconsistency stated in Theorem 1.5. One direction is given by the following lemma that follows from arguments presented in the proof of Theorem 4.1.Footnote 6
Lemma 7.5. Assume that there is no inner model with infinitely many measurable cardinals. If
![]() $\kappa $
is a singular cardinal, then there exists an injection from
$\kappa $
is a singular cardinal, then there exists an injection from
![]() $\kappa ^+$
into
$\kappa ^+$
into
![]() ${\mathcal {P}}({\kappa })$
that is definable by a
${\mathcal {P}}({\kappa })$
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
.
Proof. As in the proof of Theorem 4.1 in Section 4, we know that
![]() $0^{\text {long}}$
does not exist and we let
$0^{\text {long}}$
does not exist and we let
![]() $U_{can}$
denote the canonical sequence of measures as in [Reference Koepke31]. We again set
$U_{can}$
denote the canonical sequence of measures as in [Reference Koepke31]. We again set
![]() $U=U_{can}\restriction \kappa $
and
$U=U_{can}\restriction \kappa $
and
![]() ${\mathrm {K}}={\mathrm {K}}[U]$
. Then our assumptions imply that
${\mathrm {K}}={\mathrm {K}}[U]$
. Then our assumptions imply that
![]() $U\in {\mathrm {H}}(\kappa )^{\mathrm {K}}$
and the results of [Reference Koepke31] show that
$U\in {\mathrm {H}}(\kappa )^{\mathrm {K}}$
and the results of [Reference Koepke31] show that
![]() ${\mathrm {K}}$
is an inner model of
${\mathrm {K}}$
is an inner model of
![]() ${\mathrm {ZFC}}$
with a canonical well-ordering
${\mathrm {ZFC}}$
with a canonical well-ordering
![]() $<_{\mathrm {K}}$
. Since the domain of
$<_{\mathrm {K}}$
. Since the domain of
![]() $U_{can}$
is finite, we can again combine [Reference Koepke31, Theorem 3.9], [Reference Koepke31, Theorem 3.19] and [Reference Koepke31, Theorem 3.23] to show that
$U_{can}$
is finite, we can again combine [Reference Koepke31, Theorem 3.9], [Reference Koepke31, Theorem 3.19] and [Reference Koepke31, Theorem 3.23] to show that
![]() $\kappa ^+=(\kappa ^+)^{\mathrm {K}}$
.
$\kappa ^+=(\kappa ^+)^{\mathrm {K}}$
.
Given
![]() $\kappa \leq \gamma <\kappa ^+$
, we let
$\kappa \leq \gamma <\kappa ^+$
, we let
![]() $y_\gamma $
denote the subset of
$y_\gamma $
denote the subset of
![]() $\kappa $
that canonically codes the
$\kappa $
that canonically codes the
![]() $<_{\mathrm {K}}$
-least bijection between
$<_{\mathrm {K}}$
-least bijection between
![]() $\kappa $
and
$\kappa $
and
![]() $\gamma $
. As in the proof of Theorem 4.1, we can now conclude that the unique injection
$\gamma $
. As in the proof of Theorem 4.1, we can now conclude that the unique injection
![]() ${\iota }:{\kappa ^+}\longrightarrow {{\mathcal {P}}({\kappa })}$
with
${\iota }:{\kappa ^+}\longrightarrow {{\mathcal {P}}({\kappa })}$
with
![]() $\iota \restriction \kappa ={\mathrm {id}}_\kappa $
and
$\iota \restriction \kappa ={\mathrm {id}}_\kappa $
and
![]() $\iota (\gamma )=y_\gamma $
for all
$\iota (\gamma )=y_\gamma $
for all
![]() $\kappa \leq \gamma <\kappa ^+$
can be defined by a
$\kappa \leq \gamma <\kappa ^+$
can be defined by a
![]() $\Sigma _1$
-formula and the parameters
$\Sigma _1$
-formula and the parameters
![]() $\kappa $
and U.
$\kappa $
and U.
The next lemma is needed in the converse direction of our equiconsistency proof:
Lemma 7.6. Let U be a normal ultrafilter on a measurable cardinal
![]() $\delta $
, let
$\delta $
, let
![]() $\alpha <\delta $
, let
$\alpha <\delta $
, let
![]() $\mathcal {E}$
be a set of normal ultrafilters on cardinals smaller than
$\mathcal {E}$
be a set of normal ultrafilters on cardinals smaller than
![]() $\alpha $
and let I be a linear iteration of
$\alpha $
and let I be a linear iteration of
![]() $\langle {\mathrm {V}},\mathcal {E}\rangle $
of length less than
$\langle {\mathrm {V}},\mathcal {E}\rangle $
of length less than
![]() $\alpha $
. If
$\alpha $
. If
![]() $B\in i^I_{0,\infty }(U)$
, then there is
$B\in i^I_{0,\infty }(U)$
, then there is
![]() $A\in U$
with
$A\in U$
with
![]() $i^I_{0,\infty }(A)\subseteq B$
.
$i^I_{0,\infty }(A)\subseteq B$
.
Proof. Using [Reference Kanamori28, Exercise 12], we find a function
![]() ${f}:{[\alpha ]^{{<}\omega }}\longrightarrow {U}$
with the property that
${f}:{[\alpha ]^{{<}\omega }}\longrightarrow {U}$
with the property that
![]() $B\in {{\mathrm {ran}}(i^I_{0,\infty }(f))}$
. If we now define
$B\in {{\mathrm {ran}}(i^I_{0,\infty }(f))}$
. If we now define
then A is an element of U with the desired properties.
In order to complete the proof of Theorem 1.5, we will now use diagonal Prikry forcing and a characterisation of generic sequences for this forcing due to Fuchs [Reference Fuchs14] to construct a model without
![]() $\Sigma _1$
-definable long well-orderings from an infinite sequence of measurable cardinals.
$\Sigma _1$
-definable long well-orderings from an infinite sequence of measurable cardinals.
Proof of Theorem 1.5
Assume that
![]() $\vec {\kappa }=\langle {\kappa (n)}~\vert ~{n<\omega }\rangle $
is a strictly increasing sequence of measurable cardinals with limit
$\vec {\kappa }=\langle {\kappa (n)}~\vert ~{n<\omega }\rangle $
is a strictly increasing sequence of measurable cardinals with limit
![]() $\kappa $
. Pick a sequence
$\kappa $
. Pick a sequence
![]() $\vec {U}=\langle {U(n)}~\vert ~{n<\omega }\rangle $
with the property that
$\vec {U}=\langle {U(n)}~\vert ~{n<\omega }\rangle $
with the property that
![]() $U(n)$
is a normal ultrafilter on
$U(n)$
is a normal ultrafilter on
![]() $\kappa (n)$
for each
$\kappa (n)$
for each
![]() $n<\omega $
. Let
$n<\omega $
. Let
![]() ${\mathbb {P}}_{\vec {U}}$
denote the diagonal Prikry forcing associated to the sequence
${\mathbb {P}}_{\vec {U}}$
denote the diagonal Prikry forcing associated to the sequence
![]() $\vec {U}$
(see [Reference Gitik15, Section 1.3]), that is,
$\vec {U}$
(see [Reference Gitik15, Section 1.3]), that is,
![]() ${\mathbb {P}}_{\vec {U}}$
is the partial order defined by the following clauses:
${\mathbb {P}}_{\vec {U}}$
is the partial order defined by the following clauses:
-
○ Conditions in
 ${\mathbb {P}}_{\vec {U}}$
are sequences
${\mathbb {P}}_{\vec {U}}$
are sequences
 $p=\langle {p_n}~\vert ~{n<\omega }\rangle $
with the property that there exists a natural number
$p=\langle {p_n}~\vert ~{n<\omega }\rangle $
with the property that there exists a natural number
 $l_p$
such that
$l_p$
such that
 $p_n\in \kappa (n)$
for all
$p_n\in \kappa (n)$
for all
 $n<l_p$
and
$n<l_p$
and
 $p_n\in U(n)$
for all
$p_n\in U(n)$
for all
 $l_p\leq n<\omega $
.
$l_p\leq n<\omega $
. -
○ Given conditions p and q in
 ${\mathbb {P}}_{\vec {U}}$
, we have
${\mathbb {P}}_{\vec {U}}$
, we have
 $p\leq _{{\mathbb {P}}_{\vec {U}}}q$
if and only if
$p\leq _{{\mathbb {P}}_{\vec {U}}}q$
if and only if
 $l_q\leq l_p$
,
$l_q\leq l_p$
,
 $p_n=q_n$
for all
$p_n=q_n$
for all
 $n<l_q$
,
$n<l_q$
,
 $q_n\in p_n$
for all
$q_n\in p_n$
for all
 $l_q\leq n<l_p$
and
$l_q\leq n<l_p$
and
 $p_n\subseteq q_n$
for all
$p_n\subseteq q_n$
for all
 $l_p\leq n<\omega $
.
$l_p\leq n<\omega $
.
By [Reference Gitik15, Lemma 1.35], forcing with
![]() ${\mathbb {P}}_{\vec {U}}$
does not add bounded subsets of
${\mathbb {P}}_{\vec {U}}$
does not add bounded subsets of
![]() $\kappa $
.
$\kappa $
.
Given a filter G on
![]() ${\mathbb {P}}_{\vec {U}}$
, we let
${\mathbb {P}}_{\vec {U}}$
, we let
![]() $c_G$
denote the unique function with domain
$c_G$
denote the unique function with domain
![]() $\sup _{p\in G}l_p\leq \omega $
and
$\sup _{p\in G}l_p\leq \omega $
and
![]() $c_G(n)=p_n$
for all
$c_G(n)=p_n$
for all
![]() $p\in G$
and
$p\in G$
and
![]() $n<l_p$
. In the other direction, given a sequence c contained in the set
$n<l_p$
. In the other direction, given a sequence c contained in the set
![]() $\prod \vec {\kappa }$
of all functions
$\prod \vec {\kappa }$
of all functions
![]() $d\in {}^\omega \kappa $
with
$d\in {}^\omega \kappa $
with
![]() $d(n)<\kappa (n)$
for all
$d(n)<\kappa (n)$
for all
![]() $n<\omega $
, we let
$n<\omega $
, we let
![]() $G_c$
denote the set of all conditions p in
$G_c$
denote the set of all conditions p in
![]() ${\mathbb {P}}_{\vec {U}}$
with
${\mathbb {P}}_{\vec {U}}$
with
![]() $p_n=c(n)$
for all
$p_n=c(n)$
for all
![]() $n<l_p$
and
$n<l_p$
and
![]() $c(n)\in p_n$
for all
$c(n)\in p_n$
for all
![]() $l_p\leq n<\omega $
. It is easy to see that
$l_p\leq n<\omega $
. It is easy to see that
![]() $G_c$
is a filter on
$G_c$
is a filter on
![]() ${\mathbb {P}}_{\vec {U}}$
with
${\mathbb {P}}_{\vec {U}}$
with
![]() $c_{G_c}=c$
in this situation. Given an inner model M that contains
$c_{G_c}=c$
in this situation. Given an inner model M that contains
![]() $\vec {U}$
and
$\vec {U}$
and
![]() $c\in \prod \vec {\kappa }$
, we say that c is
$c\in \prod \vec {\kappa }$
, we say that c is
![]() $\vec {U}$
-generic over M if
$\vec {U}$
-generic over M if
![]() $G_c$
is
$G_c$
is
![]() ${\mathbb {P}}_{\vec {U}}$
-generic over M. The results of [Reference Fuchs14] then show that a sequence
${\mathbb {P}}_{\vec {U}}$
-generic over M. The results of [Reference Fuchs14] then show that a sequence
![]() $c\in \prod \vec {\kappa }$
is
$c\in \prod \vec {\kappa }$
is
![]() $\vec {U}$
-generic over an inner model M if and only if
$\vec {U}$
-generic over an inner model M if and only if
![]() $\{{n<\omega }~\vert ~{c(n)\in A_n}\}$
is a cofinite subset of
$\{{n<\omega }~\vert ~{c(n)\in A_n}\}$
is a cofinite subset of
![]() $\omega $
for every sequence
$\omega $
for every sequence
![]() $\langle {A_n\in U(n)}~\vert ~{n<\omega }\rangle $
in M. Using [Reference Grigorieff19, Theorem 3.5.1], this characterization can be used to show that the Boolean completion of
$\langle {A_n\in U(n)}~\vert ~{n<\omega }\rangle $
in M. Using [Reference Grigorieff19, Theorem 3.5.1], this characterization can be used to show that the Boolean completion of
![]() ${\mathbb {P}}_{\vec {U}}$
is weakly homogeneous and therefore every statement in the forcing language of
${\mathbb {P}}_{\vec {U}}$
is weakly homogeneous and therefore every statement in the forcing language of
![]() ${\mathbb {P}}_{\vec {U}}$
that uses only ground model elements as parameters is decided by
${\mathbb {P}}_{\vec {U}}$
that uses only ground model elements as parameters is decided by ![]() .
.
Now, let G be
![]() ${\mathbb {P}}_{\vec {U}}$
-generic over
${\mathbb {P}}_{\vec {U}}$
-generic over
![]() ${\mathrm {V}}$
and assume that, in
${\mathrm {V}}$
and assume that, in
![]() ${\mathrm {V}}[G]$
, there exists a well-ordering
${\mathrm {V}}[G]$
, there exists a well-ordering
![]() $\lhd $
of a subset D of
$\lhd $
of a subset D of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that can be defined by a
$\kappa $
that can be defined by a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_3)$
, a parameter
$\varphi (v_0,\ldots ,v_3)$
, a parameter
![]() $z\in {\mathrm {H}}(\kappa )$
and the parameter
$z\in {\mathrm {H}}(\kappa )$
and the parameter
![]() $\kappa $
. Then we can find a
$\kappa $
. Then we can find a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\psi (v_0,v_1,v_2)$
with the property that, in
$\psi (v_0,v_1,v_2)$
with the property that, in
![]() ${\mathrm {V}}[G]$
, the set D can be defined by the formula
${\mathrm {V}}[G]$
, the set D can be defined by the formula
![]() $\psi $
and the parameters
$\psi $
and the parameters
![]() $\kappa $
and z. In this situation, we know that
$\kappa $
and z. In this situation, we know that
![]() $z\in {\mathrm {V}}$
and the homogeneity properties of
$z\in {\mathrm {V}}$
and the homogeneity properties of
![]() ${\mathbb {P}}_{\vec {U}}$
imply that
${\mathbb {P}}_{\vec {U}}$
imply that
![]() $D\subseteq {\mathrm {V}}$
, because, given
$D\subseteq {\mathrm {V}}$
, because, given
![]() $y\in D$
, we know that y is the
$y\in D$
, we know that y is the
![]() $\alpha $
-th element of the well-order
$\alpha $
-th element of the well-order
![]() $\langle D,\lhd \rangle $
for some ordinal
$\langle D,\lhd \rangle $
for some ordinal
![]() $\alpha $
and therefore the set
$\alpha $
and therefore the set
![]() $\{y\}$
is definable in
$\{y\}$
is definable in
![]() ${\mathrm {V}}[G]$
by a formula with parameters in
${\mathrm {V}}[G]$
by a formula with parameters in
![]() ${\mathrm {V}}$
. In addition, we know that
${\mathrm {V}}$
. In addition, we know that
Let
![]() $\mathcal {E}$
denote the set of all normal ultrafilters on cardinals smaller than
$\mathcal {E}$
denote the set of all normal ultrafilters on cardinals smaller than
![]() $\kappa $
in
$\kappa $
in
![]() ${\mathrm {V}}$
. Apply Lemma 2.1 to
${\mathrm {V}}$
. Apply Lemma 2.1 to
![]() $\kappa $
, z and D in
$\kappa $
, z and D in
![]() ${\mathrm {V}}$
to obtain an element
${\mathrm {V}}$
to obtain an element
![]() $x_*$
of D, a system
$x_*$
of D, a system
![]() $\langle {\nu _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
of inaccessible cardinals smaller than
$\langle {\nu _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
of inaccessible cardinals smaller than
![]() $\kappa $
, a system
$\kappa $
, a system
![]() $\langle {\kappa _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
of measurable cardinals smaller than
$\langle {\kappa _s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
of measurable cardinals smaller than
![]() $\kappa $
, a system
$\kappa $
, a system
![]() $\langle {U_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
of elements of
$\langle {U_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
of elements of
![]() $\mathcal {E}$
and a system
$\mathcal {E}$
and a system
![]() $\langle {I_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
of linear iterations of
$\langle {I_s}~\vert ~{s\in {}^{{<}\omega }\kappa }\rangle $
of linear iterations of
![]() $\langle {\mathrm {V}},\mathcal {E}\rangle $
possessing the properties listed in the lemma. Next, for each
$\langle {\mathrm {V}},\mathcal {E}\rangle $
possessing the properties listed in the lemma. Next, for each
![]() $c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
, let
$c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
, let
![]() $I_c$
denote the unique iteration of
$I_c$
denote the unique iteration of
![]() $\langle {\mathrm {V}},\{{U_{c\restriction n}}~\vert ~{n<\omega }\}\rangle $
of length
$\langle {\mathrm {V}},\{{U_{c\restriction n}}~\vert ~{n<\omega }\}\rangle $
of length
![]() $\sup _{n<\omega }{\mathrm {lh}}({I_{c\restriction n}}){}$
in
$\sup _{n<\omega }{\mathrm {lh}}({I_{c\restriction n}}){}$
in
![]() ${\mathrm {V}}[G]$
with
${\mathrm {V}}[G]$
with
![]() $U^{I_c}_{\alpha }=U^{c\restriction n}_\alpha $
for all
$U^{I_c}_{\alpha }=U^{c\restriction n}_\alpha $
for all
![]() $n<\omega $
and
$n<\omega $
and
![]() $\alpha <{\mathrm {lh}}({I_{c\restriction n}}){}$
. Then
$\alpha <{\mathrm {lh}}({I_{c\restriction n}}){}$
. Then
![]() $M^{I_c}_{{\mathrm {lh}}({I_{c\restriction n}}){}}=M^{I_{c\restriction n}}_\infty $
and
$M^{I_c}_{{\mathrm {lh}}({I_{c\restriction n}}){}}=M^{I_{c\restriction n}}_\infty $
and
![]() $i^{I_c}_{0,{\mathrm {lh}}({I_{c\restriction n}}){}}=i^{I_{c\restriction n}}_{0,\infty }$
for all
$i^{I_c}_{0,{\mathrm {lh}}({I_{c\restriction n}}){}}=i^{I_{c\restriction n}}_{0,\infty }$
for all
![]() $c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
and
$c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
and
![]() $n<\omega $
with
$n<\omega $
with
![]() ${\mathrm {lh}}({I_{c\restriction n}}){}<{\mathrm {lh}}({I_c}){}$
. Moreover, we have
${\mathrm {lh}}({I_{c\restriction n}}){}<{\mathrm {lh}}({I_c}){}$
. Moreover, we have
![]() $M^{I_c}_\infty =M^{I_{c\restriction n}}_\infty $
and
$M^{I_c}_\infty =M^{I_{c\restriction n}}_\infty $
and
![]() $i^{I_c}_{0,\infty }=i^{I_{c\restriction n}}_{0,\infty }$
for all
$i^{I_c}_{0,\infty }=i^{I_{c\restriction n}}_{0,\infty }$
for all
![]() $c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
and
$c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
and
![]() $n<\omega $
with
$n<\omega $
with
![]() ${\mathrm {lh}}({I_{c\restriction n}}){}={\mathrm {lh}}({I_c}){}$
. Given
${\mathrm {lh}}({I_{c\restriction n}}){}={\mathrm {lh}}({I_c}){}$
. Given
![]() $c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
, we define
$c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
, we define
![]() $M_c=M^{I_c}_\infty $
,
$M_c=M^{I_c}_\infty $
,
![]() $\bar {c}=i^{I_c}_{0,\infty }\circ c_G$
and
$\bar {c}=i^{I_c}_{0,\infty }\circ c_G$
and
![]() $x_c=i^{I_c}_{0,\infty }(x_*)$
. In this situation, Lemma 2.2 shows that
$x_c=i^{I_c}_{0,\infty }(x_*)$
. In this situation, Lemma 2.2 shows that
![]() $M_c$
is well-founded for all
$M_c$
is well-founded for all
![]() $c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
.
$c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
.
Claim. If
![]() $c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
, then
$c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
, then
![]() $\bar {c}$
is
$\bar {c}$
is
![]() $i^{I_c}_{0,\infty }(\vec {U})$
-generic over
$i^{I_c}_{0,\infty }(\vec {U})$
-generic over
![]() $M_c$
.
$M_c$
.
Proof of the Claim
Suppose that
![]() $i^{I_c}_{0,\infty }(\vec {U})=\langle {U^{\prime \prime }(n)}~\vert ~{n<\omega }\rangle $
and fix a sequence
$i^{I_c}_{0,\infty }(\vec {U})=\langle {U^{\prime \prime }(n)}~\vert ~{n<\omega }\rangle $
and fix a sequence
![]() $\vec {C}=\langle {C_n\in U^{\prime \prime }(n)}~\vert ~{n<\omega }\rangle $
in
$\vec {C}=\langle {C_n\in U^{\prime \prime }(n)}~\vert ~{n<\omega }\rangle $
in
![]() $M_c$
. Since
$M_c$
. Since
![]() $I_c$
is a linear iteration of length at most
$I_c$
is a linear iteration of length at most
![]() $\kappa $
, we can find
$\kappa $
, we can find
![]() $n_0<\omega $
and a sequence
$n_0<\omega $
and a sequence
![]() $\vec {B}=\langle {B_n}~\vert ~{n<\omega }\rangle $
in
$\vec {B}=\langle {B_n}~\vert ~{n<\omega }\rangle $
in
![]() $M^{I_{c\restriction n_0}}_\infty $
such that either
$M^{I_{c\restriction n_0}}_\infty $
such that either
![]() ${\mathrm {lh}}({I_c}){}={\mathrm {lh}}({I_{c\restriction n_0}}){}$
and
${\mathrm {lh}}({I_c}){}={\mathrm {lh}}({I_{c\restriction n_0}}){}$
and
![]() $\vec {B}=\vec {C}$
, or
$\vec {B}=\vec {C}$
, or
![]() ${\mathrm {lh}}({I_c}){}>{\mathrm {lh}}({I_{c\restriction n_0}}){}$
and
${\mathrm {lh}}({I_c}){}>{\mathrm {lh}}({I_{c\restriction n_0}}){}$
and
![]() $i^{I_c}_{{\mathrm {lh}}({I_{c\restriction n_0}}){},\infty }(\vec {B})=\vec {C}$
. Now, pick
$i^{I_c}_{{\mathrm {lh}}({I_{c\restriction n_0}}){},\infty }(\vec {B})=\vec {C}$
. Now, pick
![]() $n_1<\omega $
with
$n_1<\omega $
with
![]() $\kappa (n)>\kappa _{c\restriction n_0}$
for all
$\kappa (n)>\kappa _{c\restriction n_0}$
for all
![]() $n_1\leq n<\omega $
. In this situation, the conclusions of Lemma 2.1 ensure that we can apply Lemma 7.6 to find a sequence
$n_1\leq n<\omega $
. In this situation, the conclusions of Lemma 2.1 ensure that we can apply Lemma 7.6 to find a sequence
![]() $\langle {A_n\in U(n)}~\vert ~{n<\omega }\rangle $
with
$\langle {A_n\in U(n)}~\vert ~{n<\omega }\rangle $
with
![]() $i^{I_c}_{0,{\mathrm {lh}}({I_{c\restriction n_0}}){}}(A_n)\subseteq B_n$
for all
$i^{I_c}_{0,{\mathrm {lh}}({I_{c\restriction n_0}}){}}(A_n)\subseteq B_n$
for all
![]() $n_1\leq n<\omega $
. Since
$n_1\leq n<\omega $
. Since
![]() $c_G$
is
$c_G$
is
![]() $\vec {U}$
-generic over
$\vec {U}$
-generic over
![]() ${\mathrm {V}}$
, we find
${\mathrm {V}}$
, we find
![]() $n_1\leq n_2<\omega $
with
$n_1\leq n_2<\omega $
with
![]() $c_G(n)\in A_n$
for all
$c_G(n)\in A_n$
for all
![]() $n_2\leq n<\omega $
. But this shows that
$n_2\leq n<\omega $
. But this shows that
![]() $\bar {c}(n)\in C_n$
holds for all
$\bar {c}(n)\in C_n$
holds for all
![]() $n_2\leq n<\omega $
. Using the characterization of generic sequences provided by [Reference Fuchs14], these computations prove the statement of the claim.
$n_2\leq n<\omega $
. Using the characterization of generic sequences provided by [Reference Fuchs14], these computations prove the statement of the claim.
Claim. If
![]() $c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
, then
$c\in ({}^\omega \kappa )^{{\mathrm {V}}[G]}$
, then
![]() $x_c\in D$
.
$x_c\in D$
.
Proof of the claim
By the previous claim, there exists a filter H on
![]() $i^{I_c}_{0,\infty }({\mathbb {P}}_{\vec {U}})$
in
$i^{I_c}_{0,\infty }({\mathbb {P}}_{\vec {U}})$
in
![]() ${\mathrm {V}}[G]$
that is generic over
${\mathrm {V}}[G]$
that is generic over
![]() $M_c$
. Since Lemma 2.2 shows that
$M_c$
. Since Lemma 2.2 shows that
![]() $i^{I_c}_{0,\infty }(\kappa )=\kappa $
and
$i^{I_c}_{0,\infty }(\kappa )=\kappa $
and
![]() $i^{I_c}_{0,\infty }(z)=z$
, we can use Equation (9) to show that
$i^{I_c}_{0,\infty }(z)=z$
, we can use Equation (9) to show that
holds in
![]() $M_c$
. This shows that
$M_c$
. This shows that
![]() $\psi (x_c,z,\kappa )$
holds in
$\psi (x_c,z,\kappa )$
holds in
![]() $M_c[H]$
and
$M_c[H]$
and
![]() $\Sigma _1$
-upwards absoluteness implies that this statement also holds in
$\Sigma _1$
-upwards absoluteness implies that this statement also holds in
![]() ${\mathrm {V}}[G]$
.
${\mathrm {V}}[G]$
.
By Lemma 2.2, our definitions ensure that the map
is an injection that is definable in
![]() ${\mathrm {V}}[G]$
from parameters contained in the ground model
${\mathrm {V}}[G]$
from parameters contained in the ground model
![]() ${\mathrm {V}}$
. Since
${\mathrm {V}}$
. Since
![]() $\iota (c_G)\in D\subseteq {\mathrm {V}}$
, this shows that, in
$\iota (c_G)\in D\subseteq {\mathrm {V}}$
, this shows that, in
![]() ${\mathrm {V}}[G]$
, the set
${\mathrm {V}}[G]$
, the set
![]() $\{c_G\}$
is definable from parameters in
$\{c_G\}$
is definable from parameters in
![]() ${\mathrm {V}}$
. Using the homogeneity properties of
${\mathrm {V}}$
. Using the homogeneity properties of
![]() ${\mathbb {P}}_{\vec {U}}$
in
${\mathbb {P}}_{\vec {U}}$
in
![]() ${\mathrm {V}}$
, we can now conclude that
${\mathrm {V}}$
, we can now conclude that
![]() $c_G$
is an element of
$c_G$
is an element of
![]() ${\mathrm {V}}$
, a contradiction.
${\mathrm {V}}$
, a contradiction.
8 Long well-orderings in
 ${\mathcal {P}}({\omega _1})$
${\mathcal {P}}({\omega _1})$
We now show that both strong large cardinal assumptions and strong forcing axioms cause analogues of the above results on the definability of long well-orders to hold for
![]() $\omega _1$
. In the following, we combine well-known consequences of the axiom of determinacy
$\omega _1$
. In the following, we combine well-known consequences of the axiom of determinacy
![]() ${\mathrm {AD}}$
with Woodin’s analysis of
${\mathrm {AD}}$
with Woodin’s analysis of
![]() ${\mathbb {P}}_{max}$
-extensions of determinacy models (see [Reference Larson32] and [Reference Woodin52]).
${\mathbb {P}}_{max}$
-extensions of determinacy models (see [Reference Larson32] and [Reference Woodin52]).
Lemma 8.1 (
 ${\mathrm {ZF}}$
)
${\mathrm {ZF}}$
)
Let
![]() $\kappa $
be an infinite cardinal. If there is an injection from
$\kappa $
be an infinite cardinal. If there is an injection from
![]() $\kappa ^+$
into
$\kappa ^+$
into
![]() ${\mathcal {P}}({\kappa })$
, then every
${\mathcal {P}}({\kappa })$
, then every
![]() ${<}\kappa ^+$
-complete ultrafilter on
${<}\kappa ^+$
-complete ultrafilter on
![]() $\kappa ^+$
is principal.
$\kappa ^+$
is principal.
Proof. Let U be a
![]() ${<}\kappa ^+$
-complete ultrafilter on
${<}\kappa ^+$
-complete ultrafilter on
![]() $\kappa ^+$
, and let
$\kappa ^+$
, and let
![]() ${\iota }:{\kappa ^+}\longrightarrow {{\mathcal {P}}({\kappa })}$
be an injection. Given
${\iota }:{\kappa ^+}\longrightarrow {{\mathcal {P}}({\kappa })}$
be an injection. Given
![]() $\alpha <\kappa $
, set
$\alpha <\kappa $
, set
Since U is an ultrafilter, there is
![]() $A\subseteq \kappa $
such that
$A\subseteq \kappa $
such that
holds for all
![]() $\alpha <\kappa $
. The
$\alpha <\kappa $
. The
![]() ${<}\kappa ^+$
-completeness of U then ensures that the set
${<}\kappa ^+$
-completeness of U then ensures that the set
is an element of U. We now know that
![]() $\iota [B]=\{A\}$
and hence the injectivity of
$\iota [B]=\{A\}$
and hence the injectivity of
![]() $\iota $
implies that B is a singleton.
$\iota $
implies that B is a singleton.
Corollary 8.2 (
 ${\mathrm {ZF}}+{\mathrm {DC}}+{\mathrm {AD}}$
)
${\mathrm {ZF}}+{\mathrm {DC}}+{\mathrm {AD}}$
)
There is no injection from
![]() $\omega _2$
into
$\omega _2$
into
![]() ${\mathcal {P}}({\omega _1})$
.
${\mathcal {P}}({\omega _1})$
.
Proof. By results of Kleinberg and Martin–Paris (see [Reference Kechris29, Section 13]), the restriction of the closed unbounded filter on
![]() $\omega _2$
to the set of all ordinals of countable cofinality is a
$\omega _2$
to the set of all ordinals of countable cofinality is a
![]() ${<}\omega _2$
-complete, nonprincipal ultrafilter on
${<}\omega _2$
-complete, nonprincipal ultrafilter on
![]() $\omega _2$
.
$\omega _2$
.
The following lemma will allow us to use the theory developed in [Reference Woodin52] to prove Theorem 1.6.(i).
Lemma 8.3. Assume that
![]() ${\mathrm {AD}}$
holds in
${\mathrm {AD}}$
holds in
![]() ${\mathrm {L}}({\mathbb {R}})$
and
${\mathrm {L}}({\mathbb {R}})$
and
![]() ${\mathrm {V}}$
is a
${\mathrm {V}}$
is a
![]() ${\mathbb {P}}_{max}$
-generic extension of
${\mathbb {P}}_{max}$
-generic extension of
![]() ${\mathrm {L}}({\mathbb {R}})$
. Then no well-ordering of a subset of
${\mathrm {L}}({\mathbb {R}})$
. Then no well-ordering of a subset of
![]() ${\mathcal {P}}({\omega _1})$
of cardinality greater than
${\mathcal {P}}({\omega _1})$
of cardinality greater than
![]() $\aleph _1$
is contained in
$\aleph _1$
is contained in
![]() ${\mathrm {OD}}({\mathbb {R}})$
.
${\mathrm {OD}}({\mathbb {R}})$
.
Proof. Assume, towards a contradiction, that there exists a subset D of
![]() ${\mathcal {P}}({\omega _1})$
of cardinality greater than
${\mathcal {P}}({\omega _1})$
of cardinality greater than
![]() $\aleph _1$
and a well-ordering
$\aleph _1$
and a well-ordering
![]() $\lhd $
of D that is contained in
$\lhd $
of D that is contained in
![]() ${\mathrm {OD}}({\mathbb {R}})$
. Then the fact that
${\mathrm {OD}}({\mathbb {R}})$
. Then the fact that
![]() ${\mathbb {P}}_{max}$
is countably closed and homogeneous in
${\mathbb {P}}_{max}$
is countably closed and homogeneous in
![]() ${\mathrm {L}}({\mathbb {R}})$
(see [Reference Woodin52, Lemma 4.38] and [Reference Woodin52, Lemma 4.43]) directly implies that D and
${\mathrm {L}}({\mathbb {R}})$
(see [Reference Woodin52, Lemma 4.38] and [Reference Woodin52, Lemma 4.43]) directly implies that D and
![]() $\lhd $
are both contained in
$\lhd $
are both contained in
![]() ${\mathrm {L}}({\mathbb {R}})$
. But this shows that
${\mathrm {L}}({\mathbb {R}})$
. But this shows that
![]() ${\mathrm {L}}({\mathbb {R}})$
is a model of
${\mathrm {L}}({\mathbb {R}})$
is a model of
![]() ${\mathrm {ZF}}+{\mathrm {DC}}+{\mathrm {AD}}$
that contains an injection from
${\mathrm {ZF}}+{\mathrm {DC}}+{\mathrm {AD}}$
that contains an injection from
![]() $\omega _2$
into
$\omega _2$
into
![]() ${\mathcal {P}}({\omega _1})$
, contradicting Corollary 8.2.
${\mathcal {P}}({\omega _1})$
, contradicting Corollary 8.2.
Proof of Theorem 1.6.(i)
Let
![]() $\lhd $
be a well-ordering of a subset of
$\lhd $
be a well-ordering of a subset of
![]() ${\mathcal {P}}({\omega _1})$
of cardinality greater than
${\mathcal {P}}({\omega _1})$
of cardinality greater than
![]() $\aleph _1$
that is definable by a
$\aleph _1$
that is definable by a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_3)$
and parameters
$\varphi (v_0,\ldots ,v_3)$
and parameters
![]() $\omega _1$
and
$\omega _1$
and
![]() $z\in {\mathrm {H}}(\aleph _1)$
.
$z\in {\mathrm {H}}(\aleph _1)$
.
First, assume that Woodin’s axiom
![]() $(*)$
holds, that is,
$(*)$
holds, that is,
![]() ${\mathrm {AD}}$
holds in
${\mathrm {AD}}$
holds in
![]() ${\mathrm {L}}({\mathbb {R}})$
and
${\mathrm {L}}({\mathbb {R}})$
and
![]() ${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
is a
${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
is a
![]() ${\mathbb {P}}_{max}$
-generic extension of
${\mathbb {P}}_{max}$
-generic extension of
![]() ${\mathrm {L}}({\mathbb {R}})$
. We now know that
${\mathrm {L}}({\mathbb {R}})$
. We now know that
![]() $\lhd $
and its domain are both elements of
$\lhd $
and its domain are both elements of
![]() ${\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathcal {P}}({\omega _1}))}$
because
${\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathcal {P}}({\omega _1}))}$
because
![]() $\Sigma _1$
-statements with parameters in
$\Sigma _1$
-statements with parameters in
![]() ${\mathrm {H}}(\aleph _2)$
are absolute between
${\mathrm {H}}(\aleph _2)$
are absolute between
![]() ${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
and
${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
and
![]() ${\mathrm {V}}$
. Since the domain of
${\mathrm {V}}$
. Since the domain of
![]() $\lhd $
has cardinality greater than
$\lhd $
has cardinality greater than
![]() $\aleph _1$
in
$\aleph _1$
in
![]() ${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
, we can now use Lemma 8.3 to derive a contradiction.
${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
, we can now use Lemma 8.3 to derive a contradiction.
Now, assume that there is a measurable cardinal above infinitely many Woodin cardinals. Then
![]() ${\mathrm {AD}}$
holds in
${\mathrm {AD}}$
holds in
![]() ${\mathrm {L}}({\mathbb {R}})$
. Note that the formula
${\mathrm {L}}({\mathbb {R}})$
. Note that the formula
![]() $\varphi $
and the parameters
$\varphi $
and the parameters
![]() $\omega _1$
and z also define
$\omega _1$
and z also define
![]() $\lhd $
in
$\lhd $
in
![]() ${\mathrm {H}}(\aleph _2)$
, and this statement can be formulated by a
${\mathrm {H}}(\aleph _2)$
, and this statement can be formulated by a
![]() $\Pi _2$
-formula with parameter z in the structure
$\Pi _2$
-formula with parameter z in the structure
![]() $\langle {\mathrm {H}}(\aleph _2),\in \rangle $
Let G be
$\langle {\mathrm {H}}(\aleph _2),\in \rangle $
Let G be
![]() ${\mathbb {P}}_{max}$
-generic over
${\mathbb {P}}_{max}$
-generic over
![]() ${\mathrm {L}}({\mathbb {R}})$
. Then the
${\mathrm {L}}({\mathbb {R}})$
. Then the
![]() $\Pi _2$
-maximality of
$\Pi _2$
-maximality of
![]() ${\mathrm {L}}({\mathbb {R}})[G]$
(see [Reference Larson32, Theorem 7.3]) implies that the formula
${\mathrm {L}}({\mathbb {R}})[G]$
(see [Reference Larson32, Theorem 7.3]) implies that the formula
![]() $\varphi $
and the parameters
$\varphi $
and the parameters
![]() $\omega _1$
and z also define a well-ordering of a subset of
$\omega _1$
and z also define a well-ordering of a subset of
![]() ${\mathcal {P}}({\omega _1})$
of cardinality greater than
${\mathcal {P}}({\omega _1})$
of cardinality greater than
![]() $\aleph _1$
in the structure
$\aleph _1$
in the structure
![]() $\langle {\mathrm {H}}(\aleph _2)^{{\mathrm {L}}({\mathbb {R}})[G]},\in \rangle $
. In particular, such a well-ordering is contained in
$\langle {\mathrm {H}}(\aleph _2)^{{\mathrm {L}}({\mathbb {R}})[G]},\in \rangle $
. In particular, such a well-ordering is contained in
![]() ${\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathbb {R}})[G]}$
, again contradicting Lemma 8.3.
${\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathbb {R}})[G]}$
, again contradicting Lemma 8.3.
9 Almost disjoint families in
 ${\mathcal {P}}({\omega _1})$
${\mathcal {P}}({\omega _1})$
Following the structure of the arguments in the previous section, we now show that both large cardinals and forcing axioms imply that large almost disjoint families of subsets of
![]() $\omega _1$
are not simply definable. The first step in these proofs is the following unpublished result of William Chan, Stephen Jackson and Nam Trang whose proof we include with their permission. This result is an application of their work on the validity of the Kurepa hypothesis in determinacy models and continues a line of groundbreaking results on definable combinatorics at
$\omega _1$
are not simply definable. The first step in these proofs is the following unpublished result of William Chan, Stephen Jackson and Nam Trang whose proof we include with their permission. This result is an application of their work on the validity of the Kurepa hypothesis in determinacy models and continues a line of groundbreaking results on definable combinatorics at
![]() $\omega _1$
(see, for example, [Reference Chan and Jackson6], [Reference Chan and Jackson7], [Reference Chan, Jackson and Trang8] and [Reference Chan, Jackson and Trang9]).
$\omega _1$
(see, for example, [Reference Chan and Jackson6], [Reference Chan and Jackson7], [Reference Chan, Jackson and Trang8] and [Reference Chan, Jackson and Trang9]).
Theorem 9.1 (Chan–Jackson–Trang,
 ${\mathrm {ZF}}+{\mathrm {DC}}_{\mathbb {R}}+{\mathrm {AD}}^+$
)
${\mathrm {ZF}}+{\mathrm {DC}}_{\mathbb {R}}+{\mathrm {AD}}^+$
)
Assume that
![]() ${\mathrm {V}}={\mathrm {L}}({\mathcal {P}}({{\mathbb {R}}}))$
holds. If A is a set of cofinal subsets of
${\mathrm {V}}={\mathrm {L}}({\mathcal {P}}({{\mathbb {R}}}))$
holds. If A is a set of cofinal subsets of
![]() $\omega _1$
, then one of the following statements holds:
$\omega _1$
, then one of the following statements holds:
-
(i) A can be well-ordered and its cardinality is less than or equal to
 $\aleph _1$
.
$\aleph _1$
. -
(ii) There are distinct
 $x,y\in A$
such that
$x,y\in A$
such that
 $x\cap y$
is unbounded in
$x\cap y$
is unbounded in
 $\omega _1$
.
$\omega _1$
.
The proof of this result makes use of the following topological fact:
Proposition 9.2 (
 ${\mathrm {ZF}}+{\mathrm {DC}}$
)
${\mathrm {ZF}}+{\mathrm {DC}}$
)
If X is a Polish space and
![]() $\langle {A_\alpha }~\vert ~{\alpha <\omega _1}\rangle $
is a sequence of pairwise disjoint nonmeager subsets of X, then there is an
$\langle {A_\alpha }~\vert ~{\alpha <\omega _1}\rangle $
is a sequence of pairwise disjoint nonmeager subsets of X, then there is an
![]() $\alpha <\omega _1$
such that the subset
$\alpha <\omega _1$
such that the subset
![]() $A_\alpha $
does not have the property of Baire.
$A_\alpha $
does not have the property of Baire.
Proof. Assume, towards a contradiction, that
![]() $A_\alpha $
has the property of Baire for all
$A_\alpha $
has the property of Baire for all
![]() $\alpha <\omega _1$
. Given
$\alpha <\omega _1$
. Given
![]() $\alpha <\omega _1$
, our assumption implies that there is a nonempty open set U with the property that
$\alpha <\omega _1$
, our assumption implies that there is a nonempty open set U with the property that
![]() $U\setminus A_\alpha $
is meager. Hence, there is a sequence
$U\setminus A_\alpha $
is meager. Hence, there is a sequence
![]() $\langle {N_\alpha }~\vert ~{\alpha <\omega _1}\rangle $
of nonempty basic open subsets of X such that
$\langle {N_\alpha }~\vert ~{\alpha <\omega _1}\rangle $
of nonempty basic open subsets of X such that
![]() $N_\alpha \setminus A_\alpha $
is meager. Pick
$N_\alpha \setminus A_\alpha $
is meager. Pick
![]() $\alpha <\beta <\omega _1$
with
$\alpha <\beta <\omega _1$
with
![]() $N_\alpha =N_\beta $
. Then
$N_\alpha =N_\beta $
. Then
![]() $N_\alpha \setminus (A_\alpha \cap A_\beta )=(N_\alpha \setminus A_\alpha )\cup (N_\alpha \setminus A_\beta )$
is meager and hence
$N_\alpha \setminus (A_\alpha \cap A_\beta )=(N_\alpha \setminus A_\alpha )\cup (N_\alpha \setminus A_\beta )$
is meager and hence
![]() $A_\alpha \cap A_\beta \neq \emptyset $
, a contradiction
$A_\alpha \cap A_\beta \neq \emptyset $
, a contradiction
Proof of Theorem 9.1
Assume, towards a contradiction, that both conclusions fail.
Claim. The set A cannot be well-ordered.
Proof of the claim
Assume, towards a contradiction, that A can be well-ordered. Then our assumptions imply that it has cardinality greater than
![]() $\aleph _1$
and hence we obtain an injection of
$\aleph _1$
and hence we obtain an injection of
![]() $\omega _2$
into
$\omega _2$
into
![]() ${\mathcal {P}}({\omega _1})$
. But this yields a contradiction, because the assumption of Corollary 8.2 are satisfied in our setting.
${\mathcal {P}}({\omega _1})$
. But this yields a contradiction, because the assumption of Corollary 8.2 are satisfied in our setting.
By combining the above claim with [Reference Caicedo and Ketchersid4, Theorem 1.4], we now obtain an injection
![]() ${\iota }:{{\mathbb {R}}}\longrightarrow {A}$
. Our assumptions then ensure that the function
${\iota }:{{\mathbb {R}}}\longrightarrow {A}$
. Our assumptions then ensure that the function
is well-defined. Given
![]() $\alpha <\omega _1$
, set
$\alpha <\omega _1$
, set
![]() $E_\alpha =c^{{-}1}\{\alpha \}\subseteq {\mathbb {R}}\times {\mathbb {R}}$
. Then
$E_\alpha =c^{{-}1}\{\alpha \}\subseteq {\mathbb {R}}\times {\mathbb {R}}$
. Then
![]() $\bigcup \{{E_\alpha }~\vert ~{\alpha <\omega _1}\}$
is dense open in
$\bigcup \{{E_\alpha }~\vert ~{\alpha <\omega _1}\}$
is dense open in
![]() ${\mathbb {R}}\times {\mathbb {R}}$
.
${\mathbb {R}}\times {\mathbb {R}}$
.
Claim. There is a
![]() $\lambda <\omega _1$
such that the set
$\lambda <\omega _1$
such that the set
![]() $\bigcup \{{E_\alpha }~\vert ~{\alpha <\lambda }\}$
is comeager in
$\bigcup \{{E_\alpha }~\vert ~{\alpha <\lambda }\}$
is comeager in
![]() ${\mathbb {R}}\times {\mathbb {R}}$
.
${\mathbb {R}}\times {\mathbb {R}}$
.
Proof of the claim
Assume that there is no
![]() $\lambda <\omega _1$
with the property that the set
$\lambda <\omega _1$
with the property that the set
![]() $\bigcup \{{E_\alpha }~\vert ~{\alpha <\lambda }\}$
is comeager. Since the ideal of meager subsets of
$\bigcup \{{E_\alpha }~\vert ~{\alpha <\lambda }\}$
is comeager. Since the ideal of meager subsets of
![]() ${\mathbb {R}}\times {\mathbb {R}}$
is closed under well-ordered unions in our setting, our assumption yields a strictly increasing function
${\mathbb {R}}\times {\mathbb {R}}$
is closed under well-ordered unions in our setting, our assumption yields a strictly increasing function
![]() ${f}:{\omega _1}\longrightarrow {\omega _1}$
with the property that
${f}:{\omega _1}\longrightarrow {\omega _1}$
with the property that
![]() $E_{f(\alpha )}$
is a nonmeager subset of
$E_{f(\alpha )}$
is a nonmeager subset of
![]() ${\mathbb {R}}\times {\mathbb {R}}$
for all
${\mathbb {R}}\times {\mathbb {R}}$
for all
![]() $\alpha <\omega _1$
. In this situation, the sequence
$\alpha <\omega _1$
. In this situation, the sequence
![]() $\langle {E_{f(\alpha )}}~\vert ~{\alpha <\omega _1}\rangle $
consists of pairwise disjoint nonmeager subsets of
$\langle {E_{f(\alpha )}}~\vert ~{\alpha <\omega _1}\rangle $
consists of pairwise disjoint nonmeager subsets of
![]() ${\mathbb {R}}\times {\mathbb {R}}$
and, since we assume that
${\mathbb {R}}\times {\mathbb {R}}$
and, since we assume that
![]() ${\mathrm {AD}}$
holds, all of these sets possess the property of Baire. This contradicts Proposition 9.2.
${\mathrm {AD}}$
holds, all of these sets possess the property of Baire. This contradicts Proposition 9.2.
By a classical result of Mycielski (see [Reference Kechris30, Theorem 19.1]), we can now find an injection
![]() ${e}:{{\mathbb {R}}}\longrightarrow {{\mathbb {R}}}$
such that for all
${e}:{{\mathbb {R}}}\longrightarrow {{\mathbb {R}}}$
such that for all
![]() $x,y\in {\mathbb {R}}$
with
$x,y\in {\mathbb {R}}$
with
![]() $x\neq y$
, there is an
$x\neq y$
, there is an
![]() $\alpha <\lambda $
with
$\alpha <\lambda $
with
![]() $\langle e(x),e(y)\rangle \in E_\alpha $
. In this situation, we know that
$\langle e(x),e(y)\rangle \in E_\alpha $
. In this situation, we know that
holds for all
![]() $x,y\in {\mathbb {R}}$
with
$x,y\in {\mathbb {R}}$
with
![]() $x\neq y$
. In particular, since the set A consists of unbounded subsets of
$x\neq y$
. In particular, since the set A consists of unbounded subsets of
![]() $\omega _1$
, we know that the map
$\omega _1$
, we know that the map
is an injection. But this shows that the reals can be well-ordered, contradicting our assumptions.
In order to transfer the above result to models of the form
![]() ${\mathrm {HOD}}({\mathbb {R}})$
of
${\mathrm {HOD}}({\mathbb {R}})$
of
![]() ${\mathbb {P}}_{max}$
-extensions, we make use of another axiom introduced by Woodin, called
${\mathbb {P}}_{max}$
-extensions, we make use of another axiom introduced by Woodin, called
![]() $\left ({*\atop *}\right )$
(see [Reference Woodin52, Definition 5.69]).
$\left ({*\atop *}\right )$
(see [Reference Woodin52, Definition 5.69]).
Lemma 9.3. Assume that
![]() ${\mathrm {AD}}$
holds in
${\mathrm {AD}}$
holds in
![]() ${\mathrm {L}}({\mathbb {R}})$
and
${\mathrm {L}}({\mathbb {R}})$
and
![]() ${\mathrm {V}}$
is a
${\mathrm {V}}$
is a
![]() ${\mathbb {P}}_{max}$
-generic extension of
${\mathbb {P}}_{max}$
-generic extension of
![]() ${\mathrm {L}}({\mathbb {R}})$
. If
${\mathrm {L}}({\mathbb {R}})$
. If
![]() $A\in {\mathrm {OD}}({\mathbb {R}})$
is a set of cardinality greater than
$A\in {\mathrm {OD}}({\mathbb {R}})$
is a set of cardinality greater than
![]() $\aleph _1$
that consists of unbounded subsets of
$\aleph _1$
that consists of unbounded subsets of
![]() $\omega _1$
, then there are distinct
$\omega _1$
, then there are distinct
![]() $x,y\in A$
with the property that
$x,y\in A$
with the property that
![]() $x\cap y$
is unbounded in
$x\cap y$
is unbounded in
![]() $\omega _1$
.
$\omega _1$
.
Proof. Assume, towards a contradiction, that the above conclusion fails.
Claim.
![]() $A\subseteq {\mathrm {L}}({\mathbb {R}})$
.
$A\subseteq {\mathrm {L}}({\mathbb {R}})$
.
Proof of the claim
Assume that
![]() $A\nsubseteq {\mathrm {L}}({\mathbb {R}})$
. Since
$A\nsubseteq {\mathrm {L}}({\mathbb {R}})$
. Since
![]() ${\mathrm {V}}={\mathrm {L}}({\mathcal {P}}({\omega _1}))$
holds and [Reference Woodin52, Corollary 5.83] shows that our assumptions imply that
${\mathrm {V}}={\mathrm {L}}({\mathcal {P}}({\omega _1}))$
holds and [Reference Woodin52, Corollary 5.83] shows that our assumptions imply that
![]() $\left ({*\atop *}\right )$
holds, we can apply [Reference Woodin52, Theorem 5.84] to find an unbounded subset U of
$\left ({*\atop *}\right )$
holds, we can apply [Reference Woodin52, Theorem 5.84] to find an unbounded subset U of
![]() $\omega _1$
and a function
$\omega _1$
and a function
![]() ${\pi }:{{}^{{<}\omega _1}2}\longrightarrow {[\omega _1]^\omega }$
such that the following statements hold:
${\pi }:{{}^{{<}\omega _1}2}\longrightarrow {[\omega _1]^\omega }$
such that the following statements hold:
-
(i) If
 $s,t\in {}^{{<}\omega _1}2$
with
$s,t\in {}^{{<}\omega _1}2$
with
 $s\subseteq t$
, then
$s\subseteq t$
, then
 $\pi (s)\subseteq \pi (t)$
and
$\pi (s)\subseteq \pi (t)$
and
 $\pi (s)\cap \alpha =\pi (t)\cap \alpha $
for all
$\pi (s)\cap \alpha =\pi (t)\cap \alpha $
for all
 $\alpha \in \pi (s)$
.
$\alpha \in \pi (s)$
. -
(ii) Given
 $s\in {}^{{<}\omega _1}2$
and
$s\in {}^{{<}\omega _1}2$
and
 $\alpha \in {{\mathrm {dom}}(s)}\cap U$
, we have
$\alpha \in {{\mathrm {dom}}(s)}\cap U$
, we have
 $\alpha \in \pi (s)$
if and only if
$\alpha \in \pi (s)$
if and only if
 $s(\alpha )=1$
.
$s(\alpha )=1$
. -
(iii) If
 $x\in {}^{\omega _1}2$
, then
$x\in {}^{\omega _1}2$
, then
 $\bar {\pi }(x)=\bigcup \{{\pi (x\restriction \alpha )}~\vert ~{\alpha <\omega _1}\}\in A$
.
$\bar {\pi }(x)=\bigcup \{{\pi (x\restriction \alpha )}~\vert ~{\alpha <\omega _1}\}\in A$
.
Pick
![]() $x,y\in {}^{\omega _1}2$
such that x has constant value
$x,y\in {}^{\omega _1}2$
such that x has constant value
![]() $1$
and y is the characteristic function of
$1$
and y is the characteristic function of
![]() $U\setminus \{\min (U)\}$
. Since
$U\setminus \{\min (U)\}$
. Since
![]() $\bar {\pi }(x),\bar {\pi }(y)\in A$
and
$\bar {\pi }(x),\bar {\pi }(y)\in A$
and
![]() $U\setminus \{\min (U)\}\subseteq \bar {\pi }(x)\cap \bar {\pi }(y)$
, we know that
$U\setminus \{\min (U)\}\subseteq \bar {\pi }(x)\cap \bar {\pi }(y)$
, we know that
![]() $\bar {\pi }(x)=\bar {\pi }(y)$
as
$\bar {\pi }(x)=\bar {\pi }(y)$
as
![]() $\bar {\pi }(x)\cap \bar {\pi }(y)$
is unbounded in
$\bar {\pi }(x)\cap \bar {\pi }(y)$
is unbounded in
![]() $\omega _1$
. But
$\omega _1$
. But
![]() $\min (U)\in \bar {\pi }(x)\setminus \bar {\pi }(y)$
, a contradiction.
$\min (U)\in \bar {\pi }(x)\setminus \bar {\pi }(y)$
, a contradiction.
Claim.
![]() $A\in {\mathrm {L}}({\mathbb {R}})$
.
$A\in {\mathrm {L}}({\mathbb {R}})$
.
Proof of the claim
Using the homogeneity of
![]() ${\mathbb {P}}_{max}$
in
${\mathbb {P}}_{max}$
in
![]() ${\mathrm {L}}({\mathbb {R}})$
, this statement follows directly from the previous claim and the fact that the set A is contained in the class
${\mathrm {L}}({\mathbb {R}})$
, this statement follows directly from the previous claim and the fact that the set A is contained in the class
![]() ${\mathrm {OD}}({\mathbb {R}})$
.
${\mathrm {OD}}({\mathbb {R}})$
.
Since [Reference Caicedo and Ketchersid4, Corollary 2.16] shows that
![]() ${\mathrm {L}}({\mathbb {R}})$
is a model of
${\mathrm {L}}({\mathbb {R}})$
is a model of
![]() ${\mathrm {DC}}+{\mathrm {AD}}^+$
, we can use Theorem 9.1 in
${\mathrm {DC}}+{\mathrm {AD}}^+$
, we can use Theorem 9.1 in
![]() ${\mathrm {L}}({\mathbb {R}})$
to conclude that, in
${\mathrm {L}}({\mathbb {R}})$
to conclude that, in
![]() ${\mathrm {L}}({\mathbb {R}})$
, the set A can be well-ordered and its cardinality is smaller than or equal to
${\mathrm {L}}({\mathbb {R}})$
, the set A can be well-ordered and its cardinality is smaller than or equal to
![]() $\aleph _1$
. But this shows that the cardinality of A in
$\aleph _1$
. But this shows that the cardinality of A in
![]() ${\mathrm {V}}$
is at most
${\mathrm {V}}$
is at most
![]() $\aleph _1$
, a contradiction.
$\aleph _1$
, a contradiction.
Proof of Theorem 1.6.(ii)
Let A be a set of cardinality greater than
![]() $\aleph _1$
that consists of unbounded subsets of
$\aleph _1$
that consists of unbounded subsets of
![]() $\omega _1$
and is definable by a
$\omega _1$
and is definable by a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
and parameters
$\varphi (v_0,v_1,v_2)$
and parameters
![]() $\omega _1$
and
$\omega _1$
and
![]() $z\in {\mathrm {H}}(\aleph _1)$
.
$z\in {\mathrm {H}}(\aleph _1)$
.
First, assume that Woodin’s axiom
![]() $(*)$
holds. Then the
$(*)$
holds. Then the
![]() $\Sigma _1$
-reflection principle implies that the formula
$\Sigma _1$
-reflection principle implies that the formula
![]() $\varphi $
and the parameters
$\varphi $
and the parameters
![]() $\omega _1$
and z also define the set A in
$\omega _1$
and z also define the set A in
![]() ${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
. But this shows that
${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
. But this shows that
![]() $A\in {\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathcal {P}}({\omega _1}))}$
and, since
$A\in {\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathcal {P}}({\omega _1}))}$
and, since
![]() ${\mathrm {AD}}$
holds in
${\mathrm {AD}}$
holds in
![]() ${\mathrm {L}}({\mathbb {R}})$
and
${\mathrm {L}}({\mathbb {R}})$
and
![]() ${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
is a
${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
is a
![]() ${\mathbb {P}}_{max}$
-generic extension of
${\mathbb {P}}_{max}$
-generic extension of
![]() ${\mathrm {L}}({\mathbb {R}})$
, we can now apply Lemma 9.3 in
${\mathrm {L}}({\mathbb {R}})$
, we can now apply Lemma 9.3 in
![]() ${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
to find distinct
${\mathrm {L}}({\mathcal {P}}({\omega _1}))$
to find distinct
![]() $x,y\in A$
with
$x,y\in A$
with
![]() $x\cap y$
unbounded in
$x\cap y$
unbounded in
![]() $\omega _1$
.
$\omega _1$
.
Next, assume that there is a measurable cardinal above infinitely many Woodin cardinals. Then
![]() ${\mathrm {AD}}$
holds in
${\mathrm {AD}}$
holds in
![]() ${\mathrm {L}}({\mathbb {R}})$
. Note that the formula
${\mathrm {L}}({\mathbb {R}})$
. Note that the formula
![]() $\varphi $
and the parameters
$\varphi $
and the parameters
![]() $\omega _1$
and z also define A in the structure
$\omega _1$
and z also define A in the structure
![]() $\langle {\mathrm {H}}(\omega _2),\in \rangle $
. Assume, towards a contradiction, that
$\langle {\mathrm {H}}(\omega _2),\in \rangle $
. Assume, towards a contradiction, that
![]() $x\cap y$
is bounded in
$x\cap y$
is bounded in
![]() $\omega _1$
for all distinct
$\omega _1$
for all distinct
![]() $x,y\in A$
. Note that, in
$x,y\in A$
. Note that, in
![]() $\langle {\mathrm {H}}(\omega _2),\in \rangle $
, the statement that
$\langle {\mathrm {H}}(\omega _2),\in \rangle $
, the statement that
![]() $\varphi $
,
$\varphi $
,
![]() $\omega _1$
and z define a set of cardinality greater than
$\omega _1$
and z define a set of cardinality greater than
![]() $\aleph _1$
that consists of unbounded subsets of
$\aleph _1$
that consists of unbounded subsets of
![]() $\omega _1$
whose pairwise intersections are countable can be expressed by a
$\omega _1$
whose pairwise intersections are countable can be expressed by a
![]() $\Pi _2$
-formula with parameter z. Let G be
$\Pi _2$
-formula with parameter z. Let G be
![]() ${\mathbb {P}}_{max}$
-generic over
${\mathbb {P}}_{max}$
-generic over
![]() ${\mathrm {L}}({\mathbb {R}})$
. Then the
${\mathrm {L}}({\mathbb {R}})$
. Then the
![]() $\Pi _2$
-maximality of
$\Pi _2$
-maximality of
![]() ${\mathrm {L}}({\mathbb {R}})[G]$
implies that, in the structure
${\mathrm {L}}({\mathbb {R}})[G]$
implies that, in the structure
![]() $\langle {\mathrm {H}}(\aleph _2)^{{\mathrm {L}}({\mathbb {R}})[G]},\in \rangle $
, the formula
$\langle {\mathrm {H}}(\aleph _2)^{{\mathrm {L}}({\mathbb {R}})[G]},\in \rangle $
, the formula
![]() $\varphi $
and the parameters
$\varphi $
and the parameters
![]() $\omega _1$
and z define a set of cardinality greater than
$\omega _1$
and z define a set of cardinality greater than
![]() $\aleph _1$
that consists of unbounded subsets of
$\aleph _1$
that consists of unbounded subsets of
![]() $\omega _1$
whose pairwise intersections are countable. In particular, such a subset of
$\omega _1$
whose pairwise intersections are countable. In particular, such a subset of
![]() ${\mathcal {P}}({\omega _1})$
exists in
${\mathcal {P}}({\omega _1})$
exists in
![]() ${\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathbb {R}})[G]}$
, contradicting Lemma 9.3.
${\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathbb {R}})[G]}$
, contradicting Lemma 9.3.
10 Concluding remarks and open questions
In the following, we discuss several questions raised by the above results, starting with questions about the optimality of the assumption of Theorem 1.1. By Theorem 1.2, the consistency strength of this assumption is optimal in the case of singular cardinals. In contrast, results of Schlicht in [Reference Schlicht44] show that, if
![]() $\kappa $
is an uncountable regular cardinal,
$\kappa $
is an uncountable regular cardinal,
![]() $\theta>\kappa $
is inaccessible and G is
$\theta>\kappa $
is inaccessible and G is
![]() ${\mathrm {Col}}({\kappa },{{<}\theta })$
-generic over
${\mathrm {Col}}({\kappa },{{<}\theta })$
-generic over
![]() ${\mathrm {V}}$
, then, in
${\mathrm {V}}$
, then, in
![]() ${\mathrm {V}}[G]$
, every subset of
${\mathrm {V}}[G]$
, every subset of
![]() $\kappa $
in
$\kappa $
in
![]() ${\mathrm {OD}}({}^\kappa {\mathrm {On}})$
either has cardinality
${\mathrm {OD}}({}^\kappa {\mathrm {On}})$
either has cardinality
![]() $\kappa $
or contains a closed subset homeomorphic to
$\kappa $
or contains a closed subset homeomorphic to
![]() ${}^\kappa 2$
. In particular, if
${}^\kappa 2$
. In particular, if
![]() $\kappa $
is not weakly compact in
$\kappa $
is not weakly compact in
![]() ${\mathrm {V}}$
, then, in
${\mathrm {V}}$
, then, in
![]() ${\mathrm {V}}[G]$
, the cardinal
${\mathrm {V}}[G]$
, the cardinal
![]() $\kappa $
is not weakly compact, the spaces
$\kappa $
is not weakly compact, the spaces
![]() ${}^\kappa 2$
and
${}^\kappa 2$
and
![]() ${}^\kappa \kappa $
are homeomorphic (see, for example, [Reference Lücke, Ros and Schlicht35, Corollary 2.3]) and for every subset D of
${}^\kappa \kappa $
are homeomorphic (see, for example, [Reference Lücke, Ros and Schlicht35, Corollary 2.3]) and for every subset D of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, there is a perfect embedding
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, there is a perfect embedding
![]() ${\iota }:{{}^\kappa \kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
${\iota }:{{}^\kappa \kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
![]() ${{\mathrm {ran}}(\iota )}\subseteq D$
. This shows that our question is only interesting when we also assume that the given cardinal
${{\mathrm {ran}}(\iota )}\subseteq D$
. This shows that our question is only interesting when we also assume that the given cardinal
![]() $\kappa $
possesses certain large cardinal properties.Footnote 7
$\kappa $
possesses certain large cardinal properties.Footnote 7
Question 10.1. Assume that
![]() $\kappa $
is a weakly compact cardinal with the property that for every subset D of
$\kappa $
is a weakly compact cardinal with the property that for every subset D of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, there is a perfect embedding
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
, there is a perfect embedding
![]() ${\iota }:{{}^\kappa \kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
${\iota }:{{}^\kappa \kappa }\longrightarrow {{\mathcal {P}}({\kappa })}$
with
![]() ${{\mathrm {ran}}(\iota )}\subseteq D$
. Is there an inner model that contains a weakly compact limit of measurable cardinals?
${{\mathrm {ran}}(\iota )}\subseteq D$
. Is there an inner model that contains a weakly compact limit of measurable cardinals?
In contrast to the singular case, we may also ask whether the conclusion of Theorem 1.1 can be established from a sequences of measurable cardinals that are bounded in a regular cardinal, but whose order type is equal their minimum.
Question 10.2. Does the assumption of Question 1.1 imply the existence of a set-sized transitive model of
![]() ${\mathrm {ZFC}}$
containing a weakly compact cardinal
${\mathrm {ZFC}}$
containing a weakly compact cardinal
![]() $\delta $
and a sequence S of measurable cardinals less than
$\delta $
and a sequence S of measurable cardinals less than
![]() $\delta $
of order-type
$\delta $
of order-type
![]() $\min (S)$
?
$\min (S)$
?
We now consider the possibility to strengthen Theorem 1.4. Since the existence of infinitely many measurable cardinals is compatible with the existence of a
![]() $\mathbf {\Sigma }^1_3$
-well-ordering of the reals (see [Reference Mitchell41, Theorem 3.6]), it is natural to ask whether the assumption of this theorem is actually consistent. The model constructed in [Reference Mitchell41, Section 1] should be the natural candidate to look for an affirmative answer to the following question.
$\mathbf {\Sigma }^1_3$
-well-ordering of the reals (see [Reference Mitchell41, Theorem 3.6]), it is natural to ask whether the assumption of this theorem is actually consistent. The model constructed in [Reference Mitchell41, Section 1] should be the natural candidate to look for an affirmative answer to the following question.
Question 10.3. Is it consistent that there exists a limit
![]() $\kappa $
of
$\kappa $
of
![]() $\omega $
-many measurable cardinals and a well-ordering of a subset of
$\omega $
-many measurable cardinals and a well-ordering of a subset of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
?
$\kappa $
?
In addition, the equiconsistency given by Theorem 1.5 motivates the question whether such implications can be extended to cardinals of higher cofinalities.
Question 10.4. Is it consistent that there exists a limit of measurable cardinals
![]() $\kappa $
and a well-ordering of a subset of
$\kappa $
and a well-ordering of a subset of
![]() ${\mathcal {P}}({\kappa })$
of cardinality greater than
${\mathcal {P}}({\kappa })$
of cardinality greater than
![]() $\kappa $
that is definable by a
$\kappa $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
?
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
?
Next, we consider simply definable almost disjoint families. The statements of Theorem 1.3 and Theorem 1.6.(ii) are motivated by a classical result of Mathias in [Reference Mathias39] showing that no maximal almost disjoint family in
![]() ${\mathcal {P}}({\omega })$
is analytic. In contrast, Miller [Reference Miller40] showed that the existence of coanalytic maximal disjoint families in
${\mathcal {P}}({\omega })$
is analytic. In contrast, Miller [Reference Miller40] showed that the existence of coanalytic maximal disjoint families in
![]() ${\mathcal {P}}({\omega })$
is consistent. This motivates the following questions:
${\mathcal {P}}({\omega })$
is consistent. This motivates the following questions:
Question 10.5.
-
(i) Does the existence of sufficiently strong large cardinals imply that no almost disjoint family of cardinality greater than
 $\aleph _1$
in
$\aleph _1$
in
 ${\mathcal {P}}({\omega _1})$
is definable by a
${\mathcal {P}}({\omega _1})$
is definable by a
 $\Pi _1$
-formula with parameters in
$\Pi _1$
-formula with parameters in
 ${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
?
${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
? -
(ii) Do sufficiently strong large cardinal properties of a cardinal
 $\kappa $
imply that no almost disjoint family of cardinality greater than
$\kappa $
imply that no almost disjoint family of cardinality greater than
 $\kappa $
in
$\kappa $
in
 ${\mathcal {P}}({\kappa })$
is definable by a
${\mathcal {P}}({\kappa })$
is definable by a
 $\Pi _1$
-formula with parameters in
$\Pi _1$
-formula with parameters in
 ${\mathrm {H}}(\kappa )\cup \{\kappa \}$
?
${\mathrm {H}}(\kappa )\cup \{\kappa \}$
?
It should be noted that our proof of Theorem 1.6.(ii) in Section 9 already shows that Woodin’s axiom
![]() $(*)$
(and therefore strong forcing axioms, see [Reference Asperó and Schindler2]) implies that no almost disjoint family of cardinality greater than
$(*)$
(and therefore strong forcing axioms, see [Reference Asperó and Schindler2]) implies that no almost disjoint family of cardinality greater than
![]() $\aleph _1$
in
$\aleph _1$
in
![]() ${\mathcal {P}}({\omega _1})$
is definable in the structure
${\mathcal {P}}({\omega _1})$
is definable in the structure
![]() $\langle {\mathrm {H}}(\aleph _2),\in \rangle $
by a formula with parameters in
$\langle {\mathrm {H}}(\aleph _2),\in \rangle $
by a formula with parameters in
![]() ${\mathrm {H}}(\aleph _1)\cup \omega _2$
, because all such families are elements of
${\mathrm {H}}(\aleph _1)\cup \omega _2$
, because all such families are elements of
![]() ${\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathcal {P}}({\omega _1}))}$
. In particular, no such family is definable by a
${\mathrm {OD}}({\mathbb {R}})^{{\mathrm {L}}({\mathcal {P}}({\omega _1}))}$
. In particular, no such family is definable by a
![]() $\Pi _1$
-formula with parameters in
$\Pi _1$
-formula with parameters in
![]() ${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
in this setting.
${\mathrm {H}}(\aleph _1)\cup \{\omega _1\}$
in this setting.
Finally, we consider the questions whether analogues of the above results hold for other types of uncountable cardinals. The following observation uses ideas from [Reference Lücke34, Section 6] and [Reference Lücke, Schindler and Schlicht37, Section 5] to show that the results of Section 9 cannot be generalized from
![]() $\omega _1$
to
$\omega _1$
to
![]() $\omega _2$
. Moreover, it shows that forcing axioms outright imply the
$\omega _2$
. Moreover, it shows that forcing axioms outright imply the
![]() $\Sigma _1$
-definability of pathological objects at
$\Sigma _1$
-definability of pathological objects at
![]() $\omega _2$
. Remember that a sequence
$\omega _2$
. Remember that a sequence
![]() $\langle {C_\alpha }~\vert ~{\alpha \in {\mathrm {Lim}}\cap \omega _1}\rangle $
is a C-sequence if
$\langle {C_\alpha }~\vert ~{\alpha \in {\mathrm {Lim}}\cap \omega _1}\rangle $
is a C-sequence if
![]() $C_\alpha $
is an unbounded subset of
$C_\alpha $
is an unbounded subset of
![]() $\alpha $
of order-type
$\alpha $
of order-type
![]() $\omega $
for every countable limit ordinal
$\omega $
for every countable limit ordinal
![]() $\alpha $
.
$\alpha $
.
Proposition 10.6.
-
(i) If the Bounded proper forcing axiom
 ${\mathrm {BPFA}}$
holds and
${\mathrm {BPFA}}$
holds and
 $\vec {C}$
is a C-sequence, then there exists an almost disjoint family of cardinality
$\vec {C}$
is a C-sequence, then there exists an almost disjoint family of cardinality
 $2^{\aleph _2}$
in
$2^{\aleph _2}$
in
 ${\mathcal {P}}({\omega _2})$
that is definable by a
${\mathcal {P}}({\omega _2})$
that is definable by a
 $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
 $\omega _2$
and
$\omega _2$
and
 $\vec {C}$
.
$\vec {C}$
. -
(ii) If
 $\omega _1=\omega _1^{\mathrm {L}}$
and
$\omega _1=\omega _1^{\mathrm {L}}$
and
 ${\mathrm {BPFA}}$
holds,Footnote 8 then there exists an almost disjoint family of cardinality
${\mathrm {BPFA}}$
holds,Footnote 8 then there exists an almost disjoint family of cardinality
 $2^{\aleph _2}$
in
$2^{\aleph _2}$
in
 ${\mathcal {P}}({\omega _2})$
that is definable by a
${\mathcal {P}}({\omega _2})$
that is definable by a
 $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
 $\omega _2$
.
$\omega _2$
. -
(iii) If there is a supercompact cardinal, then, in a generic extension of the ground model, the proper forcing axiom
 ${\mathrm {PFA}}$
holds and there exists an almost disjoint family of cardinality
${\mathrm {PFA}}$
holds and there exists an almost disjoint family of cardinality
 $2^{\aleph _2}$
in
$2^{\aleph _2}$
in
 ${\mathcal {P}}({\omega _2})$
that is definable by a
${\mathcal {P}}({\omega _2})$
that is definable by a
 $\Sigma _1$
-formula and the parameter
$\Sigma _1$
-formula and the parameter
 $\omega _2$
.
$\omega _2$
.
Proof. (i) By [Reference Caicedo and Veličković5, Theorem 2], our assumption implies the existence of a well-ordering of
![]() ${\mathrm {H}}(\aleph _2)$
of order-type
${\mathrm {H}}(\aleph _2)$
of order-type
![]() $\omega _2$
that is definable by a
$\omega _2$
that is definable by a
![]() $\Sigma _1$
-formula that only uses the sequence
$\Sigma _1$
-formula that only uses the sequence
![]() $\vec {C}$
as a parameter. In particular, there exists an injection
$\vec {C}$
as a parameter. In particular, there exists an injection
![]() ${\iota }:{{\mathrm {H}}(\aleph _2)}\longrightarrow {\omega _2}$
that is definable in the structure
${\iota }:{{\mathrm {H}}(\aleph _2)}\longrightarrow {\omega _2}$
that is definable in the structure
![]() $\langle {\mathrm {H}}(\aleph _2),\in \rangle $
by a formula with parameter
$\langle {\mathrm {H}}(\aleph _2),\in \rangle $
by a formula with parameter
![]() $\vec {C}$
. Since [Reference Lücke34, Lemma 6.4] shows that our assumption implies that the set
$\vec {C}$
. Since [Reference Lücke34, Lemma 6.4] shows that our assumption implies that the set
![]() $\{{\mathrm {H}}(\aleph _2)\}$
is definable by a
$\{{\mathrm {H}}(\aleph _2)\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\omega _2$
, we know that
$\omega _2$
, we know that
![]() $\iota $
is definable by a
$\iota $
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\omega _2$
and
$\omega _2$
and
![]() $\vec {C}$
. Given
$\vec {C}$
. Given
![]() $x\in {}^{\omega _2}2$
, we now define
$x\in {}^{\omega _2}2$
, we now define
The above computations then show that the set
![]() $A=\{{\bar {x}}~\vert ~{x\in {}^{\omega _2}2}\}$
is definable by a
$A=\{{\bar {x}}~\vert ~{x\in {}^{\omega _2}2}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\omega _2$
and
$\omega _2$
and
![]() $\vec {C}$
, and it is easy to see that A is an almost disjoint family of cardinality
$\vec {C}$
, and it is easy to see that A is an almost disjoint family of cardinality
![]() $2^{\aleph _2}$
in
$2^{\aleph _2}$
in
![]() ${\mathcal {P}}({\omega _2})$
.
${\mathcal {P}}({\omega _2})$
.
(ii) Assume that
![]() $\omega _1=\omega _1^{\mathrm {L}}$
and
$\omega _1=\omega _1^{\mathrm {L}}$
and
![]() ${\mathrm {BPFA}}$
holds. Let
${\mathrm {BPFA}}$
holds. Let
![]() $\vec {C}$
denote the
$\vec {C}$
denote the
![]() $<_{\mathrm {L}}$
-least C-sequence in
$<_{\mathrm {L}}$
-least C-sequence in
![]() ${\mathrm {L}}$
. Then
${\mathrm {L}}$
. Then
![]() $\vec {C}$
is a C-sequence and the set
$\vec {C}$
is a C-sequence and the set
![]() $\{\vec {C}\}$
is definable by a
$\{\vec {C}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\omega _2$
. Using (i), we can conclude that there exists an almost disjoint family of cardinality
$\omega _2$
. Using (i), we can conclude that there exists an almost disjoint family of cardinality
![]() $2^{\aleph _2}$
in
$2^{\aleph _2}$
in
![]() ${\mathcal {P}}({\omega _2})$
that is definable by a
${\mathcal {P}}({\omega _2})$
that is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\omega _2$
.
$\omega _2$
.
(iii) By [Reference Asperó1, Theorem 5.2], it is possible to start in a model containing a supercompact cardinal and force the validity of
![]() ${\mathrm {PFA}}$
together with the existence of a well-ordering of
${\mathrm {PFA}}$
together with the existence of a well-ordering of
![]() ${\mathrm {H}}(\aleph _2)$
of order-type
${\mathrm {H}}(\aleph _2)$
of order-type
![]() $\omega _2$
that is definable in
$\omega _2$
that is definable in
![]() $\langle {\mathrm {H}}(\aleph _2),\in \rangle $
by a formula without parameters. We can now proceed as in (i) to obtain an almost disjoint family of cardinality
$\langle {\mathrm {H}}(\aleph _2),\in \rangle $
by a formula without parameters. We can now proceed as in (i) to obtain an almost disjoint family of cardinality
![]() $2^{\aleph _2}$
in
$2^{\aleph _2}$
in
![]() ${\mathcal {P}}({\omega _2})$
that is definable by a
${\mathcal {P}}({\omega _2})$
that is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\omega _2$
in this generic extension.
$\omega _2$
in this generic extension.
Acknowledgements
The authors would like to thank William Chan for the permission to include his proof of Theorem 9.1 in this paper. In addition, the authors are thankful to the anonymous referees for the careful reading of the manuscript and several helpful comments.
Funding statement
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 842082 of the first author (Project SAIFIA: Strong Axioms of Infinity – Frameworks, Interactions and Applications). In addition, the research of the first author was supported by the Spanish Government under grant EUR2022-134032. The second author gratefully acknowledges funding from L’ORÉAL Austria, in collaboration with the Austrian UNESCO Commission and in cooperation with the Austrian Academy of Sciences - Fellowship Determinacy and Large Cardinals. Furthermore, the second author was supported by FWF Elise Richter grant number V844, START grant number Y1498, and international project number I6087. The author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission.
Competing interests
The authors have no competing interest to declare.