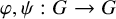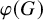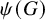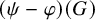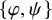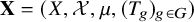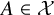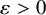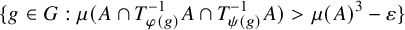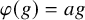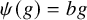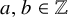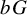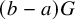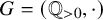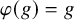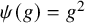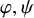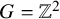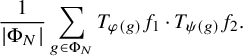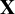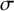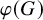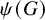1 Introduction
Let
![]() $(G,+)$
be a countable discrete abelian group. A probability measure-preserving G-system, or simply G-system for short, is a quadruple
$(G,+)$
be a countable discrete abelian group. A probability measure-preserving G-system, or simply G-system for short, is a quadruple
![]() $\textbf {X}=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
, where
$\textbf {X}=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
, where
![]() $(X,\mathcal {X},\mu )$
is a standard Borel probability space (that is, up to isomorphism of measure spaces, X is a compact metric space,
$(X,\mathcal {X},\mu )$
is a standard Borel probability space (that is, up to isomorphism of measure spaces, X is a compact metric space,
![]() $\mathcal {X}$
is the Borel
$\mathcal {X}$
is the Borel
![]() $\sigma $
-algebra and
$\sigma $
-algebra and
![]() $\mu $
is a regular Borel probability measure) and
$\mu $
is a regular Borel probability measure) and
![]() $T_g :X \to X$
,
$T_g :X \to X$
,
![]() $g \in G$
, are measure-preserving transformations, such that
$g \in G$
, are measure-preserving transformations, such that
![]() $T_{g+h}=T_g\circ T_h$
for every
$T_{g+h}=T_g\circ T_h$
for every
![]() $g,h\in G$
and
$g,h\in G$
and
![]() $T_0=Id$
. The transformation
$T_0=Id$
. The transformation
![]() $T_g:X \to X$
gives rise to a unitary operator on
$T_g:X \to X$
gives rise to a unitary operator on
![]() $L^2(\mu )$
, which we also denote by
$L^2(\mu )$
, which we also denote by
![]() $T_g$
, given by the formula
$T_g$
, given by the formula
![]() $T_g f(x) = f(T_g x)$
. We say that a G-system is ergodic if the only measurable
$T_g f(x) = f(T_g x)$
. We say that a G-system is ergodic if the only measurable
![]() $(T_g)_{g\in G}$
-invariant functions are the constant functions.
$(T_g)_{g\in G}$
-invariant functions are the constant functions.
1.1 Khintchine-type recurrence and the large intersections property
The starting point for the study of recurrence in ergodic theory is the Poincaré recurrence theorem, which states that, for any measure-preserving system
![]() $\left(X, \mathcal {X}, \mu , T \right)$
and any set
$\left(X, \mathcal {X}, \mu , T \right)$
and any set
![]() $A \in \mathcal {X}$
with
$A \in \mathcal {X}$
with
![]() $\mu (A)> 0$
, there exists
$\mu (A)> 0$
, there exists
![]() $n \in \mathbb N$
, such that
$n \in \mathbb N$
, such that
![]() $\mu (A \cap T^{-n}A)> 0$
.
$\mu (A \cap T^{-n}A)> 0$
.
Khintchine’s recurrence theorem strengthens and enhances Poincaré’s recurrence theorem by improving on the size of the intersections and the size of the set of return times.
Theorem 1.1 (Khintchine’s recurrence theorem [Reference Khintchine24])
For any measure-preserving system
![]() $\left(X, \mathcal {X}, \mu , T \right)$
, any
$\left(X, \mathcal {X}, \mu , T \right)$
, any
![]() $A \in \mathcal {X}$
and any
$A \in \mathcal {X}$
and any
![]() $\varepsilon> 0$
, the set
$\varepsilon> 0$
, the set
has bounded gaps.
Khintchine’s recurrence theorem easily extends to general semigroups, where the appropriate counterpart of ‘bounded gaps’ is the notion of syndeticity. In this paper, we deal with recurrence in countable discrete abelian groups. A subset A of a countable discrete abelian group G is said to be syndetic if there exists a finite set
![]() $F\subseteq G$
, such that
$F\subseteq G$
, such that
![]() $A+F = \{a+f : a\in A, f\in F\} = G$
.
$A+F = \{a+f : a\in A, f\in F\} = G$
.
It is natural to ask if recurrence theorems other than Poincaré’s recurrence theorem also have Khintchine-type enhancements. For instance, it follows from the IP Szemerédi theorem of Furstenberg and Katznelson [Reference Furstenberg and Katznelson20] and also from [Reference Austin3, Theorem B] that, for any abelian group G, any
![]() $k \in \mathbb N$
and any family of homomorphisms
$k \in \mathbb N$
and any family of homomorphisms
![]() $\varphi _1, \dots , \varphi _k : G \to G$
, the following holds: if
$\varphi _1, \dots , \varphi _k : G \to G$
, the following holds: if
![]() $\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
is a G-system and
$\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
is a G-system and
![]() $A \in \mathcal {X}$
has
$A \in \mathcal {X}$
has
![]() $\mu (A)> 0$
, then the set
$\mu (A)> 0$
, then the set
is syndetic.Footnote 1 With the goal of Khintchine-type enhancements in mind, this motivates the following definition:
Definition 1.2. A family of homomorphisms
![]() $\varphi _1, \dots , \varphi _k : G \to G$
has the large intersections property if the following holds: for any ergodic G-system
$\varphi _1, \dots , \varphi _k : G \to G$
has the large intersections property if the following holds: for any ergodic G-system
![]() $\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
, any
$\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
, any
![]() $A \in \mathcal {X}$
and any
$A \in \mathcal {X}$
and any
![]() $\varepsilon> 0$
, the set
$\varepsilon> 0$
, the set
is syndetic.
The large intersections property is closely related to the phenomenon of popular differences in combinatorics (see, e.g. [Reference Ackelsberg and Bergelson1, Reference Berger11, Reference Berger, Sah, Sawhney and Tidor12, Reference Mandache25, Reference Sah, Sawhney and Zhao26]).
Determining which families of homomorphisms have the large intersections property is a challenging problem with many surprising features. In the case
![]() $G = {\mathbb Z}$
and
$G = {\mathbb Z}$
and
![]() $\varphi _i(n) = in$
, the problem was resolved in [Reference Bergelson, Host and Kra8].
$\varphi _i(n) = in$
, the problem was resolved in [Reference Bergelson, Host and Kra8].
Theorem 1.3 ([Reference Bergelson, Host and Kra8], Theorems 1.2 and 1.3)
The family
![]() $\{n, 2n, \dots , kn\}$
has the large intersections property in
$\{n, 2n, \dots , kn\}$
has the large intersections property in
![]() ${\mathbb Z}$
if and only if
${\mathbb Z}$
if and only if
![]() $k \le 3$
.
$k \le 3$
.
Later work of Frantzikinakis [Reference Frantzikinakis18] and of Donoso et al. [Reference Donoso, Le, Moreira and Sun15] generalised this picture for arbitrary homomorphisms
![]() ${\mathbb Z} \to {\mathbb Z}$
, which take the form
${\mathbb Z} \to {\mathbb Z}$
, which take the form
![]() $n \mapsto an$
for some
$n \mapsto an$
for some
![]() $a \in {\mathbb Z}$
.
$a \in {\mathbb Z}$
.
Theorem 1.4 ([Reference Frantzikinakis18], special case of Theorem C; [Reference Donoso, Le, Moreira and Sun15], Theorem 1.5)
-
1. For any
 $a, b \in {{\mathbb Z}}$
, the families
$a, b \in {{\mathbb Z}}$
, the families
 $\{an,bn\}$
and
$\{an,bn\}$
and
 $\{an, bn, (a+b)n\}$
have the large intersections property (in
$\{an, bn, (a+b)n\}$
have the large intersections property (in
 ${\mathbb Z}$
).
${\mathbb Z}$
). -
2. For any
 $k \ge 4$
and any distinct and nonzero integers
$k \ge 4$
and any distinct and nonzero integers
 $a_1, \dots , a_k \in {\mathbb Z}$
, the family
$a_1, \dots , a_k \in {\mathbb Z}$
, the family
 $\{a_1n, \dots , a_kn\}$
does not have the large intersections property (in
$\{a_1n, \dots , a_kn\}$
does not have the large intersections property (in
 ${\mathbb Z}$
).
${\mathbb Z}$
).
Remark 1.5. Finitary combinatorial work of [Reference Sah, Sawhney and Zhao26, Theorem 1.6] suggests that the family
![]() $\{a_1n,a_2n,a_3n\}$
has the large intersections property if and only if
$\{a_1n,a_2n,a_3n\}$
has the large intersections property if and only if
![]() $a_i+a_j=a_k$
for some permutation
$a_i+a_j=a_k$
for some permutation
![]() $\{i,j,k\}$
of
$\{i,j,k\}$
of
![]() $\{1,2,3\}$
.
$\{1,2,3\}$
.
In [Reference Bergelson, Tao and Ziegler10], Khintchine-type recurrence results are established in the infinitely generated torsion groups
![]() $G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p{\mathbb Z}}$
.
$G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p{\mathbb Z}}$
.
Theorem 1.6 ([Reference Bergelson, Tao and Ziegler10], Theorems 1.12 and 1.13)
-
1. Fix a prime
 $p> 2$
. If
$p> 2$
. If
 $c_1, c_2 \in {\mathbb Z}/p{\mathbb Z}$
are distinct and nonzero, then
$c_1, c_2 \in {\mathbb Z}/p{\mathbb Z}$
are distinct and nonzero, then
 $\{c_1g,c_2g\}$
has the large intersections property in
$\{c_1g,c_2g\}$
has the large intersections property in
 $G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p{\mathbb Z}}$
.
$G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p{\mathbb Z}}$
. -
2. Fix a prime
 $p> 3$
. If
$p> 3$
. If
 $c_1, c_2 \in {\mathbb Z}/p{\mathbb Z}$
are distinct and nonzero and
$c_1, c_2 \in {\mathbb Z}/p{\mathbb Z}$
are distinct and nonzero and
 $c_1 + c_2 \ne 0$
, then
$c_1 + c_2 \ne 0$
, then
 $\{c_1g, c_2g, (c_1+c_2)g\}$
has the large intersections property in
$\{c_1g, c_2g, (c_1+c_2)g\}$
has the large intersections property in
 $G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p{\mathbb Z}}$
.
$G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p{\mathbb Z}}$
.
Remark 1.7. It is conjectured in [Reference Bergelson, Tao and Ziegler10, Conjecture 1.14] that, if
![]() $c_1, c_2, c_3 \in {\mathbb Z}/p{\mathbb Z}$
are distinct and nonzero and
$c_1, c_2, c_3 \in {\mathbb Z}/p{\mathbb Z}$
are distinct and nonzero and
![]() $c_i+c_j \ne c_k$
for every permutation
$c_i+c_j \ne c_k$
for every permutation
![]() $\{i,j,k\}$
of
$\{i,j,k\}$
of
![]() $\{1,2,3\}$
, then
$\{1,2,3\}$
, then
![]() $\{c_1g, c_2g, c_3g\}$
does not have the large intersections property in
$\{c_1g, c_2g, c_3g\}$
does not have the large intersections property in
![]() $G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p{\mathbb Z}}$
.
$G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p{\mathbb Z}}$
.
Khintchine-type recurrence in general abelian groups was addressed in [Reference Ackelsberg, Bergelson and Best2] and [Reference Shalom27]. For 3-point linear configurations, the following was shown in [Reference Ackelsberg, Bergelson and Best2]:
Theorem 1.8 ([Reference Ackelsberg, Bergelson and Best2], Theorem 1.10)
Let G be a countable discrete abelian group. Let
![]() $\varphi ,\psi :G \to G$
be homomorphisms. If all three of the subgroups
$\varphi ,\psi :G \to G$
be homomorphisms. If all three of the subgroups
![]() $\varphi (G)$
,
$\varphi (G)$
,
![]() $\psi (G)$
and
$\psi (G)$
and
![]() $(\psi -\varphi )(G)$
have finite index in G, then
$(\psi -\varphi )(G)$
have finite index in G, then
![]() $\{\varphi ,\psi \}$
has the large intersections property.
$\{\varphi ,\psi \}$
has the large intersections property.
Remark 1.9. Earlier work of Chu demonstrates that at least some finite index condition is necessary for large intersections. Namely, it follows from [Reference Chu13, Theorem 1.2] that the pair
![]() $\{(n,0), (0,n)\}$
, does not have the large intersections property in
$\{(n,0), (0,n)\}$
, does not have the large intersections property in
![]() ${\mathbb Z}^2$
(see [Reference Ackelsberg, Bergelson and Best2, Example 10.2]). While we do not pursue optimal lower bounds for families lacking the large intersections property in this paper, Chu also showed that, for the pair
${\mathbb Z}^2$
(see [Reference Ackelsberg, Bergelson and Best2, Example 10.2]). While we do not pursue optimal lower bounds for families lacking the large intersections property in this paper, Chu also showed that, for the pair
![]() $\{(n,0), (0,n)\}$
, the optimal lower bound is still polynomially large. In particular,
$\{(n,0), (0,n)\}$
, the optimal lower bound is still polynomially large. In particular,
![]() $\mu \left( A \cap T_{(n,0)}^{-1}A \cap T_{(0,n)}^{-1}A \right)> \mu (A)^4 - \varepsilon $
for syndetically many n (see [Reference Chu13, Theorem 1.1]).
$\mu \left( A \cap T_{(n,0)}^{-1}A \cap T_{(0,n)}^{-1}A \right)> \mu (A)^4 - \varepsilon $
for syndetically many n (see [Reference Chu13, Theorem 1.1]).
For more restricted 4-point configurations, the following result was shown in [Reference Ackelsberg, Bergelson and Best2] and independently in [Reference Shalom27]:
Theorem 1.10 ([Reference Ackelsberg, Bergelson and Best2], Theorem 1.11; [Reference Shalom27], Theorem 1.3)
Let G be a countable discrete abelian group. Let
![]() $a, b \in {\mathbb Z}$
be distinct, nonzero integers, such that all four of the subgroups
$a, b \in {\mathbb Z}$
be distinct, nonzero integers, such that all four of the subgroups
![]() $aG$
,
$aG$
,
![]() $bG$
,
$bG$
,
![]() $(a+b)G$
and
$(a+b)G$
and
![]() $(b-a)G$
have finite index in G. Then
$(b-a)G$
have finite index in G. Then
![]() $\{ag, bg, (a+b)g\}$
has the large intersections property.
$\{ag, bg, (a+b)g\}$
has the large intersections property.
1.2 Main results
In this paper, we refine the understanding of Khintchine-type recurrence for 3-point configurations in abelian groups and make substantial progress towards characterising the pairs of homomorphisms
![]() $\varphi , \psi : G \to G$
that have the large intersections property.
$\varphi , \psi : G \to G$
that have the large intersections property.
Our first result shows that the large intersections property holds for any pair of homomorphisms
![]() $\{\varphi ,\psi \}$
so long as at least two of the three subgroups in Theorem 1.8 have finite index in G. In particular, this shows that [Reference Ackelsberg, Bergelson and Best2, Conjecture 10.1] is false.
$\{\varphi ,\psi \}$
so long as at least two of the three subgroups in Theorem 1.8 have finite index in G. In particular, this shows that [Reference Ackelsberg, Bergelson and Best2, Conjecture 10.1] is false.
Theorem 1.11. Let G be a countable discrete abelian group. Let
![]() $\varphi , \psi : G \to G$
be homomorphisms, such that at least two of the three subgroups
$\varphi , \psi : G \to G$
be homomorphisms, such that at least two of the three subgroups
![]() $\varphi (G)$
,
$\varphi (G)$
,
![]() $\psi (G)$
and
$\psi (G)$
and
![]() $(\psi -\varphi )(G)$
have finite index in G. Then for any ergodic G-system
$(\psi -\varphi )(G)$
have finite index in G. Then for any ergodic G-system
![]() $\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
, any
$\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
, any
![]() $A \in \mathcal {X}$
and any
$A \in \mathcal {X}$
and any
![]() $\varepsilon>0$
, the set
$\varepsilon>0$
, the set
is syndetic.
As mentioned above (see Remark 1.9), the work of Chu [Reference Chu13] provides a counterexample to the large intersections property when all three subgroups
![]() $\varphi (G)$
,
$\varphi (G)$
,
![]() $\psi (G)$
and
$\psi (G)$
and
![]() $(\psi - \varphi )(G)$
have infinite index in G. In this paper, we give additional counterexamples for the group
$(\psi - \varphi )(G)$
have infinite index in G. In this paper, we give additional counterexamples for the group
![]() $G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
with homomorphisms
$G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
with homomorphisms
![]() $g \mapsto ag$
and
$g \mapsto ag$
and
![]() $g \mapsto bg$
for some
$g \mapsto bg$
for some
![]() $a, b \in {\mathbb Z}$
(see Theorem 1.14 below). A natural question to ask, then, is what happens when only one of the subgroups
$a, b \in {\mathbb Z}$
(see Theorem 1.14 below). A natural question to ask, then, is what happens when only one of the subgroups
![]() $\varphi (G)$
,
$\varphi (G)$
,
![]() $\psi (G)$
or
$\psi (G)$
or
![]() $(\psi -\varphi )(G)$
has finite index. Namely:
$(\psi -\varphi )(G)$
has finite index. Namely:
Question 1.12. Let G be a countable discrete abelian group, and let
![]() $\varphi :G\rightarrow G$
,
$\varphi :G\rightarrow G$
,
![]() $\psi :G\rightarrow G$
be homomorphisms, such that at least one of the subgroups
$\psi :G\rightarrow G$
be homomorphisms, such that at least one of the subgroups
![]() $\varphi (G)$
,
$\varphi (G)$
,
![]() $\psi (G)$
or
$\psi (G)$
or
![]() $(\psi -\varphi )(G)$
has finite index in G. Is it true that, for any ergodic G-system
$(\psi -\varphi )(G)$
has finite index in G. Is it true that, for any ergodic G-system
![]() $\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
, any
$\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
, any
![]() $A\in \mathcal {X}$
, and any
$A\in \mathcal {X}$
, and any
![]() $\varepsilon>0$
, the set
$\varepsilon>0$
, the set
is syndetic?
Note that, by symmetry, it is enough to provide an answer to Question 1.12 under the assumption that
![]() $(\psi -\varphi )(G)$
has finite index. Indeed, suppose
$(\psi -\varphi )(G)$
has finite index. Indeed, suppose
![]() $\psi (G)$
has finite index in G. Then, since
$\psi (G)$
has finite index in G. Then, since
![]() $(T_g)_{g \in G}$
is a measure-preserving action, we have the identity
$(T_g)_{g \in G}$
is a measure-preserving action, we have the identity
Hence, the pair
![]() $\{\varphi ,\psi \}$
has the large intersections property if and only if
$\{\varphi ,\psi \}$
has the large intersections property if and only if
![]() $\left\{\widetilde {\varphi }, \widetilde {\psi }\right\}$
has the large intersections property, where
$\left\{\widetilde {\varphi }, \widetilde {\psi }\right\}$
has the large intersections property, where
![]() $\widetilde {\varphi } = - \varphi $
and
$\widetilde {\varphi } = - \varphi $
and
![]() $\widetilde {\psi } = \psi - \varphi $
. Moreover, we have
$\widetilde {\psi } = \psi - \varphi $
. Moreover, we have
![]() $(\widetilde {\psi } - \widetilde {\varphi })(G) = \psi (G)$
, which is of finite index. A similar argument applies when
$(\widetilde {\psi } - \widetilde {\varphi })(G) = \psi (G)$
, which is of finite index. A similar argument applies when
![]() $\varphi (G)$
has finite index.
$\varphi (G)$
has finite index.
When
![]() $G = {\mathbb Z}^2$
, we can use additional tools from linear algebra to classify all pairs of homomorphisms
$G = {\mathbb Z}^2$
, we can use additional tools from linear algebra to classify all pairs of homomorphisms
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, which allows us to answer Question 1.12 affirmatively in this setting. In fact, we can give a precise description of the optimal size of intersections for all 3-point configurations in
$\psi $
, which allows us to answer Question 1.12 affirmatively in this setting. In fact, we can give a precise description of the optimal size of intersections for all 3-point configurations in
![]() ${\mathbb Z}^2$
(see Subsection 1.4 below). However, our results rely heavily on properties of
${\mathbb Z}^2$
(see Subsection 1.4 below). However, our results rely heavily on properties of
![]() $2\times 2$
matrices, and it appears that the full generality of Question 1.12 for general abelian groups and general homomoprhisms is out of reach without developing new techniques.
$2\times 2$
matrices, and it appears that the full generality of Question 1.12 for general abelian groups and general homomoprhisms is out of reach without developing new techniques.
On the other hand, in the special case
![]() $\varphi (g) = ag$
and
$\varphi (g) = ag$
and
![]() $\psi (g) = bg$
for
$\psi (g) = bg$
for
![]() $a, b \in {\mathbb Z}$
, we answer Question 1.12 affirmatively:
$a, b \in {\mathbb Z}$
, we answer Question 1.12 affirmatively:
Theorem 1.13. Let G be a countable discrete abelian group. Let
![]() $a,b\in \mathbb {Z}$
be integers, such that
$a,b\in \mathbb {Z}$
be integers, such that
![]() $(b-a)G$
has finite index in G. Then for any ergodic G-system
$(b-a)G$
has finite index in G. Then for any ergodic G-system
![]() $\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
, any
$\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
, any
![]() $A \in \mathcal {X}$
and any
$A \in \mathcal {X}$
and any
![]() $\varepsilon>0$
, the set
$\varepsilon>0$
, the set
is syndetic.
We also show that the assumption that
![]() $(b-a)G$
has finite index in G is necessary. To see this, we prove the following result:
$(b-a)G$
has finite index in G is necessary. To see this, we prove the following result:
Theorem 1.14. Let
![]() $G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
. Let
$G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
. Let
![]() $l \in \mathbb N$
. There exists a number
$l \in \mathbb N$
. There exists a number
![]() $P = P(l)$
, such that, for any
$P = P(l)$
, such that, for any
![]() $a, b \in \mathbb N$
with
$a, b \in \mathbb N$
with
![]() $p \mid \gcd (a,b)$
for some prime
$p \mid \gcd (a,b)$
for some prime
![]() $p \ge P$
, there is an ergodic G-system
$p \ge P$
, there is an ergodic G-system
![]() $\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
and a set
$\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
and a set
![]() $A \in \mathcal {X}$
with
$A \in \mathcal {X}$
with
![]() $\mu (A)> 0$
, such that
$\mu (A)> 0$
, such that
for every
![]() $g\ne 0$
.
$g\ne 0$
.
Question 1.15. Can p in the statement of Theorem 1.14 be replaced by any natural number?
1.3 Applications to geometric progressions and other multiplicative patterns
One particularly interesting corollary of Theorem 1.13 is a multiplicative version of the following large intersection theorem in [Reference Bergelson, Host and Kra8]:
Theorem 1.16 ([Reference Bergelson, Host and Kra8], Corollary 1.5)
Let
![]() $E \subseteq {\mathbb Z}$
be a set of positive upper Banach density
$E \subseteq {\mathbb Z}$
be a set of positive upper Banach density
Then, for any
![]() $\varepsilon> 0$
, the set
$\varepsilon> 0$
, the set
is syndetic.
Consider the group
![]() $G=(\mathbb {Q}_{>0},\cdot )$
. This is a multiplicative counterpart of
$G=(\mathbb {Q}_{>0},\cdot )$
. This is a multiplicative counterpart of
![]() $(\mathbb {Z},+)$
. In the group
$(\mathbb {Z},+)$
. In the group
![]() $(\mathbb Q_{>0}, \cdot )$
, the upper Banach density of a set
$(\mathbb Q_{>0}, \cdot )$
, the upper Banach density of a set
![]() $E \subseteq \mathbb Q_{>0}$
is given by
$E \subseteq \mathbb Q_{>0}$
is given by
where the supremum is taken over all Følner sequences
![]() $\Phi = (\Phi _N)_{N \in \mathbb N}$
in
$\Phi = (\Phi _N)_{N \in \mathbb N}$
in
![]() $(\mathbb Q_{>0}, \cdot )$
. An instructive class of examples of Følner sequences in
$(\mathbb Q_{>0}, \cdot )$
. An instructive class of examples of Følner sequences in
![]() $(\mathbb Q_{>0}, \cdot )$
is given by sequences of the form
$(\mathbb Q_{>0}, \cdot )$
is given by sequences of the form
 $$ \begin{align*} \Phi_N = \left\{ b_N \prod_{i=1}^N{q_i^{r_i}} : -N \le r_i \le N \right\}, \end{align*} $$
$$ \begin{align*} \Phi_N = \left\{ b_N \prod_{i=1}^N{q_i^{r_i}} : -N \le r_i \le N \right\}, \end{align*} $$
where
![]() $(q_n)_{n \in \mathbb N}$
is a sequence of generators of
$(q_n)_{n \in \mathbb N}$
is a sequence of generators of
![]() $(\mathbb Q_{>0}, \cdot )$
and
$(\mathbb Q_{>0}, \cdot )$
and
![]() $(b_N)_{N \in \mathbb N}$
is any sequence in
$(b_N)_{N \in \mathbb N}$
is any sequence in
![]() $\mathbb Q_{>0}$
. The subscript on
$\mathbb Q_{>0}$
. The subscript on
![]() $d^*_{\text {mult}}$
is to emphasise that this density is with respect to the multiplicative structure on
$d^*_{\text {mult}}$
is to emphasise that this density is with respect to the multiplicative structure on
![]() $\mathbb Q_{>0}$
rather than its additive structure. Using an ergodic version of the Furstenberg correspondence principle (see [Reference Bergelson and Ferré Moragues6, Theorem 2.8]), we deduce the following result as an immediate consequence of Theorem 1.13:
$\mathbb Q_{>0}$
rather than its additive structure. Using an ergodic version of the Furstenberg correspondence principle (see [Reference Bergelson and Ferré Moragues6, Theorem 2.8]), we deduce the following result as an immediate consequence of Theorem 1.13:
Theorem 1.17. Let
![]() $E\subseteq \mathbb {Q}_{>0}$
be a set of positive multiplicative upper Banach density
$E\subseteq \mathbb {Q}_{>0}$
be a set of positive multiplicative upper Banach density
![]() $d_{\text {mult}}^*(E)> 0$
, and let
$d_{\text {mult}}^*(E)> 0$
, and let
![]() $k\in {\mathbb Z}$
. Then for any
$k\in {\mathbb Z}$
. Then for any
![]() $\varepsilon>0$
, the sets
$\varepsilon>0$
, the sets
and
are syndetic.
Remark 1.18. The special case where
![]() $k=1$
in (2) or
$k=1$
in (2) or
![]() $k = 2$
in (3) is related to the existence of length 3 geometric progressions in sets of positive multiplicative density. Heuristically, if E were a random set, where each positive rational number
$k = 2$
in (3) is related to the existence of length 3 geometric progressions in sets of positive multiplicative density. Heuristically, if E were a random set, where each positive rational number
![]() $q\in \mathbb {Q}_{>0}$
is independently chosen to be inside E with probability
$q\in \mathbb {Q}_{>0}$
is independently chosen to be inside E with probability
![]() $\alpha $
, then the expected number of geometric progressions of length 3 and quotient q would be
$\alpha $
, then the expected number of geometric progressions of length 3 and quotient q would be
![]() $\alpha ^3$
. Now, fix any set E with
$\alpha ^3$
. Now, fix any set E with
![]() $d^*_{mult}(E) = \alpha $
. Choosing
$d^*_{mult}(E) = \alpha $
. Choosing
![]() $\varepsilon $
sufficiently small, our result implies that E contains almost as many geometric progressions with quotient q as a random set with the same density,
$\varepsilon $
sufficiently small, our result implies that E contains almost as many geometric progressions with quotient q as a random set with the same density,
![]() $\alpha $
, for a syndetic set of quotients.
$\alpha $
, for a syndetic set of quotients.
Theorem 1.14 shows that, if n and m share a large prime factor, then
![]() $\{q^n, q^m\}$
does not have the large intersections property in
$\{q^n, q^m\}$
does not have the large intersections property in
![]() $(\mathbb Q_{>0}, \cdot )$
. What happens in the case that n and m are coprime is an interesting question that we are unable to answer with our current methods:
$(\mathbb Q_{>0}, \cdot )$
. What happens in the case that n and m are coprime is an interesting question that we are unable to answer with our current methods:
Question 1.19. Suppose
![]() $n, m \in \mathbb N$
are coprime. Does the pair
$n, m \in \mathbb N$
are coprime. Does the pair
![]() $\{q^n, q^m\}$
have the large intersections property in
$\{q^n, q^m\}$
have the large intersections property in
![]() $(\mathbb Q_{>0}, \cdot )$
?
$(\mathbb Q_{>0}, \cdot )$
?
Since every
![]() $\mathbb {Z}$
-action can be lifted to a
$\mathbb {Z}$
-action can be lifted to a
![]() $(\mathbb {Q}_{>0}, \cdot )$
-action (indeed,
$(\mathbb {Q}_{>0}, \cdot )$
-action (indeed,
![]() $(\mathbb Q_{>0}, \cdot )$
is torsion-free, so
$(\mathbb Q_{>0}, \cdot )$
is torsion-free, so
![]() ${\mathbb Z}$
embeds as a subgroup), we see from Theorem 1.3 above that
${\mathbb Z}$
embeds as a subgroup), we see from Theorem 1.3 above that
![]() $\{q,q^2,\dots , q^k\}$
does not have the large intersections property for
$\{q,q^2,\dots , q^k\}$
does not have the large intersections property for
![]() $k \ge 4$
. However, we can still ask about geometric progressions of length
$k \ge 4$
. However, we can still ask about geometric progressions of length
![]() $4$
.
$4$
.
Question 1.20. Does the triple
![]() $\{q, q^2, q^3\}$
have the large intersections property in
$\{q, q^2, q^3\}$
have the large intersections property in
![]() $(\mathbb Q_{>0}, \cdot )$
?
$(\mathbb Q_{>0}, \cdot )$
?
For a discussion of where our methods come up short for answering Questions 1.19 and 1.20, see Subsection 2.7 below.
1.3.1 Patterns in
 $(\mathbb N,\cdot )$
$(\mathbb N,\cdot )$
A notion of upper Banach density can be defined in the semigroup
![]() $(\mathbb N, \cdot )$
by the formula in (1), where the supremum is now taken over Følner sequences in
$(\mathbb N, \cdot )$
by the formula in (1), where the supremum is now taken over Følner sequences in
![]() $(\mathbb N, \cdot )$
. Examples of Følner sequences in
$(\mathbb N, \cdot )$
. Examples of Følner sequences in
![]() $(\mathbb N, \cdot )$
include sequences of the form
$(\mathbb N, \cdot )$
include sequences of the form
 $$ \begin{align*} \Phi_N = \left\{ b_N \prod_{i=1}^N{p_i^{r_i}} : 0 \le r_i \le N \right\}, \end{align*} $$
$$ \begin{align*} \Phi_N = \left\{ b_N \prod_{i=1}^N{p_i^{r_i}} : 0 \le r_i \le N \right\}, \end{align*} $$
where
![]() $(p_n)_{n \in \mathbb N}$
is an enumeration of the prime numbers and
$(p_n)_{n \in \mathbb N}$
is an enumeration of the prime numbers and
![]() $(b_N)_{N \in \mathbb N}$
is any sequence in
$(b_N)_{N \in \mathbb N}$
is any sequence in
![]() $\mathbb N$
. In Section 8, we transfer Theorems 1.11 and 1.13 to the setting of cancellative abelian semigroups. As a consequence, we obtain the following result about geometric configurations in the multiplicative integers:
$\mathbb N$
. In Section 8, we transfer Theorems 1.11 and 1.13 to the setting of cancellative abelian semigroups. As a consequence, we obtain the following result about geometric configurations in the multiplicative integers:
Theorem 1.21. Let
![]() $E \subseteq \mathbb N$
be a set of positive multiplicative upper Banach density, and let
$E \subseteq \mathbb N$
be a set of positive multiplicative upper Banach density, and let
![]() $k\in {\mathbb Z}$
. Then for any
$k\in {\mathbb Z}$
. Then for any
![]() $\varepsilon>0$
, the sets
$\varepsilon>0$
, the sets
and
are (multiplicatively) syndetic in
![]() $(\mathbb N,\cdot )$
.
$(\mathbb N,\cdot )$
.
1.4 Applications to patterns in
 ${\mathbb Z}^2$
${\mathbb Z}^2$
When
![]() $G = {\mathbb Z}^2$
, we are able to give a complete picture of the phenomenon of large intersections for 3-point matrix patterns, that is, patterns of the form
$G = {\mathbb Z}^2$
, we are able to give a complete picture of the phenomenon of large intersections for 3-point matrix patterns, that is, patterns of the form
![]() $\{\vec {x}, \vec {x} + M_1\vec {n}, \vec {x} + M_2\vec {n}\}$
, where
$\{\vec {x}, \vec {x} + M_1\vec {n}, \vec {x} + M_2\vec {n}\}$
, where
![]() $\vec {x}, \vec {n} \in {\mathbb Z}^2$
and
$\vec {x}, \vec {n} \in {\mathbb Z}^2$
and
![]() $M_1, M_2$
are
$M_1, M_2$
are
![]() $2\times 2$
matrices with integer entries (note that any homomorphism
$2\times 2$
matrices with integer entries (note that any homomorphism
![]() $\varphi : {\mathbb Z}^2 \to {\mathbb Z}^2$
can be expressed as a
$\varphi : {\mathbb Z}^2 \to {\mathbb Z}^2$
can be expressed as a
![]() $2\times 2$
matrix with integer entries, so matrix patterns capture all possible configurations in
$2\times 2$
matrix with integer entries, so matrix patterns capture all possible configurations in
![]() ${\mathbb Z}^2$
that can be described within the framework of group homomorphisms).
${\mathbb Z}^2$
that can be described within the framework of group homomorphisms).
Following [Reference Bergelson, Host and Kra8], we say that the syndetic supremum of a bounded real-valued
![]() ${\mathbb Z}^2$
-sequence
${\mathbb Z}^2$
-sequence
![]() $\left( a_{n,m} \right)_{(n, m) \in {\mathbb Z}^2}$
is the quantity
$\left( a_{n,m} \right)_{(n, m) \in {\mathbb Z}^2}$
is the quantity
For
![]() $2\times 2$
integer matrices
$2\times 2$
integer matrices
![]() $M_1$
and
$M_1$
and
![]() $M_2$
and
$M_2$
and
![]() $\alpha \in (0,1)$
, we define the ergodic popular difference density by
$\alpha \in (0,1)$
, we define the ergodic popular difference density by
where the infimum is taken over all ergodic
![]() ${\mathbb Z}^2$
-systems
${\mathbb Z}^2$
-systems
![]() $\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
and sets
$\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
and sets
![]() $A \in \mathcal {X}$
with
$A \in \mathcal {X}$
with
![]() $\mu (A) = \alpha $
. This can be seen as an ergodic-theoretic analogue to the popular difference density defined in [Reference Sah, Sawhney and Zhao26]. It is natural to ask if
$\mu (A) = \alpha $
. This can be seen as an ergodic-theoretic analogue to the popular difference density defined in [Reference Sah, Sawhney and Zhao26]. It is natural to ask if
![]() $\text {epdd}_{M_1,M_2}(\alpha )$
coincides with the finitary combinatorial quantity
$\text {epdd}_{M_1,M_2}(\alpha )$
coincides with the finitary combinatorial quantity
![]() $\text {pdd}_{M_1,M_2}(\alpha )$
. Standard tools for translating between ergodic theory and combinatorics, such as Furstenberg’s correspondence principle, are insufficient for resolving this question, and we do not know the answer in general. However, in special cases where
$\text {pdd}_{M_1,M_2}(\alpha )$
. Standard tools for translating between ergodic theory and combinatorics, such as Furstenberg’s correspondence principle, are insufficient for resolving this question, and we do not know the answer in general. However, in special cases where
![]() $\text {pdd}_{M_1,M_2}(\alpha )$
is known, it is in agreement with the values of
$\text {pdd}_{M_1,M_2}(\alpha )$
is known, it is in agreement with the values of
![]() $\text {epdd}_{M_1,M_2}(\alpha )$
displayed in Table 1 below, and we suspect that
$\text {epdd}_{M_1,M_2}(\alpha )$
displayed in Table 1 below, and we suspect that
![]() $\text {pdd}_{M_1,M_2}(\alpha ) = \text {epdd}_{M_1,M_2}(\alpha )$
in the remaining cases (see Subsection 7.3 below for additional remarks on (combinatorial) popular difference densities for matrix patterns in
$\text {pdd}_{M_1,M_2}(\alpha ) = \text {epdd}_{M_1,M_2}(\alpha )$
in the remaining cases (see Subsection 7.3 below for additional remarks on (combinatorial) popular difference densities for matrix patterns in
![]() ${\mathbb Z}^2$
).
${\mathbb Z}^2$
).
Table 1 Ergodic popular difference densities for 3-point matrix patterns in
![]() ${\mathbb Z}^2$
${\mathbb Z}^2$

Theorem 1.11 provides a sufficient condition on the matrices
![]() $M_1$
and
$M_1$
and
![]() $M_2$
to guarantee that
$M_2$
to guarantee that
![]() $\text {epdd}_{M_1, M_2}(\alpha ) \ge \alpha ^3$
for
$\text {epdd}_{M_1, M_2}(\alpha ) \ge \alpha ^3$
for
![]() $\alpha \in (0,1)$
. We now seek to describe the quantity
$\alpha \in (0,1)$
. We now seek to describe the quantity
![]() $\text {epdd}_{M_1, M_2}(\alpha )$
for any pair of
$\text {epdd}_{M_1, M_2}(\alpha )$
for any pair of
![]() $2\times 2$
integer matrices
$2\times 2$
integer matrices
![]() $M_1$
and
$M_1$
and
![]() $M_2$
. Table 1 summarises ergodic popular difference densities for all 3-point matrix configurations in
$M_2$
. Table 1 summarises ergodic popular difference densities for all 3-point matrix configurations in
![]() ${\mathbb Z}^2$
(for matrices
${\mathbb Z}^2$
(for matrices
![]() $M_1, M_2$
, we let
$M_1, M_2$
, we let
![]() $r(M_1,M_2)$
be a list of the ranks of
$r(M_1,M_2)$
be a list of the ranks of
![]() $M_1$
,
$M_1$
,
![]() $M_2$
and
$M_2$
and
![]() $M_2 - M_1$
in decreasing order, and we denote by
$M_2 - M_1$
in decreasing order, and we denote by
![]() $[M_1,M_2]$
the commutator
$[M_1,M_2]$
the commutator
![]() $M_1M_2 - M_2M_1$
).
$M_1M_2 - M_2M_1$
).
The cases
![]() $r(M_1, M_2) = (2,2,2)$
and
$r(M_1, M_2) = (2,2,2)$
and
![]() $r(M_1, M_2) = (2,2,1)$
are covered directly by [Reference Ackelsberg, Bergelson and Best2, Theorem 1.10] and Theorem 1.11, respectively. Indeed, a matrix M has full rank if and only if the subgroup
$r(M_1, M_2) = (2,2,1)$
are covered directly by [Reference Ackelsberg, Bergelson and Best2, Theorem 1.10] and Theorem 1.11, respectively. Indeed, a matrix M has full rank if and only if the subgroup
![]() $M({\mathbb Z}^2) \subseteq {\mathbb Z}^2$
has finite index. More precisely,
$M({\mathbb Z}^2) \subseteq {\mathbb Z}^2$
has finite index. More precisely,
 $$ \begin{align*} [{\mathbb Z}^2 : M({\mathbb Z}^2)] = \begin{cases} \left| \det(M) \right|, & \text{if}~\det(M) \ne 0; \\ \infty, & \text{if}~\det(M) = 0. \end{cases} \end{align*} $$
$$ \begin{align*} [{\mathbb Z}^2 : M({\mathbb Z}^2)] = \begin{cases} \left| \det(M) \right|, & \text{if}~\det(M) \ne 0; \\ \infty, & \text{if}~\det(M) = 0. \end{cases} \end{align*} $$
The remaining cases are proved in Section 7.
1.5 Preliminary remarks on characteristic factors
In this paper, we approach multiple recurrence problems by determining and utilising the so-called characteristic factors, which are the factors that are responsible for the limiting behaviour of the quantity
in ergodic G-systems (see Subsection 2.2 for a discussion of factors in general and Definition 3.3 for a definition of characteristic factors). For
![]() ${\mathbb Z}$
-actions, there are two different approaches to characteristic factors for linear averages, developed independently by Host and Kra [Reference Host and Kra23] and by Ziegler [Reference Ziegler30], giving rise to factors that coincide (see [Reference Bergelson5, Appendix A]). However, in the context of G-actions, where G is an arbitrary (nonfinitely generated) countable discrete abelian group, the approaches of Host–Kra and of Ziegler may produce different factors (see Subsection 2.6 below for more details).
${\mathbb Z}$
-actions, there are two different approaches to characteristic factors for linear averages, developed independently by Host and Kra [Reference Host and Kra23] and by Ziegler [Reference Ziegler30], giving rise to factors that coincide (see [Reference Bergelson5, Appendix A]). However, in the context of G-actions, where G is an arbitrary (nonfinitely generated) countable discrete abelian group, the approaches of Host–Kra and of Ziegler may produce different factors (see Subsection 2.6 below for more details).
Our work, thus, leads to the general open question of how, in the setup of countable discrete abelian groups, the Host–Kra factors are related to the actual characteristic factors of the corresponding multiple ergodic averages (the factors obtained by Ziegler’s approach). Discerning the relationship between the Host–Kra factors and the characteristic factors may lead to a better understanding of the quantities
where
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
is a G-system,
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
is a G-system,
![]() $A \in \mathcal {X}$
and
$A \in \mathcal {X}$
and
![]() $\varphi _i:G\rightarrow G$
are homomorphisms or, more generally, polynomial maps.
$\varphi _i:G\rightarrow G$
are homomorphisms or, more generally, polynomial maps.
1.6 Structure of the paper
The paper is organised as follows. In Section 2, we introduce notation and conventions that we use throughout the paper.
Proofs of the main results appear in Sections 3–6. First, in Section 3, we establish characteristic factors for the multiple ergodic averages
when
![]() $(\psi -\varphi )(G)$
has finite index in G and prove Theorem 1.11. Then, in Section 4, we use an extension trick to simplify the characteristic factors, and in Section 5, prove a new limit formula for the extension system, leading to a proof of Theorem 1.13. Finally, we prove Theorem 1.14 in Section 6.
$(\psi -\varphi )(G)$
has finite index in G and prove Theorem 1.11. Then, in Section 4, we use an extension trick to simplify the characteristic factors, and in Section 5, prove a new limit formula for the extension system, leading to a proof of Theorem 1.13. Finally, we prove Theorem 1.14 in Section 6.
The final two sections contain applications of the main results. Using Theorem 1.11 together with additional tools from [Reference Ackelsberg, Bergelson and Best2, Reference Bergelson, Host and Kra8, Reference Bergelson and Leibman9, Reference Chu13, Reference Donoso and Sun16], we compute ergodic popular difference densities for 3-point matrix patterns in
![]() ${\mathbb Z}^2$
. In Section 8, we extend the main results (Theorems 1.11 and 1.13) to the setting of cancellative abelian semigroups.
${\mathbb Z}^2$
. In Section 8, we extend the main results (Theorems 1.11 and 1.13) to the setting of cancellative abelian semigroups.
2 Preliminaries
The goal of this section is to introduce some notations and objects that will play an important role in this paper. Throughout this section, we let G denote an arbitrary countable discrete abelian group and
![]() $\textbf {X}=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
a G-system.
$\textbf {X}=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
a G-system.
2.1 Uniform Cesàro limits
The large intersection property of a family
![]() $\{\varphi _1, \dots , \varphi _k\}$
is related to the limit behaviour of the multiple ergodic averages
$\{\varphi _1, \dots , \varphi _k\}$
is related to the limit behaviour of the multiple ergodic averages
 $$ \begin{align} \frac{1}{|\Phi_N|} \sum_{g \in \Phi_N} \prod_{i=1}^k{T_{\varphi_i(g)}f_i}, \end{align} $$
$$ \begin{align} \frac{1}{|\Phi_N|} \sum_{g \in \Phi_N} \prod_{i=1}^k{T_{\varphi_i(g)}f_i}, \end{align} $$
where
![]() $(\Phi _N)_{N \in \mathbb N}$
is a Følner sequenceFootnote 2 in G and
$(\Phi _N)_{N \in \mathbb N}$
is a Følner sequenceFootnote 2 in G and
![]() $f_1, \dots , f_k \in L^{\infty }(\mu )$
. By [Reference Austin3] and [Reference Zorin-Kranich32], the quantity in (4) converges in
$f_1, \dots , f_k \in L^{\infty }(\mu )$
. By [Reference Austin3] and [Reference Zorin-Kranich32], the quantity in (4) converges in
![]() $L^2(\mu )$
as
$L^2(\mu )$
as
![]() $N \to \infty $
, and the limit is independent of the choice of Følner sequence
$N \to \infty $
, and the limit is independent of the choice of Følner sequence
![]() $(\Phi _N)_{N \in \mathbb N}$
. For more concise notation, we define the uniform Cesàro limit
$(\Phi _N)_{N \in \mathbb N}$
. For more concise notation, we define the uniform Cesàro limit
![]() $x = \text {UC -}\lim _{g \in G}{x_g}$
if
$x = \text {UC -}\lim _{g \in G}{x_g}$
if
![]() $\frac {1}{|\Phi _N|} \sum _{g \in \Phi _N}{x_g} \to x$
for every Følner sequence
$\frac {1}{|\Phi _N|} \sum _{g \in \Phi _N}{x_g} \to x$
for every Følner sequence
![]() $(\Phi _N)_{N\in \mathbb N}$
in G.
$(\Phi _N)_{N\in \mathbb N}$
in G.
One crucial tool for handling uniform Cesàro limits is the following version of the van der Corput differencing trick:
Lemma 2.1 (van der Corput lemma, cf. [Reference Ackelsberg, Bergelson and Best2], Lemma 2.2)
Let
![]() $\mathcal {H}$
be a Hilbert space and G a countable amenable group. Let
$\mathcal {H}$
be a Hilbert space and G a countable amenable group. Let
![]() $(u_g)_{g\in G}$
be a bounded sequence in
$(u_g)_{g\in G}$
be a bounded sequence in
![]() $\mathcal {H}$
. If
$\mathcal {H}$
. If
![]() $\text {UC -}\lim _{g\in G} \left\langle u_{g+h}, u_g \right\rangle $
exists for every
$\text {UC -}\lim _{g\in G} \left\langle u_{g+h}, u_g \right\rangle $
exists for every
![]() $h\in G$
, and
$h\in G$
, and
then,
strongly.
Another useful tool for computing uniform Cesàro limits is the following ‘Fubini’ trick, which we use extensively in Section 7:
Lemma 2.2 ([Reference Bergelson and Leibman9], special case of Lemma 1.1)
Let G and H be countable discrete amenable groups, and let
![]() $(v_{h,g})_{(h,g) \in H \times G}$
be a bounded sequence. Suppose
$(v_{h,g})_{(h,g) \in H \times G}$
be a bounded sequence. Suppose
exists, and for every
![]() $g \in G$
,
$g \in G$
,
exists. Then
2.2 Factors
A factor of
![]() $\textbf {X}$
is a G-system
$\textbf {X}$
is a G-system
![]() $\textbf {Y}=(Y,\mathcal {Y},\nu ,(S_g)_{g\in G})$
together with a measurable map
$\textbf {Y}=(Y,\mathcal {Y},\nu ,(S_g)_{g\in G})$
together with a measurable map
![]() $\pi :X\to Y$
, such that
$\pi :X\to Y$
, such that
![]() $\pi _*\mu = \nu $
and
$\pi _*\mu = \nu $
and
![]() $\pi \circ T_g = S_g\circ \pi $
for all
$\pi \circ T_g = S_g\circ \pi $
for all
![]() $g\in G$
. There is a natural one-to-one correspondence between factors and
$g\in G$
. There is a natural one-to-one correspondence between factors and
![]() $(T_g)_{g \in G}$
-invariant sub-
$(T_g)_{g \in G}$
-invariant sub-
![]() $\sigma $
-algebras of
$\sigma $
-algebras of
![]() $\mathcal {X}$
. Throughout the paper, we freely move between the system
$\mathcal {X}$
. Throughout the paper, we freely move between the system
![]() $\textbf {Y}$
and the
$\textbf {Y}$
and the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\pi ^{-1}(\mathcal {Y})$
and refer to both of them as factors of
$\pi ^{-1}(\mathcal {Y})$
and refer to both of them as factors of
![]() $\textbf {X}$
. Given
$\textbf {X}$
. Given
![]() $f\in L^2(\mu )$
, we denote by
$f\in L^2(\mu )$
, we denote by
![]() $E(f|\mathcal {Y})$
the conditional expectation of f with respect to the
$E(f|\mathcal {Y})$
the conditional expectation of f with respect to the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\pi ^{-1}(\mathcal {Y})$
. We say that f is measurable with respect to
$\pi ^{-1}(\mathcal {Y})$
. We say that f is measurable with respect to
![]() $\mathcal {Y}$
if
$\mathcal {Y}$
if
![]() $f=E(f|\mathcal {Y})$
.
$f=E(f|\mathcal {Y})$
.
2.3 Factor of invariant sets
Let
![]() $\textbf {X}=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be a G-system. We write
$\textbf {X}=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be a G-system. We write
![]() $\mathcal {I}_G(X)$
for the sub-
$\mathcal {I}_G(X)$
for the sub-
![]() $\sigma $
-algebra of G-invariant sets. We say that
$\sigma $
-algebra of G-invariant sets. We say that
![]() $\textbf {X}$
is ergodic if
$\textbf {X}$
is ergodic if
![]() $\mathcal {I}_G(X)$
is the
$\mathcal {I}_G(X)$
is the
![]() $\sigma $
-algebra comprised of null and conull subsets of
$\sigma $
-algebra comprised of null and conull subsets of
![]() $(X,\mathcal {X},\mu )$
. For a subgroup
$(X,\mathcal {X},\mu )$
. For a subgroup
![]() $H \le G$
, we denote by
$H \le G$
, we denote by
![]() $\mathcal {I}_H(X)$
the sub-
$\mathcal {I}_H(X)$
the sub-
![]() $\sigma $
-algebra of H-invariant sets. Given a homomorphism
$\sigma $
-algebra of H-invariant sets. Given a homomorphism
![]() $\varphi :G\rightarrow G$
, it is convenient to denote by
$\varphi :G\rightarrow G$
, it is convenient to denote by
![]() $\mathcal {I}_{\varphi }(X)$
the
$\mathcal {I}_{\varphi }(X)$
the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {I}_{\varphi (G)}(X)$
.
$\mathcal {I}_{\varphi (G)}(X)$
.
2.4 Host–Kra factors
The Gowers–Host–Kra seminorms are an ergodic-theoretic version of the uniformity norms introduced by Gowers in [Reference Gowers22]. These seminorms were first introduced by Host and Kra in [Reference Host and Kra23] in the case of ergodic
![]() $\mathbb {Z}$
-systems, and then generalised by Chu, Frantzikinakis and Host to
$\mathbb {Z}$
-systems, and then generalised by Chu, Frantzikinakis and Host to
![]() $\mathbb {Z}$
-systems that are not necessarily ergodic in [Reference Chu, Frantzikinakis and Host14]. In [Reference Bergelson, Tao and Ziegler10, Appendix A], a general theory of Gower–Host–Kra seminorms is developed for (not necesssarily ergodic) G-systems, where G is an arbitrary countable discrete abelian group.
$\mathbb {Z}$
-systems that are not necessarily ergodic in [Reference Chu, Frantzikinakis and Host14]. In [Reference Bergelson, Tao and Ziegler10, Appendix A], a general theory of Gower–Host–Kra seminorms is developed for (not necesssarily ergodic) G-systems, where G is an arbitrary countable discrete abelian group.
Definition 2.3. Let G be a countable discrete abelian group, and let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system. Let
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system. Let
![]() $f \in L^{\infty } (X)$
, and let
$f \in L^{\infty } (X)$
, and let
![]() $k\geq 1$
be an integer. The Gowers–Host–Kra seminorm
$k\geq 1$
be an integer. The Gowers–Host–Kra seminorm
![]() $\|f\|_{U^k(G)}$
of order k of f is defined recursively by the formula
$\|f\|_{U^k(G)}$
of order k of f is defined recursively by the formula
for
![]() $k=1$
, and
$k=1$
, and
for
![]() $k>1$
, where
$k>1$
, where
![]() .
.
In [Reference Bergelson, Tao and Ziegler10, Appendix A], it is shown that the Gower–Host–Kra seminorms for general G-systems are indeed seminorms. Moreover, these seminorms correspond to factors of
![]() $\textbf {X}$
.
$\textbf {X}$
.
Proposition 2.4 (cf. [Reference Bergelson, Tao and Ziegler10], Proposition 1.10)
Let G be a countable discrete abelian group, let
![]() $\textbf {X}$
be a G-system and let
$\textbf {X}$
be a G-system and let
![]() $k\geq 0$
. There exists a unique (up to isomorphism) factor
$k\geq 0$
. There exists a unique (up to isomorphism) factor
![]() $\mathbf {Z}^{k}(X)=\left( Z^{k}(X),\mathcal {Z}^{k}(X),\mu _k,(T^{(k)}_g)_{g \in G} \right)$
of
$\mathbf {Z}^{k}(X)=\left( Z^{k}(X),\mathcal {Z}^{k}(X),\mu _k,(T^{(k)}_g)_{g \in G} \right)$
of
![]() $\textbf {X}$
with the property that for every
$\textbf {X}$
with the property that for every
![]() $f\in L^{\infty } (X)$
,
$f\in L^{\infty } (X)$
,
![]() $\|f\|_{U^{k+1}(X)}=0$
if and only if
$\|f\|_{U^{k+1}(X)}=0$
if and only if
![]() $E(f|\mathcal {Z}^{k}(X))=0$
.
$E(f|\mathcal {Z}^{k}(X))=0$
.
The factors
![]() $\mathbf {Z}^k$
guaranteed by Proposition 2.4 are called the Host–Kra factors of
$\mathbf {Z}^k$
guaranteed by Proposition 2.4 are called the Host–Kra factors of
![]() $\textbf {X}$
.
$\textbf {X}$
.
Let
![]() $\textbf {X}=\left(X,\mathcal {X},\mu ,(T_g)_{g \in G} \right)$
be a G-system. Then,
$\textbf {X}=\left(X,\mathcal {X},\mu ,(T_g)_{g \in G} \right)$
be a G-system. Then,
![]() $\mathcal {Z}^0(X)$
is the same as the
$\mathcal {Z}^0(X)$
is the same as the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {I}_G(X)$
. In particular, if
$\mathcal {I}_G(X)$
. In particular, if
![]() $\textbf {X}$
is ergodic, then
$\textbf {X}$
is ergodic, then
![]() $\mathcal {Z}^0(X)$
is trivial. In the literature,
$\mathcal {Z}^0(X)$
is trivial. In the literature,
![]() $\mathbf {Z}^1(X)$
is often called the Kronecker factor, and
$\mathbf {Z}^1(X)$
is often called the Kronecker factor, and
![]() $\mathbf {Z}^2(X)$
the Conze–Lesigne or quasi-affine factor of
$\mathbf {Z}^2(X)$
the Conze–Lesigne or quasi-affine factor of
![]() $\textbf {X}$
.
$\textbf {X}$
.
We summarise some basic results about the Host–Kra factors.
Theorem 2.5. Let G be a countable discrete abelian group, and let
![]() $\textbf {X} = (X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a ergodic G-system. Then,
$\textbf {X} = (X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a ergodic G-system. Then,
-
(i) For every
 $k\geq 1$
,
$k\geq 1$
,
 $\mathcal {Z}^{k-1}(X)\preceq \mathcal {Z}^{k}(X)$
. In other words,
$\mathcal {Z}^{k-1}(X)\preceq \mathcal {Z}^{k}(X)$
. In other words,
 $\mathbf {Z}^{k-1}(X)$
is a factor of
$\mathbf {Z}^{k-1}(X)$
is a factor of
 $\mathbf {Z}^k(X)$
. In particular,
$\mathbf {Z}^k(X)$
. In particular,
 $\mathcal {I}(X)\preceq \mathcal {Z}^k(X)$
for every
$\mathcal {I}(X)\preceq \mathcal {Z}^k(X)$
for every
 $k\geq 0$
.
$k\geq 0$
. -
(ii) The Kronecker factor of
 $\textbf {X}$
is isomorphic to a rotation on a compact abelian group. Namely, there exists a homomorphism
$\textbf {X}$
is isomorphic to a rotation on a compact abelian group. Namely, there exists a homomorphism
 $\alpha :G\rightarrow Z$
into a compact abelian group
$\alpha :G\rightarrow Z$
into a compact abelian group
 $(Z,+)$
, such that
$(Z,+)$
, such that
 $\mathbf {Z}^1(X)$
is isomorphic to
$\mathbf {Z}^1(X)$
is isomorphic to
 $(Z, (R_g)_{g \in G})$
, where
$(Z, (R_g)_{g \in G})$
, where
 $R_gz = z+\alpha (g)$
.
$R_gz = z+\alpha (g)$
. -
(iii) For every
 $k\geq 1$
, if
$k\geq 1$
, if
 $\textbf {X}$
is ergodic, then
$\textbf {X}$
is ergodic, then
 $\mathbf {Z}^k(X)$
is an extension of
$\mathbf {Z}^k(X)$
is an extension of
 $\mathbf {Z}^{k-1}(X)$
by a compact abelian group
$\mathbf {Z}^{k-1}(X)$
by a compact abelian group
 $(H,+)$
and a cocycle
$(H,+)$
and a cocycle
 $\rho :G\times Z^{k-1}(X)\rightarrow H$
. Namely,
$\rho :G\times Z^{k-1}(X)\rightarrow H$
. Namely,
 $Z^k(X)=Z^{k-1}(X)\times H$
as measure spaces, and the action is given by
$Z^k(X)=Z^{k-1}(X)\times H$
as measure spaces, and the action is given by
 $T^{(k)}_g (z,h) = (T^{(k-1)}_g z, h+\rho (g,z))$
.
$T^{(k)}_g (z,h) = (T^{(k-1)}_g z, h+\rho (g,z))$
.
Proof. The proof of
![]() $(i)$
is an immediate consequence of the monotonicity of the seminorms (see [Reference Host and Kra23, Corollary 4.4]). The proof of
$(i)$
is an immediate consequence of the monotonicity of the seminorms (see [Reference Host and Kra23, Corollary 4.4]). The proof of
![]() $(ii)$
in the generality of countable discrete abelian groups can be found in [Reference Ackelsberg, Bergelson and Best2, Lemma 2.4]. The proof of
$(ii)$
in the generality of countable discrete abelian groups can be found in [Reference Ackelsberg, Bergelson and Best2, Lemma 2.4]. The proof of
![]() $(iii)$
can be found for
$(iii)$
can be found for
![]() $\mathbb {Z}$
-actions in [Reference Host and Kra23, Proposition 6.3], and the same proof works for arbitrary countable discrete abelian groups.
$\mathbb {Z}$
-actions in [Reference Host and Kra23, Proposition 6.3], and the same proof works for arbitrary countable discrete abelian groups.
2.5 Joins and meets of factors
Let G be a countable discrete abelian group, let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system and let
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system and let
![]() $\varphi ,\psi :G\rightarrow G$
be arbitrary homomorphisms.
$\varphi ,\psi :G\rightarrow G$
be arbitrary homomorphisms.
-
1. Let
 $\mathcal {Z}^1_{\varphi }(X)$
, or just
$\mathcal {Z}^1_{\varphi }(X)$
, or just
 $\mathcal {Z}_{\varphi }(X)$
, denote the
$\mathcal {Z}_{\varphi }(X)$
, denote the
 $\sigma $
-algebra of the Kronecker factor of X with respect to the action of
$\sigma $
-algebra of the Kronecker factor of X with respect to the action of
 $\varphi (G)$
, that is, the
$\varphi (G)$
, that is, the
 $\sigma $
-algebra of the factor
$\sigma $
-algebra of the factor
 $\mathbf {Z}^1_{\varphi }(X)$
obtained by applying Proposition 2.4 for the G-system
$\mathbf {Z}^1_{\varphi }(X)$
obtained by applying Proposition 2.4 for the G-system
 $(X,\mathcal {X},\mu ,(T_{\varphi (g)})_{g\in G})$
and
$(X,\mathcal {X},\mu ,(T_{\varphi (g)})_{g\in G})$
and
 $k=1$
. More generally, let H be a subgroup of G and
$k=1$
. More generally, let H be a subgroup of G and
 $k\geq 1$
, we let
$k\geq 1$
, we let
 $\mathcal {Z}^k_H(X)$
denote the
$\mathcal {Z}^k_H(X)$
denote the
 $\sigma $
-algebra of the k-th Host–Kra factor
$\sigma $
-algebra of the k-th Host–Kra factor
 $\mathbf {Z}^k_H(X)$
with respect to the action of H.
$\mathbf {Z}^k_H(X)$
with respect to the action of H. -
2. Let
 $\mathcal {A}$
,
$\mathcal {A}$
,
 $\mathcal {A}_1,\mathcal {A}_2$
be
$\mathcal {A}_1,\mathcal {A}_2$
be
 $\sigma $
-algebras on X. Then,
$\sigma $
-algebras on X. Then,-
○ We write
 $\mathcal {A}\preceq \mathcal {X}$
if the
$\mathcal {A}\preceq \mathcal {X}$
if the
 $\sigma $
-algebra
$\sigma $
-algebra
 $\mathcal {A}$
is a sub-
$\mathcal {A}$
is a sub-
 $\sigma $
-algebra of
$\sigma $
-algebra of
 $\mathcal {X}$
.
$\mathcal {X}$
. -
○ We let
 $\mathcal {A}_1\lor \mathcal {A}_2$
denote the join of
$\mathcal {A}_1\lor \mathcal {A}_2$
denote the join of
 $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
 $\mathcal {A}_2$
, that is, the
$\mathcal {A}_2$
, that is, the
 $\sigma $
-algebra generated by
$\sigma $
-algebra generated by
 $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
 $\mathcal {A}_2$
in
$\mathcal {A}_2$
in
 $\mathcal {X}$
.
$\mathcal {X}$
. -
○ We let
 $\mathcal {A}_1\land \mathcal {A}_2$
denote the meet of
$\mathcal {A}_1\land \mathcal {A}_2$
denote the meet of
 $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
 $\mathcal {A}_2$
, that is, the maximal
$\mathcal {A}_2$
, that is, the maximal
 $\sigma $
-algebra which is also a sub-
$\sigma $
-algebra which is also a sub-
 $\sigma $
-algebra of
$\sigma $
-algebra of
 $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
 $\mathcal {A}_2$
.
$\mathcal {A}_2$
. -
○ We say that
 $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
 $\mathcal {A}_2$
are
$\mathcal {A}_2$
are
 $\mu $
-independent if their meet is trivial modulo
$\mu $
-independent if their meet is trivial modulo
 $\mu $
-null sets.
$\mu $
-null sets. -
○ More generally, we say that
 $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
 $\mathcal {A}_2$
are relatively independent over the
$\mathcal {A}_2$
are relatively independent over the
 $\sigma $
-algebra
$\sigma $
-algebra
 $\mathcal {A}$
if
$\mathcal {A}$
if
 $\mathcal {A}_1\land \mathcal {A}_2\preceq \mathcal {A}$
.
$\mathcal {A}_1\land \mathcal {A}_2\preceq \mathcal {A}$
.
-
-
3. We let
 $\mathcal {I}_{\varphi ,\psi }(X)$
denote the meet of
$\mathcal {I}_{\varphi ,\psi }(X)$
denote the meet of
 $\mathcal {I}_{\varphi }(X)$
and
$\mathcal {I}_{\varphi }(X)$
and
 $\mathcal {I}_{\psi }(X)$
and
$\mathcal {I}_{\psi }(X)$
and
 $\mathcal {Z}_{\varphi ,\psi }(X)$
the meet of
$\mathcal {Z}_{\varphi ,\psi }(X)$
the meet of
 $\mathcal {Z}_{\varphi }(X)$
and
$\mathcal {Z}_{\varphi }(X)$
and
 $\mathcal {Z}_{\psi }(X)$
. We let
$\mathcal {Z}_{\psi }(X)$
. We let
 $\mathbf {Z}_{\varphi ,\psi }(X)$
denote the factor of
$\mathbf {Z}_{\varphi ,\psi }(X)$
denote the factor of
 $\textbf {X}$
which corresponds to the
$\textbf {X}$
which corresponds to the
 $\sigma $
-algebra
$\sigma $
-algebra
 $\mathcal {Z}_{\varphi ,\psi }(X)$
.
$\mathcal {Z}_{\varphi ,\psi }(X)$
.
The next two lemmas give convenient alternative descriptions of independent and relatively independent
![]() $\sigma $
-algebras. These results are classical and can be found, for example, in [Reference Zimmer31, Proposition 1.4]; we provide short proofs for the convenience of the reader.
$\sigma $
-algebras. These results are classical and can be found, for example, in [Reference Zimmer31, Proposition 1.4]; we provide short proofs for the convenience of the reader.
Proposition 2.6 (Independent
 $\sigma $
-algebras)
$\sigma $
-algebras)
Let
![]() $\textbf {X}=(X,\mathcal {X},\mu )$
be a probability space. Two
$\textbf {X}=(X,\mathcal {X},\mu )$
be a probability space. Two
![]() $\sigma $
-algebras
$\sigma $
-algebras
![]() $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
![]() $\mathcal {A}_2$
on X are
$\mathcal {A}_2$
on X are
![]() $\mu $
-independent if and only if the following equivalent conditions hold:
$\mu $
-independent if and only if the following equivalent conditions hold:
-
(i) Any function
 $f\in L^{\infty }(X)$
measurable with respect to
$f\in L^{\infty }(X)$
measurable with respect to
 $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
 $\mathcal {A}_2$
simultaneously is a constant
$\mathcal {A}_2$
simultaneously is a constant
 $\mu $
-almost everywhere.
$\mu $
-almost everywhere. -
(ii) If
 $f\in L^{\infty }(X)$
is measurable with respect to
$f\in L^{\infty }(X)$
is measurable with respect to
 $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
 $g\in L^{\infty }(X)$
is measurable with respect to
$g\in L^{\infty }(X)$
is measurable with respect to
 $\mathcal {A}_2$
, then
$\mathcal {A}_2$
, then  $$ \begin{align*} \int_X f\cdot g~d\mu = \int_X f~d\mu \cdot \int_X g~d\mu. \end{align*} $$
$$ \begin{align*} \int_X f\cdot g~d\mu = \int_X f~d\mu \cdot \int_X g~d\mu. \end{align*} $$
Proof. The first definition of independence above is clearly equivalent to (i). We prove the equivalence between (i) and (ii).
(i)
![]() $\Rightarrow $
(ii).
$\Rightarrow $
(ii).
where the second equality holds since
![]() $E(f|\mathcal {A}_2)$
is a constant
$E(f|\mathcal {A}_2)$
is a constant
![]() $\mu $
-a.e. by (i).
$\mu $
-a.e. by (i).
For (ii)
![]() $\Rightarrow $
(i), let
$\Rightarrow $
(i), let
![]() $\widetilde {f} = f-\int f d\mu $
. Then,
$\widetilde {f} = f-\int f d\mu $
. Then,
 $$ \begin{align*} \|\widetilde{f}\|_{L^2(\mu)}^2 = \int |\widetilde{f}|^2 ~d\mu = \left|\int_X \widetilde{f} ~d\mu\right| ^2=0. \end{align*} $$
$$ \begin{align*} \|\widetilde{f}\|_{L^2(\mu)}^2 = \int |\widetilde{f}|^2 ~d\mu = \left|\int_X \widetilde{f} ~d\mu\right| ^2=0. \end{align*} $$
We conclude that
![]() $f=\int fd\mu $
.
$f=\int fd\mu $
.
Proposition 2.7 (Relatively independent
 $\sigma $
-algebras)
$\sigma $
-algebras)
Let
![]() $\textbf {X}=(X,\mathcal {X},\mu )$
be a probability space. Let
$\textbf {X}=(X,\mathcal {X},\mu )$
be a probability space. Let
![]() $\mathcal {A}_1,\mathcal {A}_2$
be two
$\mathcal {A}_1,\mathcal {A}_2$
be two
![]() $\sigma $
-algebras on X, and let
$\sigma $
-algebras on X, and let
![]() $\mathcal {A}$
be a third
$\mathcal {A}$
be a third
![]() $\sigma $
-algebra, such that
$\sigma $
-algebra, such that
![]() $\mathcal {A}\preceq \mathcal {A}_1\land \mathcal {A}_2$
. Then,
$\mathcal {A}\preceq \mathcal {A}_1\land \mathcal {A}_2$
. Then,
![]() $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
![]() $\mathcal {A}_2$
are relatively independent with respect to
$\mathcal {A}_2$
are relatively independent with respect to
![]() $\mathcal {A}$
if the following equivalent conditions hold:
$\mathcal {A}$
if the following equivalent conditions hold:
-
(i) Any function
 $f\in L^{\infty }(X)$
measurable with respect to
$f\in L^{\infty }(X)$
measurable with respect to
 $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
 $\mathcal {A}_2$
simultaneously is measurable with respect to
$\mathcal {A}_2$
simultaneously is measurable with respect to
 $\mathcal {A}$
.
$\mathcal {A}$
. -
(ii) If f is measurable with respect to
 $\mathcal {A}_1$
and g is measurable with respect to
$\mathcal {A}_1$
and g is measurable with respect to
 $\mathcal {A}_2$
, then
$\mathcal {A}_2$
, then  $$ \begin{align*} E(fg|\mathcal{A})=E(f|\mathcal{A})\cdot E(g|\mathcal{A}). \end{align*} $$
$$ \begin{align*} E(fg|\mathcal{A})=E(f|\mathcal{A})\cdot E(g|\mathcal{A}). \end{align*} $$
Proof. Condition
![]() $(i)$
is equivalent to the definition of relative independence above. Therefore, it is enough to prove the equivalence of
$(i)$
is equivalent to the definition of relative independence above. Therefore, it is enough to prove the equivalence of
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
.
$(ii)$
.
(i)
![]() $\Rightarrow $
(ii). We have
$\Rightarrow $
(ii). We have
![]() $E(fg|\mathcal {A}_1) = f\cdot E(g|\mathcal {A}_1) = f\cdot E(g|\mathcal {A})$
, where the last equality follows from
$E(fg|\mathcal {A}_1) = f\cdot E(g|\mathcal {A}_1) = f\cdot E(g|\mathcal {A})$
, where the last equality follows from
![]() $(i)$
. Now, by taking the conditional expectation over
$(i)$
. Now, by taking the conditional expectation over
![]() $\mathcal {A}$
, we have
$\mathcal {A}$
, we have
(ii)
![]() $\Rightarrow $
(i). Let
$\Rightarrow $
(i). Let
![]() $\widetilde {f} = f-E(f|\mathcal {A})$
. Then
$\widetilde {f} = f-E(f|\mathcal {A})$
. Then
![]() $E(|\widetilde {f}|^2|\mathcal {A})=E(\widetilde {f}|\mathcal {A})^2 = 0$
. In particular,
$E(|\widetilde {f}|^2|\mathcal {A})=E(\widetilde {f}|\mathcal {A})^2 = 0$
. In particular,
![]() $\int |\widetilde {f}|^2 d\mu = 0$
, thus,
$\int |\widetilde {f}|^2 d\mu = 0$
, thus,
![]() $f=E(f|\mathcal {A})$
.
$f=E(f|\mathcal {A})$
.
2.6 Characteristic factors
Let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,T)$
be an invertible ergodic measure preserving system and
$\textbf {X}=(X,\mathcal {X},\mu ,T)$
be an invertible ergodic measure preserving system and
![]() $f_1,...,f_k\in L^{\infty }(X)$
,
$f_1,...,f_k\in L^{\infty }(X)$
,
![]() $k\geq 0$
. The convergence of the multiple ergodic averages
$k\geq 0$
. The convergence of the multiple ergodic averages
 $$ \begin{align} \frac{1}{N}\sum_{n=0}^{N-1} \prod_{i=1}^k T^{in} f_i \end{align} $$
$$ \begin{align} \frac{1}{N}\sum_{n=0}^{N-1} \prod_{i=1}^k T^{in} f_i \end{align} $$
in
![]() $L^2(\mu )$
for general k was established by Host and Kra [Reference Host and Kra23] and independently, though somewhat later, by Ziegler [Reference Ziegler30].
$L^2(\mu )$
for general k was established by Host and Kra [Reference Host and Kra23] and independently, though somewhat later, by Ziegler [Reference Ziegler30].
Host and Kra proved convergence by showing that the averages in (5) are controlled by the Gowers–Host–Kra seminorms defined above. This reduces the general convergence problem to convergence under the additional assumption that each function
![]() $f_i$
is measurable with respect to the Host–Kra factor.
$f_i$
is measurable with respect to the Host–Kra factor.
Ziegler, on the other hand, studied the universal (minimal) characteristic factors for the multiple ergodic averages
 $$ \begin{align*} \frac{1}{N}\sum_{n=0}^{N-1} \prod_{i=1}^k T^{a_in} f_i, \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{n=0}^{N-1} \prod_{i=1}^k T^{a_in} f_i, \end{align*} $$
where
![]() $a_1,...,a_k\in \mathbb {Z}$
are distinct and nonzero. These are the minimal factors
$a_1,...,a_k\in \mathbb {Z}$
are distinct and nonzero. These are the minimal factors
![]() $\mathcal {Z}_{k-1}(X)$
, such that
$\mathcal {Z}_{k-1}(X)$
, such that
 $$ \begin{align*} \lim_{N\rightarrow \infty} \frac{1}{N}\sum_{n=0}^{N-1} \prod_{i=1}^k T^{a_in} f_i=0 \end{align*} $$
$$ \begin{align*} \lim_{N\rightarrow \infty} \frac{1}{N}\sum_{n=0}^{N-1} \prod_{i=1}^k T^{a_in} f_i=0 \end{align*} $$
whenever
![]() $E(f_i|\mathcal {Z}_{k-1}(X))=0$
for some i.
$E(f_i|\mathcal {Z}_{k-1}(X))=0$
for some i.
In [Reference Bergelson5, Appendix A], Leibman proved that, for
![]() ${\mathbb Z}$
-systems, the factors studied by Host and Kra coincide with the factors studied by Ziegler, thus giving these factors the name Host–Kra–Ziegler factors. Using Følner sequences in order to define averages, one can generalise the above to arbitrary countable discrete abelian groups (or even more generally, to amenable groups). However, in the setting of general abelian groups, Host–Kra factors may no longer coincide with the characteristic factors for averages of the form
${\mathbb Z}$
-systems, the factors studied by Host and Kra coincide with the factors studied by Ziegler, thus giving these factors the name Host–Kra–Ziegler factors. Using Følner sequences in order to define averages, one can generalise the above to arbitrary countable discrete abelian groups (or even more generally, to amenable groups). However, in the setting of general abelian groups, Host–Kra factors may no longer coincide with the characteristic factors for averages of the form
 $$ \begin{align*} \text{UC -}\lim_{g \in G} \prod_{i=1}^k T_{a_ig} f_i. \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{g \in G} \prod_{i=1}^k T_{a_ig} f_i. \end{align*} $$
We give a very simple example. Let p be a prime number and
![]() $\mathbb {F}_p$
be the group with p elements. We denote by
$\mathbb {F}_p$
be the group with p elements. We denote by
![]() $\mathbb {F}_p^{\infty }$
the direct sum of countably many copies of
$\mathbb {F}_p^{\infty }$
the direct sum of countably many copies of
![]() $\mathbb {F}_p$
. In [Reference Bergelson, Tao and Ziegler10], it is shown that there are many nontrivial ergodic
$\mathbb {F}_p$
. In [Reference Bergelson, Tao and Ziegler10], it is shown that there are many nontrivial ergodic
![]() $\mathbb {F}_p^{\infty }$
-systems with nontrivial Host–Kra factors
$\mathbb {F}_p^{\infty }$
-systems with nontrivial Host–Kra factors
![]() $\mathcal {Z}^k(X)$
for any
$\mathcal {Z}^k(X)$
for any
![]() $k \ge 0$
. However, the only characteristic factor for the average
$k \ge 0$
. However, the only characteristic factor for the average
is
![]() $\mathcal {X}$
. Indeed, since
$\mathcal {X}$
. Indeed, since
![]() $T_{pg}=Id$
, the average is nonzero for every
$T_{pg}=Id$
, the average is nonzero for every
![]() $f_p\not =0$
, assuming that
$f_p\not =0$
, assuming that
![]() $f_1=...=f_{p-1}=1$
(say). To overcome this technicality, one may restrict to the case where
$f_1=...=f_{p-1}=1$
(say). To overcome this technicality, one may restrict to the case where
![]() $k<p$
, but the situation is not that simple for arbitrary countable discrete abelian groups, and, in general, Host–Kra factors may not coincide with the universal characteristic factors.
$k<p$
, but the situation is not that simple for arbitrary countable discrete abelian groups, and, in general, Host–Kra factors may not coincide with the universal characteristic factors.
This phenomenon was not studied previously in the literature, but it plays an important role in this paper. More specifically, we study how the Host–Kra factor
![]() $\mathcal {Z}^1(X)$
, which coincides with the classical Kronecker factor, is related to the the universal characteristic factor,
$\mathcal {Z}^1(X)$
, which coincides with the classical Kronecker factor, is related to the the universal characteristic factor,
![]() $\mathcal {Z}_1(X)$
, for the average
$\mathcal {Z}_1(X)$
, for the average
where
![]() $f_1,f_2\in L^{\infty }(\mu )$
, in the setting of actions of countable discrete abelian groups. One of our main tools is a result which asserts, roughly speaking, that by adding eigenfunctions to the system
$f_1,f_2\in L^{\infty }(\mu )$
, in the setting of actions of countable discrete abelian groups. One of our main tools is a result which asserts, roughly speaking, that by adding eigenfunctions to the system
![]() $\textbf {X}$
, one has that the characteristic factor
$\textbf {X}$
, one has that the characteristic factor
![]() $\mathcal {Z}_1(X)$
is generated by the Host–Kra factor
$\mathcal {Z}_1(X)$
is generated by the Host–Kra factor
![]() $\mathcal {Z}^1(X)$
and the
$\mathcal {Z}^1(X)$
and the
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $2G$
-invariant functions. We also give an example that illustrates the necessity of adding eigenfunctions to the system (see Example 4.1).
$2G$
-invariant functions. We also give an example that illustrates the necessity of adding eigenfunctions to the system (see Example 4.1).
2.7 Seminorms for multiplicative configurations
We now give a brief explanation of where our methods come up short of fully answering Questions 1.19 and 1.20. As discussed above, our approach to the large intersections property is to study families of seminorms and their corresponding characteristic factors. However, in the case of Questions 1.19 and 1.20, these seminorms have somewhat exotic behaviour.
For example, Question 1.19 is related to the averages
for some ergodic
![]() $(\mathbb {Q}_{>0}, \cdot )$
-system. An application of the van der Corput lemma (Lemma 2.1) shows that (6) is equal to zero if
$(\mathbb {Q}_{>0}, \cdot )$
-system. An application of the van der Corput lemma (Lemma 2.1) shows that (6) is equal to zero if
 $$ \begin{align*} \text{UC -}\lim_{q\in \mathbb{Q}_{>0}} \left|\int \Delta_{q^m} f_1 \cdot E(\Delta_{q^m}f_2|\mathcal{I}_{q^{n-m}}(X))~d\mu \right|=0. \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{q\in \mathbb{Q}_{>0}} \left|\int \Delta_{q^m} f_1 \cdot E(\Delta_{q^m}f_2|\mathcal{I}_{q^{n-m}}(X))~d\mu \right|=0. \end{align*} $$
If the action of
![]() $T_{q^{n-m}}$
,
$T_{q^{n-m}}$
,
![]() $q\in (\mathbb {Q}_{>0}, \cdot )$
, were ergodic (e.g. if
$q\in (\mathbb {Q}_{>0}, \cdot )$
, were ergodic (e.g. if
![]() $n=m+1$
), then the above expression is manageable as we will see in this paper. Presumably, if n and m are coprime, then this expression may also be manageable, but we do not see how.
$n=m+1$
), then the above expression is manageable as we will see in this paper. Presumably, if n and m are coprime, then this expression may also be manageable, but we do not see how.
Question 1.20 is related to the average
Using the van der Corput lemma, the Cauchy–Schwarz inequality and then the van der Corput lemma again, we see that the average in (7) is zero if
 $$ \begin{align*} \text{UC -}\lim_{q_1\in\mathbb{Q}_{>0}} \left| \text{UC -}\lim_{q_2\in\mathbb{Q}_{>0}} \int \Delta_{q_1^2} \Delta_{q_2^3} f_3~d\mu \right|=0. \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{q_1\in\mathbb{Q}_{>0}} \left| \text{UC -}\lim_{q_2\in\mathbb{Q}_{>0}} \int \Delta_{q_1^2} \Delta_{q_2^3} f_3~d\mu \right|=0. \end{align*} $$
If in the expression above we had
![]() $q_1^2,q_2^2$
, or
$q_1^2,q_2^2$
, or
![]() $q_1^3,q_2^3$
, then this expression would be related to the Gowers–Host–Kra seminorm of
$q_1^3,q_2^3$
, then this expression would be related to the Gowers–Host–Kra seminorm of
![]() $f_3$
with respect to the action of all squares or cubes of
$f_3$
with respect to the action of all squares or cubes of
![]() $(\mathbb {Q}_{>0}, \cdot )$
. The above quantity is therefore some combination of the two. Again, presumably, the fact that
$(\mathbb {Q}_{>0}, \cdot )$
. The above quantity is therefore some combination of the two. Again, presumably, the fact that
![]() $2$
and
$2$
and
![]() $3$
are coprime may be useful to analyse these seminorms. Studying the structure of these new peculiar seminorms is an interesting problem that we do not pursue in this paper.
$3$
are coprime may be useful to analyse these seminorms. Studying the structure of these new peculiar seminorms is an interesting problem that we do not pursue in this paper.
3 Theorem 1.11
We first give a brief overview of the proof of Theorem 1.11. Let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system, and let
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system, and let
![]() $\varphi ,\psi :G\rightarrow G$
be arbitrary homomorphisms, such that
$\varphi ,\psi :G\rightarrow G$
be arbitrary homomorphisms, such that
![]() $(\psi -\varphi )(G)$
has finite index in G. The key component in the proof of Theorem 1.11 is the analysis of the limit behaviour of the multiple ergodic averages
$(\psi -\varphi )(G)$
has finite index in G. The key component in the proof of Theorem 1.11 is the analysis of the limit behaviour of the multiple ergodic averages
for
![]() $f_1,f_2\in L^{\infty }(X)$
. Standard arguments using the van der Corput lemma (Proposition 3.5) show that
$f_1,f_2\in L^{\infty }(X)$
. Standard arguments using the van der Corput lemma (Proposition 3.5) show that
 $$ \begin{align} \begin{aligned} \text{UC -}\lim_{g\in G}& f_1(T_{\varphi(g)}x)\cdot f_2(T_{\psi(g)}x) = \\ &\text{UC -}\lim_{g\in G} E(f_1|\mathcal{Z}_{\varphi}(X))(T_{\varphi(g)}(x)) E(f_2|\mathcal{Z}_{\psi}(X))(T_{\psi(g)}(x)) \end{aligned} ,\end{align} $$
$$ \begin{align} \begin{aligned} \text{UC -}\lim_{g\in G}& f_1(T_{\varphi(g)}x)\cdot f_2(T_{\psi(g)}x) = \\ &\text{UC -}\lim_{g\in G} E(f_1|\mathcal{Z}_{\varphi}(X))(T_{\varphi(g)}(x)) E(f_2|\mathcal{Z}_{\psi}(X))(T_{\psi(g)}(x)) \end{aligned} ,\end{align} $$
where
![]() $\mathcal {Z}_{\varphi }(X)$
and
$\mathcal {Z}_{\varphi }(X)$
and
![]() $\mathcal {Z}_{\psi }(X)$
are the
$\mathcal {Z}_{\psi }(X)$
are the
![]() $\sigma $
-algebras of the Kronecker factors of X with respect to the actions of
$\sigma $
-algebras of the Kronecker factors of X with respect to the actions of
![]() $\varphi (G)$
and
$\varphi (G)$
and
![]() $\psi (G)$
, respectively (see Subsection 2.5).
$\psi (G)$
, respectively (see Subsection 2.5).
In Theorem 1.11, we assume, furthermore, that
![]() $\varphi (G)$
has finite index in G. In this case, the factor
$\varphi (G)$
has finite index in G. In this case, the factor
![]() $\mathcal {Z}_{\varphi }(X)$
coincides with
$\mathcal {Z}_{\varphi }(X)$
coincides with
![]() $\mathcal {Z}^1_G(X)$
, the Kronecker factor of X with respect to the action of G (see Lemma 3.6). Our main observation is that one can replace
$\mathcal {Z}^1_G(X)$
, the Kronecker factor of X with respect to the action of G (see Lemma 3.6). Our main observation is that one can replace
![]() $\mathcal {Z}_{\psi }(X)$
in (9) with a smaller factor. As an illustration, we give the following example:
$\mathcal {Z}_{\psi }(X)$
in (9) with a smaller factor. As an illustration, we give the following example:
Example 3.1. Consider the additive group
![]() $G=\bigoplus _{j=1}^{\infty }\mathbb {Z}/4\mathbb {Z}$
. We use
$G=\bigoplus _{j=1}^{\infty }\mathbb {Z}/4\mathbb {Z}$
. We use
![]() $i\in \mathbb {C}$
to denote the square root of
$i\in \mathbb {C}$
to denote the square root of
![]() $-1$
, and for every natural number
$-1$
, and for every natural number
![]() $n\in \mathbb {N}$
, we let
$n\in \mathbb {N}$
, we let
![]() $C_n$
denote the group of roots of unity of degree n. We define an action of G on
$C_n$
denote the group of roots of unity of degree n. We define an action of G on
![]() $X=\left(\prod _{j\in \mathbb {N}} C_4\right)\times C_2$
by
$X=\left(\prod _{j\in \mathbb {N}} C_4\right)\times C_2$
by
 $$ \begin{align*} T_g (\textbf{x},y) = \left( (i^{g_j}x_j)_{j\in \mathbb{N}},y\cdot \prod_{j\in\mathbb{N}} (x_j^{2g_j}\cdot i^{g_j^2-g_j})\right), \end{align*} $$
$$ \begin{align*} T_g (\textbf{x},y) = \left( (i^{g_j}x_j)_{j\in \mathbb{N}},y\cdot \prod_{j\in\mathbb{N}} (x_j^{2g_j}\cdot i^{g_j^2-g_j})\right), \end{align*} $$
where
![]() $\textbf {x}=(x_1,x_2,...)\in \prod _{j\in \mathbb {N}} C_4$
and
$\textbf {x}=(x_1,x_2,...)\in \prod _{j\in \mathbb {N}} C_4$
and
![]() $g=(g_1,g_2,...)$
is any representation of g in
$g=(g_1,g_2,...)$
is any representation of g in
![]() $\bigoplus _{j=1}^{\infty }\mathbb {Z}/4{\mathbb Z}$
. The system
$\bigoplus _{j=1}^{\infty }\mathbb {Z}/4{\mathbb Z}$
. The system
![]() $(X, (T_g)_{g \in G})$
is a group extension of its Kronecker factor
$(X, (T_g)_{g \in G})$
is a group extension of its Kronecker factor
![]() $Z_G(X) = \prod _{j\in \mathbb {N}} C_4$
by the cocycle
$Z_G(X) = \prod _{j\in \mathbb {N}} C_4$
by the cocycle
 $$ \begin{align*} & \sigma : G \times \prod_{j\in\mathbb N}{C_4} \to C_2,\\ \sigma&(g,\textbf{x}) = \prod_{j\in\mathbb{N}} (x_j^{2g_j}\cdot i^{g_j^2-g_j}). \end{align*} $$
$$ \begin{align*} & \sigma : G \times \prod_{j\in\mathbb N}{C_4} \to C_2,\\ \sigma&(g,\textbf{x}) = \prod_{j\in\mathbb{N}} (x_j^{2g_j}\cdot i^{g_j^2-g_j}). \end{align*} $$
Let
![]() $\psi (g)=2g$
. We observe that the function
$\psi (g)=2g$
. We observe that the function
![]() $f(\textbf {x},y)=y$
is orthogonal to
$f(\textbf {x},y)=y$
is orthogonal to
![]() $L^2(Z^1(X))$
. On the other hand, we have
$L^2(Z^1(X))$
. On the other hand, we have
 $$ \begin{align*} T_{2g}f(\textbf{x},y) = \sigma(2g,\textbf{x})\cdot y = \prod_{j\in\mathbb{N}} (x_j^{4g_j}\cdot i^{4g_j^2-2g_j}) \cdot y = \prod_{j\in\mathbb{N}} (-1)^{g_j} y = \prod_{j\in\mathbb{N}} (-1)^{g_j} f(\textbf{x},y). \end{align*} $$
$$ \begin{align*} T_{2g}f(\textbf{x},y) = \sigma(2g,\textbf{x})\cdot y = \prod_{j\in\mathbb{N}} (x_j^{4g_j}\cdot i^{4g_j^2-2g_j}) \cdot y = \prod_{j\in\mathbb{N}} (-1)^{g_j} y = \prod_{j\in\mathbb{N}} (-1)^{g_j} f(\textbf{x},y). \end{align*} $$
In other words, f is an eigenfunction with respect to the action of
![]() $\psi (G)$
on X with eigenvalue
$\psi (G)$
on X with eigenvalue
![]() $\lambda (2g) =\prod _{j\in \mathbb {N}} (-1)^{g_j}$
. Therefore, f is measurable with respect to
$\lambda (2g) =\prod _{j\in \mathbb {N}} (-1)^{g_j}$
. Therefore, f is measurable with respect to
![]() $\mathcal {Z}_{\psi }(X)$
, and we see that
$\mathcal {Z}_{\psi }(X)$
, and we see that
![]() $\mathcal {Z}^1(X)\not = \mathcal {Z}_{\psi }(X)$
. Now, let
$\mathcal {Z}^1(X)\not = \mathcal {Z}_{\psi }(X)$
. Now, let
![]() $\varphi (g)=g$
. We claim that f does not contribute to (8). Namely, we have that
$\varphi (g)=g$
. We claim that f does not contribute to (8). Namely, we have that
for every bounded function
![]() $f_1$
. Indeed, by (9), it is enough to check this equality in the case where
$f_1$
. Indeed, by (9), it is enough to check this equality in the case where
![]() $f_1$
is an eigenfunction with respect to the action of G. Let
$f_1$
is an eigenfunction with respect to the action of G. Let
![]() $\chi (g)$
be the eigenvalue of
$\chi (g)$
be the eigenvalue of
![]() $f_1$
, we see that
$f_1$
, we see that
The eigenfunctions of X take the form
![]() $h(\textbf {x},y) = \prod _{i=1}^n x_i^{l_i}$
for some
$h(\textbf {x},y) = \prod _{i=1}^n x_i^{l_i}$
for some
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $l_1,...,l_n\in \{0,1,2,3\}$
. Therefore,
$l_1,...,l_n\in \{0,1,2,3\}$
. Therefore,
![]() $g\mapsto \chi (g)\lambda (2g)$
is a nontrivial character of G and so
$g\mapsto \chi (g)\lambda (2g)$
is a nontrivial character of G and so
Remark 3.2. In the example above, the factor
![]() $\mathbf {Z}^1(X)$
is isomorphic to
$\mathbf {Z}^1(X)$
is isomorphic to
![]() $\prod _{j\in \mathbb {N}} C_4$
equipped with the action
$\prod _{j\in \mathbb {N}} C_4$
equipped with the action
![]() $T^{(1)}_g x = (i^{g_j}\cdot x_j)_{j\in \mathbb {N}}$
, while
$T^{(1)}_g x = (i^{g_j}\cdot x_j)_{j\in \mathbb {N}}$
, while
![]() $\mathbf {Z}^2(X)=\textbf {X}$
. On the other hand, for the
$\mathbf {Z}^2(X)=\textbf {X}$
. On the other hand, for the
![]() $2G$
-system
$2G$
-system
![]() $\left( X, (T_g)_{g \in 2G} \right)$
, we have
$\left( X, (T_g)_{g \in 2G} \right)$
, we have
![]() $\mathbf {Z}_{2G}^1(X) = \textbf {X}$
.
$\mathbf {Z}_{2G}^1(X) = \textbf {X}$
.
Example 3.1 suggests that a
![]() $\psi (G)$
-eigenfunction contributes to (8) if and only if its eigenvalue coincides with an eigenvalue of the G-action. In practice, we use a result of Frantzikinakis and Host [Reference Frantzikinakis and Host19] to decompose
$\psi (G)$
-eigenfunction contributes to (8) if and only if its eigenvalue coincides with an eigenvalue of the G-action. In practice, we use a result of Frantzikinakis and Host [Reference Frantzikinakis and Host19] to decompose
![]() $f_2$
into a linear combination of eigenfunctions (see Proposition 3.12). However, since the action of
$f_2$
into a linear combination of eigenfunctions (see Proposition 3.12). However, since the action of
![]() $\psi (G)$
may not be ergodic, we have to include in our analysis the case where the
$\psi (G)$
may not be ergodic, we have to include in our analysis the case where the
![]() $\psi (G)$
-eigenvalue,
$\psi (G)$
-eigenvalue,
![]() $\lambda (\psi (g))$
, is not a constant in X, but rather a
$\lambda (\psi (g))$
, is not a constant in X, but rather a
![]() $\psi (G)$
-invariant function. We let
$\psi (G)$
-invariant function. We let
![]() $\widetilde {\mathcal {Z}}_{\psi }(X)$
be the sub-
$\widetilde {\mathcal {Z}}_{\psi }(X)$
be the sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal {Z}_{\psi }(X)$
generated by all the
$\mathcal {Z}_{\psi }(X)$
generated by all the
![]() $\psi (G)$
-eigenfunctions with eigenvalues
$\psi (G)$
-eigenfunctions with eigenvalues
![]() $\lambda (\psi (\cdot ),x):X\rightarrow \widehat G$
that coincide with an eigenvalue with respect to the G-action for
$\lambda (\psi (\cdot ),x):X\rightarrow \widehat G$
that coincide with an eigenvalue with respect to the G-action for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
. We show that one can replace
$x\in X$
. We show that one can replace
![]() $\mathcal {Z}_{\psi }(X)$
with
$\mathcal {Z}_{\psi }(X)$
with
![]() $\widetilde {\mathcal {Z}}_{\psi }(X)$
in (9). After replacing
$\widetilde {\mathcal {Z}}_{\psi }(X)$
in (9). After replacing
![]() $\mathcal {Z}_{\psi }(X)$
by
$\mathcal {Z}_{\psi }(X)$
by
![]() $\widetilde {\mathcal {Z}}_{\psi }(X)$
, the remainder of the proof of Theorem 1.11 follows by modifying previous arguments used for deducing Khintchine-type recurrence from knowledge of relevant characteristic factors (see, e.g. [Reference Ackelsberg, Bergelson and Best2, Section 8]).
$\widetilde {\mathcal {Z}}_{\psi }(X)$
, the remainder of the proof of Theorem 1.11 follows by modifying previous arguments used for deducing Khintchine-type recurrence from knowledge of relevant characteristic factors (see, e.g. [Reference Ackelsberg, Bergelson and Best2, Section 8]).
3.1 Characteristic factors
We start with a definition of characteristic factors (cf. [Reference Furstenberg and Weiss21, Section 3]).
Definition 3.3. Let G be a countable discrete abelian group, let
![]() $\varphi ,\psi :G\rightarrow G$
be arbitrary homomorphisms and let
$\varphi ,\psi :G\rightarrow G$
be arbitrary homomorphisms and let
![]() $X=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be a G-system. A factor
$X=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be a G-system. A factor
![]() $\textbf {Y}=(Y,\mathcal {Y},\nu , (S_g)_{g\in G})$
of
$\textbf {Y}=(Y,\mathcal {Y},\nu , (S_g)_{g\in G})$
of
![]() $\textbf {X}$
is called a partial characteristic factor for the pair
$\textbf {X}$
is called a partial characteristic factor for the pair
![]() $(\varphi ,\psi )$
with respect to
$(\varphi ,\psi )$
with respect to
![]() $\varphi $
if
$\varphi $
if
for every
![]() $f_1,f_2\in L^{\infty }(X)$
. We define a partial characteristic factor with respect to
$f_1,f_2\in L^{\infty }(X)$
. We define a partial characteristic factor with respect to
![]() $\psi $
similarly and say that
$\psi $
similarly and say that
![]() $\textbf {Y}$
is a characteristic factor if it is a partial characteristic factor with respect to both
$\textbf {Y}$
is a characteristic factor if it is a partial characteristic factor with respect to both
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, that is
$\psi $
, that is
for every
![]() $f_1,f_2\in L^{\infty }(X)$
.
$f_1,f_2\in L^{\infty }(X)$
.
In other words, a factor of a measure preserving system
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
is a characteristic factor for a certain multiple ergodic average, if the study of the limit behaviour of the average can be reduced to this factor. The following easy lemma is related to the well-known result of Furstenberg, which asserts that a system
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
is a characteristic factor for a certain multiple ergodic average, if the study of the limit behaviour of the average can be reduced to this factor. The following easy lemma is related to the well-known result of Furstenberg, which asserts that a system
![]() $\textbf {X}=(X,\mathcal {X},\mu ,T)$
is weakly mixing if and only if the Kronecker factor,
$\textbf {X}=(X,\mathcal {X},\mu ,T)$
is weakly mixing if and only if the Kronecker factor,
![]() $\mathcal {Z}^1(X)$
, is trivial.
$\mathcal {Z}^1(X)$
, is trivial.
Lemma 3.4. Let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g \in G})$
be a G-system, let
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g \in G})$
be a G-system, let
![]() $\varphi :G\to G$
be a homomorphism and let
$\varphi :G\to G$
be a homomorphism and let
![]() $f\in L^2(X)$
. If
$f\in L^2(X)$
. If
![]() $E(f|\mathcal {Z}_{\varphi }(X))=0$
, then for every
$E(f|\mathcal {Z}_{\varphi }(X))=0$
, then for every
![]() $h\in L^2(X)$
, we have
$h\in L^2(X)$
, we have
 $$ \begin{align*}\text{UC -}\lim_{g\in G}\left| \int_X T_{\varphi(g)} f \cdot h~d\mu \right|=0.\end{align*} $$
$$ \begin{align*}\text{UC -}\lim_{g\in G}\left| \int_X T_{\varphi(g)} f \cdot h~d\mu \right|=0.\end{align*} $$
Proof. Assume
![]() $E(f\mid \mathcal {Z}_{\varphi }(X)) = 0$
. Then by Proposition 2.4,
$E(f\mid \mathcal {Z}_{\varphi }(X)) = 0$
. Then by Proposition 2.4,
![]() $\|f\|_{U^2(\varphi (G))}=0$
, that is,
$\|f\|_{U^2(\varphi (G))}=0$
, that is,
 $$ \begin{align*} \text{UC -}\lim_{g\in G} \left|\int_X \Delta_{\varphi(g)} f d\mu \right| = 0. \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{g\in G} \left|\int_X \Delta_{\varphi(g)} f d\mu \right| = 0. \end{align*} $$
Since
![]() $\text {UC -}\lim _{g\in G} |a_g|=0 \iff \text {UC -}\lim _{g\in G} a_g^2 = 0$
for every bounded complex-valued sequence
$\text {UC -}\lim _{g\in G} |a_g|=0 \iff \text {UC -}\lim _{g\in G} a_g^2 = 0$
for every bounded complex-valued sequence
![]() $g\mapsto a_g$
, we have
$g\mapsto a_g$
, we have
The mean ergodic theorem implies that
and
. Therefore, for every
![]() $h\in L^2(X)$
, we have,
$h\in L^2(X)$
, we have,

which implies that
 $$ \begin{align*} \text{UC -}\lim_{g\in G} \left|\int_X T_{\varphi(g)}f \cdot h~ d\mu\right|=0 \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{g\in G} \left|\int_X T_{\varphi(g)}f \cdot h~ d\mu\right|=0 \end{align*} $$
as required.
Using the van der Corput lemma (Lemma 2.1), we show that
![]() $\mathcal {Z}_{\varphi }(X)$
and
$\mathcal {Z}_{\varphi }(X)$
and
![]() $\mathcal {Z}_{\psi }(X)$
are partial characteristic factors for the pair
$\mathcal {Z}_{\psi }(X)$
are partial characteristic factors for the pair
![]() $(\varphi ,\psi )$
with respect to
$(\varphi ,\psi )$
with respect to
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, respectively.
$\psi $
, respectively.
Proposition 3.5. Let
![]() $\textbf {X} = (X, \mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Let
$\textbf {X} = (X, \mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Let
![]() $\varphi , \psi : G \rightarrow G$
be homomorphisms, such that
$\varphi , \psi : G \rightarrow G$
be homomorphisms, such that
![]() $(\psi -\varphi )(G)$
has finite index in G. Then, for any
$(\psi -\varphi )(G)$
has finite index in G. Then, for any
![]() $f_1,f_2\in L^{\infty }(\mu )$
, one has
$f_1,f_2\in L^{\infty }(\mu )$
, one has
in
![]() $L^2(\mu )$
.
$L^2(\mu )$
.
Proof. We follow the argument of Furstenberg and Weiss [Reference Furstenberg and Weiss21]. By linearity and symmetry, it is enough to show that
whenever
![]() $E(f_1|\mathcal {Z}_{\varphi }(X))=0$
. Dividing through by a constant, we may assume that
$E(f_1|\mathcal {Z}_{\varphi }(X))=0$
. Dividing through by a constant, we may assume that
![]() $\|f_i\|_{\infty } \le 1$
for
$\|f_i\|_{\infty } \le 1$
for
![]() $i=1,2$
.
$i=1,2$
.
We use the van der Corput lemma with
![]() $u_g = T_{\varphi (g)} f_1\cdot T_{\psi (g)} f_2$
. For every
$u_g = T_{\varphi (g)} f_1\cdot T_{\psi (g)} f_2$
. For every
![]() $g,h\in G$
, we have
$g,h\in G$
, we have
Since the measure
![]() $\mu $
is
$\mu $
is
![]() $T_{\varphi (g)}$
-invariant, (10) is equal to
$T_{\varphi (g)}$
-invariant, (10) is equal to
Hence, by the mean ergodic theorem, we have
Since
![]() $H:=(\psi -\varphi )(G)$
has finite index in G and the action of G on X is ergodic, we can find a partition
$H:=(\psi -\varphi )(G)$
has finite index in G and the action of G on X is ergodic, we can find a partition
![]() $X=\bigcup _{i=1}^{l} A_i$
to H-invariant sets, where l is at most the index of H in G. Since
$X=\bigcup _{i=1}^{l} A_i$
to H-invariant sets, where l is at most the index of H in G. Since
![]() $f_2$
is bounded by
$f_2$
is bounded by
![]() $1$
,
$1$
,

Now, since
![]() $E(f_1|Z_{\varphi }(X))=0$
, Lemma 3.4 implies that
$E(f_1|Z_{\varphi }(X))=0$
, Lemma 3.4 implies that
, for every
![]() $1\leq i \leq k$
. The van der Corput lemma (Lemma 2.1) then implies that
$1\leq i \leq k$
. The van der Corput lemma (Lemma 2.1) then implies that
and this completes the proof.
In [Reference Bergelson5, Appendix A], Leibman proved the following result in the special case where
![]() $G=\mathbb {Z}$
. For the sake of completeness, we give a proof for arbitrary countable discrete abelian G in Appendix A.
$G=\mathbb {Z}$
. For the sake of completeness, we give a proof for arbitrary countable discrete abelian G in Appendix A.
Lemma 3.6. Let
![]() $(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be a G-system, and let
$(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be a G-system, and let
![]() $H\leq G$
be a subgroup of finite index. Then, for every
$H\leq G$
be a subgroup of finite index. Then, for every
![]() $k\geq 1$
, one has
$k\geq 1$
, one has
![]() $\mathcal {Z}^k_H(X) = \mathcal {Z}^k_G(X)$
.
$\mathcal {Z}^k_H(X) = \mathcal {Z}^k_G(X)$
.
In particular, if
![]() $\varphi (G)$
has finite index in G, then the factor
$\varphi (G)$
has finite index in G, then the factor
![]() $\mathcal {Z}_{\varphi }(X)$
coincides with
$\mathcal {Z}_{\varphi }(X)$
coincides with
![]() $\mathcal {Z}(X)$
.
$\mathcal {Z}(X)$
.
Corollary 3.7. Let G be a countable discrete abelian group, let
![]() $X=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system and let
$X=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system and let
![]() $\varphi ,\psi :G\rightarrow G$
be arbitrary homomorphisms, such that
$\varphi ,\psi :G\rightarrow G$
be arbitrary homomorphisms, such that
![]() $\varphi (G)$
and
$\varphi (G)$
and
![]() $(\psi -\varphi )(G)$
have finite index in G. Then, for any bounded functions
$(\psi -\varphi )(G)$
have finite index in G. Then, for any bounded functions
![]() $f_1,f_2\in L^{\infty }(X)$
,
$f_1,f_2\in L^{\infty }(X)$
,
Let G be a countable discrete abelian group and
![]() $\textbf {X} = (X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. By Theorem 2.5(ii), the Kronecker factor of
$\textbf {X} = (X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. By Theorem 2.5(ii), the Kronecker factor of
![]() $\textbf {X}$
,
$\textbf {X}$
,
![]() $\mathbf {Z}^1(X)$
is isomorphic to an ergodic rotation. Therefore, it is convenient to identify the Kronecker factor with the system
$\mathbf {Z}^1(X)$
is isomorphic to an ergodic rotation. Therefore, it is convenient to identify the Kronecker factor with the system
![]() $\textbf {Z}=(Z,\alpha )$
, where Z is a compact abelian group and
$\textbf {Z}=(Z,\alpha )$
, where Z is a compact abelian group and
![]() $\alpha :G\rightarrow Z$
is a homomorphism, such that
$\alpha :G\rightarrow Z$
is a homomorphism, such that
![]() $T^1_g z = z + \alpha _g$
, where
$T^1_g z = z + \alpha _g$
, where
![]() $T^1$
is the G-action on Z. The following corollary of Proposition 3.5 will be useful later on in this paper.
$T^1$
is the G-action on Z. The following corollary of Proposition 3.5 will be useful later on in this paper.
Proposition 3.8. Let
![]() $\textbf {X} = \left(X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
be an ergodic G-system with Kronecker factor
$\textbf {X} = \left(X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
be an ergodic G-system with Kronecker factor
![]() $\textbf {Z}=(Z, \alpha )$
. Let
$\textbf {Z}=(Z, \alpha )$
. Let
![]() $\varphi , \psi : G \to G$
be homomorphisms, such that
$\varphi , \psi : G \to G$
be homomorphisms, such that
![]() $(\psi - \varphi )(G)$
has finite index in G. Then, for any
$(\psi - \varphi )(G)$
has finite index in G. Then, for any
![]() $f_0, f_1, f_2 \in L^{\infty }(\mu )$
and any continuous function
$f_0, f_1, f_2 \in L^{\infty }(\mu )$
and any continuous function
![]() $\eta : Z^2 \to \mathbb {C}$
, we have
$\eta : Z^2 \to \mathbb {C}$
, we have
 $$ \begin{align*} \text{UC -}\lim_{g \in G}&~{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f_0 \cdot T_{\varphi(g)}f_1 \cdot T_{\psi(g)}f_2~d\mu}} \\ & = \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f_0 \cdot T_{\varphi(g)}E(f_1|\mathcal{Z}_{\varphi}(X)) \cdot T_{\psi(g)}E(f_2|\mathcal{Z}_{\psi}(X))~d\mu}}. \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{g \in G}&~{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f_0 \cdot T_{\varphi(g)}f_1 \cdot T_{\psi(g)}f_2~d\mu}} \\ & = \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f_0 \cdot T_{\varphi(g)}E(f_1|\mathcal{Z}_{\varphi}(X)) \cdot T_{\psi(g)}E(f_2|\mathcal{Z}_{\psi}(X))~d\mu}}. \end{align*} $$
Proof. By the Stone–Weierstrass theorem and linearity, we may assume
![]() $\eta (u,v) = \lambda _1(u)\lambda _2(v)$
for some characters
$\eta (u,v) = \lambda _1(u)\lambda _2(v)$
for some characters
![]() $\lambda _1, \lambda _2 \in \widehat {Z}$
. Let
$\lambda _1, \lambda _2 \in \widehat {Z}$
. Let
![]() $\pi : X \to Z$
be the factor map, and let
$\pi : X \to Z$
be the factor map, and let
![]() $\chi _i := \lambda _i \circ \pi $
. Note that
$\chi _i := \lambda _i \circ \pi $
. Note that
![]() $T_g\chi _i = \lambda _i(\alpha _g)\chi _i$
, so
$T_g\chi _i = \lambda _i(\alpha _g)\chi _i$
, so
![]() $\chi _i$
is a G-eigenfunction with eigenvalue
$\chi _i$
is a G-eigenfunction with eigenvalue
![]() $\lambda _i \circ \alpha $
.
$\lambda _i \circ \alpha $
.
Now, set

Since
![]() $\chi _1$
and
$\chi _1$
and
![]() $\chi _2$
are measurable with respect to the Kronecker factor
$\chi _2$
are measurable with respect to the Kronecker factor
![]() $\mathcal {Z}(X)$
, which is a sub-
$\mathcal {Z}(X)$
, which is a sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal {Z}_{\varphi }(X)$
and
$\mathcal {Z}_{\varphi }(X)$
and
![]() $\mathcal {Z}_{\psi }(X)$
, we have the identities
$\mathcal {Z}_{\psi }(X)$
, we have the identities
 $$ \begin{align*} E(h_1|\mathcal {Z}_{\varphi}(X)) & = \chi_1 \cdot E({f_1}|{\mathcal {Z}_{\varphi}(X)}), \\[6pt] E(h_2|\mathcal {Z}_{\varphi}(X)) & = \chi_2 \cdot E({f_2}|{\mathcal {Z}_{\varphi}(X)}). \end{align*} $$
$$ \begin{align*} E(h_1|\mathcal {Z}_{\varphi}(X)) & = \chi_1 \cdot E({f_1}|{\mathcal {Z}_{\varphi}(X)}), \\[6pt] E(h_2|\mathcal {Z}_{\varphi}(X)) & = \chi_2 \cdot E({f_2}|{\mathcal {Z}_{\varphi}(X)}). \end{align*} $$
Thus, applying Proposition 3.5 for the functions
![]() $h_1, h_2$
and integrating against
$h_1, h_2$
and integrating against
![]() $h_0$
, we have
$h_0$
, we have
 $$ \begin{align*} \text{UC -}\lim_{g \in G}&~{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f_0 \cdot T_{\varphi(g)}f_1 \cdot T_{\psi(g)}f_2~d\mu}} \\& = \text{UC -}\lim_{g \in G}{\int_X{h_0 \cdot T_{\varphi(g)}h_1 \cdot T_{\psi(g)}h_2~d\mu}} \\& = \text{UC -}\lim_{g \in G}{\int_X{h_0 \cdot T_{\varphi(g)} E(h_1|\mathcal {Z}_{\varphi}(X)) \cdot T_{\psi(g)} E(h_2|\mathcal {Z}_{\psi}(X))~d\mu}} \\& = \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f_0 \cdot T_{\varphi(g)} E(f_1|\mathcal {Z}_{\varphi}(X)) \cdot T_{\psi(g)} E(f_2|\mathcal {Z}_{\psi}(X))~d\mu}}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{g \in G}&~{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f_0 \cdot T_{\varphi(g)}f_1 \cdot T_{\psi(g)}f_2~d\mu}} \\& = \text{UC -}\lim_{g \in G}{\int_X{h_0 \cdot T_{\varphi(g)}h_1 \cdot T_{\psi(g)}h_2~d\mu}} \\& = \text{UC -}\lim_{g \in G}{\int_X{h_0 \cdot T_{\varphi(g)} E(h_1|\mathcal {Z}_{\varphi}(X)) \cdot T_{\psi(g)} E(h_2|\mathcal {Z}_{\psi}(X))~d\mu}} \\& = \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f_0 \cdot T_{\varphi(g)} E(f_1|\mathcal {Z}_{\varphi}(X)) \cdot T_{\psi(g)} E(f_2|\mathcal {Z}_{\psi}(X))~d\mu}}.\\[-42pt] \end{align*} $$
In the next section, we will study the factor
![]() $\mathcal {Z}_{\psi }(X)$
further.
$\mathcal {Z}_{\psi }(X)$
further.
3.2 Relative orthonormal basis
Let G be a countable discrete abelian group, and let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system. Under the assumption that the system is ergodic, it is well known that the factor
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system. Under the assumption that the system is ergodic, it is well known that the factor
![]() $\mathcal {Z}^1(X)$
admits an orthonormal basis of eigenfunctions. The following example demonstrates that this may fail for nonergodic systems.
$\mathcal {Z}^1(X)$
admits an orthonormal basis of eigenfunctions. The following example demonstrates that this may fail for nonergodic systems.
Example 3.9. Let
![]() $S^1 = \{z\in \mathbb {C} : |z|=1\}$
. Consider
$S^1 = \{z\in \mathbb {C} : |z|=1\}$
. Consider
![]() $X=S^1\times S^1$
equipped with the Borel
$X=S^1\times S^1$
equipped with the Borel
![]() $\sigma $
-algebra, the Haar probability measure
$\sigma $
-algebra, the Haar probability measure
![]() $\mu $
and the measure-preserving transformation
$\mu $
and the measure-preserving transformation
![]() $T(x,y) = (x,y\cdot x)$
. Any function
$T(x,y) = (x,y\cdot x)$
. Any function
![]() $f\in L^2(X)$
takes the form
$f\in L^2(X)$
takes the form
for some
![]() $a_{n,m}\in \mathbb {C}$
with
$a_{n,m}\in \mathbb {C}$
with
Now suppose that there exists some constant
![]() $c\in S^1$
, such that
$c\in S^1$
, such that
![]() $Tf(x,y) = c\cdot f(x,y)$
for
$Tf(x,y) = c\cdot f(x,y)$
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $(x,y)\in S^1\times S^1$
. By the uniqueness of the Fourier series, we deduce that
$(x,y)\in S^1\times S^1$
. By the uniqueness of the Fourier series, we deduce that
for every
![]() $n,m\in \mathbb {N}.$
If
$n,m\in \mathbb {N}.$
If
![]() $m\not = 0$
, this is a contradiction to (11) unless
$m\not = 0$
, this is a contradiction to (11) unless
![]() $a_{n,m}=0$
. We conclude that f is an eigenfunction if and only if it is independent of the y coordinate. In particular,
$a_{n,m}=0$
. We conclude that f is an eigenfunction if and only if it is independent of the y coordinate. In particular,
![]() $L^2(X)$
is not generated by the eigenfunctions of X.
$L^2(X)$
is not generated by the eigenfunctions of X.
On the other hand, the functions
![]() $\{x^n\}_{n\in \mathbb {N}}$
are invariant and therefore measurable with respect to
$\{x^n\}_{n\in \mathbb {N}}$
are invariant and therefore measurable with respect to
![]() $\mathcal {Z}^1(X)$
. Moreover, the functions
$\mathcal {Z}^1(X)$
. Moreover, the functions
![]() $\{y^m\}_{n\in \mathbb {N}}$
satisfy
$\{y^m\}_{n\in \mathbb {N}}$
satisfy
![]() $\Delta _n (y^m) = T^n (y^m) \cdot y^{-m} = x^{n\cdot m}$
, which is an invariant function. Hence,
$\Delta _n (y^m) = T^n (y^m) \cdot y^{-m} = x^{n\cdot m}$
, which is an invariant function. Hence,
![]() $y^m$
is also measurable with respect to
$y^m$
is also measurable with respect to
![]() $\mathcal {Z}^1(X)$
. We thus conclude that X coincides with
$\mathcal {Z}^1(X)$
. We thus conclude that X coincides with
![]() $\mathcal {Z}^1(X)$
.
$\mathcal {Z}^1(X)$
.
In order to handle nonergodic systems, Frantzikinakis and Host [Reference Frantzikinakis and Host19] came up with the following definition.
Definition 3.10. Let H be a countable discrete abelian group acting on a probability space
![]() $(X,\mathcal {X},\mu ,(T_h)_{h\in H})$
. A relative orthonormal system is a countable family
$(X,\mathcal {X},\mu ,(T_h)_{h\in H})$
. A relative orthonormal system is a countable family
![]() $(\phi _j)_{j\in \mathbb {N}}$
belonging to
$(\phi _j)_{j\in \mathbb {N}}$
belonging to
![]() $L^2(\mu )$
, such that
$L^2(\mu )$
, such that
-
(i)
 $\mathbb {E}(\left|\phi _j\right|^2\text { } | \mathcal {I}_H(X))$
has value
$\mathbb {E}(\left|\phi _j\right|^2\text { } | \mathcal {I}_H(X))$
has value
 $0$
or
$0$
or
 $1 \ \mu $
-a.e. for every
$1 \ \mu $
-a.e. for every
 $j\in \mathbb {N}$
;
$j\in \mathbb {N}$
; -
(ii)
 -a.e. for all
-a.e. for all
 $j,k\in \mathbb {N}$
with
$j,k\in \mathbb {N}$
with
 $j\not =k$
.
$j\not =k$
.The family
 $(\phi _j)_{j\in \mathbb {N}}$
is also a relative orthonormal basis if it also satisfies
$(\phi _j)_{j\in \mathbb {N}}$
is also a relative orthonormal basis if it also satisfies -
(iii) The linear space spanned by the set of functions
 $$ \begin{align*} \left\{\phi_j\psi : j \in \mathbb N, \psi \in L^{\infty}(\mu)~\text{is } H\text{-invariant}\right\} \end{align*} $$
$$ \begin{align*} \left\{\phi_j\psi : j \in \mathbb N, \psi \in L^{\infty}(\mu)~\text{is } H\text{-invariant}\right\} \end{align*} $$
is dense in
 $L^2(\mu )$
.
$L^2(\mu )$
.
We also give a definition of eigenfunctions that applies to nonergodic systems.
Definition 3.11 (H-eigenfunctions)
Let H be a countable discrete abelian group and
![]() $X=(X,\mathcal {X},\mu ,(T_h)_{h\in H})$
be an H-system. We say that
$X=(X,\mathcal {X},\mu ,(T_h)_{h\in H})$
be an H-system. We say that
![]() $f:X\rightarrow \mathbb {C}$
is an H-eigenfunction if there exists an H-invariant function
$f:X\rightarrow \mathbb {C}$
is an H-eigenfunction if there exists an H-invariant function
![]() $\lambda :X\to \widehat {H}$
, such that
$\lambda :X\to \widehat {H}$
, such that
![]() $T_h f(x) = \lambda (x,h) \cdot f(x)$
for all
$T_h f(x) = \lambda (x,h) \cdot f(x)$
for all
![]() $h\in H$
and
$h\in H$
and
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
. In this case, we also say that
$x\in X$
. In this case, we also say that
![]() $\lambda $
is the eigenvalue of f.
$\lambda $
is the eigenvalue of f.
Note that under the assumption that the H-action is ergodic, this definition coincides with the standard definition of an eigenfunction. Observe, moreover, that the functions
![]() $\{y^m\}_{m\in \mathbb {N}}$
from Example 3.9 are eigenfunctions according to this definition.
$\{y^m\}_{m\in \mathbb {N}}$
from Example 3.9 are eigenfunctions according to this definition.
Frantzikinakis and Host proved the following result:
Theorem 3.12 ([Reference Frantzikinakis and Host19], Theorem 5.2)
Let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_h)_{h\in H})$
be an H-system. Then
$\textbf {X}=(X,\mathcal {X},\mu ,(T_h)_{h\in H})$
be an H-system. Then
![]() $\mathcal {Z}_H(X)$
admits a relative orthonormal basis of eigenfunctions.
$\mathcal {Z}_H(X)$
admits a relative orthonormal basis of eigenfunctions.
The proof of Theorem 3.12 is given for
![]() $\mathbb {Z}$
-actions in [Reference Frantzikinakis and Host19], but the same argument can be easily generalised for arbitrary group actions.
$\mathbb {Z}$
-actions in [Reference Frantzikinakis and Host19], but the same argument can be easily generalised for arbitrary group actions.
3.3 Proof of Theorem 1.11
In this subsection, we prove Theorem 1.11. Example 3.1 is a good example to have in mind while reading this section.
Let
![]() $\textbf {X} = \left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
be an ergodic G-system, and let
$\textbf {X} = \left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
be an ergodic G-system, and let
![]() $\textbf {Z}=(Z,\alpha )$
be the Kronecker factor of
$\textbf {Z}=(Z,\alpha )$
be the Kronecker factor of
![]() $\textbf {X}$
. Let
$\textbf {X}$
. Let
![]() $A \in \mathcal {X}$
and
$A \in \mathcal {X}$
and
![]() $f = \mathbf {1}_A$
. We can write
$f = \mathbf {1}_A$
. We can write
where
![]() $\{\zeta _i\}_{i\in \mathbb {N}}$
is an orthonormal basis of eigenfunctions and
$\{\zeta _i\}_{i\in \mathbb {N}}$
is an orthonormal basis of eigenfunctions and
![]() $a_i\in \mathbb {C}$
. Moreover, using Theorem 3.12,
$a_i\in \mathbb {C}$
. Moreover, using Theorem 3.12,
where
![]() $\{\xi _i\}_{i\in \mathbb {N}}$
is a relative orthonormal basis of
$\{\xi _i\}_{i\in \mathbb {N}}$
is a relative orthonormal basis of
![]() $\psi (G)$
-eigenfunctions and
$\psi (G)$
-eigenfunctions and
![]() are
are
![]() $\psi (G)$
-invariant functions.
$\psi (G)$
-invariant functions.
Choose
![]() $N_1 \in \mathbb {N}$
sufficiently large so that
$N_1 \in \mathbb {N}$
sufficiently large so that
 $$ \begin{align*} \left\| f_c - \sum_{i=1}^{N_1}{a_i\zeta_i} \right\|_{2} & < \frac{\varepsilon}{8} \end{align*} $$
$$ \begin{align*} \left\| f_c - \sum_{i=1}^{N_1}{a_i\zeta_i} \right\|_{2} & < \frac{\varepsilon}{8} \end{align*} $$
and
 $$ \begin{align*} \left\| f_{\psi} - \left( \sum_{i=1}^{N_1}{b_i\xi_i}\right) \right\|_{2} & < \frac{\varepsilon}{8}. \end{align*} $$
$$ \begin{align*} \left\| f_{\psi} - \left( \sum_{i=1}^{N_1}{b_i\xi_i}\right) \right\|_{2} & < \frac{\varepsilon}{8}. \end{align*} $$
For each
![]() $j \in \mathbb {N}$
, the function
$j \in \mathbb {N}$
, the function
![]() $\xi _j$
is a
$\xi _j$
is a
![]() $\psi (G)$
-eigenfunction, so we can write
$\psi (G)$
-eigenfunction, so we can write
![]() $\xi _j \left( T_{\psi (g)}x \right) = \mu _j(x, \psi (g)) \xi _j(x)$
for some
$\xi _j \left( T_{\psi (g)}x \right) = \mu _j(x, \psi (g)) \xi _j(x)$
for some
![]() $\psi (G)$
-invariant function
$\psi (G)$
-invariant function
![]() $\mu _j : X \to \widehat {\psi (G)}$
. The group Z is compact, so
$\mu _j : X \to \widehat {\psi (G)}$
. The group Z is compact, so
![]() $\widehat Z$
is countable and we can write
$\widehat Z$
is countable and we can write
![]() $\widehat {Z} = \bigcup _{n \in \mathbb {N}}{F_n}$
, where
$\widehat {Z} = \bigcup _{n \in \mathbb {N}}{F_n}$
, where
![]() $F_1 \subseteq F_2 \subseteq \cdots $
are finite sets. Let
$F_1 \subseteq F_2 \subseteq \cdots $
are finite sets. Let
and let
![]() $C = \bigcup _{n \in \mathbb {N}}{C_n}.$
Finally, let
$C = \bigcup _{n \in \mathbb {N}}{C_n}.$
Finally, let
Note that the complement of
![]() $E_{j,n}$
consists of all
$E_{j,n}$
consists of all
![]() $x\in X$
, such that
$x\in X$
, such that
![]() $\mu _j(x,\cdot )$
belongs to a finite set. Since
$\mu _j(x,\cdot )$
belongs to a finite set. Since
![]() $\mu _j$
is measurable, we conclude that so is the complement of
$\mu _j$
is measurable, we conclude that so is the complement of
![]() $E_{j,n}$
. Hence,
$E_{j,n}$
. Hence,
![]() $E_{j,n}$
are measurable. Since
$E_{j,n}$
are measurable. Since
![]() $\bigcup _{n=1}^{\infty }{E_{j,n}} = X$
for every
$\bigcup _{n=1}^{\infty }{E_{j,n}} = X$
for every
![]() $j \in \mathbb {N}$
, there exists sufficiently large
$j \in \mathbb {N}$
, there exists sufficiently large
![]() $N_2 \in \mathbb {N}$
, such that
$N_2 \in \mathbb {N}$
, such that
 $$ \begin{align*} \left( \int_{X \setminus E_{j,N_2}}{|b_j \xi_j|^2~d\mu} \right)^{1/2} < \frac{\varepsilon}{16N_1} \end{align*} $$
$$ \begin{align*} \left( \int_{X \setminus E_{j,N_2}}{|b_j \xi_j|^2~d\mu} \right)^{1/2} < \frac{\varepsilon}{16N_1} \end{align*} $$
for
![]() $j = 1, \dots , N_1$
. Then, let
$j = 1, \dots , N_1$
. Then, let
![]() $N \ge \max \{N_1,N_2\}$
, such that: if
$N \ge \max \{N_1,N_2\}$
, such that: if
![]() $T_g\zeta _i = \chi (\alpha _g)\zeta _i$
for some
$T_g\zeta _i = \chi (\alpha _g)\zeta _i$
for some
![]() $i = 1, \dots , N_1$
, then
$i = 1, \dots , N_1$
, then
![]() $\chi \in F_N$
.
$\chi \in F_N$
.
Now, let
![]() $B_0 \in Z$
be a small neighborhood of
$B_0 \in Z$
be a small neighborhood of
![]() $0$
in Z, such that if
$0$
in Z, such that if
![]() $z \in B_0$
and
$z \in B_0$
and
![]() $\chi \in F_N$
, then
$\chi \in F_N$
, then
Let
![]() $\eta _0 : Z \to [0, \infty )$
be a continuous function supported on
$\eta _0 : Z \to [0, \infty )$
be a continuous function supported on
![]() $B_0$
normalised so that
$B_0$
normalised so that
Put
![]() $\eta (u,v) := \eta _0(u) \eta _0(v)$
. Then, by Proposition 3.8, we have
$\eta (u,v) := \eta _0(u) \eta _0(v)$
. Then, by Proposition 3.8, we have
 $$ \begin{align*} \text{UC -}\lim_{g \in G}&~{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\mu \left( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A \right)} \\ & = \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f \cdot T_{\varphi(g)}f_c \cdot T_{\psi(g)}f_{\psi}~d\mu}} \\ & = \int_X{f \cdot \text{UC -}\lim_{g \in G}{\eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c \cdot \eta_0(\alpha_{\psi(g)}) T_{\psi(g)} f_{\psi}}~d\mu}. \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{g \in G}&~{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\mu \left( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A \right)} \\ & = \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\int_X{f \cdot T_{\varphi(g)}f_c \cdot T_{\psi(g)}f_{\psi}~d\mu}} \\ & = \int_X{f \cdot \text{UC -}\lim_{g \in G}{\eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c \cdot \eta_0(\alpha_{\psi(g)}) T_{\psi(g)} f_{\psi}}~d\mu}. \end{align*} $$
From the definition of
![]() $B_0$
, if
$B_0$
, if
![]() $\alpha _{\varphi (g)} \in B_0$
, then
$\alpha _{\varphi (g)} \in B_0$
, then
![]() $\left\| T_{\varphi (g)}\zeta _i - \zeta _i \right\|_{\infty } < \frac {\varepsilon }{16N}$
for
$\left\| T_{\varphi (g)}\zeta _i - \zeta _i \right\|_{\infty } < \frac {\varepsilon }{16N}$
for
![]() $i = 1, \dots , N_1$
. Hence, for every
$i = 1, \dots , N_1$
. Hence, for every
![]() $g \in G$
, since
$g \in G$
, since
![]() $\eta _0$
is supported on
$\eta _0$
is supported on
![]() $B_0$
, we have
$B_0$
, we have
 $$ \begin{align*} \left\| \eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c - \eta_0(\alpha_{\varphi(g)})f_c \right\|_{2} \le &~\left\| \eta_0(\alpha_{\varphi(g)}) \left( T_{\varphi(g)} f_c - \sum_{i=1}^{N_1}{a_i T_{\varphi(g)} \zeta_i} \right) \right\|_{2} \\ & + \left\| \eta_0(\alpha_{\varphi(g)}) \left( \sum_{i=1}^{N_1}{a_i T_{\varphi(g)} \zeta_i} - \sum_{i=1}^{N_1}{a_i\zeta_i} \right) \right\|_{2} \\ & + \left\| \eta_0(\alpha_{\varphi(g)}) \left( \sum_{i=1}^{N_1}{a_i\zeta_i} - f_c \right) \right\|_{2} \\ \le &~\eta_0(\alpha_{\varphi(g)}) \left( \left\| f_c - \sum_{i=1}^{N_1}{a_i\zeta_i} \right\|_{2} + N_1 \frac{\varepsilon}{16N} + \left\| f_c - \sum_{i=1}^{N_1}{a_i\zeta_i} \right\|_{2} \right) \\ < &~\eta_0(\alpha_{\varphi(g)}) \left( \frac{\varepsilon}{8} + \frac{\varepsilon}{16} + \frac{\varepsilon}{8} \right) = \frac{5\varepsilon}{16} \eta_0(\alpha_{\varphi(g)}). \end{align*} $$
$$ \begin{align*} \left\| \eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c - \eta_0(\alpha_{\varphi(g)})f_c \right\|_{2} \le &~\left\| \eta_0(\alpha_{\varphi(g)}) \left( T_{\varphi(g)} f_c - \sum_{i=1}^{N_1}{a_i T_{\varphi(g)} \zeta_i} \right) \right\|_{2} \\ & + \left\| \eta_0(\alpha_{\varphi(g)}) \left( \sum_{i=1}^{N_1}{a_i T_{\varphi(g)} \zeta_i} - \sum_{i=1}^{N_1}{a_i\zeta_i} \right) \right\|_{2} \\ & + \left\| \eta_0(\alpha_{\varphi(g)}) \left( \sum_{i=1}^{N_1}{a_i\zeta_i} - f_c \right) \right\|_{2} \\ \le &~\eta_0(\alpha_{\varphi(g)}) \left( \left\| f_c - \sum_{i=1}^{N_1}{a_i\zeta_i} \right\|_{2} + N_1 \frac{\varepsilon}{16N} + \left\| f_c - \sum_{i=1}^{N_1}{a_i\zeta_i} \right\|_{2} \right) \\ < &~\eta_0(\alpha_{\varphi(g)}) \left( \frac{\varepsilon}{8} + \frac{\varepsilon}{16} + \frac{\varepsilon}{8} \right) = \frac{5\varepsilon}{16} \eta_0(\alpha_{\varphi(g)}). \end{align*} $$
Therefore,
 $$ \begin{align*} \left| \int_X{f \cdot \eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c} \right. & \left. {\cdot~\eta_0(\alpha_{\psi(g)}) T_{\psi(g)} f_{\psi}~d\mu} - \int_X{f_c \cdot f \cdot \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) T_{\psi(g)} f_{\psi}~d\mu} \right| \\& = \left| \int_X{f \cdot \eta_0(\alpha_{\psi(g)}) T_{\psi(g)}f_{\psi} \cdot \left( \eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c - \eta_0(\alpha_{\varphi(g)})f_c \right)~d\mu} \right| \\& \le \eta_0(\alpha_{\psi(g)}) \left\| \eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c - \eta_0(\alpha_{\varphi(g)})f_c \right\|_{1} \\& < \frac{5\varepsilon}{16} \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right). \end{align*} $$
$$ \begin{align*} \left| \int_X{f \cdot \eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c} \right. & \left. {\cdot~\eta_0(\alpha_{\psi(g)}) T_{\psi(g)} f_{\psi}~d\mu} - \int_X{f_c \cdot f \cdot \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) T_{\psi(g)} f_{\psi}~d\mu} \right| \\& = \left| \int_X{f \cdot \eta_0(\alpha_{\psi(g)}) T_{\psi(g)}f_{\psi} \cdot \left( \eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c - \eta_0(\alpha_{\varphi(g)})f_c \right)~d\mu} \right| \\& \le \eta_0(\alpha_{\psi(g)}) \left\| \eta_0(\alpha_{\varphi(g)}) T_{\varphi(g)} f_c - \eta_0(\alpha_{\varphi(g)})f_c \right\|_{1} \\& < \frac{5\varepsilon}{16} \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right). \end{align*} $$
Taking a Cesàro average, we have the inequality
 $$ \begin{align} \text{UC -}\lim_{g \in G}&~{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\mu \left( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A \right)} \nonumber \\ &> \int_X{f_c \cdot f \cdot \text{UC -}\lim_{g \in G}{ \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)T_{\psi(g)} f_{\psi}}~d\mu} - \frac{5\varepsilon}{16}. \end{align} $$
$$ \begin{align} \text{UC -}\lim_{g \in G}&~{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\mu \left( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A \right)} \nonumber \\ &> \int_X{f_c \cdot f \cdot \text{UC -}\lim_{g \in G}{ \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)T_{\psi(g)} f_{\psi}}~d\mu} - \frac{5\varepsilon}{16}. \end{align} $$
Now, we estimate the average
First, for each
![]() $i = 1, \dots , N_1$
, we have
$i = 1, \dots , N_1$
, we have
Next, let
![]() $1 \le j \le N_1$
. Write
$1 \le j \le N_1$
. Write
![]() $T_{\psi (g)}(b_j\xi _j) = b_j \mu _j(x, \psi (g)) \psi _j$
. If
$T_{\psi (g)}(b_j\xi _j) = b_j \mu _j(x, \psi (g)) \psi _j$
. If
![]() $\mu _j(x, \cdot ) \notin C$
, then for any
$\mu _j(x, \cdot ) \notin C$
, then for any
![]() $\chi _1, \chi _2 \in \widehat {Z}$
, the character
$\chi _1, \chi _2 \in \widehat {Z}$
, the character
![]() $g \mapsto \chi _1(\alpha _{\varphi (g)}) \chi _2(\alpha _{\psi (g)}) \mu _j(x, \psi (g))$
is nontrivial, so
$g \mapsto \chi _1(\alpha _{\varphi (g)}) \chi _2(\alpha _{\psi (g)}) \mu _j(x, \psi (g))$
is nontrivial, so
Hence, by the Stone–Weierstrass theorem,
Therefore,
where
![]() $\widetilde {f}_{\psi } = E(f|\widetilde {\mathcal {Z}}_{\psi }(X))$
and
$\widetilde {f}_{\psi } = E(f|\widetilde {\mathcal {Z}}_{\psi }(X))$
and
![]() $\widetilde {\mathcal {Z}}_{\psi }(X)$
is the factor generated by
$\widetilde {\mathcal {Z}}_{\psi }(X)$
is the factor generated by
![]() $\psi (G)$
-eigenfunctions whose eigenvalues come from C. Note that
$\psi (G)$
-eigenfunctions whose eigenvalues come from C. Note that
where
 $$ \begin{align*} \widetilde{\xi}_j(x) = \begin{cases} \xi_j(x), & \mu_j(x, \cdot) \in C; \\ 0, & \mu_j(x, \cdot) \notin C. \end{cases} \end{align*} $$
$$ \begin{align*} \widetilde{\xi}_j(x) = \begin{cases} \xi_j(x), & \mu_j(x, \cdot) \in C; \\ 0, & \mu_j(x, \cdot) \notin C. \end{cases} \end{align*} $$
We note that since C is at most countable,
![]() $\widetilde {\chi }_j$
is measurable. Moreover,
$\widetilde {\chi }_j$
is measurable. Moreover,
 $$ \begin{align*} \widetilde{f}_{\psi} - \sum_{i=1}^{N_1}b_i\widetilde{\xi}_i = E(f - \sum_{i=1}^{N_1} b_i \xi_i |\widetilde{\mathcal {Z}}_{\psi}(X)), \end{align*} $$
$$ \begin{align*} \widetilde{f}_{\psi} - \sum_{i=1}^{N_1}b_i\widetilde{\xi}_i = E(f - \sum_{i=1}^{N_1} b_i \xi_i |\widetilde{\mathcal {Z}}_{\psi}(X)), \end{align*} $$
so
 $$ \begin{align*} \left\| \widetilde{f}_{\psi} - \sum_{i=1}^{N_1}{b_i\widetilde{\xi}_i} \right\|_{2} < \frac{\varepsilon}{8}. \end{align*} $$
$$ \begin{align*} \left\| \widetilde{f}_{\psi} - \sum_{i=1}^{N_1}{b_i\widetilde{\xi}_i} \right\|_{2} < \frac{\varepsilon}{8}. \end{align*} $$
If
![]() $x \in E_{j,N}$
, then we must have
$x \in E_{j,N}$
, then we must have
![]() $\mu _j(x, \cdot ) \in C_N$
. That is,
$\mu _j(x, \cdot ) \in C_N$
. That is,
![]() $\mu _j(x, \psi (g)) = \chi _1(\alpha _{\varphi (g)}) \chi _2(\alpha _{\psi (g)})$
for some
$\mu _j(x, \psi (g)) = \chi _1(\alpha _{\varphi (g)}) \chi _2(\alpha _{\psi (g)})$
for some
![]() $\chi _1, \chi _2 \in F_N$
. Thus,
$\chi _1, \chi _2 \in F_N$
. Thus,
 $$ \begin{align*} \left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \mu_j(x, \psi(g)) - 1 \right) \right| = &~\left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \chi_1(\alpha_{\varphi(g)}) \chi_2(\alpha_{\psi(g)}) - 1 \right) \right| \\\leq &~\left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \chi_1(\alpha_{\varphi(g)}) \chi_2(\alpha_{\psi(g)}) - \chi_2(\alpha_{\psi(g)}) \right) \right| \\[6pt]& + \left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \chi_2(\alpha_{\psi(g)}) - 1 \right) \right| \\[4pt]\leq &~\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \frac{\varepsilon}{16N} + \frac{\varepsilon}{16N} \right) = \frac{\varepsilon}{8N} \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right). \end{align*} $$
$$ \begin{align*} \left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \mu_j(x, \psi(g)) - 1 \right) \right| = &~\left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \chi_1(\alpha_{\varphi(g)}) \chi_2(\alpha_{\psi(g)}) - 1 \right) \right| \\\leq &~\left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \chi_1(\alpha_{\varphi(g)}) \chi_2(\alpha_{\psi(g)}) - \chi_2(\alpha_{\psi(g)}) \right) \right| \\[6pt]& + \left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \chi_2(\alpha_{\psi(g)}) - 1 \right) \right| \\[4pt]\leq &~\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \frac{\varepsilon}{16N} + \frac{\varepsilon}{16N} \right) = \frac{\varepsilon}{8N} \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right). \end{align*} $$
Therefore,
 $$ \begin{align*} \bigg\| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) & \left( T_{\psi(g)}(b_j\widetilde{\xi}_j) - b_j\widetilde{\xi}_j \right) \bigg\|_2^2 \\ = &~\int_X{\left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( T_{\psi(g)}(b_j\widetilde{\xi}_j) - b_j\widetilde{\xi}_j \right) \right|^2~d\mu} \\ = &~\int_X{\left| b_j(x) \widetilde{\xi}_j(x) \right|^2 \left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \mu_j(x, \psi(g)) - 1 \right) \right|^2~d\mu(x)} \\ \le &~\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)^2 \left( \int_{E_{j,N}}{\left( \frac{\varepsilon}{8N} \right)^2 \left| b_j \widetilde{\xi}_j \right|^2~d\mu} + 4 \int_{X \setminus E_{j,N}}{\left| b_j \widetilde{\xi}_j \right|^2~d\mu} \right) \\ \le &~\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)^2 \left( \left( \frac{\varepsilon}{8N} \right)^2 + 4 \left( \frac{\varepsilon}{16N_1} \right)^2 \right) \le 2 \left( \frac{\varepsilon}{8N_1} \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \right)^2 .\end{align*} $$
$$ \begin{align*} \bigg\| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) & \left( T_{\psi(g)}(b_j\widetilde{\xi}_j) - b_j\widetilde{\xi}_j \right) \bigg\|_2^2 \\ = &~\int_X{\left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( T_{\psi(g)}(b_j\widetilde{\xi}_j) - b_j\widetilde{\xi}_j \right) \right|^2~d\mu} \\ = &~\int_X{\left| b_j(x) \widetilde{\xi}_j(x) \right|^2 \left| \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left( \mu_j(x, \psi(g)) - 1 \right) \right|^2~d\mu(x)} \\ \le &~\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)^2 \left( \int_{E_{j,N}}{\left( \frac{\varepsilon}{8N} \right)^2 \left| b_j \widetilde{\xi}_j \right|^2~d\mu} + 4 \int_{X \setminus E_{j,N}}{\left| b_j \widetilde{\xi}_j \right|^2~d\mu} \right) \\ \le &~\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)^2 \left( \left( \frac{\varepsilon}{8N} \right)^2 + 4 \left( \frac{\varepsilon}{16N_1} \right)^2 \right) \le 2 \left( \frac{\varepsilon}{8N_1} \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \right)^2 .\end{align*} $$
Putting together our estimates, we have
 $$ \begin{align*} \bigg\| \text{UC -}\lim_{g \in G} & {\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)T_{\psi(g)} f_{\psi}} - \widetilde{f}_{\psi} \bigg\|_2 \\ = &~\left\| \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)T_{\psi(g)} \widetilde{f}_{\psi}} - \widetilde{f}_{\psi} \right\|_{2} \\ \le &~\left\| \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) T_{\psi(g)}\widetilde{f}_{\psi} - T_{\psi(g)} \sum_{i=1}^{N_1}{b_i\widetilde{\xi}_i}} \right\|_{2} \\ & + \left\| \text{UC -}\lim_{g \in G}{\sum_{i=1}^{N_1}{ \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left(T_{\psi(g)}(b_i \widetilde{\xi}_i) - b_j \widetilde{\xi}_j \right)}} \right\|_{2} \\ & + \left\| \sum_{i=1}^{N_1}{b_i\widetilde{\xi}_i} - \widetilde{f}_{\psi} \right\|_{2} \\ < &~\frac{\varepsilon}{8} + N_1 \frac{\sqrt{2}\varepsilon}{8N_1} + \frac{\varepsilon}{8} \le \frac{(2\sqrt{2} + 5)\varepsilon}{16} < \frac{\varepsilon}{2}. \end{align*} $$
$$ \begin{align*} \bigg\| \text{UC -}\lim_{g \in G} & {\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)T_{\psi(g)} f_{\psi}} - \widetilde{f}_{\psi} \bigg\|_2 \\ = &~\left\| \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right)T_{\psi(g)} \widetilde{f}_{\psi}} - \widetilde{f}_{\psi} \right\|_{2} \\ \le &~\left\| \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) T_{\psi(g)}\widetilde{f}_{\psi} - T_{\psi(g)} \sum_{i=1}^{N_1}{b_i\widetilde{\xi}_i}} \right\|_{2} \\ & + \left\| \text{UC -}\lim_{g \in G}{\sum_{i=1}^{N_1}{ \eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) \left(T_{\psi(g)}(b_i \widetilde{\xi}_i) - b_j \widetilde{\xi}_j \right)}} \right\|_{2} \\ & + \left\| \sum_{i=1}^{N_1}{b_i\widetilde{\xi}_i} - \widetilde{f}_{\psi} \right\|_{2} \\ < &~\frac{\varepsilon}{8} + N_1 \frac{\sqrt{2}\varepsilon}{8N_1} + \frac{\varepsilon}{8} \le \frac{(2\sqrt{2} + 5)\varepsilon}{16} < \frac{\varepsilon}{2}. \end{align*} $$
Substituting back into (12), we have
 $$ \begin{align} \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\mu \left( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A \right)} &> \int_X{f_c \cdot f \cdot \widetilde{f}_{\psi}~d\mu} - \frac{13\varepsilon}{16} \nonumber \\ & \ge \mu(A)^3 - \frac{13\varepsilon}{16}. \end{align} $$
$$ \begin{align} \text{UC -}\lim_{g \in G}{\eta \left( \alpha_{\varphi(g)}, \alpha_{\psi(g)} \right) ~\mu \left( A \cap T_{\varphi(g)}^{-1}A \cap T_{\psi(g)}^{-1}A \right)} &> \int_X{f_c \cdot f \cdot \widetilde{f}_{\psi}~d\mu} - \frac{13\varepsilon}{16} \nonumber \\ & \ge \mu(A)^3 - \frac{13\varepsilon}{16}. \end{align} $$
Since
![]() $\text {UC -}\lim _{g \in G}\eta \left( \alpha _{\varphi (g)}, \alpha _{\psi (g)} \right)=1$
, it follows that the set
$\text {UC -}\lim _{g \in G}\eta \left( \alpha _{\varphi (g)}, \alpha _{\psi (g)} \right)=1$
, it follows that the set
is syndetic in G. If not, there exists a Følner sequence
![]() $(\Phi _N)_{N\in \mathbb N}$
, such that
$(\Phi _N)_{N\in \mathbb N}$
, such that
![]() $\mu (A\cap T_{\varphi (g)}^{-1}A\cap T_{\psi (g)}^{-1}A)\leq \mu (A)^3-\varepsilon $
for every
$\mu (A\cap T_{\varphi (g)}^{-1}A\cap T_{\psi (g)}^{-1}A)\leq \mu (A)^3-\varepsilon $
for every
![]() $g\in \bigcup _{N\in \mathbb {N}}\Phi _N$
. But then,
$g\in \bigcup _{N\in \mathbb {N}}\Phi _N$
. But then,
which contradicts the inequality in (13).
4 Extensions
As we have observed in Subsection 3.3, the partial characteristic factors obtained in Proposition 3.5 are not the minimal characteristic factors. For example, in Subsection 3.3, we proved that one can replace
![]() $\mathcal {Z}_{\psi }(X)$
with the smaller factor
$\mathcal {Z}_{\psi }(X)$
with the smaller factor
![]() $\widetilde {\mathcal {Z}}_{\psi }(X)$
. In this section, we develop an extension trick that will be used to further simplify the characteristic factors. These results will be useful in the proof of Theorem 1.13, where
$\widetilde {\mathcal {Z}}_{\psi }(X)$
. In this section, we develop an extension trick that will be used to further simplify the characteristic factors. These results will be useful in the proof of Theorem 1.13, where
![]() $\varphi (G)$
is no longer assumed to have finite index in G. In the example below, we illustrate our main result in the simpler case where
$\varphi (G)$
is no longer assumed to have finite index in G. In the example below, we illustrate our main result in the simpler case where
![]() $\varphi (g)=g$
,
$\varphi (g)=g$
,
![]() $\psi (g)=2g$
. The following example is based on Example 3.1.
$\psi (g)=2g$
. The following example is based on Example 3.1.
Example 4.1. Let
![]() $G=\bigoplus _{j=1}^{\infty } \mathbb {Z}/4\mathbb {Z}$
, and let
$G=\bigoplus _{j=1}^{\infty } \mathbb {Z}/4\mathbb {Z}$
, and let
![]() $X=\left(\prod _{j\in \mathbb {N}}C_4\right) \times C_2 \times C_2$
, where the action of
$X=\left(\prod _{j\in \mathbb {N}}C_4\right) \times C_2 \times C_2$
, where the action of
![]() $g\in G$
on X is given by
$g\in G$
on X is given by
 $$ \begin{align} T_g(\textbf{x},x_{\infty}, y) = \left( (i^{g_j}x_j)_{j\in \mathbb{N}}, x_{\infty} \cdot \prod_{k=1}^{\infty} (-1)^{g_k}, y\cdot \prod_{j\in\mathbb{N}} (x_j^{2g_j}\cdot i^{g_j^2-g_j})\right) \end{align} $$
$$ \begin{align} T_g(\textbf{x},x_{\infty}, y) = \left( (i^{g_j}x_j)_{j\in \mathbb{N}}, x_{\infty} \cdot \prod_{k=1}^{\infty} (-1)^{g_k}, y\cdot \prod_{j\in\mathbb{N}} (x_j^{2g_j}\cdot i^{g_j^2-g_j})\right) \end{align} $$
for
![]() $\textbf {x} = (x_1, x_2, \dots ) \in \prod _{j\in \mathbb N}{C_4}$
,
$\textbf {x} = (x_1, x_2, \dots ) \in \prod _{j\in \mathbb N}{C_4}$
,
![]() $x_{\infty } \in C_2$
and
$x_{\infty } \in C_2$
and
![]() $y \in C_2$
. Note that for
$y \in C_2$
. Note that for
![]() $g = (g_1, g_2, \dots ) \in G$
, only finitely many of the coordinates
$g = (g_1, g_2, \dots ) \in G$
, only finitely many of the coordinates
![]() $g_j \in {\mathbb Z}/4{\mathbb Z}$
are nonzero, so (14) is well defined.
$g_j \in {\mathbb Z}/4{\mathbb Z}$
are nonzero, so (14) is well defined.
As in Example 3.1, the function
![]() $f(\textbf {x},x_{\infty },y)=y$
is a
$f(\textbf {x},x_{\infty },y)=y$
is a
![]() $2G$
-eigenfunction with eigenvalue
$2G$
-eigenfunction with eigenvalue
![]() $2g\mapsto \prod _{j=1}^{\infty } (-1)^{g_j}$
. However, this time, f may have a nontrivial contribution for the average. Indeed, if we let
$2g\mapsto \prod _{j=1}^{\infty } (-1)^{g_j}$
. However, this time, f may have a nontrivial contribution for the average. Indeed, if we let
![]() $f_1(\textbf {x},x_{\infty },y) = x_{\infty }$
, then
$f_1(\textbf {x},x_{\infty },y) = x_{\infty }$
, then
![]() $f_1$
is a G-eigenfunction with eigenvalue
$f_1$
is a G-eigenfunction with eigenvalue
![]() $g\mapsto \prod _{k=1}^{\infty } (-1)^{g_k}$
and
$g\mapsto \prod _{k=1}^{\infty } (-1)^{g_k}$
and
is nonzero. Let
![]() $\varphi (g)=g$
and
$\varphi (g)=g$
and
![]() $\psi (g)=2g$
. The above computation shows that f is measurable with respect to
$\psi (g)=2g$
. The above computation shows that f is measurable with respect to
![]() $\widetilde {\mathcal {Z}}_{\psi }$
where
$\widetilde {\mathcal {Z}}_{\psi }$
where
![]() $\widetilde {\mathcal {Z}}_{\psi }$
is defined in Subsection 3.3. As a result, we deduce that
$\widetilde {\mathcal {Z}}_{\psi }$
is defined in Subsection 3.3. As a result, we deduce that
![]() $\mathcal {Z}(X)\lor \mathcal {I}_{\psi }(X)\prec \widetilde {\mathcal {Z}}_{\psi }(X)$
is a strict inclusion.
$\mathcal {Z}(X)\lor \mathcal {I}_{\psi }(X)\prec \widetilde {\mathcal {Z}}_{\psi }(X)$
is a strict inclusion.
Consider the homomorphism
![]() $\lambda :G\rightarrow S^1$
,
$\lambda :G\rightarrow S^1$
,
![]() $\lambda (g)=\prod _{j=1}^{\infty } i^{g_j}$
and observe that
$\lambda (g)=\prod _{j=1}^{\infty } i^{g_j}$
and observe that
![]() $\lambda (2g)=\prod _{j=1}^{\infty } (-1)^{g_i}$
is the eigenvalue of
$\lambda (2g)=\prod _{j=1}^{\infty } (-1)^{g_i}$
is the eigenvalue of
![]() $f_2$
. We extend X to a new system
$f_2$
. We extend X to a new system
![]() $\widetilde {X}$
, where
$\widetilde {X}$
, where
![]() $\lambda $
is an eigenvalue. Let
$\lambda $
is an eigenvalue. Let
![]() $\widetilde {X} = \left(\prod _{j\in \mathbb {N}} C_4\right) \times C_4\times C_2$
, and let the action of
$\widetilde {X} = \left(\prod _{j\in \mathbb {N}} C_4\right) \times C_4\times C_2$
, and let the action of
![]() $g\in G$
on
$g\in G$
on
![]() $\widetilde {X}$
be given by
$\widetilde {X}$
be given by
 $$ \begin{align*} S_g(\textbf{x},x_{\infty},y) = \left( (i^{g_j}x_j)_{j\in \mathbb{N}}, \lambda(g) x_{\infty}, y\cdot \prod_{j\in\mathbb{N}} (x_j^{2g_j}\cdot i^{g_j^2-g_j})\right) \end{align*} $$
$$ \begin{align*} S_g(\textbf{x},x_{\infty},y) = \left( (i^{g_j}x_j)_{j\in \mathbb{N}}, \lambda(g) x_{\infty}, y\cdot \prod_{j\in\mathbb{N}} (x_j^{2g_j}\cdot i^{g_j^2-g_j})\right) \end{align*} $$
for
![]() $\textbf {x} = (x_1, x_2, \dots ) \in \prod _{j\in \mathbb N}{C_4}$
,
$\textbf {x} = (x_1, x_2, \dots ) \in \prod _{j\in \mathbb N}{C_4}$
,
![]() $x_{\infty } \in C_4$
and
$x_{\infty } \in C_4$
and
![]() $y \in C_2$
. It is easy to see that
$y \in C_2$
. It is easy to see that
![]() $\widetilde {\textbf {X}} = (\widetilde {X},(S_g)_{g\in G})$
is an extension of
$\widetilde {\textbf {X}} = (\widetilde {X},(S_g)_{g\in G})$
is an extension of
![]() $\textbf {X}$
with respect to the factor map
$\textbf {X}$
with respect to the factor map
![]() $\pi (\textbf {x},x_{\infty },y) = (\textbf {x},x_{\infty }^2,y)$
. Observe that now the function
$\pi (\textbf {x},x_{\infty },y) = (\textbf {x},x_{\infty }^2,y)$
. Observe that now the function
![]() $h(\textbf {x},x_{\infty },y)=x_{\infty }$
on
$h(\textbf {x},x_{\infty },y)=x_{\infty }$
on
![]() $\widetilde {X}$
is an eigenfunction with eigenvalue
$\widetilde {X}$
is an eigenfunction with eigenvalue
![]() $\lambda $
and we deduce that
$\lambda $
and we deduce that
![]() is a
is a
![]() $2G$
-invariant function on
$2G$
-invariant function on
![]() $\widetilde {X}$
. This means that
$\widetilde {X}$
. This means that
![]() is measurable with respect to the
is measurable with respect to the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\widetilde {Z}(\widetilde {X})\lor \mathcal {I}_{\psi }(\widetilde {X})$
. In fact, one can show that now we have an equality
$\widetilde {Z}(\widetilde {X})\lor \mathcal {I}_{\psi }(\widetilde {X})$
. In fact, one can show that now we have an equality
![]() $\mathcal {Z}(X)\lor \mathcal {I}_{\psi }(\widetilde {X})=\widetilde {\mathcal {Z}}_{\psi }(\widetilde {X})$
.
$\mathcal {Z}(X)\lor \mathcal {I}_{\psi }(\widetilde {X})=\widetilde {\mathcal {Z}}_{\psi }(\widetilde {X})$
.
Definition 4.2. Let G be a countable discrete abelian group, and let
![]() $\varphi :G\rightarrow G$
be a homomorphism. We say that a character
$\varphi :G\rightarrow G$
be a homomorphism. We say that a character
![]() $\chi \in \widehat G$
factors through
$\chi \in \widehat G$
factors through
![]() $\varphi $
is
$\varphi $
is
![]() $\chi =\lambda \circ \varphi $
for some
$\chi =\lambda \circ \varphi $
for some
![]() $\lambda \in \widehat G$
.
$\lambda \in \widehat G$
.
The main result in this section is the following theorem.
Theorem 4.3. Let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g \in G})$
be an ergodic G-system. Let
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g \in G})$
be an ergodic G-system. Let
![]() $\varphi ,\psi : G \to G$
be homomorphisms. For any countable set
$\varphi ,\psi : G \to G$
be homomorphisms. For any countable set
![]() $C \subseteq \widehat {G}$
of characters that factor through
$C \subseteq \widehat {G}$
of characters that factor through
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, there exists an ergodic extension
$\psi $
, there exists an ergodic extension
![]() $\widetilde {\textbf {X}}$
of
$\widetilde {\textbf {X}}$
of
![]() $\textbf {X}$
with the following property: for any
$\textbf {X}$
with the following property: for any
![]() $\chi \in C$
, there exist G-eigenvalues
$\chi \in C$
, there exist G-eigenvalues
![]() $\lambda ,\mu $
of
$\lambda ,\mu $
of
![]() $\widetilde {\textbf {X}}$
, such that
$\widetilde {\textbf {X}}$
, such that
![]() $\lambda (\varphi (g))=\mu (\psi (g))=\chi (g)$
.
$\lambda (\varphi (g))=\mu (\psi (g))=\chi (g)$
.
The fact that
![]() $\widetilde {\textbf {X}}$
in Theorem 4.3 is ergodic will be important in our proof. In preparation for proving that
$\widetilde {\textbf {X}}$
in Theorem 4.3 is ergodic will be important in our proof. In preparation for proving that
![]() $\widetilde {\textbf {X}}$
is ergodic, we need the following definition.
$\widetilde {\textbf {X}}$
is ergodic, we need the following definition.
Definition 4.4. Let
![]() $(X,G)$
be an ergodic system and U a compact abelian group. A cocycle is a measurable map
$(X,G)$
be an ergodic system and U a compact abelian group. A cocycle is a measurable map
![]() $\rho :G\times X\rightarrow U$
satisfying
$\rho :G\times X\rightarrow U$
satisfying
![]() $\rho (g+g',x) = \rho (g,x)\cdot \rho (g',T_gx)$
for every
$\rho (g+g',x) = \rho (g,x)\cdot \rho (g',T_gx)$
for every
![]() $g,g'\in G$
and
$g,g'\in G$
and
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
. Two cocycles
$x\in X$
. Two cocycles
![]() $\rho ,\rho ':G\times X\rightarrow U$
are said to be cohomologous if there exists a measurable map
$\rho ,\rho ':G\times X\rightarrow U$
are said to be cohomologous if there exists a measurable map
![]() $F:X\rightarrow U$
, such that
$F:X\rightarrow U$
, such that
![]() $\rho (g,x)\cdot \rho '(g,x)^{-1} = \Delta _g F(x)$
for all
$\rho (g,x)\cdot \rho '(g,x)^{-1} = \Delta _g F(x)$
for all
![]() $g\in G$
and
$g\in G$
and
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X$
. The image of
$x\in X$
. The image of
![]() $\rho $
,
$\rho $
,
![]() $U_{\rho }$
, is defined to be the minimal closed subgroup generated by
$U_{\rho }$
, is defined to be the minimal closed subgroup generated by
![]() $\{\rho (g,x) : g\in G, x\in X\}$
. The cocycle
$\{\rho (g,x) : g\in G, x\in X\}$
. The cocycle
![]() $\rho $
is said to be minimal if it is not cohomologous to any cocycle
$\rho $
is said to be minimal if it is not cohomologous to any cocycle
![]() $\rho '$
with
$\rho '$
with
![]() $U_{\rho '}\lneqq U_{\rho }$
.
$U_{\rho '}\lneqq U_{\rho }$
.
In [Reference Zimmer31], Zimmer proved that every cocycle is cohomologous to a minimal cocycle and established the following criterion for ergodicity.
Lemma 4.5 ([Reference Zimmer31], Corollary 3.8)
Let
![]() $\textbf {X}=\left(X,\mathcal {X},\mu ,(T_g)_{g \in G}\right)$
be an ergodic G-system, U a compact abelian group and
$\textbf {X}=\left(X,\mathcal {X},\mu ,(T_g)_{g \in G}\right)$
be an ergodic G-system, U a compact abelian group and
![]() $\rho : G \times X \to U$
a cocycle. Then,
$\rho : G \times X \to U$
a cocycle. Then,
![]() $\textbf {X}\times _{\rho } U$
is ergodic if and only if
$\textbf {X}\times _{\rho } U$
is ergodic if and only if
![]() $\rho $
is minimal and
$\rho $
is minimal and
![]() $U=U_{\rho }$
.
$U=U_{\rho }$
.
We are now set to prove Theorem 4.3.
Proof of Theorem 4.3
Let
![]() $\{\chi _i : i\in \mathbb {N}\}$
be an enumeration of the elements in C. By assumption, for every
$\{\chi _i : i\in \mathbb {N}\}$
be an enumeration of the elements in C. By assumption, for every
![]() $i\in \mathbb {N}$
, there exist homomorphisms
$i\in \mathbb {N}$
, there exist homomorphisms
![]() $\chi _i^{\varphi },\chi _i^{\psi }:G\rightarrow S^1$
, such that
$\chi _i^{\varphi },\chi _i^{\psi }:G\rightarrow S^1$
, such that
![]() $\chi _i^{\varphi }(\varphi (g)) = \chi _i^{\psi }(\psi (g))= \chi _i(g)$
. Let
$\chi _i^{\varphi }(\varphi (g)) = \chi _i^{\psi }(\psi (g))= \chi _i(g)$
. Let
![]() $I=\mathbb {N}\times \{\varphi ,\psi \}$
, and let
$I=\mathbb {N}\times \{\varphi ,\psi \}$
, and let
![]() $\widetilde {\chi }:G\rightarrow (S^1)^{I}$
be the homomorphism whose
$\widetilde {\chi }:G\rightarrow (S^1)^{I}$
be the homomorphism whose
![]() $(i,\varphi )$
-coordinate is
$(i,\varphi )$
-coordinate is
![]() $\chi _i^{\varphi }$
and
$\chi _i^{\varphi }$
and
![]() $(j,\psi )$
-coordinate is
$(j,\psi )$
-coordinate is
![]() $\chi _j^{\psi }$
for every
$\chi _j^{\psi }$
for every
![]() $i,j\in \mathbb {N}$
. By Zimmer’s theory, there exists a minimal cocycle
$i,j\in \mathbb {N}$
. By Zimmer’s theory, there exists a minimal cocycle
![]() $\rho :G\times X\rightarrow (S^1)^{I}$
which is cohomologous to
$\rho :G\times X\rightarrow (S^1)^{I}$
which is cohomologous to
![]() $\widetilde {\chi }$
, where the latter is viewed as a
$\widetilde {\chi }$
, where the latter is viewed as a
![]() $G\times X\rightarrow (S^1)^{I}$
function that is independent of
$G\times X\rightarrow (S^1)^{I}$
function that is independent of
![]() $x\in X$
. This means that there exists a measurable map
$x\in X$
. This means that there exists a measurable map
![]() $F:X\rightarrow (S^1)^{I}$
, such that
$F:X\rightarrow (S^1)^{I}$
, such that
![]() $\rho _g = \widetilde {\chi }(g)\cdot \Delta _g F$
. Let V be the image of
$\rho _g = \widetilde {\chi }(g)\cdot \Delta _g F$
. Let V be the image of
![]() $\rho $
, then, by Lemma 4.5,
$\rho $
, then, by Lemma 4.5,
![]() $\widetilde {X}=X\times _{\rho } V$
is ergodic. Now, for every coordinate
$\widetilde {X}=X\times _{\rho } V$
is ergodic. Now, for every coordinate
![]() $t\in I$
, consider the projection map
$t\in I$
, consider the projection map
![]() $\pi _t:(S^1)^{I}\rightarrow S^1$
. By restricting
$\pi _t:(S^1)^{I}\rightarrow S^1$
. By restricting
![]() $\pi _t$
to V, we get a homomorphism
$\pi _t$
to V, we get a homomorphism
![]() $\tau _t :V\rightarrow S^1$
. Then, the function
$\tau _t :V\rightarrow S^1$
. Then, the function
![]() $\phi _{i,\varphi }(x,v) := \tau _{i,\varphi }(v)\cdot \pi _{i,\varphi } F(x)$
is an eigenfunction with eigenvalue
$\phi _{i,\varphi }(x,v) := \tau _{i,\varphi }(v)\cdot \pi _{i,\varphi } F(x)$
is an eigenfunction with eigenvalue
![]() $\Delta _g \phi _{i,\varphi }(x,v) = \chi _i^{\varphi }(g)$
and
$\Delta _g \phi _{i,\varphi }(x,v) = \chi _i^{\varphi }(g)$
and
![]() $\phi _{j,\psi }(x,v)=\tau _{j,\psi }(v)\cdot \pi _{j,\psi } F(x)$
is an eigenfunction with eigenvalue
$\phi _{j,\psi }(x,v)=\tau _{j,\psi }(v)\cdot \pi _{j,\psi } F(x)$
is an eigenfunction with eigenvalue
![]() $\Delta _g \phi _{j,\psi }(x,v) = \chi _j^{\psi }(g)$
. This completes the proof.
$\Delta _g \phi _{j,\psi }(x,v) = \chi _j^{\psi }(g)$
. This completes the proof.
4.1 Characteristic factors related to Theorem 1.13
The goal of this subsection is to prove a stronger version of Propositions 3.5 and 3.8 with smaller characteristic factors. We will use the above extension theorem in order to express these characteristic factors in terms of
![]() $\mathcal {Z}_{\varphi ,\psi }(X)$
and the invariant
$\mathcal {Z}_{\varphi ,\psi }(X)$
and the invariant
![]() $\sigma $
-algebras,
$\sigma $
-algebras,
![]() $\mathcal {I}_{\varphi }(X)$
and
$\mathcal {I}_{\varphi }(X)$
and
![]() $\mathcal {I}_{\psi }(X)$
. Then, using a result of Tao and Ziegler [Reference Tao and Ziegler29] (see Theorem 4.8 below), we will reduce matters further to studying the Conze–Lesigne factor
$\mathcal {I}_{\psi }(X)$
. Then, using a result of Tao and Ziegler [Reference Tao and Ziegler29] (see Theorem 4.8 below), we will reduce matters further to studying the Conze–Lesigne factor
![]() $\mathcal {Z}^2(X)$
with respect to the action of G, which is already well understood for arbitrary countable discrete abelian groups (see [Reference Ackelsberg, Bergelson and Best2], [Reference Shalom27]).
$\mathcal {Z}^2(X)$
with respect to the action of G, which is already well understood for arbitrary countable discrete abelian groups (see [Reference Ackelsberg, Bergelson and Best2], [Reference Shalom27]).
We start with a lemma.
Lemma 4.6. Let
![]() $\textbf {X}=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be an ergodic G-system. Let
$\textbf {X}=(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be an ergodic G-system. Let
![]() $\mathcal {I}_{\varphi \times \psi }(X\times X)$
denote the
$\mathcal {I}_{\varphi \times \psi }(X\times X)$
denote the
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $(T_{\varphi (g)}\times T_{\psi (g)})_{g\in G}$
-invariant sets in
$(T_{\varphi (g)}\times T_{\psi (g)})_{g\in G}$
-invariant sets in
![]() $X\times X$
. Then,
$X\times X$
. Then,
Proof. Let
![]() $f_1,f_2\in L^{\infty }(X)$
be arbitrary functions and
$f_1,f_2\in L^{\infty }(X)$
be arbitrary functions and
![]() $f(x,y)=f_1(x)f_2(y)$
. Then, by the mean ergodic theorem, we have that
$f(x,y)=f_1(x)f_2(y)$
. Then, by the mean ergodic theorem, we have that
in
![]() $L^2(\mu \times \mu )$
. By the van der Corput lemma,
$L^2(\mu \times \mu )$
. By the van der Corput lemma,
![]() $E(f|\mathcal {I}_{\varphi \times \psi }(X\times X))=0$
if
$E(f|\mathcal {I}_{\varphi \times \psi }(X\times X))=0$
if

Since
![]() $\varphi (G)\times \psi (G)$
is measure-preserving, the above is equal to
$\varphi (G)\times \psi (G)$
is measure-preserving, the above is equal to
 $$ \begin{align*} \text{UC -}\lim_{h\in G}\left(\left|\int_X \Delta_{\varphi(h)}f_1(x) d\mu(x)\right|\right) \left(\left|\int_X \Delta_{\psi(h)}f_2(y) d\mu(y) \right|\right) \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{h\in G}\left(\left|\int_X \Delta_{\varphi(h)}f_1(x) d\mu(x)\right|\right) \left(\left|\int_X \Delta_{\psi(h)}f_2(y) d\mu(y) \right|\right) \end{align*} $$
which by the Cauchy–Schwarz inequality is bounded above by
We deduce that if
![]() $E(f|\mathcal {Z}_{\varphi }(X)\times \mathcal {Z}_{\psi }(X))=0$
, then
$E(f|\mathcal {Z}_{\varphi }(X)\times \mathcal {Z}_{\psi }(X))=0$
, then
![]() $E\left(f|\mathcal {I}_{\varphi \times \psi }(X\times X)\right)=0$
. Since linear combinations of functions of the form
$E\left(f|\mathcal {I}_{\varphi \times \psi }(X\times X)\right)=0$
. Since linear combinations of functions of the form
with
![]() $f_1,f_2\in L^{\infty }(X)$
are dense in
$f_1,f_2\in L^{\infty }(X)$
are dense in
![]() $L^{\infty }(X\times X)$
, we deduce that the same holds for every bounded function on
$L^{\infty }(X\times X)$
, we deduce that the same holds for every bounded function on
![]() $X\times X$
, and this completes the proof.
$X\times X$
, and this completes the proof.
Using Theorem 4.3, we can now prove the following useful result.
Lemma 4.7. Let G be a countable discrete abelian group, and let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Suppose that
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Suppose that
![]() $\varphi ,\psi :G\rightarrow G$
are arbitrary homomorphisms, such that
$\varphi ,\psi :G\rightarrow G$
are arbitrary homomorphisms, such that
![]() $(\psi -\varphi )(G)$
has finite index in G. Then, there exists an ergodic extension
$(\psi -\varphi )(G)$
has finite index in G. Then, there exists an ergodic extension
![]() $\pi \colon \widetilde {X} \to X$
, such that
$\pi \colon \widetilde {X} \to X$
, such that
Proof. Let
![]() $\{\zeta _i\}_{i\in \mathbb {N}}$
be a relative orthonormal basis of eigenfunctions for
$\{\zeta _i\}_{i\in \mathbb {N}}$
be a relative orthonormal basis of eigenfunctions for
![]() $\mathcal {Z}_{\varphi }(X)$
and
$\mathcal {Z}_{\varphi }(X)$
and
![]() $\{\xi _i\}_{i\in \mathbb {N}}$
be the same for
$\{\xi _i\}_{i\in \mathbb {N}}$
be the same for
![]() $\mathcal {Z}_{\psi }(X)$
. For every
$\mathcal {Z}_{\psi }(X)$
. For every
![]() $i,j \in \mathbb N$
, let
$i,j \in \mathbb N$
, let
![]() $\lambda _i:\varphi (G)\times X\rightarrow \mathbb {C}$
and
$\lambda _i:\varphi (G)\times X\rightarrow \mathbb {C}$
and
![]() $\mu _j:\psi (G)\times X\rightarrow \mathbb {C}$
denote the eigenvalues of
$\mu _j:\psi (G)\times X\rightarrow \mathbb {C}$
denote the eigenvalues of
![]() $\zeta _i$
and
$\zeta _i$
and
![]() $\xi _j$
, respectively. Our goal is to study the functions
$\xi _j$
, respectively. Our goal is to study the functions
![]() $f\in L^{\infty }(X^2)$
which are
$f\in L^{\infty }(X^2)$
which are
![]() $(T_{\varphi (g)}\times T_{\psi (g)})_{g\in G}$
-invariant. By Lemma 4.6, we can write any such function as
$(T_{\varphi (g)}\times T_{\psi (g)})_{g\in G}$
-invariant. By Lemma 4.6, we can write any such function as

where
![]() $c_{i,j}$
is a
$c_{i,j}$
is a
![]() $\varphi (G)\times \psi (G)$
-invariant function. Since f is
$\varphi (G)\times \psi (G)$
-invariant function. Since f is
![]() $T_{\varphi (g)}\times T_{\psi (g)}$
-invariant, we deduce that
$T_{\varphi (g)}\times T_{\psi (g)}$
-invariant, we deduce that
Hypothetically, if
![]() $c_{i,j}$
was a constant, then unless it is zero (and then can be removed from the summation), the equation above implies that
$c_{i,j}$
was a constant, then unless it is zero (and then can be removed from the summation), the equation above implies that
![]() $\lambda _i(\varphi (g),\cdot ) = \mu _j(\psi (g),\cdot )=\chi (g)$
for some character
$\lambda _i(\varphi (g),\cdot ) = \mu _j(\psi (g),\cdot )=\chi (g)$
for some character
![]() $\chi \in \widehat G$
. In this special case, we can apply Theorem 4.3 in order to find an extension where
$\chi \in \widehat G$
. In this special case, we can apply Theorem 4.3 in order to find an extension where
![]() $\lambda _i$
and
$\lambda _i$
and
![]() $\mu _j$
are eigenvalues. This means that we can express the lift of
$\mu _j$
are eigenvalues. This means that we can express the lift of
![]() to
to
![]() $\widetilde {X}$
as a product of a tensor product of G-eigenfunctions (whose eigenvalues are
$\widetilde {X}$
as a product of a tensor product of G-eigenfunctions (whose eigenvalues are
![]() $\lambda _i$
and
$\lambda _i$
and
![]() $\mu _j$
) and a
$\mu _j$
) and a
![]() $\varphi (G)\times \psi (G)$
-invariant function, which completes the proof in this special case. Below, we generalise the above to arbitrary
$\varphi (G)\times \psi (G)$
-invariant function, which completes the proof in this special case. Below, we generalise the above to arbitrary
![]() $c_{i,j}$
.
$c_{i,j}$
.
Let
![]() $C_{i,j} = \{(x,y)\in X\times X : c_{i,j}(x,y)\not = 0\}$
. Then,
$C_{i,j} = \{(x,y)\in X\times X : c_{i,j}(x,y)\not = 0\}$
. Then,
![]() for every
for every
![]() $(x,y)\in C_{i,j}$
and all
$(x,y)\in C_{i,j}$
and all
![]() $g\in G$
. Hence,
$g\in G$
. Hence,
![]() $g\mapsto \lambda _i(\varphi (g),x)$
and
$g\mapsto \lambda _i(\varphi (g),x)$
and
![]() $g\mapsto \mu _j(\psi (g),y)$
are equal to the same character
$g\mapsto \mu _j(\psi (g),y)$
are equal to the same character
![]() $\chi \in \widehat G$
which factors through
$\chi \in \widehat G$
which factors through
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
simultaneously for all
$\psi $
simultaneously for all
![]() $(x,y)\in C_{i,j}$
. Now, for every
$(x,y)\in C_{i,j}$
. Now, for every
![]() $\chi \in \widehat G$
, we let
$\chi \in \widehat G$
, we let
and set
 $$ \begin{align*} C:=\{\chi\in\widehat G : J_{\chi}\not = \emptyset\} \text{ and } J:=\bigcup_{\chi\in C} J_{\chi}. \end{align*} $$
$$ \begin{align*} C:=\{\chi\in\widehat G : J_{\chi}\not = \emptyset\} \text{ and } J:=\bigcup_{\chi\in C} J_{\chi}. \end{align*} $$
Our first observation is that
 $$ \begin{align} f(x,y) = \sum_{(i,j)\in J} c_{i,j}(x,y) \zeta_i(x) \xi_j(y). \end{align} $$
$$ \begin{align} f(x,y) = \sum_{(i,j)\in J} c_{i,j}(x,y) \zeta_i(x) \xi_j(y). \end{align} $$
Indeed, if
![]() $(i,j)\not \in J$
, then for every
$(i,j)\not \in J$
, then for every
![]() $\chi $
,
$\chi $
,
![]() $(i,j)\not \in J_{\chi }$
, but then from the computation above
$(i,j)\not \in J_{\chi }$
, but then from the computation above
![]() $\mu (C_{i,j})=0$
and
$\mu (C_{i,j})=0$
and
![]() $c_{i,j}=0$
for
$c_{i,j}=0$
for
![]() $(\mu \times \mu )$
-a.e.
$(\mu \times \mu )$
-a.e.
![]() $(x,y)\in X\times X$
.
$(x,y)\in X\times X$
.
Claim. The set C is at most countable.
Proof of the claim
We use the fact that in a probability space there can be at most countably many disjoint sets of positive measure. Assume by contradiction that C is uncountable. Since there are only countably many
![]() $(i,j)\in \mathbb {N}^2$
, we deduce that there exists some
$(i,j)\in \mathbb {N}^2$
, we deduce that there exists some
![]() $(i_0,j_0)$
which belongs to
$(i_0,j_0)$
which belongs to
![]() $J_{\chi }$
for all
$J_{\chi }$
for all
![]() $\chi $
in an uncountable subset of
$\chi $
in an uncountable subset of
![]() $\widehat G$
. But since the sets
$\widehat G$
. But since the sets
are disjoint for different
![]() $\chi $
’s and of positive measure, we obtain a contradiction. This proves the claim.
$\chi $
’s and of positive measure, we obtain a contradiction. This proves the claim.
Now, we return to the proof of the lemma. Since C is at most countable, we can apply Theorem 4.3. We see that there exists an ergodic extension
![]() $\pi :\widetilde {X}\rightarrow X$
, such that for every
$\pi :\widetilde {X}\rightarrow X$
, such that for every
![]() $\chi \in C$
, there exist G-eigenvalues
$\chi \in C$
, there exist G-eigenvalues
![]() $\chi ^{\varphi },\chi ^{\psi }:G\rightarrow S^1$
with
$\chi ^{\varphi },\chi ^{\psi }:G\rightarrow S^1$
with
![]() $\chi ^{\varphi }(\varphi (g))=\chi (g)$
and
$\chi ^{\varphi }(\varphi (g))=\chi (g)$
and
![]() $\chi ^{\psi }(\psi (g))=\chi (g)$
. Let
$\chi ^{\psi }(\psi (g))=\chi (g)$
. Let
![]() $m_{\chi }^{\varphi },m_{\chi }^{\psi } :\widetilde {X}\rightarrow S^1$
be the corresponding eigenfunctions. Now, fix some
$m_{\chi }^{\varphi },m_{\chi }^{\psi } :\widetilde {X}\rightarrow S^1$
be the corresponding eigenfunctions. Now, fix some
![]() $(i,j)\in J$
, and let
$(i,j)\in J$
, and let
![]() $\chi \in C$
be, such that
$\chi \in C$
be, such that
![]() $\lambda _i(\varphi (g),x)=\mu _j(\psi (g),y)=\chi (g)$
whenever
$\lambda _i(\varphi (g),x)=\mu _j(\psi (g),y)=\chi (g)$
whenever
![]() $c_{i,j}(x,y)\not =0$
. We deduce that
$c_{i,j}(x,y)\not =0$
. We deduce that
is a
![]() $\varphi (G)\times \psi (G)$
-invariant function. Since
$\varphi (G)\times \psi (G)$
-invariant function. Since
![]() $c_{i,j}$
is also
$c_{i,j}$
is also
![]() $\varphi (G)\times \psi (G)$
-invariant, we deduce by equation (15) that
$\varphi (G)\times \psi (G)$
-invariant, we deduce by equation (15) that
![]() $f\circ \pi $
is a linear combination of products of eigenfunctions
$f\circ \pi $
is a linear combination of products of eigenfunctions
and some
![]() $\varphi (G)\times \psi (G)$
-invariant functions. Equivalently, the lift of f to
$\varphi (G)\times \psi (G)$
-invariant functions. Equivalently, the lift of f to
![]() $\widetilde {X}\times \widetilde {X}$
is measurable with respect to the
$\widetilde {X}\times \widetilde {X}$
is measurable with respect to the
![]() $\sigma $
-algebra
$\sigma $
-algebra
as required.
The following result of Tao and Ziegler [Reference Tao and Ziegler29] plays in important role in our work.
Theorem 4.8 ([Reference Tao and Ziegler29], Theorem 1.19)
Let G be a countable discrete abelian group, and let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g \in G})$
be a G-system. Let
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g \in G})$
be a G-system. Let
![]() $H_1,H_2$
be two subgroups of G, and denote by
$H_1,H_2$
be two subgroups of G, and denote by
![]() $H_1+H_2$
the subgroup of G generated by
$H_1+H_2$
the subgroup of G generated by
![]() $H_1$
and
$H_1$
and
![]() $H_2$
. Then, for every
$H_2$
. Then, for every
![]() $d_1,d_2\in \mathbb {N}$
, one has
$d_1,d_2\in \mathbb {N}$
, one has
In particular, by setting
![]() $d_1=d_2=1$
and using Lemma 3.6, we deduce:
$d_1=d_2=1$
and using Lemma 3.6, we deduce:
Lemma 4.9. Let G be a countable discrete abelian group and
![]() $(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system, and let
$(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system, and let
![]() $\varphi ,\psi :G\rightarrow G$
be homomorphisms, such that
$\varphi ,\psi :G\rightarrow G$
be homomorphisms, such that
![]() $(\psi - \varphi )(G)$
has finite index in G. Then,
$(\psi - \varphi )(G)$
has finite index in G. Then,
![]() $\mathcal {Z}_{\varphi ,\psi }(X)\preceq \mathcal {Z}_G^2(X)$
.
$\mathcal {Z}_{\varphi ,\psi }(X)\preceq \mathcal {Z}_G^2(X)$
.
We combine this with the results in Section 3 to deduce the following version of Theorem 3.5.
Theorem 4.10. Let G be a countable discrete abelian group and
![]() $\textbf {X} = (X, \mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Suppose that
$\textbf {X} = (X, \mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Suppose that
![]() $\varphi , \psi : G \rightarrow G$
are arbitrary homomorphisms, such that
$\varphi , \psi : G \rightarrow G$
are arbitrary homomorphisms, such that
![]() $(\psi -\varphi )(G)$
has finite index in G. There exists an ergodic extension
$(\psi -\varphi )(G)$
has finite index in G. There exists an ergodic extension
![]() $\pi :(\widetilde {X},\widetilde {\mu })\rightarrow (X,\mu )$
, such that for any
$\pi :(\widetilde {X},\widetilde {\mu })\rightarrow (X,\mu )$
, such that for any
![]() $f_0,f_1,f_2\in L^{\infty }(\mu )$
$f_0,f_1,f_2\in L^{\infty }(\mu )$
 $$ \begin{align*} &\text{UC -}\lim_{g\in G} \int_{X} f_0\cdot T_{\varphi(g)} f_1\cdot T_{\psi(g)} f_2~ d\mu =\\ &\text{UC -}\lim_{g\in G} \int_{\widetilde{X}} \widetilde{f}_0\cdot T_{\varphi(g)} E(\widetilde{f}_1|\mathcal {Z}_{G}^2(\widetilde{X})\lor \mathcal {I}_{\varphi}(\widetilde{X})) \cdot T_{\psi(g)} E(\widetilde{f}_2|\mathcal {Z}_{G}^2(\widetilde{X})\lor \mathcal {I}_{\psi}(\widetilde{X}))~ d\widetilde{\mu} \end{align*} $$
$$ \begin{align*} &\text{UC -}\lim_{g\in G} \int_{X} f_0\cdot T_{\varphi(g)} f_1\cdot T_{\psi(g)} f_2~ d\mu =\\ &\text{UC -}\lim_{g\in G} \int_{\widetilde{X}} \widetilde{f}_0\cdot T_{\varphi(g)} E(\widetilde{f}_1|\mathcal {Z}_{G}^2(\widetilde{X})\lor \mathcal {I}_{\varphi}(\widetilde{X})) \cdot T_{\psi(g)} E(\widetilde{f}_2|\mathcal {Z}_{G}^2(\widetilde{X})\lor \mathcal {I}_{\psi}(\widetilde{X}))~ d\widetilde{\mu} \end{align*} $$
in
![]() $L^2(\widetilde {X})$
, where
$L^2(\widetilde {X})$
, where
![]() $\widetilde {f}_i:=f_i\circ \pi $
denotes the lift of
$\widetilde {f}_i:=f_i\circ \pi $
denotes the lift of
![]() $f_i$
to the extension
$f_i$
to the extension
![]() $\widetilde {X}$
.
$\widetilde {X}$
.
Recall that the factors
![]() $\mathcal {Z}_{\varphi }(X)$
and
$\mathcal {Z}_{\varphi }(X)$
and
![]() $\mathcal {Z}_{\psi }(X)$
are relatively independent over
$\mathcal {Z}_{\psi }(X)$
are relatively independent over
![]() $\mathcal {Z}_{\varphi ,\psi }(X)$
. To put this fact to use, we need to introduce a construction known as a fibre product:
$\mathcal {Z}_{\varphi ,\psi }(X)$
. To put this fact to use, we need to introduce a construction known as a fibre product:
Definition 4.11 (The fibre product over a factor.)
For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $\textbf {Y}_i=(Y_i, \mathcal {Y}_i,\mu _i,(S^{(i)}_g)_{g\in G})$
be G-systems. Suppose that
$\textbf {Y}_i=(Y_i, \mathcal {Y}_i,\mu _i,(S^{(i)}_g)_{g\in G})$
be G-systems. Suppose that
![]() $\textbf {Y}=(Y,\mathcal {Y},\nu ,(S_g)_{g\in G})$
is a common factor, and let
$\textbf {Y}=(Y,\mathcal {Y},\nu ,(S_g)_{g\in G})$
is a common factor, and let
![]() $\pi _i:Y_i\rightarrow Y$
,
$\pi _i:Y_i\rightarrow Y$
,
![]() $i=1,2$
denote the factor maps. The fibre product of
$i=1,2$
denote the factor maps. The fibre product of
![]() $\mathit{\boldsymbol Y}_1$
and
$\mathit{\boldsymbol Y}_1$
and
![]() $\mathit{\boldsymbol Y}_2$
over
$\mathit{\boldsymbol Y}_2$
over
![]() $\mathit{\boldsymbol Y}$
is the system
$\mathit{\boldsymbol Y}$
is the system
![]() , where
, where
and
where
is the disintegration of the measure
![]() $\mu _i$
over Y for
$\mu _i$
over Y for
![]() $i=1,2$
.
$i=1,2$
.
We will use the following result from [Reference Zimmer31]:
Theorem 4.12. Let G be a countable discrete abelian group, and let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system. Let
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system. Let
![]() $\textbf {Y}_1=(Y_1, \mathcal {A}_1,\mu _1,(T^{(1)}_g)_{g\in G})$
and
$\textbf {Y}_1=(Y_1, \mathcal {A}_1,\mu _1,(T^{(1)}_g)_{g\in G})$
and
![]() $\textbf {Y}_2=(Y_2,\mathcal {A}_2,\mu _2,(T^{(2)}_g)_{g\in G})$
be two factors of X with factor maps
$\textbf {Y}_2=(Y_2,\mathcal {A}_2,\mu _2,(T^{(2)}_g)_{g\in G})$
be two factors of X with factor maps
![]() $\pi _i:X\rightarrow Y_i$
for
$\pi _i:X\rightarrow Y_i$
for
![]() $i=1,2$
, and let
$i=1,2$
, and let
![]() $\textbf {Y}=(Y,\nu )$
be their meet. Then, the
$\textbf {Y}=(Y,\nu )$
be their meet. Then, the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {A}_1\lor \mathcal {A}_2$
corresponds to the fibre product
$\mathcal {A}_1\lor \mathcal {A}_2$
corresponds to the fibre product
![]() $\textbf {Y}_1\times _{\textbf {Y}} \textbf {Y}_2$
.
$\textbf {Y}_1\times _{\textbf {Y}} \textbf {Y}_2$
.
Remark 4.13. In particular, Theorem 4.12 implies that
![]() $\textbf {Y}_1\times _{\textbf {Y}}\textbf {Y}_2$
is a factor of
$\textbf {Y}_1\times _{\textbf {Y}}\textbf {Y}_2$
is a factor of
![]() $\textbf {X}$
. We note that Zimmer also proved the other direction, namely, that two factors
$\textbf {X}$
. We note that Zimmer also proved the other direction, namely, that two factors
![]() $\mathcal {Y}_1$
and
$\mathcal {Y}_1$
and
![]() $\mathcal {Y}_2$
are relatively independent over a third factor
$\mathcal {Y}_2$
are relatively independent over a third factor
![]() $\mathcal {Y}$
if and only if the fibre product
$\mathcal {Y}$
if and only if the fibre product
![]() $\textbf {Y}_1 \times _{\textbf {Y}} \textbf {Y}_2$
is a factor of
$\textbf {Y}_1 \times _{\textbf {Y}} \textbf {Y}_2$
is a factor of
![]() $\textbf {X}$
(see [Reference Zimmer31, Proposition 1.5]).
$\textbf {X}$
(see [Reference Zimmer31, Proposition 1.5]).
We also need the following result:
Theorem 4.14 (cf. [Reference Host and Kra23], Proposition 4.6)
Let
![]() $\pi :(Y,\mathcal {Y},\nu ,(S_g)_{g\in G})\rightarrow (X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a factor map between G-systems, and let
$\pi :(Y,\mathcal {Y},\nu ,(S_g)_{g\in G})\rightarrow (X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a factor map between G-systems, and let
![]() $k\geq 1$
. Then,
$k\geq 1$
. Then,
![]() $\pi ^{-1}(\mathcal {Z}^k(X)) = \mathcal {Z}^k(Y)\land \pi ^{-1}(\mathcal {X})$
.
$\pi ^{-1}(\mathcal {Z}^k(X)) = \mathcal {Z}^k(Y)\land \pi ^{-1}(\mathcal {X})$
.
Host and Kra [Reference Host and Kra23] proved Theorem 4.14 for
![]() $\mathbb {Z}$
-actions, but the argument extends easily to arbitrary countable discrete abelian groups.
$\mathbb {Z}$
-actions, but the argument extends easily to arbitrary countable discrete abelian groups.
We now have all the requisite tools to prove Theorem 4.10.
Proof of Theorem 4.10
By the previous result, we see that if
![]() $f_0,f_1$
or
$f_0,f_1$
or
![]() $f_2$
are orthogonal to functions measurable with respect to the
$f_2$
are orthogonal to functions measurable with respect to the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {Z}_{\varphi }(X) \lor \mathcal {Z}_{\psi }(X)$
, then the averages above are zero. Therefore, by Theorem 4.12, the factor
$\mathcal {Z}_{\varphi }(X) \lor \mathcal {Z}_{\psi }(X)$
, then the averages above are zero. Therefore, by Theorem 4.12, the factor
![]() $\mathbf {Z}_{\varphi }(X)\times _{\mathbf {Z}_{\varphi ,\psi }(X)}\mathbf {Z}_{\psi }(X)$
is a characteristic factor. We may therefore assume without loss of generality that
$\mathbf {Z}_{\varphi }(X)\times _{\mathbf {Z}_{\varphi ,\psi }(X)}\mathbf {Z}_{\psi }(X)$
is a characteristic factor. We may therefore assume without loss of generality that
![]() $\textbf {X}=\mathbf {Z}_{\varphi }(X)\times _{\mathbf {Z}_{\varphi ,\psi }(X)}\mathbf {Z}_{\psi }(X)$
. For the sake of simplicity of notations, we write
$\textbf {X}=\mathbf {Z}_{\varphi }(X)\times _{\mathbf {Z}_{\varphi ,\psi }(X)}\mathbf {Z}_{\psi }(X)$
. For the sake of simplicity of notations, we write
![]() $\mu _{\varphi ,\psi }$
for the measure
$\mu _{\varphi ,\psi }$
for the measure
![]() $\mu _{Z_{\varphi }(X)}\times _{Z_{\varphi ,\psi }(X)} \mu _{Z_{\psi }(X)}$
on
$\mu _{Z_{\varphi }(X)}\times _{Z_{\varphi ,\psi }(X)} \mu _{Z_{\psi }(X)}$
on
![]() $Z_{\varphi (X)}\times _{Z_{\varphi ,\psi }(X)}Z_{\psi }(X)$
. By linearity, it suffices to prove the theorem in the case where
$Z_{\varphi (X)}\times _{Z_{\varphi ,\psi }(X)}Z_{\psi }(X)$
. By linearity, it suffices to prove the theorem in the case where
and
for some
![]() $f_1^{\varphi },f_2^{\varphi }:Z_{\varphi }(X)\rightarrow \mathbb {C}$
and
$f_1^{\varphi },f_2^{\varphi }:Z_{\varphi }(X)\rightarrow \mathbb {C}$
and
![]() $f_1^{\psi },f_2^{\psi } : Z_{\psi }(X)\rightarrow \mathbb {C}$
. Then,
$f_1^{\psi },f_2^{\psi } : Z_{\psi }(X)\rightarrow \mathbb {C}$
. Then,

By Proposition 3.5, (16) is equal to
 $$ \begin{align} \begin{aligned} \text{UC -}\lim_{g\in G} \underset{Z_{\varphi}(X)\times Z_{\psi}(X)}{\int} f_0&(x,y) \cdot T_{\varphi(g)}\left(f_1^{\varphi}\cdot E(f_1^{\psi}|\mathcal {Z}_{\varphi,\psi}(X))\right)(x) \\ & T_{\psi(g)} \left(E(f_2^{\varphi}|\mathcal {Z}_{\varphi,\psi}(X))\cdot f_2^{\psi}\right)(y)~d\mu_{\varphi,\psi}(x,y). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \text{UC -}\lim_{g\in G} \underset{Z_{\varphi}(X)\times Z_{\psi}(X)}{\int} f_0&(x,y) \cdot T_{\varphi(g)}\left(f_1^{\varphi}\cdot E(f_1^{\psi}|\mathcal {Z}_{\varphi,\psi}(X))\right)(x) \\ & T_{\psi(g)} \left(E(f_2^{\varphi}|\mathcal {Z}_{\varphi,\psi}(X))\cdot f_2^{\psi}\right)(y)~d\mu_{\varphi,\psi}(x,y). \end{aligned} \end{align} $$
Note that we used the fact that
![]() $E(h|\mathcal {Z}_{\varphi ,\psi }(X))(x)=E(h|\mathcal {Z}_{\varphi ,\psi }(X))(y)$
for
$E(h|\mathcal {Z}_{\varphi ,\psi }(X))(x)=E(h|\mathcal {Z}_{\varphi ,\psi }(X))(y)$
for
![]() $\mu _{\varphi ,\psi }$
a.e.
$\mu _{\varphi ,\psi }$
a.e.
![]() $x,y$
. By the mean ergodic theorem, applied to the transformation
$x,y$
. By the mean ergodic theorem, applied to the transformation
![]() $T_{\varphi }\times T_{\psi }$
, the limit in (17) converges to
$T_{\varphi }\times T_{\psi }$
, the limit in (17) converges to

By Lemma 4.7, we can find an ergodic extension
![]() $\pi :\widetilde {X}\rightarrow X$
(independent of
$\pi :\widetilde {X}\rightarrow X$
(independent of
![]() $f_0,f_1,f_2$
), such that
$f_0,f_1,f_2$
), such that
![]() $\pi ^{-1}\left(\mathcal {I}_{\varphi \times \psi }(X)\right)$
is a sub-
$\pi ^{-1}\left(\mathcal {I}_{\varphi \times \psi }(X)\right)$
is a sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
. Now, by applying the same argument as above with
![]() $\widetilde {f}_0,\widetilde {f}_1$
and
$\widetilde {f}_0,\widetilde {f}_1$
and
![]() $\widetilde {f}_2$
instead of
$\widetilde {f}_2$
instead of
![]() $f_0,f_1$
and
$f_0,f_1$
and
![]() $f_2$
, and using Theorem 4.14 in order to replace
$f_2$
, and using Theorem 4.14 in order to replace
![]() $\pi ^{-1}(\mathcal {Z}_{\varphi ,\psi }(X))$
with
$\pi ^{-1}(\mathcal {Z}_{\varphi ,\psi }(X))$
with
![]() $\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})$
, we deduce that:
$\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})$
, we deduce that:

where
![]() $\widetilde {\mu }_{\varphi ,\psi }$
is the lift of
$\widetilde {\mu }_{\varphi ,\psi }$
is the lift of
![]() $\mu _{\varphi ,\psi }$
to
$\mu _{\varphi ,\psi }$
to
![]() $\widetilde {X}$
.
$\widetilde {X}$
.
We return to the proof of the theorem. By linearity, it is enough to show that if
![]() $E(\widetilde {f}_1|\mathcal {Z}_{G}^2(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X}))=0$
or
$E(\widetilde {f}_1|\mathcal {Z}_{G}^2(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X}))=0$
or
![]() $E(\widetilde {f}_2|\mathcal {Z}_{G}^2(\widetilde {X})\lor \mathcal {I}_{\psi }(\widetilde {X}))=0$
, then (18) is zero. By symmetry and Lemma 4.9, we may assume without loss of generality that
$E(\widetilde {f}_2|\mathcal {Z}_{G}^2(\widetilde {X})\lor \mathcal {I}_{\psi }(\widetilde {X}))=0$
, then (18) is zero. By symmetry and Lemma 4.9, we may assume without loss of generality that
![]() $E(\widetilde {f}_1|\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X}))=0$
. Since
$E(\widetilde {f}_1|\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X}))=0$
. Since
![]() $\mathcal {Z}_{\varphi }(\widetilde {X}),\mathcal {Z}_{\psi }(\widetilde {X})$
are relatively independent over
$\mathcal {Z}_{\varphi }(\widetilde {X}),\mathcal {Z}_{\psi }(\widetilde {X})$
are relatively independent over
![]() $\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})$
, they are also relatively independent over the larger
$\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})$
, they are also relatively independent over the larger
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})$
. We deduce, by Proposition 2.7, that
$\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})$
. We deduce, by Proposition 2.7, that
Claim.
![]() $E(\widetilde {f}_1^{\psi }|\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})) =E(\widetilde {f}_1^{\psi }|\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})) $
.
$E(\widetilde {f}_1^{\psi }|\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})) =E(\widetilde {f}_1^{\psi }|\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})) $
.
Proof of the claim
![]() $\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})$
is a factor of
$\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})$
is a factor of
![]() $\mathcal {Z}_{\varphi }(\widetilde {X})$
. By Theorem 4.14,
$\mathcal {Z}_{\varphi }(\widetilde {X})$
. By Theorem 4.14,
![]() $\widetilde {f}_1^{\psi }$
is measurable with respect to
$\widetilde {f}_1^{\psi }$
is measurable with respect to
![]() $\mathcal {Z}_{\psi }(\widetilde {X})$
, and this and
$\mathcal {Z}_{\psi }(\widetilde {X})$
, and this and
![]() $\mathcal {Z}_{\varphi }(\widetilde {X})$
are relatively independent over
$\mathcal {Z}_{\varphi }(\widetilde {X})$
are relatively independent over
![]() $\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})$
, so the claim follows.
$\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})$
, so the claim follows.
Equation (19) and the claim imply that
is orthogonal to all functions measurable with respect to
![]() $\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})$
, and so it is also orthogonal to those measurable with respect to
$\mathcal {Z}_{\varphi ,\psi }(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})$
, and so it is also orthogonal to those measurable with respect to
![]() $\mathcal {Z}(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})$
. Since
$\mathcal {Z}(\widetilde {X})\lor \mathcal {I}_{\varphi }(\widetilde {X})$
. Since
![]() $\pi ^{-1}(\mathcal {I}_{\varphi \times \psi }(X))$
is a sub-
$\pi ^{-1}(\mathcal {I}_{\varphi \times \psi }(X))$
is a sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() , this implies that (18) is equal to zero as required.
, this implies that (18) is equal to zero as required.
As a corollary, we also have the following stronger counterpart of Proposition 3.8.
Corollary 4.15. In the settings of Theorem 4.10. Let
![]() $\eta :Z(\widetilde {X})\rightarrow \mathbb {C}$
be a continuous function and
$\eta :Z(\widetilde {X})\rightarrow \mathbb {C}$
be a continuous function and
![]() $f_0,f_1,f_2\in L^{\infty }(X)$
. Let
$f_0,f_1,f_2\in L^{\infty }(X)$
. Let
![]() $\alpha _g$
denote the rotation of
$\alpha _g$
denote the rotation of
![]() $g\in G$
on
$g\in G$
on
![]() $Z(\widetilde {X})$
. If
$Z(\widetilde {X})$
. If
![]() $a, b \in {\mathbb Z}$
are coprime, then
$a, b \in {\mathbb Z}$
are coprime, then
where
![]() $\widetilde {f}_i = f_i \circ \pi $
is the lift of
$\widetilde {f}_i = f_i \circ \pi $
is the lift of
![]() $f_i$
to
$f_i$
to
![]() $\widetilde {X}$
for
$\widetilde {X}$
for
![]() $i=0,1,2$
.
$i=0,1,2$
.
Proof. Since
![]() $\eta $
is measurable with respect to
$\eta $
is measurable with respect to
![]() $\mathcal {Z}(\widetilde {X})$
, it is a linear combination of characters. Therefore, it is enough to prove the equality in the special case where
$\mathcal {Z}(\widetilde {X})$
, it is a linear combination of characters. Therefore, it is enough to prove the equality in the special case where
![]() $\eta $
itself is a character. Then, since a and b are coprime, we can find
$\eta $
itself is a character. Then, since a and b are coprime, we can find
![]() $t,s\in \mathbb {Z}$
, such that
$t,s\in \mathbb {Z}$
, such that
![]() $ta+sb=1$
. Set
$ta+sb=1$
. Set
![]() $h_0 =\widetilde {f}_0\cdot \eta ^{-(t+s)}$
,
$h_0 =\widetilde {f}_0\cdot \eta ^{-(t+s)}$
,
![]() $h_1 = \widetilde {f}_1\cdot \eta ^s$
and
$h_1 = \widetilde {f}_1\cdot \eta ^s$
and
![]() $h_2=\widetilde {f}_2\cdot \eta ^t$
. Arguing as in Theorem 4.10, we have
$h_2=\widetilde {f}_2\cdot \eta ^t$
. Arguing as in Theorem 4.10, we have
 $$ \begin{align} &\text{UC -}\lim_{g\in G} \int_{\widetilde{X}} h_0\cdot T_{ag} h_1\cdot T_{bg} h_2 ~d\widetilde{\mu} =\nonumber\\ &\text{UC -}\lim_{g\in G} \int_{\widetilde{X}} h_0\cdot T_{ag} E(h_1|\mathcal{Z}_G^2(\widetilde{X}) \lor \mathcal {I}_a(\widetilde{X})) \cdot T_{bg} E(h_2|\mathcal{Z}_G^2(\widetilde{X}) \lor \mathcal {I}_b(\widetilde{X}))~ d\widetilde{\mu}. \end{align} $$
$$ \begin{align} &\text{UC -}\lim_{g\in G} \int_{\widetilde{X}} h_0\cdot T_{ag} h_1\cdot T_{bg} h_2 ~d\widetilde{\mu} =\nonumber\\ &\text{UC -}\lim_{g\in G} \int_{\widetilde{X}} h_0\cdot T_{ag} E(h_1|\mathcal{Z}_G^2(\widetilde{X}) \lor \mathcal {I}_a(\widetilde{X})) \cdot T_{bg} E(h_2|\mathcal{Z}_G^2(\widetilde{X}) \lor \mathcal {I}_b(\widetilde{X}))~ d\widetilde{\mu}. \end{align} $$
Now, since
![]() $\eta $
is measurable with respect to
$\eta $
is measurable with respect to
![]() $\mathcal {Z}(\widetilde {X})$
, it is also measurable with respect to
$\mathcal {Z}(\widetilde {X})$
, it is also measurable with respect to
![]() $\mathcal {Z}_G^2(\widetilde {X}) \lor \mathcal {I}_a(\widetilde {X})$
and
$\mathcal {Z}_G^2(\widetilde {X}) \lor \mathcal {I}_a(\widetilde {X})$
and
![]() $\mathcal {Z}_G^2(\widetilde {X}) \lor \mathcal {I}_b(\widetilde {X})$
, so the claim follows by rewriting
$\mathcal {Z}_G^2(\widetilde {X}) \lor \mathcal {I}_b(\widetilde {X})$
, so the claim follows by rewriting
![]() $h_i$
in terms of
$h_i$
in terms of
![]() $\eta $
and
$\eta $
and
![]() $\widetilde {f}_i$
on both sides of equation (20).
$\widetilde {f}_i$
on both sides of equation (20).
5 A limit formula for
 $\{ag, bg\}$
$\{ag, bg\}$
Let G be a countable discrete abelian group and
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. In this section, we restrict ourselves to the homomorphisms
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. In this section, we restrict ourselves to the homomorphisms
![]() $\varphi (g)=ag,\psi (g)=bg$
, where
$\varphi (g)=ag,\psi (g)=bg$
, where
![]() $a,b\in \mathbb {Z}$
. By Theorem 4.10, we see that it is enough to analyse the ergodic average
$a,b\in \mathbb {Z}$
. By Theorem 4.10, we see that it is enough to analyse the ergodic average
in the case where X is a Conze–Lesigne system (i.e.
![]() $X=Z^2(X)$
).
$X=Z^2(X)$
).
Under certain assumptions on a and b, two different (but related) formulas were obtained previously in [Reference Ackelsberg, Bergelson and Best2] and in [Reference Shalom27] (see Theorems 5.1 and 5.2 below). Neither of the previously obtained formulas is sufficient for our purposes, so we prove a new one in this section.
5.1 Previous limit formulas
Assuming all of the subgroups
![]() $aG$
,
$aG$
,
![]() $bG$
,
$bG$
,
![]() $(a+b)G$
and
$(a+b)G$
and
![]() $(b-a)G$
have finite index in G, a limit formula was obtained in [Reference Ackelsberg, Bergelson and Best2] for the multiple ergodic averages in (21) by analysing a Mackey group associated to the abelian extension corresponding to the Conze–Lesigne factor (the relevant terminology is defined in the next subsection). For compact groups Z and H, let
$(b-a)G$
have finite index in G, a limit formula was obtained in [Reference Ackelsberg, Bergelson and Best2] for the multiple ergodic averages in (21) by analysing a Mackey group associated to the abelian extension corresponding to the Conze–Lesigne factor (the relevant terminology is defined in the next subsection). For compact groups Z and H, let
![]() $\mathcal {M}(Z,H)$
denote the space of measurable functions
$\mathcal {M}(Z,H)$
denote the space of measurable functions
![]() $f : Z \to H$
equipped with the topology of convergence in measure (with respect to the Haar probability measure).
$f : Z \to H$
equipped with the topology of convergence in measure (with respect to the Haar probability measure).
Theorem 5.1 ([Reference Ackelsberg, Bergelson and Best2], Theorem 7.1)
Let G be a countable discrete abelian group. Let
![]() $a,b\in \mathbb {Z}$
, such that
$a,b\in \mathbb {Z}$
, such that
![]() $aG$
,
$aG$
,
![]() $bG$
,
$bG$
,
![]() $(a+b)G$
and
$(a+b)G$
and
![]() $(b-a)G$
have finite index in G. Let
$(b-a)G$
have finite index in G. Let
![]() $k_1' = -ab(a+b)$
,
$k_1' = -ab(a+b)$
,
![]() $k_2'=ab(a+b)$
and
$k_2'=ab(a+b)$
and
![]() $k_3' = -ab(b-a)$
. Set
$k_3' = -ab(b-a)$
. Set
![]() $D=\text {gcd}(k_1',k_2',k_3')$
and
$D=\text {gcd}(k_1',k_2',k_3')$
and
![]() $k_i=\frac {k_i'}{D}$
for
$k_i=\frac {k_i'}{D}$
for
![]() $i=1,2,3$
. Let
$i=1,2,3$
. Let
![]() $c_1,c_2,c_3\in \mathbb {Z}$
so that
$c_1,c_2,c_3\in \mathbb {Z}$
so that
![]() $\sum _{i=1}^3 k_ic_i=1$
. Let
$\sum _{i=1}^3 k_ic_i=1$
. Let
![]() $\textbf {X} = \textbf {Z}\times _{\sigma } H$
be as in Theorem 2.5(iii). There is a function
$\textbf {X} = \textbf {Z}\times _{\sigma } H$
be as in Theorem 2.5(iii). There is a function
![]() $\psi :Z\times Z\rightarrow H$
, such that
$\psi :Z\times Z\rightarrow H$
, such that
![]() $\psi (0,z)=0$
for every
$\psi (0,z)=0$
for every
![]() $z\in Z$
and
$z\in Z$
and
![]() $t\mapsto \psi (t,\cdot )$
is a continuous map from Z to
$t\mapsto \psi (t,\cdot )$
is a continuous map from Z to
![]() $\mathcal {M}(Z,H)$
, and for every
$\mathcal {M}(Z,H)$
, and for every
![]() $f_1,f_2,f_3\in L^{\infty }(\mu )$
,
$f_1,f_2,f_3\in L^{\infty }(\mu )$
,
 $$ \begin{align*} \text{UC -}\lim_{g\in G} f_1(T_{ag}x)f_2(T_{bg}x)f_3(T_{(a+b)g}x) = \int_{Z\times H^2} \prod_{i=1}^3 f_i(z+a_it,h+d_iu+a_i^2v+c_i\psi(t,z)~ du~dv~dt, \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{g\in G} f_1(T_{ag}x)f_2(T_{bg}x)f_3(T_{(a+b)g}x) = \int_{Z\times H^2} \prod_{i=1}^3 f_i(z+a_it,h+d_iu+a_i^2v+c_i\psi(t,z)~ du~dv~dt, \end{align*} $$
in
![]() $L^2(\mu )$
, where
$L^2(\mu )$
, where
![]() $x=(z,h)\in Z\times H$
, and
$x=(z,h)\in Z\times H$
, and
![]() $a_1=a,a_2=b,a_3=a+b$
.
$a_1=a,a_2=b,a_3=a+b$
.
Assuming that
![]() $(b-a)$
is even, the last author proved the following result.
$(b-a)$
is even, the last author proved the following result.
Theorem 5.2 ([Reference Shalom27], Corollary 6.2)
Let G be a countable discrete abelian group. Let
![]() $a,b\in \mathbb {Z}$
be, such that
$a,b\in \mathbb {Z}$
be, such that
![]() $(b-a)$
is even and
$(b-a)$
is even and
![]() $(b-a)G$
has finite index in G. Let
$(b-a)G$
has finite index in G. Let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system, such that
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system, such that
![]() $\textbf {X}=\mathbf {Z}^2(X)$
. Then, there exists an ergodic extension
$\textbf {X}=\mathbf {Z}^2(X)$
. Then, there exists an ergodic extension
![]() $\pi :Y\rightarrow X$
which is isomorphic to a
$\pi :Y\rightarrow X$
which is isomorphic to a
![]() $2$
-step nilpotent coset systemFootnote 3 and for every
$2$
-step nilpotent coset systemFootnote 3 and for every
![]() $f_1,f_2,f_3\in L^{\infty }(X)$
,
$f_1,f_2,f_3\in L^{\infty }(X)$
,
 $$ \begin{align*}&\text{UC -}\lim_{g\in G} \widetilde{f}_1(T_{ag}y\Gamma) f_2(T_{bg}y\Gamma) f_3(T_{(a+b)g}y\Gamma) =\\& \int_{\mathcal {G}/\Gamma} \int_{\mathcal {G}_2} \widetilde{f}_1(yy_1^ay_2^{\binom{a}{2}}) \widetilde{f}_2(yy_1^by_2^{\binom{b}{2}}\Gamma)\widetilde{f}_3(yy_1^{a+b}y_2^{\binom{a+b}{2}}\Gamma)~ d\mu_{\mathcal{G}_2}(y_2)~d\mu_{\mathcal{G}/\Gamma}(y\Gamma). \end{align*} $$
$$ \begin{align*}&\text{UC -}\lim_{g\in G} \widetilde{f}_1(T_{ag}y\Gamma) f_2(T_{bg}y\Gamma) f_3(T_{(a+b)g}y\Gamma) =\\& \int_{\mathcal {G}/\Gamma} \int_{\mathcal {G}_2} \widetilde{f}_1(yy_1^ay_2^{\binom{a}{2}}) \widetilde{f}_2(yy_1^by_2^{\binom{b}{2}}\Gamma)\widetilde{f}_3(yy_1^{a+b}y_2^{\binom{a+b}{2}}\Gamma)~ d\mu_{\mathcal{G}_2}(y_2)~d\mu_{\mathcal{G}/\Gamma}(y\Gamma). \end{align*} $$
The above formula fails if
![]() $b-a$
is odd (see [Reference Shalom27, Example 6.3]).
$b-a$
is odd (see [Reference Shalom27, Example 6.3]).
Observe that in the formulas in Theorems 5.1 and 5.2, we can take
![]() $f_3\equiv 1$
and get a limit formula for the averages we are interested in. However, for the sake of our argument, we need a limit formula for every
$f_3\equiv 1$
and get a limit formula for the averages we are interested in. However, for the sake of our argument, we need a limit formula for every
![]() $a,b\in \mathbb {Z}$
regardless of the indices of the subgroups
$a,b\in \mathbb {Z}$
regardless of the indices of the subgroups
![]() $aG$
,
$aG$
,
![]() $bG$
and
$bG$
and
![]() $(a\pm b)G$
and the parity of
$(a\pm b)G$
and the parity of
![]() $b-a$
. Below, we remove the finite index assumptions in Theorem 5.1.
$b-a$
. Below, we remove the finite index assumptions in Theorem 5.1.
5.2 Mackey group
Let G be a countable discrete abelian group, and let
![]() $\textbf {X}= (X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Suppose that
$\textbf {X}= (X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Suppose that
![]() $X=Z^2(X)$
, then, by Theorem 2.5, we can write
$X=Z^2(X)$
, then, by Theorem 2.5, we can write
![]() $\textbf {X} = \textbf {Z} \times _{\sigma } H$
, where
$\textbf {X} = \textbf {Z} \times _{\sigma } H$
, where
![]() $\textbf {Z} = (Z, \alpha )$
is the Kronecker factor, H is a compact abelian group and
$\textbf {Z} = (Z, \alpha )$
is the Kronecker factor, H is a compact abelian group and
![]() $\sigma :G\times Z\rightarrow H$
is a cocycle.
$\sigma :G\times Z\rightarrow H$
is a cocycle.
We now define a Mackey group associated to the cocycle
![]() $\sigma $
. Let
$\sigma $
. Let
and define
![]() $S_gw = (w_1 + \alpha _{ag}, w_2 + \alpha _{bg})$
for
$S_gw = (w_1 + \alpha _{ag}, w_2 + \alpha _{bg})$
for
![]() $g \in G$
,
$g \in G$
,
![]() $w = (w_1, w_2) \in W$
. Let
$w = (w_1, w_2) \in W$
. Let
![]() $\widetilde {\sigma }_g(w) := \left( \sigma _{ag}(w_1), \sigma _{bg}(w_2) \right)$
. Then the Mackey group
$\widetilde {\sigma }_g(w) := \left( \sigma _{ag}(w_1), \sigma _{bg}(w_2) \right)$
. Then the Mackey group
![]() $M = M(a,b)$
is the closed subgroup of H with annihilator given by
$M = M(a,b)$
is the closed subgroup of H with annihilator given by
We will show that the Mackey group is a product of subgroups of H. For
![]() $c \in {\mathbb Z}$
, let
$c \in {\mathbb Z}$
, let
![]() $M_c \le H$
be the closed subgroup with annihilator
$M_c \le H$
be the closed subgroup with annihilator
Proposition 5.3. Let
![]() $a, b \in {\mathbb Z}$
be coprime, and let
$a, b \in {\mathbb Z}$
be coprime, and let
![]() $M = M(a,b)$
be the Mackey group. Then
$M = M(a,b)$
be the Mackey group. Then
![]() $M = M_a \times M_b$
.
$M = M_a \times M_b$
.
The proof of Proposition 5.3 relies heavily on results from [Reference Ackelsberg, Bergelson and Best2, Section 7], which we restate here for ease of reference.
5.3 Cocycle identities
The following result gives a convenient characterisation of coboundaries (recall that a cocycle
![]() $\rho : G \times Z \to S^1$
is a coboundary if
$\rho : G \times Z \to S^1$
is a coboundary if
![]() $\rho _g = \Delta _g F$
for some measurable function
$\rho _g = \Delta _g F$
for some measurable function
![]() $F : Z \to S^1$
).
$F : Z \to S^1$
).
Proposition 5.4 ([Reference Ackelsberg, Bergelson and Best2], Proposition 7.12)
Let
![]() $\mathbf {Z}$
be a Kronecker system and
$\mathbf {Z}$
be a Kronecker system and
![]() $\rho : G \times Z \to S^1$
a cocycle. The following are equivalent:
$\rho : G \times Z \to S^1$
a cocycle. The following are equivalent:
-
(i)
 $\rho $
is a coboundary;
$\rho $
is a coboundary; -
(ii) for any sequence
 $(g_n)_{n \in \mathbb {N}}$
in G with
$(g_n)_{n \in \mathbb {N}}$
in G with
 $\alpha _{g_n} \to 0$
in Z, we have
$\alpha _{g_n} \to 0$
in Z, we have
 $\rho _{g_n}(z) \to 1$
in
$\rho _{g_n}(z) \to 1$
in
 $L^2(Z)$
.
$L^2(Z)$
.
The next proposition gives three equivalent characterisations of Conze–Lesigne (or quasi-affine) cocycles.
Proposition 5.5 ([Reference Ackelsberg, Bergelson and Best2], Proposition 7.15)
Let
![]() $\mathbf {Z}$
be an ergodic Kronecker system and
$\mathbf {Z}$
be an ergodic Kronecker system and
![]() $\rho : G \times Z \to S^1$
a cocycle. The following are equivalent:
$\rho : G \times Z \to S^1$
a cocycle. The following are equivalent:
-
(i) for any sequence
 $(g_n)_{n \in \mathbb {N}}$
in G with
$(g_n)_{n \in \mathbb {N}}$
in G with
 $\alpha _{g_n} \to 0$
in Z, there is a sequence
$\alpha _{g_n} \to 0$
in Z, there is a sequence
 of affine functions, such that
of affine functions, such that
 in
in
 $L^2(Z)$
;
$L^2(Z)$
; -
(ii) for every
 $t \in Z$
, is cohomologous to a character;
$t \in Z$
, is cohomologous to a character; $$ \begin{align*} \frac{\rho_g(z+t)}{\rho_g(z)} \end{align*} $$
$$ \begin{align*} \frac{\rho_g(z+t)}{\rho_g(z)} \end{align*} $$
-
(iii) there is a Borel set
 $A \subseteq Z$
with
$A \subseteq Z$
with
 $m_Z(A)> 0$
, such that is cohomologous to a character for every
$m_Z(A)> 0$
, such that is cohomologous to a character for every $$ \begin{align*} \frac{\rho_g(z+t)}{\rho_g(z)} \end{align*} $$
$$ \begin{align*} \frac{\rho_g(z+t)}{\rho_g(z)} \end{align*} $$
 $t \in A$
.
$t \in A$
.
Lemma 5.6 ([Reference Ackelsberg, Bergelson and Best2], Lemma 7.19)
Let
![]() $\mathbf {Z}$
be an ergodic Kronecker system and
$\mathbf {Z}$
be an ergodic Kronecker system and
![]() $\rho : G \times Z \to S^1$
a cocycle. Suppose
$\rho : G \times Z \to S^1$
a cocycle. Suppose
![]() $\left( \alpha _{g_n} \right)$
converges (to
$\left( \alpha _{g_n} \right)$
converges (to
![]() $0$
) in Z and
$0$
) in Z and
![]() are affine functions, such that
are affine functions, such that
![]() converges (to
converges (to
![]() $1$
) in
$1$
) in
![]() $L^2(Z)$
. Then, for every
$L^2(Z)$
. Then, for every
![]() $a \in \mathbb {N}$
,
$a \in \mathbb {N}$
,
 $$ \begin{align*} c_n^a \lambda_n \left( \binom{a}{2} \alpha_{g_n} \right) \lambda_n^a(z) \rho_{ag_n}(z) \end{align*} $$
$$ \begin{align*} c_n^a \lambda_n \left( \binom{a}{2} \alpha_{g_n} \right) \lambda_n^a(z) \rho_{ag_n}(z) \end{align*} $$
converges (to
![]() $1$
) in
$1$
) in
![]() $L^2(Z)$
.
$L^2(Z)$
.
Lemma 5.7 ([Reference Ackelsberg, Bergelson and Best2], Lemma 7.23)
Let
![]() $\mathbf {Z} \times _{\sigma } H$
be an ergodic Conze–Lesigne G-system. Suppose
$\mathbf {Z} \times _{\sigma } H$
be an ergodic Conze–Lesigne G-system. Suppose
![]() $a \in {\mathbb Z}$
and
$a \in {\mathbb Z}$
and
![]() $aG$
has finite index in G. Then,
$aG$
has finite index in G. Then,
![]() $aH = H$
.
$aH = H$
.
Lemma 5.8 ([Reference Ackelsberg, Bergelson and Best2], Lemma 7.25)
Let Z be a compact abelian group. Let
![]() $c_1, c_2 \in S^1$
and
$c_1, c_2 \in S^1$
and
![]() $\lambda _1, \lambda _2 \in \widehat {Z}$
. If
$\lambda _1, \lambda _2 \in \widehat {Z}$
. If
![]() $\lambda _1 \ne \lambda _2$
, then
$\lambda _1 \ne \lambda _2$
, then
5.4 Proof of Proposition 5.3
We will prove Proposition 5.3 via the next three lemmas. Rather than proving directly that
![]() $M = M_a \times M_b$
, we will instead show the dual identity
$M = M_a \times M_b$
, we will instead show the dual identity
![]() $M^{\perp } = M_a^{\perp } \times M_b^{\perp }$
. First, we show
$M^{\perp } = M_a^{\perp } \times M_b^{\perp }$
. First, we show
![]() $M_a^{\perp } \times M_b^{\perp } \subseteq M^{\perp }$
:
$M_a^{\perp } \times M_b^{\perp } \subseteq M^{\perp }$
:
Lemma 5.9. In the setup of Proposition 5.3,
![]() $M_a^{\perp } \times M_b^{\perp } \subseteq M^{\perp }$
.
$M_a^{\perp } \times M_b^{\perp } \subseteq M^{\perp }$
.
Proof. Let
![]() $\chi _1 \in M_a^{\perp }$
and
$\chi _1 \in M_a^{\perp }$
and
![]() $\chi _2 \in M_b^{\perp }$
. We want to show
$\chi _2 \in M_b^{\perp }$
. We want to show
![]() . Let
. Let
![]() $(g_n)_{n \in \mathbb {N}}$
be a sequence in G, such that
$(g_n)_{n \in \mathbb {N}}$
be a sequence in G, such that
![]() $(\alpha _{ag_n}, \alpha _{bg_n}) \to 0$
in W. By Proposition 5.4, it suffices to show
$(\alpha _{ag_n}, \alpha _{bg_n}) \to 0$
in W. By Proposition 5.4, it suffices to show
in
![]() $L^2(W)$
. Now, since a and b are coprime, we have
$L^2(W)$
. Now, since a and b are coprime, we have
![]() $\alpha _{g_n} \to 0$
in Z. Since
$\alpha _{g_n} \to 0$
in Z. Since
![]() $\chi _1 \in M_a^{\perp }$
, it follows that
$\chi _1 \in M_a^{\perp }$
, it follows that
in
![]() $L^2(Z)$
by Proposition 5.4. Similarly,
$L^2(Z)$
by Proposition 5.4. Similarly,
in
![]() $L^2(Z)$
. Combining (23) and (24), we have
$L^2(Z)$
. Combining (23) and (24), we have
in
![]() $L^2(Z \times Z)$
. That is, (22) holds.
$L^2(Z \times Z)$
. That is, (22) holds.
Before establishing the reverse inclusion,
![]() $M^{\perp } \subseteq M_a^{\perp } \times M_b^{\perp }$
, we need the following result:
$M^{\perp } \subseteq M_a^{\perp } \times M_b^{\perp }$
, we need the following result:
Lemma 5.10. In the setup of Proposition 5.3,
Proof. Let
![]() . By the argument in the proof of [Reference Ackelsberg, Bergelson and Best2, Theorem 7.26], we have
. By the argument in the proof of [Reference Ackelsberg, Bergelson and Best2, Theorem 7.26], we have
![]() $\chi _1^a \chi _2^b = \chi _1^{a^2} \chi _2^{b^2} = 1$
. Therefore,
$\chi _1^a \chi _2^b = \chi _1^{a^2} \chi _2^{b^2} = 1$
. Therefore,
By assumption,
![]() $(b-a)G$
has finite index in G. It follows that
$(b-a)G$
has finite index in G. It follows that
![]() $\widehat {H}$
does not contain any
$\widehat {H}$
does not contain any
![]() $(b-a)$
-torsion elements (see Lemma 5.7), so
$(b-a)$
-torsion elements (see Lemma 5.7), so
![]() $\chi _1^a = 1$
. We immediately deduce
$\chi _1^a = 1$
. We immediately deduce
![]() $\chi _2^b = \chi _1^{-a} = 1$
as well.
$\chi _2^b = \chi _1^{-a} = 1$
as well.
Lemma 5.11. In the setup of Proposition 5.3,
![]() $M^{\perp } \subseteq M_a^{\perp } \times M_b^{\perp }$
.
$M^{\perp } \subseteq M_a^{\perp } \times M_b^{\perp }$
.
Proof. Let
![]() . We want to show
. We want to show
![]() $\chi _1 \in M_a^{\perp }$
and
$\chi _1 \in M_a^{\perp }$
and
![]() $\chi _2 \in M_b^{\perp }$
. For notational convenience, let
$\chi _2 \in M_b^{\perp }$
. For notational convenience, let
![]() $a_1 = a$
and
$a_1 = a$
and
![]() $a_2 = b$
. Let
$a_2 = b$
. Let
![]() $(g_n)_{n \in \mathbb {N}}$
be a sequence in G, such that
$(g_n)_{n \in \mathbb {N}}$
be a sequence in G, such that
![]() $\alpha _{g_n} \to 0$
in Z. By Proposition 5.4, it suffices to show
$\alpha _{g_n} \to 0$
in Z. By Proposition 5.4, it suffices to show
in
![]() $L^2(Z)$
for
$L^2(Z)$
for
![]() $i = 1, 2$
.
$i = 1, 2$
.
Now,
![]() $(\alpha _{ag_n}, \alpha _{bg_n}) \to 0$
in W, so
$(\alpha _{ag_n}, \alpha _{bg_n}) \to 0$
in W, so
in
![]() $L^2(W)$
by Proposition 5.4. Moreover, since
$L^2(W)$
by Proposition 5.4. Moreover, since
![]() $\chi _i \circ \sigma $
is a Conze–Lesigne cocycle, we have
$\chi _i \circ \sigma $
is a Conze–Lesigne cocycle, we have
in
![]() $L^2(Z)$
for some sequences
$L^2(Z)$
for some sequences
![]() $(c_{i,n})_{n \in \mathbb {N}}$
in
$(c_{i,n})_{n \in \mathbb {N}}$
in
![]() $S^1$
and
$S^1$
and
![]() $\left( \lambda _{i,n} \right)_{n \in \mathbb {N}}$
in
$\left( \lambda _{i,n} \right)_{n \in \mathbb {N}}$
in
![]() $\widehat {Z}$
(see Proposition 5.5).
$\widehat {Z}$
(see Proposition 5.5).
It follows by Lemma 5.6 that
in
![]() $L^2(Z)$
. On the other hand, by Lemma 5.10, we have
$L^2(Z)$
. On the other hand, by Lemma 5.10, we have
![]() $\chi _i^{a_i} = 1$
, so raising (27) to the
$\chi _i^{a_i} = 1$
, so raising (27) to the
![]() $a_i$
-th power gives
$a_i$
-th power gives
in
![]() $L^2(Z)$
. Hence, by Lemma 5.8,
$L^2(Z)$
. Hence, by Lemma 5.8,
![]() $\lambda _{i,n}^{a_i} = 1$
for all sufficiently large n, and
$\lambda _{i,n}^{a_i} = 1$
for all sufficiently large n, and
![]() $c_{i,n}^{a_i} \to 1$
. Therefore, (28) simplifies to
$c_{i,n}^{a_i} \to 1$
. Therefore, (28) simplifies to
in
![]() $L^2(Z)$
, where
$L^2(Z)$
, where
![]() $d_{i,n} = \lambda _{i,n}^{\binom {a_i}{2}} \left( \alpha _{g_n} \right)$
.
$d_{i,n} = \lambda _{i,n}^{\binom {a_i}{2}} \left( \alpha _{g_n} \right)$
.
The numbers a and b are coprime, so at least one of them is odd. Without loss of generality, assume a is odd. Then a divides
![]() $\binom {a}{2}$
, so
$\binom {a}{2}$
, so
![]() $\lambda _{1,n}^{\binom {a}{2}} = 1$
. Hence,
$\lambda _{1,n}^{\binom {a}{2}} = 1$
. Hence,
![]() $d_{1,n} = 1$
for all large n, so (25) follows from (29) for
$d_{1,n} = 1$
for all large n, so (25) follows from (29) for
![]() $i = 1$
. It remains to show if (25) holds for
$i = 1$
. It remains to show if (25) holds for
![]() $i = 2$
.
$i = 2$
.
Combining the identities in (29) for
![]() $i = 1, 2$
and using
$i = 1, 2$
and using
![]() $d_{1,n} = 1$
, we have
$d_{1,n} = 1$
, we have
in
![]() $L^2(Z \times Z)$
. That is,
$L^2(Z \times Z)$
. That is,
in
![]() $L^2(W)$
. Comparing with (26), this implies
$L^2(W)$
. Comparing with (26), this implies
![]() $d_{2,n} \to 1$
. Therefore, (25) follows from (29) for
$d_{2,n} \to 1$
. Therefore, (25) follows from (29) for
![]() $i = 2$
.
$i = 2$
.
Proposition 5.3 follows immediately from Lemmas 5.9 and 5.11.
5.5 Limit formula
With the help of Proposition 5.3, we will now prove a limit formula for the averages
![]() $\text {UC -}\lim _{g\in G} T_{ag} f_1 T_{bg} f_2$
. We need to define one more object related to the cocycle
$\text {UC -}\lim _{g\in G} T_{ag} f_1 T_{bg} f_2$
. We need to define one more object related to the cocycle
![]() $\sigma $
before stating the limit formula. For a compact space K, let
$\sigma $
before stating the limit formula. For a compact space K, let
![]() $\mathcal {M}(Z, K)$
denote the space of measurable functions
$\mathcal {M}(Z, K)$
denote the space of measurable functions
![]() $Z \to K$
equipped with the topology of convergence in measure.
$Z \to K$
equipped with the topology of convergence in measure.
Proposition 5.12. Let
![]() $\textbf {X} = \mathbf {Z} \times _{\sigma } H$
be an ergodic Conze–Lesigne system. Let
$\textbf {X} = \mathbf {Z} \times _{\sigma } H$
be an ergodic Conze–Lesigne system. Let
![]() $c \in {\mathbb Z}$
. There exists a function
$c \in {\mathbb Z}$
. There exists a function
![]() $\psi _c : Z \times Z \to H/M_c$
, such that
$\psi _c : Z \times Z \to H/M_c$
, such that
-
(1) for every
 $g \in G$
,
$g \in G$
,  $$ \begin{align*} \psi_c(\alpha_g, z) \equiv \sigma_{cg}(z) \pmod{M_c}, \end{align*} $$
$$ \begin{align*} \psi_c(\alpha_g, z) \equiv \sigma_{cg}(z) \pmod{M_c}, \end{align*} $$
and
-
(2) the map
 $Z \ni t \mapsto \psi _c(t, \cdot ) \in \mathcal {M}(Z, H/M_c)$
is continuous.
$Z \ni t \mapsto \psi _c(t, \cdot ) \in \mathcal {M}(Z, H/M_c)$
is continuous.
In order to prove Proposition 5.12, we use the following characterisation of convergence in measure:
Lemma 5.13 ([Reference Ackelsberg, Bergelson and Best2], 7.28)
Let
![]() $(f_n)_{n \in \mathbb {N}}$
be a sequence of functions in
$(f_n)_{n \in \mathbb {N}}$
be a sequence of functions in
![]() $\mathcal {M}(Z,H)$
. Then
$\mathcal {M}(Z,H)$
. Then
![]() $f_n \to f$
in
$f_n \to f$
in
![]() $\mathcal {M}(Z,H)$
if and only if
$\mathcal {M}(Z,H)$
if and only if
![]() $\chi \circ f_n \to \chi \circ f$
in
$\chi \circ f_n \to \chi \circ f$
in
![]() $L^2(Z)$
for every character
$L^2(Z)$
for every character
![]() $\chi \in \widehat {H}$
.
$\chi \in \widehat {H}$
.
Proof of Proposition 5.12
Given a sequence
![]() $(g_n)_{n \in \mathbb {N}}$
in G, such that
$(g_n)_{n \in \mathbb {N}}$
in G, such that
![]() $(\alpha _{g_n})_{n \in \mathbb {N}}$
is convergent in Z, we want to show that the sequence
$(\alpha _{g_n})_{n \in \mathbb {N}}$
is convergent in Z, we want to show that the sequence
converges in
![]() $\mathcal {M}(Z, H/M_c)$
. Equivalently, by Lemma 5.13, we must show that
$\mathcal {M}(Z, H/M_c)$
. Equivalently, by Lemma 5.13, we must show that
converges in
![]() $L^2(Z)$
for every
$L^2(Z)$
for every
![]() $\chi \in \widehat {H/M_c} = M_c^{\perp }$
.
$\chi \in \widehat {H/M_c} = M_c^{\perp }$
.
Let
![]() $\chi \in M_a^{\perp }$
. By the definition of
$\chi \in M_a^{\perp }$
. By the definition of
![]() $M_c$
, the cocycle
$M_c$
, the cocycle
![]() $\chi \left( \sigma _{cg}(z) \right)$
is a coboundary over
$\chi \left( \sigma _{cg}(z) \right)$
is a coboundary over
![]() $(Z, \alpha )$
. Hence, by Proposition 5.4, there is a continuous map
$(Z, \alpha )$
. Hence, by Proposition 5.4, there is a continuous map
![]() $t \mapsto \varphi (t, \cdot ) \in L^2(Z)$
, such that
$t \mapsto \varphi (t, \cdot ) \in L^2(Z)$
, such that
![]() $\varphi (\alpha _g, z) = \chi \left( \sigma _{cg}(z) \right)$
. Therefore,
$\varphi (\alpha _g, z) = \chi \left( \sigma _{cg}(z) \right)$
. Therefore,
in
![]() $L^2(Z)$
, where
$L^2(Z)$
, where
![]() $t = \lim _{n \to \infty }{\alpha _{g_n}} \in Z$
.
$t = \lim _{n \to \infty }{\alpha _{g_n}} \in Z$
.
By the Kuratowski and Ryll-Nardzewski measurable selection theorem (see [Reference Srivastava28, Section 5.2]), there exists a measurable map
![]() $\iota _a : H/M_a \to H$
, such that
$\iota _a : H/M_a \to H$
, such that
![]() $\pi _a(\iota _a(x)) = x$
, where
$\pi _a(\iota _a(x)) = x$
, where
![]() $\pi _a$
is the canonical projection
$\pi _a$
is the canonical projection
![]() $\pi _a : H \to H/M_a$
. Let
$\pi _a : H \to H/M_a$
. Let
![]() $\psi _1 = \iota _a \circ \psi _a$
and
$\psi _1 = \iota _a \circ \psi _a$
and
![]() $\psi _2 = \iota _b \circ \psi _b$
. We can now state and prove a general limit formula for Conze–Lesigne systems:
$\psi _2 = \iota _b \circ \psi _b$
. We can now state and prove a general limit formula for Conze–Lesigne systems:
Theorem 5.14. Let
![]() $\textbf {X} = \mathbf {Z} \times _{\sigma } H$
be an ergodic Conze–Lesigne system. Let
$\textbf {X} = \mathbf {Z} \times _{\sigma } H$
be an ergodic Conze–Lesigne system. Let
![]() $a, b \in Z$
. Let
$a, b \in Z$
. Let
![]() $M = M(a,b) = M_a \times M_b$
. Then for any
$M = M(a,b) = M_a \times M_b$
. Then for any
![]() $f_1, f_2 \in L^{\infty }(\mu )$
, we have
$f_1, f_2 \in L^{\infty }(\mu )$
, we have
 $$ \begin{align} \text{UC -}\lim_{g \in G}&{f_1(T_{ag}(z,x)) f_2(T_{bg}(z,x))} \nonumber \\ & = \int_{Z \times M_a \times M_b}{f_1(z + at, x + u + \psi_1(t,z)) f_2(z + bt, x + v + \psi_2(t,z))~dt~du~dv} \end{align} $$
$$ \begin{align} \text{UC -}\lim_{g \in G}&{f_1(T_{ag}(z,x)) f_2(T_{bg}(z,x))} \nonumber \\ & = \int_{Z \times M_a \times M_b}{f_1(z + at, x + u + \psi_1(t,z)) f_2(z + bt, x + v + \psi_2(t,z))~dt~du~dv} \end{align} $$
in
![]() $L^2(Z \times H)$
.
$L^2(Z \times H)$
.
Remark 5.15. We have defined the functions
![]() $\psi _i$
by lifting
$\psi _i$
by lifting
![]() $\psi _a$
and
$\psi _a$
and
![]() $\psi _b$
to the group H from
$\psi _b$
to the group H from
![]() $H/M_a$
and
$H/M_a$
and
![]() $H/M_b$
respectively. If
$H/M_b$
respectively. If
![]() $\psi ^{\prime }_1$
is another functions with
$\psi ^{\prime }_1$
is another functions with
![]() $\pi _a(\psi ^{\prime }_1) = \psi _a$
, then for any
$\pi _a(\psi ^{\prime }_1) = \psi _a$
, then for any
![]() $t, z \in Z$
, we have
$t, z \in Z$
, we have
![]() $\psi ^{\prime }_1(t,z) - \psi _1(t,z) \in M_a$
. Since the Haar measure on
$\psi ^{\prime }_1(t,z) - \psi _1(t,z) \in M_a$
. Since the Haar measure on
![]() $M_a$
is invariant under shifts coming from
$M_a$
is invariant under shifts coming from
![]() $M_a$
, the expression on the right-hand side of (30) is unchanged when
$M_a$
, the expression on the right-hand side of (30) is unchanged when
![]() $\psi _1$
is replaced by
$\psi _1$
is replaced by
![]() $\psi ^{\prime }_1$
. The same is true for replacing
$\psi ^{\prime }_1$
. The same is true for replacing
![]() $\psi _2$
by
$\psi _2$
by
![]() $\psi ^{\prime }_2$
, so it does not matter which lifts of
$\psi ^{\prime }_2$
, so it does not matter which lifts of
![]() $\psi _a$
and
$\psi _a$
and
![]() $\psi _b$
we choose.
$\psi _b$
we choose.
Proof. For notational convenience, let
![]() $\psi = (\psi _1, \psi _2) : Z \times Z \to H^2$
, and let
$\psi = (\psi _1, \psi _2) : Z \times Z \to H^2$
, and let
![]() $m_M$
denote the Haar measure on the Mackey group
$m_M$
denote the Haar measure on the Mackey group
![]() $M = M_a \times M_b$
.
$M = M_a \times M_b$
.
It suffices to prove the formula in (30) for functions of the form
with
and
![]() $\chi _i \in \widehat {H}$
. In this case, the right-hand side of (30) is equal to
$\chi _i \in \widehat {H}$
. In this case, the right-hand side of (30) is equal to
where
.
We now consider two cases. First, if
![]() $\widetilde {\chi } \notin M^{\perp }$
, then
$\widetilde {\chi } \notin M^{\perp }$
, then
![]() $\int _M{\widetilde {\chi }~dm_M} = 0$
, so the right-hand side of (30) is equal to zero. Moreover, for every
$\int _M{\widetilde {\chi }~dm_M} = 0$
, so the right-hand side of (30) is equal to zero. Moreover, for every
![]() $\lambda \in M^{\perp }$
and almost every
$\lambda \in M^{\perp }$
and almost every
![]() $z, t \in Z$
, we have
$z, t \in Z$
, we have
Therefore, the left-hand side of (30) is also zero (see [Reference Ackelsberg, Bergelson and Best2, Proposition 7.10]).
Now suppose
![]() $\widetilde {\chi } \in M^{\perp }$
so that
$\widetilde {\chi } \in M^{\perp }$
so that
![]() $\int _M{\widetilde {\chi }~dm_M} = 1$
. For
$\int _M{\widetilde {\chi }~dm_M} = 1$
. For
![]() $g \in G$
and
$g \in G$
and
![]() $(z,x) \in Z \times H$
, we can write
$(z,x) \in Z \times H$
, we can write
Thus, letting
we have
Since
![]() $\widetilde {\chi }$
annihilates the Mackey group M, we see by Proposition 5.12(ii) that
$\widetilde {\chi }$
annihilates the Mackey group M, we see by Proposition 5.12(ii) that
![]() $Z \ni t \mapsto \widetilde {\chi }(\psi (t,\cdot )) \in L^2(Z)$
is continuous, and so
$Z \ni t \mapsto \widetilde {\chi }(\psi (t,\cdot )) \in L^2(Z)$
is continuous, and so
![]() $Z \ni t \mapsto \varphi _t \in L^2(Z \times H)$
is also continuous. Therefore, for any
$Z \ni t \mapsto \varphi _t \in L^2(Z \times H)$
is also continuous. Therefore, for any
![]() $\xi \in L^2(Z \times H)$
, since the system
$\xi \in L^2(Z \times H)$
, since the system
![]() $(Z, \alpha )$
is uniquely ergodic, we have
$(Z, \alpha )$
is uniquely ergodic, we have
That is
weakly in
![]() $L^2(Z \times H)$
. By more general results on norm convergence on multiple ergodic averages (see [Reference Austin3, Reference Zorin-Kranich32]), it follows that (31) holds strongly. The right-hand side of (30) is also equal to
$L^2(Z \times H)$
. By more general results on norm convergence on multiple ergodic averages (see [Reference Austin3, Reference Zorin-Kranich32]), it follows that (31) holds strongly. The right-hand side of (30) is also equal to
![]() $\int _Z{\varphi _t(z,x)~dt}$
, so the formula in (30) holds when
$\int _Z{\varphi _t(z,x)~dt}$
, so the formula in (30) holds when
![]() $\widetilde {\chi } \in M^{\perp }$
.
$\widetilde {\chi } \in M^{\perp }$
.
5.6 Proof of Theorem 1.13
We first prove the theorem in the special case where a and b are coprime.
Let
![]() $f = \mathbf {1}_A$
. By Theorem 4.15, there is an extension
$f = \mathbf {1}_A$
. By Theorem 4.15, there is an extension
![]() $\widetilde {\textbf {X}}$
of
$\widetilde {\textbf {X}}$
of
![]() $\textbf {X}$
, such that
$\textbf {X}$
, such that
 $$ \begin{align*} \text{UC -}\lim_{g \in G}&~{\eta(\alpha_g)~\int_{\widetilde{X}}{\widetilde{f} \cdot T_{ag} \widetilde{f} \cdot T_{bg} \widetilde{f}~d\widetilde{\mu}}} \\ & = \text{UC -}\lim_{g \in G}{\eta(\alpha_g)~\int_{\widetilde{X}}{\widetilde{f} \cdot T_{ag} E(\widetilde{f}|\mathcal {Z}_{G}^2(\widetilde{X})) \vee \mathcal {I}_a(\widetilde{X})) \cdot T_{ag} E({\widetilde{f}}|{\mathcal {Z}_{G}^2(\widetilde{X}) \vee \mathcal {I}_b(\widetilde{X})})~d\widetilde{\mu}}}, \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{g \in G}&~{\eta(\alpha_g)~\int_{\widetilde{X}}{\widetilde{f} \cdot T_{ag} \widetilde{f} \cdot T_{bg} \widetilde{f}~d\widetilde{\mu}}} \\ & = \text{UC -}\lim_{g \in G}{\eta(\alpha_g)~\int_{\widetilde{X}}{\widetilde{f} \cdot T_{ag} E(\widetilde{f}|\mathcal {Z}_{G}^2(\widetilde{X})) \vee \mathcal {I}_a(\widetilde{X})) \cdot T_{ag} E({\widetilde{f}}|{\mathcal {Z}_{G}^2(\widetilde{X}) \vee \mathcal {I}_b(\widetilde{X})})~d\widetilde{\mu}}}, \end{align*} $$
where
![]() $\widetilde {f}$
is the lift of f to
$\widetilde {f}$
is the lift of f to
![]() $\widetilde {X}$
. For notational convenience, let
$\widetilde {X}$
. For notational convenience, let
![]() $\widetilde {f}_a := E(\widetilde {f}|\mathcal {Z}_{G}^2(\widetilde {X}) \vee \mathcal {I}_a(\widetilde {X}))$
and
$\widetilde {f}_a := E(\widetilde {f}|\mathcal {Z}_{G}^2(\widetilde {X}) \vee \mathcal {I}_a(\widetilde {X}))$
and
![]() $\widetilde {f}_b := E({\widetilde {f}}|{\mathcal {Z}_{G}^2(\widetilde {X}) \vee \mathcal {I}_b(\widetilde {X})})$
. We can therefore write
$\widetilde {f}_b := E({\widetilde {f}}|{\mathcal {Z}_{G}^2(\widetilde {X}) \vee \mathcal {I}_b(\widetilde {X})})$
. We can therefore write
 $$ \begin{align*} \widetilde{f}_a & = \sum_{i\in\mathbb{N}}{c_ih_i}, \\ \widetilde{f}_b & = \sum_{j\in\mathbb{N}}{d_jk_j}, \end{align*} $$
$$ \begin{align*} \widetilde{f}_a & = \sum_{i\in\mathbb{N}}{c_ih_i}, \\ \widetilde{f}_b & = \sum_{j\in\mathbb{N}}{d_jk_j}, \end{align*} $$
where each
![]() $c_i$
is
$c_i$
is
![]() $aG$
-invariant,
$aG$
-invariant,
![]() $d_j$
is
$d_j$
is
![]() $bG$
-invariant and
$bG$
-invariant and
![]() $h_i, k_j$
are
$h_i, k_j$
are
![]() $\mathcal {Z}_G^2(\widetilde {X})$
-measurable. By Theorem 2.5(iii), we can write
$\mathcal {Z}_G^2(\widetilde {X})$
-measurable. By Theorem 2.5(iii), we can write
![]() $\mathbf {Z}_G^2(\widetilde {X}) = \widetilde {\mathbf {Z}} \times _{\sigma } H$
. Then, by Theorem 5.14,
$\mathbf {Z}_G^2(\widetilde {X}) = \widetilde {\mathbf {Z}} \times _{\sigma } H$
. Then, by Theorem 5.14,
 $$ \begin{align*} & \text{UC -}\lim_{g \in G}{\eta(\alpha_g)~\mu \left( A \cap T_{ag}^{-1}A \cap T_{bg}^{-1}A \right)} \\ & = \text{UC -}\lim_{g \in G}{\eta(\alpha_g)~\int_{\widetilde{X}}{\widetilde{f} \cdot T_{ag} \widetilde{f}_a \cdot T_{ag} \widetilde{f_b}~d\widetilde{\mu}}}\\ & = \sum_{i,j\in\mathbb{N}}{\int_{\widetilde{X}}{c_i d_j \widetilde{f} \cdot \text{UC -}\lim_{g \in G}{\eta(\alpha_g)~T_{ag}h_i \cdot T_{bg} k_j~d\widetilde{\mu}}}} \\ & = \sum_{i,j\in\mathbb{N}}{\int_{\widetilde{X} \times Z \times M_a \times M_b}{c_i(x) d_j(x) \widetilde{f}(x) \eta(t) h_i \left( \pi_Z(x)+at, \pi_H(x)+u+\psi_1(t,z) \right)}} \\ & \qquad \qquad \qquad {{k_j \left( \pi_Z(x)+bt, \pi_H(x)+v+\psi_2(t,z) \right)~d\widetilde{\mu}(x)~dt~du~dv}}, \end{align*} $$
$$ \begin{align*} & \text{UC -}\lim_{g \in G}{\eta(\alpha_g)~\mu \left( A \cap T_{ag}^{-1}A \cap T_{bg}^{-1}A \right)} \\ & = \text{UC -}\lim_{g \in G}{\eta(\alpha_g)~\int_{\widetilde{X}}{\widetilde{f} \cdot T_{ag} \widetilde{f}_a \cdot T_{ag} \widetilde{f_b}~d\widetilde{\mu}}}\\ & = \sum_{i,j\in\mathbb{N}}{\int_{\widetilde{X}}{c_i d_j \widetilde{f} \cdot \text{UC -}\lim_{g \in G}{\eta(\alpha_g)~T_{ag}h_i \cdot T_{bg} k_j~d\widetilde{\mu}}}} \\ & = \sum_{i,j\in\mathbb{N}}{\int_{\widetilde{X} \times Z \times M_a \times M_b}{c_i(x) d_j(x) \widetilde{f}(x) \eta(t) h_i \left( \pi_Z(x)+at, \pi_H(x)+u+\psi_1(t,z) \right)}} \\ & \qquad \qquad \qquad {{k_j \left( \pi_Z(x)+bt, \pi_H(x)+v+\psi_2(t,z) \right)~d\widetilde{\mu}(x)~dt~du~dv}}, \end{align*} $$
where
![]() $(\pi _Z(x), \pi _H(x)) \in Z \times H$
is the projection of
$(\pi _Z(x), \pi _H(x)) \in Z \times H$
is the projection of
![]() $x \in \widetilde {X}$
onto the Conze–Lesigne factor
$x \in \widetilde {X}$
onto the Conze–Lesigne factor
![]() $Z \times H$
. By choosing
$Z \times H$
. By choosing
![]() $\eta : Z \to [0, \infty )$
concentrated on a small neighborhood of
$\eta : Z \to [0, \infty )$
concentrated on a small neighborhood of
![]() $0$
(as in the proof of Theorem 1.11; see Subsection 3.3), it remains to show the inequality:
$0$
(as in the proof of Theorem 1.11; see Subsection 3.3), it remains to show the inequality:
 $$ \begin{align} \sum_{i,j}{\int_{\widetilde{X} \times M_a \times M_b}{c_i(x) d_j(x) \widetilde{f}(x) h_i \left( \pi_Z(x), \pi_H(x)+u \right) k_j \left( \pi_Z(x), \pi_H(x)+v \right)~d\widetilde{\mu}(x)~du~dv}} \ge \mu(A)^3. \end{align} $$
$$ \begin{align} \sum_{i,j}{\int_{\widetilde{X} \times M_a \times M_b}{c_i(x) d_j(x) \widetilde{f}(x) h_i \left( \pi_Z(x), \pi_H(x)+u \right) k_j \left( \pi_Z(x), \pi_H(x)+v \right)~d\widetilde{\mu}(x)~du~dv}} \ge \mu(A)^3. \end{align} $$
Let
![]() $\mathcal {W}_1$
be the
$\mathcal {W}_1$
be the
![]() $\sigma $
-algebra generated by functions
$\sigma $
-algebra generated by functions
![]() $f \in L^{\infty }(Z \times H)$
, such that
$f \in L^{\infty }(Z \times H)$
, such that
![]() $f(z, x + y) = f(z,x)$
for every
$f(z, x + y) = f(z,x)$
for every
![]() $y \in M_a$
. Similarly, let
$y \in M_a$
. Similarly, let
![]() $\mathcal {W}_2$
be the
$\mathcal {W}_2$
be the
![]() $\sigma $
-algebra generated by functions
$\sigma $
-algebra generated by functions
![]() $f \in L^{\infty }(Z \times H)$
, such that
$f \in L^{\infty }(Z \times H)$
, such that
![]() $f(z, x + y) = f(z,x)$
for every
$f(z, x + y) = f(z,x)$
for every
![]() $y \in M_b$
. Then the left-hand side of (32) is equal to
$y \in M_b$
. Then the left-hand side of (32) is equal to
By [Reference Chu13, Lemma 1.6], the quantity in (33) is bounded below by
![]() $\left( \int _{\widetilde {X}}{\widetilde {f}~d\widetilde {\mu }} \right)^3 = \mu (A)^3$
, so (32) holds.
$\left( \int _{\widetilde {X}}{\widetilde {f}~d\widetilde {\mu }} \right)^3 = \mu (A)^3$
, so (32) holds.
Now suppose
![]() $a,b\in \mathbb {Z}$
are arbitrary integers and write
$a,b\in \mathbb {Z}$
are arbitrary integers and write
![]() $a=a'\cdot d$
and
$a=a'\cdot d$
and
![]() $b=b'\cdot d$
, where
$b=b'\cdot d$
, where
![]() $d=\text {gcd}(a,b)$
and
$d=\text {gcd}(a,b)$
and
![]() $a',b'$
are coprime. Since
$a',b'$
are coprime. Since
![]() $(b-a)G$
has finite index in G, we deduce that so does
$(b-a)G$
has finite index in G, we deduce that so does
![]() $dG$
. Therefore, we can find finitely many ergodic
$dG$
. Therefore, we can find finitely many ergodic
![]() $dG$
-invariant measures
$dG$
-invariant measures
![]() $\{\mu _i\}_{i=1}^l$
, such that
$\{\mu _i\}_{i=1}^l$
, such that
![]() $\mu = \frac {1}{l}\sum _{i=1}^l \mu _i$
and all of the systems
$\mu = \frac {1}{l}\sum _{i=1}^l \mu _i$
and all of the systems
![]() $\textbf {X}_i=(X,\mathcal {X},\mu _i,dG)$
admit the same Kronecker factor. By the argument above, we can find a suitable
$\textbf {X}_i=(X,\mathcal {X},\mu _i,dG)$
admit the same Kronecker factor. By the argument above, we can find a suitable
![]() $\eta $
satisfying:
$\eta $
satisfying:
for all
![]() $i=1,...,l$
, and
$i=1,...,l$
, and
![]() $\text {UC -}\lim _{g\in dG} \eta (\alpha _g)=1$
. Therefore, by Jensen’s inequality, we have
$\text {UC -}\lim _{g\in dG} \eta (\alpha _g)=1$
. Therefore, by Jensen’s inequality, we have
As in the proof of Theorem 1.11, we conclude that
is syndetic. Since
![]() $dG$
has finite index in G, this implies that
$dG$
has finite index in G, this implies that
is syndetic, as required.
![]() $\Box $
$\Box $
6 Proof of Theorem 1.14
In this section, we prove Theorem 1.14, restated here for the convenience of the reader:
Theorem 6.1 (Theorem 1.14)
Let
![]() $G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
. Let
$G = \bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
. Let
![]() $l \in \mathbb N$
. There exists
$l \in \mathbb N$
. There exists
![]() $P = P(l)$
, such that, for any
$P = P(l)$
, such that, for any
![]() $a, b \in \mathbb N$
with
$a, b \in \mathbb N$
with
![]() $p \mid \gcd (a,b)$
for some prime
$p \mid \gcd (a,b)$
for some prime
![]() $p \ge P$
, there is an ergodic G-system
$p \ge P$
, there is an ergodic G-system
![]() $\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
and a set
$\left( X, \mathcal {X}, \mu , (T_g)_{g \in G} \right)$
and a set
![]() $A \in \mathcal {X}$
with
$A \in \mathcal {X}$
with
![]() $\mu (A)> 0$
, such that
$\mu (A)> 0$
, such that
for every
![]() $g\ne 0$
.
$g\ne 0$
.
Rather than constructing a
![]() $\bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
-system directly, we will instead construct a
$\bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
-system directly, we will instead construct a
![]() $\bigoplus _{n=1}^{\infty }{{\mathbb Z}/p^2{\mathbb Z}}$
-system. Since
$\bigoplus _{n=1}^{\infty }{{\mathbb Z}/p^2{\mathbb Z}}$
-system. Since
![]() $\bigoplus _{n=1}^{\infty }{{\mathbb Z}/p^2{\mathbb Z}}$
is a quotient of
$\bigoplus _{n=1}^{\infty }{{\mathbb Z}/p^2{\mathbb Z}}$
is a quotient of
![]() $\bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
, the system we construct can be lifted to an ergodic
$\bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
, the system we construct can be lifted to an ergodic
![]() $\bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
-system. Hence, Theorem 1.14 follows from:
$\bigoplus _{n=1}^{\infty }{{\mathbb Z}}$
-system. Hence, Theorem 1.14 follows from:
Theorem 6.2. For any
![]() $a,b,l \in \mathbb N$
, there exists a prime p (sufficiently large), an ergodic
$a,b,l \in \mathbb N$
, there exists a prime p (sufficiently large), an ergodic
![]() $\bigoplus _{n=1}^{\infty }\mathbb {Z}/p^2\mathbb {Z}$
-system
$\bigoplus _{n=1}^{\infty }\mathbb {Z}/p^2\mathbb {Z}$
-system
![]() $\textbf {X} = \left( X, \mathcal {X}, \mu , (T_g)_{g \in \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p^2{\mathbb Z}}} \right)$
and a set
$\textbf {X} = \left( X, \mathcal {X}, \mu , (T_g)_{g \in \bigoplus _{n=1}^{\infty }{{\mathbb Z}/p^2{\mathbb Z}}} \right)$
and a set
![]() $A \in \mathcal {X}$
with
$A \in \mathcal {X}$
with
![]() $\mu (A)> 0$
, such that
$\mu (A)> 0$
, such that
for every
![]() $g \ne 0$
.
$g \ne 0$
.
The proof of Theorem 6.2 is based on the following result of Behrend [Reference Behrend4].
Theorem 6.3. Let
![]() $a,b\in \mathbb {N}$
be distinct and nonzero. There is an absolute constant
$a,b\in \mathbb {N}$
be distinct and nonzero. There is an absolute constant
![]() $c> 0$
, such that: for every
$c> 0$
, such that: for every
![]() $N\in \mathbb {N}$
, there is a subset
$N\in \mathbb {N}$
, there is a subset
![]() $B\subseteq \{0,1,...,N-1\}$
, such that
$B\subseteq \{0,1,...,N-1\}$
, such that
![]() $|B|>N\cdot e^{-c\sqrt {\log (N)}}$
and B contains no configurations of the form
$|B|>N\cdot e^{-c\sqrt {\log (N)}}$
and B contains no configurations of the form
![]() $\{n,n+am,n+bm\}$
for
$\{n,n+am,n+bm\}$
for
![]() $m\not = 0$
.
$m\not = 0$
.
For every prime number p, let
![]() $C_p=\{z\in \mathbb {C} : z^p =1\}$
denote the group of all roots of unity of order p and let
$C_p=\{z\in \mathbb {C} : z^p =1\}$
denote the group of all roots of unity of order p and let
![]() be the first p-th root of unity in
be the first p-th root of unity in
![]() $\mathbb {C}$
. The following is an immediate corollary of Behrend’s theorem.
$\mathbb {C}$
. The following is an immediate corollary of Behrend’s theorem.
Lemma 6.4. Let
![]() $a,b\in \mathbb {N}$
be distinct, then, for every l, there exists a sufficiently large prime p and a subset
$a,b\in \mathbb {N}$
be distinct, then, for every l, there exists a sufficiently large prime p and a subset
![]() $B\subseteq C_p$
of size
$B\subseteq C_p$
of size
![]() $|B|>p^{1-\frac {1}{l-1}}$
which contains no configurations of the form
$|B|>p^{1-\frac {1}{l-1}}$
which contains no configurations of the form
![]() $\{y,y\cdot x^a,y\cdot x^b\}$
for
$\{y,y\cdot x^a,y\cdot x^b\}$
for
![]() $x\not =1$
.
$x\not =1$
.
Throughout this section, we let
![]() $\mathcal {T}_p := C_p^{\mathbb {N}}$
and
$\mathcal {T}_p := C_p^{\mathbb {N}}$
and
![]() $G_p:= \bigoplus _{i\in I} \mathbb {Z}/p\mathbb {Z}$
.
$G_p:= \bigoplus _{i\in I} \mathbb {Z}/p\mathbb {Z}$
.
We start by giving a proof that the large intersection property fails for nonergodic systems.
Lemma 6.5. Let
![]() $a,b \in \mathbb {Z}$
be distinct and nonzero. For every
$a,b \in \mathbb {Z}$
be distinct and nonzero. For every
![]() $L\in \mathbb {N}$
, there is a
$L\in \mathbb {N}$
, there is a
![]() $P=P(L)$
, such that for every prime
$P=P(L)$
, such that for every prime
![]() $p\geq P$
, there is a
$p\geq P$
, there is a
![]() $G_p$
-system
$G_p$
-system
![]() $(X,\mathcal {X},\mu ,(T_g)_{g\in G_p})$
, such that, for every
$(X,\mathcal {X},\mu ,(T_g)_{g\in G_p})$
, such that, for every
![]() $l\leq L$
, there is a measurable set
$l\leq L$
, there is a measurable set
![]() $A=A(l)$
with
$A=A(l)$
with
![]() $\mu (A)>0$
and
$\mu (A)>0$
and
for every
![]() $g\not =0$
.
$g\not =0$
.
This result was previously established in [Reference Ackelsberg, Bergelson and Best2, Proposition 10.11], but we give a different proof that will be useful later on.
Proof. Let p be a prime number, and let
![]() $X_p=\mathcal {T}_p\times C_p$
. We equip
$X_p=\mathcal {T}_p\times C_p$
. We equip
![]() $X_p$
with the Borel
$X_p$
with the Borel
![]() $\sigma $
-algebra, the Haar measure
$\sigma $
-algebra, the Haar measure
![]() $\mu $
and the action of
$\mu $
and the action of
![]() $G_p$
by
$G_p$
by
 $$ \begin{align*}T_g(x,u) = (x,\prod_{i=1}^{\infty} x_i^{g_i} u). \end{align*} $$
$$ \begin{align*}T_g(x,u) = (x,\prod_{i=1}^{\infty} x_i^{g_i} u). \end{align*} $$
Now, fix a subset
![]() $B\subseteq C_p$
which avoids configurations of the form
$B\subseteq C_p$
which avoids configurations of the form
![]() $\{y,y\cdot x^{a}, y\cdot x^{b}\}$
whenever
$\{y,y\cdot x^{a}, y\cdot x^{b}\}$
whenever
![]() $x\not =1$
, and let
$x\not =1$
, and let
![]() $A=\mathcal {T}_p\times B$
. It is easy to see that
$A=\mathcal {T}_p\times B$
. It is easy to see that
![]() $\mu (A) = \frac {|B|}{p}$
and we have
$\mu (A) = \frac {|B|}{p}$
and we have
 $$ \begin{align*} \mu(A\cap T_{ag} A\cap T_{bg} A) = \int_{\mathcal{T}_p^2} 1_B(y) 1_B\left(y\prod_{i\in I}x^{ag_i}\right) 1_B\left(y\prod_{i\in I}x^{bg_i}\right) dx dy &=\\ \int_{\mathcal{T}_p^2} 1_B(y) 1_B\left(y\cdot \left(\prod_{\{i~:~ g_i\not = 0\}} x_i\right)^a\right) 1_B\left(y\cdot \left(\prod_{\{i~:~ g_i\not = 0\}} x_i\right)^b\right) dx dy &=\\ \mu_{\mathcal{T}_p^2}\left(\left\{(y,x)\in\mathcal{T}_p^2 : \left\{y,y\cdot \left(\prod_{\{i~:~ g_i\not = 0\}} x_i\right)^a, y\cdot \left(\prod_{\{i~:~ g_i\not = 0\}} x_i\right)^b\right\}\subset B\right\}\right). \end{align*} $$
$$ \begin{align*} \mu(A\cap T_{ag} A\cap T_{bg} A) = \int_{\mathcal{T}_p^2} 1_B(y) 1_B\left(y\prod_{i\in I}x^{ag_i}\right) 1_B\left(y\prod_{i\in I}x^{bg_i}\right) dx dy &=\\ \int_{\mathcal{T}_p^2} 1_B(y) 1_B\left(y\cdot \left(\prod_{\{i~:~ g_i\not = 0\}} x_i\right)^a\right) 1_B\left(y\cdot \left(\prod_{\{i~:~ g_i\not = 0\}} x_i\right)^b\right) dx dy &=\\ \mu_{\mathcal{T}_p^2}\left(\left\{(y,x)\in\mathcal{T}_p^2 : \left\{y,y\cdot \left(\prod_{\{i~:~ g_i\not = 0\}} x_i\right)^a, y\cdot \left(\prod_{\{i~:~ g_i\not = 0\}} x_i\right)^b\right\}\subset B\right\}\right). \end{align*} $$
But,
 $\left\{y,y\cdot \left(\prod _{\{i~:~ g_i\not = 0\}} x_i\right)^a, y\cdot \left(\prod _{\{i~:~ g_i\not = 0\}} x_i\right)^b\right\}\subset B$
if and only if
$\left\{y,y\cdot \left(\prod _{\{i~:~ g_i\not = 0\}} x_i\right)^a, y\cdot \left(\prod _{\{i~:~ g_i\not = 0\}} x_i\right)^b\right\}\subset B$
if and only if
![]() $\prod _{\{i~:~ g_i\not = 0\}} x_i=1$
. Since
$\prod _{\{i~:~ g_i\not = 0\}} x_i=1$
. Since
![]() $g\not =0$
, we deduce that
$g\not =0$
, we deduce that
![]() $\mu (A\cap T_{ag} A\cap T_{bg} A) = \frac {|B|}{p^2} = \frac {p^{l-2}}{|B|^{l-1}} \mu (A)^l$
. Now, choose P sufficiently large for which there exists a set B with
$\mu (A\cap T_{ag} A\cap T_{bg} A) = \frac {|B|}{p^2} = \frac {p^{l-2}}{|B|^{l-1}} \mu (A)^l$
. Now, choose P sufficiently large for which there exists a set B with
![]() $|B|>p^{1-\frac {1}{l-1}}$
(Lemma 6.4). Then,
$|B|>p^{1-\frac {1}{l-1}}$
(Lemma 6.4). Then,
![]() $\mu (A\cap T_{ag} A\cap T_{bg} A)<\mu (A)^l$
as required.
$\mu (A\cap T_{ag} A\cap T_{bg} A)<\mu (A)^l$
as required.
Roughly speaking, the idea in this section is to construct an ergodic p-th root for the system above.
We fix some P sufficiently large as in Lemma 6.5, and let
![]() $p>P$
be a prime number. For convenience of notations, we let
$p>P$
be a prime number. For convenience of notations, we let
![]() and
and
![]() $\eta = e^{2\pi i/{p^2}}$
. We define an action of
$\eta = e^{2\pi i/{p^2}}$
. We define an action of
![]() $G=\bigoplus _{n\in \mathbb {N}}\mathbb {Z}/p^2\mathbb {Z}$
on
$G=\bigoplus _{n\in \mathbb {N}}\mathbb {Z}/p^2\mathbb {Z}$
on
![]() $\mathcal {T}$
by setting
$\mathcal {T}$
by setting
![]() $S_g x= \zeta (g) x$
, where
$S_g x= \zeta (g) x$
, where
![]() . Since the image of
. Since the image of
![]() $\zeta $
is dense in
$\zeta $
is dense in
![]() $\mathcal {T}$
, the action is ergodic.
$\mathcal {T}$
, the action is ergodic.
Now, we extend this action to the product space
![]() $X=\mathcal {T}\times C_{p^2}$
. Let
$X=\mathcal {T}\times C_{p^2}$
. Let
![]() $\varphi :C_p\rightarrow C_{p^2}$
be the map
$\varphi :C_p\rightarrow C_{p^2}$
be the map
where
![]() $|x|_p = x\ \mod p$
. Then,
$|x|_p = x\ \mod p$
. Then,
![]() $\varphi $
is a cross-section of the canonical projection
$\varphi $
is a cross-section of the canonical projection
![]() $C_{p^2}\rightarrow C_p$
, and we have that
$C_{p^2}\rightarrow C_p$
, and we have that
![]() $\varphi (x)^p = x$
, and
$\varphi (x)^p = x$
, and
![]() . Our goal is to define an action
. Our goal is to define an action
![]() $(T_g)_{g\in G}$
on X, such that
$(T_g)_{g\in G}$
on X, such that
![]() $T_{pg}(t,u) = (t,\prod _{i\in \mathbb {N}} t_i^{pg_i}\cdot u)$
.
$T_{pg}(t,u) = (t,\prod _{i\in \mathbb {N}} t_i^{pg_i}\cdot u)$
.
We do so in two steps. We define an action
![]() $T^{\prime }_g$
on X which satisfies that
$T^{\prime }_g$
on X which satisfies that
![]() $T^{\prime }_{e_i} (t,u) = (S_{e_i} t , \varphi (t_i) u)$
, for every
$T^{\prime }_{e_i} (t,u) = (S_{e_i} t , \varphi (t_i) u)$
, for every
![]() $i\in \mathbb {N}$
, where
$i\in \mathbb {N}$
, where
![]() $e_i\in \bigoplus _{n=1}^{\infty } \mathbb {Z}/p^n\mathbb {Z}$
is the i-th unit vector. Writing
$e_i\in \bigoplus _{n=1}^{\infty } \mathbb {Z}/p^n\mathbb {Z}$
is the i-th unit vector. Writing
![]() $g=\sum _{i\in \mathbb {N}}g_ie_i$
and using the group law, we get the following action:
$g=\sum _{i\in \mathbb {N}}g_ie_i$
and using the group law, we get the following action:

where an empty product
![]() $\prod _{k=0}^{-1}{x_k}$
is equal to 1.
$\prod _{k=0}^{-1}{x_k}$
is equal to 1.
Unfortunately, this action is not what we are looking for. Indeed,

To fix that, we let
be a p-th root of
and change the action accordingly:

Lemma 6.6. For every
![]() $t\in \mathcal {T}$
,
$t\in \mathcal {T}$
,
![]() $u\in C_{p^2}$
and
$u\in C_{p^2}$
and
![]() $g\in G$
, we have
$g\in G$
, we have
Proof. The proof is a direct computation. Indeed, it suffices to prove that (36) holds for
![]() $g=e_j$
for every
$g=e_j$
for every
![]() $j\in \mathbb {N}$
. Let
$j\in \mathbb {N}$
. Let
![]() $j\in \mathbb {N}$
be arbitrary. Since
$j\in \mathbb {N}$
be arbitrary. Since
is of order p,
![]() $S_{pg}t = t$
. As for the second coordinate, observe that
$S_{pg}t = t$
. As for the second coordinate, observe that

The first equality follows because the product is independent on
![]() $t_j$
and always equals to
$t_j$
and always equals to
, and the last equality follows from the definition of
![]() $\xi $
. This completes the proof of the lemma.
$\xi $
. This completes the proof of the lemma.
The main difficulty in the proof is showing that this action is ergodic.
Lemma 6.7. The action in (35) on X is ergodic.
Proof. We use Zimmer's criterion for ergodicity [Reference Zimmer31, Lemma 4.5]. Since the action of G on
![]() $\mathcal {T}$
is ergodic, it is enough to show that the cocycle
$\mathcal {T}$
is ergodic, it is enough to show that the cocycle
![]() $\sigma :G\times \mathcal {T}\rightarrow C_{p^2}$
,
$\sigma :G\times \mathcal {T}\rightarrow C_{p^2}$
,
![]() is minimal. Since
is minimal. Since
![]() $C_p$
is the largest proper subgroup of
$C_p$
is the largest proper subgroup of
![]() $C_{p^2}$
, it is enough to show that
$C_{p^2}$
, it is enough to show that
![]() $\sigma $
is not cohomologous to a cocycle taking values in
$\sigma $
is not cohomologous to a cocycle taking values in
![]() $C_p$
. Suppose, by contradiction, that there exists a cocycle
$C_p$
. Suppose, by contradiction, that there exists a cocycle
![]() $\tau :\mathcal {T}\rightarrow C_p$
cohomologous to
$\tau :\mathcal {T}\rightarrow C_p$
cohomologous to
![]() $\sigma $
. Since
$\sigma $
. Since
![]() $\tau ^p=1$
, we deduce that
$\tau ^p=1$
, we deduce that
![]() is a coboundary. Therefore, there exists
is a coboundary. Therefore, there exists
![]() $F:\mathcal {T}\rightarrow S^1$
, such that
$F:\mathcal {T}\rightarrow S^1$
, such that
for every
![]() $g\in G$
and
$g\in G$
and
![]() $t\in T$
. Observe that for every
$t\in T$
. Observe that for every
![]() $g,h\in G$
,
$g,h\in G$
,
![]() $\Delta _h\sigma ^p(g,t)$
is a constant in t. Therefore, by (37),
$\Delta _h\sigma ^p(g,t)$
is a constant in t. Therefore, by (37),
![]() $\Delta _{h_1}\Delta _{h_2}F$
is a constant for every
$\Delta _{h_1}\Delta _{h_2}F$
is a constant for every
![]() $h_1,h_2\in G$
. Let
$h_1,h_2\in G$
. Let
![]() $s\in \mathcal {T}$
and define
$s\in \mathcal {T}$
and define
![]() $\Delta _s F(x) = \frac {F(sx)}{F(x)}$
. We claim that
$\Delta _s F(x) = \frac {F(sx)}{F(x)}$
. We claim that
![]() $\Delta _s F(x)$
is an eigenfunction. Let
$\Delta _s F(x)$
is an eigenfunction. Let
![]() $g_1,g_2\in G$
, then
$g_1,g_2\in G$
, then
![]() $\Delta _{g_1}\Delta _{g_2} \Delta _s F(x) = \Delta _s \Delta _{g_1} \Delta _{g_2} F(x)=1$
. Hence, by ergodicity,
$\Delta _{g_1}\Delta _{g_2} \Delta _s F(x) = \Delta _s \Delta _{g_1} \Delta _{g_2} F(x)=1$
. Hence, by ergodicity,
![]() $\Delta _{g_2}\Delta _{s}F$
is constant and
$\Delta _{g_2}\Delta _{s}F$
is constant and
![]() $\Delta _s F$
is an eigenfunction for every
$\Delta _s F$
is an eigenfunction for every
![]() $s\in Z$
. Recall that translations by
$s\in Z$
. Recall that translations by
![]() $s\in Z$
are continuous with respect to the
$s\in Z$
are continuous with respect to the
![]() $L^2$
-norm. In particular, there exists an open subgroup
$L^2$
-norm. In particular, there exists an open subgroup
![]() $U\leq \mathcal {T}$
, such that
$U\leq \mathcal {T}$
, such that
for all
![]() $s\in U$
. By ergodicity, the multiplicity of each eigenvalue is
$s\in U$
. By ergodicity, the multiplicity of each eigenvalue is
![]() $1$
. Since eigenfunctions with different eigenvalues are orthogonal, it follows that
$1$
. Since eigenfunctions with different eigenvalues are orthogonal, it follows that
![]() $\Delta _s F$
is a constant for all
$\Delta _s F$
is a constant for all
![]() $s\in U$
. Otherwise,
$s\in U$
. Otherwise,
![]() $\Delta _s F$
is orthogonal to
$\Delta _s F$
is orthogonal to
![]() $1$
, and then
$1$
, and then
which contradicts (38). Now, choose
![]() $g\in G$
, such that
$g\in G$
, such that
![]() (such g must exist by density). Then, if we take
(such g must exist by density). Then, if we take
![]() , equation (37) implies that
, equation (37) implies that
![]() $\sigma ^p(g,\cdot )$
is a constant. As
$\sigma ^p(g,\cdot )$
is a constant. As
![]() $\sigma ^p(g,t)$
clearly depends on t, this is a contradiction.
$\sigma ^p(g,t)$
clearly depends on t, this is a contradiction.
We now complete the proof of Theorem 6.2. Let
![]() $B\subseteq C_p$
be as in Lemma 6.4. Let
$B\subseteq C_p$
be as in Lemma 6.4. Let
![]() $\pi :C_{p^2}\rightarrow C_p$
be the map
$\pi :C_{p^2}\rightarrow C_p$
be the map
![]() $\pi _i(x) = x_1^p$
, and let
$\pi _i(x) = x_1^p$
, and let
![]() $A=\mathcal {T}\times \widetilde {B}$
, where
$A=\mathcal {T}\times \widetilde {B}$
, where
![]() $\widetilde {B} = \pi ^{-1}(B)$
. Then,
$\widetilde {B} = \pi ^{-1}(B)$
. Then,
![]() $\mu _X(A) = \frac {|B|}{p}$
, and, as in the proof of Lemma 6.5,
$\mu _X(A) = \frac {|B|}{p}$
, and, as in the proof of Lemma 6.5,
 $$ \begin{align*} \mu_X(A\cap T_{apg} A \cap T_{bpg} A)=\frac{|B|}{p^2}=\frac{p^{l-2}}{|B|^{l-1}}\mu_X(A)^l<\mu_X(A)^{l}. \end{align*} $$
$$ \begin{align*} \mu_X(A\cap T_{apg} A \cap T_{bpg} A)=\frac{|B|}{p^2}=\frac{p^{l-2}}{|B|^{l-1}}\mu_X(A)^l<\mu_X(A)^{l}. \end{align*} $$
This completes the proof.
![]() $\Box $
$\Box $
7 3-point configurations in
 ${\mathbb Z}^2$
${\mathbb Z}^2$
In this section, we establish ergodic popular difference densities for all 3-point matrix patterns in
![]() ${\mathbb Z}^2$
. The results are summarised in Table 1 in the Introduction.
${\mathbb Z}^2$
. The results are summarised in Table 1 in the Introduction.
7.1 Ergodic popular difference densities when
 $r(M_1, M_2) = (2,1,1)$
$r(M_1, M_2) = (2,1,1)$
The following theorem gives an affirmative answer to Question 1.12 for the group
![]() $G = {\mathbb Z}^2$
:
$G = {\mathbb Z}^2$
:
Theorem 7.1. Suppose
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are
$M_2$
are
![]() $2\times 2$
matrices, such that
$2\times 2$
matrices, such that
![]() $r(M_1, M_2) = (2,1,1)$
. Then, for any
$r(M_1, M_2) = (2,1,1)$
. Then, for any
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
![]() $\text {epdd}_{M_1, M_2}(\alpha ) = \alpha ^3$
.
$\text {epdd}_{M_1, M_2}(\alpha ) = \alpha ^3$
.
An example of the configurations handled by Theorem 7.1 is the class of all axis-aligned right triangles in
![]() ${\mathbb Z}^2$
,
${\mathbb Z}^2$
,
![]() $\{(a,b), (a+n,b), (a,b+m)\}$
, which corresponds to the choice of matrices
$\{(a,b), (a+n,b), (a,b+m)\}$
, which corresponds to the choice of matrices
 $$ \begin{align*} M_1 = \left( \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad M_2 = \left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right).\\[-36pt] \end{align*} $$
$$ \begin{align*} M_1 = \left( \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad M_2 = \left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right).\\[-36pt] \end{align*} $$
Proof of Theorem 7.1
Without loss of generality, we may assume
![]() $\text {rk}(M_1) = \text {rk}(M_2) = 1$
and
$\text {rk}(M_1) = \text {rk}(M_2) = 1$
and
![]() $\text {rk}(M_2 - M_1) = 2$
. Indeed, if
$\text {rk}(M_2 - M_1) = 2$
. Indeed, if
![]() $\text {rk}(M_1) = 2$
, we may rearrange the expression
$\text {rk}(M_1) = 2$
, we may rearrange the expression
and the new matrices
![]() $N_1 = M_1-M_2$
and
$N_1 = M_1-M_2$
and
![]() $N_2 = -M_2$
satisfy the desired conditions.
$N_2 = -M_2$
satisfy the desired conditions.
We now break the proof into two cases depending on the diagonalisability of
![]() $M_1$
and
$M_1$
and
![]() $M_2$
. Note that, since
$M_2$
. Note that, since
![]() $M_i$
has rank 1, its characteristic polynomial is of the form
$M_i$
has rank 1, its characteristic polynomial is of the form
![]() $x(x-a)$
for some
$x(x-a)$
for some
![]() $a \in {\mathbb Z}$
. Hence, if
$a \in {\mathbb Z}$
. Hence, if
![]() $M_i$
has a nonzero eigenvalue, then it has an integer eigenvalue (in this case, equal to a) and is diagonalisable.
$M_i$
has a nonzero eigenvalue, then it has an integer eigenvalue (in this case, equal to a) and is diagonalisable.
Case 1:
![]() $M_1$
or
$M_1$
or
![]() $M_2$
has a nonzero eigenvalue.
$M_2$
has a nonzero eigenvalue.
Without loss of generality, we may assume that
![]() $M_1$
has a nonzero eigenvalue and is therefore diagonalisable. Hence, there is a nonsingular
$M_1$
has a nonzero eigenvalue and is therefore diagonalisable. Hence, there is a nonsingular
![]() $2\times 2$
integer matrix P, an integer
$2\times 2$
integer matrix P, an integer
![]() $a \in {\mathbb Z}$
and a rank 1 matrix
$a \in {\mathbb Z}$
and a rank 1 matrix
![]() $N_2$
with integer entries, such that
$N_2$
with integer entries, such that
 $$ \begin{align*} M_1P = P\left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right), \qquad M_2P = PN_2 \qquad \text{and} \qquad \text{rk} \left( N_2 - \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \right) = 2. \end{align*} $$
$$ \begin{align*} M_1P = P\left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right), \qquad M_2P = PN_2 \qquad \text{and} \qquad \text{rk} \left( N_2 - \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \right) = 2. \end{align*} $$
It is straightforward to check that, in order to satisfy the constraints on rank,
![]() $N_2$
must be of the form
$N_2$
must be of the form
 $$ \begin{align*} N_2 = \left( \begin{array}{cc} cd & c \\ bd & b \end{array} \right) \end{align*} $$
$$ \begin{align*} N_2 = \left( \begin{array}{cc} cd & c \\ bd & b \end{array} \right) \end{align*} $$
with
![]() $b \ne 0$
. By changing to the basis
$b \ne 0$
. By changing to the basis
![]() $\binom {1}{-d}, \binom {0}{1}$
, we may further assume
$\binom {1}{-d}, \binom {0}{1}$
, we may further assume
![]() $d = 0$
.
$d = 0$
.
Suppose
![]() $\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
is a measure-preserving
$\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
is a measure-preserving
![]() ${\mathbb Z}^2$
-system (we do not need to assume that the system is ergodic here), and let
${\mathbb Z}^2$
-system (we do not need to assume that the system is ergodic here), and let
![]() $A \in \mathcal {X}$
with
$A \in \mathcal {X}$
with
![]() $\mu (A) = \alpha $
. Define a new
$\mu (A) = \alpha $
. Define a new
![]() ${\mathbb Z}^2$
-action by
${\mathbb Z}^2$
-action by
![]() $S_{\vec {n}} := T_{P\vec {n}}$
. Then,
$S_{\vec {n}} := T_{P\vec {n}}$
. Then,
Now put
![]() $S_1 := S_{(a,0)}$
and
$S_1 := S_{(a,0)}$
and
![]() $S_2 := S_{(c,b)}$
. By Lemma 2.2 and the mean ergodic theorem, we have
$S_2 := S_{(c,b)}$
. By Lemma 2.2 and the mean ergodic theorem, we have
 $$ \begin{align*} \text{UC -}\lim_{\vec{n} \in {\mathbb Z}^2}{\mu \left( A \cap T_{M_1P\vec{n}}^{-1}A \cap T_{M_2P\vec{n}}^{-1}A \right)} & = \text{UC -}\lim_{n_2 \in {\mathbb Z}}{\text{UC -}\lim_{n_1 \in {\mathbb Z}}{\mu \left( A \cap S_1^{-n_1}A \cap S_2^{-n_2}A \right)}} \\ & = \int_X{\mathbf{1}_A \cdot E(\mathbf{1}_A \mid \mathcal {I}(S_1)) \cdot E(\mathbf{1}_A \mid \mathcal {I}(S_2))} \\ & \ge \alpha^3, \end{align*} $$
$$ \begin{align*} \text{UC -}\lim_{\vec{n} \in {\mathbb Z}^2}{\mu \left( A \cap T_{M_1P\vec{n}}^{-1}A \cap T_{M_2P\vec{n}}^{-1}A \right)} & = \text{UC -}\lim_{n_2 \in {\mathbb Z}}{\text{UC -}\lim_{n_1 \in {\mathbb Z}}{\mu \left( A \cap S_1^{-n_1}A \cap S_2^{-n_2}A \right)}} \\ & = \int_X{\mathbf{1}_A \cdot E(\mathbf{1}_A \mid \mathcal {I}(S_1)) \cdot E(\mathbf{1}_A \mid \mathcal {I}(S_2))} \\ & \ge \alpha^3, \end{align*} $$
where the inequality in the last line follows from [Reference Chu13, Lemma 1.6]. Therefore, for any
![]() $\varepsilon> 0$
, the set
$\varepsilon> 0$
, the set
is syndetic. Noting that P is nonsingular, it follows that the set
![]() $P(R_{\varepsilon })$
is also syndetic in
$P(R_{\varepsilon })$
is also syndetic in
![]() ${\mathbb Z}^2$
. But for any
${\mathbb Z}^2$
. But for any
![]() $\vec {m} \in P(R_{\varepsilon })$
, we have
$\vec {m} \in P(R_{\varepsilon })$
, we have
This shows
![]() $\text {epdd}_{M_1, M_2}(\alpha ) \ge \alpha ^3$
.
$\text {epdd}_{M_1, M_2}(\alpha ) \ge \alpha ^3$
.
To see the upper bound
![]() $\text {epdd}_{M_1,M_2}(\alpha ) \le \alpha ^3$
, let
$\text {epdd}_{M_1,M_2}(\alpha ) \le \alpha ^3$
, let
![]() $\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
be mixing of order 3. Then, for any
$\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
be mixing of order 3. Then, for any
![]() $A \in \mathcal {X}$
, we have
$A \in \mathcal {X}$
, we have
![]() $\mu \left( A \cap T_{\vec {n}}^{-1}A \cap T_{\vec {m}}^{-1}A \right) \to \mu (A)^3$
as
$\mu \left( A \cap T_{\vec {n}}^{-1}A \cap T_{\vec {m}}^{-1}A \right) \to \mu (A)^3$
as
![]() $\vec {n}, \vec {m}, \vec {m}-\vec {n} \to \infty $
. Let P be a nonsingular
$\vec {n}, \vec {m}, \vec {m}-\vec {n} \to \infty $
. Let P be a nonsingular
![]() $2\times 2$
matrix with integer entries and
$2\times 2$
matrix with integer entries and
![]() $a, b, c \in {\mathbb Z}$
with
$a, b, c \in {\mathbb Z}$
with
![]() $a, b \ne 0$
, such that
$a, b \ne 0$
, such that
 $$ \begin{align*} PM_1 = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right)P \qquad \text{and} \qquad PM_2 = \left( \begin{array}{cc} 0 & c \\ 0 & b \end{array} \right)P. \end{align*} $$
$$ \begin{align*} PM_1 = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right)P \qquad \text{and} \qquad PM_2 = \left( \begin{array}{cc} 0 & c \\ 0 & b \end{array} \right)P. \end{align*} $$
The group of transformations
![]() $\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
is still mixing of order 3. Write
$\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
is still mixing of order 3. Write
![]() $\vec {m} = P\vec {n}$
for
$\vec {m} = P\vec {n}$
for
![]() $\vec {n} \in {\mathbb Z}^2$
. If
$\vec {n} \in {\mathbb Z}^2$
. If
![]() $m_1 \to \infty $
and
$m_1 \to \infty $
and
![]() $m_2 \to \infty $
, then
$m_2 \to \infty $
, then
Hence, for any
![]() $\varepsilon> 0$
, there is a finite set
$\varepsilon> 0$
, there is a finite set
![]() $F \subseteq {\mathbb Z}$
, such that
$F \subseteq {\mathbb Z}$
, such that
A union of finitely many lines in
![]() ${\mathbb Z}^2$
is not syndetic, so
${\mathbb Z}^2$
is not syndetic, so
Case 2:
![]() $M_1$
and
$M_1$
and
![]() $M_2$
have no nonzero eigenvalues.
$M_2$
have no nonzero eigenvalues.
Since
![]() $M_1$
has rank 1, there is a nonsingular
$M_1$
has rank 1, there is a nonsingular
![]() $2\times 2$
integer matrix P, a nonzero integer
$2\times 2$
integer matrix P, a nonzero integer
![]() $a \in {\mathbb Z}$
and a rank 1 matrix
$a \in {\mathbb Z}$
and a rank 1 matrix
![]() $N_2$
with integer entries and characteristic polynomial
$N_2$
with integer entries and characteristic polynomial
![]() $x^2$
, such that
$x^2$
, such that
 $$ \begin{align*} M_1P = P\left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right), \qquad M_2P = PN_2 \qquad \text{and} \qquad \text{rk} \left( N_2 - \left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right) \right) = 2. \end{align*} $$
$$ \begin{align*} M_1P = P\left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right), \qquad M_2P = PN_2 \qquad \text{and} \qquad \text{rk} \left( N_2 - \left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right) \right) = 2. \end{align*} $$
Write
 $$ \begin{align*} N_2 = \left( \begin{array}{cc} s & t \\ u & v \end{array} \right). \end{align*} $$
$$ \begin{align*} N_2 = \left( \begin{array}{cc} s & t \\ u & v \end{array} \right). \end{align*} $$
Since
![]() $N_2$
has characteristic polynomial
$N_2$
has characteristic polynomial
![]() $x^2$
, we have
$x^2$
, we have
![]() $s + v = 0$
and
$s + v = 0$
and
![]() $sv = tu$
. Therefore, if
$sv = tu$
. Therefore, if
![]() $u = 0$
, then
$u = 0$
, then
![]() $s = v = 0$
. But then
$s = v = 0$
. But then
 $$ \begin{align*} N_2 - \left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right) = \left( \begin{array}{cc} 0 & t-a \\ 0 & 0 \end{array} \right) \end{align*} $$
$$ \begin{align*} N_2 - \left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right) = \left( \begin{array}{cc} 0 & t-a \\ 0 & 0 \end{array} \right) \end{align*} $$
has rank at most 1. Thus, we must have
![]() $u \ne 0$
. It follows that
$u \ne 0$
. It follows that
![]() $N_2$
can be written in the form
$N_2$
can be written in the form
 $$ \begin{align*} N_2 = \left( \begin{array}{cc} db & -d^2b \\ b & -db \end{array} \right) \end{align*} $$
$$ \begin{align*} N_2 = \left( \begin{array}{cc} db & -d^2b \\ b & -db \end{array} \right) \end{align*} $$
for some
![]() $b, d$
with
$b, d$
with
![]() $b \ne 0$
. Changing to the basis
$b \ne 0$
. Changing to the basis
![]() $\binom {1}{0}, \binom {d}{1}$
, we may assume
$\binom {1}{0}, \binom {d}{1}$
, we may assume
![]() $d = 0$
so that
$d = 0$
so that
 $$ \begin{align*} N_2 = \left( \begin{array}{cc} 0 & 0 \\ b & 0 \end{array} \right). \end{align*} $$
$$ \begin{align*} N_2 = \left( \begin{array}{cc} 0 & 0 \\ b & 0 \end{array} \right). \end{align*} $$
Given a
![]() ${\mathbb Z}^2$
-system
${\mathbb Z}^2$
-system
![]() $\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
, note that
$\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
, note that
Hence, replacing
![]() $(n_1,n_2)$
by
$(n_1,n_2)$
by
![]() $(n_2,n_1)$
, we reduce to Case 1.
$(n_2,n_1)$
, we reduce to Case 1.
7.2 Ergodic popular difference densities when
 $r(M_1,M_2) = (1,1,1)$
$r(M_1,M_2) = (1,1,1)$
For matrix configurations with
![]() $r(M_1, M_2) = (1,1,1)$
, we must distinguish between several cases. First, when
$r(M_1, M_2) = (1,1,1)$
, we must distinguish between several cases. First, when
![]() $M_1$
and
$M_1$
and
![]() $M_2$
commute, a construction based on Behrend’s theorem shows that the ergodic popular difference density decays faster than any polynomial:
$M_2$
commute, a construction based on Behrend’s theorem shows that the ergodic popular difference density decays faster than any polynomial:
Theorem 7.2. Suppose
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are commuting
$M_2$
are commuting
![]() $2\times 2$
matrices, such that
$2\times 2$
matrices, such that
![]() $r(M_1, M_2) = (1,1,1)$
. Then, for any sufficiently small
$r(M_1, M_2) = (1,1,1)$
. Then, for any sufficiently small
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
![]() $\text {epdd}_{M_1, M_2}(\alpha ) < \alpha ^{c\log (1/\alpha )}$
, where
$\text {epdd}_{M_1, M_2}(\alpha ) < \alpha ^{c\log (1/\alpha )}$
, where
![]() $c> 0$
is an absolute constant.
$c> 0$
is an absolute constant.
Theorem 7.2 applies to collinear 3-point configurations up to scaling and translation.
Proof of Theorem 7.2
We first distinguish between two cases depending on diagonalisability of
![]() $M_1$
and
$M_1$
and
![]() $M_2$
.
$M_2$
.
Case 1:
![]() $M_1$
or
$M_1$
or
![]() $M_2$
has a nonzero eigenvalue.
$M_2$
has a nonzero eigenvalue.
Without loss of generality, assume
![]() $M_1$
has a nonzero eigenvalue and is therefore diagonalisable. Since
$M_1$
has a nonzero eigenvalue and is therefore diagonalisable. Since
![]() $M_2$
and
$M_2$
and
![]() $M_2 - M_1$
are also rank 1 and commute with
$M_2 - M_1$
are also rank 1 and commute with
![]() $M_1$
, there exists a nonsingular
$M_1$
, there exists a nonsingular
![]() $2\times 2$
matrix P with integer entries and
$2\times 2$
matrix P with integer entries and
![]() $a, b \in {\mathbb Z}$
be distinct and nonzero, such that
$a, b \in {\mathbb Z}$
be distinct and nonzero, such that
 $$ \begin{align} PM_1 = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right)P \qquad \text{and} \qquad PM_2 = \left( \begin{array}{cc} b & 0 \\ 0 & 0 \end{array} \right)P. \end{align} $$
$$ \begin{align} PM_1 = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right)P \qquad \text{and} \qquad PM_2 = \left( \begin{array}{cc} b & 0 \\ 0 & 0 \end{array} \right)P. \end{align} $$
Case 2:
![]() $M_1$
and
$M_1$
and
![]() $M_2$
have no nonzero eigenvalues.
$M_2$
have no nonzero eigenvalues.
Using the condition
![]() $r(M_1,M_2) = (1,1,1)$
, there is a nonsingular
$r(M_1,M_2) = (1,1,1)$
, there is a nonsingular
![]() $2\times 2$
integer matrix P, a nonzero integer
$2\times 2$
integer matrix P, a nonzero integer
![]() $a \in {\mathbb Z}$
and a rank 1 matrix
$a \in {\mathbb Z}$
and a rank 1 matrix
![]() $N_2$
with integer entries and characteristic polynomial
$N_2$
with integer entries and characteristic polynomial
![]() $x^2$
, such that
$x^2$
, such that
 $$ \begin{align*} M_1P = P\left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right), \qquad M_2P = PN_2 \qquad \text{and} \qquad \text{rk} \left( N_2 - \left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right) \right) = 1. \end{align*} $$
$$ \begin{align*} M_1P = P\left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right), \qquad M_2P = PN_2 \qquad \text{and} \qquad \text{rk} \left( N_2 - \left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right) \right) = 1. \end{align*} $$
Moreover,
![]() $N_2$
commutes with the matrix
$N_2$
commutes with the matrix
 $\left( \begin {array}{cc} 0 & a \\ 0 & 0 \end {array} \right)$
. Write
$\left( \begin {array}{cc} 0 & a \\ 0 & 0 \end {array} \right)$
. Write
 $$ \begin{align*} N_2 = \left( \begin{array}{cc} s & t \\ u & v \end{array} \right). \end{align*} $$
$$ \begin{align*} N_2 = \left( \begin{array}{cc} s & t \\ u & v \end{array} \right). \end{align*} $$
Note that
 $$ \begin{align*} \left[ \left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right), \left( \begin{array}{cc} s & t \\ u & v \end{array} \right) \right] = \left( \begin{array}{cc} au & a(v-s) \\ 0 & au \end{array} \right), \end{align*} $$
$$ \begin{align*} \left[ \left( \begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right), \left( \begin{array}{cc} s & t \\ u & v \end{array} \right) \right] = \left( \begin{array}{cc} au & a(v-s) \\ 0 & au \end{array} \right), \end{align*} $$
so
![]() $u = 0$
and
$u = 0$
and
![]() $v = s$
. On the other hand, since
$v = s$
. On the other hand, since
![]() $N_2$
has characteristic polynomial
$N_2$
has characteristic polynomial
![]() $x^2$
, we have
$x^2$
, we have
![]() $s + v = 0$
and
$s + v = 0$
and
![]() $sv = tu$
. Hence,
$sv = tu$
. Hence,
![]() $s = v = 0$
, and
$s = v = 0$
, and
![]() $N_2$
is of the form
$N_2$
is of the form
 $$ \begin{align*} N_2 = \left( \begin{array}{cc} 0 & b \\ 0 & 0 \end{array} \right) \end{align*} $$
$$ \begin{align*} N_2 = \left( \begin{array}{cc} 0 & b \\ 0 & 0 \end{array} \right) \end{align*} $$
with
![]() $b \notin \{0,a\}$
.
$b \notin \{0,a\}$
.
Now, replacing
![]() $(n_1,n_2) \in {\mathbb Z}^2$
by
$(n_1,n_2) \in {\mathbb Z}^2$
by
![]() $(n_2,n_1) \in {\mathbb Z}^2$
and using the identity
$(n_2,n_1) \in {\mathbb Z}^2$
and using the identity
 $$ \begin{align*} \left( \begin{array}{cc} 0 & c \\ 0 & 0 \end{array} \right) \left( \begin{array}{c} n_2 \\ n_1 \end{array} \right) = \left( \begin{array}{cc} c & 0 \\ 0 & 0 \end{array} \right) \left( \begin{array}{c} n_1 \\ n_2 \end{array} \right) \end{align*} $$
$$ \begin{align*} \left( \begin{array}{cc} 0 & c \\ 0 & 0 \end{array} \right) \left( \begin{array}{c} n_2 \\ n_1 \end{array} \right) = \left( \begin{array}{cc} c & 0 \\ 0 & 0 \end{array} \right) \left( \begin{array}{c} n_1 \\ n_2 \end{array} \right) \end{align*} $$
for
![]() $c \in {\mathbb Z}$
, we can reduce Case 2 to Case 1.
$c \in {\mathbb Z}$
, we can reduce Case 2 to Case 1.
Without loss of generality, let P be a nonsingular
![]() $2\times 2$
matrix with integer entries and
$2\times 2$
matrix with integer entries and
![]() $a, b \in {\mathbb Z}$
distinct and nonzero, such that (39) holds. Put
$a, b \in {\mathbb Z}$
distinct and nonzero, such that (39) holds. Put
![]() $d := \left| \det (P) \right| \in \mathbb N$
.
$d := \left| \det (P) \right| \in \mathbb N$
.
Define
![]() $S : \mathbb {T}^2 \to \mathbb {T}^2$
by
$S : \mathbb {T}^2 \to \mathbb {T}^2$
by
![]() $S(x,y) := (x, y+x)$
. Let
$S(x,y) := (x, y+x)$
. Let
![]() $R : \mathbb {T}^2 \to \mathbb {T}^2$
be the transformation
$R : \mathbb {T}^2 \to \mathbb {T}^2$
be the transformation
![]() $R(x,y) = (2x, 2y + x)$
. Both S and R preserve the Haar probability measure
$R(x,y) = (2x, 2y + x)$
. Both S and R preserve the Haar probability measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {T}^2$
. We claim that the
$\mathbb {T}^2$
. We claim that the
![]() $({\mathbb Z}_{\ge 0})^2$
-action generated by S and R is ergodic (with respect to
$({\mathbb Z}_{\ge 0})^2$
-action generated by S and R is ergodic (with respect to
![]() $\mu $
). To see this, suppose
$\mu $
). To see this, suppose
![]() $f \in L^2(\mathbb {T}^2)$
is simultaneously S- and R-invariant, and expand f as a Fourier series
$f \in L^2(\mathbb {T}^2)$
is simultaneously S- and R-invariant, and expand f as a Fourier series
where
![]() $e(t) := e(2\pi i t)$
. Then
$e(t) := e(2\pi i t)$
. Then
Therefore, since
![]() $Sf = f$
, we have
$Sf = f$
, we have
![]() $c_{n,m} = c_{n-m,m}$
for all
$c_{n,m} = c_{n-m,m}$
for all
![]() $n,m \in {\mathbb Z}$
. By Parseval’s identity,
$n,m \in {\mathbb Z}$
. By Parseval’s identity,
![]() $\sum _{n,m}{|c_{n,m}|^2} = \|f\|_2^2 < \infty $
, so
$\sum _{n,m}{|c_{n,m}|^2} = \|f\|_2^2 < \infty $
, so
![]() $c_{n,m} = 0$
whenever
$c_{n,m} = 0$
whenever
![]() $m \ne 0$
. That is,
$m \ne 0$
. That is,
![]() $f(x,y) = \sum _n{c_{n,0}e(nx)}$
. Now,
$f(x,y) = \sum _n{c_{n,0}e(nx)}$
. Now,
Hence, since
![]() $Rf = f$
, we have
$Rf = f$
, we have
![]() $c_{2n,0} = c_{n,0}$
for every
$c_{2n,0} = c_{n,0}$
for every
![]() $n \in {\mathbb Z}$
. Applying Parseval’s identity once again, we conclude that
$n \in {\mathbb Z}$
. Applying Parseval’s identity once again, we conclude that
![]() $c_{n,0} = 0$
for
$c_{n,0} = 0$
for
![]() $n \ne 0$
. Thus,
$n \ne 0$
. Thus,
![]() $f(x,y) = c_{0,0}$
is a constant function.
$f(x,y) = c_{0,0}$
is a constant function.
Fix
![]() $\alpha \in (0,1)$
. By [Reference Bergelson, Host and Kra8, Theorem 1.3], there exists a set
$\alpha \in (0,1)$
. By [Reference Bergelson, Host and Kra8, Theorem 1.3], there exists a set
![]() $A \subseteq \mathbb {T}^2$
with
$A \subseteq \mathbb {T}^2$
with
![]() $\mu (A) = \alpha $
, such that
$\mu (A) = \alpha $
, such that
![]() $\mu \left( A \cap S^{-an}A \cap S^{-bn} A \right) < \alpha ^{c\log (1/\alpha )}$
for
$\mu \left( A \cap S^{-an}A \cap S^{-bn} A \right) < \alpha ^{c\log (1/\alpha )}$
for
![]() $n \ne 0$
, where
$n \ne 0$
, where
![]() $c> 0$
is an absolute constant.Footnote 4
$c> 0$
is an absolute constant.Footnote 4
Let
![]() $\left( X, \mathcal {X}, \nu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
be an ergodic
$\left( X, \mathcal {X}, \nu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
be an ergodic
![]() ${\mathbb Z}^2$
-system and
${\mathbb Z}^2$
-system and
![]() $B \in \mathcal {X}$
with
$B \in \mathcal {X}$
with
![]() $\nu (B) = \alpha $
, such that
$\nu (B) = \alpha $
, such that
for every
![]() $\vec {n},\vec {m} \in {\mathbb Z} \times {\mathbb Z}_{\geq 0}$
(note that, because R is noninvertible, we cannot simply take
$\vec {n},\vec {m} \in {\mathbb Z} \times {\mathbb Z}_{\geq 0}$
(note that, because R is noninvertible, we cannot simply take
![]() $X = \mathbb {T}^2$
,
$X = \mathbb {T}^2$
,
![]() $\nu = \mu $
,
$\nu = \mu $
,
![]() $B = A$
and
$B = A$
and
![]() $T_{\vec {n}} = S^{n_1}R^{n_2}$
). Then, let
$T_{\vec {n}} = S^{n_1}R^{n_2}$
). Then, let
![]() $\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
for
$\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
for
![]() $\vec {n} \in {\mathbb Z}^2$
.
$\vec {n} \in {\mathbb Z}^2$
.
Since
![]() $[{\mathbb Z}^2 : P({\mathbb Z}^2)] = \left| \det (P) \right| = d < \infty $
, the system
$[{\mathbb Z}^2 : P({\mathbb Z}^2)] = \left| \det (P) \right| = d < \infty $
, the system
![]() $\left( X, \mathcal {X}, \nu , (\widetilde {T}_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
has at most d ergodic components. Hence, we may write the ergodic decomposition as
$\left( X, \mathcal {X}, \nu , (\widetilde {T}_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
has at most d ergodic components. Hence, we may write the ergodic decomposition as
![]() $\nu = \frac {1}{k} \sum _{i=1}^k{\nu _i}$
for some
$\nu = \frac {1}{k} \sum _{i=1}^k{\nu _i}$
for some
![]() $k \le d$
and some measure
$k \le d$
and some measure
![]() $\nu _i$
. For some
$\nu _i$
. For some
![]() $1 \le i \le k$
, we must have
$1 \le i \le k$
, we must have
![]() $\nu _i(B) \ge \alpha $
. Without loss of generality, we may therefore assume
$\nu _i(B) \ge \alpha $
. Without loss of generality, we may therefore assume
![]() $\nu _1(B) \ge \alpha $
.
$\nu _1(B) \ge \alpha $
.
Let
![]() $\vec {n} \in {\mathbb Z}^2 \setminus \{0\}$
. Let
$\vec {n} \in {\mathbb Z}^2 \setminus \{0\}$
. Let
![]() $\vec {m} = P\vec {n} \in {\mathbb Z}^2$
. Then
$\vec {m} = P\vec {n} \in {\mathbb Z}^2$
. Then
 $$ \begin{align*} \nu_1 \left( B \cap \widetilde{T}_{M_1\vec{n}}^{-1}B \cap \widetilde{T}_{M_2\vec{n}}^{-1}B \right) & = \nu_1 \left( B \cap T_{(am_1,0)}^{-1}B \cap T_{(bm_1,0)}^{-1}B \right) \\ & \le d \cdot \mu \left( A \cap S^{-am_1}A \cap S^{-bm_1}A \right). \end{align*} $$
$$ \begin{align*} \nu_1 \left( B \cap \widetilde{T}_{M_1\vec{n}}^{-1}B \cap \widetilde{T}_{M_2\vec{n}}^{-1}B \right) & = \nu_1 \left( B \cap T_{(am_1,0)}^{-1}B \cap T_{(bm_1,0)}^{-1}B \right) \\ & \le d \cdot \mu \left( A \cap S^{-am_1}A \cap S^{-bm_1}A \right). \end{align*} $$
Hence, if
![]() $\nu _1 \left( B \cap \widetilde {T}_{M_1\vec {n}}^{-1}B \cap \widetilde {T}_{M_2\vec {n}}^{-1}B \right)> d \cdot \alpha ^{c\log (1/\alpha )}$
, then
$\nu _1 \left( B \cap \widetilde {T}_{M_1\vec {n}}^{-1}B \cap \widetilde {T}_{M_2\vec {n}}^{-1}B \right)> d \cdot \alpha ^{c\log (1/\alpha )}$
, then
![]() $m_1 = 0$
. But since P is nonsingular,
$m_1 = 0$
. But since P is nonsingular,
where
![]() $\vec {v}$
is the vector
$\vec {v}$
is the vector
![]() $P^{-1} \binom {0}{1} \in \mathbb Q^2$
. Such a set is never syndetic, so
$P^{-1} \binom {0}{1} \in \mathbb Q^2$
. Such a set is never syndetic, so
![]() $\text {epdd}_{M_1,M_2}(\alpha ) \le d \cdot \alpha ^{c\log (1/\alpha )}$
. For
$\text {epdd}_{M_1,M_2}(\alpha ) \le d \cdot \alpha ^{c\log (1/\alpha )}$
. For
![]() $c' < c$
and
$c' < c$
and
![]() $\alpha $
sufficiently small, one has
$\alpha $
sufficiently small, one has
![]() $d \cdot \alpha ^{c\log (1/\alpha )} < \alpha ^{c'\log (1/\alpha )}$
, so this completes the proof.
$d \cdot \alpha ^{c\log (1/\alpha )} < \alpha ^{c'\log (1/\alpha )}$
, so this completes the proof.
Now suppose
![]() $r(M_1, M_2) = (1,1,1)$
, and
$r(M_1, M_2) = (1,1,1)$
, and
![]() $M_1$
and
$M_1$
and
![]() $M_2$
do not commute. In this case,
$M_2$
do not commute. In this case,
![]() $M_1$
or
$M_1$
or
![]() $M_2$
must be diagonalisable,Footnote 5 so we assume without loss of generality that
$M_2$
must be diagonalisable,Footnote 5 so we assume without loss of generality that
![]() $M_1$
is diagonalisable. We then distinguish between two cases, depending on the form of
$M_1$
is diagonalisable. We then distinguish between two cases, depending on the form of
![]() $M_2$
when
$M_2$
when
![]() $M_1$
is diagonalised. Call the pair of matrices
$M_1$
is diagonalised. Call the pair of matrices
![]() $(M_1, M_2)$
row-like if there is a nonsingular
$(M_1, M_2)$
row-like if there is a nonsingular
![]() $2\times 2$
matrix P with rational entries and rational numbers
$2\times 2$
matrix P with rational entries and rational numbers
![]() $a, b, c \in \mathbb Q$
with
$a, b, c \in \mathbb Q$
with
![]() $a, b \ne 0$
, such that
$a, b \ne 0$
, such that
 $$ \begin{align*} PM_1P^{-1} = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad PM_2P^{-1} = \left( \begin{array}{cc} c & b \\ 0 & 0 \end{array} \right). \end{align*} $$
$$ \begin{align*} PM_1P^{-1} = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad PM_2P^{-1} = \left( \begin{array}{cc} c & b \\ 0 & 0 \end{array} \right). \end{align*} $$
Similarly, call the pair
![]() $(M_1, M_2)$
column-like if there is a nonsingular
$(M_1, M_2)$
column-like if there is a nonsingular
![]() $2\times 2$
matrix P with rational entries and rational numbers
$2\times 2$
matrix P with rational entries and rational numbers
![]() $a, b, c \in \mathbb Q$
with
$a, b, c \in \mathbb Q$
with
![]() $a, b \ne 0$
, such that
$a, b \ne 0$
, such that
 $$ \begin{align*} PM_1P^{-1} = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad PM_2P^{-1} = \left( \begin{array}{cc} c & 0 \\ b & 0 \end{array} \right). \end{align*} $$
$$ \begin{align*} PM_1P^{-1} = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad PM_2P^{-1} = \left( \begin{array}{cc} c & 0 \\ b & 0 \end{array} \right). \end{align*} $$
For row-like configurations, we can use the ‘Fubini’ property of uniform Cesàro limits (Lemma 2.2) to show
![]() $\text {epdd}(\alpha ) = \alpha ^3$
:
$\text {epdd}(\alpha ) = \alpha ^3$
:
Theorem 7.3. Suppose
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are
$M_2$
are
![]() $2\times 2$
matrices with
$2\times 2$
matrices with
![]() $r(M_1, M_2) = (1,1,1)$
, such that
$r(M_1, M_2) = (1,1,1)$
, such that
![]() $(M_1, M_2)$
is row-like. Then, for any
$(M_1, M_2)$
is row-like. Then, for any
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
![]() $\text {epdd}_{M_1,M_2}(\alpha ) = \alpha ^3$
.
$\text {epdd}_{M_1,M_2}(\alpha ) = \alpha ^3$
.
Proof. Let P be a nonsingular
![]() $2\times 2$
matrix with integer entries, such that
$2\times 2$
matrix with integer entries, such that
 $$ \begin{align*} M_1P = P\left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad M_2P = P\left( \begin{array}{cc} c & b \\ 0 & 0 \end{array} \right). \end{align*} $$
$$ \begin{align*} M_1P = P\left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad M_2P = P\left( \begin{array}{cc} c & b \\ 0 & 0 \end{array} \right). \end{align*} $$
By changing to the basis
![]() $\binom {b}{-c}, \binom {0}{1}$
, we may assume
$\binom {b}{-c}, \binom {0}{1}$
, we may assume
![]() $c = 0$
.
$c = 0$
.
Let
![]() $\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
be a measure-preserving system, and let
$\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
be a measure-preserving system, and let
![]() $A \in \mathcal {X}$
with
$A \in \mathcal {X}$
with
![]() $\mu (A) = \alpha> 0$
. Define a new
$\mu (A) = \alpha> 0$
. Define a new
![]() ${\mathbb Z}^2$
-action by
${\mathbb Z}^2$
-action by
![]() $\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
, and let
$\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
, and let
![]() $S := \widetilde {T}_{(1,0)}$
. Then
$S := \widetilde {T}_{(1,0)}$
. Then
Thus, by Lemma 2.2, we have
Since P is nonsingular, it follows that
Now we will show
![]() $\text {epdd}_{M_1,M_2}(\alpha ) \le \alpha ^3$
. Let P be a nonsingular
$\text {epdd}_{M_1,M_2}(\alpha ) \le \alpha ^3$
. Let P be a nonsingular
![]() $2\times 2$
matrix with integer entries and
$2\times 2$
matrix with integer entries and
![]() $a, b, c \in {\mathbb Z}$
with
$a, b, c \in {\mathbb Z}$
with
![]() $a, b \ne 0$
, such that
$a, b \ne 0$
, such that
 $$ \begin{align*} PM_1 = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right)P \qquad \text{and} \qquad PM_2 = \left( \begin{array}{cc} 0 & b\\ 0 & 0 \end{array} \right)P. \end{align*} $$
$$ \begin{align*} PM_1 = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right)P \qquad \text{and} \qquad PM_2 = \left( \begin{array}{cc} 0 & b\\ 0 & 0 \end{array} \right)P. \end{align*} $$
Let
![]() $\left( X, \mathcal {X}, \mu , S, R \right)$
be an ergodic
$\left( X, \mathcal {X}, \mu , S, R \right)$
be an ergodic
![]() ${\mathbb Z}^2$
-system, such that S is mixing of order 3. Define
${\mathbb Z}^2$
-system, such that S is mixing of order 3. Define
![]() $T_{\vec {n}} := S^{n_1}R^{n_2}$
and
$T_{\vec {n}} := S^{n_1}R^{n_2}$
and
![]() $\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
for
$\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
for
![]() $\vec {n} \in {\mathbb Z}^2$
. Then, for
$\vec {n} \in {\mathbb Z}^2$
. Then, for
![]() $A \in \mathcal {X}$
and
$A \in \mathcal {X}$
and
![]() $\vec {m} = P\vec {n} \in {\mathbb Z}^2$
, we have
$\vec {m} = P\vec {n} \in {\mathbb Z}^2$
, we have
Since S is mixing of order 3, given
![]() $\varepsilon> 0$
, there exists a finite set
$\varepsilon> 0$
, there exists a finite set
![]() $F \subseteq {\mathbb Z}$
, such that
$F \subseteq {\mathbb Z}$
, such that
 $$ \begin{align*} & \left\{ \vec{n} \in {\mathbb Z}^2 : \mu \left( A \cap \widetilde{T}_{M_1\vec{n}}^{-1}A \cap \widetilde{T}_{M_2\vec{n}}^{-1}A \right)> \mu(A)^3 + \varepsilon \right\} \\ & \quad \subseteq P^{-1} \left( \left\{ \vec{m} \in {\mathbb Z}^2 : m_1 \in F, m_2 \in F,~\text{or}~bm_2 - am_1 \in F \right\} \right). \end{align*} $$
$$ \begin{align*} & \left\{ \vec{n} \in {\mathbb Z}^2 : \mu \left( A \cap \widetilde{T}_{M_1\vec{n}}^{-1}A \cap \widetilde{T}_{M_2\vec{n}}^{-1}A \right)> \mu(A)^3 + \varepsilon \right\} \\ & \quad \subseteq P^{-1} \left( \left\{ \vec{m} \in {\mathbb Z}^2 : m_1 \in F, m_2 \in F,~\text{or}~bm_2 - am_1 \in F \right\} \right). \end{align*} $$
This set is a union of finitely many lines in
![]() ${\mathbb Z}^2$
, so it is not syndetic. Hence,
${\mathbb Z}^2$
, so it is not syndetic. Hence,
The prototypical column-like configuration is the class of axis-aligned isosceles right triangles, for which it is known by previous work of Chu [Reference Chu13] and Donoso and Sun [Reference Donoso and Sun16] that
![]() $\alpha ^4 \le \text {epdd}(\alpha ) \le \alpha ^{4-o(1)}$
, where the
$\alpha ^4 \le \text {epdd}(\alpha ) \le \alpha ^{4-o(1)}$
, where the
![]() $o(1)$
term refers to a small positive value tending to
$o(1)$
term refers to a small positive value tending to
![]() $0$
as
$0$
as
![]() $\alpha \to 0$
. We prove that these bounds extend to all column-like configurations:
$\alpha \to 0$
. We prove that these bounds extend to all column-like configurations:
Theorem 7.4. Suppose
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are
$M_2$
are
![]() $2\times 2$
matrices with
$2\times 2$
matrices with
![]() $r(M_1, M_2) = (1,1,1)$
, such that
$r(M_1, M_2) = (1,1,1)$
, such that
![]() $(M_1, M_2)$
is column-like. Then, for any
$(M_1, M_2)$
is column-like. Then, for any
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
![]() $\text {epdd}_{M_1,M_2}(\alpha ) \ge \alpha ^4$
. Moreover, for any
$\text {epdd}_{M_1,M_2}(\alpha ) \ge \alpha ^4$
. Moreover, for any
![]() $l < 4$
and all sufficiently small
$l < 4$
and all sufficiently small
![]() $\alpha $
(depending on l), one has
$\alpha $
(depending on l), one has
![]() $\text {epdd}_{M_1,M_2}(\alpha ) \le \alpha ^l$
.
$\text {epdd}_{M_1,M_2}(\alpha ) \le \alpha ^l$
.
Proof. Let
![]() $\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
be an ergodic
$\left( X, \mathcal {X}, \mu , (T_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
be an ergodic
![]() ${\mathbb Z}^2$
-system. Since the pair
${\mathbb Z}^2$
-system. Since the pair
![]() $(M_1, M_2)$
is column-like, there exists a nonsingular
$(M_1, M_2)$
is column-like, there exists a nonsingular
![]() $2\times 2$
matrix P with integer entries and integers
$2\times 2$
matrix P with integer entries and integers
![]() $a, b, c \in {\mathbb Z}$
with
$a, b, c \in {\mathbb Z}$
with
![]() $a, b \ne 0$
, such that
$a, b \ne 0$
, such that
 $$ \begin{align*} M_1P = P\left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad M_2P = P\left( \begin{array}{cc} c & 0 \\ b & 0 \end{array} \right). \end{align*} $$
$$ \begin{align*} M_1P = P\left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right) \qquad \text{and} \qquad M_2P = P\left( \begin{array}{cc} c & 0 \\ b & 0 \end{array} \right). \end{align*} $$
Then, for any
![]() $\vec {n} \in {\mathbb Z}^2$
, we have
$\vec {n} \in {\mathbb Z}^2$
, we have
Letting
![]() $S := T_{P(a,0)}$
and
$S := T_{P(a,0)}$
and
![]() $R := T_{P(c,b)}$
, we therefore have the identity
$R := T_{P(c,b)}$
, we therefore have the identity
Now, since T is ergodic and P is nonsingular, the
![]() ${\mathbb Z}^2$
-action generated by S and R has finitely many ergodic components. Thus, by [Reference Chu13, Theorem 1.1],
${\mathbb Z}^2$
-action generated by S and R has finitely many ergodic components. Thus, by [Reference Chu13, Theorem 1.1],
is syndetic in
![]() ${\mathbb Z}$
.Footnote 6 It follows that
${\mathbb Z}$
.Footnote 6 It follows that
is syndetic in
![]() ${\mathbb Z}^2$
. Hence,
${\mathbb Z}^2$
. Hence,
![]() $\text {epdd}_{M_1,M_2}(\alpha ) \ge \alpha ^4$
.
$\text {epdd}_{M_1,M_2}(\alpha ) \ge \alpha ^4$
.
Let
![]() $l < 4$
. By [Reference Donoso and Sun16, Theorem 1.2], there exists an ergodic
$l < 4$
. By [Reference Donoso and Sun16, Theorem 1.2], there exists an ergodic
![]() ${\mathbb Z}^2$
-system
${\mathbb Z}^2$
-system
![]() $\left( X, \mathcal {X}, \mu , S, R \right)$
and a set
$\left( X, \mathcal {X}, \mu , S, R \right)$
and a set
![]() $A \in \mathcal {X}$
, such that
$A \in \mathcal {X}$
, such that
![]() $\mu \left( A \cap S^{-n}A \cap R^{-n}A \right) < \mu (A)^l$
for every
$\mu \left( A \cap S^{-n}A \cap R^{-n}A \right) < \mu (A)^l$
for every
![]() $n \ne 0$
. Since the pair
$n \ne 0$
. Since the pair
![]() $(M_1,M_2)$
is column-like, there is a nonsingular
$(M_1,M_2)$
is column-like, there is a nonsingular
![]() $2\times 2$
matrix P with integer entries and integers
$2\times 2$
matrix P with integer entries and integers
![]() $a,b,c \in {\mathbb Z}$
with
$a,b,c \in {\mathbb Z}$
with
![]() $a, b \ne 0$
, such that
$a, b \ne 0$
, such that
 $$ \begin{align*} PM_1 = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right)P \qquad \text{and} \qquad PM_2 = \left( \begin{array}{cc} c & 0 \\ b & 0 \end{array} \right)P. \end{align*} $$
$$ \begin{align*} PM_1 = \left( \begin{array}{cc} a & 0 \\ 0 & 0 \end{array} \right)P \qquad \text{and} \qquad PM_2 = \left( \begin{array}{cc} c & 0 \\ b & 0 \end{array} \right)P. \end{align*} $$
Define
![]() $T_{\vec {n}} := S^{bn_1}(R^aS^{-c})^{n_2}$
, and let
$T_{\vec {n}} := S^{bn_1}(R^aS^{-c})^{n_2}$
, and let
![]() $\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
for
$\widetilde {T}_{\vec {n}} := T_{P\vec {n}}$
for
![]() $n \in {\mathbb Z}^2$
. Note that
$n \in {\mathbb Z}^2$
. Note that
![]() $\left( X, \mathcal {X}, \mu , (\widetilde {T}_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
has finitely many ergodic components. To be more precise, the ergodic decomposition has the form
$\left( X, \mathcal {X}, \mu , (\widetilde {T}_{\vec {n}})_{\vec {n} \in {\mathbb Z}^2} \right)$
has finitely many ergodic components. To be more precise, the ergodic decomposition has the form
![]() $\mu = \frac {1}{k} \sum _{i=1}^k{\mu _i}$
with
$\mu = \frac {1}{k} \sum _{i=1}^k{\mu _i}$
with
![]() $k \le d := \left| ab\det (P) \right|$
. Without loss of generality, we may assume
$k \le d := \left| ab\det (P) \right|$
. Without loss of generality, we may assume
![]() $\mu _1(A) \ge \mu (A)$
.
$\mu _1(A) \ge \mu (A)$
.
Now, for any
![]() $\vec {n} \ne 0$
, we have
$\vec {n} \ne 0$
, we have
where
![]() $\vec {m} = P\vec {n} \in {\mathbb Z}^2$
. Therefore,
$\vec {m} = P\vec {n} \in {\mathbb Z}^2$
. Therefore,
where
![]() $\vec {v} = P^{-1}\binom {0}{1} \in \mathbb Q^2$
. The set
$\vec {v} = P^{-1}\binom {0}{1} \in \mathbb Q^2$
. The set
![]() $\mathbb Q \vec {v} \cap {\mathbb Z}^2$
is not syndetic, so this shows
$\mathbb Q \vec {v} \cap {\mathbb Z}^2$
is not syndetic, so this shows
![]() $\text {epdd}_{M_1,M_2}(\alpha ) \le d \cdot \alpha ^l$
for
$\text {epdd}_{M_1,M_2}(\alpha ) \le d \cdot \alpha ^l$
for
![]() $\alpha = \mu (A)$
. Moreover, for any
$\alpha = \mu (A)$
. Moreover, for any
![]() $l' < l$
, we have the inequality
$l' < l$
, we have the inequality
![]() $d \cdot \alpha ^l < \alpha ^{l'}$
for all
$d \cdot \alpha ^l < \alpha ^{l'}$
for all
![]() $\alpha> 0$
sufficiently small.
$\alpha> 0$
sufficiently small.
7.3 Finitary combinatorial consequences and open questions
There are two cases in which our ergodic-theoretic results directly imply finitary combinatorial analogues. Namely, when
![]() $r(M_1,M_2) = (2,1,1)$
and when
$r(M_1,M_2) = (2,1,1)$
and when
![]() $(M_1,M_2)$
is a row-like pair of noncommuting matrices with
$(M_1,M_2)$
is a row-like pair of noncommuting matrices with
![]() $r(M_1,M_2) = (1,1,1)$
, we establish the bound
$r(M_1,M_2) = (1,1,1)$
, we establish the bound
![]() $\text {epdd}_{M_1,M_2}(\alpha ) \ge \alpha ^3$
with the help of the ‘Fubini’ property for uniform Cesàro limits (Lemma 2.2), and this allows us to avoid assuming that the underlying
$\text {epdd}_{M_1,M_2}(\alpha ) \ge \alpha ^3$
with the help of the ‘Fubini’ property for uniform Cesàro limits (Lemma 2.2), and this allows us to avoid assuming that the underlying
![]() ${\mathbb Z}^2$
-system is ergodic. For this reason, we can obtain the following combinatorial result:
${\mathbb Z}^2$
-system is ergodic. For this reason, we can obtain the following combinatorial result:
Theorem 7.5. Let
![]() $M_1, M_2$
be
$M_1, M_2$
be
![]() $2\times 2$
matrices with integer entries. Suppose that either
$2\times 2$
matrices with integer entries. Suppose that either
-
(i)
 $r(M_1,M_2) = (2,1,1)$
, or
$r(M_1,M_2) = (2,1,1)$
, or -
(ii)
 $r(M_1,M_2) = (1,1,1)$
,
$r(M_1,M_2) = (1,1,1)$
,
 $M_1$
and
$M_1$
and
 $M_2$
do not commute, and
$M_2$
do not commute, and
 $(M_1,M_2)$
is row-like.
$(M_1,M_2)$
is row-like.
Then, for any
![]() $\alpha , \varepsilon> 0$
, there exists
$\alpha , \varepsilon> 0$
, there exists
![]() $N_0 = N_0(\alpha , \varepsilon ) \in \mathbb N$
, such that, if
$N_0 = N_0(\alpha , \varepsilon ) \in \mathbb N$
, such that, if
![]() $N \ge N_0$
and
$N \ge N_0$
and
![]() $A \subseteq \{1, \dots , N\}^2$
has
$A \subseteq \{1, \dots , N\}^2$
has
![]() $|A| \ge \alpha N^2$
, then there exists
$|A| \ge \alpha N^2$
, then there exists
![]() $\vec {n} \in {\mathbb Z}^2$
with
$\vec {n} \in {\mathbb Z}^2$
with
![]() $M_1\vec {n}, M_2\vec {n}, (M_2-M_1)\vec {n} \ne 0$
, such that
$M_1\vec {n}, M_2\vec {n}, (M_2-M_1)\vec {n} \ne 0$
, such that
Proof. Let
![]() $\alpha , \varepsilon> 0$
, and suppose no such
$\alpha , \varepsilon> 0$
, and suppose no such
![]() $N_0$
exists. Then, there is an increasing sequence
$N_0$
exists. Then, there is an increasing sequence
![]() $(N_k)_{k \in \mathbb N}$
in
$(N_k)_{k \in \mathbb N}$
in
![]() $\mathbb N$
and sets
$\mathbb N$
and sets
![]() $A_k \subseteq \{1, \dots , N_k\}^2$
with
$A_k \subseteq \{1, \dots , N_k\}^2$
with
![]() $|A_k| \ge \alpha N_k^2$
, such that
$|A_k| \ge \alpha N_k^2$
, such that
whenever
![]() $M_1\vec {n}, M_2\vec {n}, (M_2-M_1)\vec {n} \ne 0$
.
$M_1\vec {n}, M_2\vec {n}, (M_2-M_1)\vec {n} \ne 0$
.
For notational convenience, let
![]() $A_{k,0} := {\mathbb Z}^2 \setminus A_k$
and
$A_{k,0} := {\mathbb Z}^2 \setminus A_k$
and
![]() $A_{k,1} := A_k$
. By passing to a subsequence if necessary, we may assume without loss of generality that
$A_{k,1} := A_k$
. By passing to a subsequence if necessary, we may assume without loss of generality that
 $$ \begin{align} \lim_{k \to \infty}{\frac{\left| \left( A_{k,i_1} - \vec{n}_1 \right) \cap \dots \cap \left( A_{k,i_r} - \vec{n}_r \right) \cap \{1, \dots, N_k\}^2 \right|}{N_k^2}} \end{align} $$
$$ \begin{align} \lim_{k \to \infty}{\frac{\left| \left( A_{k,i_1} - \vec{n}_1 \right) \cap \dots \cap \left( A_{k,i_r} - \vec{n}_r \right) \cap \{1, \dots, N_k\}^2 \right|}{N_k^2}} \end{align} $$
exists for all
![]() $r \in \mathbb N$
,
$r \in \mathbb N$
,
![]() $\vec {n}_1, \dots , \vec {n}_r \in {\mathbb Z}^2$
and
$\vec {n}_1, \dots , \vec {n}_r \in {\mathbb Z}^2$
and
![]() $i_1, \dots , i_r \in \{0,1\}$
. Hence, we may define a measure
$i_1, \dots , i_r \in \{0,1\}$
. Hence, we may define a measure
![]() $\mu $
on the sequence space
$\mu $
on the sequence space
![]() $\{0,1\}^{{\mathbb Z}^2}$
by setting
$\{0,1\}^{{\mathbb Z}^2}$
by setting
equal to the limit in (40) and extending with the use of Kolmogorov’s extension theorem. Since
![]() $\left( \{1, \dots , N_k\}^2 \right)_{k \in \mathbb N}$
is a Følner sequence in
$\left( \{1, \dots , N_k\}^2 \right)_{k \in \mathbb N}$
is a Følner sequence in
![]() ${\mathbb Z}^2$
, the measure
${\mathbb Z}^2$
, the measure
![]() $\mu $
is invariant under the shift transformations
$\mu $
is invariant under the shift transformations
![]() $(T_{\vec {n}}x)(\vec {m}) := x(\vec {m}+\vec {n})$
.
$(T_{\vec {n}}x)(\vec {m}) := x(\vec {m}+\vec {n})$
.
Let
![]() $A := \{x \in X : x(\vec {0}) = 1\}$
. Then
$A := \{x \in X : x(\vec {0}) = 1\}$
. Then
![]() $\mu (A) = \lim _{k \to \infty }{\frac {|A_k|}{N_k^2}} \ge \alpha $
. On the other hand, if
$\mu (A) = \lim _{k \to \infty }{\frac {|A_k|}{N_k^2}} \ge \alpha $
. On the other hand, if
![]() $M_1\vec {n}, M_2\vec {n}, (M_2-M_1)\vec {n} \ne 0$
, then
$M_1\vec {n}, M_2\vec {n}, (M_2-M_1)\vec {n} \ne 0$
, then
 $$ \begin{align*} \mu \left( A \cap T_{M_1\vec{n}}^{-1}A \cap T_{M_2\vec{n}}^{-1}A \right) & = \mu \left( \{x \in X : x(\vec{0}) = x(M_1\vec{n}) = x(M_2\vec{n}) = 1\} \right) \\ & = \lim_{k \to \infty}{\frac{\left| A_k \cap \left( A_k - M_1\vec{n} \right) \cap \left( A_k - M_2\vec{n} \right) \right|} {N_k^2}} \\ & \le \alpha^3 - \varepsilon. \end{align*} $$
$$ \begin{align*} \mu \left( A \cap T_{M_1\vec{n}}^{-1}A \cap T_{M_2\vec{n}}^{-1}A \right) & = \mu \left( \{x \in X : x(\vec{0}) = x(M_1\vec{n}) = x(M_2\vec{n}) = 1\} \right) \\ & = \lim_{k \to \infty}{\frac{\left| A_k \cap \left( A_k - M_1\vec{n} \right) \cap \left( A_k - M_2\vec{n} \right) \right|} {N_k^2}} \\ & \le \alpha^3 - \varepsilon. \end{align*} $$
Hence,
 $$ \begin{align*} R_{\varepsilon} & := \left\{ \vec{n} \in {\mathbb Z}^2 : \mu \left( A \cap T_{M_1\vec{n}}^{-1}A \cap T_{M_2\vec{n}}^{-1}A \right)> \mu(A)^3 - \varepsilon \right\} \\ & \subseteq \ker(M_1) \cup \ker(M_2) \cup \ker(M_2-M_1). \end{align*} $$
$$ \begin{align*} R_{\varepsilon} & := \left\{ \vec{n} \in {\mathbb Z}^2 : \mu \left( A \cap T_{M_1\vec{n}}^{-1}A \cap T_{M_2\vec{n}}^{-1}A \right)> \mu(A)^3 - \varepsilon \right\} \\ & \subseteq \ker(M_1) \cup \ker(M_2) \cup \ker(M_2-M_1). \end{align*} $$
But by the proofs of Theorems 7.1 and 7.3,
![]() $R_{\varepsilon }$
is a syndetic subset of
$R_{\varepsilon }$
is a syndetic subset of
![]() ${\mathbb Z}^2$
, so this is a contradiction.
${\mathbb Z}^2$
, so this is a contradiction.
For general 3-point matrix patterns in
![]() ${\mathbb Z}^2$
, it remains an open problem to fully determine (finitary combinatorial) popular difference densities. One particularly attractive case, which can be seen as a finitary version of Question 1.12 for the group
${\mathbb Z}^2$
, it remains an open problem to fully determine (finitary combinatorial) popular difference densities. One particularly attractive case, which can be seen as a finitary version of Question 1.12 for the group
![]() $G = {\mathbb Z}^2$
, is the following:
$G = {\mathbb Z}^2$
, is the following:
Conjecture 7.6. Let
![]() $M_1$
and
$M_1$
and
![]() $M_2$
be
$M_2$
be
![]() $2\times 2$
matrices with integer entries, such that
$2\times 2$
matrices with integer entries, such that
![]() $M_2 - M_1$
has full rank. Then, for any
$M_2 - M_1$
has full rank. Then, for any
![]() $\alpha , \varepsilon> 0$
, there exists
$\alpha , \varepsilon> 0$
, there exists
![]() $N_0 = N_0(\alpha , \varepsilon ) \in \mathbb N$
, such that, if
$N_0 = N_0(\alpha , \varepsilon ) \in \mathbb N$
, such that, if
![]() $N \ge N_0$
and
$N \ge N_0$
and
![]() $A \subseteq \{1, \dots , N\}^2$
has cardinality
$A \subseteq \{1, \dots , N\}^2$
has cardinality
![]() $|A| \ge \alpha N^2$
, then there exists
$|A| \ge \alpha N^2$
, then there exists
![]() $\vec {n} \in {\mathbb Z}^2$
with
$\vec {n} \in {\mathbb Z}^2$
with
![]() $M_1\vec {n}, M_2\vec {n} \ne 0$
, such that
$M_1\vec {n}, M_2\vec {n} \ne 0$
, such that
The special case when
![]() $M_1, M_2$
and
$M_1, M_2$
and
![]() $M_2 - M_1$
are all invertible, Conjecture 7.6 was verified by [Reference Berger, Sah, Sawhney and Tidor12, Theorem 1.1]. Moreover, Theorem 7.5 shows that Conjecture 7.6 holds when
$M_2 - M_1$
are all invertible, Conjecture 7.6 was verified by [Reference Berger, Sah, Sawhney and Tidor12, Theorem 1.1]. Moreover, Theorem 7.5 shows that Conjecture 7.6 holds when
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are both rank 1 matrices. The most interesting remaining case is when
$M_2$
are both rank 1 matrices. The most interesting remaining case is when
![]() $M_1$
has full rank and
$M_1$
has full rank and
![]() $M_2$
is a rank 1 matrix.
$M_2$
is a rank 1 matrix.
Finally, the column-like family of configurations
![]() $\{(a,b), (a+n,b), (a,b+n)\}$
, known as corners, has been well studied from the perspective of popular differences in finitary combinatorics. In particular, it is known that the popular difference density for corners is of the form
$\{(a,b), (a+n,b), (a,b+n)\}$
, known as corners, has been well studied from the perspective of popular differences in finitary combinatorics. In particular, it is known that the popular difference density for corners is of the form
![]() $\alpha ^{4-o(1)}$
(see [Reference Berger11] and also [Reference Fox, Sah, Sawhney, Stoner and Zhao17, Reference Mandache25] for an analogous result in a finite characteristic setting). To the authors’ knowledge, such results are not known for general column-like matrix patterns, but we anticipate that techniques for handling corners should apply in this generality with only minor modifications needed.
$\alpha ^{4-o(1)}$
(see [Reference Berger11] and also [Reference Fox, Sah, Sawhney, Stoner and Zhao17, Reference Mandache25] for an analogous result in a finite characteristic setting). To the authors’ knowledge, such results are not known for general column-like matrix patterns, but we anticipate that techniques for handling corners should apply in this generality with only minor modifications needed.
8 Khintchine-type recurrence for actions of semigroups
As a consequence of Theorem 1.13, we obtain the following combinatorial result. For any set
![]() $E \subseteq \mathbb Q_{>0}$
of positive multiplicative upper Banach density
$E \subseteq \mathbb Q_{>0}$
of positive multiplicative upper Banach density
![]() $d^*_{mult}(E)> 0$
and any
$d^*_{mult}(E)> 0$
and any
![]() $\varepsilon> 0$
, there exists
$\varepsilon> 0$
, there exists
![]() $q \in \mathbb Q_{>0} \setminus \{1\}$
, such that
$q \in \mathbb Q_{>0} \setminus \{1\}$
, such that
(in fact, the set of such q is multiplicatively syndetic). More generally, for any countable field
![]() $\mathbb F$
, any set
$\mathbb F$
, any set
![]() $E \subseteq \mathbb F^{\times }$
of positive multiplicative upper Banach density
$E \subseteq \mathbb F^{\times }$
of positive multiplicative upper Banach density
![]() $d_{mult}^*(E)> 0$
and any
$d_{mult}^*(E)> 0$
and any
![]() $\varepsilon> 0$
, the set of
$\varepsilon> 0$
, the set of
![]() $x \in \mathbb F^{\times }$
, such that
$x \in \mathbb F^{\times }$
, such that
is multiplicatively syndetic.Footnote 7 This is suggestive of the following problem. Let R be an integral domain (for example, R can be the ring
![]() ${\mathbb Z}$
, the ring of integers of a number field or the polynomial ring
${\mathbb Z}$
, the ring of integers of a number field or the polynomial ring
![]() $\mathbb F[t]$
over a finite field
$\mathbb F[t]$
over a finite field
![]() $\mathbb F$
). Given a set
$\mathbb F$
). Given a set
![]() $E \subseteq R^{\times }$
of positive multiplicative upper Banach density
$E \subseteq R^{\times }$
of positive multiplicative upper Banach density
![]() $d^*_{R, mult}(E)> 0$
and
$d^*_{R, mult}(E)> 0$
and
![]() $\varepsilon> 0$
, does there exist
$\varepsilon> 0$
, does there exist
![]() $r \in R \setminus \{1\}$
, such that
$r \in R \setminus \{1\}$
, such that
where
![]() $E/r := \left\{ t \in R : rt \in E \right\}$
for
$E/r := \left\{ t \in R : rt \in E \right\}$
for
![]() $r \in R$
? The goal of this section is to transfer our results into the setting of cancellative abelian semigroups in order to answer this question affirmatively.
$r \in R$
? The goal of this section is to transfer our results into the setting of cancellative abelian semigroups in order to answer this question affirmatively.
8.1 The group generated by a cancellative abelian semigroup
Let
![]() $(S, +)$
be a countable cancellative abelian semigroup. That is, S is a countable set equipped with a commutative and associative binary operation
$(S, +)$
be a countable cancellative abelian semigroup. That is, S is a countable set equipped with a commutative and associative binary operation
![]() $+$
, such that if
$+$
, such that if
![]() $s + t = s + r$
for some
$s + t = s + r$
for some
![]() $r, s, t \in S$
, then
$r, s, t \in S$
, then
![]() $t = r$
.
$t = r$
.
We can define a group
![]() $G_S$
as the set of formal differences
$G_S$
as the set of formal differences
![]() $\left\{ s - t : s, t \in S \right\}$
where we identify
$\left\{ s - t : s, t \in S \right\}$
where we identify
![]() $s - t$
and
$s - t$
and
![]() $s' - t'$
if
$s' - t'$
if
![]() $s+t' = s'+t$
. More formally, we may define an equivalence relation
$s+t' = s'+t$
. More formally, we may define an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $S^2$
by
$S^2$
by
![]() $(s,t) \sim (s',t')$
if
$(s,t) \sim (s',t')$
if
![]() $s+t' = s'+t$
. Then
$s+t' = s'+t$
. Then
![]() $G_S$
is the set of equivalence classes
$G_S$
is the set of equivalence classes
![]() $S^2/\sim $
with the operation
$S^2/\sim $
with the operation
![]() $[(s,t)] + [(s',t')] := [(s+s', t+t')]$
. It is easy to check that this operation is well defined because S is cancellative. Moreover,
$[(s,t)] + [(s',t')] := [(s+s', t+t')]$
. It is easy to check that this operation is well defined because S is cancellative. Moreover,
![]() $G_S$
has an identity
$G_S$
has an identity
![]() $0 := [(s,s)]$
, and for any
$0 := [(s,s)]$
, and for any
![]() $s, t \in S$
, we have
$s, t \in S$
, we have
![]() $[(s,t)] + [(t,s)] = 0$
. Thus,
$[(s,t)] + [(t,s)] = 0$
. Thus,
![]() $G_S$
is a group. Note that there is a natural embedding
$G_S$
is a group. Note that there is a natural embedding
![]() $S \to G_S$
given by
$S \to G_S$
given by
![]() $s\mapsto [(s+s,s)]$
.
$s\mapsto [(s+s,s)]$
.
8.2 Notions of largeness
For a set
![]() $E \subseteq S$
and an element
$E \subseteq S$
and an element
![]() $t \in S$
, let
$t \in S$
, let
![]() $E - t := \{s \in S : s+t \in E\}$
and
$E - t := \{s \in S : s+t \in E\}$
and
![]() $E + t := \{s+t : s \in S\}$
. The following definition summarises combinatorial notions of largeness that we will use, some of which are defined above in the setting of abelian groups.
$E + t := \{s+t : s \in S\}$
. The following definition summarises combinatorial notions of largeness that we will use, some of which are defined above in the setting of abelian groups.
Definition 8.1. Let
![]() $(S, +)$
be a countable cancellative abelian semigroup.
$(S, +)$
be a countable cancellative abelian semigroup.
-
○ A set
 $E \subseteq S$
is syndetic if there are finitely many elements
$E \subseteq S$
is syndetic if there are finitely many elements
 $t_1, \dots , t_k \in S$
, such that
$t_1, \dots , t_k \in S$
, such that
 $\bigcup _{i=1}^k{(E - t_i)} = S$
.
$\bigcup _{i=1}^k{(E - t_i)} = S$
. -
○ A set
 $T \subseteq S$
is thick if for any finite set
$T \subseteq S$
is thick if for any finite set
 $F \subseteq S$
, there exists
$F \subseteq S$
, there exists
 $t \in S$
, such that
$t \in S$
, such that
 $F + t \subseteq T$
.
$F + t \subseteq T$
. -
○ A set
 $P \subseteq S$
is piecewise syndetic if there is a syndetic set
$P \subseteq S$
is piecewise syndetic if there is a syndetic set
 $E \subseteq S$
and a thick set
$E \subseteq S$
and a thick set
 $T \subseteq S$
, such that
$T \subseteq S$
, such that
 $P = E \cap T$
.
$P = E \cap T$
. -
○ A sequence
 $(F_N)_{N \in \mathbb N}$
of finite subsets of S is a Følner sequence if, for any
$(F_N)_{N \in \mathbb N}$
of finite subsets of S is a Følner sequence if, for any
 $t \in S$
,
$t \in S$
,  $$ \begin{align*} \frac{\left| (F_N+t) \triangle F_N \right|}{|F_N|} \to 0. \end{align*} $$
$$ \begin{align*} \frac{\left| (F_N+t) \triangle F_N \right|}{|F_N|} \to 0. \end{align*} $$
-
○ The lower Banach density of a set
 $E \subseteq S$
is the quantity
$E \subseteq S$
is the quantity  $$ \begin{align*} d_*(E) := \inf{\left\{ \liminf_{N \to \infty}{\frac{\left| E \cap F_N \right|}{|F_N|}} : (F_N)_{N \in \mathbb N} \text{ is a F}{\unicode{xf8}}\text{lner sequence in } S \right\}}. \end{align*} $$
$$ \begin{align*} d_*(E) := \inf{\left\{ \liminf_{N \to \infty}{\frac{\left| E \cap F_N \right|}{|F_N|}} : (F_N)_{N \in \mathbb N} \text{ is a F}{\unicode{xf8}}\text{lner sequence in } S \right\}}. \end{align*} $$
-
○ The upper Banach density of a set
 $E \subseteq S$
is the quantity
$E \subseteq S$
is the quantity  $$ \begin{align*} d^*(E) := \sup{\left\{ \limsup_{N \to \infty}{\frac{\left| E \cap F_N \right|}{|F_N|}} : (F_N)_{N \in \mathbb N} \text{ is a F}{\unicode{xf8}}\text{lner sequence in } S \right\}}. \end{align*} $$
$$ \begin{align*} d^*(E) := \sup{\left\{ \limsup_{N \to \infty}{\frac{\left| E \cap F_N \right|}{|F_N|}} : (F_N)_{N \in \mathbb N} \text{ is a F}{\unicode{xf8}}\text{lner sequence in } S \right\}}. \end{align*} $$
The following is a standard characterisation of syndetic and thick sets (see, e.g. [Reference Bergelson, Hindman and McCutcheon7, Section 2]).
Proposition 8.2. Let
![]() $(S, +)$
be a countable cancellative abelian semigroup.
$(S, +)$
be a countable cancellative abelian semigroup.
-
1. E is syndetic if and only if
 $d_*(E)> 0$
if and only if
$d_*(E)> 0$
if and only if
 $E \cap T \ne \emptyset $
for any thick set
$E \cap T \ne \emptyset $
for any thick set
 $T \subseteq S$
;
$T \subseteq S$
; -
2. T is thick if and only if
 $d^*(T) = 1$
if and only if
$d^*(T) = 1$
if and only if
 $T \cap E \ne \emptyset $
for any syndetic set
$T \cap E \ne \emptyset $
for any syndetic set
 $E \subseteq S$
.
$E \subseteq S$
.
Lemma 8.3. Let
![]() $(S,+)$
be a countable cancellative abelian semigroup. Then S is thick in
$(S,+)$
be a countable cancellative abelian semigroup. Then S is thick in
![]() $G_S$
.
$G_S$
.
Proof. Let
![]() $F \subseteq G_S$
be a finite set. Write
$F \subseteq G_S$
be a finite set. Write
![]() $F = \{s_i - t_i : 1 \le i \le k\}$
, where
$F = \{s_i - t_i : 1 \le i \le k\}$
, where
![]() $s_i, t_i \in S$
. Put
$s_i, t_i \in S$
. Put
![]() $t = \sum _{i=1}^k{t_i} \in S$
. Then
$t = \sum _{i=1}^k{t_i} \in S$
. Then
 $$ \begin{align*} F + t = \left\{ s_i + \sum_{j \ne i}{t_j} : 1 \le i \le k \right\} \subseteq S. \end{align*} $$
$$ \begin{align*} F + t = \left\{ s_i + \sum_{j \ne i}{t_j} : 1 \le i \le k \right\} \subseteq S. \end{align*} $$
The fact that S is thick in
![]() $G_S$
is closely related to the fact that any Følner sequence in S is also a Følner sequence in
$G_S$
is closely related to the fact that any Følner sequence in S is also a Følner sequence in
![]() $G_S$
, from which we deduce the following density result:
$G_S$
, from which we deduce the following density result:
Proposition 8.4. Let
![]() $E \subseteq S$
. Then
$E \subseteq S$
. Then
![]() $d_S^*(E) = d_{G_S}^*(E)$
.
$d_S^*(E) = d_{G_S}^*(E)$
.
Proof. To show the inequality
![]() $d_{G_S}^*(E) \ge d_S^*(E)$
, it suffices to show that any Følner sequence in S is a Følner sequence in
$d_{G_S}^*(E) \ge d_S^*(E)$
, it suffices to show that any Følner sequence in S is a Følner sequence in
![]() $G_S$
. Let
$G_S$
. Let
![]() $(F_N)_{N \in \mathbb N}$
be a Følner sequence in S, and let
$(F_N)_{N \in \mathbb N}$
be a Følner sequence in S, and let
![]() $x \in G_S$
. We want to show
$x \in G_S$
. We want to show
Write
![]() $x = s-t$
with
$x = s-t$
with
![]() $s, t \in S$
. Then
$s, t \in S$
. Then
Hence,
![]() $(F_N)_{N \in \mathbb N}$
is a Følner sequence in
$(F_N)_{N \in \mathbb N}$
is a Følner sequence in
![]() $G_S$
as claimed.
$G_S$
as claimed.
Now we show the reverse inequality
![]() $d_S^*(E) \ge d_{G_S}^*(E)$
. If
$d_S^*(E) \ge d_{G_S}^*(E)$
. If
![]() $d_{G_S}^*(E) = 0$
, there is nothing to show, so assume
$d_{G_S}^*(E) = 0$
, there is nothing to show, so assume
![]() $d_{G_S}^*(E)> 0$
. Let m be an invariant mean on
$d_{G_S}^*(E)> 0$
. Let m be an invariant mean on
![]() $G_S$
, such that
$G_S$
, such that
![]() $m(E) = d_{G_S}^*(E)$
. Put
$m(E) = d_{G_S}^*(E)$
. Put
![]() $c = m(S) \ge m(E)> 0$
. Then,
$c = m(S) \ge m(E)> 0$
. Then,
![]() $\widetilde {m} := \frac {1}{c}m$
is an invariant mean on S. Moreover,
$\widetilde {m} := \frac {1}{c}m$
is an invariant mean on S. Moreover,
![]() $\widetilde {m}(E) = \frac {1}{c}m(E) \ge m(E) = d_{G_S}^*(E)$
. Therefore,
$\widetilde {m}(E) = \frac {1}{c}m(E) \ge m(E) = d_{G_S}^*(E)$
. Therefore,
![]() $d_S^*(E) \ge \widetilde {m}(E) \ge d_{G_S}^*(E)$
.
$d_S^*(E) \ge \widetilde {m}(E) \ge d_{G_S}^*(E)$
.
Lemma 8.5. Suppose
![]() $E \subseteq G_S$
is syndetic in
$E \subseteq G_S$
is syndetic in
![]() $G_S$
. Then,
$G_S$
. Then,
![]() $E \cap S$
is syndetic in S.
$E \cap S$
is syndetic in S.
Proof. Let
![]() $x_1, \dots , x_k \in G_S$
, such that
$x_1, \dots , x_k \in G_S$
, such that
![]() $\bigcup _{i=1}^k{(E - x_i)} = G_S$
. By Lemma 8.3, S is thick, so we may assume
$\bigcup _{i=1}^k{(E - x_i)} = G_S$
. By Lemma 8.3, S is thick, so we may assume
![]() $x_i \in S$
for each
$x_i \in S$
for each
![]() $i = 1, \dots , k$
. We claim
$i = 1, \dots , k$
. We claim
 $$ \begin{align*} \bigcup_{i=1}^k{\left( (E \cap S) - x_i \right)} \supseteq S. \end{align*} $$
$$ \begin{align*} \bigcup_{i=1}^k{\left( (E \cap S) - x_i \right)} \supseteq S. \end{align*} $$
It suffices to check
![]() $(E \cap S) - x_i \supseteq (E - x_i) \cap S$
for each
$(E \cap S) - x_i \supseteq (E - x_i) \cap S$
for each
![]() $i = 1, \dots , k$
. Suppose
$i = 1, \dots , k$
. Suppose
![]() $y \in (E - x_i) \cap S$
, and let
$y \in (E - x_i) \cap S$
, and let
![]() $t \in E$
, such that
$t \in E$
, such that
![]() $t - x_i = y$
. Then,
$t - x_i = y$
. Then,
![]() $t = y + x_i \in S + S \subseteq S$
. Hence,
$t = y + x_i \in S + S \subseteq S$
. Hence,
![]() $y \in (E \cap S) - x_i$
as desired.
$y \in (E \cap S) - x_i$
as desired.
8.3 Extending main results to actions of cancellative abelian semigroups
Any homomorphism
![]() $\varphi : S \to S$
extends uniquely to a homomorphism
$\varphi : S \to S$
extends uniquely to a homomorphism
![]() $\widetilde {\varphi } : G_S \to G_S$
via
$\widetilde {\varphi } : G_S \to G_S$
via
![]() $\widetilde {\varphi } \left( s - t \right) = \varphi (s) - \varphi (t)$
. To extend our Khintchine-type results to the semigroup setting, we need a condition on
$\widetilde {\varphi } \left( s - t \right) = \varphi (s) - \varphi (t)$
. To extend our Khintchine-type results to the semigroup setting, we need a condition on
![]() $\varphi $
characterising when
$\varphi $
characterising when
![]() $\widetilde {\varphi }(G_S)$
has finite index in
$\widetilde {\varphi }(G_S)$
has finite index in
![]() $G_S$
.
$G_S$
.
Proposition 8.6. Let
![]() $(S, +)$
be a countable cancellative abelian semigroup. Let
$(S, +)$
be a countable cancellative abelian semigroup. Let
![]() $\varphi : S \to S$
be a homomorphism, and let
$\varphi : S \to S$
be a homomorphism, and let
![]() $\widetilde {\varphi } : G_S \to G_S$
be the group homomorphism
$\widetilde {\varphi } : G_S \to G_S$
be the group homomorphism
![]() $\widetilde {\varphi }(s-t) := \varphi (s) - \varphi (t)$
. The following are equivalent:
$\widetilde {\varphi }(s-t) := \varphi (s) - \varphi (t)$
. The following are equivalent:
-
(i)
 $\varphi (S)$
is a piecewise syndetic subset of S;
$\varphi (S)$
is a piecewise syndetic subset of S; -
(ii)
 $\widetilde {\varphi }(G_S)$
has finite index in
$\widetilde {\varphi }(G_S)$
has finite index in
 $G_S$
.
$G_S$
.
Proof. Let
![]() $T := \varphi (S)$
, and let
$T := \varphi (S)$
, and let
![]() $H := \widetilde {\varphi }(G_S)$
. Note that
$H := \widetilde {\varphi }(G_S)$
. Note that
![]() $H = T - T = G_T$
.
$H = T - T = G_T$
.
(i)
![]() $\implies $
(ii). Suppose T is piecewise syndetic in S. Then,
$\implies $
(ii). Suppose T is piecewise syndetic in S. Then,
![]() $d_S^*(T)> 0$
. Thus, by Proposition 8.4,
$d_S^*(T)> 0$
. Thus, by Proposition 8.4,
![]() $d_{G_S}^*(H) \ge d_{G_S}^*(T) = d_S^*(T)> 0$
. But in the group
$d_{G_S}^*(H) \ge d_{G_S}^*(T) = d_S^*(T)> 0$
. But in the group
![]() $G_S$
, we have the identity
$G_S$
, we have the identity
so
![]() $[G_S:H] < \infty $
.
$[G_S:H] < \infty $
.
(ii)
![]() $\implies $
(i). Suppose H has finite index in
$\implies $
(i). Suppose H has finite index in
![]() $G_S$
. Then, H is a syndetic subset of
$G_S$
. Then, H is a syndetic subset of
![]() $G_S$
, so
$G_S$
, so
![]() $H \cap S$
is syndetic in S by Lemma 8.5. Moreover, by Lemma 8.3, T is a thick subset of H. Let
$H \cap S$
is syndetic in S by Lemma 8.5. Moreover, by Lemma 8.3, T is a thick subset of H. Let
![]() $\widetilde {T} := T \cup (S \setminus H)$
so that
$\widetilde {T} := T \cup (S \setminus H)$
so that
![]() $T = \widetilde {T} \cap (H \cap S)$
. We claim that
$T = \widetilde {T} \cap (H \cap S)$
. We claim that
![]() $\widetilde {T}$
is thick in S.
$\widetilde {T}$
is thick in S.
Let
![]() $F \subseteq S$
be a finite set. Put
$F \subseteq S$
be a finite set. Put
![]() $F_1 = F \cap H$
and
$F_1 = F \cap H$
and
![]() $F_2 = F \setminus H$
. Since T is a thick subset of H, there exists
$F_2 = F \setminus H$
. Since T is a thick subset of H, there exists
![]() $x \in H$
, such that
$x \in H$
, such that
![]() $F_1 + x \subseteq T$
. Write
$F_1 + x \subseteq T$
. Write
![]() $x = s - t$
with
$x = s - t$
with
![]() $s, t \in T \subseteq H \cap S$
. Then,
$s, t \in T \subseteq H \cap S$
. Then,
![]() $F_1 + s = F_1 + x + t \subseteq T + t \subseteq T$
. Now, since
$F_1 + s = F_1 + x + t \subseteq T + t \subseteq T$
. Now, since
![]() $s \in H \cap S$
and H is a group, we have
$s \in H \cap S$
and H is a group, we have
![]() $F_2 + s \subseteq S \setminus H$
. Thus,
$F_2 + s \subseteq S \setminus H$
. Thus,
![]() $F + s = (F_1 + s) \cup (F_2 + s) \subseteq T \cup (S \setminus H) = \widetilde {T}$
.
$F + s = (F_1 + s) \cup (F_2 + s) \subseteq T \cup (S \setminus H) = \widetilde {T}$
.
This shows that
![]() $\widetilde {T}$
is a thick subset of S, so
$\widetilde {T}$
is a thick subset of S, so
![]() $T = \widetilde {T} \cap (H \cap S)$
is piecewise syndetic in S.
$T = \widetilde {T} \cap (H \cap S)$
is piecewise syndetic in S.
Now we can extend Theorems 1.11 and 1.13 to the semigroup setting:
Theorem 8.7. Let
![]() $(S, +)$
be a countable cancellative abelian semigroup. Let
$(S, +)$
be a countable cancellative abelian semigroup. Let
![]() $\varphi , \psi : S \to S$
be homomorphisms. If at least two of the three subsemigroups
$\varphi , \psi : S \to S$
be homomorphisms. If at least two of the three subsemigroups
![]() $\varphi (S)$
,
$\varphi (S)$
,
![]() $\psi (S)$
and
$\psi (S)$
and
![]() $(\varphi + \psi )(S)$
are piecewise syndetic in S, then, for any set
$(\varphi + \psi )(S)$
are piecewise syndetic in S, then, for any set
![]() $E \subseteq S$
with positive upper Banach density
$E \subseteq S$
with positive upper Banach density
![]() $d_S^*(E)> 0$
and any
$d_S^*(E)> 0$
and any
![]() $\varepsilon> 0$
, the set
$\varepsilon> 0$
, the set
is syndetic in S.
Remark 8.8. We use the pair
![]() $\{\varphi , \varphi + \psi \}$
rather than
$\{\varphi , \varphi + \psi \}$
rather than
![]() $\{\varphi , \psi \}$
since the difference
$\{\varphi , \psi \}$
since the difference
![]() $\psi - \varphi $
is not necessarily defined as a map into S.
$\psi - \varphi $
is not necessarily defined as a map into S.
Proof. By Proposition 8.4, we have
![]() $\delta := d_{G_S}^*(E) = d_S^*(E)> 0$
. Let
$\delta := d_{G_S}^*(E) = d_S^*(E)> 0$
. Let
![]() $\widetilde {\varphi }$
and
$\widetilde {\varphi }$
and
![]() $\widetilde {\psi }$
be the extensions of
$\widetilde {\psi }$
be the extensions of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
to
$\psi $
to
![]() $G_S$
. By Proposition 8.6, at least two of the subgroups
$G_S$
. By Proposition 8.6, at least two of the subgroups
![]() $\widetilde {\varphi }(G_S)$
,
$\widetilde {\varphi }(G_S)$
,
![]() $\widetilde {\psi }(G_S)$
and
$\widetilde {\psi }(G_S)$
and
![]() $\left( \widetilde {\varphi } + \widetilde {\psi } \right)(G_S)$
have finite index in
$\left( \widetilde {\varphi } + \widetilde {\psi } \right)(G_S)$
have finite index in
![]() $G_S$
. Hence, by Theorem 1.11, the set
$G_S$
. Hence, by Theorem 1.11, the set
is syndetic in
![]() $G_S$
.
$G_S$
.
By Lemma 8.5, the set
![]() $R \cap S$
is syndetic in S. But
$R \cap S$
is syndetic in S. But
so this completes the proof.
Theorem 8.9. Let
![]() $(S, +)$
be a countable cancellative abelian semigroup. Let
$(S, +)$
be a countable cancellative abelian semigroup. Let
![]() $a, b \in \mathbb N$
. If at least one of the three subsemigroups
$a, b \in \mathbb N$
. If at least one of the three subsemigroups
![]() $aS$
,
$aS$
,
![]() $bS$
or
$bS$
or
![]() $(a+b)S$
is piecewise syndetic in S, then, for any set
$(a+b)S$
is piecewise syndetic in S, then, for any set
![]() $E \subseteq S$
with positive upper Banach density
$E \subseteq S$
with positive upper Banach density
![]() $d_S^*(E)> 0$
and any
$d_S^*(E)> 0$
and any
![]() $\varepsilon> 0$
, the set
$\varepsilon> 0$
, the set
is syndetic in S.
8.4 Two combinatorial questions
Applying Theorem 8.9 in the semigroup
![]() $(\mathbb N, \cdot )$
, for any
$(\mathbb N, \cdot )$
, for any
![]() $E \subseteq \mathbb N$
with positive multiplicative upper Banach density
$E \subseteq \mathbb N$
with positive multiplicative upper Banach density
![]() $d_{mult}^*(E)> 0$
, any
$d_{mult}^*(E)> 0$
, any
![]() $k \in \mathbb N$
and any
$k \in \mathbb N$
and any
![]() $\varepsilon> 0$
, the set of
$\varepsilon> 0$
, the set of
![]() $m \in \mathbb N$
, such that
$m \in \mathbb N$
, such that
is multiplicatively syndetic in
![]() $\mathbb N$
. It is natural to ask if a finitary variant of this result holds.
$\mathbb N$
. It is natural to ask if a finitary variant of this result holds.
Question 8.10. Let
![]() $p_1, p_2, \dots $
be an enumeration of the positive prime numbers. Let
$p_1, p_2, \dots $
be an enumeration of the positive prime numbers. Let
![]() $\delta , \varepsilon> 0$
, and let
$\delta , \varepsilon> 0$
, and let
![]() $k \in \mathbb N$
. Does there exists
$k \in \mathbb N$
. Does there exists
![]() $N = N(k, \delta , \varepsilon ) \in \mathbb N$
, such that the following holds: for any
$N = N(k, \delta , \varepsilon ) \in \mathbb N$
, such that the following holds: for any
![]() $n \ge N$
and any set
$n \ge N$
and any set
![]() $A \subseteq \left\{ p_1^{r_1} \dots p_n^{r_n} : 0 \le r_i \le n \right\}$
with
$A \subseteq \left\{ p_1^{r_1} \dots p_n^{r_n} : 0 \le r_i \le n \right\}$
with
![]() $|A| \ge \delta n^n$
, there exists
$|A| \ge \delta n^n$
, there exists
![]() $y \in \mathbb N \setminus \{1\}$
, such that
$y \in \mathbb N \setminus \{1\}$
, such that
Now, we describe an application of Theorem 8.7. Let
![]() $p_1, p_2, \dots $
and
$p_1, p_2, \dots $
and
![]() $q_1, q_2, \dots $
be enumerations of the positive prime numbers. The map
$q_1, q_2, \dots $
be enumerations of the positive prime numbers. The map
![]() $\varphi : \mathbb N \to \mathbb N$
defined by
$\varphi : \mathbb N \to \mathbb N$
defined by
![]() $\varphi \left( \prod _{i=1}^n{p_i^{r_i}} \right) := \prod _{i=1}^n{q_i^{r_i}}$
is an automorphism of the semigroup
$\varphi \left( \prod _{i=1}^n{p_i^{r_i}} \right) := \prod _{i=1}^n{q_i^{r_i}}$
is an automorphism of the semigroup
![]() $(\mathbb N, \cdot )$
. Hence, by Theorem 8.7, if
$(\mathbb N, \cdot )$
. Hence, by Theorem 8.7, if
![]() $E \subseteq \mathbb N$
has positive multiplicative upper Banach density
$E \subseteq \mathbb N$
has positive multiplicative upper Banach density
![]() $d_{mult}^*(E)> 0$
and
$d_{mult}^*(E)> 0$
and
![]() $\varepsilon> 0$
, then there is a multiplicatively syndetic set of numbers
$\varepsilon> 0$
, then there is a multiplicatively syndetic set of numbers
![]() $y = \prod _{i=1}^n{p_i^{r_i}} \in \mathbb N$
, such that
$y = \prod _{i=1}^n{p_i^{r_i}} \in \mathbb N$
, such that
 $$ \begin{align} d_{mult}^* \left( \left\{x \in \mathbb N : \left\{ x, x\prod_{i=1}^n{p_i^{r_i}}, x\prod_{i=1}^n{q_i^{r_i}} \right\} \subseteq E \right\} \right)> d_{mult}^*(E)^3 - \varepsilon. \end{align} $$
$$ \begin{align} d_{mult}^* \left( \left\{x \in \mathbb N : \left\{ x, x\prod_{i=1}^n{p_i^{r_i}}, x\prod_{i=1}^n{q_i^{r_i}} \right\} \subseteq E \right\} \right)> d_{mult}^*(E)^3 - \varepsilon. \end{align} $$
The IP Szemerédi theorem of Furstenberg and Katznelson [Reference Furstenberg and Katznelson20] implies that, for any
![]() $k \in \mathbb N$
and any multiplicative automorphisms
$k \in \mathbb N$
and any multiplicative automorphisms
![]() $\varphi _1, \dots , \varphi _k : \mathbb N \to \mathbb N$
, the set of
$\varphi _1, \dots , \varphi _k : \mathbb N \to \mathbb N$
, the set of
![]() $m \in \mathbb N$
, such that
$m \in \mathbb N$
, such that
is a multiplicative IP
![]() $^*$
set and, hence, multiplicatively syndetic. It is therefore natural to ask if a large intersections variant holds for families of more than two multiplicative automorphisms:
$^*$
set and, hence, multiplicatively syndetic. It is therefore natural to ask if a large intersections variant holds for families of more than two multiplicative automorphisms:
Question 8.11. Let
![]() $p_1, p_2, \dots $
be the enumeration of the positive prime numbers in increasing order. For each
$p_1, p_2, \dots $
be the enumeration of the positive prime numbers in increasing order. For each
![]() $j \in \mathbb N$
, let
$j \in \mathbb N$
, let
![]() $q_{j,1}, q_{j,2}, \dots $
be a distinct enumeration of the positive prime numbers. For which
$q_{j,1}, q_{j,2}, \dots $
be a distinct enumeration of the positive prime numbers. For which
![]() $k \in \mathbb N$
does the following hold: for any
$k \in \mathbb N$
does the following hold: for any
![]() $E \subseteq \mathbb N$
with
$E \subseteq \mathbb N$
with
![]() $d_{mult}^*(E)> 0$
and any
$d_{mult}^*(E)> 0$
and any
![]() $\varepsilon> 0$
, there exists
$\varepsilon> 0$
, there exists
![]() $y = \prod _{i=1}^n{p_i^{r_i}} \in \mathbb N \setminus \{1\}$
, such that
$y = \prod _{i=1}^n{p_i^{r_i}} \in \mathbb N \setminus \{1\}$
, such that
 $$ \begin{align} d_{mult}^* \left( \left\{x \in \mathbb N : \left\{ x, x\prod_{i=1}^n{q_{1,i}^{r_i}}, x\prod_{i=1}^n{q_{2,i}^{r_i}} , \dots, x\prod_{i=1}^n{q_{k,i}^{r_i}} \right\} \subseteq E \right\} \right)> d_{mult}^*(E)^{k+1} - \varepsilon. \end{align} $$
$$ \begin{align} d_{mult}^* \left( \left\{x \in \mathbb N : \left\{ x, x\prod_{i=1}^n{q_{1,i}^{r_i}}, x\prod_{i=1}^n{q_{2,i}^{r_i}} , \dots, x\prod_{i=1}^n{q_{k,i}^{r_i}} \right\} \subseteq E \right\} \right)> d_{mult}^*(E)^{k+1} - \varepsilon. \end{align} $$
Note that (42) holds for
![]() $k \le 2$
(see (41) and the discussion above).
$k \le 2$
(see (41) and the discussion above).
A Proof of Lemma 3.6
In this section we prove Lemma 3.6, restated here for the convenience of the reader:
Lemma A.1 (Lemma 3.5)
Let
![]() $(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be a G-system, and let
$(X,\mathcal {X},\mu , (T_g)_{g\in G})$
be a G-system, and let
![]() $H\leq G$
be a subgroup of finite index. Then, for every
$H\leq G$
be a subgroup of finite index. Then, for every
![]() $k\geq 1$
, one has
$k\geq 1$
, one has
![]() $\mathcal {Z}^k_H(X) = \mathcal {Z}^k_G(X)$
.
$\mathcal {Z}^k_H(X) = \mathcal {Z}^k_G(X)$
.
We follow the arguments in [Reference Bergelson5, Appendix A] and generalise them to arbitrary countable discrete abelian groups. We start with some background related to the Host–Kra parallelepipeds construction.
Definition A.2. Let G be a countable discrete abelian group, and let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g))$
be a G-system. For every
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g))$
be a G-system. For every
![]() $k\geq 0$
, we define a G-system
$k\geq 0$
, we define a G-system
![]() $\textbf {X}_G^{[k]} = (X^{[k]},\mathcal {X}^{[k]}, \mu ^{[k]}, (T^{[k]}_g)_{g\in G})$
inductively by setting
$\textbf {X}_G^{[k]} = (X^{[k]},\mathcal {X}^{[k]}, \mu ^{[k]}, (T^{[k]}_g)_{g\in G})$
inductively by setting
![]() $X_G^{[0]}=X$
, and
$X_G^{[0]}=X$
, and
![]() $X_G^{[k+1]} = X_G^{[k]}\times _{\mathcal {I}(X_G^{[k]})}X_G^{[k]}$
, where
$X_G^{[k+1]} = X_G^{[k]}\times _{\mathcal {I}(X_G^{[k]})}X_G^{[k]}$
, where
![]() $\mathcal {I}(X_G^{[k]})$
is the
$\mathcal {I}(X_G^{[k]})$
is the
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $(T_g^{[k]})_{g\in G}$
-invariant functions.
$(T_g^{[k]})_{g\in G}$
-invariant functions.
Host and Kra [Reference Host and Kra23] proved the following result for
![]() $\mathbb {Z}$
-systems, but the same proof works for arbitrary countable discrete abelian groups.
$\mathbb {Z}$
-systems, but the same proof works for arbitrary countable discrete abelian groups.
Theorem A.3 ([Reference Host and Kra23], Proposition 4.7)
![]() $\mathcal {Z}^k_G(X)$
is the minimal
$\mathcal {Z}^k_G(X)$
is the minimal
![]() $\sigma $
-algebra with the property that
$\sigma $
-algebra with the property that
![]() $\mathcal {I}(X^{[k]})$
is a sub-
$\mathcal {I}(X^{[k]})$
is a sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $(\mathcal {Z}^k_G(X))^{[k]}$
.
$(\mathcal {Z}^k_G(X))^{[k]}$
.
Let
![]() $X=\bigcup _{\alpha \in J}X_{\alpha }$
be a partition of X to G-invariant sets. Then,
$X=\bigcup _{\alpha \in J}X_{\alpha }$
be a partition of X to G-invariant sets. Then,
![]() $X_G^{[k]} = \bigcup _{\alpha \in J} X_{\alpha }^{[k]}$
,
$X_G^{[k]} = \bigcup _{\alpha \in J} X_{\alpha }^{[k]}$
,
![]() $\mathcal {I}(X^{[k]}) = \bigvee _{\alpha \in J} \mathcal {I}(X_{\alpha }^{[k]})$
and
$\mathcal {I}(X^{[k]}) = \bigvee _{\alpha \in J} \mathcal {I}(X_{\alpha }^{[k]})$
and
![]() $\mathcal {Z}^k_G(X) =\bigvee _{\alpha \in J} \mathcal {Z}^k_G(X_{\alpha })$
. Therefore, by the ergodic decomposition, it is enough to prove Lemma 3.6 in the case where the G-action is ergodic.
$\mathcal {Z}^k_G(X) =\bigvee _{\alpha \in J} \mathcal {Z}^k_G(X_{\alpha })$
. Therefore, by the ergodic decomposition, it is enough to prove Lemma 3.6 in the case where the G-action is ergodic.
The following lemma gives the easy inclusion in Lemma 3.6.
Lemma A.4. In the setting of Lemma 3.6,
![]() $\mathcal {Z}_G^k(X)\preceq \mathcal {Z}_H^k(X)$
.
$\mathcal {Z}_G^k(X)\preceq \mathcal {Z}_H^k(X)$
.
Proof. The proof is immediate by Theorem A.3 and since any
![]() $(T_g^{[k]})_{g\in G}$
-invariant function is also a
$(T_g^{[k]})_{g\in G}$
-invariant function is also a
![]() $(T_h^{[k]})_{h\in H}$
-invariant function.
$(T_h^{[k]})_{h\in H}$
-invariant function.
We need the following observation.
Lemma A.5. Let G be a countable discrete abelian group, let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic measure preserving G-system and let
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic measure preserving G-system and let
![]() $H\leq G$
be a subgroup of finite index. Then,
$H\leq G$
be a subgroup of finite index. Then,
![]() $\mathcal {I}_H(X)\preceq \mathcal {Z}_G(X)$
.
$\mathcal {I}_H(X)\preceq \mathcal {Z}_G(X)$
.
Proof. The group
![]() $G/H$
acts ergodically by unitary transformations on
$G/H$
acts ergodically by unitary transformations on
![]() $\mathcal {H}=L^2(X,\mathcal {I}_H,\mu |_{\mathcal {I}_H})$
. Since
$\mathcal {H}=L^2(X,\mathcal {I}_H,\mu |_{\mathcal {I}_H})$
. Since
![]() $G/H$
is a finite abelian group, the unitary representation splits into a direct sum of one-dimensional irreducible representations. In other words,
$G/H$
is a finite abelian group, the unitary representation splits into a direct sum of one-dimensional irreducible representations. In other words,
![]() $\mathcal {H}$
is generated by eigenfunctions of the action of
$\mathcal {H}$
is generated by eigenfunctions of the action of
![]() $G/H$
, which are measurable with respect to
$G/H$
, which are measurable with respect to
![]() $\mathcal {Z}_G(X)$
. This completes the proof.
$\mathcal {Z}_G(X)$
. This completes the proof.
Now, we prove the
![]() $k=1$
case of Lemma 3.6 under the additional assumption that the action of H is ergodic.
$k=1$
case of Lemma 3.6 under the additional assumption that the action of H is ergodic.
Lemma A.6. Let G be countable discrete abelian groups, and let
![]() $H \le G$
be a finite index subgroup. Let
$H \le G$
be a finite index subgroup. Let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system, and suppose the action of H is ergodic. Then,
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system, and suppose the action of H is ergodic. Then,
![]() $\mathcal {Z}_H(X)=\mathcal {Z}_G(X)$
.
$\mathcal {Z}_H(X)=\mathcal {Z}_G(X)$
.
Proof. The group
![]() $G/H$
is finite, and therefore it is a direct product of finite cyclic groups. In particular, we can find
$G/H$
is finite, and therefore it is a direct product of finite cyclic groups. In particular, we can find
![]() $d \in \mathbb N$
and a sequence of subgroups
$d \in \mathbb N$
and a sequence of subgroups
![]() $H_0 = H \le H_1 \le \dots \le H_d \le G$
, such that
$H_0 = H \le H_1 \le \dots \le H_d \le G$
, such that
![]() $G/H_d$
and
$G/H_d$
and
![]() $H_i/H_{i-1}$
,
$H_i/H_{i-1}$
,
![]() $1\leq i \leq d$
, are cyclic groups of prime order. Using a proof by induction on d, we may assume without loss of generality that
$1\leq i \leq d$
, are cyclic groups of prime order. Using a proof by induction on d, we may assume without loss of generality that
![]() $G/H$
is cyclic and of prime order. Let
$G/H$
is cyclic and of prime order. Let
![]() $g_0\in G$
be a representative of a generator of
$g_0\in G$
be a representative of a generator of
![]() $G/H$
and
$G/H$
and
![]() $l:=[G:H]$
be a prime number. By the ergodicity of H, the
$l:=[G:H]$
be a prime number. By the ergodicity of H, the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {Z}_H(X)$
is generated by H-eigenfunctions. Hence, it is enough to show that every H-eigenfunction f is a linear combination of G-eigenfunctions. Let
$\mathcal {Z}_H(X)$
is generated by H-eigenfunctions. Hence, it is enough to show that every H-eigenfunction f is a linear combination of G-eigenfunctions. Let
![]() $\lambda :H\rightarrow S^1$
be the eigenvalue of f, and observe that for any l-th root
$\lambda :H\rightarrow S^1$
be the eigenvalue of f, and observe that for any l-th root
of
![]() $\lambda (lg_0)$
, the function
$\lambda (lg_0)$
, the function
is a G-eigenfunction. Now, since

f is measurable with respect to
![]() $\mathcal {Z}_G(X)$
, and this completes the proof.
$\mathcal {Z}_G(X)$
, and this completes the proof.
Let G be a countable discrete abelian group, and let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system. If the system
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be a G-system. If the system
![]() $\textbf {X}$
is ergodic, it follows from the definition that
$\textbf {X}$
is ergodic, it follows from the definition that
![]() $X_G^{[1]}$
is the Cartesian product of X with itself, and the measure is the product measure. As a consequence of Lemma A.6, we have:
$X_G^{[1]}$
is the Cartesian product of X with itself, and the measure is the product measure. As a consequence of Lemma A.6, we have:
Lemma A.7. If the action of H on X is ergodic, then
Proof. The inclusion
![]() $\mathcal {I}(X_G^{[1]})\preceq \mathcal {I}(X_H^{[1]}))$
is trivial. Now, let
$\mathcal {I}(X_G^{[1]})\preceq \mathcal {I}(X_H^{[1]}))$
is trivial. Now, let
![]() $f:X\times X\rightarrow \mathbb {C}$
be a
$f:X\times X\rightarrow \mathbb {C}$
be a
![]() $(T_h\times T_h)_{h\in H}$
invariant function. By Lemma A.6, we can find an orthonormal basis of G-eigenfunctions
$(T_h\times T_h)_{h\in H}$
invariant function. By Lemma A.6, we can find an orthonormal basis of G-eigenfunctions
![]() $\{f_i\}_{i\in \mathbb {N}}$
for
$\{f_i\}_{i\in \mathbb {N}}$
for
![]() $\mathcal {Z}_H(X)$
. By Lemma 4.6, there exist constants
$\mathcal {Z}_H(X)$
. By Lemma 4.6, there exist constants
![]() $a_{i,j}\in \mathbb {C}$
for all
$a_{i,j}\in \mathbb {C}$
for all
![]() $i,j\in \mathbb {N}$
, such that
$i,j\in \mathbb {N}$
, such that

Applying the H-action and using the uniqueness of the decomposition, we see that
![]() $a_{i,j}=0$
unless
$a_{i,j}=0$
unless
![]() $i=j$
. In particular, f is spanned by the G-invariant functions
$i=j$
. In particular, f is spanned by the G-invariant functions
. Thus, f is measurable with respect to
![]() $\mathcal {I}(X_G^2)$
and the claim follows.
$\mathcal {I}(X_G^2)$
and the claim follows.
We use Lemma A.7 to prove the following:
Proposition A.8. If the action of H on X is ergodic, then for
![]() $k \ge 0$
, one has
$k \ge 0$
, one has
Proof. We prove the claim by induction on k. The case
![]() $k=0$
is trivial.
$k=0$
is trivial.
Assume that for some
![]() $k \ge 0$
,
$k \ge 0$
,
![]() $\mathcal {I}(X_H^{[k]}) = \mathcal {I}(X_G^{[k]})$
and
$\mathcal {I}(X_H^{[k]}) = \mathcal {I}(X_G^{[k]})$
and
![]() $\mu _G^{[k]}= \mu _H^{[k]}$
. It is immediate that
$\mu _G^{[k]}= \mu _H^{[k]}$
. It is immediate that
By the ergodic decomposition theorem, applied with respect to the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {I}(X_G^{[k]})$
, we can find a partition
$\mathcal {I}(X_G^{[k]})$
, we can find a partition
![]() $X_G^{[k]}=\bigcup _{\alpha \in J} X_{\alpha }$
of
$X_G^{[k]}=\bigcup _{\alpha \in J} X_{\alpha }$
of
![]() $X_G^{[k]}$
to
$X_G^{[k]}$
to
![]() $(T_g^{[k]})_{g\in G}$
invariant sets. Let
$(T_g^{[k]})_{g\in G}$
invariant sets. Let
![]() $S_g^{\alpha }$
be the restriction of
$S_g^{\alpha }$
be the restriction of
![]() $T_g^{[k]}$
to the set
$T_g^{[k]}$
to the set
![]() $X_{\alpha }$
. By the induction hypothesis, the action of
$X_{\alpha }$
. By the induction hypothesis, the action of
![]() $(S_h^{\alpha })_{h\in H}$
on
$(S_h^{\alpha })_{h\in H}$
on
![]() $X_{\alpha }$
is ergodic. Hence, by Lemma A.7, we have
$X_{\alpha }$
is ergodic. Hence, by Lemma A.7, we have
as required.
Proposition A.8 establishes Lemma 3.6 in the case where the action of H is ergodic. Now, we assume that the H-action is nonergodic. As in the proof of Lemma A.6, we may assume without loss of generality that
![]() $G/H$
is cyclic of order l for some prime l. In particular, there exists a partition
$G/H$
is cyclic of order l for some prime l. In particular, there exists a partition
![]() $X=\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} X_i$
into H-invariant sets and some
$X=\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} X_i$
into H-invariant sets and some
![]() $g_0\in G$
, such that
$g_0\in G$
, such that
![]() $T_{g_0} X_i = X_{i+1}$
,
$T_{g_0} X_i = X_{i+1}$
,
![]() $i \in {\mathbb Z}/l{\mathbb Z}$
.
$i \in {\mathbb Z}/l{\mathbb Z}$
.
We need the following technical lemma.
Lemma A.9. Let G be a countable discrete abelian group, and let
![]() $\textbf {Y}=(Y,\mathcal {Y},\nu ,(T_g)_{g\in G})$
be an ergodic G-system. Suppose that there exists some
$\textbf {Y}=(Y,\mathcal {Y},\nu ,(T_g)_{g\in G})$
be an ergodic G-system. Suppose that there exists some
![]() $g_0\in G$
and H-invariant subsets
$g_0\in G$
and H-invariant subsets
![]() $Y_i$
, such that
$Y_i$
, such that
![]() $Y=\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} Y_i$
and
$Y=\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} Y_i$
and
![]() $T_{g_0} Y_i = Y_{i+1}$
for
$T_{g_0} Y_i = Y_{i+1}$
for
![]() $i \in {\mathbb Z}/l{\mathbb Z}$
. Then,
$i \in {\mathbb Z}/l{\mathbb Z}$
. Then,
![]() $Y\times _{\mathcal {I}_G(Y)} Y = \bigcup _{i,j\in {\mathbb Z}/l{\mathbb Z}} Y_{i,j}$
where
$Y\times _{\mathcal {I}_G(Y)} Y = \bigcup _{i,j\in {\mathbb Z}/l{\mathbb Z}} Y_{i,j}$
where
![]() $Y_{i,i}=Y_i\times _{\mathcal {I}_H(Y_i)} Y_i$
and
$Y_{i,i}=Y_i\times _{\mathcal {I}_H(Y_i)} Y_i$
and
![]() $T_{sg_0}\times T_{tg_0}$
is an isomorphism between
$T_{sg_0}\times T_{tg_0}$
is an isomorphism between
![]() $Y_{i,i}$
and
$Y_{i,i}$
and
![]() $Y_{i+s, i+t}$
,
$Y_{i+s, i+t}$
,
![]() $i \in {\mathbb Z}/l{\mathbb Z}$
.
$i \in {\mathbb Z}/l{\mathbb Z}$
.
Proof. Let
![]() $A\in \mathcal {I}_G(Y)$
be a measurable G-invariant subset of Y. For each
$A\in \mathcal {I}_G(Y)$
be a measurable G-invariant subset of Y. For each
![]() $0\leq i \leq l-1$
,
$0\leq i \leq l-1$
,
![]() $A_i = A\cap Y_i$
is an H-invariant set. In particular,
$A_i = A\cap Y_i$
is an H-invariant set. In particular,
![]() $A_0$
is H-invariant and
$A_0$
is H-invariant and
![]() $A_i=T_{ig_0}A_0$
. We deduce that the mapping
$A_i=T_{ig_0}A_0$
. We deduce that the mapping
![]() $A\mapsto A\cap Y_0$
is an isomorphism between
$A\mapsto A\cap Y_0$
is an isomorphism between
![]() $\mathcal {I}_G(Y)$
and
$\mathcal {I}_G(Y)$
and
![]() $\mathcal {I}_H(Y_0)$
. Using the ergodic decomposition, we can find a partition
$\mathcal {I}_H(Y_0)$
. Using the ergodic decomposition, we can find a partition
of
![]() $Y_0$
to H-invariant sets. For every
$Y_0$
to H-invariant sets. For every
![]() $\alpha \in I$
, and
$\alpha \in I$
, and
![]() $i\not =0$
, let
$i\not =0$
, let
![]() $Y_{i,\alpha } = T_{ig_0} Y_{0,\alpha }$
and
$Y_{i,\alpha } = T_{ig_0} Y_{0,\alpha }$
and
![]() $Y_{\alpha } = \bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} Y_{i,\alpha }$
. Then,
$Y_{\alpha } = \bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} Y_{i,\alpha }$
. Then,
![]() $Y=\bigcup _{\alpha \in I} Y_{\alpha }$
is the ergodic decomposition of Y with respect to the factor
$Y=\bigcup _{\alpha \in I} Y_{\alpha }$
is the ergodic decomposition of Y with respect to the factor
![]() $\mathcal {I}_G(Y)$
. Thus, if we let
$\mathcal {I}_G(Y)$
. Thus, if we let
![]() $Y_{i,j}=\bigcup _{\alpha \in I} Y_{i,\alpha }\times Y_{j,\alpha }$
, we have,
$Y_{i,j}=\bigcup _{\alpha \in I} Y_{i,\alpha }\times Y_{j,\alpha }$
, we have,
 $$ \begin{align*} Y_G^{[1]} = \bigcup_{\alpha\in I} (Y_{\alpha}\times_{\mathcal{I}_G(Y_{\alpha})} Y_{\alpha}) = \bigcup_{\alpha\in I}\bigcup_{i,j\in{\mathbb Z}/l{\mathbb Z}} (Y_{i,\alpha}\times Y_{j,\alpha}) =\bigcup_{i,j\in{\mathbb Z}/l{\mathbb Z}}\bigcup_{\alpha\in I}\ (Y_{i,\alpha}\times Y_{j,\alpha}) =\bigcup_{i,j\in{\mathbb Z}/l{\mathbb Z}} Y_{i,j}. \end{align*} $$
$$ \begin{align*} Y_G^{[1]} = \bigcup_{\alpha\in I} (Y_{\alpha}\times_{\mathcal{I}_G(Y_{\alpha})} Y_{\alpha}) = \bigcup_{\alpha\in I}\bigcup_{i,j\in{\mathbb Z}/l{\mathbb Z}} (Y_{i,\alpha}\times Y_{j,\alpha}) =\bigcup_{i,j\in{\mathbb Z}/l{\mathbb Z}}\bigcup_{\alpha\in I}\ (Y_{i,\alpha}\times Y_{j,\alpha}) =\bigcup_{i,j\in{\mathbb Z}/l{\mathbb Z}} Y_{i,j}. \end{align*} $$
In particular,
![]() $Y_{i,i} = \bigcup _{\alpha \in I} (Y_{i,\alpha }\times Y_{i,\alpha }) = Y_i\times Y_i$
, as required.
$Y_{i,i} = \bigcup _{\alpha \in I} (Y_{i,\alpha }\times Y_{i,\alpha }) = Y_i\times Y_i$
, as required.
Recall that
![]() $G=\bigcup _{i=0}^{l-1} ig_0+H$
. It follows from Lemma A.9 that for
$G=\bigcup _{i=0}^{l-1} ig_0+H$
. It follows from Lemma A.9 that for
![]() $i,j \in {\mathbb Z}/l{\mathbb Z}$
,
$i,j \in {\mathbb Z}/l{\mathbb Z}$
,
Therefore, the subsets
![]() $V_i = \bigcup _{j\in {\mathbb Z}/l{\mathbb Z}} Y_{j,j+i}$
,
$V_i = \bigcup _{j\in {\mathbb Z}/l{\mathbb Z}} Y_{j,j+i}$
,
![]() $i \in {\mathbb Z}/l{\mathbb Z}$
form a partition of
$i \in {\mathbb Z}/l{\mathbb Z}$
form a partition of
![]() $Y\times _{\mathcal {I}_G(Y)} Y$
into
$Y\times _{\mathcal {I}_G(Y)} Y$
into
![]() $(T_g\times T_g)_{g\in G}$
-invariant sets. Furthermore,
$(T_g\times T_g)_{g\in G}$
-invariant sets. Furthermore,
![]() $\text {Id}\times T_{ig_0}$
is an isomorphism between
$\text {Id}\times T_{ig_0}$
is an isomorphism between
![]() $V_0$
and
$V_0$
and
![]() $V_i$
.
$V_i$
.
We use Lemma A.9 to show the following:
Lemma A.10. Let
![]() $\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Let
$\textbf {X}=(X,\mathcal {X},\mu ,(T_g)_{g\in G})$
be an ergodic G-system. Let
![]() $X=\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} X_i$
be a partition into H-invariant sets and let
$X=\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} X_i$
be a partition into H-invariant sets and let
![]() $g_0\in G$
be as above. Then, for any
$g_0\in G$
be as above. Then, for any
![]() $k\geq 0$
, there exists a partition
$k\geq 0$
, there exists a partition
![]() $X_G^{[k]} = \bigcup _{j\in ({\mathbb Z}/l{\mathbb Z})^k} W_j$
, into
$X_G^{[k]} = \bigcup _{j\in ({\mathbb Z}/l{\mathbb Z})^k} W_j$
, into
![]() $(T_g^{[k]})_{g\in G}$
-invariant sets, such that
$(T_g^{[k]})_{g\in G}$
-invariant sets, such that
![]() $W_0 =\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} (X_i)_H^{[k]} $
and
$W_0 =\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} (X_i)_H^{[k]} $
and
![]() $T_{g_0}^{[k]}\left((X_i)_H^{[k]} \right)=(X_{i+1})_H^{[k]}$
. Furthermore, for every
$T_{g_0}^{[k]}\left((X_i)_H^{[k]} \right)=(X_{i+1})_H^{[k]}$
. Furthermore, for every
![]() $j\in ({\mathbb Z}/l{\mathbb Z})^k$
, there exists an isomorphism of measure spaces
$j\in ({\mathbb Z}/l{\mathbb Z})^k$
, there exists an isomorphism of measure spaces
![]() $\tau _j:W_0\rightarrow W_j$
, which in every coordinate of
$\tau _j:W_0\rightarrow W_j$
, which in every coordinate of
![]() $X^{[k]}$
is a power of
$X^{[k]}$
is a power of
![]() $T_{g_0}$
.
$T_{g_0}$
.
Proof. We induct on k. The case
![]() $k=0$
is trivial.
$k=0$
is trivial.
Assume that the claim holds for some
![]() $k\geq 0$
. Then
$k\geq 0$
. Then
 $$ \begin{align*} X_G^{[k+1]} = X_G^{[k]}\times_{\mathcal{I}(X_G^{[k]})}X_G^{[k]} =\bigcup_{j\in({\mathbb Z}/l{\mathbb Z})^k} (W_j\times_{\mathcal{I}(W_j)} W_j). \end{align*} $$
$$ \begin{align*} X_G^{[k+1]} = X_G^{[k]}\times_{\mathcal{I}(X_G^{[k]})}X_G^{[k]} =\bigcup_{j\in({\mathbb Z}/l{\mathbb Z})^k} (W_j\times_{\mathcal{I}(W_j)} W_j). \end{align*} $$
Fix
![]() $j \in ({\mathbb Z}/l{\mathbb Z})^k$
. Since the isomorphism
$j \in ({\mathbb Z}/l{\mathbb Z})^k$
. Since the isomorphism
![]() $\tau _j:W_0\rightarrow W_j$
commutes with
$\tau _j:W_0\rightarrow W_j$
commutes with
![]() $(T_g^{[k]})_{g\in G}$
, it induces an isomorphism
$(T_g^{[k]})_{g\in G}$
, it induces an isomorphism
![]() $\tau _j\times \tau _j:W_0\times _{\mathcal {I}(W_0)} W_0\rightarrow W_j\times _{\mathcal {I}(W_j)} W_j$
. By assumption,
$\tau _j\times \tau _j:W_0\times _{\mathcal {I}(W_0)} W_0\rightarrow W_j\times _{\mathcal {I}(W_j)} W_j$
. By assumption,
![]() $W_0 = \bigcup _{i\in {\mathbb Z}/l{\mathbb Z}}(X_i)_H^{[k]}$
, and by Lemma A.9,
$W_0 = \bigcup _{i\in {\mathbb Z}/l{\mathbb Z}}(X_i)_H^{[k]}$
, and by Lemma A.9,
![]() $W_0\times _{\mathcal {I}(W_0)}W_0$
can be partitioned into
$W_0\times _{\mathcal {I}(W_0)}W_0$
can be partitioned into
![]() $(T_g^{[k+1]})_{g\in G}$
-invariant sets
$(T_g^{[k+1]})_{g\in G}$
-invariant sets
![]() $\{V_i\}_{i\in {\mathbb Z}/l{\mathbb Z}}$
, such that
$\{V_i\}_{i\in {\mathbb Z}/l{\mathbb Z}}$
, such that
 $$ \begin{align*} V_0 = \bigcup_{i\in{\mathbb Z}/l{\mathbb Z}}\left( (X_i)_H^{[k]}\times_{\mathcal{I}\left((X_i)_H^{[k]}\right)} (X_i)_H^{[k]}\right) =\bigcup_{i\in{\mathbb Z}/l{\mathbb Z}} (X_i)_H^{[k+1]}. \end{align*} $$
$$ \begin{align*} V_0 = \bigcup_{i\in{\mathbb Z}/l{\mathbb Z}}\left( (X_i)_H^{[k]}\times_{\mathcal{I}\left((X_i)_H^{[k]}\right)} (X_i)_H^{[k]}\right) =\bigcup_{i\in{\mathbb Z}/l{\mathbb Z}} (X_i)_H^{[k+1]}. \end{align*} $$
Moreover,
![]() $V_0$
is isomorphic to
$V_0$
is isomorphic to
![]() $V_j$
via an isomorphism whose projections are powers of
$V_j$
via an isomorphism whose projections are powers of
![]() $T_{g_0}^{[k]}$
. Since
$T_{g_0}^{[k]}$
. Since
![]() $W_0$
is isomorphic to
$W_0$
is isomorphic to
![]() $W_j$
, this completes the proof.
$W_j$
, this completes the proof.
We recall that it suffices to establish the proof of Lemma 3.6 in the case where the G-action is ergodic and
![]() $G/H$
is a cyclic group of order l for some
$G/H$
is a cyclic group of order l for some
![]() $l>0$
. As before, we find a partition
$l>0$
. As before, we find a partition
![]() $X=\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} X_i$
of X into H-invariant sets and some
$X=\bigcup _{i\in {\mathbb Z}/l{\mathbb Z}} X_i$
of X into H-invariant sets and some
![]() $g_0\in G$
, such that
$g_0\in G$
, such that
![]() $T_{g_0} (X_i) = X_{i+1}$
for
$T_{g_0} (X_i) = X_{i+1}$
for
![]() $i \in {\mathbb Z}/l{\mathbb Z}$
.
$i \in {\mathbb Z}/l{\mathbb Z}$
.
Proof of Lemma 3.6
Let
![]() $k\geq 0$
, and let
$k\geq 0$
, and let
![]() $\{W_i\}_{i\in ({\mathbb Z}/l{\mathbb Z})^k}$
be as in Lemma A.10. Since
$\{W_i\}_{i\in ({\mathbb Z}/l{\mathbb Z})^k}$
be as in Lemma A.10. Since
![]() $X_0,...,X_{l-1}$
are disjoint
$X_0,...,X_{l-1}$
are disjoint
![]() $(T_h)_{h\in H}$
-invariant subsets of X, we have
$(T_h)_{h\in H}$
-invariant subsets of X, we have
![]() $\mathcal {I}(X_H^{[k]}) = \prod _{i\in {\mathbb Z}/l{\mathbb Z}} \mathcal {I}\left((X_i)_H^{[k]}\right)$
and
$\mathcal {I}(X_H^{[k]}) = \prod _{i\in {\mathbb Z}/l{\mathbb Z}} \mathcal {I}\left((X_i)_H^{[k]}\right)$
and
![]() $Z^k_H(X)=\prod _{i\in {\mathbb Z}/l{\mathbb Z}} Z^k_H(X_i)$
. Let B be a
$Z^k_H(X)=\prod _{i\in {\mathbb Z}/l{\mathbb Z}} Z^k_H(X_i)$
. Let B be a
![]() $(T_h^{[k]})_{h\in H}$
-invariant subset of
$(T_h^{[k]})_{h\in H}$
-invariant subset of
![]() $(X_i)_H^{[k]}$
. For every
$(X_i)_H^{[k]}$
. For every
![]() $j\in {\mathbb Z}/l{\mathbb Z}$
, let
$j\in {\mathbb Z}/l{\mathbb Z}$
, let
![]() $A_j=(T_{(j-i)g_0}^{[k]})(B)$
and
$A_j=(T_{(j-i)g_0}^{[k]})(B)$
and
![]() $A=\bigcup _{j\in {\mathbb Z}/l{\mathbb Z}} A_j$
. By definition,
$A=\bigcup _{j\in {\mathbb Z}/l{\mathbb Z}} A_j$
. By definition,
![]() $A\subseteq W_0$
is a
$A\subseteq W_0$
is a
![]() $(T_g^{[k]})_{g\in G}$
-invariant set. Therefore, by Theorem A.3,
$(T_g^{[k]})_{g\in G}$
-invariant set. Therefore, by Theorem A.3,
![]() $A\in \left(\mathcal {Z}^k_G(X)\right)^{[k]}$
. Since
$A\in \left(\mathcal {Z}^k_G(X)\right)^{[k]}$
. Since
![]() $X_i$
is
$X_i$
is
![]() $(T_h^{[k]})$
-invariant, by Lemma A.5,
$(T_h^{[k]})$
-invariant, by Lemma A.5,
![]() $X_i\in \mathcal {Z}^1_G(X)$
. Therefore,
$X_i\in \mathcal {Z}^1_G(X)$
. Therefore,
![]() $B=A_i = A\cap \left(X_i\right)_H^{[k]}$
is an element of
$B=A_i = A\cap \left(X_i\right)_H^{[k]}$
is an element of
![]() $\left(\mathcal {Z}^k_G(X)\right)^{[k]}$
. Since B is arbitrary, and this holds for all
$\left(\mathcal {Z}^k_G(X)\right)^{[k]}$
. Since B is arbitrary, and this holds for all
![]() $i\in {\mathbb Z}/l{\mathbb Z}$
, we deduce that
$i\in {\mathbb Z}/l{\mathbb Z}$
, we deduce that
![]() $\mathcal {I}(X_H^{[k]})\preceq \mathcal {Z}^k_G(X)$
. By Theorem A.3, we have
$\mathcal {I}(X_H^{[k]})\preceq \mathcal {Z}^k_G(X)$
. By Theorem A.3, we have
![]() $\mathcal {Z}^k_H(X)\preceq \mathcal {Z}_G^k(X)$
. Lemma A.4 provides the other inclusion, and this completes the proof.
$\mathcal {Z}^k_H(X)\preceq \mathcal {Z}_G^k(X)$
. Lemma A.4 provides the other inclusion, and this completes the proof.
Conflict of Interest
The authors have no conflict of interest to declare.
Funding statement
The third author is supported by European Research Council grant ErgComNum 682150 and Israel Science Foundation grant 2112/20.