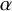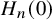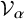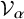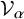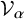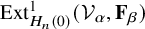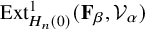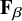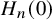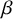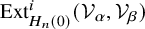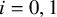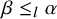1 Introduction
The first systematic work on the representation theory of the
![]() $0$
-Hecke algebras was made by Norton [Reference Norton25], who completely classified all projective indecomposable modules and simple modules, up to isomorphism, for all
$0$
-Hecke algebras was made by Norton [Reference Norton25], who completely classified all projective indecomposable modules and simple modules, up to isomorphism, for all
![]() $0$
-Hecke algebras of finite type. In the case where
$0$
-Hecke algebras of finite type. In the case where
![]() $H_n(0)$
, the
$H_n(0)$
, the
![]() $0$
-Hecke algebra of type
$0$
-Hecke algebra of type
![]() $A_{n-1}$
, they are naturally parametrised by compositions of n. For each composition
$A_{n-1}$
, they are naturally parametrised by compositions of n. For each composition
![]() $\alpha $
of n, let us denote by
$\alpha $
of n, let us denote by
![]() $\mathbf {P}_{\alpha }$
and
$\mathbf {P}_{\alpha }$
and
![]() $\mathbf {F}_{\alpha }$
the projective indecomposable module and the simple module corresponding
$\mathbf {F}_{\alpha }$
the projective indecomposable module and the simple module corresponding
![]() $\alpha $
, respectively (see Subsection 2.3). These modules were again studied intensively in the 2000s (for instance, see [Reference Denton13, Reference Hivert, Novelli and Thibon19, Reference Huang20]). In particular, Huang [Reference Huang20] studied the induced modules
$\alpha $
, respectively (see Subsection 2.3). These modules were again studied intensively in the 2000s (for instance, see [Reference Denton13, Reference Hivert, Novelli and Thibon19, Reference Huang20]). In particular, Huang [Reference Huang20] studied the induced modules
![]() $\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}}$
of projective indecomposable modules by using the combinatorial objects called standard ribbon tableaux, where
$\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}}$
of projective indecomposable modules by using the combinatorial objects called standard ribbon tableaux, where
![]() ${\boldsymbol {\unicode{x3b1} }}$
in bold-face ranges over the set of generalised compositions.
${\boldsymbol {\unicode{x3b1} }}$
in bold-face ranges over the set of generalised compositions.
In [Reference Duchamp, Krob, Leclerc and Thibon15, Reference Krob and Thibon22], it was shown that the representation theory of the 0-Hecke algebras of type A has a deep connection to the ring
![]() $\mathrm {QSym}$
of quasisymmetric functions. Letting
$\mathrm {QSym}$
of quasisymmetric functions. Letting
![]() $\mathcal {G}_0(H_n(0))$
be the Grothendieck group of the category of finitely generated
$\mathcal {G}_0(H_n(0))$
be the Grothendieck group of the category of finitely generated
![]() $H_n(0)$
-modules, their direct sum over all
$H_n(0)$
-modules, their direct sum over all
![]() $n\ge 0$
endowed with the induction product is isomorphic to
$n\ge 0$
endowed with the induction product is isomorphic to
![]() $\mathrm {QSym}$
via the quasisymmetric characteristic
$\mathrm {QSym}$
via the quasisymmetric characteristic
Here, for a composition
![]() $\alpha $
of n,
$\alpha $
of n,
![]() $[\mathbf {F}_{\alpha }]$
is the equivalence class of
$[\mathbf {F}_{\alpha }]$
is the equivalence class of
![]() $\mathbf {F}_{\alpha }$
inside
$\mathbf {F}_{\alpha }$
inside
![]() $\mathcal {G}_0(H_n(0))$
, and
$\mathcal {G}_0(H_n(0))$
, and
![]() $F_{\alpha }$
is the fundamental quasisymmetric function attached to
$F_{\alpha }$
is the fundamental quasisymmetric function attached to
![]() $\alpha $
(for more information; see Subsection 2.2).
$\alpha $
(for more information; see Subsection 2.2).
Suppose that
![]() $\alpha $
ranges over the set of all compositions of n. In the mid-2010s, Berg, Bergeron, Saliola, Serrano and Zabrocki [Reference Berg, Bergeron, Saliola, Serrano and Zabrocki4] introduced the immaculate functions
$\alpha $
ranges over the set of all compositions of n. In the mid-2010s, Berg, Bergeron, Saliola, Serrano and Zabrocki [Reference Berg, Bergeron, Saliola, Serrano and Zabrocki4] introduced the immaculate functions
![]() $\mathfrak {S}_{\alpha }$
by applying noncommutative Bernstein operators to the constant power series
$\mathfrak {S}_{\alpha }$
by applying noncommutative Bernstein operators to the constant power series
![]() $1$
, the identity of the ring
$1$
, the identity of the ring
![]() $\mathrm {NSym}$
of noncommutative symmetric functions. These functions form a basis of
$\mathrm {NSym}$
of noncommutative symmetric functions. These functions form a basis of
![]() $\mathrm {NSym}$
. Then the authors defined the dual immaculate function
$\mathrm {NSym}$
. Then the authors defined the dual immaculate function
![]() $\mathfrak {S}^{\ast }_{\alpha }$
as the quasisymmetric function dual to
$\mathfrak {S}^{\ast }_{\alpha }$
as the quasisymmetric function dual to
![]() $\mathfrak {S}_{\alpha }$
under the appropriate pairing between
$\mathfrak {S}_{\alpha }$
under the appropriate pairing between
![]() $\mathrm {QSym}$
and
$\mathrm {QSym}$
and
![]() $\mathrm {NSym}$
; thus
$\mathrm {NSym}$
; thus
![]() $\mathfrak {S}^{\ast }_{\alpha }$
s also form a basis of
$\mathfrak {S}^{\ast }_{\alpha }$
s also form a basis of
![]() $\mathrm {QSym}$
. Due to their nice properties, the immaculate and dual immaculate functions have since drawn the attention of many mathematicians (see [Reference Berg, Bergeron, Saliola, Serrano and Zabrocki6, Reference Bergeron, Sánchez-Ortega and Zabrocki7, Reference Campbell10, Reference Campbell11, Reference Gao and Yang17, Reference Grinberg18, Reference Mason and Searles24]). In a subsequent paper [Reference Berg, Bergeron, Saliola, Serrano and Zabrocki5], the same authors successfully construct a cyclic indecomposable
$\mathrm {QSym}$
. Due to their nice properties, the immaculate and dual immaculate functions have since drawn the attention of many mathematicians (see [Reference Berg, Bergeron, Saliola, Serrano and Zabrocki6, Reference Bergeron, Sánchez-Ortega and Zabrocki7, Reference Campbell10, Reference Campbell11, Reference Gao and Yang17, Reference Grinberg18, Reference Mason and Searles24]). In a subsequent paper [Reference Berg, Bergeron, Saliola, Serrano and Zabrocki5], the same authors successfully construct a cyclic indecomposable
![]() $H_n(0)$
-module
$H_n(0)$
-module
![]() $\mathcal {V}_{\alpha }$
with
$\mathcal {V}_{\alpha }$
with
![]() $\mathrm {ch}(\mathcal {V}_{\alpha })=\mathfrak {S}^{\ast }_{\alpha }$
by using combinatorial objects called standard immaculate tableaux. Although several notable properties have recently been revealed in [Reference Choi, Kim, Nam and Oh12, Reference Jung, Kim, Lee and Oh21], the structure of
$\mathrm {ch}(\mathcal {V}_{\alpha })=\mathfrak {S}^{\ast }_{\alpha }$
by using combinatorial objects called standard immaculate tableaux. Although several notable properties have recently been revealed in [Reference Choi, Kim, Nam and Oh12, Reference Jung, Kim, Lee and Oh21], the structure of
![]() $\mathcal {V}_{\alpha }$
is not yet well known, especially compared to
$\mathcal {V}_{\alpha }$
is not yet well known, especially compared to
![]() $\mathfrak {S}^{\ast }_{\alpha }$
.
$\mathfrak {S}^{\ast }_{\alpha }$
.
The studies of the
![]() $0$
-Hecke algebras from the homological viewpoint can be found in [Reference Cabanes9, Reference Duchamp, Hivert and Thibon14, Reference Fayers16]. For type A, Duchamp, Hivert and Thibon [Reference Duchamp, Hivert and Thibon14, Section 4] construct all nonisomorphic 2-dimensional indecomposable modules and use this result to calculate
$0$
-Hecke algebras from the homological viewpoint can be found in [Reference Cabanes9, Reference Duchamp, Hivert and Thibon14, Reference Fayers16]. For type A, Duchamp, Hivert and Thibon [Reference Duchamp, Hivert and Thibon14, Section 4] construct all nonisomorphic 2-dimensional indecomposable modules and use this result to calculate
![]() $\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\alpha },\mathbf {F}_{\beta })$
for all compositions
$\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\alpha },\mathbf {F}_{\beta })$
for all compositions
![]() $\alpha , \beta $
of n.
$\alpha , \beta $
of n.
Moreover, when
![]() $n \le 4$
, they show that its Poincaré series is given by the
$n \le 4$
, they show that its Poincaré series is given by the
![]() $(\alpha ,\beta )$
entry of the inverse of
$(\alpha ,\beta )$
entry of the inverse of
![]() $(-q)$
-Cartan matrix. For all finite types, Fayers [Reference Fayers16, Section 5] shows that
$(-q)$
-Cartan matrix. For all finite types, Fayers [Reference Fayers16, Section 5] shows that
![]() $\dim \mathrm {Ext}^1_{\mathcal {\bullet }}(M,N) =1$
or
$\dim \mathrm {Ext}^1_{\mathcal {\bullet }}(M,N) =1$
or
![]() $0$
for all simple modules M and N. He also classifies when the dimension equals
$0$
for all simple modules M and N. He also classifies when the dimension equals
![]() $1$
. However, to the best knowledge of the authors, little is known about Ext-groups other than simple (and projective) modules.
$1$
. However, to the best knowledge of the authors, little is known about Ext-groups other than simple (and projective) modules.
In this paper, we study homological properties of
![]() $\mathcal {V}_{\alpha }$
s. To be precise, we explicitly describe a minimal projective presentation and a minimal injective presentation of
$\mathcal {V}_{\alpha }$
s. To be precise, we explicitly describe a minimal projective presentation and a minimal injective presentation of
![]() $\mathcal {V}_{\alpha }$
. By employing these presentations, we calculate
$\mathcal {V}_{\alpha }$
. By employing these presentations, we calculate
In addition, we calculate
for all
![]() $\beta \le _l \alpha $
, where
$\beta \le _l \alpha $
, where
![]() $\le _l$
represents the lexicographic order on compositions. In the following, let us explain our results in more detail.
$\le _l$
represents the lexicographic order on compositions. In the following, let us explain our results in more detail.
Let
![]() $\alpha = (\alpha _1,\alpha _2,\ldots , \alpha _{\ell (\alpha )})$
be a composition of n. The first main result concerns a minimal projective presentation of
$\alpha = (\alpha _1,\alpha _2,\ldots , \alpha _{\ell (\alpha )})$
be a composition of n. The first main result concerns a minimal projective presentation of
![]() $\mathcal {V}_{\alpha }$
. The projective cover
$\mathcal {V}_{\alpha }$
. The projective cover
![]() $\Phi : \mathbf {P}_{\alpha } \rightarrow \mathcal {V}_{\alpha }$
, of
$\Phi : \mathbf {P}_{\alpha } \rightarrow \mathcal {V}_{\alpha }$
, of
![]() $\mathcal {V}_{\alpha }$
has already been provided in [Reference Choi, Kim, Nam and Oh12, Theorem 3.2]. Let
$\mathcal {V}_{\alpha }$
has already been provided in [Reference Choi, Kim, Nam and Oh12, Theorem 3.2]. Let
![]() $\mathcal {I}(\alpha ) := \{1 \le i \le \ell (\alpha )-1 \mid \alpha _{i+1} \neq 1 \}$
, and for each
$\mathcal {I}(\alpha ) := \{1 \le i \le \ell (\alpha )-1 \mid \alpha _{i+1} \neq 1 \}$
, and for each
![]() $i \in \mathcal {I}(\alpha )$
, let
$i \in \mathcal {I}(\alpha )$
, let
![]() ${\boldsymbol {\unicode{x3b1} }}^{(i)}$
be the generalised composition
${\boldsymbol {\unicode{x3b1} }}^{(i)}$
be the generalised composition
Then we construct a
![]() $\mathbb C$
-linear map
$\mathbb C$
-linear map
which turns out to be an
![]() $H_n(0)$
-module homomorphism. Additionally, we show that
$H_n(0)$
-module homomorphism. Additionally, we show that
 $$\begin{align*}\ker (\Phi) = \mathrm{Im}(\partial_1) \quad \text{and} \quad \ker(\partial_1) \subseteq \mathrm{rad} \left(\bigoplus_{i \in \mathcal{I}(\alpha)} \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}^{(i)}} \right). \end{align*}$$
$$\begin{align*}\ker (\Phi) = \mathrm{Im}(\partial_1) \quad \text{and} \quad \ker(\partial_1) \subseteq \mathrm{rad} \left(\bigoplus_{i \in \mathcal{I}(\alpha)} \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}^{(i)}} \right). \end{align*}$$
Hence we obtain the following minimal projective presentation of
![]() $\mathcal {V}_{\alpha }$
$\mathcal {V}_{\alpha }$

which enables us to derive that
 $$\begin{align*}\mathrm{Ext}_{H_n(0)}^1(\mathcal{V}_{\alpha},\mathbf{F}_{\beta}) \cong \begin{cases} \mathbb C & \text{if } \beta \in \mathcal{J}(\alpha),\\ 0 & \text{otherwise} \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{Ext}_{H_n(0)}^1(\mathcal{V}_{\alpha},\mathbf{F}_{\beta}) \cong \begin{cases} \mathbb C & \text{if } \beta \in \mathcal{J}(\alpha),\\ 0 & \text{otherwise} \end{cases} \end{align*}$$
with
![]() $\mathcal {J}(\alpha ) := \bigcup _{i \in \mathcal {I}(\alpha )} [{\boldsymbol {\unicode{x3b1} }}^{(i)}]$
. Here, given a generalised composition
$\mathcal {J}(\alpha ) := \bigcup _{i \in \mathcal {I}(\alpha )} [{\boldsymbol {\unicode{x3b1} }}^{(i)}]$
. Here, given a generalised composition
![]() ${\boldsymbol {\unicode{x3b1} }} = \alpha ^{(1)} \oplus \alpha ^{(2)} \oplus \cdots \oplus \alpha ^{(p)}$
, we are using the notation
${\boldsymbol {\unicode{x3b1} }} = \alpha ^{(1)} \oplus \alpha ^{(2)} \oplus \cdots \oplus \alpha ^{(p)}$
, we are using the notation
![]() $[{\boldsymbol {\unicode{x3b1} }}]$
to denote the set of all compositions of the form
$[{\boldsymbol {\unicode{x3b1} }}]$
to denote the set of all compositions of the form
where
![]() $\square $
is the concatenation
$\square $
is the concatenation
![]() $\cdot $
or near concatenation
$\cdot $
or near concatenation
![]() $\odot $
(Theorem 3.3).
$\odot $
(Theorem 3.3).
The second main result concerns a minimal injective presentation of
![]() $\mathcal {V}_{\alpha }$
. Since
$\mathcal {V}_{\alpha }$
. Since
![]() $H_n(0)$
is a Frobenius algebra, every finitely generated injective
$H_n(0)$
is a Frobenius algebra, every finitely generated injective
![]() $H_n(0)$
-module is projective. But unlike the projective cover of
$H_n(0)$
-module is projective. But unlike the projective cover of
![]() $\mathcal {V}_{\alpha }$
, there are no known results for an injective hull of
$\mathcal {V}_{\alpha }$
, there are no known results for an injective hull of
![]() $\mathcal {V}_{\alpha }$
. We consider the generalised composition
$\mathcal {V}_{\alpha }$
. We consider the generalised composition
where
Then we construct an injective
![]() $H_n(0)$
-module homomorphism
$H_n(0)$
-module homomorphism
![]() $\epsilon : \mathcal {V}_{\alpha } \rightarrow \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
and prove that it is an injective hull of
$\epsilon : \mathcal {V}_{\alpha } \rightarrow \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
and prove that it is an injective hull of
![]() $\mathcal {V}_{\alpha }$
, equivalently,
$\mathcal {V}_{\alpha }$
, equivalently,
![]() $\mathrm {soc}(\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}) \subseteq \epsilon (\mathcal {V}_{\alpha })$
(Theorem 4.1). The next step is to find a map
$\mathrm {soc}(\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}) \subseteq \epsilon (\mathcal {V}_{\alpha })$
(Theorem 4.1). The next step is to find a map
![]() $\partial ^1: \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}} \to \boldsymbol {I}$
with
$\partial ^1: \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}} \to \boldsymbol {I}$
with
![]() $\boldsymbol {I}$
injective such that
$\boldsymbol {I}$
injective such that
is a minimal injective presentation. To do this, to each index
![]() $1 \leq j \leq m$
, we assign the generalised composition
$1 \leq j \leq m$
, we assign the generalised composition
 $$ \begin{align*}\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}: = \begin{cases} (\alpha_{k_1}-1) \oplus \cdots \oplus (\alpha_{k_j} - 2) \oplus \cdots \oplus (\alpha_{k_m}, 1^{\ell(\alpha)-k_j+1}) \oplus (1^{k_j-1}) & \text{ if } 1 \leq j < m, \\ (\alpha_{k_1}-1 ) \oplus \cdots \oplus (\alpha_{k_{m-1}}-1) \oplus \left((\alpha_{k_m}-1,1^{\ell(\alpha)-k_j+1}) \cdot (1^{k_j-1})\right) & \text{ if } j = m. \end{cases} \end{align*} $$
$$ \begin{align*}\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}: = \begin{cases} (\alpha_{k_1}-1) \oplus \cdots \oplus (\alpha_{k_j} - 2) \oplus \cdots \oplus (\alpha_{k_m}, 1^{\ell(\alpha)-k_j+1}) \oplus (1^{k_j-1}) & \text{ if } 1 \leq j < m, \\ (\alpha_{k_1}-1 ) \oplus \cdots \oplus (\alpha_{k_{m-1}}-1) \oplus \left((\alpha_{k_m}-1,1^{\ell(\alpha)-k_j+1}) \cdot (1^{k_j-1})\right) & \text{ if } j = m. \end{cases} \end{align*} $$
Then we construct a
![]() $\mathbb C$
-linear map
$\mathbb C$
-linear map
which turns out to be an
![]() $H_n(0)$
-module homomorphism. We also show that
$H_n(0)$
-module homomorphism. We also show that
Hence we have the following minimal injective presentation of
![]() $\mathcal {V}_{\alpha }$
:
$\mathcal {V}_{\alpha }$
:
Let
![]() $\Omega ^{-1}(\mathcal {V}_{\alpha })$
be the cosyzygy module of
$\Omega ^{-1}(\mathcal {V}_{\alpha })$
be the cosyzygy module of
![]() $\mathcal {V}_{\alpha }$
, the cokernel of
$\mathcal {V}_{\alpha }$
, the cokernel of
![]() $\epsilon $
. Applying the formula
$\epsilon $
. Applying the formula
![]() $\mathrm {Ext}_{H_n(0)}^1(\mathbf {F}_{\beta },\mathcal {V}_{\alpha }) \cong \mathrm {Hom}_{H_n(0)}(\mathbf {F}_{\beta }, \Omega ^{-1}(\mathcal {V}_{\alpha }))$
to this minimal injective presentation enables us to derive that
$\mathrm {Ext}_{H_n(0)}^1(\mathbf {F}_{\beta },\mathcal {V}_{\alpha }) \cong \mathrm {Hom}_{H_n(0)}(\mathbf {F}_{\beta }, \Omega ^{-1}(\mathcal {V}_{\alpha }))$
to this minimal injective presentation enables us to derive that
 $$\begin{align*}\mathrm{Ext}_{H_n(0)}^1(\mathbf{F}_{\beta},\mathcal{V}_{\alpha}) \cong \begin{cases} \mathbb C^{[\mathcal{L}(\alpha):\beta^{\mathrm{r}}]} & \text{if } \beta^{\mathrm{r}} \in \mathcal{L}(\alpha),\\ 0 & \text{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{Ext}_{H_n(0)}^1(\mathbf{F}_{\beta},\mathcal{V}_{\alpha}) \cong \begin{cases} \mathbb C^{[\mathcal{L}(\alpha):\beta^{\mathrm{r}}]} & \text{if } \beta^{\mathrm{r}} \in \mathcal{L}(\alpha),\\ 0 & \text{otherwise,} \end{cases} \end{align*}$$
where
![]() $\mathcal {L}(\alpha )$
is the multiset
$\mathcal {L}(\alpha )$
is the multiset
![]() $\bigcup _{1 \leq j \leq m} [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
,
$\bigcup _{1 \leq j \leq m} [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
,
![]() $\beta ^{\mathrm {r}}$
the reverse composition of
$\beta ^{\mathrm {r}}$
the reverse composition of
![]() $\beta $
and
$\beta $
and
![]() $[\mathcal {L}(\alpha ):\beta ^{\mathrm {r}}]$
the multiplicity of
$[\mathcal {L}(\alpha ):\beta ^{\mathrm {r}}]$
the multiplicity of
![]() $\beta ^{\mathrm {r}}$
in
$\beta ^{\mathrm {r}}$
in
![]() $\mathcal {L}(\alpha )$
(Theorem 4.3).
$\mathcal {L}(\alpha )$
(Theorem 4.3).
The third main result concerns
![]() $\mathrm {Ext}^i_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
for
$\mathrm {Ext}^i_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
for
![]() $i=0,1$
. We show that whenever
$i=0,1$
. We show that whenever
![]() $\beta \le _l \alpha $
,
$\beta \le _l \alpha $
,
 $$ \begin{align*} \mathrm{Ext}_{H_n(0)}^1(\mathcal{V}_{\alpha},\mathcal{V}_{\beta}) = 0 \qquad \text{and} \qquad \mathrm{Ext}_{H_n(0)}^0(\mathcal{V}_{\alpha}, \mathcal{V}_{\beta}) \cong\begin{cases} \mathbb C & \text{if } \beta = \alpha, \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \mathrm{Ext}_{H_n(0)}^1(\mathcal{V}_{\alpha},\mathcal{V}_{\beta}) = 0 \qquad \text{and} \qquad \mathrm{Ext}_{H_n(0)}^0(\mathcal{V}_{\alpha}, \mathcal{V}_{\beta}) \cong\begin{cases} \mathbb C & \text{if } \beta = \alpha, \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
Given a finite-dimensional
![]() $H_n(0)$
-module M, we say that M is rigid if
$H_n(0)$
-module M, we say that M is rigid if
![]() $\mathrm {Ext}_{H_n(0)}^1(M,M)=0$
and essentially rigid if
$\mathrm {Ext}_{H_n(0)}^1(M,M)=0$
and essentially rigid if
![]() $\mathrm {Hom}_{H_n(0)}(\Omega (M),M)=0$
, where
$\mathrm {Hom}_{H_n(0)}(\Omega (M),M)=0$
, where
![]() $\Omega (M)$
is the syzygy module of M. With this definition, we also prove that
$\Omega (M)$
is the syzygy module of M. With this definition, we also prove that
![]() $\mathcal {V}_{\alpha }$
is essentially rigid for every composition
$\mathcal {V}_{\alpha }$
is essentially rigid for every composition
![]() $\alpha $
of n (Theorem 5.4). In the case where
$\alpha $
of n (Theorem 5.4). In the case where
![]() $\beta>_l \alpha $
, the structure of
$\beta>_l \alpha $
, the structure of
![]() $\mathrm {Ext}^i_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
for
$\mathrm {Ext}^i_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
for
![]() $i=0,1$
is still beyond our understanding. For instance, each map in
$i=0,1$
is still beyond our understanding. For instance, each map in
![]() $\mathrm {Ext}^0_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
is completely determined by the value of a cyclic generator of
$\mathrm {Ext}^0_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
is completely determined by the value of a cyclic generator of
![]() $\mathcal {V}_{\alpha }$
. However, at the moment, it seems difficult to characterise all possible values the generator can have. Instead, we view
$\mathcal {V}_{\alpha }$
. However, at the moment, it seems difficult to characterise all possible values the generator can have. Instead, we view
![]() $\mathrm {Ext}^0_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
as the set of
$\mathrm {Ext}^0_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
as the set of
![]() $H_n(0)$
-module homomorphisms from
$H_n(0)$
-module homomorphisms from
![]() $\mathbf {P}_{\alpha }$
to
$\mathbf {P}_{\alpha }$
to
![]() $\mathcal {V}_{\beta }$
that vanish on
$\mathcal {V}_{\beta }$
that vanish on
![]() $\Omega (\mathcal {V}_{\alpha })$
. The most important reason for taking this view is that we know a minimal generating set of
$\Omega (\mathcal {V}_{\alpha })$
. The most important reason for taking this view is that we know a minimal generating set of
![]() $\mathcal {V}_{\alpha }$
as well as a combinatorial description of
$\mathcal {V}_{\alpha }$
as well as a combinatorial description of
![]() $\dim _{\mathbb C}\mathrm {Ext}^0_{H_n(0)}(\mathbf {P}_{\alpha }, \mathcal {V}_{\beta })$
. An approach in this direction is given in Theorem 5.6.
$\dim _{\mathbb C}\mathrm {Ext}^0_{H_n(0)}(\mathbf {P}_{\alpha }, \mathcal {V}_{\beta })$
. An approach in this direction is given in Theorem 5.6.
This paper is organised as follows. In Section 2, we introduce the prerequisites on the
![]() $0$
-Hecke algebra, including the quasisymmetric characteristic, standard ribbon tableaux, standard immaculate tableaux and
$0$
-Hecke algebra, including the quasisymmetric characteristic, standard ribbon tableaux, standard immaculate tableaux and
![]() $H_n(0)$
-modules associated to such tableaux. In Section 3, we provide a minimal projective presentation of
$H_n(0)$
-modules associated to such tableaux. In Section 3, we provide a minimal projective presentation of
![]() $\mathcal {V}_{\alpha }$
and
$\mathcal {V}_{\alpha }$
and
![]() $\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathbf {F}_{\beta })$
. And in Section 4, we provide a minimal injective presentation of
$\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathbf {F}_{\beta })$
. And in Section 4, we provide a minimal injective presentation of
![]() $\mathcal {V}_{\alpha }$
and
$\mathcal {V}_{\alpha }$
and
![]() $\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\beta },\mathcal {V}_{\alpha })$
. In Section 5, we investigate
$\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\beta },\mathcal {V}_{\alpha })$
. In Section 5, we investigate
![]() $\mathrm {Ext}^i_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
for
$\mathrm {Ext}^i_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
for
![]() $i=0,1$
. Section 6 is devoted to proving the first and second main results of this paper. In the last section, we provide some future directions to pursue.
$i=0,1$
. Section 6 is devoted to proving the first and second main results of this paper. In the last section, we provide some future directions to pursue.
2 Preliminaries
In this section, n denotes a nonnegative integer. Define
![]() $[n]$
to be
$[n]$
to be
![]() $\{1,2,\ldots , n\}$
if
$\{1,2,\ldots , n\}$
if
![]() $n> 0$
or
$n> 0$
or
![]() $\emptyset $
otherwise. In addition, we set
$\emptyset $
otherwise. In addition, we set
![]() $[-1]:=\emptyset $
. For positive integers
$[-1]:=\emptyset $
. For positive integers
![]() $i\le j$
, set
$i\le j$
, set
![]() $[i,j]:=\{i,i+1,\ldots , j\}$
.
$[i,j]:=\{i,i+1,\ldots , j\}$
.
2.1 Compositions and their diagrams
A composition
![]() $\alpha $
of a nonnegative integer n, denoted by
$\alpha $
of a nonnegative integer n, denoted by
![]() $\alpha \models n$
, is a finite ordered list of positive integers
$\alpha \models n$
, is a finite ordered list of positive integers
![]() $(\alpha _1, \alpha _2, \ldots , \alpha _k)$
satisfying
$(\alpha _1, \alpha _2, \ldots , \alpha _k)$
satisfying
![]() $\sum _{i=1}^k \alpha _i = n$
. For each
$\sum _{i=1}^k \alpha _i = n$
. For each
![]() $1 \le i \le k$
, let us call
$1 \le i \le k$
, let us call
![]() $\alpha _i$
a part of
$\alpha _i$
a part of
![]() $\alpha $
. And we call
$\alpha $
. And we call
![]() $k =: \ell (\alpha )$
the length of
$k =: \ell (\alpha )$
the length of
![]() $\alpha $
and
$\alpha $
and
![]() $n =:|\alpha |$
the size of
$n =:|\alpha |$
the size of
![]() $\alpha $
. For convenience, we define the empty composition
$\alpha $
. For convenience, we define the empty composition
![]() $\emptyset $
to be the unique composition of size and length
$\emptyset $
to be the unique composition of size and length
![]() $0$
. A generalised composition
$0$
. A generalised composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
of n is a formal sum
${\boldsymbol {\unicode{x3b1} }}$
of n is a formal sum
![]() $\alpha ^{(1)} \oplus \alpha ^{(2)} \oplus \cdots \oplus \alpha ^{(k)}$
, where
$\alpha ^{(1)} \oplus \alpha ^{(2)} \oplus \cdots \oplus \alpha ^{(k)}$
, where
![]() $\alpha ^{(i)} \models n_i$
for positive integers
$\alpha ^{(i)} \models n_i$
for positive integers
![]() $n_i$
s with
$n_i$
s with
![]() $n_1 + n_2 + \cdots + n_k = n$
.
$n_1 + n_2 + \cdots + n_k = n$
.
For
![]() $\alpha = (\alpha _1, \alpha _2, \ldots , \alpha _{\ell (\alpha )}) \models n$
, we define the composition diagram
$\alpha = (\alpha _1, \alpha _2, \ldots , \alpha _{\ell (\alpha )}) \models n$
, we define the composition diagram
![]() $\mathtt {cd}(\alpha )$
of
$\mathtt {cd}(\alpha )$
of
![]() $\alpha $
as a left-justified array of n boxes where the ith row from the top has
$\alpha $
as a left-justified array of n boxes where the ith row from the top has
![]() $\alpha _i$
boxes for
$\alpha _i$
boxes for
![]() $1 \le i \le k$
. We also define the ribbon diagram
$1 \le i \le k$
. We also define the ribbon diagram
![]() $\mathtt {rd}(\alpha )$
of
$\mathtt {rd}(\alpha )$
of
![]() $\alpha $
by the connected skew diagram without
$\alpha $
by the connected skew diagram without
![]() $2 \times 2$
boxes, such that the ith column from the left has
$2 \times 2$
boxes, such that the ith column from the left has
![]() $\alpha _i$
boxes. Then for a generalised composition
$\alpha _i$
boxes. Then for a generalised composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
of n, we define the generalised ribbon diagram
${\boldsymbol {\unicode{x3b1} }}$
of n, we define the generalised ribbon diagram
![]() $\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
of
$\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
of
![]() ${\boldsymbol {\unicode{x3b1} }}$
to be the skew diagram whose connected components are
${\boldsymbol {\unicode{x3b1} }}$
to be the skew diagram whose connected components are
![]() $\mathtt {rd}(\alpha ^{(1)}), \mathtt {rd}(\alpha ^{(2)}), \ldots , \mathtt {rd}(\alpha ^{(k)})$
such that
$\mathtt {rd}(\alpha ^{(1)}), \mathtt {rd}(\alpha ^{(2)}), \ldots , \mathtt {rd}(\alpha ^{(k)})$
such that
![]() $\mathtt {rd}(\alpha ^{(i+1)})$
is strictly to the northeast of
$\mathtt {rd}(\alpha ^{(i+1)})$
is strictly to the northeast of
![]() $\mathtt {rd}(\alpha ^{(i)})$
for
$\mathtt {rd}(\alpha ^{(i)})$
for
![]() $i = 1, 2, \ldots , k-1$
. For example, if
$i = 1, 2, \ldots , k-1$
. For example, if
![]() $\alpha = (3,1,2)$
and
$\alpha = (3,1,2)$
and
![]() ${\boldsymbol {\unicode{x3b1} }} = (2,1) \oplus (1,1)$
, then
${\boldsymbol {\unicode{x3b1} }} = (2,1) \oplus (1,1)$
, then

Given
![]() $\alpha = (\alpha _1, \alpha _2, \ldots ,\alpha _{\ell (\alpha )}) \models n$
and
$\alpha = (\alpha _1, \alpha _2, \ldots ,\alpha _{\ell (\alpha )}) \models n$
and
![]() $I = \{i_1 < i_2 < \cdots < i_k\} \subset [n-1]$
, let
$I = \{i_1 < i_2 < \cdots < i_k\} \subset [n-1]$
, let
 $$ \begin{align*} &\mathrm{set}(\alpha) := \{\alpha_1,\alpha_1+\alpha_2,\ldots, \alpha_1 + \alpha_2 + \cdots + \alpha_{\ell(\alpha)-1}\}, \\ &\mathrm{comp}(I) := (i_1,i_2 - i_1,\ldots,n-i_k). \end{align*} $$
$$ \begin{align*} &\mathrm{set}(\alpha) := \{\alpha_1,\alpha_1+\alpha_2,\ldots, \alpha_1 + \alpha_2 + \cdots + \alpha_{\ell(\alpha)-1}\}, \\ &\mathrm{comp}(I) := (i_1,i_2 - i_1,\ldots,n-i_k). \end{align*} $$
The set of compositions of n is in bijection with the set of subsets of
![]() $[n-1]$
under the correspondence
$[n-1]$
under the correspondence
![]() $\alpha \mapsto \mathrm {set}(\alpha )$
(or
$\alpha \mapsto \mathrm {set}(\alpha )$
(or
![]() $I \mapsto \mathrm {comp}(I)$
). Let
$I \mapsto \mathrm {comp}(I)$
). Let
![]() $\alpha ^{\mathrm {r}}$
denote the composition
$\alpha ^{\mathrm {r}}$
denote the composition
![]() $(\alpha _{\ell (\alpha )}, \alpha _{\ell (\alpha )-1}, \ldots , \alpha _1)$
.
$(\alpha _{\ell (\alpha )}, \alpha _{\ell (\alpha )-1}, \ldots , \alpha _1)$
.
For compositions
![]() $\alpha = (\alpha _{1}, \alpha _{2}, \ldots , \alpha _{k})$
and
$\alpha = (\alpha _{1}, \alpha _{2}, \ldots , \alpha _{k})$
and
![]() $\beta = (\beta _{1}, \beta _{2}, \ldots , \beta _{l})$
, let
$\beta = (\beta _{1}, \beta _{2}, \ldots , \beta _{l})$
, let
![]() $\alpha \cdot \beta $
be the concatenation and
$\alpha \cdot \beta $
be the concatenation and
![]() $\alpha \odot \beta $
the near concatenation of
$\alpha \odot \beta $
the near concatenation of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. In other words,
$\beta $
. In other words,
![]() $ \alpha \cdot \beta = (\alpha _1, \alpha _2, \ldots , \alpha _k, \beta _1, \beta _2, \ldots , \beta _l)$
and
$ \alpha \cdot \beta = (\alpha _1, \alpha _2, \ldots , \alpha _k, \beta _1, \beta _2, \ldots , \beta _l)$
and
![]() $\alpha \odot \beta = (\alpha _1,\ldots , \alpha _{k-1},\alpha _k + \beta _1,\beta _2, \ldots , \beta _l)$
. For a generalised composition
$\alpha \odot \beta = (\alpha _1,\ldots , \alpha _{k-1},\alpha _k + \beta _1,\beta _2, \ldots , \beta _l)$
. For a generalised composition
![]() ${\boldsymbol {\unicode{x3b1} }} = \alpha ^{(1)} \oplus \alpha ^{(2)} \oplus \cdots \oplus \alpha ^{(m)}$
, define
${\boldsymbol {\unicode{x3b1} }} = \alpha ^{(1)} \oplus \alpha ^{(2)} \oplus \cdots \oplus \alpha ^{(m)}$
, define
2.2 The
 $0$
-Hecke algebra and the quasisymmetric characteristic
$0$
-Hecke algebra and the quasisymmetric characteristic
The symmetric group
![]() $\Sigma _n$
is generated by simple transpositions
$\Sigma _n$
is generated by simple transpositions
![]() $s_i := (i \ i \hspace {-.5ex} + \hspace {-.5ex} 1)$
with
$s_i := (i \ i \hspace {-.5ex} + \hspace {-.5ex} 1)$
with
![]() $1 \le i \le n-1$
. An expression for
$1 \le i \le n-1$
. An expression for
![]() $\sigma \in \Sigma _n$
of the form
$\sigma \in \Sigma _n$
of the form
![]() $s_{i_1} s_{i_2} \cdots s_{i_p}$
that uses the minimal number of simple transpositions is called a reduced expression for
$s_{i_1} s_{i_2} \cdots s_{i_p}$
that uses the minimal number of simple transpositions is called a reduced expression for
![]() $\sigma $
. The number of simple transpositions in any reduced expression for
$\sigma $
. The number of simple transpositions in any reduced expression for
![]() $\sigma $
, denoted by
$\sigma $
, denoted by
![]() $\ell (\sigma )$
, is called the length of
$\ell (\sigma )$
, is called the length of
![]() $\sigma $
.
$\sigma $
.
The
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_n(0)$
is the
$H_n(0)$
is the
![]() $\mathbb C$
-algebra generated by
$\mathbb C$
-algebra generated by
![]() $\pi _1, \pi _2, \ldots ,\pi _{n-1}$
subject to the following relations:
$\pi _1, \pi _2, \ldots ,\pi _{n-1}$
subject to the following relations:
 $$ \begin{align*} \pi_i^2 &= \pi_i \quad \text{for } 1\le i \le n-1,\\ \pi_i \pi_{i+1} \pi_i &= \pi_{i+1} \pi_i \pi_{i+1} \quad \text{for } 1\le i \le n-2,\\ \pi_i \pi_j &=\pi_j \pi_i \quad \text{if } |i-j| \ge 2. \end{align*} $$
$$ \begin{align*} \pi_i^2 &= \pi_i \quad \text{for } 1\le i \le n-1,\\ \pi_i \pi_{i+1} \pi_i &= \pi_{i+1} \pi_i \pi_{i+1} \quad \text{for } 1\le i \le n-2,\\ \pi_i \pi_j &=\pi_j \pi_i \quad \text{if } |i-j| \ge 2. \end{align*} $$
Pick up any reduced expression
![]() $s_{i_1} s_{i_2} \cdots s_{i_p}$
for a permutation
$s_{i_1} s_{i_2} \cdots s_{i_p}$
for a permutation
![]() $\sigma \in \Sigma _n$
. It is well known that the element
$\sigma \in \Sigma _n$
. It is well known that the element
![]() $\pi _{\sigma } := \pi _{i_1} \pi _{i_2} \cdots \pi _{i_p}$
is independent of the choice of reduced expressions and
$\pi _{\sigma } := \pi _{i_1} \pi _{i_2} \cdots \pi _{i_p}$
is independent of the choice of reduced expressions and
![]() $\{\pi _{\sigma } \mid \sigma \in \Sigma _n\}$
is a basis for
$\{\pi _{\sigma } \mid \sigma \in \Sigma _n\}$
is a basis for
![]() $H_n(0)$
. For later use, set
$H_n(0)$
. For later use, set
for all
![]() $1 \le i \le j \le n-1$
.
$1 \le i \le j \le n-1$
.
Let
![]() $\mathcal {R}(H_n(0))$
denote the
$\mathcal {R}(H_n(0))$
denote the
![]() $\mathbb Z$
-span of (representatives of) the isomorphism classes of finite-dimensional representations of
$\mathbb Z$
-span of (representatives of) the isomorphism classes of finite-dimensional representations of
![]() $H_n(0)$
. The isomorphism class corresponding to an
$H_n(0)$
. The isomorphism class corresponding to an
![]() $H_n(0)$
-module M will be denoted by
$H_n(0)$
-module M will be denoted by
![]() $[M]$
. The Grothendieck group
$[M]$
. The Grothendieck group
![]() $\mathcal {G}_0(H_n(0))$
is the quotient of
$\mathcal {G}_0(H_n(0))$
is the quotient of
![]() $\mathcal {R}(H_n(0))$
modulo the relations
$\mathcal {R}(H_n(0))$
modulo the relations
![]() $[M] = [M'] + [M"]$
whenever there exists a short exact sequence
$[M] = [M'] + [M"]$
whenever there exists a short exact sequence
![]() $0 \rightarrow M' \rightarrow M \rightarrow M" \rightarrow 0$
. The equivalence classes of irreducible representations of
$0 \rightarrow M' \rightarrow M \rightarrow M" \rightarrow 0$
. The equivalence classes of irreducible representations of
![]() $H_n(0)$
form a free
$H_n(0)$
form a free
![]() $\mathbb Z$
-basis for
$\mathbb Z$
-basis for
![]() $\mathcal {G}_0(H_n(0))$
. Let
$\mathcal {G}_0(H_n(0))$
. Let
According to [Reference Norton25], there are
![]() $2^{n-1}$
distinct irreducible representations of
$2^{n-1}$
distinct irreducible representations of
![]() $H_n(0)$
. They are naturally indexed by compositions of n. Let
$H_n(0)$
. They are naturally indexed by compositions of n. Let
![]() $\mathbf {F}_{\alpha }$
denote the
$\mathbf {F}_{\alpha }$
denote the
![]() $1$
-dimensional
$1$
-dimensional
![]() $\mathbb C$
-vector space corresponding to
$\mathbb C$
-vector space corresponding to
![]() $\alpha \models n$
, spanned by a vector
$\alpha \models n$
, spanned by a vector
![]() $v_{\alpha }$
. For each
$v_{\alpha }$
. For each
![]() $1\le i \le n-1$
, define an action of the generator
$1\le i \le n-1$
, define an action of the generator
![]() $\pi _i$
of
$\pi _i$
of
![]() $H_n(0)$
as follows:
$H_n(0)$
as follows:
 $$\begin{align*}\pi_i \cdot v_{\alpha} = \begin{cases} 0 & i \in \mathrm{set}(\alpha),\\ v_{\alpha} & i \notin \mathrm{set}(\alpha). \end{cases} \end{align*}$$
$$\begin{align*}\pi_i \cdot v_{\alpha} = \begin{cases} 0 & i \in \mathrm{set}(\alpha),\\ v_{\alpha} & i \notin \mathrm{set}(\alpha). \end{cases} \end{align*}$$
Then
![]() $\mathbf {F}_{\alpha }$
is an irreducible
$\mathbf {F}_{\alpha }$
is an irreducible
![]() $1$
-dimensional
$1$
-dimensional
![]() $H_n(0)$
-representation.
$H_n(0)$
-representation.
In the following, let us review the connection between
![]() $\mathcal {G}$
and the ring
$\mathcal {G}$
and the ring
![]() $\mathrm {QSym}$
of quasisymmetric functions. Quasisymmetric functions are power series of bounded degree in variables
$\mathrm {QSym}$
of quasisymmetric functions. Quasisymmetric functions are power series of bounded degree in variables
![]() $x_{1},x_{2},x_{3},\ldots $
with coefficients in
$x_{1},x_{2},x_{3},\ldots $
with coefficients in
![]() $\mathbb Z$
that are shift invariant in the sense that the coefficient of the monomial
$\mathbb Z$
that are shift invariant in the sense that the coefficient of the monomial
![]() $x_{1}^{\alpha _{1}}x_{2}^{\alpha _{2}}\cdots x_{k}^{\alpha _{k}}$
is equal to the coefficient of the monomial
$x_{1}^{\alpha _{1}}x_{2}^{\alpha _{2}}\cdots x_{k}^{\alpha _{k}}$
is equal to the coefficient of the monomial
![]() $x_{i_{1}}^{\alpha _{1}}x_{i_{2}}^{\alpha _{2}}\cdots x_{i_{k}}^{\alpha _{k}}$
for any strictly increasing sequence of positive integers
$x_{i_{1}}^{\alpha _{1}}x_{i_{2}}^{\alpha _{2}}\cdots x_{i_{k}}^{\alpha _{k}}$
for any strictly increasing sequence of positive integers
![]() $i_{1}<i_{2}<\cdots <i_{k}$
indexing the variables and any positive integer sequence
$i_{1}<i_{2}<\cdots <i_{k}$
indexing the variables and any positive integer sequence
![]() $(\alpha _{1},\alpha _{2},\ldots ,\alpha _{k})$
of exponents.
$(\alpha _{1},\alpha _{2},\ldots ,\alpha _{k})$
of exponents.
Given a composition
![]() $\alpha $
, the fundamental quasisymmetric function
$\alpha $
, the fundamental quasisymmetric function
![]() $F_{\alpha }$
is defined by
$F_{\alpha }$
is defined by
![]() $F_{\emptyset } = 1$
and
$F_{\emptyset } = 1$
and
 $$\begin{align*}F_{\alpha} = \sum_{\substack{1 \le i_1 \le i_2 \le \cdots \le i_k \\ i_j < i_{j+1} \text{ if } j \in \mathrm{set}(\alpha)}} x_{i_1} x_{i_2} \cdots x_{i_k}. \end{align*}$$
$$\begin{align*}F_{\alpha} = \sum_{\substack{1 \le i_1 \le i_2 \le \cdots \le i_k \\ i_j < i_{j+1} \text{ if } j \in \mathrm{set}(\alpha)}} x_{i_1} x_{i_2} \cdots x_{i_k}. \end{align*}$$
It is well known that
![]() $\{F_{\alpha } \mid \alpha \text { is a composition}\}$
is a basis for
$\{F_{\alpha } \mid \alpha \text { is a composition}\}$
is a basis for
![]() $\mathrm {QSym}$
. In [Reference Duchamp, Krob, Leclerc and Thibon15], Duchamp, Krob, Leclerc and Thibon show that, when
$\mathrm {QSym}$
. In [Reference Duchamp, Krob, Leclerc and Thibon15], Duchamp, Krob, Leclerc and Thibon show that, when
![]() $\mathcal {G}$
is equipped with induction product, the linear map
$\mathcal {G}$
is equipped with induction product, the linear map
called the quasisymmetric characteristic, is a ring isomorphism.
2.3 Projective modules of the
 $0$
-Hecke algebra
$0$
-Hecke algebra
We begin this subsection by recalling that
![]() $H_n(0)$
is a Frobenius algebra. Hence it is self-injective, so that finitely generated projective and injective modules coincide (see [Reference Duchamp, Hivert and Thibon14, Proposition 4.1], [Reference Fayers16, Proposition 4.1] and [Reference Benson3, Proposition 1.6.2]).
$H_n(0)$
is a Frobenius algebra. Hence it is self-injective, so that finitely generated projective and injective modules coincide (see [Reference Duchamp, Hivert and Thibon14, Proposition 4.1], [Reference Fayers16, Proposition 4.1] and [Reference Benson3, Proposition 1.6.2]).
It was Norton [Reference Norton25] who first classified all projective indecomposable modules of
![]() $H_n(0)$
up to isomorphism that bijectively correspond to compositions of n. Later, Huang [Reference Huang20] provided a combinatorial description of these modules and their induction products as well by using standard ribbon tableaux of generalised composition shape. We review Huang’s description very briefly here.
$H_n(0)$
up to isomorphism that bijectively correspond to compositions of n. Later, Huang [Reference Huang20] provided a combinatorial description of these modules and their induction products as well by using standard ribbon tableaux of generalised composition shape. We review Huang’s description very briefly here.
Definition 2.1. For a generalised composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
of n, a standard ribbon tableau (SRT) of shape
${\boldsymbol {\unicode{x3b1} }}$
of n, a standard ribbon tableau (SRT) of shape
![]() ${\boldsymbol {\unicode{x3b1} }}$
is a filling of
${\boldsymbol {\unicode{x3b1} }}$
is a filling of
![]() $\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
with
$\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
with
![]() $\{1,2,\ldots ,n\}$
such that the entries are all distinct, the entries in each row are increasing from left to right, and the entries in each column are increasing from top to bottom.
$\{1,2,\ldots ,n\}$
such that the entries are all distinct, the entries in each row are increasing from left to right, and the entries in each column are increasing from top to bottom.
Let
![]() $\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
denote the set of all
$\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
denote the set of all
![]() $\mathrm {SRT}$
x of shape
$\mathrm {SRT}$
x of shape
![]() ${\boldsymbol {\unicode{x3b1} }}$
. For
${\boldsymbol {\unicode{x3b1} }}$
. For
![]() $T \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
, let
$T \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
, let
Define an
![]() $H_n(0)$
-action on the
$H_n(0)$
-action on the
![]() $\mathbb C$
-span of
$\mathbb C$
-span of
![]() $\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
by
$\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
by
 $$ \begin{align} \pi_i \cdot T = \begin{cases} T & \text{if } i \notin \mathrm{Des}(T),\\ 0 & \text{if } i \text{ and } i+1 \text{ are in the same row of } T,\\ s_i \cdot T & \text{if } i \text{ appears strictly below } i+1 \text{ in } T \end{cases} \end{align} $$
$$ \begin{align} \pi_i \cdot T = \begin{cases} T & \text{if } i \notin \mathrm{Des}(T),\\ 0 & \text{if } i \text{ and } i+1 \text{ are in the same row of } T,\\ s_i \cdot T & \text{if } i \text{ appears strictly below } i+1 \text{ in } T \end{cases} \end{align} $$
for
![]() $1\le i \le n-1$
and
$1\le i \le n-1$
and
![]() $T \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
. Here
$T \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
. Here
![]() $s_i \cdot T$
is obtained from T by swapping i and
$s_i \cdot T$
is obtained from T by swapping i and
![]() $i+1$
. The resulting module is denoted by
$i+1$
. The resulting module is denoted by
![]() $\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
. It is known that the set
$\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
. It is known that the set
![]() $\{\mathbf {P}_{\alpha } \mid \alpha \models n\}$
forms a complete family of non-isomorphic projective indecomposable
$\{\mathbf {P}_{\alpha } \mid \alpha \models n\}$
forms a complete family of non-isomorphic projective indecomposable
![]() $H_n(0)$
-modules and
$H_n(0)$
-modules and
![]() $\mathbf {P}_{\alpha } /\mathrm {rad}(\mathbf {P}_{\alpha }) \cong \mathbf {F}_{\alpha }$
, where
$\mathbf {P}_{\alpha } /\mathrm {rad}(\mathbf {P}_{\alpha }) \cong \mathbf {F}_{\alpha }$
, where
![]() $\mathrm {rad}(\mathbf {P}_{\alpha })$
is the radical of
$\mathrm {rad}(\mathbf {P}_{\alpha })$
is the radical of
![]() $\mathbf {P}_{\alpha }$
(for details; see [Reference Huang20, Reference Norton25]).
$\mathbf {P}_{\alpha }$
(for details; see [Reference Huang20, Reference Norton25]).
Remark 2.2. It should be pointed out that the ribbon diagram and
![]() $H_n(0)$
-action used here are slightly different from those in Huang’s work [Reference Huang20]. He describes the
$H_n(0)$
-action used here are slightly different from those in Huang’s work [Reference Huang20]. He describes the
![]() $H_n(0)$
-action on
$H_n(0)$
-action on
![]() $\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
in terms of
$\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
in terms of
![]() $\overline {\pi }_i$
s, where
$\overline {\pi }_i$
s, where
![]() $\overline {\pi }_i= \pi _i -1$
. On the other hand, we use
$\overline {\pi }_i= \pi _i -1$
. On the other hand, we use
![]() $\pi _i$
s because the
$\pi _i$
s because the
![]() $H_n(0)$
-action on
$H_n(0)$
-action on
![]() $\mathcal {V}_{\alpha }$
is described in terms of
$\mathcal {V}_{\alpha }$
is described in terms of
![]() $\pi _i$
s. This leads us to adjust Huang’s ribbon diagram to the form of
$\pi _i$
s. This leads us to adjust Huang’s ribbon diagram to the form of
![]() $\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
.
$\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
.
Given any generalised composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
, let
${\boldsymbol {\unicode{x3b1} }}$
, let
![]() $T_{\boldsymbol {\unicode{x3b1} }} \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
be the
$T_{\boldsymbol {\unicode{x3b1} }} \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
be the
![]() $\mathrm {SRT}$
obtained by filling
$\mathrm {SRT}$
obtained by filling
![]() $\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
with entries
$\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
with entries
![]() $1, 2, \ldots , n$
from top to bottom and from left to right. Since
$1, 2, \ldots , n$
from top to bottom and from left to right. Since
![]() $\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}}$
is cyclically generated by
$\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}}$
is cyclically generated by
![]() $T_{\boldsymbol {\unicode{x3b1} }}$
, we call
$T_{\boldsymbol {\unicode{x3b1} }}$
, we call
![]() $T_{\boldsymbol {\unicode{x3b1} }}$
the source tableau of
$T_{\boldsymbol {\unicode{x3b1} }}$
the source tableau of
![]() $\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
. For any
$\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
. For any
![]() $\mathrm {SRT} T$
, let
$\mathrm {SRT} T$
, let
![]() $\mathbf {w}(T)$
be the word obtained by reading the entries from left to right, starting with the bottom row. Using this reading, Huang [Reference Huang20] shows the following result.
$\mathbf {w}(T)$
be the word obtained by reading the entries from left to right, starting with the bottom row. Using this reading, Huang [Reference Huang20] shows the following result.
Theorem 2.3 ([Reference Huang20, Theorem 3.3]).
Let
![]() ${\boldsymbol {\unicode{x3b1} }}$
be a generalised composition of n. Then
${\boldsymbol {\unicode{x3b1} }}$
be a generalised composition of n. Then
![]() $\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
is isomorphic to
$\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
is isomorphic to
![]() $\bigoplus _{\beta \in [{\boldsymbol {\unicode{x3b1} }}]} \mathbf {P}_{\beta }$
as an
$\bigoplus _{\beta \in [{\boldsymbol {\unicode{x3b1} }}]} \mathbf {P}_{\beta }$
as an
![]() $H_n(0)$
-module.
$H_n(0)$
-module.
For later use, for every generalised composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
of n, we define a partial order
${\boldsymbol {\unicode{x3b1} }}$
of n, we define a partial order
![]() $\le $
on
$\le $
on
![]() $\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
by
$\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }})$
by
As usual, whenever
![]() $T \le T'$
, the notation
$T \le T'$
, the notation
![]() $[T, T']$
denotes the interval
$[T, T']$
denotes the interval
![]() $\{U \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}) \mid T \le U \le T'\}$
.
$\{U \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}) \mid T \le U \le T'\}$
.
2.4 The
 $H_n(0)$
-action on standard immaculate tableaux
$H_n(0)$
-action on standard immaculate tableaux
Noncommutative Bernstein operators were introduced by Berg, Bergeron, Saliola, Serrano and Zabrocki [Reference Berg, Bergeron, Saliola, Serrano and Zabrocki4]. Applied to the identity of the ring
![]() $\mathrm {NSym}$
of noncommutative symmetric functions, they yield the immaculate functions, which form a basis of
$\mathrm {NSym}$
of noncommutative symmetric functions, they yield the immaculate functions, which form a basis of
![]() $\mathrm {NSym}$
. Soon after, using the combinatorial objects called standard immaculate tableaux, they constructed indecomposable
$\mathrm {NSym}$
. Soon after, using the combinatorial objects called standard immaculate tableaux, they constructed indecomposable
![]() $H_n(0)$
-modules whose quasisymmetric characteristics are the quasisymmetric functions that are dual to immaculate functions (see [Reference Berg, Bergeron, Saliola, Serrano and Zabrocki5]).
$H_n(0)$
-modules whose quasisymmetric characteristics are the quasisymmetric functions that are dual to immaculate functions (see [Reference Berg, Bergeron, Saliola, Serrano and Zabrocki5]).
Definition 2.4. Let
![]() $\alpha \models n$
. A standard immaculate tableau (SIT) of shape
$\alpha \models n$
. A standard immaculate tableau (SIT) of shape
![]() $\alpha $
is a filling
$\alpha $
is a filling
![]() $\mathscr {T}$
of the composition diagram
$\mathscr {T}$
of the composition diagram
![]() $\mathtt {cd}(\alpha )$
with
$\mathtt {cd}(\alpha )$
with
![]() $\{1,2,\ldots ,n\}$
such that the entries are all distinct, the entries in each row increase from left to right, and the entries in the first column increase from top to bottom.
$\{1,2,\ldots ,n\}$
such that the entries are all distinct, the entries in each row increase from left to right, and the entries in the first column increase from top to bottom.
We denote the set of all SITx of shape
![]() $\alpha $
by
$\alpha $
by
![]() $\mathrm {SIT}(\alpha )$
. For
$\mathrm {SIT}(\alpha )$
. For
![]() $\mathscr {T} \in \mathrm {SIT}(\alpha )$
, let
$\mathscr {T} \in \mathrm {SIT}(\alpha )$
, let
Define an
![]() $H_n(0)$
-action on
$H_n(0)$
-action on
![]() $\mathbb C$
-span of
$\mathbb C$
-span of
![]() $\mathrm {SIT}(\alpha )$
by
$\mathrm {SIT}(\alpha )$
by
 $$ \begin{align} \pi_i \cdot \mathscr{T} = \begin{cases} \mathscr{T} & \text{if } i \notin \mathrm{Des}(\mathscr{T}),\\ 0 & \text{if } i \text{ and } i+1 \text{ are in the first column of } \mathscr{T},\\ s_i \cdot \mathscr{T} & \text{otherwise} \end{cases} \end{align} $$
$$ \begin{align} \pi_i \cdot \mathscr{T} = \begin{cases} \mathscr{T} & \text{if } i \notin \mathrm{Des}(\mathscr{T}),\\ 0 & \text{if } i \text{ and } i+1 \text{ are in the first column of } \mathscr{T},\\ s_i \cdot \mathscr{T} & \text{otherwise} \end{cases} \end{align} $$
for
![]() $1\le i \le n-1$
and
$1\le i \le n-1$
and
![]() $\mathscr {T} \in \mathrm {SIT}(\alpha )$
. Here
$\mathscr {T} \in \mathrm {SIT}(\alpha )$
. Here
![]() $s_i \cdot \mathscr {T}$
is obtained from
$s_i \cdot \mathscr {T}$
is obtained from
![]() $\mathscr {T}$
by swapping i and
$\mathscr {T}$
by swapping i and
![]() $i+1$
. The resulting module is denoted by
$i+1$
. The resulting module is denoted by
![]() $\mathcal {V}_{\alpha }$
.
$\mathcal {V}_{\alpha }$
.
Let
![]() $\mathscr {T}_{\alpha } \in \mathrm {SIT}(\alpha )$
be the SIT obtained by filling
$\mathscr {T}_{\alpha } \in \mathrm {SIT}(\alpha )$
be the SIT obtained by filling
![]() $\mathtt {cd}(\alpha )$
with entries
$\mathtt {cd}(\alpha )$
with entries
![]() $1, 2, \ldots , n$
from left to right and from top to bottom.
$1, 2, \ldots , n$
from left to right and from top to bottom.
Theorem 2.5 ([Reference Berg, Bergeron, Saliola, Serrano and Zabrocki5]).
For
![]() $\alpha \models n$
,
$\alpha \models n$
,
![]() $\mathcal {V}_{\alpha }$
is a cyclic indecomposable
$\mathcal {V}_{\alpha }$
is a cyclic indecomposable
![]() $H_n(0)$
-module generated by
$H_n(0)$
-module generated by
![]() $\mathscr {T}_{\alpha }$
whose quasisymmetric characteristic is the dual immaculate quasisymmetric function
$\mathscr {T}_{\alpha }$
whose quasisymmetric characteristic is the dual immaculate quasisymmetric function
![]() $\mathfrak {S}^*_{\alpha }$
.
$\mathfrak {S}^*_{\alpha }$
.
Convention. Regardless of a ribbon diagram or composition diagram, columns are numbered from left to right. To avoid possible confusion, we adopt the following notation:
-
(i) Let T be a filling of the ribbon diagram
 $\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
.
$\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
.-
-
 $T^i_j$
= the entry at the ith box from the top of the jth column
$T^i_j$
= the entry at the ith box from the top of the jth column -
-
 $T_j^{-1}$
= the entry at the bottom-most box in the jth column
$T_j^{-1}$
= the entry at the bottom-most box in the jth column -
-
 $T^{\bullet }_j$
= the set of all entries in the jth column
$T^{\bullet }_j$
= the set of all entries in the jth column
-
-
(ii) Let
 $\mathscr {T}$
be a filling of the composition diagram
$\mathscr {T}$
be a filling of the composition diagram
 $\mathtt {cd}(\alpha )$
.
$\mathtt {cd}(\alpha )$
.-
-
 $\mathscr {T}_{i,j}$
= the entry at the box in the ith row (from the top) and in the jth column
$\mathscr {T}_{i,j}$
= the entry at the box in the ith row (from the top) and in the jth column
-
3 A minimal projective presentation of
 $\mathcal {V}_{\alpha }$
and
$\mathcal {V}_{\alpha }$
and
 $\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathbf {F}_{\beta })$
$\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathbf {F}_{\beta })$
From now on,
![]() $\alpha $
denotes an arbitrarily chosen composition of n. We here construct a minimal projective presentation of
$\alpha $
denotes an arbitrarily chosen composition of n. We here construct a minimal projective presentation of
![]() $\mathcal {V}_{\alpha }$
. Using this, we compute
$\mathcal {V}_{\alpha }$
. Using this, we compute
![]() $\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathbf {F}_{\beta })$
for each
$\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathbf {F}_{\beta })$
for each
![]() $\beta \models n$
.
$\beta \models n$
.
Firstly, let us introduce necessary terminologies and notation. Let
![]() $A,B$
be finitely generated
$A,B$
be finitely generated
![]() $H_n(0)$
-modules. A surjective
$H_n(0)$
-modules. A surjective
![]() $H_n(0)$
-module homomorphism
$H_n(0)$
-module homomorphism
![]() $f:A\to B$
is called an essential epimorphism if an
$f:A\to B$
is called an essential epimorphism if an
![]() $H_n(0)$
-module homomorphism
$H_n(0)$
-module homomorphism
![]() $g: X\to A$
is surjective whenever
$g: X\to A$
is surjective whenever
![]() $f \circ g:X\to B$
is surjective. A projective cover of A is an essential epimorphism
$f \circ g:X\to B$
is surjective. A projective cover of A is an essential epimorphism
![]() $f:P\to A$
with P projective that always exists and is unique up to isomorphism. It is well known that
$f:P\to A$
with P projective that always exists and is unique up to isomorphism. It is well known that
![]() $f:P\to A$
is an essential epimorphism if and only if
$f:P\to A$
is an essential epimorphism if and only if
![]() $\ker (f) \subset \mathrm {rad}(P)$
(for instance, see [Reference Auslander, Reiten and Smalø1, Proposition I.3.6]). For simplicity, when f is clear in the context, we just write
$\ker (f) \subset \mathrm {rad}(P)$
(for instance, see [Reference Auslander, Reiten and Smalø1, Proposition I.3.6]). For simplicity, when f is clear in the context, we just write
![]() $\Omega (A)$
for
$\Omega (A)$
for
![]() $\ker (f)$
and call it the syzygy module of A. An exact sequence
$\ker (f)$
and call it the syzygy module of A. An exact sequence
with projective modules
![]() $P_0$
and
$P_0$
and
![]() $P_1$
is called a minimal projective presentation if the
$P_1$
is called a minimal projective presentation if the
![]() $H_n(0)$
-module homomorphisms
$H_n(0)$
-module homomorphisms
![]() $\epsilon : P_0 \rightarrow A$
and
$\epsilon : P_0 \rightarrow A$
and
![]() $\partial _1: P_1 \rightarrow \Omega (A)$
are projective covers of A and
$\partial _1: P_1 \rightarrow \Omega (A)$
are projective covers of A and
![]() $\Omega (A)$
, respectively.
$\Omega (A)$
, respectively.
Next, let us review the projective cover of
![]() $\mathcal {V}_{\alpha }$
obtained in [Reference Choi, Kim, Nam and Oh12]. Given any
$\mathcal {V}_{\alpha }$
obtained in [Reference Choi, Kim, Nam and Oh12]. Given any
![]() $T \in \mathrm {SRT}(\alpha )$
, let
$T \in \mathrm {SRT}(\alpha )$
, let
![]() $\mathscr {T}_T$
be the filling of
$\mathscr {T}_T$
be the filling of
![]() $\mathtt {cd}(\alpha )$
given by
$\mathtt {cd}(\alpha )$
given by
![]() $(\mathscr {T}_T)_{i,j} = T^{j}_{i}$
. Then we define a
$(\mathscr {T}_T)_{i,j} = T^{j}_{i}$
. Then we define a
![]() $\mathbb C$
-linear map
$\mathbb C$
-linear map
![]() $\Phi : \mathbf {P}_{\alpha } \rightarrow \mathcal {V}_{\alpha }$
by
$\Phi : \mathbf {P}_{\alpha } \rightarrow \mathcal {V}_{\alpha }$
by
 $$ \begin{align} \Phi(T) = \begin{cases} \mathscr{T}_T & \text{if } \mathscr{T}_T \text{ is an SIT,}\\ 0 & \text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} \Phi(T) = \begin{cases} \mathscr{T}_T & \text{if } \mathscr{T}_T \text{ is an SIT,}\\ 0 & \text{otherwise.} \end{cases} \end{align} $$
For example, if
![]() $\alpha = (1,2,2)$
and
$\alpha = (1,2,2)$
and

then

Therefore,
![]() $\Phi (T_1) = \mathscr {T}_{T_1}$
and
$\Phi (T_1) = \mathscr {T}_{T_1}$
and
![]() $\Phi (T_2) = 0$
.
$\Phi (T_2) = 0$
.
Theorem 3.1 ([Reference Choi, Kim, Nam and Oh12, Theorem 3.2]).
For
![]() $\alpha \models n$
,
$\alpha \models n$
,
![]() $\Phi : \mathbf {P}_{\alpha } \rightarrow \mathcal {V}_{\alpha }$
is a projective cover of
$\Phi : \mathbf {P}_{\alpha } \rightarrow \mathcal {V}_{\alpha }$
is a projective cover of
![]() $\mathcal {V}_{\alpha }$
.
$\mathcal {V}_{\alpha }$
.
Now, let us construct a projective cover of
![]() $\Omega (\mathcal {V}_{\alpha })$
for each
$\Omega (\mathcal {V}_{\alpha })$
for each
![]() $\alpha \models n$
. To do this, we provide necessary notation. For each integer
$\alpha \models n$
. To do this, we provide necessary notation. For each integer
![]() $0\le i \le \ell (\alpha )-1$
, we set
$0\le i \le \ell (\alpha )-1$
, we set
![]() $m_i$
to be
$m_i$
to be
![]() $\sum _{j = 1}^{i}\alpha _j$
for
$\sum _{j = 1}^{i}\alpha _j$
for
![]() $i> 0$
and
$i> 0$
and
![]() $m_0 = 0$
. Let
$m_0 = 0$
. Let
Given
![]() $i \in \mathcal {I}(\alpha )$
, let
$i \in \mathcal {I}(\alpha )$
, let
and
Given an SRT
![]() $\tau $
of shape
$\tau $
of shape
![]() ${\boldsymbol {\unicode{x3b1} }}^{(i)} (i \in \mathcal {I}(\alpha ))$
, define
${\boldsymbol {\unicode{x3b1} }}^{(i)} (i \in \mathcal {I}(\alpha ))$
, define
![]() $L(\tau )$
to be the filling of
$L(\tau )$
to be the filling of
![]() $\mathtt {rd}(\alpha )$
whose entries in each column are increasing from top to bottom and whose columns are given as follows: for
$\mathtt {rd}(\alpha )$
whose entries in each column are increasing from top to bottom and whose columns are given as follows: for
![]() $1 \le p \le \ell (\alpha )$
,
$1 \le p \le \ell (\alpha )$
,
 $$ \begin{align} L(\tau)_p^{\bullet} = \begin{cases} \tau_i^{\bullet} \setminus \{\tau_i^1\} & \text{if } p = i,\\ \tau_{i+1}^{\bullet} \cup \{\tau_i^1\} & \text{if } p = i+1,\\ \tau_p^{\bullet} & \text{otherwise.}\\ \end{cases} \end{align} $$
$$ \begin{align} L(\tau)_p^{\bullet} = \begin{cases} \tau_i^{\bullet} \setminus \{\tau_i^1\} & \text{if } p = i,\\ \tau_{i+1}^{\bullet} \cup \{\tau_i^1\} & \text{if } p = i+1,\\ \tau_p^{\bullet} & \text{otherwise.}\\ \end{cases} \end{align} $$
Example 3.2. For
 we have
we have

For each
![]() $i \in \mathcal {I}(\alpha )$
, we define a
$i \in \mathcal {I}(\alpha )$
, we define a
![]() $\mathbb C$
-linear map
$\mathbb C$
-linear map
![]() $ \partial _1^{(i)}: \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow H_n(0) \cdot T^{(i)}_{\alpha }$
by
$ \partial _1^{(i)}: \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow H_n(0) \cdot T^{(i)}_{\alpha }$
by
 $$\begin{align*}\partial_1^{(i)} (\tau) = \begin{cases} L(\tau) & \text{if } L(\tau) \in \mathrm{SRT}(\alpha),\\ 0 & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\partial_1^{(i)} (\tau) = \begin{cases} L(\tau) & \text{if } L(\tau) \in \mathrm{SRT}(\alpha),\\ 0 & \text{otherwise.} \end{cases} \end{align*}$$
Then we define a
![]() $\mathbb C$
-linear map
$\mathbb C$
-linear map
![]() $\partial _1 : \bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow \mathbf {P}_{\alpha }$
by
$\partial _1 : \bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow \mathbf {P}_{\alpha }$
by
Theorem 3.3 (This will be proven in Subsection 6.1).
Let
![]() $\alpha $
be a composition of n.
$\alpha $
be a composition of n.
-
(a)
 $\mathrm {Im}(\partial _1) = \Omega (\mathcal {V}_{\alpha })$
and
$\mathrm {Im}(\partial _1) = \Omega (\mathcal {V}_{\alpha })$
and
 $\partial _1 : \bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow \Omega (\mathcal {V}_{\alpha })$
is a projective cover of
$\partial _1 : \bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow \Omega (\mathcal {V}_{\alpha })$
is a projective cover of
 $\Omega (\mathcal {V}_{\alpha })$
.
$\Omega (\mathcal {V}_{\alpha })$
. -
(b) Let
 $\mathcal {J}(\alpha ) := \bigcup _{i \in \mathcal {I}(\alpha )} [{\boldsymbol {\unicode{x3b1} }}^{(i)}]$
. Then we have
$\mathcal {J}(\alpha ) := \bigcup _{i \in \mathcal {I}(\alpha )} [{\boldsymbol {\unicode{x3b1} }}^{(i)}]$
. Then we have  $$\begin{align*}\mathrm{Ext}_{H_n(0)}^1(\mathcal{V}_{\alpha},\mathbf{F}_{\beta}) \cong \begin{cases} \mathbb C & \text{if } \beta \in \mathcal{J}(\alpha), \\ 0 & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{Ext}_{H_n(0)}^1(\mathcal{V}_{\alpha},\mathbf{F}_{\beta}) \cong \begin{cases} \mathbb C & \text{if } \beta \in \mathcal{J}(\alpha), \\ 0 & \text{otherwise.} \end{cases} \end{align*}$$
Example 3.4. Let
![]() $\alpha = (1,2,1)$
. Then we have that
$\alpha = (1,2,1)$
. Then we have that
![]() $\mathcal {I}(\alpha ) = \{1\}$
and
$\mathcal {I}(\alpha ) = \{1\}$
and
![]() ${\boldsymbol {\unicode{x3b1} }}^{(1)} = (2,1) \oplus (1)$
.
${\boldsymbol {\unicode{x3b1} }}^{(1)} = (2,1) \oplus (1)$
.
(a) The map
![]() $\partial _1: \mathbf {P}_{(2,1) \oplus (1)} \rightarrow \mathbf {P}_{(1,2,1)}$
is illustrated in Figure 1, where the entries i in red in each SRT
$\partial _1: \mathbf {P}_{(2,1) \oplus (1)} \rightarrow \mathbf {P}_{(1,2,1)}$
is illustrated in Figure 1, where the entries i in red in each SRT
![]() $T$
are used to indicate that
$T$
are used to indicate that
![]() $\pi _i \cdot T = 0$
.
$\pi _i \cdot T = 0$
.

Figure 1
![]() $\partial _1: \mathbf {P}_{(2,1) \oplus (1)} \rightarrow \mathbf {P}_{(1,2,1)}$
.
$\partial _1: \mathbf {P}_{(2,1) \oplus (1)} \rightarrow \mathbf {P}_{(1,2,1)}$
.
(b) Note that
![]() $\mathcal {J}(\alpha ) = [{\boldsymbol {\unicode{x3b1} }}^{(1)}] = \{(2,2),(2,1,1)\}$
. By Theorem 3.3(b), we have
$\mathcal {J}(\alpha ) = [{\boldsymbol {\unicode{x3b1} }}^{(1)}] = \{(2,2),(2,1,1)\}$
. By Theorem 3.3(b), we have
 $$\begin{align*}\dim \mathrm{Ext}_{H_n(0)}^1(\mathcal{V}_{(1,2,1)},\mathbf{F}_{\beta}) = \begin{cases} 1 & \text{ if } \beta = (2,2) \text{ or } (2,1,1), \\ 0 & \text{ otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\dim \mathrm{Ext}_{H_n(0)}^1(\mathcal{V}_{(1,2,1)},\mathbf{F}_{\beta}) = \begin{cases} 1 & \text{ if } \beta = (2,2) \text{ or } (2,1,1), \\ 0 & \text{ otherwise.} \end{cases} \end{align*}$$
4 A minimal injective presentation of
 $\mathcal {V}_{\alpha }$
and
$\mathcal {V}_{\alpha }$
and
 $\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\beta },\mathcal {V}_{\alpha })$
$\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\beta },\mathcal {V}_{\alpha })$
As before,
![]() $\alpha $
denotes an arbitrarily chosen composition of n. In this section, we construct a minimal injective presentation of
$\alpha $
denotes an arbitrarily chosen composition of n. In this section, we construct a minimal injective presentation of
![]() $\mathcal {V}_{\alpha }$
. Using this, we compute
$\mathcal {V}_{\alpha }$
. Using this, we compute
![]() $\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\beta },\mathcal {V}_{\alpha })$
for each
$\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\beta },\mathcal {V}_{\alpha })$
for each
![]() $\beta \models n$
.
$\beta \models n$
.
Let us introduce necessary terminologies and notation. Let
![]() $M,N$
be finitely generated
$M,N$
be finitely generated
![]() $H_n(0)$
-modules with
$H_n(0)$
-modules with
![]() $N \subsetneq M$
. We say that M is an essential extension of N if
$N \subsetneq M$
. We say that M is an essential extension of N if
![]() $X\cap N \ne 0$
for all nonzero submodules X of M. An injective
$X\cap N \ne 0$
for all nonzero submodules X of M. An injective
![]() $H_n(0)$
-module homomorphism
$H_n(0)$
-module homomorphism
![]() $\iota : M \rightarrow \boldsymbol {I}$
with
$\iota : M \rightarrow \boldsymbol {I}$
with
![]() $\boldsymbol {I}$
injective is called an injective hull of M if
$\boldsymbol {I}$
injective is called an injective hull of M if
![]() $\boldsymbol {I}$
is an essential extension of
$\boldsymbol {I}$
is an essential extension of
![]() $\iota (M)$
that always exists and is unique up to isomorphism. By [Reference Lam23, Theorem 3.30 and Exercise 3.6.12], it follows that
$\iota (M)$
that always exists and is unique up to isomorphism. By [Reference Lam23, Theorem 3.30 and Exercise 3.6.12], it follows that
![]() $\boldsymbol {I}$
is an injective hull of M if and only if
$\boldsymbol {I}$
is an injective hull of M if and only if
![]() $\iota (M) \supseteq \mathrm {soc}(\boldsymbol {I})$
. Here
$\iota (M) \supseteq \mathrm {soc}(\boldsymbol {I})$
. Here
![]() $\mathrm {soc}(\boldsymbol {I})$
is the socle of
$\mathrm {soc}(\boldsymbol {I})$
is the socle of
![]() $\boldsymbol {I}$
: that is, the sum of all simple submodules of
$\boldsymbol {I}$
: that is, the sum of all simple submodules of
![]() $\boldsymbol {I}$
. When
$\boldsymbol {I}$
. When
![]() $\iota $
is clear in the context, we write
$\iota $
is clear in the context, we write
![]() $\Omega ^{-1}(M)$
for
$\Omega ^{-1}(M)$
for
![]() $\mathrm {Coker} (\iota )$
and call it the cosyzygy module of M. An exact sequence
$\mathrm {Coker} (\iota )$
and call it the cosyzygy module of M. An exact sequence
with injective modules
![]() $\boldsymbol {I}_0$
and
$\boldsymbol {I}_0$
and
![]() $\boldsymbol {I}_1$
is called a minimal injective presentation if the
$\boldsymbol {I}_1$
is called a minimal injective presentation if the
![]() $H_n(0)$
-module homomorphisms
$H_n(0)$
-module homomorphisms
![]() $\iota : M \rightarrow \boldsymbol {I}_0$
and
$\iota : M \rightarrow \boldsymbol {I}_0$
and
![]() $\partial ^1: \Omega ^{-1}(M) \rightarrow \boldsymbol {I}_1$
are injective hulls of M and
$\partial ^1: \Omega ^{-1}(M) \rightarrow \boldsymbol {I}_1$
are injective hulls of M and
![]() $\Omega ^{-1}(M)$
, respectively.
$\Omega ^{-1}(M)$
, respectively.
We first describe an injective hull of
![]() $\mathcal {V}_{\alpha }$
. Let
$\mathcal {V}_{\alpha }$
. Let
We write the elements of
![]() $\mathcal {K}(\alpha )$
as
$\mathcal {K}(\alpha )$
as
![]() $k_0:=0 < k_1 < k_2 < \cdots < k_m$
. Let
$k_0:=0 < k_1 < k_2 < \cdots < k_m$
. Let
 $$ \begin{align*} \underline{{\boldsymbol{\unicode{x3b1}}}} &:= (\alpha_{k_1} -1) \oplus (\alpha_{k_2}-1) \oplus \cdots \oplus \left((\alpha_{k_m}-1) \odot (1^{\ell(\alpha)})\right) \\ & \ = (\alpha_{k_1} -1) \oplus (\alpha_{k_2}-1) \oplus \cdots \oplus (\alpha_{k_{m-1}}-1) \oplus (\alpha_{k_m},1^{\ell(\alpha)-1}). \end{align*} $$
$$ \begin{align*} \underline{{\boldsymbol{\unicode{x3b1}}}} &:= (\alpha_{k_1} -1) \oplus (\alpha_{k_2}-1) \oplus \cdots \oplus \left((\alpha_{k_m}-1) \odot (1^{\ell(\alpha)})\right) \\ & \ = (\alpha_{k_1} -1) \oplus (\alpha_{k_2}-1) \oplus \cdots \oplus (\alpha_{k_{m-1}}-1) \oplus (\alpha_{k_m},1^{\ell(\alpha)-1}). \end{align*} $$
Let us depict
![]() $\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
in a pictorial manner. When
$\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
in a pictorial manner. When
![]() $j=0$
, we define
$j=0$
, we define
![]() $\mathtt {S}_{k_0}$
to be the vertical strip consisting of all the boxes in the first column of
$\mathtt {S}_{k_0}$
to be the vertical strip consisting of all the boxes in the first column of
![]() $\mathtt {cd}(\alpha )$
. For
$\mathtt {cd}(\alpha )$
. For
![]() $1 \le j \le m$
, we define
$1 \le j \le m$
, we define
![]() $\mathtt {S}_{k_j}$
as the horizontal strip consisting of the boxes in the
$\mathtt {S}_{k_j}$
as the horizontal strip consisting of the boxes in the
![]() $k_j$
th row of
$k_j$
th row of
![]() $\mathtt {cd}(\alpha )$
(from the top), except for the leftmost box. Then
$\mathtt {cd}(\alpha )$
(from the top), except for the leftmost box. Then
![]() $\underline {{\boldsymbol {\unicode{x3b1} }}}$
is defined by the generalised composition obtained by placing
$\underline {{\boldsymbol {\unicode{x3b1} }}}$
is defined by the generalised composition obtained by placing
![]() $\mathtt {S}_{k_0},\mathtt {S}_{k_1},\ldots , \mathtt {S}_{k_m}$
in the following manner:
$\mathtt {S}_{k_0},\mathtt {S}_{k_1},\ldots , \mathtt {S}_{k_m}$
in the following manner:
-
(i)
 $\mathtt {S}_{k_0}$
is placed horizontally at the topmost row in the new diagram.
$\mathtt {S}_{k_0}$
is placed horizontally at the topmost row in the new diagram. -
(ii)
 $\mathtt {S}_{k_m}$
is placed vertically to the lower-left of
$\mathtt {S}_{k_m}$
is placed vertically to the lower-left of
 $\mathtt {S}_{k_0}$
so that
$\mathtt {S}_{k_0}$
so that
 $\mathtt {S}_{k_0}$
and
$\mathtt {S}_{k_0}$
and
 $\mathtt {S}_{k_m}$
are connected.
$\mathtt {S}_{k_m}$
are connected. -
(iii) For
 $j=m-1,m-2, \ldots , 1$
, place
$j=m-1,m-2, \ldots , 1$
, place
 $\mathtt {S}_{k_j}$
vertically to the lower-left of
$\mathtt {S}_{k_j}$
vertically to the lower-left of
 $\mathtt {S}_{k_{j+1}}$
so that they are not connected to each other.
$\mathtt {S}_{k_{j+1}}$
so that they are not connected to each other.
Figure 2 illustrates the above procedure.

Figure 2 The construction of
![]() $\mathtt {rd}( \underline {{\boldsymbol {\unicode{x3b1} }}})$
when
$\mathtt {rd}( \underline {{\boldsymbol {\unicode{x3b1} }}})$
when
![]() $\alpha =(2,1,3^2,1)$
.
$\alpha =(2,1,3^2,1)$
.
For simplicity, we introduce the following notation:
-
• For an SIT
 $\mathscr {T}$
and a subdiagram
$\mathscr {T}$
and a subdiagram
 $\mathtt {S}$
of shape of
$\mathtt {S}$
of shape of
 $\mathscr {T}$
, we denote by
$\mathscr {T}$
, we denote by
 $\mathscr {T}(\mathtt {S})$
the set of entries of
$\mathscr {T}(\mathtt {S})$
the set of entries of
 $\mathscr {T}$
in
$\mathscr {T}$
in
 $\mathtt {S}$
.
$\mathtt {S}$
. -
• For an SRT T and a subdiagram
 $\mathtt {S}$
of shape of T, we denote by
$\mathtt {S}$
of shape of T, we denote by
 $T(\mathtt {S})$
the set of entries of T in
$T(\mathtt {S})$
the set of entries of T in
 $\mathtt {S}$
.
$\mathtt {S}$
.
For
![]() $\mathscr {T} \in \mathrm {SIT}(\alpha )$
, let
$\mathscr {T} \in \mathrm {SIT}(\alpha )$
, let
![]() ${T^{\mathscr {T}}}$
be the tableau of
${T^{\mathscr {T}}}$
be the tableau of
![]() $\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
defined by
$\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
defined by
Extending the assignment
![]() $\mathscr {T} \mapsto T^{\mathscr {T}}$
by linearity, we define the
$\mathscr {T} \mapsto T^{\mathscr {T}}$
by linearity, we define the
![]() $\mathbb C$
-linear map
$\mathbb C$
-linear map
which is obviously injective.
Theorem 4.1 (This will be proven in Subsection 6.2).
![]() $\epsilon : \mathcal {V}_{\alpha } \to \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
is an injective hull of
$\epsilon : \mathcal {V}_{\alpha } \to \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
is an injective hull of
![]() $\mathcal {V}_{\alpha }$
.
$\mathcal {V}_{\alpha }$
.
For later use, we provide bases of
![]() $\epsilon (\mathcal {V}_{\alpha })$
and
$\epsilon (\mathcal {V}_{\alpha })$
and
![]() $\Omega ^{-1}(\mathcal {V}_{\alpha })$
. From the injectivity of
$\Omega ^{-1}(\mathcal {V}_{\alpha })$
. From the injectivity of
![]() $\epsilon $
, we derive that
$\epsilon $
, we derive that
![]() $\epsilon (\mathcal {V}_{\alpha })$
is spanned by
$\epsilon (\mathcal {V}_{\alpha })$
is spanned by
and
![]() $\Omega ^{-1}(\mathcal {V}_{\alpha })$
is spanned by
$\Omega ^{-1}(\mathcal {V}_{\alpha })$
is spanned by
![]() $\{T + \epsilon (\mathcal {V}_{\alpha }) \mid T \in \Theta (\mathcal {V}_{\alpha })\}$
with
$\{T + \epsilon (\mathcal {V}_{\alpha }) \mid T \in \Theta (\mathcal {V}_{\alpha })\}$
with
Example 4.2. If
![]() $\alpha = (1,2,2) \models 5$
, then
$\alpha = (1,2,2) \models 5$
, then
![]() $\mathcal {K}(\alpha ) = \{0,2,3\}$
and
$\mathcal {K}(\alpha ) = \{0,2,3\}$
and
![]() $\underline {{\boldsymbol {\unicode{x3b1} }}} = (1)\oplus (2,1^2)$
. For
$\underline {{\boldsymbol {\unicode{x3b1} }}} = (1)\oplus (2,1^2)$
. For
 , one sees that
, one sees that
 . The map
. The map
![]() $\epsilon :\mathcal {V}_{\alpha } \rightarrow \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
is illustrated in Figure 3, where the red entries i in tableaux are used to indicate that
$\epsilon :\mathcal {V}_{\alpha } \rightarrow \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
is illustrated in Figure 3, where the red entries i in tableaux are used to indicate that
![]() $\pi _i$
acts on them as zero.
$\pi _i$
acts on them as zero.

Figure 3
![]() $\epsilon : \mathcal {V}_{(1,2,2)} \rightarrow \mathbf {P}_{(1)\oplus (2,1,1)}$
.
$\epsilon : \mathcal {V}_{(1,2,2)} \rightarrow \mathbf {P}_{(1)\oplus (2,1,1)}$
.
We next describe an injective hull of
![]() $\Omega ^{-1}(\mathcal {V}_{\alpha })$
. To do this, we need an
$\Omega ^{-1}(\mathcal {V}_{\alpha })$
. To do this, we need an
![]() $H_n(0)$
-module homomorphism
$H_n(0)$
-module homomorphism
![]() $\partial ^1: \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}\rightarrow \boldsymbol {I}$
with
$\partial ^1: \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}\rightarrow \boldsymbol {I}$
with
![]() $\boldsymbol {I}$
an injective module satisfying that
$\boldsymbol {I}$
an injective module satisfying that
![]() $\ker (\partial ^1)=\epsilon (\mathcal {V}_{\alpha })$
.
$\ker (\partial ^1)=\epsilon (\mathcal {V}_{\alpha })$
.
First, we provide the required injective module
![]() $\boldsymbol {I}$
. For
$\boldsymbol {I}$
. For
![]() $1 \leq j \leq m$
, define
$1 \leq j \leq m$
, define
![]() $\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}$
to be the generalised composition
$\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}$
to be the generalised composition
 $$ \begin{align*} \underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}: = \left\{ \begin{array}{ll} (\alpha_{k_1}-1) \oplus \cdots \oplus (\alpha_{k_j} - 2) \oplus \cdots \oplus (\alpha_{k_m}, 1^{\ell(\alpha)-k_j+1}) \oplus (1^{k_j-1}) & \quad \text{if } 1 \leq j < m, \\ (\alpha_{k_1}-1 ) \oplus \cdots \oplus (\alpha_{k_{m-1}}-1) \oplus \left((\alpha_{k_m}-1,1^{\ell(\alpha)-k_j+1}) \cdot (1^{k_j-1})\right) & \quad \text{if } j = m. \end{array} \right. \end{align*} $$
$$ \begin{align*} \underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}: = \left\{ \begin{array}{ll} (\alpha_{k_1}-1) \oplus \cdots \oplus (\alpha_{k_j} - 2) \oplus \cdots \oplus (\alpha_{k_m}, 1^{\ell(\alpha)-k_j+1}) \oplus (1^{k_j-1}) & \quad \text{if } 1 \leq j < m, \\ (\alpha_{k_1}-1 ) \oplus \cdots \oplus (\alpha_{k_{m-1}}-1) \oplus \left((\alpha_{k_m}-1,1^{\ell(\alpha)-k_j+1}) \cdot (1^{k_j-1})\right) & \quad \text{if } j = m. \end{array} \right. \end{align*} $$
Then we set
 $$ \begin{align} \boldsymbol{I}:=\bigoplus_{1 \leq j \leq m}\mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}. \end{align} $$
$$ \begin{align} \boldsymbol{I}:=\bigoplus_{1 \leq j \leq m}\mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}. \end{align} $$
In the following, we provide a pictorial description of
![]() $\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)})$
. We begin by recalling that
$\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)})$
. We begin by recalling that
![]() $\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
consists of the horizontal strip
$\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
consists of the horizontal strip
![]() $\mathtt {S}_{k_0}$
and the vertical strips
$\mathtt {S}_{k_0}$
and the vertical strips
![]() $\mathtt {S}_{k_1},\ldots ,\mathtt {S}_{k_m}$
. For each
$\mathtt {S}_{k_1},\ldots ,\mathtt {S}_{k_m}$
. For each
![]() $-1\le r \le m$
, we denote by
$-1\le r \le m$
, we denote by
![]() $\mathtt {S}^{\prime }_{k_r}$
the connected horizontal strip of length
$\mathtt {S}^{\prime }_{k_r}$
the connected horizontal strip of length
 $$ \begin{align*} |\mathtt{S}^{\prime}_{k_r}|:= \begin{cases} k_j-1 & \text{ if } r = -1,\\ \ell(\alpha)-k_j+2 & \text{ if } r = 0, \\ |\mathtt{S}_{k_r}| - \delta_{r,j} & \text{ if } 1 \leq r \leq m, \end{cases} \end{align*} $$
$$ \begin{align*} |\mathtt{S}^{\prime}_{k_r}|:= \begin{cases} k_j-1 & \text{ if } r = -1,\\ \ell(\alpha)-k_j+2 & \text{ if } r = 0, \\ |\mathtt{S}_{k_r}| - \delta_{r,j} & \text{ if } 1 \leq r \leq m, \end{cases} \end{align*} $$
where
![]() $k_{-1} := -1$
. With this preparation,
$k_{-1} := -1$
. With this preparation,
![]() $\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}$
is defined to be the generalised composition obtained by placing
$\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}$
is defined to be the generalised composition obtained by placing
![]() $\mathtt {S}^{\prime }_{k_{-1}},\mathtt {S}^{\prime }_{k_0},\mathtt {S}^{\prime }_{k_1},\ldots ,\mathtt {S}^{\prime }_{k_m}$
in the following way:
$\mathtt {S}^{\prime }_{k_{-1}},\mathtt {S}^{\prime }_{k_0},\mathtt {S}^{\prime }_{k_1},\ldots ,\mathtt {S}^{\prime }_{k_m}$
in the following way:
-
(i)
 $\mathtt {S}^{\prime }_{k_1}$
is placed vertically to the leftmost column in the diagram we will create.
$\mathtt {S}^{\prime }_{k_1}$
is placed vertically to the leftmost column in the diagram we will create. -
(ii) For
 $j = 2,3,\ldots , m$
,
$j = 2,3,\ldots , m$
,
 $\mathtt {S}^{\prime }_{k_j}$
is placed vertically to the upper-right of
$\mathtt {S}^{\prime }_{k_j}$
is placed vertically to the upper-right of
 $\mathtt {S}^{\prime }_{k_{j-1}}$
so that they are not connected to each other.
$\mathtt {S}^{\prime }_{k_{j-1}}$
so that they are not connected to each other. -
(iii)
 $\mathtt {S}^{\prime }_{k_0}$
is placed horizontally to
$\mathtt {S}^{\prime }_{k_0}$
is placed horizontally to
 $\mathtt {S}^{\prime }_{k_m}$
so that they are connected.
$\mathtt {S}^{\prime }_{k_m}$
so that they are connected. -
(iv) In the case where
 $j \neq m$
,
$j \neq m$
,
 $\mathtt {S}^{\prime }_{k_{-1}}$
is placed horizontally to the upper-right of
$\mathtt {S}^{\prime }_{k_{-1}}$
is placed horizontally to the upper-right of
 $\mathtt {S}^{\prime }_{k_0}$
so that they are disconnected. In the case where
$\mathtt {S}^{\prime }_{k_0}$
so that they are disconnected. In the case where
 $j = m$
,
$j = m$
,
 $\mathtt {S}^{\prime }_{k_{-1}}$
is placed horizontally to the upper-right of
$\mathtt {S}^{\prime }_{k_{-1}}$
is placed horizontally to the upper-right of
 $\mathtt {S}^{\prime }_{k_0}$
so that they are connected.
$\mathtt {S}^{\prime }_{k_0}$
so that they are connected.
Figure 4 illustrates the above procedure.

Figure 4 The construction of
![]() $\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(1)})$
and
$\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(1)})$
and
![]() $\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)})$
when
$\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)})$
when
![]() $\alpha = (1,3,2,1)$
.
$\alpha = (1,3,2,1)$
.
Now, let us construct
![]() $\partial ^1: \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}\rightarrow \boldsymbol {I}$
. Choose any tableau T in
$\partial ^1: \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}\rightarrow \boldsymbol {I}$
. Choose any tableau T in
![]() $\mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
. Recall that
$\mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
. Recall that
![]() $\mathbf {w}(T)$
is the word obtained by reading the entries of T from left to right, starting with the bottom row. Let
$\mathbf {w}(T)$
is the word obtained by reading the entries of T from left to right, starting with the bottom row. Let
![]() $\mathbf {w}(T) = w_1 w_2 \cdots w_n$
. For each
$\mathbf {w}(T) = w_1 w_2 \cdots w_n$
. For each
![]() $1 \leq j \leq m$
, we consider the subword
$1 \leq j \leq m$
, we consider the subword
![]() $\mathbf {w}_{T;j}$
of
$\mathbf {w}_{T;j}$
of
![]() $\mathbf {w}(T)$
defined by
$\mathbf {w}(T)$
defined by
where the subscripts
![]() $u_i(j)$
s are defined via the following recursion:
$u_i(j)$
s are defined via the following recursion:
 $$ \begin{align*} &u_1(j) = \sum_{1 \le r \le j} (\alpha_{k_r}-1),\\ &u_{i+1}(j) = \min \{u_i(j) < u \le n - \ell(\alpha) \mid w_u < w_{u_i(j)} \} \quad (i \ge 1), \text{ and }\\ &l_j := \max \{i \mid u_i(j) < \infty \}. \end{align*} $$
$$ \begin{align*} &u_1(j) = \sum_{1 \le r \le j} (\alpha_{k_r}-1),\\ &u_{i+1}(j) = \min \{u_i(j) < u \le n - \ell(\alpha) \mid w_u < w_{u_i(j)} \} \quad (i \ge 1), \text{ and }\\ &l_j := \max \{i \mid u_i(j) < \infty \}. \end{align*} $$
In the second identity, whenever
![]() $\{u_i(j) < u \le n - \ell (\alpha ) \mid w_u < w_{u_i(j)} \}=\emptyset $
, we set
$\{u_i(j) < u \le n - \ell (\alpha ) \mid w_u < w_{u_i(j)} \}=\emptyset $
, we set
![]() $u_{i+1}(j):=\infty $
. Henceforth we simply write
$u_{i+1}(j):=\infty $
. Henceforth we simply write
![]() $u_i$
s for
$u_i$
s for
![]() $u_i(j)$
s and thus
$u_i(j)$
s and thus
![]() $\mathbf {w}_{T;j}= w_{u_1} w_{u_2} \cdots w_{u_{l_j}}$
. Given an arbitrary word w, we use
$\mathbf {w}_{T;j}= w_{u_1} w_{u_2} \cdots w_{u_{l_j}}$
. Given an arbitrary word w, we use
![]() $\textsf {end}(w)$
to denote the last letter of w. With the notations above, we introduce the following two sets:
$\textsf {end}(w)$
to denote the last letter of w. With the notations above, we introduce the following two sets:
 $$ \begin{align*} \begin{aligned} \mathtt{A}_{T;j} &: = \{y \in T(\mathtt{S}_{k_0}) \mid y> \textsf{end}(\mathbf{w}_{T;j})\}, \\ \mathcal{P}(\mathtt{A}_{T;j}) &: = \left\{ A \subseteq \mathtt{A}_{T;j} \mid |A| = \ell(\alpha)-k_j+1 \right\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathtt{A}_{T;j} &: = \{y \in T(\mathtt{S}_{k_0}) \mid y> \textsf{end}(\mathbf{w}_{T;j})\}, \\ \mathcal{P}(\mathtt{A}_{T;j}) &: = \left\{ A \subseteq \mathtt{A}_{T;j} \mid |A| = \ell(\alpha)-k_j+1 \right\}. \end{aligned} \end{align*} $$
For
![]() $A \in \mathcal {P}(\mathtt {A}_{T;j})$
, we define
$A \in \mathcal {P}(\mathtt {A}_{T;j})$
, we define
![]() $\tau _{T;j;A}$
to be an SRT of shape
$\tau _{T;j;A}$
to be an SRT of shape
![]() $\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}$
that is uniquely determined by the following conditions:
$\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}$
that is uniquely determined by the following conditions:
-
(i)
 $\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_{-1}}) = T(\mathtt {S}_{k_0}) \setminus A$
,
$\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_{-1}}) = T(\mathtt {S}_{k_0}) \setminus A$
, -
(ii)
 $\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_0}) =\{\textsf {end}(\mathbf {w}_{T;j})\} \cup A$
,
$\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_0}) =\{\textsf {end}(\mathbf {w}_{T;j})\} \cup A$
, -
(iii)
 $\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_r}) = T(\mathtt {S}_{k_r})$
for
$\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_r}) = T(\mathtt {S}_{k_r})$
for
 $1 \leq r < j$
,
$1 \leq r < j$
, -
(iv)
 $\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_j}) = T(\mathtt {S}_{k_j}) \setminus \{w_{u_1} \}$
, and
$\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_j}) = T(\mathtt {S}_{k_j}) \setminus \{w_{u_1} \}$
, and -
(v) for
 $j < r \leq m$
,
$j < r \leq m$
,
 $\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_r})$
is obtained from
$\tau _{T;j;A}(\mathtt {S}^{\prime }_{k_r})$
is obtained from
 $T(\mathtt {S}_{k_r})$
by substituting
$T(\mathtt {S}_{k_r})$
by substituting
 $w_{u_{i}}$
with
$w_{u_{i}}$
with
 $w_{u_{i-1}}$
for
$w_{u_{i-1}}$
for
 $w_{u_{i}}$
s (
$w_{u_{i}}$
s (
 $1 < i \le l_j$
) contained in
$1 < i \le l_j$
) contained in
 $T(\mathtt {S}_{k_r})$
.
$T(\mathtt {S}_{k_r})$
.
We next explain the notion of the signature
![]() $\mathrm {sgn}(A)$
of A. Enumerate the elements in
$\mathrm {sgn}(A)$
of A. Enumerate the elements in
![]() $\mathtt {A}_{T;j}$
in the increasing order
$\mathtt {A}_{T;j}$
in the increasing order
Then let
![]() $A^1_{T;j}$
be the set of the consecutive
$A^1_{T;j}$
be the set of the consecutive
![]() $(\ell (\alpha )-k_j+1)$
elements starting from the rightmost and moving to the left, precisely,
$(\ell (\alpha )-k_j+1)$
elements starting from the rightmost and moving to the left, precisely,
There is a natural right
![]() $\Sigma _{|\mathtt {A}_{T;j}|}$
-action on
$\Sigma _{|\mathtt {A}_{T;j}|}$
-action on
![]() $\mathtt {A}_{T;j}$
given by
$\mathtt {A}_{T;j}$
given by
We define
![]() $\mathrm {sgn}(A) := (-1)^{\ell (\omega ^1)}$
, where
$\mathrm {sgn}(A) := (-1)^{\ell (\omega ^1)}$
, where
![]() $\omega ^1$
is any minimal length permutation in
$\omega ^1$
is any minimal length permutation in
![]() $\{\omega \in \Sigma _{|\mathtt {A}_{T;j}|} \mid A = A^1_{T;j} \cdot \omega \}$
.
$\{\omega \in \Sigma _{|\mathtt {A}_{T;j}|} \mid A = A^1_{T;j} \cdot \omega \}$
.
For each
![]() $1 \leq j \leq m$
, set
$1 \leq j \leq m$
, set
 $$ \begin{align*} {\boldsymbol{\tau}}_{T;j}:= \displaystyle \sum_{A \in \mathcal{P}(\mathtt{A}_{T;j})} \mathrm{sgn}(A) \tau_{T;j;A}, \end{align*} $$
$$ \begin{align*} {\boldsymbol{\tau}}_{T;j}:= \displaystyle \sum_{A \in \mathcal{P}(\mathtt{A}_{T;j})} \mathrm{sgn}(A) \tau_{T;j;A}, \end{align*} $$
where the summation in the right-hand side is zero in the case where
![]() $\mathcal {P}(\mathtt {A}_{T;j})=\emptyset $
. Finally, we define a
$\mathcal {P}(\mathtt {A}_{T;j})=\emptyset $
. Finally, we define a
![]() $\mathbb C$
-linear map
$\mathbb C$
-linear map
 $$ \begin{align*} \partial^1: \mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}}\rightarrow \boldsymbol{I}, \quad T \mapsto \sum_{1 \leq j \leq m} {\boldsymbol{\tau}}_{T;j} \end{align*} $$
$$ \begin{align*} \partial^1: \mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}}\rightarrow \boldsymbol{I}, \quad T \mapsto \sum_{1 \leq j \leq m} {\boldsymbol{\tau}}_{T;j} \end{align*} $$
with
![]() $\boldsymbol {I}$
in equation (4.2).
$\boldsymbol {I}$
in equation (4.2).
Theorem 4.3 (This will be proven in Subsection 6.3).
Let
![]() $\alpha $
be a composition of n.
$\alpha $
be a composition of n.
-
(a)
 $\partial ^1: \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}} \rightarrow \boldsymbol {I}$
is an
$\partial ^1: \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}} \rightarrow \boldsymbol {I}$
is an
 $H_n(0)$
-module homomorphism.
$H_n(0)$
-module homomorphism. -
(b) The sequence
is exact.
-
(c) The
 $H_n(0)$
-module homomorphism induced from
$H_n(0)$
-module homomorphism induced from $$\begin{align*}\overline{\partial^1}: \Omega^{-1}(\mathcal{V}_{\alpha}) \rightarrow \boldsymbol{I}, \quad T + \epsilon(\mathcal{V}_{\alpha}) \mapsto \partial^1(T) \quad (T \in \Theta(\mathcal{V}_{\alpha})) \end{align*}$$
$$\begin{align*}\overline{\partial^1}: \Omega^{-1}(\mathcal{V}_{\alpha}) \rightarrow \boldsymbol{I}, \quad T + \epsilon(\mathcal{V}_{\alpha}) \mapsto \partial^1(T) \quad (T \in \Theta(\mathcal{V}_{\alpha})) \end{align*}$$
 $\partial ^1$
is an injective hull of
$\partial ^1$
is an injective hull of
 $\Omega ^{-1}(\mathcal {V}_{\alpha })$
.
$\Omega ^{-1}(\mathcal {V}_{\alpha })$
.
-
(d) Let
 $\mathcal {L}(\alpha ) := \bigcup _{1 \leq j \leq m} [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
, which is viewed as a multiset. Then we have where
$\mathcal {L}(\alpha ) := \bigcup _{1 \leq j \leq m} [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
, which is viewed as a multiset. Then we have where $$\begin{align*}\mathrm{Ext}_{H_n(0)}^1(\mathbf{F}_{\beta},\mathcal{V}_{\alpha}) \cong \begin{cases} \mathbb C^{[\mathcal{L}(\alpha):\beta^{\mathrm{r}}]} & \text{ if } \beta^{\mathrm{r}} \in \mathcal{L}(\alpha)\\ 0 & \text{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{Ext}_{H_n(0)}^1(\mathbf{F}_{\beta},\mathcal{V}_{\alpha}) \cong \begin{cases} \mathbb C^{[\mathcal{L}(\alpha):\beta^{\mathrm{r}}]} & \text{ if } \beta^{\mathrm{r}} \in \mathcal{L}(\alpha)\\ 0 & \text{otherwise,} \end{cases} \end{align*}$$
 $[\mathcal {L}(\alpha ):\beta ^{\mathrm {r}}]$
denotes the multiplicity of
$[\mathcal {L}(\alpha ):\beta ^{\mathrm {r}}]$
denotes the multiplicity of
 $\beta ^{\mathrm {r}}$
in
$\beta ^{\mathrm {r}}$
in
 $\mathcal {L}(\alpha )$
.
$\mathcal {L}(\alpha )$
.
Example 4.4. Let
![]() $\alpha = (2,1,2,3) \models 8$
. Then
$\alpha = (2,1,2,3) \models 8$
. Then
![]() $\mathcal {K}(\alpha ) = \{0,1,3,4\}$
and
$\mathcal {K}(\alpha ) = \{0,1,3,4\}$
and
![]() $\underline {{\boldsymbol {\unicode{x3b1} }}} = (1) \oplus (1) \oplus (3,1^3)$
. By definition, we get
$\underline {{\boldsymbol {\unicode{x3b1} }}} = (1) \oplus (1) \oplus (3,1^3)$
. By definition, we get
 $$ \begin{align*} \underline{{\boldsymbol{\unicode{x3b1}}}}_{(1)} & = (1) \oplus (3,1^4), \\ \underline{{\boldsymbol{\unicode{x3b1}}}}_{(2)} & = (1) \oplus (3,1^2) \oplus (1^2), \\ \underline{{\boldsymbol{\unicode{x3b1}}}}_{(3)} & = (1) \oplus (1) \oplus (2^2,1^2). \end{align*} $$
$$ \begin{align*} \underline{{\boldsymbol{\unicode{x3b1}}}}_{(1)} & = (1) \oplus (3,1^4), \\ \underline{{\boldsymbol{\unicode{x3b1}}}}_{(2)} & = (1) \oplus (3,1^2) \oplus (1^2), \\ \underline{{\boldsymbol{\unicode{x3b1}}}}_{(3)} & = (1) \oplus (1) \oplus (2^2,1^2). \end{align*} $$
(a) Let

. Then one sees that
 $$ \begin{align*} \begin{array}{llll} \mathbf{w}_{T;1} = 6 \ 2 \quad & \quad \textsf{end}(\mathbf{w}_{T;1}) = 2 \quad & \mathtt{A}_{T;1} = \{3, 7,8\} \quad & \quad \mathcal{P}(\mathtt{A}_{T;1}) = \emptyset,\\ \mathbf{w}_{T;2} = 2 & \quad \textsf{end}(\mathbf{w}_{T;2}) = 2 & \mathtt{A}_{T;2} = \{3,7,8 \} & \quad \mathcal{P}(\mathtt{A}_{T;2}) = \{\{3,7\},\{3,8\},\{7,8\}\}, \\ \mathbf{w}_{T;3} = 4 & \quad \textsf{end}(\mathbf{w}_{T;3}) = 4 & \mathtt{A}_{T;3} = \{7,8 \} & \quad \mathcal{P}(\mathtt{A}_{T;3}) = \{\{7\},\{8\} \}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{llll} \mathbf{w}_{T;1} = 6 \ 2 \quad & \quad \textsf{end}(\mathbf{w}_{T;1}) = 2 \quad & \mathtt{A}_{T;1} = \{3, 7,8\} \quad & \quad \mathcal{P}(\mathtt{A}_{T;1}) = \emptyset,\\ \mathbf{w}_{T;2} = 2 & \quad \textsf{end}(\mathbf{w}_{T;2}) = 2 & \mathtt{A}_{T;2} = \{3,7,8 \} & \quad \mathcal{P}(\mathtt{A}_{T;2}) = \{\{3,7\},\{3,8\},\{7,8\}\}, \\ \mathbf{w}_{T;3} = 4 & \quad \textsf{end}(\mathbf{w}_{T;3}) = 4 & \mathtt{A}_{T;3} = \{7,8 \} & \quad \mathcal{P}(\mathtt{A}_{T;3}) = \{\{7\},\{8\} \}. \end{array} \end{align*} $$
Since

it follows that
Therefore,
(b) Note that
 $$ \begin{align*} [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(1)}] & = \left\{(1,3,1^4), (4,1^4)\right\}, \\ [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(2)}] & = \left\{(1,3,1^4),(1,3,1,2,1),(4,1^4),(4,1,2,1)\right\}, \\ [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(3)}] & = \left\{(1^2,2^2,1^2),(1,3,2,1^2),(2^3,1^2),(4,2,1^2) \right\}. \end{align*} $$
$$ \begin{align*} [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(1)}] & = \left\{(1,3,1^4), (4,1^4)\right\}, \\ [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(2)}] & = \left\{(1,3,1^4),(1,3,1,2,1),(4,1^4),(4,1,2,1)\right\}, \\ [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(3)}] & = \left\{(1^2,2^2,1^2),(1,3,2,1^2),(2^3,1^2),(4,2,1^2) \right\}. \end{align*} $$
Theorem 4.3(d) implies that
 $$ \begin{align*} \dim \mathrm{Ext}^1_{H_n(0)}(\mathbf{F}_{\beta},\mathcal{V}_{\alpha}) = \begin{cases} 1 & \text{ if } \beta^{\mathrm{r}} \in \mathcal{L}(\alpha) \setminus \{(1, 3, 1^4),(4, 1^4)\}, \\ 2 & \text{ if } \beta^{\mathrm{r}} \in \{(1,3,1^4), (4, 1^4)\}, \\ 0 & \text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \dim \mathrm{Ext}^1_{H_n(0)}(\mathbf{F}_{\beta},\mathcal{V}_{\alpha}) = \begin{cases} 1 & \text{ if } \beta^{\mathrm{r}} \in \mathcal{L}(\alpha) \setminus \{(1, 3, 1^4),(4, 1^4)\}, \\ 2 & \text{ if } \beta^{\mathrm{r}} \in \{(1,3,1^4), (4, 1^4)\}, \\ 0 & \text{ otherwise.} \end{cases} \end{align*} $$
5
 $\mathrm {Ext}^i_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
with
$\mathrm {Ext}^i_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
with
 $i=0,1$
$i=0,1$
In the previous sections, we computed
![]() $\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathbf {F}_{\beta })$
and
$\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathbf {F}_{\beta })$
and
![]() $\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\beta }, \mathcal {V}_{\alpha })$
. In this section, we focus on
$\mathrm {Ext}^1_{H_n(0)}(\mathbf {F}_{\beta }, \mathcal {V}_{\alpha })$
. In this section, we focus on
![]() $\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
and
$\mathrm {Ext}^1_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
and
![]() $\mathrm {Ext}^0_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })\, (=\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta }))$
.
$\mathrm {Ext}^0_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })\, (=\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta }))$
.
Let
![]() $M, N$
be finite-dimensional
$M, N$
be finite-dimensional
![]() $H_n(0)$
-modules. Given a short exact sequence
$H_n(0)$
-modules. Given a short exact sequence
with
![]() $(P_0,\pi )$
a projective cover of M, it is well known that
$(P_0,\pi )$
a projective cover of M, it is well known that
where
![]() $\iota ^{\ast}\!:\mathrm {Hom}_{H_n(0)}(P_0, N) \to \mathrm {Hom}_{H_n(0)}(\Omega (M),N)$
is given by composition with
$\iota ^{\ast}\!:\mathrm {Hom}_{H_n(0)}(P_0, N) \to \mathrm {Hom}_{H_n(0)}(\Omega (M),N)$
is given by composition with
![]() $\iota $
. The kernel of
$\iota $
. The kernel of
![]() $\iota ^{\ast }$
equals
$\iota ^{\ast }$
equals
and therefore
This says that
![]() $\mathrm {Ext}_{H_n(0)}^1(M,N)=0$
if and only if, as
$\mathrm {Ext}_{H_n(0)}^1(M,N)=0$
if and only if, as
![]() $\mathbb C$
-vector spaces,
$\mathbb C$
-vector spaces,
Definition 5.1. Given a finite-dimensional
![]() $H_n(0)$
-module M, we say that M is rigid if
$H_n(0)$
-module M, we say that M is rigid if
![]() $\mathrm {Ext}_{H_n(0)}^1 (M,M)=0$
and essentially rigid if
$\mathrm {Ext}_{H_n(0)}^1 (M,M)=0$
and essentially rigid if
![]() $\mathrm {Hom}_{H_n(0)}(\Omega (M),M)=0$
.
$\mathrm {Hom}_{H_n(0)}(\Omega (M),M)=0$
.
Whenever M is essentially rigid, one has that
![]() $\mathrm {Hom}_{H_n(0)}(P_0, M) \cong \mathrm {End}_{H_n(0)}(M).$
Typical examples of essentially rigid
$\mathrm {Hom}_{H_n(0)}(P_0, M) \cong \mathrm {End}_{H_n(0)}(M).$
Typical examples of essentially rigid
![]() $H_n(0)$
-modules are simple modules and projective modules. The syzygy and cosyzygy modules of a rigid module are also rigid since
$H_n(0)$
-modules are simple modules and projective modules. The syzygy and cosyzygy modules of a rigid module are also rigid since
![]() $\mathrm {Ext}_{H_n(0)}^1(M,N)=\mathrm {Ext}_{H_n(0)}^1(\Omega (M),\Omega (N))$
and
$\mathrm {Ext}_{H_n(0)}^1(M,N)=\mathrm {Ext}_{H_n(0)}^1(\Omega (M),\Omega (N))$
and
![]() $M \cong \Omega \Omega ^{-1}(M) \oplus (\mathrm {projective})$
(for example, see [Reference Benson3]).
$M \cong \Omega \Omega ^{-1}(M) \oplus (\mathrm {projective})$
(for example, see [Reference Benson3]).
Let us use
![]() $\le _l$
to represent the lexicographic order on compositions of n. Using the results in the preceding sections, we derive some interesting results on
$\le _l$
to represent the lexicographic order on compositions of n. Using the results in the preceding sections, we derive some interesting results on
![]() $\mathrm {Ext}_{H_n(0)}^1(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
. To do this, we need the following lemmas.
$\mathrm {Ext}_{H_n(0)}^1(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
. To do this, we need the following lemmas.
Lemma 5.2 ([Reference Benson3, Lemma 1.7.6]).
Let M be a finite-dimensional
![]() $H_n(0)$
-module. Then
$H_n(0)$
-module. Then
![]() $\dim \mathrm {Hom}_{H_n(0)}( \mathbf {P}_{\alpha }, M)$
is the multiplicity of
$\dim \mathrm {Hom}_{H_n(0)}( \mathbf {P}_{\alpha }, M)$
is the multiplicity of
![]() $\mathbf {F}_{\alpha }$
as a composition factors of M.
$\mathbf {F}_{\alpha }$
as a composition factors of M.
Lemma 5.3 ([Reference Berg, Bergeron, Saliola, Serrano and Zabrocki4, Proposition 3.37]).
The dual immaculate functions
![]() $\mathfrak {S}^*_{\alpha }$
are fundamental positive. Specifically, they expand as
$\mathfrak {S}^*_{\alpha }$
are fundamental positive. Specifically, they expand as
![]() $\mathfrak {S}^*_{\alpha }=\sum _{\beta \le _l \alpha }L_{\alpha , \beta }F_{\beta }$
, where
$\mathfrak {S}^*_{\alpha }=\sum _{\beta \le _l \alpha }L_{\alpha , \beta }F_{\beta }$
, where
![]() $L_{\alpha , \beta }$
denotes the number of standard immaculate tableaux
$L_{\alpha , \beta }$
denotes the number of standard immaculate tableaux
![]() $\mathscr {T}$
of shape
$\mathscr {T}$
of shape
![]() $\alpha $
and descent composition
$\alpha $
and descent composition
![]() $\beta $
: that is,
$\beta $
: that is,
![]() $\mathrm {comp}(\mathrm {Des}(\mathscr {T})) = \beta $
.
$\mathrm {comp}(\mathrm {Des}(\mathscr {T})) = \beta $
.
We now state the main result of this section.
Theorem 5.4. Let
![]() $\alpha $
be a composition of n.
$\alpha $
be a composition of n.
-
(a) For all
 $\beta \le _l \alpha $
,
$\beta \le _l \alpha $
,
 $\mathrm {Ext}_{H_n(0)}^1(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })=0.$
In particular,
$\mathrm {Ext}_{H_n(0)}^1(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })=0.$
In particular,
 $\mathcal {V}_{\alpha }$
is essentially rigid.
$\mathcal {V}_{\alpha }$
is essentially rigid. -
(b) For all
 $\beta \le _l \alpha $
, we have
$\beta \le _l \alpha $
, we have  $$\begin{align*}\mathrm{Hom}_{H_n(0)}(\mathcal{V}_{\alpha}, \mathcal{V}_{\beta}) \cong\begin{cases} \mathbb C & \text{if } \beta =\alpha,\\ 0 & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{Hom}_{H_n(0)}(\mathcal{V}_{\alpha}, \mathcal{V}_{\beta}) \cong\begin{cases} \mathbb C & \text{if } \beta =\alpha,\\ 0 & \text{otherwise.} \end{cases} \end{align*}$$
-
(c) Let M be any nonzero quotient of
 $\mathcal {V}_{\alpha }$
. Then
$\mathcal {V}_{\alpha }$
. Then
 $\mathrm {End}_{H_n(0)}(M) \cong \mathbb C$
.
$\mathrm {End}_{H_n(0)}(M) \cong \mathbb C$
.
Proof. (a) Due to Theorem 3.3, there is a projective resolution of
![]() $\mathcal {V}_{\alpha }$
of the form
$\mathcal {V}_{\alpha }$
of the form
Hence, for the assertion, it suffices to show that
 $$\begin{align*}\mathrm{Hom}_{H_n(0)}\left(\bigoplus_{i \in \mathcal{I}(\alpha)} \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}^{(i)}},\mathcal{V}_{\beta} \right)=0. \end{align*}$$
$$\begin{align*}\mathrm{Hom}_{H_n(0)}\left(\bigoplus_{i \in \mathcal{I}(\alpha)} \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}^{(i)}},\mathcal{V}_{\beta} \right)=0. \end{align*}$$
Observe that
 $$ \begin{align*} \dim\mathrm{Hom}_{H_n(0)}\left(\bigoplus_{i \in \mathcal{I}(\alpha)} \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}^{(i)}},\mathcal{V}_{\beta} \right) &=\sum_{ \gamma \in \mathcal{J}(\alpha)}\dim\mathrm{Hom}_{H_n(0)}\left(\mathbf{P}_{\gamma},\mathcal{V}_{\beta} \right)\\ &=\sum_{ \gamma \in \mathcal{J}(\alpha)} [\mathcal{V}_{\beta}:\mathbf{F}_{\gamma}] \quad \text{ (by Lemma \hyperlink{lemma1}{5.2})}. \end{align*} $$
$$ \begin{align*} \dim\mathrm{Hom}_{H_n(0)}\left(\bigoplus_{i \in \mathcal{I}(\alpha)} \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}^{(i)}},\mathcal{V}_{\beta} \right) &=\sum_{ \gamma \in \mathcal{J}(\alpha)}\dim\mathrm{Hom}_{H_n(0)}\left(\mathbf{P}_{\gamma},\mathcal{V}_{\beta} \right)\\ &=\sum_{ \gamma \in \mathcal{J}(\alpha)} [\mathcal{V}_{\beta}:\mathbf{F}_{\gamma}] \quad \text{ (by Lemma \hyperlink{lemma1}{5.2})}. \end{align*} $$
Here,
![]() $[\mathcal {V}_{\beta }:\mathbf {F}_{\gamma }]$
denotes the multiplicity of
$[\mathcal {V}_{\beta }:\mathbf {F}_{\gamma }]$
denotes the multiplicity of
![]() $\mathbf {F}_{\gamma }$
as a composition factor of
$\mathbf {F}_{\gamma }$
as a composition factor of
![]() $\mathcal {V}_{\beta }$
and thus equals the coefficient of
$\mathcal {V}_{\beta }$
and thus equals the coefficient of
![]() $F_{\gamma }$
in the expansion of
$F_{\gamma }$
in the expansion of
![]() $\mathfrak {S}^*_{\beta }$
into fundamental quasisymmetric functions. From Lemma 5.3, it follows that this coefficient vanishes unless
$\mathfrak {S}^*_{\beta }$
into fundamental quasisymmetric functions. From Lemma 5.3, it follows that this coefficient vanishes unless
![]() $\beta \ge _l \gamma $
. Since
$\beta \ge _l \gamma $
. Since
![]() $\alpha <_l \gamma $
for all
$\alpha <_l \gamma $
for all
![]() $\gamma \in \mathcal {J}(\alpha )$
, the assumption
$\gamma \in \mathcal {J}(\alpha )$
, the assumption
![]() $\beta \le _l \alpha $
yields the desired result.
$\beta \le _l \alpha $
yields the desired result.
(b) Combining equation (5.2) with (a) yields that
But by Lemma 5.2 and Lemma 5.3, we see that
 $$ \begin{align*} \dim\mathrm{Hom}_{H_n(0)}(\mathbf{P}_{\alpha}, \mathcal{V}_{\beta})=L_{\beta, \alpha}= \begin{cases} 1 & \text{ if } \beta =\alpha\\ 0 & \text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \dim\mathrm{Hom}_{H_n(0)}(\mathbf{P}_{\alpha}, \mathcal{V}_{\beta})=L_{\beta, \alpha}= \begin{cases} 1 & \text{ if } \beta =\alpha\\ 0 & \text{ otherwise.} \end{cases} \end{align*} $$
This justifies the assertion since
![]() $\dim \mathrm {End}_{H_n(0)}( \mathcal {V}_{\alpha })\ge 1$
.
$\dim \mathrm {End}_{H_n(0)}( \mathcal {V}_{\alpha })\ge 1$
.
(c) Let
![]() $f:\mathbf {P}_{\alpha } \to M$
be a surjective
$f:\mathbf {P}_{\alpha } \to M$
be a surjective
![]() $H_n(0)$
-module homomorphism. Then
$H_n(0)$
-module homomorphism. Then
and therefore
Now the assertion follows from the inequality
![]() $[M: \mathbf {F}_{\alpha }]\le [\mathcal {V}_{\alpha }: \mathbf {F}_{\alpha }]=L_{\alpha , \alpha }=1$
.
$[M: \mathbf {F}_{\alpha }]\le [\mathcal {V}_{\alpha }: \mathbf {F}_{\alpha }]=L_{\alpha , \alpha }=1$
.
Remark 5.5. To the best of the authors’ knowledge, the classification or distribution of indecomposable rigid modules is completely unknown. For the reader’s understanding, we provide some related examples.
-
(a) Let
 . A simple computation shows that M is a rigid indecomposable module. But since
. A simple computation shows that M is a rigid indecomposable module. But since
 $\dim \mathrm {Hom}_{H_5(0)}(\Omega (M), M) = 1$
, it is not essentially rigid.
$\dim \mathrm {Hom}_{H_5(0)}(\Omega (M), M) = 1$
, it is not essentially rigid. -
(b) Let
 . By adding two Vs appropriately, one can produce a nonsplit sequence Hence V is a nonrigid indecomposable module.
. By adding two Vs appropriately, one can produce a nonsplit sequence Hence V is a nonrigid indecomposable module.
Theorem 5.4 (b) is no longer valid unless
![]() $\beta \le _l \alpha $
. In view of
$\beta \le _l \alpha $
. In view of
![]() $\mathcal {V}_{\alpha } \cong \mathbf {P}_{\alpha } / \Omega (\mathcal {V}_{\alpha })$
, one can view
$\mathcal {V}_{\alpha } \cong \mathbf {P}_{\alpha } / \Omega (\mathcal {V}_{\alpha })$
, one can view
![]() $\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
as the
$\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
as the
![]() $\mathbb C$
-vector space consisting of
$\mathbb C$
-vector space consisting of
![]() $H_n(0)$
-module homomorphisms from
$H_n(0)$
-module homomorphisms from
![]() $\mathbf {P}_{\alpha }$
to
$\mathbf {P}_{\alpha }$
to
![]() $\mathcal {V}_{\beta }$
that vanish on
$\mathcal {V}_{\beta }$
that vanish on
![]() $\Omega (\mathcal {V}_{\alpha })$
. Therefore, to understand
$\Omega (\mathcal {V}_{\alpha })$
. Therefore, to understand
![]() $\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
, it is indispensable to understand
$\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
, it is indispensable to understand
![]() $\mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha }, \mathcal {V}_{\beta })$
first. To do this, let us fix a linear extension
$\mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha }, \mathcal {V}_{\beta })$
first. To do this, let us fix a linear extension
![]() $\preccurlyeq _{L}^{\mathrm {r}}$
of the partial order
$\preccurlyeq _{L}^{\mathrm {r}}$
of the partial order
![]() $\preccurlyeq ^{\mathrm {r}}$
on
$\preccurlyeq ^{\mathrm {r}}$
on
![]() $\mathrm {SIT}(\beta )$
given by
$\mathrm {SIT}(\beta )$
given by
Given
![]() $f\in \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
, let
$f\in \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
, let
![]() $f(T_{\alpha })=\sum _{\mathscr {T} \in \mathrm {SIT}(\beta )}c_{f,\mathscr {T}}\mathscr {T}$
. We define
$f(T_{\alpha })=\sum _{\mathscr {T} \in \mathrm {SIT}(\beta )}c_{f,\mathscr {T}}\mathscr {T}$
. We define
![]() ${\mathsf {Lead}}(f)$
to be the largest tableau in
${\mathsf {Lead}}(f)$
to be the largest tableau in
![]() $\{\mathscr {T} \in \mathrm {SIT}(\beta ): c_{f,\mathscr {T}}\ne 0\}$
with respect to
$\{\mathscr {T} \in \mathrm {SIT}(\beta ): c_{f,\mathscr {T}}\ne 0\}$
with respect to
![]() $\preccurlyeq _{L}^{\mathrm {r}}$
. When
$\preccurlyeq _{L}^{\mathrm {r}}$
. When
![]() $f=0$
,
$f=0$
,
![]() ${\mathsf {Lead}}(f)$
is set to be
${\mathsf {Lead}}(f)$
is set to be
![]() $\emptyset $
.
$\emptyset $
.
Theorem 5.6. Let
![]() $\alpha , \beta $
be compositions of n, and let
$\alpha , \beta $
be compositions of n, and let
![]() ${\mathfrak B}$
be the set of standard immaculate tableaux U of shape
${\mathfrak B}$
be the set of standard immaculate tableaux U of shape
![]() $\beta $
with
$\beta $
with
![]() $\mathrm {Des}(U)=\mathrm {set}(\alpha )$
.
$\mathrm {Des}(U)=\mathrm {set}(\alpha )$
.
-
(a) For each standard immaculate tableau U of shape
 $\beta $
with
$\beta $
with
 $\mathrm {Des}(U)=\mathrm {set}(\alpha )$
, there exists a unique homomorphism
$\mathrm {Des}(U)=\mathrm {set}(\alpha )$
, there exists a unique homomorphism
 $f_U\in \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
such that
$f_U\in \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
such that
 ${\mathsf {Lead}}(f)=U$
,
${\mathsf {Lead}}(f)=U$
,
 $c_{f,U}=1$
and
$c_{f,U}=1$
and
 $c_{f,U'}=0$
for all
$c_{f,U'}=0$
for all
 $U'\in {\mathfrak B}\setminus \{U\}$
.
$U'\in {\mathfrak B}\setminus \{U\}$
. -
(b) The dimension of
 $\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
is the same as the dimension of
$\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
is the same as the dimension of  $$\begin{align*}\{(c_U)_{U\in {\mathfrak B}} \in \mathbb C^{|{\mathfrak B}|}: \sum_{U}c_U \,\pi_{[m_{i-1} + 1, m_i]} \cdot f_U(T_{\alpha})=0 \text{ for all } i \in \mathcal{I}(\alpha) \}. \end{align*}$$
$$\begin{align*}\{(c_U)_{U\in {\mathfrak B}} \in \mathbb C^{|{\mathfrak B}|}: \sum_{U}c_U \,\pi_{[m_{i-1} + 1, m_i]} \cdot f_U(T_{\alpha})=0 \text{ for all } i \in \mathcal{I}(\alpha) \}. \end{align*}$$
Proof. (a) Observe that every homomorphism in
![]() $\mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
is completely determined by the value at the source tableau
$\mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
is completely determined by the value at the source tableau
![]() $T_{\alpha }$
of
$T_{\alpha }$
of
![]() $\mathbf {P}_{\alpha }$
. We claim that
$\mathbf {P}_{\alpha }$
. We claim that
![]() $\mathrm {Des}({\mathsf {Lead}}(f)) =\mathrm {set}(\alpha )$
for all nonzero
$\mathrm {Des}({\mathsf {Lead}}(f)) =\mathrm {set}(\alpha )$
for all nonzero
![]() $f\in \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
. To begin with, from the equalities
$f\in \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
. To begin with, from the equalities
![]() $f(\pi _i \cdot T_{\alpha })=f(T_{\alpha })$
for all
$f(\pi _i \cdot T_{\alpha })=f(T_{\alpha })$
for all
![]() $i\notin \mathrm {Des}(T_{\alpha })=\mathrm {set}(\alpha )$
, we see that f satisfies the condition that
$i\notin \mathrm {Des}(T_{\alpha })=\mathrm {set}(\alpha )$
, we see that f satisfies the condition that
![]() $\mathrm {Des}({\mathsf {Lead}}(f)) \subseteq \mathrm {set}(\alpha )$
. Recall that we set
$\mathrm {Des}({\mathsf {Lead}}(f)) \subseteq \mathrm {set}(\alpha )$
. Recall that we set
![]() $m_i:=\sum _{1\le k \le i}\alpha _i$
for all
$m_i:=\sum _{1\le k \le i}\alpha _i$
for all
![]() $1\le i \le \ell (\alpha )$
in Section 3. Suppose that there is an index j such that
$1\le i \le \ell (\alpha )$
in Section 3. Suppose that there is an index j such that
Then
But this is absurd since
whereas
So the claim is verified.
For each
![]() $U \in {\mathfrak B}$
, consider the
$U \in {\mathfrak B}$
, consider the
![]() $\mathbb C$
-vector space
$\mathbb C$
-vector space
Write
![]() ${\mathfrak B}$
as
${\mathfrak B}$
as
![]() $\{U_1\preccurlyeq _{L}^{\mathrm {r}}U_{2} \preccurlyeq _{L}^{\mathrm {r}} \cdots \preccurlyeq _{L}^{\mathrm {r}} U_{l-1} \preccurlyeq _{L}^{\mathrm {r}} U_{l}\}$
, where
$\{U_1\preccurlyeq _{L}^{\mathrm {r}}U_{2} \preccurlyeq _{L}^{\mathrm {r}} \cdots \preccurlyeq _{L}^{\mathrm {r}} U_{l-1} \preccurlyeq _{L}^{\mathrm {r}} U_{l}\}$
, where
![]() $l=|{\mathfrak B}|$
. For any
$l=|{\mathfrak B}|$
. For any
![]() $f,g \in H(U_i)$
, it holds that
$f,g \in H(U_i)$
, it holds that
with
![]() $H(U_0):=0$
. This implies that
$H(U_0):=0$
. This implies that
![]() $\dim H(U_i)/H(U_{i-1}) \le 1$
for all
$\dim H(U_i)/H(U_{i-1}) \le 1$
for all
![]() $1\le i \le l$
.
$1\le i \le l$
.
Combining these inequalities with the equality
![]() $\dim \mathrm {Hom}_{H_n(0)}\left (\mathbf {P}_{\alpha },\mathcal {V}_{\beta } \right )=|{\mathfrak B}|$
, we deduce that, for each
$\dim \mathrm {Hom}_{H_n(0)}\left (\mathbf {P}_{\alpha },\mathcal {V}_{\beta } \right )=|{\mathfrak B}|$
, we deduce that, for each
![]() $U\in {\mathfrak B}$
, there exists a unique
$U\in {\mathfrak B}$
, there exists a unique
![]() $f_U\in \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
with the desired property.
$f_U\in \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\alpha },\mathcal {V}_{\beta })$
with the desired property.
(b) By (a), one sees that
![]() $\{f_U: U\in {\mathfrak B}\}$
forms a basis for
$\{f_U: U\in {\mathfrak B}\}$
forms a basis for
![]() $\mathrm {Hom}_{H_n(0)}\left (\mathbf {P}_{\alpha },\mathcal {V}_{\beta } \right )$
. Since
$\mathrm {Hom}_{H_n(0)}\left (\mathbf {P}_{\alpha },\mathcal {V}_{\beta } \right )$
. Since
![]() $\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
is isomorphic to the
$\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
is isomorphic to the
![]() $\mathbb C$
-vector space consisting of
$\mathbb C$
-vector space consisting of
![]() $H_n(0)$
-module homomorphisms from
$H_n(0)$
-module homomorphisms from
![]() $\mathbf {P}_{\alpha }$
to
$\mathbf {P}_{\alpha }$
to
![]() $\mathcal {V}_{\beta }$
which vanish on
$\mathcal {V}_{\beta }$
which vanish on
![]() $\Omega (\mathcal {V}_{\alpha })$
, our assertion follows from Lemma 6.2, which says that
$\Omega (\mathcal {V}_{\alpha })$
, our assertion follows from Lemma 6.2, which says that
![]() $\{\pi _{[m_{i-1} + 1, m_i]} \cdot T_{\alpha } \,: \, i \in \mathcal {I}(\alpha )\}$
is a generating set of
$\{\pi _{[m_{i-1} + 1, m_i]} \cdot T_{\alpha } \,: \, i \in \mathcal {I}(\alpha )\}$
is a generating set of
![]() $\Omega (\mathcal {V}_{\alpha })$
.
$\Omega (\mathcal {V}_{\alpha })$
.
Example 5.7. (a) Let
![]() $\alpha =(1,1,2,1)$
and
$\alpha =(1,1,2,1)$
and
![]() $\beta =(1,2,2)$
. Then
$\beta =(1,2,2)$
. Then

and

Note that
![]() $\mathcal {I}(\alpha )=\{2\}$
and
$\mathcal {I}(\alpha )=\{2\}$
and
![]() $m_1=1, m_2=2$
. Since
$m_1=1, m_2=2$
. Since
![]() $\pi _{2} \cdot f_U(T_{\alpha })=0$
, it follows that
$\pi _{2} \cdot f_U(T_{\alpha })=0$
, it follows that
![]() $\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
is
$\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
is
![]() $1$
-dimensional.
$1$
-dimensional.
(b) Let
![]() $\alpha =(1,1,3,2)$
and
$\alpha =(1,1,3,2)$
and
![]() $\beta =(2,3,2)$
. Then
$\beta =(2,3,2)$
. Then

and
![]() $f_{U_i}(T_{\alpha })=U_i$
for
$f_{U_i}(T_{\alpha })=U_i$
for
![]() $i=1,2,3$
. Note that
$i=1,2,3$
. Note that
![]() $\mathcal {I}(\alpha )=\{2,3\}$
and
$\mathcal {I}(\alpha )=\{2,3\}$
and
![]() $m_1=1, m_2=2, m_3 = 5$
. Since
$m_1=1, m_2=2, m_3 = 5$
. Since
![]() $\pi _{2} \cdot f_{U_i}(T_{\alpha }) =0$
for all
$\pi _{2} \cdot f_{U_i}(T_{\alpha }) =0$
for all
![]() $1\le i \le 3$
and
$1\le i \le 3$
and

it follows that
![]() $\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
is
$\mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha },\mathcal {V}_{\beta })$
is
![]() $1$
-dimensional.
$1$
-dimensional.
We end up with an interesting consequence of Theorem 4.3, where we successfully compute
![]() $\mathrm {Ext}_{H_n(0)}^1(\mathbf {F}_{\beta },\mathcal {V}_{\alpha })$
by constructing an injective hull of
$\mathrm {Ext}_{H_n(0)}^1(\mathbf {F}_{\beta },\mathcal {V}_{\alpha })$
by constructing an injective hull of
![]() $\Omega ^{-1}(\mathcal {V}_{\alpha })$
. To compute it in a different way, let us consider a short exact sequence
$\Omega ^{-1}(\mathcal {V}_{\alpha })$
. To compute it in a different way, let us consider a short exact sequence
Here,
![]() $\iota $
is the natural injection. Then we have
$\iota $
is the natural injection. Then we have
where
![]() $\iota ^{\ast }: \mathrm {Hom}_{H_n(0)}( \mathbf {P}_{\beta } ,\mathcal {V}_{\alpha } )\rightarrow \mathrm {Hom}_{H_n(0)}({\mathrm {rad}}(\mathbf {P}_{\beta }),\mathcal {V}_{\alpha } ) $
is given by composition by with
$\iota ^{\ast }: \mathrm {Hom}_{H_n(0)}( \mathbf {P}_{\beta } ,\mathcal {V}_{\alpha } )\rightarrow \mathrm {Hom}_{H_n(0)}({\mathrm {rad}}(\mathbf {P}_{\beta }),\mathcal {V}_{\alpha } ) $
is given by composition by with
![]() $\iota $
. By equation (5.1), one has that
$\iota $
. By equation (5.1), one has that
 $$ \begin{align*} \dim \mathrm{Im}\, \iota^{\ast} &=\dim \mathrm{Hom}_{H_n(0)}\left(\mathbf{P}_{\beta},\mathcal{V}_{\alpha} \right)-\dim \mathrm{Hom}_{H_n(0)}\left(\mathbf{F}_{\beta},\mathcal{V}_{\alpha} \right)\\ &=[\mathcal{V}_{\alpha}:\mathbf{F}_{\beta}]-[\mathrm{soc}(\mathcal{V}_{\alpha}):\mathbf{F}_{\beta}]\\ &=L_{\alpha, \beta}-[[\underline{{\boldsymbol{\unicode{x3b1}}}}]:\beta^{\mathrm{r}}] \quad \text{(by Lemma 5.3 and Theorem 4.1)}, \end{align*} $$
$$ \begin{align*} \dim \mathrm{Im}\, \iota^{\ast} &=\dim \mathrm{Hom}_{H_n(0)}\left(\mathbf{P}_{\beta},\mathcal{V}_{\alpha} \right)-\dim \mathrm{Hom}_{H_n(0)}\left(\mathbf{F}_{\beta},\mathcal{V}_{\alpha} \right)\\ &=[\mathcal{V}_{\alpha}:\mathbf{F}_{\beta}]-[\mathrm{soc}(\mathcal{V}_{\alpha}):\mathbf{F}_{\beta}]\\ &=L_{\alpha, \beta}-[[\underline{{\boldsymbol{\unicode{x3b1}}}}]:\beta^{\mathrm{r}}] \quad \text{(by Lemma 5.3 and Theorem 4.1)}, \end{align*} $$
where
![]() $[[\underline {{\boldsymbol {\unicode{x3b1} }}}]:\beta ^{\mathrm {r}}]$
is the multiplicity of
$[[\underline {{\boldsymbol {\unicode{x3b1} }}}]:\beta ^{\mathrm {r}}]$
is the multiplicity of
![]() $\beta ^{\mathrm {r}} \in [\underline {{\boldsymbol {\unicode{x3b1} }}}]$
. Comparing Theorem 4.3 with equation (5.3) yields the following result.
$\beta ^{\mathrm {r}} \in [\underline {{\boldsymbol {\unicode{x3b1} }}}]$
. Comparing Theorem 4.3 with equation (5.3) yields the following result.
Corollary 5.8. Let
![]() $\alpha , \beta $
be compositions of n. Then we have
$\alpha , \beta $
be compositions of n. Then we have
6 Proof of Theorems
6.1 Proof of Theorem 3.3
We first prove that
![]() $\Omega (\mathcal {V}_{\alpha })$
is generated by
$\Omega (\mathcal {V}_{\alpha })$
is generated by
![]() $\{T^{(i)}_{\alpha } \mid i \in \mathcal {I}(\alpha )\}$
. By the definition of
$\{T^{(i)}_{\alpha } \mid i \in \mathcal {I}(\alpha )\}$
. By the definition of
![]() $\Phi $
, one can easily derive that
$\Phi $
, one can easily derive that
Given
![]() $\sigma \in \Sigma _n$
, let
$\sigma \in \Sigma _n$
, let
The left weak Bruhat order
![]() $\preceq _L$
on
$\preceq _L$
on
![]() $\Sigma _n$
is the partial order on
$\Sigma _n$
is the partial order on
![]() $\Sigma _n$
whose covering relation
$\Sigma _n$
whose covering relation
![]() $\preceq _L^c$
is defined as follows:
$\preceq _L^c$
is defined as follows:
![]() $\sigma \preceq _L^c s_i \sigma $
if and only if
$\sigma \preceq _L^c s_i \sigma $
if and only if
![]() $i \notin \mathrm {Des}_L(\sigma )$
. It should be remarked that a word of length n can be confused with a permutation in
$i \notin \mathrm {Des}_L(\sigma )$
. It should be remarked that a word of length n can be confused with a permutation in
![]() $\Sigma _n$
if each of
$\Sigma _n$
if each of
![]() $1,2,\ldots , n$
appears in it exactly once.
$1,2,\ldots , n$
appears in it exactly once.
The following lemma plays a key role in proving Lemma 6.2.
Lemma 6.1 ([Reference Björner and Brenti8, Proposition 3.1.2 (vi)]).
Suppose that
![]() $i \in \mathrm {Des}_R(\sigma ) \cap \mathrm {Des}_R(\rho )$
. Then
$i \in \mathrm {Des}_R(\sigma ) \cap \mathrm {Des}_R(\rho )$
. Then
![]() $\sigma \preceq _L \rho $
if and only if
$\sigma \preceq _L \rho $
if and only if
![]() $\sigma s_i \preceq _L \rho s_i$
.
$\sigma s_i \preceq _L \rho s_i$
.
Lemma 6.2. For each
![]() $i \in \mathcal {I}(\alpha )$
,
$i \in \mathcal {I}(\alpha )$
,
![]() $H_n(0) \cdot T^{(i)}_{\alpha } = \mathbb C\{T \in \mathrm {SRT}(\alpha ) \mid T_i^1> T_{i+1}^1 \}$
. Thus,
$H_n(0) \cdot T^{(i)}_{\alpha } = \mathbb C\{T \in \mathrm {SRT}(\alpha ) \mid T_i^1> T_{i+1}^1 \}$
. Thus,
![]() $\Omega (\mathcal {V}_{\alpha }) = \sum _{i\in \mathcal {I}(\alpha )} H_n(0) \cdot T^{(i)}_{\alpha }$
.
$\Omega (\mathcal {V}_{\alpha }) = \sum _{i\in \mathcal {I}(\alpha )} H_n(0) \cdot T^{(i)}_{\alpha }$
.
Proof. For simplicity, let
![]() $\mathrm {SRT}(\alpha )^{(i)}$
be the set of
$\mathrm {SRT}(\alpha )^{(i)}$
be the set of
![]() $\mathrm {SRT}$
x of shape
$\mathrm {SRT}$
x of shape
![]() $\alpha $
such that the topmost entry in the ith column is greater than that in the
$\alpha $
such that the topmost entry in the ith column is greater than that in the
![]() $(i+1)$
st column.
$(i+1)$
st column.
We first show that
![]() $H_n(0) \cdot T^{(i)}_{\alpha }$
is included in the
$H_n(0) \cdot T^{(i)}_{\alpha }$
is included in the
![]() $\mathbb C$
-span of
$\mathbb C$
-span of
![]() $\mathrm {SRT}(\alpha )^{(i)}$
, equivalently
$\mathrm {SRT}(\alpha )^{(i)}$
, equivalently
![]() $\pi _{\sigma } \cdot T^{(i)}_{\alpha } \in \mathrm {SRT}(\alpha )^{(i)} \cup \{0\}$
for all
$\pi _{\sigma } \cdot T^{(i)}_{\alpha } \in \mathrm {SRT}(\alpha )^{(i)} \cup \{0\}$
for all
![]() $\sigma \in \Sigma _n$
. Suppose that there exists
$\sigma \in \Sigma _n$
. Suppose that there exists
![]() $\sigma \in \Sigma _n$
such that
$\sigma \in \Sigma _n$
such that
![]() $\pi _{\sigma } \cdot T^{(i)}_{\alpha } \neq 0$
and
$\pi _{\sigma } \cdot T^{(i)}_{\alpha } \neq 0$
and
![]() $\pi _{\sigma } \cdot T^{(i)}_{\alpha } \notin \mathrm {SRT}(\alpha )^{(i)}$
. Let
$\pi _{\sigma } \cdot T^{(i)}_{\alpha } \notin \mathrm {SRT}(\alpha )^{(i)}$
. Let
![]() $\sigma _0$
be such a permutation with minimal length and j a left descent of
$\sigma _0$
be such a permutation with minimal length and j a left descent of
![]() $\sigma _0$
. By the minimality of
$\sigma _0$
. By the minimality of
![]() $\sigma _0$
, we have
$\sigma _0$
, we have
![]() $\pi _{s_j \sigma _0} \cdot T^{(i)}_{\alpha } \in \mathrm {SRT}(\alpha )^{(i)}$
, and therefore
$\pi _{s_j \sigma _0} \cdot T^{(i)}_{\alpha } \in \mathrm {SRT}(\alpha )^{(i)}$
, and therefore
By the definition of the
![]() $\pi _j$
-action on
$\pi _j$
-action on
![]() $\mathrm {SRT}(\alpha )$
, we have
$\mathrm {SRT}(\alpha )$
, we have
However, since
![]() $\pi _j \cdot (\pi _{s_j \sigma _0} \cdot T^{(i)}_{\alpha }) = \pi _{\sigma _0} \cdot T^{(i)}_{\alpha }$
, this contradicts the assumption that
$\pi _j \cdot (\pi _{s_j \sigma _0} \cdot T^{(i)}_{\alpha }) = \pi _{\sigma _0} \cdot T^{(i)}_{\alpha }$
, this contradicts the assumption that
![]() $\pi _{\sigma _0} \cdot T^{(i)}_{\alpha } \notin \mathrm {SRT}(\alpha )^{(i)}$
.
$\pi _{\sigma _0} \cdot T^{(i)}_{\alpha } \notin \mathrm {SRT}(\alpha )^{(i)}$
.
We next show the opposite inclusion
![]() $\mathrm {SRT}(\alpha )^{(i)} \subseteq H_n(0) \cdot T^{(i)}_{\alpha }$
. Our strategy is to use [Reference Huang20, Theorem 3.3], which implicitly says that for
$\mathrm {SRT}(\alpha )^{(i)} \subseteq H_n(0) \cdot T^{(i)}_{\alpha }$
. Our strategy is to use [Reference Huang20, Theorem 3.3], which implicitly says that for
![]() $T_1, T_2 \in \mathrm {SRT}(\alpha )$
,
$T_1, T_2 \in \mathrm {SRT}(\alpha )$
,
![]() $T_2 \in H_n(0) \cdot T_1$
if and only if
$T_2 \in H_n(0) \cdot T_1$
if and only if
![]() $\mathbf {w}(T_1) \preceq _L \mathbf {w}(T_2)$
. Here,
$\mathbf {w}(T_1) \preceq _L \mathbf {w}(T_2)$
. Here,
![]() $\mathbf {w}(T_i) \,(i=1,2)$
denotes the word obtained from
$\mathbf {w}(T_i) \,(i=1,2)$
denotes the word obtained from
![]() $T_i$
by reading the entries from left to right starting with the bottom row. For each
$T_i$
by reading the entries from left to right starting with the bottom row. For each
![]() $T \in \mathrm {SRT}(\alpha )^{(i)}$
, we define
$T \in \mathrm {SRT}(\alpha )^{(i)}$
, we define
![]() $\tau _T$
to be the filling of
$\tau _T$
to be the filling of
![]() $\mathtt {rd}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
whose entries in each column are increasing from top to bottom and whose columns are given as follows: for
$\mathtt {rd}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
whose entries in each column are increasing from top to bottom and whose columns are given as follows: for
![]() $1 \le p \le \ell (\alpha )$
,
$1 \le p \le \ell (\alpha )$
,
 $$ \begin{align} (\tau_T)_p^{\bullet} = \begin{cases} T_i^{\bullet} \cup \{T_{i+1}^1\} & \text{if } p = i,\\ T_{i+1}^{\bullet} \setminus \{ T_{i+1}^1 \} & \text{if } p = i+1,\\ T_p^{\bullet} & \text{otherwise.}\\ \end{cases} \end{align} $$
$$ \begin{align} (\tau_T)_p^{\bullet} = \begin{cases} T_i^{\bullet} \cup \{T_{i+1}^1\} & \text{if } p = i,\\ T_{i+1}^{\bullet} \setminus \{ T_{i+1}^1 \} & \text{if } p = i+1,\\ T_p^{\bullet} & \text{otherwise.}\\ \end{cases} \end{align} $$
The inequality
![]() $(\tau _T)_i^1 < (\tau _T)_{i+1}^{-1}$
shows that
$(\tau _T)_i^1 < (\tau _T)_{i+1}^{-1}$
shows that
![]() $\tau _T \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
. Combining
$\tau _T \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
. Combining
with
![]() $\tau _{T^{(i)}_{\alpha }} = T_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
(=the source tableau of
$\tau _{T^{(i)}_{\alpha }} = T_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
(=the source tableau of
![]() $\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
) yields that
$\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
) yields that
![]() $\mathbf {w}(\tau _{T^{(i)}_{\alpha }}) \preceq _L \mathbf {w}(\tau _T)$
for
$\mathbf {w}(\tau _{T^{(i)}_{\alpha }}) \preceq _L \mathbf {w}(\tau _T)$
for
![]() $T \in \mathrm {SRT}(\alpha )^{(i)}$
. Moreover, for each
$T \in \mathrm {SRT}(\alpha )^{(i)}$
. Moreover, for each
![]() $m_i \le j < m_{i+1}$
, it holds that
$m_i \le j < m_{i+1}$
, it holds that
Here,
![]() $s_{m_i} s_{m_i + 1} \cdots s_{j - 1}$
is regarded as the identity when
$s_{m_i} s_{m_i + 1} \cdots s_{j - 1}$
is regarded as the identity when
![]() $j = m_i$
. Finally, applying Lemma 6.1 to equation (6.2) yields that
$j = m_i$
. Finally, applying Lemma 6.1 to equation (6.2) yields that
![]() $\mathbf {w}(T^{(i)}_{\alpha }) \preceq _L \mathbf {w}(T)$
, as required.
$\mathbf {w}(T^{(i)}_{\alpha }) \preceq _L \mathbf {w}(T)$
, as required.
Combining Lemma 6.2 with the equalities
![]() $L(\tau )_i^1 = \tau _i^2$
and
$L(\tau )_i^1 = \tau _i^2$
and
![]() $L(\tau )_{i+1}^1 = \min (\tau _i^1, \tau _{i+1}^1)$
, we derive that
$L(\tau )_{i+1}^1 = \min (\tau _i^1, \tau _{i+1}^1)$
, we derive that
![]() $\partial ^{(i)}_1$
is well-defined.
$\partial ^{(i)}_1$
is well-defined.
Lemma 6.3. For
![]() $i \in \mathcal {I}(\alpha )$
,
$i \in \mathcal {I}(\alpha )$
,
![]() $\partial _1^{(i)}: \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow H_n(0) \cdot T^{(i)}_{\alpha }$
is a surjective
$\partial _1^{(i)}: \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow H_n(0) \cdot T^{(i)}_{\alpha }$
is a surjective
![]() $H_n(0)$
-module homomorphism.
$H_n(0)$
-module homomorphism.
Proof. For each
![]() $T \in H_n(0) \cdot T^{(i)}_{\alpha }$
, let
$T \in H_n(0) \cdot T^{(i)}_{\alpha }$
, let
![]() $\tau _T$
be the filling of
$\tau _T$
be the filling of
![]() $\mathtt {rd}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
defined in equation (6.1). The surjectivity of
$\mathtt {rd}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
defined in equation (6.1). The surjectivity of
![]() $\partial _1^{(i)}$
is straightforward since
$\partial _1^{(i)}$
is straightforward since
![]() $\tau _T \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
and
$\tau _T \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
and
![]() $L(\tau _T)=T$
. Thus, to prove our assertion, it suffices to show that
$L(\tau _T)=T$
. Thus, to prove our assertion, it suffices to show that
for all
![]() $k = 1,2, \ldots , n-1$
and
$k = 1,2, \ldots , n-1$
and
![]() $\tau \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
.
$\tau \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
.
Case 1:
![]() $\pi _k \cdot \tau = \tau $
. If
$\pi _k \cdot \tau = \tau $
. If
![]() $\partial _1^{(i)}(\tau ) = 0$
, then there is nothing to prove. Suppose that
$\partial _1^{(i)}(\tau ) = 0$
, then there is nothing to prove. Suppose that
![]() $\partial _1^{(i)}(\tau ) \neq 0$
: that is,
$\partial _1^{(i)}(\tau ) \neq 0$
: that is,
![]() $L(\tau ) \in \mathrm {SRT}(\alpha )$
. We claim that
$L(\tau ) \in \mathrm {SRT}(\alpha )$
. We claim that
![]() $k \notin \mathrm {Des}(L(\tau ))$
. If
$k \notin \mathrm {Des}(L(\tau ))$
. If
![]() $k = \tau _i^1$
and
$k = \tau _i^1$
and
![]() $k+1 = \tau _i^2$
, then
$k+1 = \tau _i^2$
, then
![]() $k \in L(\tau )_{i+1}^{\bullet }$
and
$k \in L(\tau )_{i+1}^{\bullet }$
and
![]() $k+1 \in L(\tau )_i^{\bullet }$
. If
$k+1 \in L(\tau )_i^{\bullet }$
. If
![]() $k \in \tau _{i+1}^{\bullet }$
and
$k \in \tau _{i+1}^{\bullet }$
and
![]() $k+1 = \tau _i^1$
, then both k and
$k+1 = \tau _i^1$
, then both k and
![]() $k+1$
are in
$k+1$
are in
![]() $L(\tau )_{i+1}^{\bullet }$
. In the remaining cases, from the fact that k is weakly right of
$L(\tau )_{i+1}^{\bullet }$
. In the remaining cases, from the fact that k is weakly right of
![]() $k+1$
in
$k+1$
in
![]() $\tau $
, it follows that k is weakly right of
$\tau $
, it follows that k is weakly right of
![]() $k+1$
in
$k+1$
in
![]() $L(\tau )$
. For any cases, we can see that
$L(\tau )$
. For any cases, we can see that
![]() $k \notin \mathrm {Des}(L(\tau ))$
.
$k \notin \mathrm {Des}(L(\tau ))$
.
Case 2:
![]() $\pi _k \cdot \tau = 0$
. If
$\pi _k \cdot \tau = 0$
. If
![]() $\partial _1^{(i)}(\tau ) = 0$
, then there is nothing to prove. Suppose that
$\partial _1^{(i)}(\tau ) = 0$
, then there is nothing to prove. Suppose that
![]() $\partial _1^{(i)}(\tau ) \neq 0$
. Since k and
$\partial _1^{(i)}(\tau ) \neq 0$
. Since k and
![]() $k+1$
are in the same row of
$k+1$
are in the same row of
![]() $\tau $
, k is the top and
$\tau $
, k is the top and
![]() $k+1$
is the bottom for some two consecutive columns of
$k+1$
is the bottom for some two consecutive columns of
![]() $\tau $
. If
$\tau $
. If
![]() $k \neq \tau _i^1$
, then k and
$k \neq \tau _i^1$
, then k and
![]() $k+1$
are still in the same row of
$k+1$
are still in the same row of
![]() $L(\tau )$
, so
$L(\tau )$
, so
![]() $\pi _k \cdot L(\tau ) = \pi _k \cdot \partial _1^{(i)}(\tau ) = 0$
, as required. Assume that
$\pi _k \cdot L(\tau ) = \pi _k \cdot \partial _1^{(i)}(\tau ) = 0$
, as required. Assume that
![]() $k = \tau _i^1$
. Note that
$k = \tau _i^1$
. Note that
![]() $|\tau _i^{\bullet }| = \alpha _i +1 \geq 2$
and
$|\tau _i^{\bullet }| = \alpha _i +1 \geq 2$
and
![]() $\tau _i^2$
greater than both k and
$\tau _i^2$
greater than both k and
![]() $k+1$
. By the definition of
$k+1$
. By the definition of
![]() $L(\tau )$
, we have that
$L(\tau )$
, we have that
![]() $L(\tau )_i^1 = \tau _i^2> L(\tau )_{i+1}^{-1} = k+1$
. This implies that
$L(\tau )_i^1 = \tau _i^2> L(\tau )_{i+1}^{-1} = k+1$
. This implies that
![]() $\partial _1^{(i)}(\tau )=0$
, which contradicts our assumption
$\partial _1^{(i)}(\tau )=0$
, which contradicts our assumption
![]() $\partial _1^{(i)}(\tau ) \neq 0$
.
$\partial _1^{(i)}(\tau ) \neq 0$
.
Case 3:
![]() $\pi _k \cdot \tau = s_k \cdot \tau $
. First, consider the case where
$\pi _k \cdot \tau = s_k \cdot \tau $
. First, consider the case where
![]() $\partial _1^{(i)}(\tau ) = 0$
: that is,
$\partial _1^{(i)}(\tau ) = 0$
: that is,
![]() $L(\tau ) \notin \mathrm {SRT}(\alpha )$
. Then
$L(\tau ) \notin \mathrm {SRT}(\alpha )$
. Then
![]() $\tau $
must satisfy either
$\tau $
must satisfy either
![]() $\tau _i^2> \tau _{i+1}^{-1}$
or
$\tau _i^2> \tau _{i+1}^{-1}$
or
![]() $\min (\tau _i^1, \tau _{i+1}^1)> \tau _{i+2}^{-1}$
. Thus, to
$\min (\tau _i^1, \tau _{i+1}^1)> \tau _{i+2}^{-1}$
. Thus, to
![]() $L(\pi _k \cdot \tau ) \in \mathrm {SRT}(\alpha )$
, either
$L(\pi _k \cdot \tau ) \in \mathrm {SRT}(\alpha )$
, either
![]() $\tau _i^2 = k+1$
and
$\tau _i^2 = k+1$
and
![]() $\tau _{i+1}^{-1}=k$
or
$\tau _{i+1}^{-1}=k$
or
![]() $\min (\tau _i^1, \tau _{i+1}^1)= k+1$
and
$\min (\tau _i^1, \tau _{i+1}^1)= k+1$
and
![]() $\tau _{i+2}^{-1}=k$
. However, these are absurd because k is strictly left of
$\tau _{i+2}^{-1}=k$
. However, these are absurd because k is strictly left of
![]() $k+1$
in
$k+1$
in
![]() $\tau $
.
$\tau $
.
Next, consider the case where
![]() $\partial _1^{(i)}(\tau ) \neq 0$
: that is,
$\partial _1^{(i)}(\tau ) \neq 0$
: that is,
![]() $L(\tau ) \in \mathrm {SRT}(\alpha )$
. Since
$L(\tau ) \in \mathrm {SRT}(\alpha )$
. Since
![]() $\pi _k \cdot \tau = s_k \cdot \tau $
, k is strictly left of
$\pi _k \cdot \tau = s_k \cdot \tau $
, k is strictly left of
![]() $k+1$
in
$k+1$
in
![]() $\tau $
. Therefore, k is weakly left of
$\tau $
. Therefore, k is weakly left of
![]() $k+1$
in
$k+1$
in
![]() $L(\tau )$
by the definition of
$L(\tau )$
by the definition of
![]() $L(\tau )$
. Hence if neither k and
$L(\tau )$
. Hence if neither k and
![]() $k+1$
are in the same column in
$k+1$
are in the same column in
![]() $L(\tau )$
, nor are they in the same row in
$L(\tau )$
, nor are they in the same row in
![]() $L(\tau )$
, then
$L(\tau )$
, then
![]() $\pi _k \cdot L(\tau ) = s_k \cdot L(\tau )$
. Therefore, in such case, we have that
$\pi _k \cdot L(\tau ) = s_k \cdot L(\tau )$
. Therefore, in such case, we have that
Suppose that k and
![]() $k+1$
are in the same column in
$k+1$
are in the same column in
![]() $L(\tau )$
. This is possible only the case where
$L(\tau )$
. This is possible only the case where
![]() $k = \tau _i^1$
and
$k = \tau _i^1$
and
![]() $k+1 \in \tau _{i+1}^{\bullet }$
since k is strictly left of
$k+1 \in \tau _{i+1}^{\bullet }$
since k is strictly left of
![]() $k+1$
in
$k+1$
in
![]() $\tau $
. Moreover,
$\tau $
. Moreover,
![]() $k+1 \neq \tau _{i+1}^{-1}$
since
$k+1 \neq \tau _{i+1}^{-1}$
since
![]() $\pi _k \cdot \tau = s_k \cdot \tau $
. Hence
$\pi _k \cdot \tau = s_k \cdot \tau $
. Hence
![]() $k+1 = (\pi _k \cdot \tau )_{i}^1$
and
$k+1 = (\pi _k \cdot \tau )_{i}^1$
and
![]() $k \in (\pi _k \cdot \tau )_{i+1}^{\bullet }$
, which implies that
$k \in (\pi _k \cdot \tau )_{i+1}^{\bullet }$
, which implies that
![]() $L(\tau ) = L(\pi _k \cdot \tau )$
. Therefore, we have
$L(\tau ) = L(\pi _k \cdot \tau )$
. Therefore, we have
Here the second equality follows from the assumption that k and
![]() $k+1$
are in the same column in
$k+1$
are in the same column in
![]() $L(\tau )$
.
$L(\tau )$
.
Suppose that k and
![]() $k+1$
are in the same row in
$k+1$
are in the same row in
![]() $L(\tau )$
. Then
$L(\tau )$
. Then
![]() $\pi _k \cdot L(\tau ) = 0$
. In addition, since
$\pi _k \cdot L(\tau ) = 0$
. In addition, since
![]() $\pi _k \cdot \tau = s_k \cdot \tau $
, we have that either
$\pi _k \cdot \tau = s_k \cdot \tau $
, we have that either
![]() $L(\tau _{i+1}^1) = k$
and
$L(\tau _{i+1}^1) = k$
and
![]() $L(\tau )_{i+2}^{-1} = k+1$
, or
$L(\tau )_{i+2}^{-1} = k+1$
, or
![]() $L(\tau )_i^1 = k$
and
$L(\tau )_i^1 = k$
and
![]() $L(\tau )_{i+1}^{-1} = k+1$
. In the case where
$L(\tau )_{i+1}^{-1} = k+1$
. In the case where
![]() $L(\tau )_{i+1}^1 = k$
and
$L(\tau )_{i+1}^1 = k$
and
![]() $L(\tau )_{i+2}^{-1} = k+1$
, the assumption
$L(\tau )_{i+2}^{-1} = k+1$
, the assumption
![]() $\pi _k \cdot \tau = s_k \cdot \tau $
implies that
$\pi _k \cdot \tau = s_k \cdot \tau $
implies that
![]() $L(\pi _k \cdot \tau )_{i+1}^1 = k+1$
and
$L(\pi _k \cdot \tau )_{i+1}^1 = k+1$
and
![]() $L(\pi _k \cdot \tau )_{i+2}^{-1} = k$
. Thus,
$L(\pi _k \cdot \tau )_{i+2}^{-1} = k$
. Thus,
![]() $L(\pi _k \cdot \tau ) \notin \mathrm {SRT}(\alpha )$
: that is,
$L(\pi _k \cdot \tau ) \notin \mathrm {SRT}(\alpha )$
: that is,
![]() $\partial _1^{(i)}(\pi _k \cdot \tau ) = 0$
as desired. In the case where
$\partial _1^{(i)}(\pi _k \cdot \tau ) = 0$
as desired. In the case where
![]() $L(\tau )_i^1 = k$
and
$L(\tau )_i^1 = k$
and
![]() $L(\tau )_{i+1}^{-1} = k+1$
, one can easily see that
$L(\tau )_{i+1}^{-1} = k+1$
, one can easily see that
![]() $L(\pi _k \cdot \tau ) \notin \mathrm {SRT}(\alpha )$
. Thus
$L(\pi _k \cdot \tau ) \notin \mathrm {SRT}(\alpha )$
. Thus
![]() $\pi _k \cdot \partial _1^{(i)}(\tau ) = 0 = \partial _1^{(i)}(\pi _k \cdot \tau )$
.
$\pi _k \cdot \partial _1^{(i)}(\tau ) = 0 = \partial _1^{(i)}(\pi _k \cdot \tau )$
.
Due to Lemma 6.2 and Lemma 6.3, we can view
![]() $\partial _1 = \sum _{i \in \mathcal {I}(\alpha )} \partial _1^{(i)}$
as an
$\partial _1 = \sum _{i \in \mathcal {I}(\alpha )} \partial _1^{(i)}$
as an
![]() $H_n(0)$
-module homomorphism from
$H_n(0)$
-module homomorphism from
![]() $\bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
onto
$\bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
onto
![]() $\Omega (\mathcal {V}_{\alpha })$
. Now, we verify that
$\Omega (\mathcal {V}_{\alpha })$
. Now, we verify that
![]() $\partial _1$
is an essential epimorphism: that is,
$\partial _1$
is an essential epimorphism: that is,
![]() $\ker (\partial _1) \subseteq \mathrm {rad}(\bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}})$
.
$\ker (\partial _1) \subseteq \mathrm {rad}(\bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}})$
.
To ease notation, we write
![]() $\boldsymbol {\tau }_{(i)}$
for the source tableau
$\boldsymbol {\tau }_{(i)}$
for the source tableau
![]() $\tau _{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
in
$\tau _{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
in
![]() $\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
. When
$\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})$
. When
![]() $i \neq \ell (\alpha )-1$
, we can see that
$i \neq \ell (\alpha )-1$
, we can see that
 $$\begin{align*}\begin{aligned} (\boldsymbol{\tau}_{(i)})_{i+1}^q &= m_i+1+q \quad \text{for } 1 \leq q \leq \alpha_{i+1}-1\, \text{, and} \\ (\boldsymbol{\tau}_{(i)})_{i+2}^q &= m_{i+1}+q \quad \text{for } 1 \leq q \leq \alpha_{i+2}\, , \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} (\boldsymbol{\tau}_{(i)})_{i+1}^q &= m_i+1+q \quad \text{for } 1 \leq q \leq \alpha_{i+1}-1\, \text{, and} \\ (\boldsymbol{\tau}_{(i)})_{i+2}^q &= m_{i+1}+q \quad \text{for } 1 \leq q \leq \alpha_{i+2}\, , \end{aligned} \end{align*}$$
where
![]() $m_i = \sum _{j = 1}^{i}\alpha _j$
. Let
$m_i = \sum _{j = 1}^{i}\alpha _j$
. Let
![]() $\hat {\boldsymbol {\tau }}_{(i)}$
denote the
$\hat {\boldsymbol {\tau }}_{(i)}$
denote the
![]() $\mathrm {SRT}$
of shape
$\mathrm {SRT}$
of shape
![]() ${\boldsymbol {\unicode{x3b1} }}^{(i)}$
such that
${\boldsymbol {\unicode{x3b1} }}^{(i)}$
such that
 $$ \begin{align*} \begin{aligned} (\hat{\boldsymbol{\tau}}_{(i)})_{i+1}^q &= m_i+1+ \alpha_{i+2}+q \quad \text{for } 1 \leq q \leq \alpha_{i+1}-1\, , \\ (\hat{\boldsymbol{\tau}}_{(i)})_{i+2}^q &= m_{i}+1+q \quad \text{for } 1 \leq q \leq \alpha_{i+2}\, \text{, and} \\ (\hat{\boldsymbol{\tau}}_{(i)})_p &= (\boldsymbol{\tau}_{(i)})_p \quad \text{for }p \neq i, i+1. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (\hat{\boldsymbol{\tau}}_{(i)})_{i+1}^q &= m_i+1+ \alpha_{i+2}+q \quad \text{for } 1 \leq q \leq \alpha_{i+1}-1\, , \\ (\hat{\boldsymbol{\tau}}_{(i)})_{i+2}^q &= m_{i}+1+q \quad \text{for } 1 \leq q \leq \alpha_{i+2}\, \text{, and} \\ (\hat{\boldsymbol{\tau}}_{(i)})_p &= (\boldsymbol{\tau}_{(i)})_p \quad \text{for }p \neq i, i+1. \end{aligned} \end{align*} $$
For example, if
![]() $\alpha = (1,3,3,1)$
and
$\alpha = (1,3,3,1)$
and
![]() $i = 1$
, then
$i = 1$
, then

Observe that
![]() $(\boldsymbol {\tau }_{(i)})^{\bullet }_j = (\hat {\boldsymbol {\tau }}_{(i)})^{\bullet }_j$
for
$(\boldsymbol {\tau }_{(i)})^{\bullet }_j = (\hat {\boldsymbol {\tau }}_{(i)})^{\bullet }_j$
for
![]() $j \neq i+1, i+2$
.
$j \neq i+1, i+2$
.
Lemma 6.4. For
![]() $i \in \mathcal {I}(\alpha )$
,
$i \in \mathcal {I}(\alpha )$
,
![]() $\ker (\partial _1^{(i)}) \subseteq \mathrm {rad}(\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} )$
.
$\ker (\partial _1^{(i)}) \subseteq \mathrm {rad}(\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} )$
.
Proof. If
![]() $i = \ell (\alpha )-1$
, then
$i = \ell (\alpha )-1$
, then
![]() ${\boldsymbol {\unicode{x3b1} }}^{(i)}$
is a composition. Therefore,
${\boldsymbol {\unicode{x3b1} }}^{(i)}$
is a composition. Therefore,
![]() $\mathrm {rad}(\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}})$
is the
$\mathrm {rad}(\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}})$
is the
![]() $\mathbb C$
-span of
$\mathbb C$
-span of
![]() $\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})\setminus \{ \boldsymbol {\tau }_{(i)} \}$
. Since
$\mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})\setminus \{ \boldsymbol {\tau }_{(i)} \}$
. Since
![]() $\partial _1^{(i)}(\boldsymbol {\tau }_{(i)}) \neq 0$
, this implies that
$\partial _1^{(i)}(\boldsymbol {\tau }_{(i)}) \neq 0$
, this implies that
![]() $\ker (\partial _1^{(i)}) \subseteq \mathrm {rad}(\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} )$
.
$\ker (\partial _1^{(i)}) \subseteq \mathrm {rad}(\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} )$
.
Suppose that
![]() $i \neq \ell (\alpha )-1$
. Let
$i \neq \ell (\alpha )-1$
. Let
 $$ \begin{align} \begin{aligned} \beta^{(1)} & = (\alpha_1, \alpha_2, \ldots, \alpha_{i-1}, \alpha_i +1, \alpha_{i+1} - 1, \alpha_{i+2} , \alpha_{i+3}, \ldots, \alpha_{\ell(\alpha)}), \\ \beta^{(2)} & = (\alpha_1, \alpha_2, \ldots, \alpha_{i-1}, \alpha_i +1, \alpha_{i+1} - 1 + \alpha_{i+2} , \alpha_{i+3}, \ldots, \alpha_{\ell(\alpha)}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \beta^{(1)} & = (\alpha_1, \alpha_2, \ldots, \alpha_{i-1}, \alpha_i +1, \alpha_{i+1} - 1, \alpha_{i+2} , \alpha_{i+3}, \ldots, \alpha_{\ell(\alpha)}), \\ \beta^{(2)} & = (\alpha_1, \alpha_2, \ldots, \alpha_{i-1}, \alpha_i +1, \alpha_{i+1} - 1 + \alpha_{i+2} , \alpha_{i+3}, \ldots, \alpha_{\ell(\alpha)}). \end{aligned} \end{align} $$
To ease notation, we denote the source tableaux of
![]() $\mathbf {P}_{\beta ^{(1)}}$
and
$\mathbf {P}_{\beta ^{(1)}}$
and
![]() $\mathbf {P}_{\beta ^{(2)}}$
by
$\mathbf {P}_{\beta ^{(2)}}$
by
![]() $\tau ^{(1)}$
and
$\tau ^{(1)}$
and
![]() $\tau ^{(2)}$
, respectively. By Theorem 2.3, we may choose an
$\tau ^{(2)}$
, respectively. By Theorem 2.3, we may choose an
![]() $H_n(0)$
-module isomorphism
$H_n(0)$
-module isomorphism
Let
 $$ \begin{align*}f(\boldsymbol{\tau}_{(i)}) = \sum_{\tau \in \mathrm{SRT}(\beta^{(1)})} c_{\tau} \tau + \sum_{\tau \in \mathrm{SRT}(\beta^{(2)})} d_{\tau} \tau \quad \text{for } c_{\tau}, d_{\tau} \in {\mathbb C}. \end{align*} $$
$$ \begin{align*}f(\boldsymbol{\tau}_{(i)}) = \sum_{\tau \in \mathrm{SRT}(\beta^{(1)})} c_{\tau} \tau + \sum_{\tau \in \mathrm{SRT}(\beta^{(2)})} d_{\tau} \tau \quad \text{for } c_{\tau}, d_{\tau} \in {\mathbb C}. \end{align*} $$
Since
![]() $f(\boldsymbol {\tau }_{(i)})$
is a generator of
$f(\boldsymbol {\tau }_{(i)})$
is a generator of
![]() $\mathbf {P}_{\beta ^{(1)}} \oplus \mathbf {P}_{\beta ^{(2)}}$
,
$\mathbf {P}_{\beta ^{(1)}} \oplus \mathbf {P}_{\beta ^{(2)}}$
,
![]() $c_{\tau ^{(1)}}$
and
$c_{\tau ^{(1)}}$
and
![]() $d_{\tau ^{(2)}}$
are nonzero.
$d_{\tau ^{(2)}}$
are nonzero.
We claim that
![]() $[\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]^{\mathrm {c}} \subset \mathrm {rad} (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}})$
. Take any
$[\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]^{\mathrm {c}} \subset \mathrm {rad} (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}})$
. Take any
![]() $\tau \notin [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}]$
. To get
$\tau \notin [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}]$
. To get
![]() $\tau $
from
$\tau $
from
![]() $\boldsymbol {\tau }_{(i)}$
, there should exist an
$\boldsymbol {\tau }_{(i)}$
, there should exist an
![]() $H_n(0)$
-action switching two entries such that at least one of them lies apart from the
$H_n(0)$
-action switching two entries such that at least one of them lies apart from the
![]() $(i+1)$
st and
$(i+1)$
st and
![]() $(i+2)$
nd columns. Thus there exist
$(i+2)$
nd columns. Thus there exist
![]() $\sigma , \rho \in \Sigma _n$
and
$\sigma , \rho \in \Sigma _n$
and
![]() $k \notin [m_i+2, m_{i+2} - 1]$
such that
$k \notin [m_i+2, m_{i+2} - 1]$
such that
Ignoring the columns filled with entries
![]() $[m_i+2, m_{i+2}]$
, we can see that all
$[m_i+2, m_{i+2}]$
, we can see that all
![]() $\pi _{\rho } \cdot \boldsymbol {\tau }_{(i)}$
,
$\pi _{\rho } \cdot \boldsymbol {\tau }_{(i)}$
,
![]() $\tau ^{(1)}$
and
$\tau ^{(1)}$
and
![]() $\tau ^{(2)}$
are the same. This implies that
$\tau ^{(2)}$
are the same. This implies that
![]() $\pi _k \cdot \tau ^{(j)} = s_k \cdot \tau ^{(j)}$
for
$\pi _k \cdot \tau ^{(j)} = s_k \cdot \tau ^{(j)}$
for
![]() $j = 1,2$
. In all, we have
$j = 1,2$
. In all, we have
 $$ \begin{align*} f(\tau) &= \pi_{\sigma} \pi_k \pi_{\rho} \cdot f(\boldsymbol{\tau}_{(i)})\\ &= \pi_{\sigma} \pi_k \pi_{\rho} \cdot \left( \sum_{\tau \in \mathrm{SRT}(\beta^{(1)})} c_{\tau} \tau + \sum_{\tau \in \mathrm{SRT}(\beta^{(2)})} d_{\tau} \tau \right) \\ &= \sum_{\substack{\tau \in \mathrm{SRT}(\beta^{(1)}) \\ \tau> \tau^{(1)} }} c^{\prime}_{\tau} \tau + \sum_{\substack{\tau \in \mathrm{SRT}(\beta^{(2)}) \\ \tau > \tau^{(2)} }} d^{\prime}_{\tau} \tau \end{align*} $$
$$ \begin{align*} f(\tau) &= \pi_{\sigma} \pi_k \pi_{\rho} \cdot f(\boldsymbol{\tau}_{(i)})\\ &= \pi_{\sigma} \pi_k \pi_{\rho} \cdot \left( \sum_{\tau \in \mathrm{SRT}(\beta^{(1)})} c_{\tau} \tau + \sum_{\tau \in \mathrm{SRT}(\beta^{(2)})} d_{\tau} \tau \right) \\ &= \sum_{\substack{\tau \in \mathrm{SRT}(\beta^{(1)}) \\ \tau> \tau^{(1)} }} c^{\prime}_{\tau} \tau + \sum_{\substack{\tau \in \mathrm{SRT}(\beta^{(2)}) \\ \tau > \tau^{(2)} }} d^{\prime}_{\tau} \tau \end{align*} $$
for some
![]() $c^{\prime }_{\tau }, d^{\prime }_{\tau } \in \mathbb C$
. This implies that
$c^{\prime }_{\tau }, d^{\prime }_{\tau } \in \mathbb C$
. This implies that
![]() $f(\tau ) \in \mathrm {rad}(\mathbf {P}_{\beta ^{(1)}} \oplus \mathbf {P}_{\beta ^{(2)}})$
, and hence
$f(\tau ) \in \mathrm {rad}(\mathbf {P}_{\beta ^{(1)}} \oplus \mathbf {P}_{\beta ^{(2)}})$
, and hence
![]() $\tau \in \mathrm {rad}(\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}})$
.
$\tau \in \mathrm {rad}(\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}})$
.
By virtue of the above discussion, to complete our assertion, it is enough to show that
![]() $\ker (\partial _1^{(i)}) \subseteq \mathbb C [\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]^{\mathrm {c}}$
, or equivalently,
$\ker (\partial _1^{(i)}) \subseteq \mathbb C [\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]^{\mathrm {c}}$
, or equivalently,
![]() $L(\tau ) \in \mathrm {SRT}(\alpha )$
for every
$L(\tau ) \in \mathrm {SRT}(\alpha )$
for every
![]() $\tau \in [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}]$
. But this is obvious since
$\tau \in [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}]$
. But this is obvious since
![]() $L(\tau )_i^1 = \tau _i^2 = m_{i-1}+2$
,
$L(\tau )_i^1 = \tau _i^2 = m_{i-1}+2$
,
![]() $L(\tau )_{i+1}^1 = \tau _{i}^{1} = m_{i-1}+1$
and
$L(\tau )_{i+1}^1 = \tau _{i}^{1} = m_{i-1}+1$
and
![]() $L(\tau )_{i+1}^{-1}, L(\tau )_{i+2}^{-1} \in [m_i+2, m_{i+2}]$
.
$L(\tau )_{i+1}^{-1}, L(\tau )_{i+2}^{-1} \in [m_i+2, m_{i+2}]$
.
We are now in place to prove Theorem 3.3.
Proof of Theorem 3.3.
(a) As mentioned after the proof of Lemma 6.3,
![]() $\partial _1: \bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow \Omega (\mathcal {V}_{\alpha })$
is a surjective
$\partial _1: \bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \rightarrow \Omega (\mathcal {V}_{\alpha })$
is a surjective
![]() $H_n(0)$
-module homomorphism. Therefore, we only need to check
$H_n(0)$
-module homomorphism. Therefore, we only need to check
![]() $\ker (\partial _1) \subseteq \mathrm {rad} \left (\bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \right )$
to complete the proof of the assertion. Let
$\ker (\partial _1) \subseteq \mathrm {rad} \left (\bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \right )$
to complete the proof of the assertion. Let
In the proof of Lemma 6.4, we see that
![]() $[\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]^{\mathrm {c}} \subseteq \mathrm {rad} \, \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
for
$[\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]^{\mathrm {c}} \subseteq \mathrm {rad} \, \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
for
![]() $i \in \mathcal {I}(\alpha )$
and thus
$i \in \mathcal {I}(\alpha )$
and thus
![]() $\mathbf {B} \subseteq \mathrm {rad} \left (\bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \right )$
.
$\mathbf {B} \subseteq \mathrm {rad} \left (\bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}} \right )$
.
In the following, we will prove
![]() $\ker (\partial _1) \subseteq \mathbf {B}$
, which is obviously a stronger inclusion than necessary. We begin by collecting the following properties, which were shown in the proof of Lemma 6.4: For all
$\ker (\partial _1) \subseteq \mathbf {B}$
, which is obviously a stronger inclusion than necessary. We begin by collecting the following properties, which were shown in the proof of Lemma 6.4: For all
![]() $i \in \mathcal {I}(\alpha )$
,
$i \in \mathcal {I}(\alpha )$
,
![]() $1\le j < i$
and
$1\le j < i$
and
![]() $\tau \in [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}]$
,
$\tau \in [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}]$
,
 $$ \begin{align*} &\ker(\partial_1^{(i)}) \subseteq \mathbb C[\boldsymbol{\tau}_{(i)}, \hat{\boldsymbol{\tau}}_{(i)}]^{\mathrm{c}},\\ &\partial_1^{(i)}(\tau)_i^1 = m_{i-1}+2\, \text{ and} \\ &\partial_1^{(i)}(\tau)_j^1 = m_{j-1} +1. \end{align*} $$
$$ \begin{align*} &\ker(\partial_1^{(i)}) \subseteq \mathbb C[\boldsymbol{\tau}_{(i)}, \hat{\boldsymbol{\tau}}_{(i)}]^{\mathrm{c}},\\ &\partial_1^{(i)}(\tau)_i^1 = m_{i-1}+2\, \text{ and} \\ &\partial_1^{(i)}(\tau)_j^1 = m_{j-1} +1. \end{align*} $$
Therefore, for any
![]() $i, j \in \mathcal {I}(\alpha )$
with
$i, j \in \mathcal {I}(\alpha )$
with
![]() $j < i$
, if
$j < i$
, if
![]() $\tau \in [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}] \subset \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
and
$\tau \in [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}] \subset \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}$
and
![]() $\tau ' \in [\boldsymbol {\tau }_{(j)},\hat {\boldsymbol {\tau }}_{(j)}] \subset \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(j)}}$
, then
$\tau ' \in [\boldsymbol {\tau }_{(j)},\hat {\boldsymbol {\tau }}_{(j)}] \subset \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(j)}}$
, then
![]() $\partial _1(\tau )_j^1 = \partial _1^{(i)} (\tau )_j^1 = m_{j-1} + 1$
and
$\partial _1(\tau )_j^1 = \partial _1^{(i)} (\tau )_j^1 = m_{j-1} + 1$
and
![]() $\partial _1(\tau ')_j^1 = \partial _1^{(j)} (\tau ')_j^1 = m_{j-1} + 2$
: that is,
$\partial _1(\tau ')_j^1 = \partial _1^{(j)} (\tau ')_j^1 = m_{j-1} + 2$
: that is,
![]() $\partial _1(\tau ) \neq \partial _1(\tau ')$
. This implies that that the set
$\partial _1(\tau ) \neq \partial _1(\tau ')$
. This implies that that the set
![]() $\{\partial _1(\tau ) \mid \tau \in [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}] \text { for } i \in \mathcal {I}(\alpha )\}$
is linearly independent, hence every
$\{\partial _1(\tau ) \mid \tau \in [\boldsymbol {\tau }_{(i)},\hat {\boldsymbol {\tau }}_{(i)}] \text { for } i \in \mathcal {I}(\alpha )\}$
is linearly independent, hence every
![]() $\mathbf {x} \in \ker (\partial _1) \setminus \{0\}$
is decomposed as
$\mathbf {x} \in \ker (\partial _1) \setminus \{0\}$
is decomposed as
![]() $\mathbf {x} = \mathbf {x}^{(1)} + \mathbf {x}^{(2)}$
for some
$\mathbf {x} = \mathbf {x}^{(1)} + \mathbf {x}^{(2)}$
for some
![]() $\mathbf {x}^{(1)} \in \mathbf {T}$
and
$\mathbf {x}^{(1)} \in \mathbf {T}$
and
![]() $\mathbf {x}^{(2)} \in \mathbf {B} \setminus \{0\}$
.
$\mathbf {x}^{(2)} \in \mathbf {B} \setminus \{0\}$
.
We claim that
![]() $\mathbf {x}^{(1)} = 0$
. Suppose on the contrary that
$\mathbf {x}^{(1)} = 0$
. Suppose on the contrary that
![]() $\mathbf {x}^{(1)} \neq 0$
. Let
$\mathbf {x}^{(1)} \neq 0$
. Let
Since
![]() $\partial _1(\mathbf {x}^{(1)}) \neq 0$
, there exists
$\partial _1(\mathbf {x}^{(1)}) \neq 0$
, there exists
![]() $T \in \mathrm {SRT}(\alpha ) \cap \Omega (\mathcal {V}_{\alpha })$
such that
$T \in \mathrm {SRT}(\alpha ) \cap \Omega (\mathcal {V}_{\alpha })$
such that
![]() $c_{T} \neq 0$
. In addition, since
$c_{T} \neq 0$
. In addition, since
![]() $\mathrm {SRT}(\alpha ) \cap \Omega (\mathcal {V}_{\alpha }) $
is linearly independent and
$\mathrm {SRT}(\alpha ) \cap \Omega (\mathcal {V}_{\alpha }) $
is linearly independent and
![]() $\partial _1(\mathbf {x}) = 0$
, we have
$\partial _1(\mathbf {x}) = 0$
, we have
![]() $c_{T} = -d_{T}$
. Therefore, there exist
$c_{T} = -d_{T}$
. Therefore, there exist
![]() $i,j \in \mathcal {I}(\alpha )$
,
$i,j \in \mathcal {I}(\alpha )$
,
![]() $\tau _{\mathbf {T}} \in [\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]$
and
$\tau _{\mathbf {T}} \in [\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]$
and
![]() $\tau _{\mathbf {B}} \in [\boldsymbol {\tau }_{(j)}, \hat {\boldsymbol {\tau }}_{(j)}]^{\mathrm {c}}$
such that
$\tau _{\mathbf {B}} \in [\boldsymbol {\tau }_{(j)}, \hat {\boldsymbol {\tau }}_{(j)}]^{\mathrm {c}}$
such that
![]() $\partial _1(\tau _{\mathbf {T}}) = T = \partial _1(\tau _{\mathbf {B}})$
. Since
$\partial _1(\tau _{\mathbf {T}}) = T = \partial _1(\tau _{\mathbf {B}})$
. Since
![]() $\{\partial _1(\tau ) \mid \tau \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})\} \setminus \{0\}$
is linearly independent, we have
$\{\partial _1(\tau ) \mid \tau \in \mathrm {SRT}({\boldsymbol {\unicode{x3b1} }}^{(i)})\} \setminus \{0\}$
is linearly independent, we have
![]() $i \neq j$
. Note that
$i \neq j$
. Note that
![]() $\partial _1(\tau _{\mathbf {B}}) = \partial _1^{(j)}(\tau _{\mathbf {B}}) \in H_n(0)\cdot T^{(j)}_{\alpha }$
. By Lemma 6.2, we have
$\partial _1(\tau _{\mathbf {B}}) = \partial _1^{(j)}(\tau _{\mathbf {B}}) \in H_n(0)\cdot T^{(j)}_{\alpha }$
. By Lemma 6.2, we have
![]() $T_j^1> T_{j+1}^1$
. On the other hand, since
$T_j^1> T_{j+1}^1$
. On the other hand, since
![]() $T = \partial _1^{(i)}(\tau _{\mathbf {T}})$
and
$T = \partial _1^{(i)}(\tau _{\mathbf {T}})$
and
![]() $\tau _{\mathbf {T}} \in [\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]$
, T is equal to
$\tau _{\mathbf {T}} \in [\boldsymbol {\tau }_{(i)}, \hat {\boldsymbol {\tau }}_{(i)}]$
, T is equal to
![]() $T^{(i)}_{\alpha }$
except for the
$T^{(i)}_{\alpha }$
except for the
![]() $(i+1)$
st and
$(i+1)$
st and
![]() $(i+2)$
nd columns. Note that the
$(i+2)$
nd columns. Note that the
![]() $(i+1)$
st and
$(i+1)$
st and
![]() $(i+2)$
nd columns of them are filled with
$(i+2)$
nd columns of them are filled with
![]() $\{ (\tau _{\mathbf {T}})_i^1 \} \cup [m_i+2, m_{i+2}]$
and
$\{ (\tau _{\mathbf {T}})_i^1 \} \cup [m_i+2, m_{i+2}]$
and
![]() $T_{i+1}^1 = \partial _1^{(i)}(\tau _{\mathbf {T}})_{i+1}^1 = m_{i-1} + 1$
. This shows that
$T_{i+1}^1 = \partial _1^{(i)}(\tau _{\mathbf {T}})_{i+1}^1 = m_{i-1} + 1$
. This shows that
![]() $T_j^1 < T_{j+1}^1$
, which is absurd. Hence
$T_j^1 < T_{j+1}^1$
, which is absurd. Hence
![]() $\mathbf {x}^{(1)} = 0$
, and it follows that
$\mathbf {x}^{(1)} = 0$
, and it follows that
![]() $\ker (\partial _1) \subseteq \mathbf {B}$
, as required.
$\ker (\partial _1) \subseteq \mathbf {B}$
, as required.
(b) For all
![]() $\beta \models n$
, it is known that
$\beta \models n$
, it is known that
with
![]() $P_1:=\displaystyle { \bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}}$
(for instance, see [Reference Benson3, Corollary 2.5.4]). In the case with projective indecomposable modules, one has that
$P_1:=\displaystyle { \bigoplus _{i \in \mathcal {I}(\alpha )} \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}^{(i)}}}$
(for instance, see [Reference Benson3, Corollary 2.5.4]). In the case with projective indecomposable modules, one has that
![]() $\dim \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\gamma },\mathbf {F}_{\gamma '})=\delta _{\gamma ,\gamma '}$
for all
$\dim \mathrm {Hom}_{H_n(0)}(\mathbf {P}_{\gamma },\mathbf {F}_{\gamma '})=\delta _{\gamma ,\gamma '}$
for all
![]() $\gamma , \gamma ' \models n$
(see [Reference Benson3, Lemma 1.7.5]). This tells us that
$\gamma , \gamma ' \models n$
(see [Reference Benson3, Lemma 1.7.5]). This tells us that
![]() $\dim \mathrm {Ext}_{H_n(0)}^1(\mathcal {V}_{\alpha },\mathbf {F}_{\beta })$
counts the multiplicity of
$\dim \mathrm {Ext}_{H_n(0)}^1(\mathcal {V}_{\alpha },\mathbf {F}_{\beta })$
counts the multiplicity of
![]() $\mathbf {P}_{\beta }$
in the decomposition of
$\mathbf {P}_{\beta }$
in the decomposition of
![]() $P_1$
into indecomposables. The indecomposables that occur in the decomposition are precisely
$P_1$
into indecomposables. The indecomposables that occur in the decomposition are precisely
![]() $\mathbf {P}_{\beta }$
with
$\mathbf {P}_{\beta }$
with
![]() $\beta \in \mathcal {J}(\alpha )$
. We claim that all of them are multiplicity-free. For
$\beta \in \mathcal {J}(\alpha )$
. We claim that all of them are multiplicity-free. For
![]() $i \in \mathcal {I}(\alpha )$
, note that
$i \in \mathcal {I}(\alpha )$
, note that
![]() $[{\boldsymbol {\unicode{x3b1} }}^{(i)}]=\{\beta ^{(1)}, \beta ^{(2)}\}$
with
$[{\boldsymbol {\unicode{x3b1} }}^{(i)}]=\{\beta ^{(1)}, \beta ^{(2)}\}$
with
![]() $\beta ^{(1)}, \beta ^{(2)}$
in equation (6.3). Obviously
$\beta ^{(1)}, \beta ^{(2)}$
in equation (6.3). Obviously
![]() $\beta ^{(1)}$
and
$\beta ^{(1)}$
and
![]() $\beta ^{(2)}$
are distinct. Furthermore, for
$\beta ^{(2)}$
are distinct. Furthermore, for
![]() $i<j$
,
$i<j$
,
![]() $[{\boldsymbol {\unicode{x3b1} }}^{(i)}]$
and
$[{\boldsymbol {\unicode{x3b1} }}^{(i)}]$
and
![]() $[{\boldsymbol {\unicode{x3b1} }}^{(j)}]$
are disjoint since the ith entry of the compositions in the former is
$[{\boldsymbol {\unicode{x3b1} }}^{(j)}]$
are disjoint since the ith entry of the compositions in the former is
![]() $\alpha _i+1$
, whereas that of the compositions in the latter is
$\alpha _i+1$
, whereas that of the compositions in the latter is
![]() $\alpha _i$
. Hence the claim is verified, which completes the proof.
$\alpha _i$
. Hence the claim is verified, which completes the proof.
6.2 Proof of Theorem 4.1
We begin by introducing the necessary terminologies, notations and lemmas. First, we recall the notation related to parabolic subgroups of
![]() $\Sigma _n$
. For each subset I of
$\Sigma _n$
. For each subset I of
![]() $[n-1]$
, we write
$[n-1]$
, we write
![]() $(\Sigma _n)_I$
for the parabolic subgroup of
$(\Sigma _n)_I$
for the parabolic subgroup of
![]() $\Sigma _n$
generated by simple transpositions
$\Sigma _n$
generated by simple transpositions
![]() $s_i$
with
$s_i$
with
![]() $i\in I$
and
$i\in I$
and
![]() $w_0(I)$
for the longest element of
$w_0(I)$
for the longest element of
![]() $(\Sigma _n)_I$
. When I is a subinterval
$(\Sigma _n)_I$
. When I is a subinterval
![]() $[k_1,k_2]$
of
$[k_1,k_2]$
of
![]() $[n-1]$
and
$[n-1]$
and
![]() $c \in I$
, we write
$c \in I$
, we write
![]() $(\Sigma _n)_I^{(c)}$
for
$(\Sigma _n)_I^{(c)}$
for
 $$ \begin{align*} \left\{ \sigma \in (\Sigma_{n})_I \, \middle| \, \genfrac{}{}{0pt}{}{ \ \sigma(k_1) < \sigma(k_1 + 1) < \cdots < \sigma(c) \text{ and} }{\sigma(c + 1) < \sigma(c + 2) < \cdots < \sigma(k_2+1)} \right\} \end{align*} $$
$$ \begin{align*} \left\{ \sigma \in (\Sigma_{n})_I \, \middle| \, \genfrac{}{}{0pt}{}{ \ \sigma(k_1) < \sigma(k_1 + 1) < \cdots < \sigma(c) \text{ and} }{\sigma(c + 1) < \sigma(c + 2) < \cdots < \sigma(k_2+1)} \right\} \end{align*} $$
and
![]() $w_0(I;c)$
for the longest element of
$w_0(I;c)$
for the longest element of
![]() $(\Sigma _n)_I^{(c)}$
(see [Reference Björner and Brenti8, Chapter 2]).
$(\Sigma _n)_I^{(c)}$
(see [Reference Björner and Brenti8, Chapter 2]).
Next, we introduce the sink tableau of
![]() $\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
. Given a generalised composition
$\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
. Given a generalised composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
of n,
${\boldsymbol {\unicode{x3b1} }}$
of n,
![]() $\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
contains a unique tableau T such that
$\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
contains a unique tableau T such that
![]() $\pi _i \cdot T = 0$
or T for all
$\pi _i \cdot T = 0$
or T for all
![]() $i \in [n-1]$
. We call it the sink tableau of
$i \in [n-1]$
. We call it the sink tableau of
![]() $\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
, denoted by
$\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
, denoted by
![]() $T^{\leftarrow }_{\boldsymbol {\unicode{x3b1} }}$
. Explicitly,
$T^{\leftarrow }_{\boldsymbol {\unicode{x3b1} }}$
. Explicitly,
![]() $T^{\leftarrow }_{\boldsymbol {\unicode{x3b1} }}$
is obtained by filling in
$T^{\leftarrow }_{\boldsymbol {\unicode{x3b1} }}$
is obtained by filling in
![]() $\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
with entries
$\mathtt {rd}({\boldsymbol {\unicode{x3b1} }})$
with entries
![]() $1, 2, \ldots , n$
from left to right and from top to bottom. Let us define a bijection
$1, 2, \ldots , n$
from left to right and from top to bottom. Let us define a bijection
 $$\begin{align*}\chi_{\boldsymbol{\unicode{x3b1}}}: \mathrm{SRT}({\boldsymbol{\unicode{x3b1}}}) \rightarrow \bigcup_{\beta \in [{\boldsymbol{\unicode{x3b1}}}]} \mathrm{SRT}(\beta), \quad T \mapsto T', \end{align*}$$
$$\begin{align*}\chi_{\boldsymbol{\unicode{x3b1}}}: \mathrm{SRT}({\boldsymbol{\unicode{x3b1}}}) \rightarrow \bigcup_{\beta \in [{\boldsymbol{\unicode{x3b1}}}]} \mathrm{SRT}(\beta), \quad T \mapsto T', \end{align*}$$
where
![]() $T'$
is uniquely determined by the condition
$T'$
is uniquely determined by the condition
![]() $\mathbf {w}(T) = \mathbf {w}(T')$
. With this bijection, we define
$\mathbf {w}(T) = \mathbf {w}(T')$
. With this bijection, we define
For
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}]$
, we let
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}]$
, we let
For each
![]() $1 \le i \le n-1$
, let
$1 \le i \le n-1$
, let
![]() $\overline {\pi }_i := \pi _i -1$
. Pick up any reduced expression
$\overline {\pi }_i := \pi _i -1$
. Pick up any reduced expression
![]() $s_{i_1}\cdots s_{i_p}$
for
$s_{i_1}\cdots s_{i_p}$
for
![]() $\sigma \in \Sigma _n$
. Let
$\sigma \in \Sigma _n$
. Let
![]() $\overline {\pi }_{\sigma }$
be the element of
$\overline {\pi }_{\sigma }$
be the element of
![]() $H_n(0)$
defined by
$H_n(0)$
defined by
![]() $\overline {\pi }_{\sigma } := \overline {\pi }_{i_1} \cdots \overline {\pi }_{i_p}$
. It is well known that the element
$\overline {\pi }_{\sigma } := \overline {\pi }_{i_1} \cdots \overline {\pi }_{i_p}$
. It is well known that the element
![]() $\overline {\pi }_{\sigma }$
is independent of the choice of reduced expressions.
$\overline {\pi }_{\sigma }$
is independent of the choice of reduced expressions.
Lemma 6.5 [Reference Jung, Kim, Lee and Oh21, Lemma 3 (1)].
For any
![]() $\sigma , \rho \in \Sigma _n$
,
$\sigma , \rho \in \Sigma _n$
,
![]() $\pi _{\sigma } \overline {\pi }_{\rho }$
is nonzero if and only if
$\pi _{\sigma } \overline {\pi }_{\rho }$
is nonzero if and only if
![]() $\ell (\sigma \rho ) = \ell (\sigma ) + \ell (\rho )$
.
$\ell (\sigma \rho ) = \ell (\sigma ) + \ell (\rho )$
.
The following lemma gives an explicit description for
![]() $\mathrm {soc}(\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}})$
.
$\mathrm {soc}(\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}})$
.
Lemma 6.6. For
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}]$
,
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}]$
,
![]() $\mathbb C T^{\leftarrow }_{\beta }$
is isomorphic to
$\mathbb C T^{\leftarrow }_{\beta }$
is isomorphic to
![]() $\mathbb C\left ( \overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}\right )$
as an
$\mathbb C\left ( \overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}\right )$
as an
![]() $H_n(0)$
-module.
$H_n(0)$
-module.
Proof. First, we claim that
![]() $\overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
is stabilised under the action of
$\overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
is stabilised under the action of
![]() $\pi _i$
for all
$\pi _i$
for all
![]() $i \in \mathrm {Des}(T_{\beta }^{\leftarrow })^{\mathrm {c}}$
. Note that
$i \in \mathrm {Des}(T_{\beta }^{\leftarrow })^{\mathrm {c}}$
. Note that
![]() $\overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
is of the form
$\overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
is of the form
 $$ \begin{align} \sum_{T \in [{T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}}, T_{\underline{{\boldsymbol{\unicode{x3b1}}}}}^{\leftarrow}]} c_T T \quad \text{for some } c_T \in {\mathbb Z}. \end{align} $$
$$ \begin{align} \sum_{T \in [{T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}}, T_{\underline{{\boldsymbol{\unicode{x3b1}}}}}^{\leftarrow}]} c_T T \quad \text{for some } c_T \in {\mathbb Z}. \end{align} $$
But from the definitions of
![]() ${T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
and
${T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
and
![]() $T_{\underline {{\boldsymbol {\unicode{x3b1} }}}}^{\leftarrow }$
, it follows that
$T_{\underline {{\boldsymbol {\unicode{x3b1} }}}}^{\leftarrow }$
, it follows that
![]() $\pi _i \cdot T = T$
for
$\pi _i \cdot T = T$
for
![]() $i \in \mathrm {Des}(T_{\beta }^{\leftarrow })^{\mathrm {c}}$
. Thus our claim is verified.
$i \in \mathrm {Des}(T_{\beta }^{\leftarrow })^{\mathrm {c}}$
. Thus our claim is verified.
Next, we claim that
![]() $\pi _i \cdot (\overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}) = 0$
for all
$\pi _i \cdot (\overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}) = 0$
for all
![]() $i \in \mathrm {Des}(T_{\beta }^{\leftarrow })$
. Take any
$i \in \mathrm {Des}(T_{\beta }^{\leftarrow })$
. Take any
![]() $i \in \mathrm {Des}(T_{\beta }^{\leftarrow })$
. Note that
$i \in \mathrm {Des}(T_{\beta }^{\leftarrow })$
. Note that
![]() $T(\mathtt {S}_{k_0}) = \{1,2,\ldots ,\ell (\alpha )\}$
for any
$T(\mathtt {S}_{k_0}) = \{1,2,\ldots ,\ell (\alpha )\}$
for any
![]() $T \in [{T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}, T_{\underline {{\boldsymbol {\unicode{x3b1} }}}}^{\leftarrow }]$
. Therefore, if
$T \in [{T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}, T_{\underline {{\boldsymbol {\unicode{x3b1} }}}}^{\leftarrow }]$
. Therefore, if
![]() $1 \leq i < \ell (\alpha )$
, then
$1 \leq i < \ell (\alpha )$
, then
![]() $\pi _i \overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}} = 0$
by equation (6.4). In the case where
$\pi _i \overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}} = 0$
by equation (6.4). In the case where
![]() $i \ge \ell (\alpha )$
,
$i \ge \ell (\alpha )$
,
![]() $i \in \mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}$
and thus
$i \in \mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}$
and thus
![]() $\pi _i \overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})}= 0$
by Lemma 6.5.
$\pi _i \overline {\pi }_{w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}})}= 0$
by Lemma 6.5.
Example 6.7. Given
![]() $\alpha = (2^3)$
, let
$\alpha = (2^3)$
, let
![]() $\beta = (1^2,2,1^2)$
and
$\beta = (1^2,2,1^2)$
and
![]() $\gamma = (2^2,1^2)$
be compositions in
$\gamma = (2^2,1^2)$
be compositions in
![]() $[\underline {{\boldsymbol {\unicode{x3b1} }}}] = [(1) \oplus (1) \oplus (2,1^2)]$
. Note that
$[\underline {{\boldsymbol {\unicode{x3b1} }}}] = [(1) \oplus (1) \oplus (2,1^2)]$
. Note that

Since
![]() $\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}} = \{4,5\}$
and
$\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}} = \{4,5\}$
and
![]() $\mathtt {J}_{\gamma ;\underline {{\boldsymbol {\unicode{x3b1} }}}} = \{4\}$
, it follows that
$\mathtt {J}_{\gamma ;\underline {{\boldsymbol {\unicode{x3b1} }}}} = \{4\}$
, it follows that
![]() $w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}) = s_4 s_5 s_4$
and
$w_0(\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}) = s_4 s_5 s_4$
and
![]() $w_0(\mathtt {J}_{\gamma ;\underline {{\boldsymbol {\unicode{x3b1} }}}}) = s_4 $
. Thus we have
$w_0(\mathtt {J}_{\gamma ;\underline {{\boldsymbol {\unicode{x3b1} }}}}) = s_4 $
. Thus we have

Proof of Theorem 4.1.
We first claim that
![]() $\epsilon : \mathcal {V}_{\alpha } \to \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
is an
$\epsilon : \mathcal {V}_{\alpha } \to \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
is an
![]() $H_n(0)$
-module homomorphism: that is,
$H_n(0)$
-module homomorphism: that is,
Let us fix
![]() $1 \le i \le n-1$
and
$1 \le i \le n-1$
and
![]() $\mathscr {T} \in \mathrm {SIT}(\alpha )$
. Let
$\mathscr {T} \in \mathrm {SIT}(\alpha )$
. Let
![]() $0 \leq x, y \leq m$
be integers satisfying that
$0 \leq x, y \leq m$
be integers satisfying that
![]() $i \in \mathscr {T}(\mathtt {S}_{k_x})$
and
$i \in \mathscr {T}(\mathtt {S}_{k_x})$
and
![]() $i+1 \in \mathscr {T}(\mathtt {S}_{k_y})$
.
$i+1 \in \mathscr {T}(\mathtt {S}_{k_y})$
.
Case 1:
![]() $\pi _i \cdot \mathscr {T} = \mathscr {T}$
. First we handle the case where
$\pi _i \cdot \mathscr {T} = \mathscr {T}$
. First we handle the case where
![]() $x=0$
. Then i will be placed in the top row in
$x=0$
. Then i will be placed in the top row in
![]() ${T^{\mathscr {T}}}$
. In view of the given condition
${T^{\mathscr {T}}}$
. In view of the given condition
![]() $\pi _i \cdot \mathscr {T} = \mathscr {T}$
, one sees that
$\pi _i \cdot \mathscr {T} = \mathscr {T}$
, one sees that
![]() $x \neq y$
. This implies that
$x \neq y$
. This implies that
![]() $i+1$
is strictly below i in
$i+1$
is strictly below i in
![]() ${T^{\mathscr {T}}}$
. Next we handle the case where
${T^{\mathscr {T}}}$
. Next we handle the case where
![]() $x>0$
. The condition
$x>0$
. The condition
![]() $\pi _i \cdot \mathscr {T} = \mathscr {T}$
says that
$\pi _i \cdot \mathscr {T} = \mathscr {T}$
says that
![]() $0 < x \leq y$
; thus
$0 < x \leq y$
; thus
![]() $i+1$
is strictly below i in
$i+1$
is strictly below i in
![]() ${T^{\mathscr {T}}}$
. In either case, it is immediate from equation (2.1) that
${T^{\mathscr {T}}}$
. In either case, it is immediate from equation (2.1) that
![]() $\pi _i \cdot {T^{\mathscr {T}}} = {T^{\mathscr {T}}}$
.
$\pi _i \cdot {T^{\mathscr {T}}} = {T^{\mathscr {T}}}$
.
Case 2:
![]() $\pi _i \cdot \mathscr {T} = 0$
. From equation (2.2), it follows that i and
$\pi _i \cdot \mathscr {T} = 0$
. From equation (2.2), it follows that i and
![]() $i+1$
are in the first column in
$i+1$
are in the first column in
![]() $\mathscr {T}$
: that is,
$\mathscr {T}$
: that is,
![]() $x = y = 0$
. Hence, in
$x = y = 0$
. Hence, in
![]() ${T^{\mathscr {T}}}$
, both of them will appear in
${T^{\mathscr {T}}}$
, both of them will appear in
![]() ${T^{\mathscr {T}}}(\mathtt {S}_{k_0})$
. As in Case 1, one can derive from equation (2.1) that
${T^{\mathscr {T}}}(\mathtt {S}_{k_0})$
. As in Case 1, one can derive from equation (2.1) that
![]() $\pi _i \cdot {T^{\mathscr {T}}} = 0$
.
$\pi _i \cdot {T^{\mathscr {T}}} = 0$
.
Case 3:
![]() $\pi _i \cdot \mathscr {T} = s_i \cdot \mathscr {T}$
. We claim that
$\pi _i \cdot \mathscr {T} = s_i \cdot \mathscr {T}$
. We claim that
![]() $\epsilon (s_i \cdot \mathscr {T}) = s_i \cdot {T^{\mathscr {T}}}$
. Observe that i appears strictly above
$\epsilon (s_i \cdot \mathscr {T}) = s_i \cdot {T^{\mathscr {T}}}$
. Observe that i appears strictly above
![]() $i+1$
in
$i+1$
in
![]() $\mathscr {T}$
. If
$\mathscr {T}$
. If
![]() $i+1 \in \mathscr {T}(\mathtt {S}_{k_0})$
, then we see that
$i+1 \in \mathscr {T}(\mathtt {S}_{k_0})$
, then we see that
![]() $i \notin \mathscr {T}(\mathtt {S}_{k_0})$
, which means i appears strictly left of
$i \notin \mathscr {T}(\mathtt {S}_{k_0})$
, which means i appears strictly left of
![]() $i+1$
in
$i+1$
in
![]() ${T^{\mathscr {T}}}$
. Otherwise, we also see that
${T^{\mathscr {T}}}$
. Otherwise, we also see that
![]() $i \notin \mathscr {T}(\mathtt {S}_{k_0})$
. More precisely, if
$i \notin \mathscr {T}(\mathtt {S}_{k_0})$
. More precisely, if
![]() $i+1 \notin \mathscr {T}(\mathtt {S}_{k_0})$
and
$i+1 \notin \mathscr {T}(\mathtt {S}_{k_0})$
and
![]() $i \in \mathscr {T}(\mathtt {S}_{k_0})$
, then
$i \in \mathscr {T}(\mathtt {S}_{k_0})$
, then
![]() $\mathscr {T}$
is not an SIT since the entries in the row containing
$\mathscr {T}$
is not an SIT since the entries in the row containing
![]() $i+1$
of
$i+1$
of
![]() $\mathscr {T}$
do not increase from left to right. It follows from the construction of
$\mathscr {T}$
do not increase from left to right. It follows from the construction of
![]() ${T^{\mathscr {T}}}$
that i is strictly below
${T^{\mathscr {T}}}$
that i is strictly below
![]() $i+1$
in
$i+1$
in
![]() ${T^{\mathscr {T}}}$
. In either case, it holds that
${T^{\mathscr {T}}}$
. In either case, it holds that
![]() $T^{s_i \cdot \mathscr {T}} = s_i \cdot {T^{\mathscr {T}}}$
. Thus we conclude that
$T^{s_i \cdot \mathscr {T}} = s_i \cdot {T^{\mathscr {T}}}$
. Thus we conclude that
We next claim that
![]() $\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
is an essential extension of
$\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}$
is an essential extension of
![]() $\epsilon (\mathcal {V}_{\alpha })$
. To do this, we see that
$\epsilon (\mathcal {V}_{\alpha })$
. To do this, we see that
![]() $\mathrm {soc}(\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}) \subset \epsilon (\mathcal {V}_{\alpha })$
. Note that
$\mathrm {soc}(\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}) \subset \epsilon (\mathcal {V}_{\alpha })$
. Note that
 $$ \begin{align*} \mathrm{soc}(\mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}}) \cong \mathrm{soc} \Big(\bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}]} \mathbf{P}_{\beta} \Big) \cong \bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}]} \mathbb C T^{\leftarrow}_{\beta}. \end{align*} $$
$$ \begin{align*} \mathrm{soc}(\mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}}) \cong \mathrm{soc} \Big(\bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}]} \mathbf{P}_{\beta} \Big) \cong \bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}]} \mathbb C T^{\leftarrow}_{\beta}. \end{align*} $$
In view of Lemma 6.6, one sees that
 $$ \begin{align} \mathrm{soc}(\mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}}) = \bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}]} \mathbb C\left( \overline{\pi}_{w_0(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}})} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}}\right). \end{align} $$
$$ \begin{align} \mathrm{soc}(\mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}}) = \bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}]} \mathbb C\left( \overline{\pi}_{w_0(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}})} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}}\right). \end{align} $$
Choose any
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}]$
. Then
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}]$
. Then
 $$ \begin{align*} \overline{\pi}_{w_0(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}})} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}} = \sum_{\sigma \in (\Sigma_n)_{\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}}} (-1)^{\ell(w_0(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}})) - \ell(\sigma)} \pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}}. \end{align*} $$
$$ \begin{align*} \overline{\pi}_{w_0(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}})} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}} = \sum_{\sigma \in (\Sigma_n)_{\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}}} (-1)^{\ell(w_0(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}})) - \ell(\sigma)} \pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}}. \end{align*} $$
For
![]() $\sigma \in (\Sigma _n)_{\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
, since
$\sigma \in (\Sigma _n)_{\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
, since
![]() $(\pi _{\sigma } \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}})(\mathtt {S}_{k_0}) = \{1,2, \ldots , \ell (\alpha )\}$
, we have
$(\pi _{\sigma } \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}})(\mathtt {S}_{k_0}) = \{1,2, \ldots , \ell (\alpha )\}$
, we have
 $$ \begin{align*} (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}})^1_{m+k_j-1} < \begin{cases} (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}})^{1}_j & \text{if } 1 \leq j < m, \\[1ex] (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}})^{2}_j & \text{if } j = m. \end{cases} \end{align*} $$
$$ \begin{align*} (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}})^1_{m+k_j-1} < \begin{cases} (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}})^{1}_j & \text{if } 1 \leq j < m, \\[1ex] (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}}})^{2}_j & \text{if } j = m. \end{cases} \end{align*} $$
It means
![]() $\pi _{\sigma } \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}} \in \epsilon (\mathcal {V}_{\alpha })$
for all
$\pi _{\sigma } \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}} \in \epsilon (\mathcal {V}_{\alpha })$
for all
![]() $\sigma \in (\Sigma _n)_{\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
. Combining this with equation (6.5) yields that
$\sigma \in (\Sigma _n)_{\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}}}$
. Combining this with equation (6.5) yields that
![]() $\mathrm {soc}(\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}) \subset \epsilon (\mathcal {V}_{\alpha })$
.
$\mathrm {soc}(\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}}) \subset \epsilon (\mathcal {V}_{\alpha })$
.
6.3 Proof of Theorem 4.3
Throughout this section, let us fix an integer
![]() $1 \le j \le m$
unless otherwise stated.
$1 \le j \le m$
unless otherwise stated.
Let
![]() $T \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
. In the same notation as in Section 4, we claim that
$T \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
. In the same notation as in Section 4, we claim that
This is because if
![]() $T^{1+\delta _{j,m}}_j < T^1_{m+k_j-1}$
, then
$T^{1+\delta _{j,m}}_j < T^1_{m+k_j-1}$
, then
![]() $\textsf {end}(\mathbf {w}_{T;j}) < T^1_{m+k_j-1}$
and therefore
$\textsf {end}(\mathbf {w}_{T;j}) < T^1_{m+k_j-1}$
and therefore
![]() ${\boldsymbol {\tau }}_{T;j} \neq 0$
. Otherwise,
${\boldsymbol {\tau }}_{T;j} \neq 0$
. Otherwise,
![]() ${\boldsymbol {\tau }}_{T;j}$
should be zero since
${\boldsymbol {\tau }}_{T;j}$
should be zero since
![]() $\textsf {end}(\mathbf {w}_{T;j})> T^1_{m+k_j-1}$
.
$\textsf {end}(\mathbf {w}_{T;j})> T^1_{m+k_j-1}$
.
Let
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. Recall that
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. Recall that
![]() ${T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}} = \chi _{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}^{-1}(T^{\leftarrow }_{\beta })$
and
${T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}} = \chi _{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}^{-1}(T^{\leftarrow }_{\beta })$
and
Note that if
![]() $\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \leq \ell (\alpha )$
, then
$\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \leq \ell (\alpha )$
, then
Set
 $$ \begin{align*}\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}:= \begin{cases} \mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}} \setminus \{|\mathtt{S}^{\prime}_{k_0}|\} & \text{if } 1 \leq \min(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}) \leq \ell(\alpha), \\ \mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}} & \text{otherwise,} \end{cases} \end{align*} $$
$$ \begin{align*}\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}:= \begin{cases} \mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}} \setminus \{|\mathtt{S}^{\prime}_{k_0}|\} & \text{if } 1 \leq \min(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}) \leq \ell(\alpha), \\ \mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}} & \text{otherwise,} \end{cases} \end{align*} $$
and
 $$ \begin{align*}\boldsymbol{w_0}(\beta;j):= \begin{cases} w_0([\ell(\alpha)];|\mathtt{S}^{\prime}_{k_0}|) \cdot w_0(\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}) & \text{if } 1 \leq \min(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}) \leq \ell(\alpha), \\ w_0(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}) & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}\boldsymbol{w_0}(\beta;j):= \begin{cases} w_0([\ell(\alpha)];|\mathtt{S}^{\prime}_{k_0}|) \cdot w_0(\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}) & \text{if } 1 \leq \min(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}) \leq \ell(\alpha), \\ w_0(\mathtt{J}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}) & \text{otherwise.} \end{cases} \end{align*} $$
In view of equation (6.7), we know that every element of
![]() $(\Sigma _{n})_{[\ell (\alpha )]}^{(|\mathtt {S}^{\prime }_{k_0}|)}$
commutes with that of
$(\Sigma _{n})_{[\ell (\alpha )]}^{(|\mathtt {S}^{\prime }_{k_0}|)}$
commutes with that of
![]() $(\Sigma _n)_{\widehat {\mathtt { J}}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}$
. The following lemma is necessary to show that
$(\Sigma _n)_{\widehat {\mathtt { J}}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}$
. The following lemma is necessary to show that
![]() $\mathrm {soc}(\bigoplus _{1 \leq j \leq m}\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \subseteq \mathrm {Im}(\overline {\partial ^1})$
.
$\mathrm {soc}(\bigoplus _{1 \leq j \leq m}\mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \subseteq \mathrm {Im}(\overline {\partial ^1})$
.
Lemma 6.8. For
![]() $1 \leq j \leq m$
and
$1 \leq j \leq m$
and
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
,
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
,
![]() $\mathbb C T^{\leftarrow }_{\beta } \cong \mathbb C (\overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}})$
as
$\mathbb C T^{\leftarrow }_{\beta } \cong \mathbb C (\overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}})$
as
![]() $H_n(0)$
-modules.
$H_n(0)$
-modules.
Proof. Let
![]() $1 \leq j \leq m$
and
$1 \leq j \leq m$
and
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. If
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. If
![]() $\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}})> \ell (\alpha )$
, then one can prove the assertion in the same way as in Lemma 6.6. We now assume that
$\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}})> \ell (\alpha )$
, then one can prove the assertion in the same way as in Lemma 6.6. We now assume that
![]() $\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \leq \ell (\alpha )$
. We first show that
$\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \leq \ell (\alpha )$
. We first show that
for
![]() $i \notin \mathrm {Des}(T^{\leftarrow }_{\beta })$
. Since
$i \notin \mathrm {Des}(T^{\leftarrow }_{\beta })$
. Since
 $$ \begin{align*} \overline{\pi}_{\boldsymbol{w_0}(\beta;j)} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} = \sum_{T \in [{T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}, T_{\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}^{\leftarrow}]} c_T T \quad \text{for some } c_T \in \mathbb Z, \end{align*} $$
$$ \begin{align*} \overline{\pi}_{\boldsymbol{w_0}(\beta;j)} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} = \sum_{T \in [{T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}, T_{\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}^{\leftarrow}]} c_T T \quad \text{for some } c_T \in \mathbb Z, \end{align*} $$
it suffices to show that
![]() $\pi _i \cdot T = T$
for
$\pi _i \cdot T = T$
for
![]() $i \notin \mathrm {Des}(T_{\beta }^{\leftarrow })$
and
$i \notin \mathrm {Des}(T_{\beta }^{\leftarrow })$
and
![]() $T \in [{T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}, T_{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}^{\leftarrow }]$
. Since
$T \in [{T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}, T_{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}^{\leftarrow }]$
. Since
![]() $\{1,2,\ldots , \ell (\alpha )\}\subseteq \mathrm {Des}(T^{\leftarrow }_{\beta })$
by definition, we only consider that
$\{1,2,\ldots , \ell (\alpha )\}\subseteq \mathrm {Des}(T^{\leftarrow }_{\beta })$
by definition, we only consider that
![]() $i \geq \ell (\alpha )+1$
. If
$i \geq \ell (\alpha )+1$
. If
![]() $i=\ell (\alpha )+1$
, then the assertion follows from the fact that
$i=\ell (\alpha )+1$
, then the assertion follows from the fact that
![]() $T(\mathtt {S}^{\prime }_{k_0})\cup T(\mathtt {S}^{\prime }_{k_{-1}}) = \{1,2,\ldots ,\ell (\alpha )+1\}$
. Otherwise, from the definitions of
$T(\mathtt {S}^{\prime }_{k_0})\cup T(\mathtt {S}^{\prime }_{k_{-1}}) = \{1,2,\ldots ,\ell (\alpha )+1\}$
. Otherwise, from the definitions of
![]() ${T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}$
and
${T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}$
and
![]() $T_{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}^{\leftarrow }$
, it follows that
$T_{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}^{\leftarrow }$
, it follows that
![]() $\pi _i \cdot T = T$
for
$\pi _i \cdot T = T$
for
![]() $i \notin \mathrm {Des}(T_{\beta }^{\leftarrow })$
. Thus our claim is verified.
$i \notin \mathrm {Des}(T_{\beta }^{\leftarrow })$
. Thus our claim is verified.
We next show that
![]() $\pi _i \cdot (\overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}) = 0$
for
$\pi _i \cdot (\overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}) = 0$
for
![]() $i \in \mathrm {Des}(T^{\leftarrow }_{\beta })$
. Take any
$i \in \mathrm {Des}(T^{\leftarrow }_{\beta })$
. Take any
![]() $i \in \mathrm {Des}(T_{\beta }^{\leftarrow })$
. If
$i \in \mathrm {Des}(T_{\beta }^{\leftarrow })$
. If
![]() $i> \ell (\alpha ) + 1$
, then
$i> \ell (\alpha ) + 1$
, then
![]() $i \in \widehat {\mathtt {J}}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}$
. Therefore, by Lemma 6.5, we have
$i \in \widehat {\mathtt {J}}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}$
. Therefore, by Lemma 6.5, we have
![]() $\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} = 0$
, which implies
$\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} = 0$
, which implies
![]() $\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot T^{\leftarrow }_{\beta ,\underline {{\boldsymbol {\unicode{x3b1} }}}} = 0$
. Suppose that
$\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot T^{\leftarrow }_{\beta ,\underline {{\boldsymbol {\unicode{x3b1} }}}} = 0$
. Suppose that
![]() $i \le \ell (\alpha ) + 1$
. Since
$i \le \ell (\alpha ) + 1$
. Since
![]() $\ell (\alpha ) + 1 \notin \mathrm {Des}(T^{\leftarrow }_{\beta })$
, we have that
$\ell (\alpha ) + 1 \notin \mathrm {Des}(T^{\leftarrow }_{\beta })$
, we have that
![]() $1 \le i \le \ell (\alpha )$
. If
$1 \le i \le \ell (\alpha )$
. If
![]() $i \in \mathrm {Des}_L(\boldsymbol {w_0}(\beta ;j))$
, then
$i \in \mathrm {Des}_L(\boldsymbol {w_0}(\beta ;j))$
, then
![]() $\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} = 0$
. Thus,
$\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} = 0$
. Thus,
![]() $\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot T^{\leftarrow }_{\beta ,\underline {{\boldsymbol {\unicode{x3b1} }}}} = 0$
. Otherwise, we have
$\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot T^{\leftarrow }_{\beta ,\underline {{\boldsymbol {\unicode{x3b1} }}}} = 0$
. Otherwise, we have
![]() $s_i w_0([\ell (\alpha )];|\mathtt {S}^{\prime }_{k_0}|) = \sigma s_{i'}$
for some
$s_i w_0([\ell (\alpha )];|\mathtt {S}^{\prime }_{k_0}|) = \sigma s_{i'}$
for some
![]() $\sigma \in (\Sigma _{n})_{[\ell (\alpha )]}^{(|\mathtt {S}^{\prime }_{k_0}|)}$
and
$\sigma \in (\Sigma _{n})_{[\ell (\alpha )]}^{(|\mathtt {S}^{\prime }_{k_0}|)}$
and
![]() $1\le i' \le \ell (\alpha )$
with
$1\le i' \le \ell (\alpha )$
with
![]() $i' \neq |\mathtt {S}^{\prime }_{k_0}|$
since
$i' \neq |\mathtt {S}^{\prime }_{k_0}|$
since
![]() $w_0([\ell (\alpha )];|\mathtt {S}^{\prime }_{k_0}|)$
is the unique longest element in
$w_0([\ell (\alpha )];|\mathtt {S}^{\prime }_{k_0}|)$
is the unique longest element in
![]() $(\Sigma _{n})_{[\ell (\alpha )]}^{(|\mathtt {S}^{\prime }_{k_0}|)}$
. Combining this with [Reference Jung, Kim, Lee and Oh21, Lemma 1], we have that
$(\Sigma _{n})_{[\ell (\alpha )]}^{(|\mathtt {S}^{\prime }_{k_0}|)}$
. Combining this with [Reference Jung, Kim, Lee and Oh21, Lemma 1], we have that
![]() $\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} = \mathbf {h} \pi _{i'}$
for some
$\pi _i \overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} = \mathbf {h} \pi _{i'}$
for some
![]() $\mathbf {h} \in H_n(0)$
and
$\mathbf {h} \in H_n(0)$
and
![]() $1 \le i' \le \ell (\alpha )$
with
$1 \le i' \le \ell (\alpha )$
with
![]() $i' \neq |\mathtt {S}^{\prime }_{k_0}|$
. Since
$i' \neq |\mathtt {S}^{\prime }_{k_0}|$
. Since
![]() $\pi _{i'} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}} = 0$
for all
$\pi _{i'} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}} = 0$
for all
![]() $1 \le i' \le \ell (\alpha )$
with
$1 \le i' \le \ell (\alpha )$
with
![]() $i' \neq |\mathtt {S}^{\prime }_{k_0}|$
, it follows that
$i' \neq |\mathtt {S}^{\prime }_{k_0}|$
, it follows that
Example 6.9. Let
![]() $\alpha = (2,1,2,3) \models 8$
. Note that
$\alpha = (2,1,2,3) \models 8$
. Note that
![]() $\mathcal {K}(\alpha ) = \{0,1,3,4\}$
and
$\mathcal {K}(\alpha ) = \{0,1,3,4\}$
and
![]() $\ell (\alpha )=4$
. Then
$\ell (\alpha )=4$
. Then
![]() $\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)} = (1) \oplus (3,1^2) \oplus (1^2)$
. Let
$\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)} = (1) \oplus (3,1^2) \oplus (1^2)$
. Let
![]() $\beta = (1,3,1^4)$
and
$\beta = (1,3,1^4)$
and
![]() $\gamma = (1,3,1,2,1)$
in
$\gamma = (1,3,1,2,1)$
in
![]() $[\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)}]$
. Note that
$[\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)}]$
. Note that

Here the entries i in red in each SRT T are being used to indicate that
![]() $\pi _i \cdot T = 0$
. Since
$\pi _i \cdot T = 0$
. Since
![]() $\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)}}) = 3 \le \ell (\alpha )$
and
$\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)}}) = 3 \le \ell (\alpha )$
and
![]() $ \min (\mathtt {J}_{\gamma ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)}}) = 7> \ell (\alpha )$
,
$ \min (\mathtt {J}_{\gamma ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)}}) = 7> \ell (\alpha )$
,
Therefore, by Lemma 6.8, we have
From now on, suppose that
![]() $n \ge 3$
. Fix
$n \ge 3$
. Fix
![]() $l \in [2, n-1]$
and
$l \in [2, n-1]$
and
![]() $c \in [2,l]$
. For
$c \in [2,l]$
. For
![]() $\omega \in \left (\Sigma _{n}\right )_{[l]}^{(c)}$
, let
$\omega \in \left (\Sigma _{n}\right )_{[l]}^{(c)}$
, let
![]() $\Delta (\omega )$
be the permutation in
$\Delta (\omega )$
be the permutation in
![]() $\left (\Sigma _{n}\right )_{[l]}^{(c)}$
such that
$\left (\Sigma _{n}\right )_{[l]}^{(c)}$
such that
![]() $\Delta (\omega )(i)=\omega (1) + i-1$
for
$\Delta (\omega )(i)=\omega (1) + i-1$
for
![]() $1\le i \le c$
. Then we consider the map
$1\le i \le c$
. Then we consider the map
It can be easily seen that
 $$ \begin{align} \begin{aligned} &\bullet\, \phi(\omega)(i) = i \text{ for } 1 \leq i \leq \omega(1), \\ &\bullet\, \phi(\omega)(\omega(1)+1) <\phi(\omega)(\omega(1)+2) < \cdots <\phi(\omega)(\omega(1)+c-1),\\ &\bullet\,\phi(\omega)(\omega(1)+c) <\phi(\omega)(\omega(1)+c+1) < \cdots <\phi(\omega)(l+1) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\bullet\, \phi(\omega)(i) = i \text{ for } 1 \leq i \leq \omega(1), \\ &\bullet\, \phi(\omega)(\omega(1)+1) <\phi(\omega)(\omega(1)+2) < \cdots <\phi(\omega)(\omega(1)+c-1),\\ &\bullet\,\phi(\omega)(\omega(1)+c) <\phi(\omega)(\omega(1)+c+1) < \cdots <\phi(\omega)(l+1) \end{aligned} \end{align} $$
and particularly
![]() $\phi $
is an injective map. Note that
$\phi $
is an injective map. Note that
![]() $\omega (1)$
can have values belonging to
$\omega (1)$
can have values belonging to
![]() $[l-c+2]$
. For
$[l-c+2]$
. For
![]() $1 \leq u \leq l-c+2$
, equation (6.8) implies that
$1 \leq u \leq l-c+2$
, equation (6.8) implies that
Here
![]() $(\Sigma _n)^{(l+1)}_{[u + 1, l]}$
is set to be
$(\Sigma _n)^{(l+1)}_{[u + 1, l]}$
is set to be
![]() $\{\mathrm {id}\}$
. Hence, letting
$\{\mathrm {id}\}$
. Hence, letting
![]() $\Delta _u$
be the permutation in
$\Delta _u$
be the permutation in
![]() $\left (\Sigma _{n}\right )_{[l]}^{(c)}$
such that
$\left (\Sigma _{n}\right )_{[l]}^{(c)}$
such that
![]() $\Delta _u(i) = u+i-1$
for
$\Delta _u(i) = u+i-1$
for
![]() $1 \leq i \leq c$
, we have the following decomposition:
$1 \leq i \leq c$
, we have the following decomposition:
 $$ \begin{align} \left(\Sigma_{n}\right)_{[l]}^{(c)} = \bigsqcup_{1 \le u \le l - c + 2} \left\{\zeta \Delta_u \mid \zeta \in (\Sigma_n)^{(c + u - 1)}_{[u + 1, l]} \right\}. \end{align} $$
$$ \begin{align} \left(\Sigma_{n}\right)_{[l]}^{(c)} = \bigsqcup_{1 \le u \le l - c + 2} \left\{\zeta \Delta_u \mid \zeta \in (\Sigma_n)^{(c + u - 1)}_{[u + 1, l]} \right\}. \end{align} $$
In the following, for each
![]() $\omega \in \left (\Sigma _{n}\right )_{[l]}^{(c)}$
, we will show that
$\omega \in \left (\Sigma _{n}\right )_{[l]}^{(c)}$
, we will show that
![]() $\pi _{\omega } = \pi _{\phi (\omega )} \pi _{\Delta (\omega )}$
. Note that
$\pi _{\omega } = \pi _{\phi (\omega )} \pi _{\Delta (\omega )}$
. Note that
Since
![]() $\phi (\omega ) \in (\Sigma _n)_{[\omega (1) + 1, l]}^{(c + \omega (1) - 1)}$
,
$\phi (\omega ) \in (\Sigma _n)_{[\omega (1) + 1, l]}^{(c + \omega (1) - 1)}$
,
From the construction of
![]() $\phi $
, one sees that
$\phi $
, one sees that
![]() $\phi (\omega )(\omega (1) + i) = \omega (i + 1)$
, and thus
$\phi (\omega )(\omega (1) + i) = \omega (i + 1)$
, and thus
Combining this equality with equation (6.10) yields that
 $$ \begin{align*} \ell(\phi(\omega)) + \ell(\Delta(\omega)) & = \sum_{1 \le i \le c -1} \left( \omega(i + 1) - \omega(1) - i \right) + c(\omega(1)-1) \\ & = \sum_{1 \leq i \leq c} (\omega(i)-i) = \ell(\omega). \end{align*} $$
$$ \begin{align*} \ell(\phi(\omega)) + \ell(\Delta(\omega)) & = \sum_{1 \le i \le c -1} \left( \omega(i + 1) - \omega(1) - i \right) + c(\omega(1)-1) \\ & = \sum_{1 \leq i \leq c} (\omega(i)-i) = \ell(\omega). \end{align*} $$
Since
![]() $\omega = \phi (\omega ) \Delta (\omega )$
, we have that
$\omega = \phi (\omega ) \Delta (\omega )$
, we have that
![]() $\Delta (\omega ) \preceq _L \omega $
, and thus
$\Delta (\omega ) \preceq _L \omega $
, and thus
Let
![]() $1 \le j \le m$
and
$1 \le j \le m$
and
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. For
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. For
![]() $\sigma \preceq _L \boldsymbol {w_0}(\beta ;j)$
, we define
$\sigma \preceq _L \boldsymbol {w_0}(\beta ;j)$
, we define
![]() $T_{j;\beta }(\sigma )$
to be the filling of
$T_{j;\beta }(\sigma )$
to be the filling of
![]() $\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
such that the column strip
$\mathtt {rd}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
such that the column strip
![]() $\mathtt {S}_{k_r}$
(
$\mathtt {S}_{k_r}$
(
![]() $1 \leq r \leq m$
) is filled with the entries of
$1 \leq r \leq m$
) is filled with the entries of
 $$ \begin{align*}\begin{cases} (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}})(\mathtt{S}^{\prime}_{k_j}) \cup \{\min((\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}})(\mathtt{S}^{\prime}_{k_0}))\} & \text{ if } r = j,\\ (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}})(\mathtt{S}^{\prime}_{k_r}) & \text{ otherwise } \end{cases} \end{align*} $$
$$ \begin{align*}\begin{cases} (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}})(\mathtt{S}^{\prime}_{k_j}) \cup \{\min((\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}})(\mathtt{S}^{\prime}_{k_0}))\} & \text{ if } r = j,\\ (\pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}})(\mathtt{S}^{\prime}_{k_r}) & \text{ otherwise } \end{cases} \end{align*} $$
in such a way that the entries increase from top to bottom and the row strip
![]() $\mathtt {S}_{k_0}$
is filled with the entries of
$\mathtt {S}_{k_0}$
is filled with the entries of
in such a way that the entries increase from left to right.
Example 6.10. Let us revisit Example 6.9. Recall
![]() $\beta =(1,3,1^4)$
and
$\beta =(1,3,1^4)$
and
![]() $\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)} =(1) \oplus (3,1^2) \oplus (1^2)$
. For
$\underline {{\boldsymbol {\unicode{x3b1} }}}_{(2)} =(1) \oplus (3,1^2) \oplus (1^2)$
. For
![]() $\sigma = s_{[1,3]}, s_4s_{[1,3]}$
and
$\sigma = s_{[1,3]}, s_4s_{[1,3]}$
and
![]() $s_{[3,4]}s_{[1,3]}$
, it holds that
$s_{[3,4]}s_{[1,3]}$
, it holds that
![]() $\sigma \preceq _L \boldsymbol {w_0}(\beta ;2)$
and
$\sigma \preceq _L \boldsymbol {w_0}(\beta ;2)$
and

Using these, we can check that

for all
![]() $\sigma = s_{[1,3]}, s_4s_{[1,3]},s_3s_4s_{[1,3]}$
.
$\sigma = s_{[1,3]}, s_4s_{[1,3]},s_3s_4s_{[1,3]}$
.
If there is no confusion for j and
![]() $\beta $
, then we simply write
$\beta $
, then we simply write
![]() $T(\sigma )$
for
$T(\sigma )$
for
![]() $T_{j;\beta }(\sigma )$
. For
$T_{j;\beta }(\sigma )$
. For
![]() $\Theta (\mathcal {V}_{\alpha })$
defined in equation (4.1), we have the following lemma.
$\Theta (\mathcal {V}_{\alpha })$
defined in equation (4.1), we have the following lemma.
Lemma 6.11. Suppose we have a pair
![]() $(j,\beta )$
with
$(j,\beta )$
with
![]() $1 \le j \le m$
and
$1 \le j \le m$
and
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
satisfying that
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
satisfying that
![]() $\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \leq \ell (\alpha )$
. Then for every permutation
$\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \leq \ell (\alpha )$
. Then for every permutation
![]() $\sigma \in \Sigma _n$
with
$\sigma \in \Sigma _n$
with
![]() $\sigma \preceq _L \boldsymbol {w_0}(\beta ;j)$
, it holds that
$\sigma \preceq _L \boldsymbol {w_0}(\beta ;j)$
, it holds that
![]() $T(\sigma ) \in \Theta (\mathcal {V}_{\alpha })$
.
$T(\sigma ) \in \Theta (\mathcal {V}_{\alpha })$
.
Proof. It is clear that
![]() $T(\sigma ) \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
. Thus, for the assertion, we have only to show that
$T(\sigma ) \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
. Thus, for the assertion, we have only to show that
![]() $T(\sigma )_j^{1+\delta _{j,m}} < T(\sigma )^1_{m+k_j-1}$
. Note that
$T(\sigma )_j^{1+\delta _{j,m}} < T(\sigma )^1_{m+k_j-1}$
. Note that
which implies that
Since
![]() $|\mathtt {S}^{\prime }_{k_{-1}}| = k_j-1$
, it follows that
$|\mathtt {S}^{\prime }_{k_{-1}}| = k_j-1$
, it follows that
![]() $\min ((\pi _{\sigma } \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}})(\mathtt {S}^{\prime }_{k_0})) \leq k_j$
. On the other hand, from the observation that
$\min ((\pi _{\sigma } \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}})(\mathtt {S}^{\prime }_{k_0})) \leq k_j$
. On the other hand, from the observation that
![]() $T(\sigma )^1_{m+k_j-1}$
is the
$T(\sigma )^1_{m+k_j-1}$
is the
![]() $k_j$
th smallest element in the set
$k_j$
th smallest element in the set
we see that
![]() $k_j < T(\sigma )^1_{m+k_j-1}$
. As a consequence, we derive the following inequality:
$k_j < T(\sigma )^1_{m+k_j-1}$
. As a consequence, we derive the following inequality:
We are now ready to prove Theorem 4.3.
Proof of Theorem 4.3.
(a) Given
![]() $1 \le i \le n-1$
and
$1 \le i \le n-1$
and
![]() $T \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
, we have three cases.
$T \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})$
, we have three cases.
Case 1:
![]() $\pi _i \cdot T = T$
. We claim that
$\pi _i \cdot T = T$
. We claim that
![]() $i \notin \mathrm {Des}(\tau _{T;j;A})$
for all
$i \notin \mathrm {Des}(\tau _{T;j;A})$
for all
![]() $1 \leq j \leq m$
and
$1 \leq j \leq m$
and
![]() $A \in \mathcal {P}(\mathtt {A}_{T;j})$
. Fix
$A \in \mathcal {P}(\mathtt {A}_{T;j})$
. Fix
![]() $j \in [m]$
and
$j \in [m]$
and
![]() $A \in \mathcal {P}(\mathtt {A}_{T;j})$
. Since
$A \in \mathcal {P}(\mathtt {A}_{T;j})$
. Since
![]() $i \notin \mathrm {Des}(T)$
, i is weakly right of
$i \notin \mathrm {Des}(T)$
, i is weakly right of
![]() $i+1$
in T. If neither i nor
$i+1$
in T. If neither i nor
![]() $i+1$
appears in
$i+1$
appears in
![]() $\mathbf {w}_{T;j}$
, then i and
$\mathbf {w}_{T;j}$
, then i and
![]() $i+1$
still hold their positions in
$i+1$
still hold their positions in
![]() $\tau _{T;j;A}$
, so
$\tau _{T;j;A}$
, so
![]() $i \notin \mathrm {Des}(\tau _{T;j;A})$
. If i appears in
$i \notin \mathrm {Des}(\tau _{T;j;A})$
. If i appears in
![]() $\mathbf {w}_{T;j}$
and
$\mathbf {w}_{T;j}$
and
![]() $i+1$
does not appear in
$i+1$
does not appear in
![]() $\mathbf {w}_{T;j}$
, then
$\mathbf {w}_{T;j}$
, then
![]() $i+1$
holds its position in
$i+1$
holds its position in
![]() $\tau _{T;j;A}$
but i is moved to the right in
$\tau _{T;j;A}$
but i is moved to the right in
![]() $\tau _{T;j;A}$
, so
$\tau _{T;j;A}$
, so
![]() $i \notin \mathrm {Des}(\tau _{T;j;A})$
. Suppose that i does not appear in
$i \notin \mathrm {Des}(\tau _{T;j;A})$
. Suppose that i does not appear in
![]() $\mathbf {w}_{T;j}$
and
$\mathbf {w}_{T;j}$
and
![]() $i+1 = w_{u_k}$
for some
$i+1 = w_{u_k}$
for some
![]() $1 \le k \le l$
, where
$1 \le k \le l$
, where
![]() $\mathbf {w}_{T;j} = w_{u_1} w_{u_2} \cdots w_{u_l}$
. By the definition of
$\mathbf {w}_{T;j} = w_{u_1} w_{u_2} \cdots w_{u_l}$
. By the definition of
![]() $\mathbf {w}_{T;j}$
,
$\mathbf {w}_{T;j}$
,
![]() $w_{u_{k+1}} < i$
and appears strictly left of i if
$w_{u_{k+1}} < i$
and appears strictly left of i if
![]() $k < l$
, and
$k < l$
, and
![]() $i \in T(\mathtt {S}_{k_0})$
if
$i \in T(\mathtt {S}_{k_0})$
if
![]() $k = l$
. Thus,
$k = l$
. Thus,
![]() $i \notin \mathrm {Des}(\tau _{T;j;A})$
.
$i \notin \mathrm {Des}(\tau _{T;j;A})$
.
Case 2:
![]() $\pi _i \cdot T = 0$
. We claim that
$\pi _i \cdot T = 0$
. We claim that
![]() $\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = 0$
for all
$\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = 0$
for all
![]() $1 \leq j \leq m$
. Fix
$1 \leq j \leq m$
. Fix
![]() $j \in [m]$
. Since
$j \in [m]$
. Since
![]() $i, i+1 \in T(\mathtt {S}_0)$
by the shape of T,
$i, i+1 \in T(\mathtt {S}_0)$
by the shape of T,
![]() $\textsf {end}(\mathbf {w}_{T;j}) \neq i, i+1$
. So we have from the definition of
$\textsf {end}(\mathbf {w}_{T;j}) \neq i, i+1$
. So we have from the definition of
![]() $\mathtt {A}_{T;j}$
that either
$\mathtt {A}_{T;j}$
that either
![]() $i, i+1 \notin \mathtt {A}_{T;j}$
or
$i, i+1 \notin \mathtt {A}_{T;j}$
or
![]() $i, i+1 \in \mathtt {A}_{T;j}$
. If
$i, i+1 \in \mathtt {A}_{T;j}$
. If
![]() $i, i+1 \notin \mathtt {A}_{T;j}$
, then
$i, i+1 \notin \mathtt {A}_{T;j}$
, then
![]() $i,i+1 \in \tau _{T;j;A}(\mathtt {S}^{\prime }_{k_{-1}})$
for all
$i,i+1 \in \tau _{T;j;A}(\mathtt {S}^{\prime }_{k_{-1}})$
for all
![]() $A \in \mathcal {P}(\mathtt {A}_{T;j})$
, so
$A \in \mathcal {P}(\mathtt {A}_{T;j})$
, so
![]() $\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = 0$
. If
$\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = 0$
. If
![]() $i, i+1 \in \mathtt {A}_{T;j}$
, then
$i, i+1 \in \mathtt {A}_{T;j}$
, then
![]() $\mathcal {P}(\mathtt {A}_{T;j}) = \mathcal {X} \cup \mathcal {Y} \cup \mathcal {Z}$
, where
$\mathcal {P}(\mathtt {A}_{T;j}) = \mathcal {X} \cup \mathcal {Y} \cup \mathcal {Z}$
, where
 $$ \begin{align*} \mathcal{X} & := \{ A \in \mathcal{P}(\mathtt{A}_{T;j}) \mid i \in A, \ i+1 \notin A \} \\ \mathcal{Y} & := \{ A \in \mathcal{P}(\mathtt{A}_{T;j}) \mid i \notin A, \ i+1 \in A \} \\ \mathcal{Z} & :=\{ A \in \mathcal{P}(\mathtt{A}_{T;j}) \mid i,i+1 \in A \} \cup \{ A \in \mathcal{P}(\mathtt{A}_{T;j}) \mid i,i+1 \notin A \} \end{align*} $$
$$ \begin{align*} \mathcal{X} & := \{ A \in \mathcal{P}(\mathtt{A}_{T;j}) \mid i \in A, \ i+1 \notin A \} \\ \mathcal{Y} & := \{ A \in \mathcal{P}(\mathtt{A}_{T;j}) \mid i \notin A, \ i+1 \in A \} \\ \mathcal{Z} & :=\{ A \in \mathcal{P}(\mathtt{A}_{T;j}) \mid i,i+1 \in A \} \cup \{ A \in \mathcal{P}(\mathtt{A}_{T;j}) \mid i,i+1 \notin A \} \end{align*} $$
Note that
![]() $\pi _i \cdot \tau _{T;j;A} = 0$
for any
$\pi _i \cdot \tau _{T;j;A} = 0$
for any
![]() $A \in \mathcal {Z}$
. Therefore, the claim can be shown by proving that
$A \in \mathcal {Z}$
. Therefore, the claim can be shown by proving that
 $$ \begin{align} \pi_i \left(\sum_{A \in \mathcal{X}} \mathrm{sgn}(A)\tau_{T;j;A} + \sum_{A \in \mathcal{Y}} \mathrm{sgn}(A)\tau_{T;j;A} \right) = 0. \end{align} $$
$$ \begin{align} \pi_i \left(\sum_{A \in \mathcal{X}} \mathrm{sgn}(A)\tau_{T;j;A} + \sum_{A \in \mathcal{Y}} \mathrm{sgn}(A)\tau_{T;j;A} \right) = 0. \end{align} $$
Let us consider the bijection
![]() $f: \mathcal {X} \rightarrow \mathcal {Y}$
by
$f: \mathcal {X} \rightarrow \mathcal {Y}$
by
Since
![]() $\mathrm {sgn}(A) + \mathrm {sgn}(f(A)) = 0$
and
$\mathrm {sgn}(A) + \mathrm {sgn}(f(A)) = 0$
and
![]() $\tau _{T;j;f(A)} = s_i \cdot \tau _{T;j;A}$
, we obtain equation (6.12).
$\tau _{T;j;f(A)} = s_i \cdot \tau _{T;j;A}$
, we obtain equation (6.12).
Case 3:
![]() $\pi _i \cdot T = s_i \cdot T$
. We claim that
$\pi _i \cdot T = s_i \cdot T$
. We claim that
![]() $\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = {\boldsymbol {\tau }}_{(\pi _i \cdot T);j}$
for all
$\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = {\boldsymbol {\tau }}_{(\pi _i \cdot T);j}$
for all
![]() $1 \leq j \leq m$
. Fix
$1 \leq j \leq m$
. Fix
![]() $1 \leq j \leq m$
with
$1 \leq j \leq m$
with
![]() ${\boldsymbol {\tau }}_{T;j} \neq 0$
. If
${\boldsymbol {\tau }}_{T;j} \neq 0$
. If
![]() $i+1 \notin T(\mathtt {S}_{k_0})$
, then
$i+1 \notin T(\mathtt {S}_{k_0})$
, then
![]() $\textsf {end}(\mathbf {w}_{T;j}) = \textsf {end}(\mathbf {w}_{\pi _i \cdot T;j})$
and
$\textsf {end}(\mathbf {w}_{T;j}) = \textsf {end}(\mathbf {w}_{\pi _i \cdot T;j})$
and
![]() $\mathtt {A}_{T;j} = \mathtt {A}_{(\pi _i \cdot T);j}$
, so
$\mathtt {A}_{T;j} = \mathtt {A}_{(\pi _i \cdot T);j}$
, so
![]() $\mathcal {P}(\mathtt {A}_{T;j}) = \mathcal {P}(\mathtt {A}_{(\pi _i \cdot T);j})$
. This implies that
$\mathcal {P}(\mathtt {A}_{T;j}) = \mathcal {P}(\mathtt {A}_{(\pi _i \cdot T);j})$
. This implies that
 $$ \begin{align*} \pi_i \cdot {\boldsymbol{\tau}}_{T;j} = \pi_i \left(\sum_{A\in \mathcal{P}(\mathtt{A}_{T;j})} \mathrm{sgn}(A) \tau_{T;j;A}\right) = \sum_{A\in \mathcal{P}(\mathtt{A}_{\pi_i \cdot T;j})} \mathrm{sgn}(A) \tau_{\pi_i \cdot T;j;A} = {\boldsymbol{\tau}}_{(\pi_i\cdot T);j}. \end{align*} $$
$$ \begin{align*} \pi_i \cdot {\boldsymbol{\tau}}_{T;j} = \pi_i \left(\sum_{A\in \mathcal{P}(\mathtt{A}_{T;j})} \mathrm{sgn}(A) \tau_{T;j;A}\right) = \sum_{A\in \mathcal{P}(\mathtt{A}_{\pi_i \cdot T;j})} \mathrm{sgn}(A) \tau_{\pi_i \cdot T;j;A} = {\boldsymbol{\tau}}_{(\pi_i\cdot T);j}. \end{align*} $$
Let us assume that
![]() $i+1 \in T(\mathtt {S}_{k_0})$
. First, we consider the case where
$i+1 \in T(\mathtt {S}_{k_0})$
. First, we consider the case where
![]() $\textsf {end}(\mathbf {w}_{T;j}) = i$
. Combining the assumption
$\textsf {end}(\mathbf {w}_{T;j}) = i$
. Combining the assumption
![]() ${\boldsymbol {\tau }}_{T;j} \neq 0$
with equation (6.6) yields that
${\boldsymbol {\tau }}_{T;j} \neq 0$
with equation (6.6) yields that
![]() $T^1_{m+k_j-1}> i$
. In addition, for any
$T^1_{m+k_j-1}> i$
. In addition, for any
![]() $A \in \mathcal {P}(\mathtt {A}_{T;j})$
with
$A \in \mathcal {P}(\mathtt {A}_{T;j})$
with
![]() $i+1 \in A$
, we have
$i+1 \in A$
, we have
![]() $\pi _i \cdot \tau _{T;j;A} = 0$
. Therefore,
$\pi _i \cdot \tau _{T;j;A} = 0$
. Therefore,
 $$ \begin{align} \pi_i \cdot {\boldsymbol{\tau}}_{T;j} = \sum_{\substack{A \in \mathcal{P}(\mathtt{A}_{T;j}) \\ i+1 \notin A} } \mathrm{sgn}(A) \ \pi_i \cdot \tau_{T;j;A}. \end{align} $$
$$ \begin{align} \pi_i \cdot {\boldsymbol{\tau}}_{T;j} = \sum_{\substack{A \in \mathcal{P}(\mathtt{A}_{T;j}) \\ i+1 \notin A} } \mathrm{sgn}(A) \ \pi_i \cdot \tau_{T;j;A}. \end{align} $$
On the other hand, since
![]() $\textsf {end}(\mathbf {w}_{\pi _i \cdot T;j}) = i+1$
, we have
$\textsf {end}(\mathbf {w}_{\pi _i \cdot T;j}) = i+1$
, we have
This implies that
 $$ \begin{align} {\boldsymbol{\tau}}_{\pi_i \cdot T;j} = \sum_{A \in \mathcal{P}(\mathtt{A}_{\pi_i \cdot T;j})} \mathrm{sgn}(A) \tau_{\pi_i \cdot T;j;A} = \sum_{\substack{A \in \mathcal{P}(\mathtt{A}_{T;j}) \\ i+1 \notin A} } \mathrm{sgn}(A) \ \tau_{\pi_i \cdot T;j;A}. \end{align} $$
$$ \begin{align} {\boldsymbol{\tau}}_{\pi_i \cdot T;j} = \sum_{A \in \mathcal{P}(\mathtt{A}_{\pi_i \cdot T;j})} \mathrm{sgn}(A) \tau_{\pi_i \cdot T;j;A} = \sum_{\substack{A \in \mathcal{P}(\mathtt{A}_{T;j}) \\ i+1 \notin A} } \mathrm{sgn}(A) \ \tau_{\pi_i \cdot T;j;A}. \end{align} $$
For any
![]() $A \in \mathcal {P}(\mathtt {A}_{T;j})$
with
$A \in \mathcal {P}(\mathtt {A}_{T;j})$
with
![]() $i+1 \notin A$
, one can see that
$i+1 \notin A$
, one can see that
![]() $\pi _i \cdot \tau _{T;j;A} = \tau _{\pi _i \cdot T;j;A}$
. Combining this equality with the equalities given by equations (6.13) and (6.14), we have
$\pi _i \cdot \tau _{T;j;A} = \tau _{\pi _i \cdot T;j;A}$
. Combining this equality with the equalities given by equations (6.13) and (6.14), we have
![]() $\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = {\boldsymbol {\tau }}_{\pi _i \cdot T;j}$
.
$\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = {\boldsymbol {\tau }}_{\pi _i \cdot T;j}$
.
Next, we consider the case where
![]() $\textsf {end}(\mathbf {w}_{T;j}) \neq i$
. Then one sees that
$\textsf {end}(\mathbf {w}_{T;j}) \neq i$
. Then one sees that
 $$ \begin{align*} \mathtt{A}_{(\pi_i \cdot T);j} = \begin{cases} \mathtt{A}_{T;j} & \text{ if } \textsf{end}(\mathbf{w}_{T;j})> i, \\ (\mathtt{A}_{T;j} \setminus \{i+1\})\cup \{ i\} & \text{ if } \textsf{end}(\mathbf{w}_{T;j}) < i. \end{cases} \end{align*} $$
$$ \begin{align*} \mathtt{A}_{(\pi_i \cdot T);j} = \begin{cases} \mathtt{A}_{T;j} & \text{ if } \textsf{end}(\mathbf{w}_{T;j})> i, \\ (\mathtt{A}_{T;j} \setminus \{i+1\})\cup \{ i\} & \text{ if } \textsf{end}(\mathbf{w}_{T;j}) < i. \end{cases} \end{align*} $$
In the former case, one can see that
![]() $\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = {\boldsymbol {\tau }}_{(\pi _i \cdot T);j}$
by mimicking the proof of the case where
$\pi _i \cdot {\boldsymbol {\tau }}_{T;j} = {\boldsymbol {\tau }}_{(\pi _i \cdot T);j}$
by mimicking the proof of the case where
![]() $i+1 \notin T(\mathtt {S}_{k_0})$
. For the latter case, set
$i+1 \notin T(\mathtt {S}_{k_0})$
. For the latter case, set
 $$ \begin{align*} f: \mathcal{P}(\mathtt{A}_{T;j}) \rightarrow \mathcal{P}(\mathtt{A}_{(\pi_i \cdot T);j}), \quad A \mapsto f(A) := \begin{cases} (A \setminus \{i+1 \})\cup \{ i\} & \text{ if } i+1 \in A, \\ A & \text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} f: \mathcal{P}(\mathtt{A}_{T;j}) \rightarrow \mathcal{P}(\mathtt{A}_{(\pi_i \cdot T);j}), \quad A \mapsto f(A) := \begin{cases} (A \setminus \{i+1 \})\cup \{ i\} & \text{ if } i+1 \in A, \\ A & \text{ otherwise.} \end{cases} \end{align*} $$
It is clear that f is bijective. Moreover, since
![]() $\mathrm {sgn}(A) = \mathrm {sgn}(f(A))$
and
$\mathrm {sgn}(A) = \mathrm {sgn}(f(A))$
and
![]() $\pi _i \cdot \tau _{T;j;A} = \tau _{(\pi _i\cdot T);j;f(A)}$
, it follows that
$\pi _i \cdot \tau _{T;j;A} = \tau _{(\pi _i\cdot T);j;f(A)}$
, it follows that
 $$\begin{align*}\pi_i \cdot {\boldsymbol{\tau}}_{T;j} =\sum_{A \in \mathcal{P}(\mathtt{A}_{T;j})} \mathrm{sgn} (A) \pi_i \cdot \tau_{T;j;A} =\sum_{f(A) \in \mathcal{P}(\mathtt{A}_{(\pi_i \cdot T);j})} \mathrm{sgn} (f(A)) \tau_{(\pi_i\cdot T);j;f(A)} = {\boldsymbol{\tau}}_{(\pi_i \cdot T);j}. \end{align*}$$
$$\begin{align*}\pi_i \cdot {\boldsymbol{\tau}}_{T;j} =\sum_{A \in \mathcal{P}(\mathtt{A}_{T;j})} \mathrm{sgn} (A) \pi_i \cdot \tau_{T;j;A} =\sum_{f(A) \in \mathcal{P}(\mathtt{A}_{(\pi_i \cdot T);j})} \mathrm{sgn} (f(A)) \tau_{(\pi_i\cdot T);j;f(A)} = {\boldsymbol{\tau}}_{(\pi_i \cdot T);j}. \end{align*}$$
(b) Let us show
![]() $\ker (\partial ^1) \supseteq \epsilon (\mathcal {V}_{\alpha })$
. Recall that
$\ker (\partial ^1) \supseteq \epsilon (\mathcal {V}_{\alpha })$
. Recall that
Therefore, it suffices to show that
Let
![]() $T \in \{ T \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}}) \mid T_j^{1+\delta _{j,m}}> T^1_{m+k_j-1} \text { for all } 1\leq j \leq m \}$
. For every
$T \in \{ T \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}}) \mid T_j^{1+\delta _{j,m}}> T^1_{m+k_j-1} \text { for all } 1\leq j \leq m \}$
. For every
![]() $1\leq j \leq m$
, there exists
$1\leq j \leq m$
, there exists
![]() $j'>j$
such that
$j'>j$
such that
![]() $\textsf {end}(\mathbf {w}_{T;j}) = T_{j'}^{1+\delta _{j',m}}$
. By definition, one has
$\textsf {end}(\mathbf {w}_{T;j}) = T_{j'}^{1+\delta _{j',m}}$
. By definition, one has
so
![]() $\mathcal {P}(\mathtt {A}_{T;j}) = \emptyset $
. By definition,
$\mathcal {P}(\mathtt {A}_{T;j}) = \emptyset $
. By definition,
![]() ${\boldsymbol {\tau }}_{T;j} = 0$
, and thus
${\boldsymbol {\tau }}_{T;j} = 0$
, and thus
![]() $T \in \ker (\partial ^1)$
.
$T \in \ker (\partial ^1)$
.
Let us show
![]() $\ker (\partial ^1) \subseteq \epsilon (\mathcal {V}_{\alpha })$
. Suppose that there exists
$\ker (\partial ^1) \subseteq \epsilon (\mathcal {V}_{\alpha })$
. Suppose that there exists
![]() $x \in \ker (\partial ^1) \setminus \epsilon (\mathcal {V}_{\alpha })$
. Let
$x \in \ker (\partial ^1) \setminus \epsilon (\mathcal {V}_{\alpha })$
. Let
![]() $x = \sum _{T \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})} c_T T$
with
$x = \sum _{T \in \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}})} c_T T$
with
![]() $c_T \in \mathbb C$
. Since
$c_T \in \mathbb C$
. Since
![]() $\partial ^1(T) = 0$
for all T satisfying that
$\partial ^1(T) = 0$
for all T satisfying that
![]() $T_j^{1+\delta _{j,m}}> T^1_{m+k_j-1}~(1\leq j \leq m)$
, all Ts in the expansion of x are contained in
$T_j^{1+\delta _{j,m}}> T^1_{m+k_j-1}~(1\leq j \leq m)$
, all Ts in the expansion of x are contained in
![]() $\Theta (\mathcal {V}_{\alpha })$
(see equation (4.1)). Define
$\Theta (\mathcal {V}_{\alpha })$
(see equation (4.1)). Define
and choose any tableau U in
![]() $\textsf {supp}(x)$
such that
$\textsf {supp}(x)$
such that
![]() $\mathbf {w}(U)$
is maximal in
$\mathbf {w}(U)$
is maximal in
![]() $\{\mathbf {w}(T): T \in \textsf {supp}(x)\}$
with respect to the Bruhat order. Let
$\{\mathbf {w}(T): T \in \textsf {supp}(x)\}$
with respect to the Bruhat order. Let
 $$ \begin{align*} J & := \{j \in [m] \mid \mathcal{P}(\mathtt{A}_{U;j}) \neq \emptyset \} \text{ and}\\ \tau_0 &:= \tau_{U;\max(J);A^1_{U; \max(J)}}. \end{align*} $$
$$ \begin{align*} J & := \{j \in [m] \mid \mathcal{P}(\mathtt{A}_{U;j}) \neq \emptyset \} \text{ and}\\ \tau_0 &:= \tau_{U;\max(J);A^1_{U; \max(J)}}. \end{align*} $$
It should be noted that J is nonempty because
![]() $U \in \Theta (\mathcal {V}_{\alpha })$
, and the coefficient of
$U \in \Theta (\mathcal {V}_{\alpha })$
, and the coefficient of
![]() $\tau _0$
is nonzero in the expansion of
$\tau _0$
is nonzero in the expansion of
![]() $\partial ^1(U)$
in terms of
$\partial ^1(U)$
in terms of
![]() $\bigcup _{1 \le j \le m} \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)})$
. Note that
$\bigcup _{1 \le j \le m} \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)})$
. Note that
![]() $\partial ^1(x) = \partial ^1(c_U U) + \partial ^1(x - c_U U)$
and
$\partial ^1(x) = \partial ^1(c_U U) + \partial ^1(x - c_U U)$
and
 $$ \begin{align*} \partial^1(x - c_U U) & = \sum_{T \in \textsf{supp}(x) \setminus \{U\}} c_T \left( \sum_{1\le j \le m} {\boldsymbol{\tau}}_{T;j} \right) \\ & = \sum_{T \in \textsf{supp}(x) \setminus \{U\}} c_T \left( \sum_{1\le j \le m} \sum_{A \in \mathcal{P}(\mathtt{A}_{T;j})} \mathrm{sgn}(A) \tau_{T;j;A} \right). \end{align*} $$
$$ \begin{align*} \partial^1(x - c_U U) & = \sum_{T \in \textsf{supp}(x) \setminus \{U\}} c_T \left( \sum_{1\le j \le m} {\boldsymbol{\tau}}_{T;j} \right) \\ & = \sum_{T \in \textsf{supp}(x) \setminus \{U\}} c_T \left( \sum_{1\le j \le m} \sum_{A \in \mathcal{P}(\mathtt{A}_{T;j})} \mathrm{sgn}(A) \tau_{T;j;A} \right). \end{align*} $$
We claim that there is no triple
![]() $(T,j,A)$
with
$(T,j,A)$
with
![]() $T \in \textsf {supp}(x) \setminus \{U\}$
,
$T \in \textsf {supp}(x) \setminus \{U\}$
,
![]() $1\le j \le m$
and
$1\le j \le m$
and
![]() $A \in \mathcal {P}(\mathtt {A}_{T;j})$
such that
$A \in \mathcal {P}(\mathtt {A}_{T;j})$
such that
![]() $\tau _{T;j;A} = \tau _0$
. Suppose not: that is,
$\tau _{T;j;A} = \tau _0$
. Suppose not: that is,
![]() $\tau _0 = \tau _{T;j;A}$
for some
$\tau _0 = \tau _{T;j;A}$
for some
![]() $(T,j,A)$
. Comparing the shapes of
$(T,j,A)$
. Comparing the shapes of
![]() $\tau _0$
and
$\tau _0$
and
![]() $\tau _{T;j;A}$
, we see that j must be
$\tau _{T;j;A}$
, we see that j must be
![]() $\max (J)$
. Let
$\max (J)$
. Let
![]() $\mathbf {w}(T) = w_1 w_2 \cdots w_n$
. According to the definition of
$\mathbf {w}(T) = w_1 w_2 \cdots w_n$
. According to the definition of
![]() $\mathbf {w}_{T;\max (J)}$
in equation (4.3), it is a decreasing subword
$\mathbf {w}_{T;\max (J)}$
in equation (4.3), it is a decreasing subword
![]() $w_{u_1} w_{u_2} \cdots w_{u_l}$
of
$w_{u_1} w_{u_2} \cdots w_{u_l}$
of
![]() $\mathbf {w}(T)$
subject to the conditions
$\mathbf {w}(T)$
subject to the conditions
Since
![]() $\tau _{T;\max (J);A} = \tau _0$
, one has that
$\tau _{T;\max (J);A} = \tau _0$
, one has that
where
![]() $\mathbf {w}(T), \mathbf {w}(U)$
are viewed as permutations and
$\mathbf {w}(T), \mathbf {w}(U)$
are viewed as permutations and
![]() $(a~b)$
denotes a transposition. For
$(a~b)$
denotes a transposition. For
![]() $\sigma \in \Sigma _n$
and
$\sigma \in \Sigma _n$
and
![]() $a,b \in [n]$
, it is stated in [Reference Björner and Brenti8, Lemma 2.1.4] that
$a,b \in [n]$
, it is stated in [Reference Björner and Brenti8, Lemma 2.1.4] that
![]() $\sigma \prec \sigma \cdot (a \ b)$
and
$\sigma \prec \sigma \cdot (a \ b)$
and
![]() $\ell (\sigma \cdot (a \ b)) = \ell (\sigma ) + 1$
if and only if
$\ell (\sigma \cdot (a \ b)) = \ell (\sigma ) + 1$
if and only if
![]() $\sigma (a) < \sigma (b)$
and there is no c such that
$\sigma (a) < \sigma (b)$
and there is no c such that
![]() $\sigma (a) < \sigma (c) < \sigma (b)$
. Here
$\sigma (a) < \sigma (c) < \sigma (b)$
. Here
![]() $\prec $
is the Bruhat order. Combining this with equation (6.15) yields that
$\prec $
is the Bruhat order. Combining this with equation (6.15) yields that
![]() $\mathbf {w}(U) \prec \mathbf {w}(T)$
. This contradicts the maximality of U; thus our claim is verified. It tells us that the coefficient of
$\mathbf {w}(U) \prec \mathbf {w}(T)$
. This contradicts the maximality of U; thus our claim is verified. It tells us that the coefficient of
![]() $\tau _0$
in the expansion of
$\tau _0$
in the expansion of
![]() $\partial ^1(x)$
in terms of
$\partial ^1(x)$
in terms of
![]() $\bigcup _{1 \le j \le m} \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)})$
is nonzero, which is absurd by the assumption that
$\bigcup _{1 \le j \le m} \mathrm {SRT}(\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)})$
is nonzero, which is absurd by the assumption that
![]() $x \in \ker (\partial ^1)$
. Consequently, we can conclude that there is no
$x \in \ker (\partial ^1)$
. Consequently, we can conclude that there is no
![]() $x \in \ker (\partial ^1) \setminus \epsilon (\mathcal {V}_{\alpha })$
.
$x \in \ker (\partial ^1) \setminus \epsilon (\mathcal {V}_{\alpha })$
.
(c) Observe the following
![]() $H_n(0)$
-module isomorphisms:
$H_n(0)$
-module isomorphisms:
 $$ \begin{align*} \mathrm{soc} \left(\bigoplus_{1 \leq j \leq m}\mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}} \right) & \underset{\text{Theorem~2.3}}{\cong} \bigoplus_{1 \leq j \leq m} \bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}]} \mathrm{soc}(\mathbf{P}_{\beta}) \cong \bigoplus_{1 \leq j \leq m}\bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}]} \mathbb C T^{\leftarrow}_{\beta} \\ & \hspace{0.55ex} \underset{\text{Lemma~6.8}}{\cong}\mathbb C \left( \overline{\pi}_{\boldsymbol{w_0}(\beta;j)} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} \right) \end{align*} $$
$$ \begin{align*} \mathrm{soc} \left(\bigoplus_{1 \leq j \leq m}\mathbf{P}_{\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}} \right) & \underset{\text{Theorem~2.3}}{\cong} \bigoplus_{1 \leq j \leq m} \bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}]} \mathrm{soc}(\mathbf{P}_{\beta}) \cong \bigoplus_{1 \leq j \leq m}\bigoplus_{\beta \in [\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}]} \mathbb C T^{\leftarrow}_{\beta} \\ & \hspace{0.55ex} \underset{\text{Lemma~6.8}}{\cong}\mathbb C \left( \overline{\pi}_{\boldsymbol{w_0}(\beta;j)} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} \right) \end{align*} $$
Hence our assertion can be verified by showing that
![]() $\overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}} \in \mathrm {Im}(\overline {\partial ^1})$
for
$\overline {\pi }_{\boldsymbol {w_0}(\beta ;j)} \cdot {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}} \in \mathrm {Im}(\overline {\partial ^1})$
for
![]() $1 \le j \le m$
and
$1 \le j \le m$
and
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. Let us fix
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. Let us fix
![]() $j \in [m]$
and
$j \in [m]$
and
![]() $\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. To begin with, we note that
$\beta \in [\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}]$
. To begin with, we note that
 $$ \begin{align} \overline{\pi}_{\boldsymbol{w_0}(\beta;j)} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} = \sum_{\sigma \preceq_L \boldsymbol{w_0}(\beta;j)} (-1)^{\ell(\boldsymbol{w_0}(\beta;j)) - \ell(\sigma)} \pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{align} $$
$$ \begin{align} \overline{\pi}_{\boldsymbol{w_0}(\beta;j)} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} = \sum_{\sigma \preceq_L \boldsymbol{w_0}(\beta;j)} (-1)^{\ell(\boldsymbol{w_0}(\beta;j)) - \ell(\sigma)} \pi_{\sigma} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{align} $$
According to the definition of
![]() $\boldsymbol {w_0}(\beta ;j)$
, we divide into the following two cases.
$\boldsymbol {w_0}(\beta ;j)$
, we divide into the following two cases.
Case 1:
![]() $\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}})> \ell (\alpha )$
. For
$\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}})> \ell (\alpha )$
. For
![]() $\sigma \preceq _L \boldsymbol {w_0}(\beta ;j) = w_0(\widehat {\mathtt {J}}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}})$
, it holds that
$\sigma \preceq _L \boldsymbol {w_0}(\beta ;j) = w_0(\widehat {\mathtt {J}}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}})$
, it holds that
 $$ \begin{align} \begin{aligned} & T(\sigma)^{1+\delta_{j,m}}_{j} = |\mathtt{S}^{\prime}_{k_{-1}}|+1, \\ & T(\sigma)^1_{m+k_{j}-1}=|\mathtt{S}^{\prime}_{k_{-1}}|+2 \text{ and } \\ & T(\sigma)^{1+\delta_{j',m}}_{j'}> T(\sigma)^1_{m+k_{j'}-1} \qquad \text{ if }1 \leq j' \leq m \text{ and } j'\neq j. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & T(\sigma)^{1+\delta_{j,m}}_{j} = |\mathtt{S}^{\prime}_{k_{-1}}|+1, \\ & T(\sigma)^1_{m+k_{j}-1}=|\mathtt{S}^{\prime}_{k_{-1}}|+2 \text{ and } \\ & T(\sigma)^{1+\delta_{j',m}}_{j'}> T(\sigma)^1_{m+k_{j'}-1} \qquad \text{ if }1 \leq j' \leq m \text{ and } j'\neq j. \end{aligned} \end{align} $$
Moreover, the definition of
![]() $T(\sigma )$
says that
$T(\sigma )$
says that
Putting these together, we can derive the following equalities:
 $$ \begin{align} \begin{aligned} \overline{\partial^1}(T(\sigma) + \epsilon(\mathcal{V}_{\alpha})) &= \sum_{1 \leq r \leq m}{\boldsymbol{\tau}}_{T(\sigma);r}\\ &={\boldsymbol{\tau}}_{T(\sigma);j} &\text{(by equation } (6.17))\;\\ &=\tau_{T(\sigma);j;A^1} &\text{(by equation } (6.18)). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \overline{\partial^1}(T(\sigma) + \epsilon(\mathcal{V}_{\alpha})) &= \sum_{1 \leq r \leq m}{\boldsymbol{\tau}}_{T(\sigma);r}\\ &={\boldsymbol{\tau}}_{T(\sigma);j} &\text{(by equation } (6.17))\;\\ &=\tau_{T(\sigma);j;A^1} &\text{(by equation } (6.18)). \end{aligned} \end{align} $$
Since
![]() $\tau _{T(\sigma );j;A^1} = \pi _{\sigma } \cdot \tau _{T(\mathrm {id});j;A^1}$
and
$\tau _{T(\sigma );j;A^1} = \pi _{\sigma } \cdot \tau _{T(\mathrm {id});j;A^1}$
and
![]() $\tau _{T(\mathrm {id});j;A^1} = {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}$
, we see that
$\tau _{T(\mathrm {id});j;A^1} = {T^{\leftarrow }_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}$
, we see that
Finally, putting equations (6.16) and (6.20) together yields that
 $$ \begin{align*} \overline{\pi}_{\boldsymbol{w_0}(\beta;j)} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} = \sum_{\sigma \preceq_L \boldsymbol{w_0}(\beta;j)} (-1)^{\ell(\boldsymbol{w_0}(\beta;j)) - \ell(\sigma)} \, \overline{\partial^1}(T(\sigma) + \epsilon(\mathcal{V}_{\alpha})), \end{align*} $$
$$ \begin{align*} \overline{\pi}_{\boldsymbol{w_0}(\beta;j)} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} = \sum_{\sigma \preceq_L \boldsymbol{w_0}(\beta;j)} (-1)^{\ell(\boldsymbol{w_0}(\beta;j)) - \ell(\sigma)} \, \overline{\partial^1}(T(\sigma) + \epsilon(\mathcal{V}_{\alpha})), \end{align*} $$
which verifies the assertion.
Case 2:
![]() $\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \le \ell (\alpha )$
. Let
$\min (\mathtt {J}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}) \le \ell (\alpha )$
. Let
![]() $\sigma \preceq _L \boldsymbol {w_0}(\beta ;j)$
. Since
$\sigma \preceq _L \boldsymbol {w_0}(\beta ;j)$
. Since
we can write
![]() $\sigma $
as
$\sigma $
as
![]() $\sigma ' \sigma "$
for some
$\sigma ' \sigma "$
for some
![]() $\sigma ' \in (\Sigma _{n})_{\widehat {\mathtt {J}}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}$
and
$\sigma ' \in (\Sigma _{n})_{\widehat {\mathtt {J}}_{\beta ;\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}}$
and
![]() $\sigma " \in (\Sigma _{n})_{[\ell (\alpha )]}^{(|\mathtt {S}^{\prime }_{k_0}|)}$
. Therefore, the right-hand side of equation (6.16) can be rewritten as
$\sigma " \in (\Sigma _{n})_{[\ell (\alpha )]}^{(|\mathtt {S}^{\prime }_{k_0}|)}$
. Therefore, the right-hand side of equation (6.16) can be rewritten as
 $$ \begin{align} \sum_{\sigma \preceq_L \boldsymbol{w_0}(\beta;j)} (-1)^{ \ell( w_0(\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}})) + \ell( w_0([\ell(\alpha)];|\mathtt{S}^{\prime}_{k_0}|)) -(\ell(\sigma') + \ell(\sigma"))} \pi_{\sigma'} \pi_{\sigma"} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{align} $$
$$ \begin{align} \sum_{\sigma \preceq_L \boldsymbol{w_0}(\beta;j)} (-1)^{ \ell( w_0(\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}})) + \ell( w_0([\ell(\alpha)];|\mathtt{S}^{\prime}_{k_0}|)) -(\ell(\sigma') + \ell(\sigma"))} \pi_{\sigma'} \pi_{\sigma"} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{align} $$
Since
![]() $\{\sigma \in \Sigma _n \mid \sigma \preceq _L \boldsymbol {w_0}(\beta ;j)\}$
can be decomposed into
$\{\sigma \in \Sigma _n \mid \sigma \preceq _L \boldsymbol {w_0}(\beta ;j)\}$
can be decomposed into
 $$\begin{align*}\bigsqcup_{\sigma' \in (\Sigma_{n})_{\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}} \bigsqcup_{\sigma" \in (\Sigma_{n})_{[\ell(\alpha)]}^{(|\mathtt{S}^{\prime}_{k_0}|)}} \{\sigma' \sigma"\}, \end{align*}$$
$$\begin{align*}\bigsqcup_{\sigma' \in (\Sigma_{n})_{\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}} \bigsqcup_{\sigma" \in (\Sigma_{n})_{[\ell(\alpha)]}^{(|\mathtt{S}^{\prime}_{k_0}|)}} \{\sigma' \sigma"\}, \end{align*}$$
equation (6.21) can also be rewritten as
 $$ \begin{align} \sum_{\sigma' \in (\Sigma_{n})_{\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}} (-1)^{\mathcal{N}(\sigma')} \pi_{\sigma'} \underbrace{\sum_{\sigma" \in (\Sigma_{n})_{[\ell(\alpha)]}^{(|\mathtt{S}^{\prime}_{k_0}|)}} (-1)^{\mathcal{M}(\sigma")} \pi_{\sigma"} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}}_{(\textsf{P})}. \end{align} $$
$$ \begin{align} \sum_{\sigma' \in (\Sigma_{n})_{\widehat{\mathtt{J}}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}} (-1)^{\mathcal{N}(\sigma')} \pi_{\sigma'} \underbrace{\sum_{\sigma" \in (\Sigma_{n})_{[\ell(\alpha)]}^{(|\mathtt{S}^{\prime}_{k_0}|)}} (-1)^{\mathcal{M}(\sigma")} \pi_{\sigma"} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}}_{(\textsf{P})}. \end{align} $$
Here we are using the notation
Note that
![]() $\ell (\alpha )-|\mathtt {S}^{\prime }_{k_0}|+2 = |\mathtt {S}^{\prime }_{k_{-1}}|+1$
since
$\ell (\alpha )-|\mathtt {S}^{\prime }_{k_0}|+2 = |\mathtt {S}^{\prime }_{k_{-1}}|+1$
since
![]() $\ell (\alpha )+1 = |\mathtt {S}^{\prime }_{k_0}|+|\mathtt {S}^{\prime }_{k_{-1}}|$
. In view of equations (6.9) and (6.11), we see that the summation
$\ell (\alpha )+1 = |\mathtt {S}^{\prime }_{k_0}|+|\mathtt {S}^{\prime }_{k_{-1}}|$
. In view of equations (6.9) and (6.11), we see that the summation
![]() $(\textsf {P})$
in equation (6.22) equals
$(\textsf {P})$
in equation (6.22) equals
 $$ \begin{align*} \sum_{1 \le u \le |\mathtt{S}^{\prime}_{k_{-1}}|+1} \sum_{\zeta \in \left(\Sigma_{n}\right)_{[u+1,\ell(\alpha)]}^{(|\mathtt{S}^{\prime}_{k_0}|+u-1)}} (-1)^{\mathcal{M}(\zeta \Delta_u)} \pi_{\zeta} \pi_{\Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{align*} $$
$$ \begin{align*} \sum_{1 \le u \le |\mathtt{S}^{\prime}_{k_{-1}}|+1} \sum_{\zeta \in \left(\Sigma_{n}\right)_{[u+1,\ell(\alpha)]}^{(|\mathtt{S}^{\prime}_{k_0}|+u-1)}} (-1)^{\mathcal{M}(\zeta \Delta_u)} \pi_{\zeta} \pi_{\Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{align*} $$
For each
![]() $1 \le u \le |\mathtt {S}^{\prime }_{k_{-1}}|+1$
, we claim that
$1 \le u \le |\mathtt {S}^{\prime }_{k_{-1}}|+1$
, we claim that
 $$ \begin{align*} \sum_{\zeta \in \left(\Sigma_{n}\right)_{[u+1,\ell(\alpha)]}^{(|\mathtt{S}^{\prime}_{k_0}|+u-1)}} (-1)^{\mathcal{M}(\zeta \Delta_u)} \pi_{\zeta \Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} = (-1)^{|\mathtt{S}^{\prime}_{k_{-1}}|-u} \partial^1(T(\Delta_u)), \end{align*} $$
$$ \begin{align*} \sum_{\zeta \in \left(\Sigma_{n}\right)_{[u+1,\ell(\alpha)]}^{(|\mathtt{S}^{\prime}_{k_0}|+u-1)}} (-1)^{\mathcal{M}(\zeta \Delta_u)} \pi_{\zeta \Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}} = (-1)^{|\mathtt{S}^{\prime}_{k_{-1}}|-u} \partial^1(T(\Delta_u)), \end{align*} $$
which will give rise to
The last of the proof will be devoted to the verification of this claim. We fix
![]() $u \in [1,|\mathtt {S}^{\prime }_{k_{-1}}|+1]$
and observe that
$u \in [1,|\mathtt {S}^{\prime }_{k_{-1}}|+1]$
and observe that
 $$ \begin{align*} &T(\Delta_u)(\mathtt{S}_{k_0}) =[\ell(\alpha) + 1]\setminus\{u\} \text{ and}\\ &\min \left(T(\Delta_u)(\mathtt{S}_{k_{j'}})\right)> \ell(\alpha) + 1 \quad \text{if } 1 \leq j' \leq m \text{ and } j' \neq j. \end{align*} $$
$$ \begin{align*} &T(\Delta_u)(\mathtt{S}_{k_0}) =[\ell(\alpha) + 1]\setminus\{u\} \text{ and}\\ &\min \left(T(\Delta_u)(\mathtt{S}_{k_{j'}})\right)> \ell(\alpha) + 1 \quad \text{if } 1 \leq j' \leq m \text{ and } j' \neq j. \end{align*} $$
This implies that
![]() $T(\Delta _u)^{1+\delta _{j',m}}_{j'}> T(\Delta _u)^1_{m+k_{j'}-1}$
, and therefore
$T(\Delta _u)^{1+\delta _{j',m}}_{j'}> T(\Delta _u)^1_{m+k_{j'}-1}$
, and therefore
 $$ \begin{align} \partial^1(T(\Delta_u)) = {\boldsymbol{\tau}}_{T(\Delta_u);j} = \sum_{A \in \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})} \mathrm{sgn}(A) \tau_{T(\Delta_u);j;A}. \end{align} $$
$$ \begin{align} \partial^1(T(\Delta_u)) = {\boldsymbol{\tau}}_{T(\Delta_u);j} = \sum_{A \in \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})} \mathrm{sgn}(A) \tau_{T(\Delta_u);j;A}. \end{align} $$
Combining Lemma 6.11 with equation (6.6) shows that the summation given in the last term is nonzero. In what follows, we transform this summation into a form suitable for proving our claim. For this purpose, we need to analyse
![]() $\mathcal {P}(\mathtt {A}_{T(\Delta _u);j})$
. Since
$\mathcal {P}(\mathtt {A}_{T(\Delta _u);j})$
. Since
![]() $\mathtt {A}_{T(\Delta _u);j} = [u+1,\ell (\alpha )+1]$
and
$\mathtt {A}_{T(\Delta _u);j} = [u+1,\ell (\alpha )+1]$
and
![]() $\ell (\alpha )-k_j+1 = |\mathtt {S}^{\prime }_{k_0}| - 1$
, it follows that
$\ell (\alpha )-k_j+1 = |\mathtt {S}^{\prime }_{k_0}| - 1$
, it follows that
 $$ \begin{align*} \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})=\binom{[u+1,\ell(\alpha)+1]}{|\mathtt{S}^{\prime}_{k_0}| - 1}. \end{align*} $$
$$ \begin{align*} \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})=\binom{[u+1,\ell(\alpha)+1]}{|\mathtt{S}^{\prime}_{k_0}| - 1}. \end{align*} $$
Thus we have the natural bijection
where
![]() $\psi (A)$
denotes the permutation in
$\psi (A)$
denotes the permutation in
![]() $(\Sigma _n)^{(|\mathtt {S}^{\prime }_{k_0}|-1)}_{[\ell (\alpha )-u]}$
such that
$(\Sigma _n)^{(|\mathtt {S}^{\prime }_{k_0}|-1)}_{[\ell (\alpha )-u]}$
such that
![]() $\psi (A)(i) = a_i - u$
for
$\psi (A)(i) = a_i - u$
for
![]() $1 \leq i \leq |\mathtt {S}^{\prime }_{k_0}|-1$
. Recall that there is a natural right
$1 \leq i \leq |\mathtt {S}^{\prime }_{k_0}|-1$
. Recall that there is a natural right
![]() $\Sigma _{|\mathtt {A}_{T(\Delta _u);j}|}$
-action on
$\Sigma _{|\mathtt {A}_{T(\Delta _u);j}|}$
-action on
![]() $\mathtt {A}_{T(\Delta _u);j}$
given by equation (4.4). Put
$\mathtt {A}_{T(\Delta _u);j}$
given by equation (4.4). Put
Since
![]() $|\mathtt {A}_{T(\Delta _u);j}| = \ell (\alpha ) - u + 1$
, we may identify
$|\mathtt {A}_{T(\Delta _u);j}| = \ell (\alpha ) - u + 1$
, we may identify
![]() $\Sigma _{|\mathtt {A}_{T(\Delta _u);j}|}$
with
$\Sigma _{|\mathtt {A}_{T(\Delta _u);j}|}$
with
![]() $(\Sigma _n)_{[\ell (\alpha )-u]}$
. Note that
$(\Sigma _n)_{[\ell (\alpha )-u]}$
. Note that
![]() $\psi (A)$
is the unique permutation in
$\psi (A)$
is the unique permutation in
![]() $(\Sigma _n)^{(|\mathtt {S}^{\prime }_{k_0}| - 1)}_{[\ell (\alpha )-u]}$
that gives
$(\Sigma _n)^{(|\mathtt {S}^{\prime }_{k_0}| - 1)}_{[\ell (\alpha )-u]}$
that gives
![]() $A^0$
when acting on A: that is,
$A^0$
when acting on A: that is,
![]() $A \cdot \psi (A) = A^0$
. Since
$A \cdot \psi (A) = A^0$
. Since
we have that
Applying this identity to equation (6.23) yields that
 $$ \begin{align} \partial^1(T(\Delta_u)) & = \sum_{A \in \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})} (-1)^{\ell(w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1)) -\ \ell(\psi(A))} \tau_{T(\Delta_u);j;A}. \end{align} $$
$$ \begin{align} \partial^1(T(\Delta_u)) & = \sum_{A \in \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})} (-1)^{\ell(w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1)) -\ \ell(\psi(A))} \tau_{T(\Delta_u);j;A}. \end{align} $$
Consider the bijection
From the constructions of
![]() $T(\Delta _u)$
and
$T(\Delta _u)$
and
![]() $\tau _{T(\Delta _u);j;A^0}$
, we can derive the identities
$\tau _{T(\Delta _u);j;A^0}$
, we can derive the identities
As a consequence,
 $$ \begin{align*} \partial^1(T(\Delta_u)) & \overset{(6.24)}{=} \sum_{A \in \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})} (-1)^{\ell( w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1) ) -\ \ell(\psi(A))} \tau_{T(\Delta_u);j;A} \\ & \overset{(6.25)}{=} \sum_{A \in \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})} (-1)^{\ell( w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1) )-\ell({\theta}_u(\psi(A)))} \pi_{{\theta}_u(\psi(A))}\pi_{\Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{align*} $$
$$ \begin{align*} \partial^1(T(\Delta_u)) & \overset{(6.24)}{=} \sum_{A \in \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})} (-1)^{\ell( w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1) ) -\ \ell(\psi(A))} \tau_{T(\Delta_u);j;A} \\ & \overset{(6.25)}{=} \sum_{A \in \mathcal{P}(\mathtt{A}_{T(\Delta_u);j})} (-1)^{\ell( w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1) )-\ell({\theta}_u(\psi(A)))} \pi_{{\theta}_u(\psi(A))}\pi_{\Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{align*} $$
Making use of the bijection
![]() ${\theta }_u \circ \psi : \mathcal {P}(\mathtt {A}_{T(\Delta _u);j}) \rightarrow (\Sigma _n)^{(|\mathtt {S}^{\prime }_{k_0}|-1+u)}_{[u+1,\ell (\alpha )]}$
, we can rewrite the second summation as
${\theta }_u \circ \psi : \mathcal {P}(\mathtt {A}_{T(\Delta _u);j}) \rightarrow (\Sigma _n)^{(|\mathtt {S}^{\prime }_{k_0}|-1+u)}_{[u+1,\ell (\alpha )]}$
, we can rewrite the second summation as
 $$ \begin{align} \begin{aligned} \sum_{\xi \in (\Sigma_n)^{(|\mathtt{S}^{\prime}_{k_0}|-1+u)}_{[u+1,\ell(\alpha)]}} (-1)^{\ell( w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1) )-\ell(\zeta)} \pi_{\zeta} \pi_{\Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sum_{\xi \in (\Sigma_n)^{(|\mathtt{S}^{\prime}_{k_0}|-1+u)}_{[u+1,\ell(\alpha)]}} (-1)^{\ell( w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1) )-\ell(\zeta)} \pi_{\zeta} \pi_{\Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}. \end{aligned} \end{align} $$
Note that
 $$ \begin{align*} \ell\left( w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1) \right) -\ell(\zeta) &=(|\mathtt{S}^{\prime}_{k_0}|-1)(\ell(\alpha)-u-|\mathtt{S}^{\prime}_{k_0}|+1) - \ell(\zeta)\\ &=(|\mathtt{S}^{\prime}_{k_0}|-1)(|\mathtt{S}^{\prime}_{k_{-1}}|-u) - \ell(\zeta)\\ &= \mathcal{M}(\zeta\Delta_u) - |\mathtt{S}^{\prime}_{k_{-1}}|+u. \end{align*} $$
$$ \begin{align*} \ell\left( w_0([\ell(\alpha)-u];|\mathtt{S}^{\prime}_{k_0}|-1) \right) -\ell(\zeta) &=(|\mathtt{S}^{\prime}_{k_0}|-1)(\ell(\alpha)-u-|\mathtt{S}^{\prime}_{k_0}|+1) - \ell(\zeta)\\ &=(|\mathtt{S}^{\prime}_{k_0}|-1)(|\mathtt{S}^{\prime}_{k_{-1}}|-u) - \ell(\zeta)\\ &= \mathcal{M}(\zeta\Delta_u) - |\mathtt{S}^{\prime}_{k_{-1}}|+u. \end{align*} $$
By substituting
![]() $\mathcal {M}(\zeta \Delta _u) - |\mathtt {S}^{\prime }_{k_{-1}}|+u$
for
$\mathcal {M}(\zeta \Delta _u) - |\mathtt {S}^{\prime }_{k_{-1}}|+u$
for
![]() $\ell \left ( w_0([\ell (\alpha )-u];|\mathtt {S}^{\prime }_{k_0}|-1)\right ) -\ell (\zeta )$
in equation (6.26), we finally obtain that
$\ell \left ( w_0([\ell (\alpha )-u];|\mathtt {S}^{\prime }_{k_0}|-1)\right ) -\ell (\zeta )$
in equation (6.26), we finally obtain that
 $$\begin{align*}\partial^1(T(\Delta_u)) = (-1)^{|\mathtt{S}^{\prime}_{k_{-1}}| - u} \sum_{\zeta \in (\Sigma_n)^{(|\mathtt{S}^{\prime}_{k_0}|-1+u)}_{[u+1,\ell(\alpha)]}} (-1)^{\mathcal{M}(\zeta\Delta_u)} \pi_{\zeta} \pi_{\Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}, \end{align*}$$
$$\begin{align*}\partial^1(T(\Delta_u)) = (-1)^{|\mathtt{S}^{\prime}_{k_{-1}}| - u} \sum_{\zeta \in (\Sigma_n)^{(|\mathtt{S}^{\prime}_{k_0}|-1+u)}_{[u+1,\ell(\alpha)]}} (-1)^{\mathcal{M}(\zeta\Delta_u)} \pi_{\zeta} \pi_{\Delta_u} \cdot {T^{\leftarrow}_{\beta;\underline{{\boldsymbol{\unicode{x3b1}}}}_{(j)}}}, \end{align*}$$
as required.
(d) It is well known that
(see [Reference Benson3, Corollary 2.5.4]). This immediately yields that
By (c), one sees that
![]() $\mathrm {soc}(\Omega ^{-1}(\mathcal {V}_{\alpha }))$
equals the socle of
$\mathrm {soc}(\Omega ^{-1}(\mathcal {V}_{\alpha }))$
equals the socle of
![]() $\bigoplus _{1 \leq j \leq m} \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}$
. So we are done.
$\bigoplus _{1 \leq j \leq m} \mathbf {P}_{\underline {{\boldsymbol {\unicode{x3b1} }}}_{(j)}}$
. So we are done.
7 Further avenues
(a) For each
![]() $\alpha \models n$
, let
$\alpha \models n$
, let
be a minimal projective presentation of
![]() $\mathbf {F}_{\alpha }$
. From [Reference Benson3, Corollary 2.5.4], we know that
$\mathbf {F}_{\alpha }$
. From [Reference Benson3, Corollary 2.5.4], we know that
![]() $\dim \mathrm {Ext}_{H_n(0)}^1(\mathbf {F}_{\alpha },\mathbf {F}_{\beta })$
counts the multiplicity of
$\dim \mathrm {Ext}_{H_n(0)}^1(\mathbf {F}_{\alpha },\mathbf {F}_{\beta })$
counts the multiplicity of
![]() $\mathbf {P}_{\beta }$
in the decomposition of
$\mathbf {P}_{\beta }$
in the decomposition of
![]() $P_1$
into indecomposable modules, equivalently,
$P_1$
into indecomposable modules, equivalently,
 $$ \begin{align*} P_1 \cong \bigoplus_{\beta \models n} \mathbf{P}_{\beta}^{\dim \mathrm{Ext}^1_{H_n(0)} (\mathbf{F}_{\alpha},\mathbf{F}_{\beta})}. \end{align*} $$
$$ \begin{align*} P_1 \cong \bigoplus_{\beta \models n} \mathbf{P}_{\beta}^{\dim \mathrm{Ext}^1_{H_n(0)} (\mathbf{F}_{\alpha},\mathbf{F}_{\beta})}. \end{align*} $$
This dimension has been computed in [Reference Duchamp, Hivert and Thibon14, Section 4] and [Reference Fayers16, Theorem 5.1]. However, to the best of the authors’ knowledge, no description for
![]() $\partial _1$
is available yet. It would be nice to find an explicit description of
$\partial _1$
is available yet. It would be nice to find an explicit description of
![]() $\partial _1$
, especially in a combinatorial manner. If this is done successfully, by taking an anti-automorphism twist introduced in [Reference Jung, Kim, Lee and Oh21, Section 3.4] to equation (7.1), we can also derive a minimal injective presentation for
$\partial _1$
, especially in a combinatorial manner. If this is done successfully, by taking an anti-automorphism twist introduced in [Reference Jung, Kim, Lee and Oh21, Section 3.4] to equation (7.1), we can also derive a minimal injective presentation for
![]() $\mathbf {F}_{\alpha }$
.
$\mathbf {F}_{\alpha }$
.
(b) Besides dual immaculate functions, the problem of constructing
![]() $H_n(0)$
-modules has been considered for the following quasisymmetric functions: the quasisymmetric Schur functions in [Reference Tewari and van Willigenburg27, Reference Tewari and van Willigenburg28], the extended Schur functions in [Reference Searles26], the Young row-strict quasisymmetric Schur functions in [Reference Bardwell and Searles2], the Young quasisymmetric Schur functions in [Reference Choi, Kim, Nam and Oh12] and the images of all these quasisymmetric functions under certain involutions on
$H_n(0)$
-modules has been considered for the following quasisymmetric functions: the quasisymmetric Schur functions in [Reference Tewari and van Willigenburg27, Reference Tewari and van Willigenburg28], the extended Schur functions in [Reference Searles26], the Young row-strict quasisymmetric Schur functions in [Reference Bardwell and Searles2], the Young quasisymmetric Schur functions in [Reference Choi, Kim, Nam and Oh12] and the images of all these quasisymmetric functions under certain involutions on
![]() $\mathrm {QSym}$
in [Reference Jung, Kim, Lee and Oh21]. Although these modules are built in a very similar way, their homological properties have not been well studied. The study of their projective and injective presentations will be pursued in the near future with appropriate modifications to the method used in this paper.
$\mathrm {QSym}$
in [Reference Jung, Kim, Lee and Oh21]. Although these modules are built in a very similar way, their homological properties have not been well studied. The study of their projective and injective presentations will be pursued in the near future with appropriate modifications to the method used in this paper.
(c) By virtue of Lemma 5.2 and Lemma 5.3, we have a combinatorial description for
![]() $\dim \mathrm {Hom}_{H_n(0)}(\mathbf{P}_{\alpha }, \mathcal {V}_{\beta })$
. However, no similar one is known for
$\dim \mathrm {Hom}_{H_n(0)}(\mathbf{P}_{\alpha }, \mathcal {V}_{\beta })$
. However, no similar one is known for
![]() $\dim \mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
except when
$\dim \mathrm {Hom}_{H_n(0)}(\mathcal {V}_{\alpha }, \mathcal {V}_{\beta })$
except when
![]() $\beta \le _l \alpha $
. It would be interesting to find such a description that holds for all
$\beta \le _l \alpha $
. It would be interesting to find such a description that holds for all
![]() $\alpha , \beta \models n$
.
$\alpha , \beta \models n$
.
Acknowledgements
The authors are grateful to the anonymous referees for their careful readings of the manuscript and valuable advice. And the authors would like to thank So-Yeon Lee for helping with computer programming. This work benefited from computations using SageMath.
Conflicts of Interest
None.
Funding statement
The first author was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (No. NRF-2019R1C1C1010668 and No. NRF-2020R1A5A1016126). The second author was supported by an NRF grant funded by the Korean Government (No. NRF-2019R1A2C4069647 and No. NRF-2020R1A5A1016126). The third author was supported by the Basic Science Research Program through the NRF, funded by the Ministry of Education (No. NRF-2019R1I1A1A01062658). The fourth author was supported by an NRF grant funded by the Korean Government (No. NRF-2020R1F1A1A01071055).