Hostname: page-component-7479d7b7d-68ccn Total loading time: 0 Render date: 2024-07-09T16:14:16.288Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERATION OF SECOND MAXIMAL SUBGROUPS AND THE EXISTENCE OF SPECIAL PRIMES

Part of: Probabilistic methods in group theory Representation theory of groups

Published online by Cambridge University Press:  07 November 2017

TIMOTHY C. BURNESS ,
MARTIN W. LIEBECK  and
ANER SHALEV
TIMOTHY C. BURNESS
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, UK; t.burness@bristol.ac.uk
MARTIN W. LIEBECK
Affiliation:
Department of Mathematics, Imperial College, London SW7 2BZ, UK; m.liebeck@imperial.ac.uk
ANER SHALEV
Affiliation:
Institute of Mathematics, Hebrew University, Jerusalem 91904, Israel; shalev@math.huji.ac.il

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 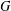$G$ be a finite almost simple group. It is well known that $G$ can be generated by three elements, and in previous work we showed that 6 generators suffice for all maximal subgroups of 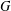$G$. In this paper, we consider subgroups at the next level of the subgroup lattice—the so-called second maximal subgroups. We prove that with the possible exception of some families of rank 1 groups of Lie type, the number of generators of every second maximal subgroup of $G$ is bounded by an absolute constant. We also show that such a bound holds without any exceptions if and only if there are only finitely many primes $r$ for which there is a prime power 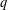$q$ such that 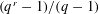$(q^{r}-1)/(q-1)$ is prime. The latter statement is a formidable open problem in Number Theory. Applications to random generation and polynomial growth are also given.

MSC classification

Primary: 20D06: Simple groups
Secondary: 20D30: Series and lattices of subgroups 20P05: Probabilistic methods in group theory
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e25
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Aschbacher, M., ‘On the maximal subgroups of the finite classical groups’, Invent. Math. 76 (1984), 469–514.CrossRefGoogle Scholar
Aschbacher, M., ‘On intervals in subgroup lattices of finite groups’, J. Amer. Math. Soc. 21 (2008), 809–830.Google Scholar
Aschbacher, M. and Guralnick, R., ‘Some applications of the first cohomology group’, J. Algebra 90 (1984), 446–460.CrossRefGoogle Scholar
Azad, H., Barry, M. and Seitz, G. M., ‘On the structure of parabolic subgroups’, Comm. Algebra 18 (1990), 551–562.Google Scholar
Basile, A., ‘Second maximal subgroups of the finite alternating and symmetric groups’, PhD Thesis, Australian National University, 2001, arXiv:0810.3721.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: the user language’, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Bray, J. N., Holt, D. F. and Roney-Dougal, C. M., The Maximal Subgroups of the Low-dimensional Finite Classical Groups, London Mathematical Society Lecture Note Series, 407 (Cambridge University Press, Cambridge, 2013).CrossRefGoogle Scholar
Burness, T. C., Liebeck, M. W. and Shalev, A., ‘Generation and random generation: From simple groups to maximal subgroups’, Adv. Math. 248 (2013), 59–95.CrossRefGoogle Scholar
Burness, T. C., O’Brien, E. A. and Wilson, R. A., ‘Base sizes for sporadic simple groups’, Israel J. Math. 177 (2010), 307–334.Google Scholar
Carter, R. W., Simple Groups of Lie Type (John Wiley and Sons, London–New York–Sydney, 1972).Google Scholar
Cohen, A. M., Liebeck, M. W., Saxl, J. and Seitz, G. M., ‘The local maximal subgroups of exceptional groups of Lie type’, Proc. Lond. Math. Soc. (3) 64 (1992), 21–48.Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups, (Oxford University Press, Eynsham, 1985).Google Scholar
Dalla Volta, F. and Lucchini, A., ‘Generation of almost simple groups’, J. Algebra 178 (1995), 194–223.CrossRefGoogle Scholar
Dickson, L. E., Linear Groups with an Exposition of the Galois Field Theory (Teubner, Leipzig, 1901), (Dover reprint 1958).Google Scholar
Feit, W., ‘An interval in the subgroup lattice of a finite group which is isomorphic to M 7 ’, Algebra Universalis 17 (1983), 220–221.Google Scholar
Jaikin-Zapirain, A. and Pyber, L., ‘Random generation of finite and profinite groups and group enumeration’, Ann. of Math. (2) 173 (2011), 769–814.Google Scholar
Kantor, W. M. and Lubotzky, A., ‘The probability of generating a finite classical group’, Geom. Dedicata 36 (1990), 67–87.CrossRefGoogle Scholar
Kleidman, P. B., ‘The maximal subgroups of the finite 8-dimensional orthogonal groups P𝛺8 +(q) and of their automorphism groups’, J. Algebra 110 (1987), 173–242.Google Scholar
Kleidman, P. B. and Liebeck, M. W., The Subgroup Structure of the Finite Classical Groups, London Mathematical Society Lecture Note Series, 129 (Cambridge University Press, Cambridge, 1990).Google Scholar
Liebeck, M. W., Martin, B. M. S. and Shalev, A., ‘On conjugacy classes of maximal subgroups of finite simple groups, and a related zeta function’, Duke Math. J. 128 (2005), 541–557.Google Scholar
Liebeck, M. W., Praeger, C. E. and Saxl, J., ‘A classification of the maximal subgroups of the finite alternating and symmetric groups’, J. Algebra 111 (1987), 365–383.Google Scholar
Liebeck, M. W., Saxl, J. and Seitz, G. M., ‘Subgroups of maximal rank in finite exceptional groups of Lie type’, Proc. Lond. Math. Soc. (3) 65 (1992), 297–325.CrossRefGoogle Scholar
Liebeck, M. W. and Seitz, G. M., ‘Maximal subgroups of exceptional groups of Lie type, finite and algebraic’, Geom. Dedicata 36 (1990), 353–387.Google Scholar
Liebeck, M. W. and Seitz, G. M., ‘A survey of of maximal subgroups of exceptional groups of Lie type’, inGroups, Combinatorics and Geometry (Durham, 2001) (World Science Publishing, River Edge, NJ, 2003), 139–146.Google Scholar
Liebeck, M. W. and Shalev, A., ‘The probability of generating a finite simple group’, Geom. Dedicata 56 (1995), 103–113.CrossRefGoogle Scholar
Lubotzky, A., ‘The expected number of random elements to generate a finite group’, J. Algebra 257 (2002), 452–459.CrossRefGoogle Scholar
Lucchini, A. and Menegazzo, F., ‘Generators for finite groups with a unique minimal normal subgroup’, Rend. Semin. Mat. Univ. Padova 98 (1997), 173–191.Google Scholar
Mann, A., ‘Positively finitely generated groups’, Forum Math. 8 (1996), 429–459.Google Scholar
Mann, A. and Shalev, A., ‘Simple groups, maximal subgroups, and probabilistic aspects of profinite groups’, Israel J. Math. 96 (1996), 449–468.Google Scholar
Pak, I., ‘On probability of generating a finite group’, Preprint, 1999, http://www.math.ucla.edu/∼pak/papers/sim.pdf.Google Scholar
Pálfy, P. P., ‘On Feit’s examples of intervals in subgroup lattices’, J. Algebra 116 (1988), 471–479.Google Scholar
Steinberg, R., ‘Generators for simple groups’, Canad. J. Math. 14 (1962), 277–283.Google Scholar
Suzuki, M., ‘On a class of doubly transitive groups’, Ann. of Math. (2) 75 (1962), 105–145.Google Scholar
Thévenaz, J., ‘Maximal subgroups of direct products’, J. Algebra 198 (1997), 352–361.Google Scholar
Ward, H. N., ‘On Ree’s series of simple groups’, Trans. Amer. Math. Soc. 121 (1966), 62–89.Google Scholar
Wilson, R. A. et al. , ‘A World-Wide-Web Atlas of finite group representations’, http://brauer.maths.qmul.ac.uk/Atlas/v3/.Google Scholar