Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
EnglishFrançais
Forum of Mathematics, Sigma Forum of Mathematics, Sigma

Article contents

GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  30 June 2020

ANDREA LUCCHINI ,
CLAUDE MARION  and
GARETH TRACEY
ANDREA LUCCHINI
Affiliation:
Dipartimento di Matematica Tullio Levi-Civita, Università degli Studi di Padova, 35121-IPadova, Italy; lucchini@math.unipd.it
CLAUDE MARION
Affiliation:
CMUP, Departamento de Matemática, Universidade do Porto, 4169-007Porto, Portugal; claude.marion@fc.up.pt
GARETH TRACEY
Affiliation:
Department of Mathematical Sciences, University of Bath, BathBA2 7AY, UK; gmt29@bath.ac.uk
Corresponding
E-mail address:
lucchini@math.unipd.it
claude.marion@fc.up.pt
gmt29@bath.ac.uk
Save pdf (0.45 mb)

Abstract

For a finite group 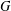$G$ , let 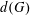$d(G)$ denote the minimal number of elements required to generate 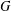$G$ . In this paper, we prove sharp upper bounds on 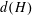$d(H)$ whenever 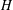$H$ is a maximal subgroup of a finite almost simple group. In particular, we show that 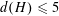$d(H)\leqslant 5$ and that 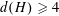$d(H)\geqslant 4$ if and only if 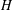$H$ occurs in a known list. This improves a result of Burness, Liebeck and Shalev. The method involves the theory of crowns in finite groups.

MSC classification

Primary: 20F05: Generators, relations, and presentations
Secondary: 20D05: Finite simple groups and their classification 20E28: Maximal subgroups
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e32
Creative Commons
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Aschbacher, M., ‘On the maximal subgroups of the finite classical groups’, Invent. Math. 76 (1984), 469–514.CrossRefGoogle Scholar
Aschbacher, M. and Guralnick, R., ‘Some applications of the first cohomology group’, J. Algebra 90 (1984), 446–460.CrossRefGoogle Scholar
Aschbacher, M. and Scott, L., ‘Maximal subgroups of finite groups’, J. Algebra 92 (1985), 44–80.CrossRefGoogle Scholar
Aschbacher, M. and Seitz, G. M., ‘Involutions in Chevalley groups over fields of even order’, Nagoya Math. J. 63 (1976), 1–91.CrossRefGoogle Scholar
Azad, H., Barry, M. and Seitz, G., ‘On the structure of parabolic subgroups’, Comm. Algebra 18(2) (1990), 551–562.CrossRefGoogle Scholar
Ballester-Bolinches, A. and Ezquerro, L. M., Classes of Finite Groups, Mathematics and Its Applications (Springer), 584 (Springer, Dordrecht, 2006).Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Bourbaki, N., Groupes et algèbres de Lie - Chapitres 4,5, et 6, 2nd edn, (Springer, Berlin, Heidelberg, Paris, 1972).Google Scholar
Bray, J. N., Holt, D. F. and Roney-Dougal, C. M., The Maximal Subgroups of the Low-Dimensional Finite Classical Groups, Lecture Note Series, 407 (London Mathematical Society, Cambridge, 2013).CrossRefGoogle Scholar
Burness, T., Liebeck, M. and Shalev, A., ‘Generation and random generation: From simple groups to maximal subgroups’, Adv. Math. 248 (2013), 59–95.CrossRefGoogle Scholar
Cameron, P., Lucchini, A. and Roney-Dougal, C., ‘Generating sets of finite groups’, Trans. Amer. Math. Soc. 370(9) (2018), 6751–6770.CrossRefGoogle Scholar
Carter, R., ‘Centralizers of semisimple elements in finite groups of Lie type’, Proc. Lond. Math. Soc. 37 (1978), 491–507.CrossRefGoogle Scholar
Cohen, A., Liebeck, M., Saxl, J. and Seitz, G., ‘The local maximal subgroups of the exceptional groups of Lie type, finite and algebraic’, Proc. Lond. Math. Soc. 64(3) (1992), 21–48.CrossRefGoogle Scholar
Connor, T. and Leemans, D., ‘An atlas of subgroup lattices of finite almost simple groups’, Ars Math. Contemp. 8 (2015), 259–266.CrossRefGoogle Scholar
Conway, J., Curtis, R., Norton, S., Parker, R. and Wilson, R., Atlas of Finite Groups, (Oxford University Press, Eynsham, 1985).Google Scholar
Curtis, C. W. and Reiner, I., Representation Theory of Finite Groups and Associative Algebras, (AMS Chelsea Publishing, Providence, RI, 2006), Reprint of the 1962 original.CrossRefGoogle Scholar
Dalla Volta, F. and Lucchini, A., ‘Generation of almost simple groups’, J. Algebra 178 (1995), 194–223.CrossRefGoogle Scholar
Dalla Volta, F. and Lucchini, A., ‘Finite groups that need more generators than any proper quotient’, J. Aust. Math. Soc. 64 (1998), 82–91.Google Scholar
Dalla Volta, F., Lucchini, A. and Morini, F., ‘On the probability of generating a minimal d-generated group’, J. Aust. Math. Soc. 71 (2001), 177–185.CrossRefGoogle Scholar
Detomi, E. and Lucchini, A., ‘Crowns and factorization of the probabilistic zeta function of a finite group’, J. Algebra 265 (2003), 651–668.CrossRefGoogle Scholar
Detomi, E. and Lucchini, A., ‘Probabilistic generation of finite groups with a unique minimal normal subgroup’, J. Lond. Math. Soc. 87 (2013), 689–706.CrossRefGoogle Scholar
Flaass, D., ‘2-local subgroups of Fischer’s groups’, Mat. Zametki 35 (1984), 333–342.Google Scholar
Förster, P., ‘Chief factors, crowns, and the generalized Jordan–Hölder theorem’, Comm. Algebra 16 (1988), 1627–1638.CrossRefGoogle Scholar
Gaschütz, W., ‘Praefrattinigruppen’, Arch. Math. 13 (1962), 418–426.CrossRefGoogle Scholar
Gorenstein, D. and Lyons, R., ‘The local structure of finite groups of characteristic 2 type’, Mem. Amer. Math. Soc. 42 (1983), 1–731.Google Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups Number Three, Mathematical Surveys and Monographs, 40 (3) (American Mathematical Society, Providence, 1991).Google Scholar
Holmes, P. E. and Wilson, R. A., ‘A new computer construction of the Monster using 2-local subgroups’, J. Lond. Math. Soc. 67 (2003), 349–364.CrossRefGoogle Scholar
Humphreys, J., Linear Algebraic Groups, (Springer, New York, 1975).CrossRefGoogle Scholar
Jiménez-Seral, P. and Lafuente, J. P., ‘On complemented non-abelian chief factors of a finite group’, Israel J. Math. 106 (1998), 177–188.CrossRefGoogle Scholar
Kleidman, P., ‘The maximal subgroups of the finite 8-dimensional orthogonal groups P𝛺8+(q) and of their automorphism groups’, J. Algebra 110 (1987), 173–242.CrossRefGoogle Scholar
Kleidman, P. and Liebeck, M., The Subgroup Structure of the Finite Classical Groups, London Mathematical Society Lecture Note Series, 129 (Cambridge University Press, 1990).CrossRefGoogle Scholar
Kleidman, P., Parker, R. and Wilson, R., ‘The maximal subgroups of the Fisher group Fi 23’, J. Lond. Math. Soc. 39 (1989), 89–101.CrossRefGoogle Scholar
Kleidman, P. and Wilson, R., ‘The maximal subgroups of Fi 22’, Math. Proc. Cambridge Philos. Soc. 102 (1987), 17–23.CrossRefGoogle Scholar
Liebeck, M., Saxl, J. and Seitz, G., ‘Subgroups of maximal rank in finite exceptional groups of Lie type’, Proc. Lond. Math. Soc. (3) 65 (1992), 297–325.CrossRefGoogle Scholar
Liebeck, M. and Seitz, G., ‘Maximal subgroups of exceptional groups of Lie type, finite and algebraic’, Geom. Dedicata 35(1–3) (1990), 353–387.CrossRefGoogle Scholar
Linton, S. and Wilson, R., ‘The maximal subgroups of the Fischer groups Fi 24 and Fi 24′’, Proc. Lond. Math. Soc. 63 (1991), 113–164.CrossRefGoogle Scholar
Lucchini, A. and Menegazzo, F., ‘Generators for finite groups with a unique minimal normal subgroup’, Rend. Semin. Mat. Univ. Padova 98 (1997), 173–191.Google Scholar
Lucchini, A. and Morini, F., ‘On the probability of generating finite groups with a unique minimal normal subgroup’, Pac. J. Math. 203 (2002), 429–440.CrossRefGoogle Scholar
Lyndon, R. and Schupp, P., Combinatorial Group Theory (Springer, Berlin, 1977).Google Scholar
Malle, G. and Testerman, D., Linear Algebraic Groups and Finite Groups of Lie Type, Cambridge Studies in Advanced Mathematics, 133 (Cambridge University Press, Cambridge, 2011).CrossRefGoogle Scholar
Meierfrankenfeld, U. and Shpectorov, S. V., ‘Maximal 2-local subgroups of the Monster and Baby Monster’, Preprint, 2002. Michigan State University, Available from http://www.mth.msu.edu/meier/Preprints/2monster/maxmon.pdf.Google Scholar
Menezes, N., Quick, M. and Roney-Dougal, C., ‘The probability of generating a finite simple group’, Israel J. Math. 198(1) (2013), 371–392.CrossRefGoogle Scholar
Miller, G., ‘On the groups generated by two operators’, Bull. Amer. Math. Soc. 7 (1901), 424–426.CrossRefGoogle Scholar
Norton, S. and Wilson, R., ‘Maximal subgroups of the Harada–Norton Group’, J. Algebra 103 (1986), 362–376.CrossRefGoogle Scholar
Norton, S. and Wilson, R., ‘A correction to the 41-structure of the Monster, a construction of a new maximal subgroup Ł 2(41) and a new Moonshine phenomenon’, J. Lond. Math. Soc. 87 (2013), 943–962.CrossRefGoogle Scholar
Seitz, G., ‘Generation of finite groups of Lie type’, Trans. Amer. Math. Soc. 271 (1982), 351–407.CrossRefGoogle Scholar
Steinberg, R., ‘Generators for simple groups’, Canad. J. Math. 14 (1962), 277–283.CrossRefGoogle Scholar
Wilson, R., ‘The maximal subgroups of Conway’s group Co 1’, J.  Algebra 85 (1983), 144–165.CrossRefGoogle Scholar
Wilson, R., ‘Some subgroups of the Baby Monster’, Invent. Math. 89 (1987), 197–218.CrossRefGoogle Scholar
Wilson, R., ‘The local subgroups of the Fischer groups’, J. Lond. Math. Soc. (2) 36 (1987), 77–94.CrossRefGoogle Scholar
Wilson, R., ‘The maximal subgroups of the Baby Monster, I’, J. Algebra 211 (1999), 1–14.CrossRefGoogle Scholar
Wilson, R., Parker, R., Nickerson, S., Breuer, T. and Bray, J., ‘AtlasRep, A GAP Interface to the Atlas of Group Representations’, Version 1.5.1 (2016), http://www.math.rwth-aachen.de/∼Thomas.Breuer/atlasrep.Google Scholar
Wilson, R. et al. , ‘A World-Wide-Web Atlas of finite group representations’,http://brauer.maths.qmul.ac.uk/Atlas/v3/.Google Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 115 *
View data table for this chart

* Views captured on Cambridge Core between 30th June 2020 - 23rd January 2021. This data will be updated every 24 hours.

Access
Open access
Hostname: page-component-76cb886bbf-gtgjg Total loading time: 0.318 Render date: 2021-01-23T05:43:52.659Z Query parameters: { "hasAccess": "1", "openAccess": "1", "isLogged": "0", "lang": "en" } Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false }

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *