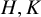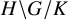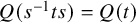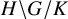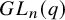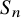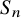1 Introduction
This paper develops tools which allow projecting a random walk on a group to a Markov chain on special equivalence classes of the group. Fourier analysis on the group can then be harnessed to give sharp analysis of rates of convergence to stationarity for the Markov chain on equivalence classes. We begin with a motivating example.
Example 1.1 (Coagulation-fragmentation processes).
In chemistry and physics, coagulation-fragmentation processes are models used to capture the behavior of ‘blobs’ that combine and break up over time. These processes are used in population genetics to model the merging and splitting of family groups. A simple mean field model considers n unlabeled particles in a partition
![]() $\lambda = (\lambda _1, \dots , \lambda _k)$
,
$\lambda = (\lambda _1, \dots , \lambda _k)$
,
![]() ,
,
![]() $\sum _{i = 1}^k \lambda _i = n$
. At each step of the process, a pair of particles is chosen uniformly at random and the partition evolves according to the rules:
$\sum _{i = 1}^k \lambda _i = n$
. At each step of the process, a pair of particles is chosen uniformly at random and the partition evolves according to the rules:
-
1. If the particles are in distinct blocks, combine the blocks.
-
2. If the particles are in the same block, break the block uniformly into two blocks.
-
3. If the same particle is chosen twice, do nothing.
This defines a Markov chain on partitions of n. Natural questions are:
-
• What is the stationary distribution
 $\pi (\lambda )$
?
$\pi (\lambda )$
? -
• How does the process evolve?
-
• How long to reach stationarity?
All of these questions can be answered by considering the random transpositions process on the symmetric group
![]() $S_n$
. The transition probabilities for this process are constant on conjugacy classes, the conjugacy classes are indexed by partitions and the conjugacy class containing the current permutation of the walk evolves as the coagulation-fragmentation process on partitions. The answers are (see section 2.3):
$S_n$
. The transition probabilities for this process are constant on conjugacy classes, the conjugacy classes are indexed by partitions and the conjugacy class containing the current permutation of the walk evolves as the coagulation-fragmentation process on partitions. The answers are (see section 2.3):
-
• The stationary distribution is
 $\pi (\lambda ) = \prod _{i=1}^n 1/(i^{a_i} a_i!)$
for a partition
$\pi (\lambda ) = \prod _{i=1}^n 1/(i^{a_i} a_i!)$
for a partition
 $\lambda $
with
$\lambda $
with
 $a_i$
parts of size i.
$a_i$
parts of size i. -
• Starting at
 $\lambda = 1^n$
, the pieces evolve as the connected components of a growing Erdős-Rényi random graph process: Initially there are n vertices and no edges. Random edges are added to the graph so that the connected components correspond to the parts of a partition
$\lambda = 1^n$
, the pieces evolve as the connected components of a growing Erdős-Rényi random graph process: Initially there are n vertices and no edges. Random edges are added to the graph so that the connected components correspond to the parts of a partition
 $\lambda $
of n. This works as long as there are no repeated edges
$\lambda $
of n. This works as long as there are no repeated edges
 $(i, j)$
(so for number of steps of smaller order than n). Repeated edges can be easily handled so that there is a tight connection between the growth of the random graph and the random transpositions Markov chain. In particular, random transpositions mix in order
$(i, j)$
(so for number of steps of smaller order than n). Repeated edges can be easily handled so that there is a tight connection between the growth of the random graph and the random transpositions Markov chain. In particular, random transpositions mix in order
 $(1/2)n \log n$
, which is the same amount of time for the random graph to become connected. See [Reference Berestycki, Schramm and Zeitouni6] for more details.
$(1/2)n \log n$
, which is the same amount of time for the random graph to become connected. See [Reference Berestycki, Schramm and Zeitouni6] for more details. -
• It takes order
 $n \log n$
steps to reach stationarity.
$n \log n$
steps to reach stationarity.
The coagulation-fragmentation process is a special case of a double coset walk: Let G be a finite group,
![]() $H, K$
subgroups of G. The equivalence relation
$H, K$
subgroups of G. The equivalence relation
partitions the group into double cosets
![]() $H \backslash G / K$
. Let
$H \backslash G / K$
. Let
![]() $Q(s)$
be a probability measure on G. That is,
$Q(s)$
be a probability measure on G. That is,
![]() $0 \le Q(s) \le 1$
for all
$0 \le Q(s) \le 1$
for all
![]() $s \in G$
and
$s \in G$
and
![]() $\sum _{s \in G} Q(s) = 1$
. Further assume
$\sum _{s \in G} Q(s) = 1$
. Further assume
![]() $Q(s)$
is a class function: It is constant on conjugacy classes, that is,
$Q(s)$
is a class function: It is constant on conjugacy classes, that is,
![]() $Q(s) = Q(t^{-1} s t)$
for all
$Q(s) = Q(t^{-1} s t)$
for all
![]() $s, t \in G$
. Then Q defines a random walk on G by repeated multiplication of random elements chosen according to Q. In other words, the random walk is induced by convolution,
$s, t \in G$
. Then Q defines a random walk on G by repeated multiplication of random elements chosen according to Q. In other words, the random walk is induced by convolution,
![]() $Q^{*k}(s) = \sum _{t \in G} Q(t) Q^{*(k-1)}(s t^{-1})$
and a single transition step has probability
$Q^{*k}(s) = \sum _{t \in G} Q(t) Q^{*(k-1)}(s t^{-1})$
and a single transition step has probability
![]() $P(x, y) = Q(yx^{-1})$
.
$P(x, y) = Q(yx^{-1})$
.
This random walk induces a random process on the space of double cosets. While usually a function of a Markov chain is no longer a Markov chain, in this situation the image of the random walk on
![]() $H \backslash G / K$
is Markov. Section 2.2 proves the following general result. Throughout, we pick double coset representatives
$H \backslash G / K$
is Markov. Section 2.2 proves the following general result. Throughout, we pick double coset representatives
![]() $x \in G$
and write x for
$x \in G$
and write x for
![]() $H x K$
.
$H x K$
.
Theorem 1.2. For
![]() $Q(s) = Q(t^{-1} s t)$
a probability on G, the induced process on
$Q(s) = Q(t^{-1} s t)$
a probability on G, the induced process on
![]() $H \backslash G / K$
is Markov with the following properties.
$H \backslash G / K$
is Markov with the following properties.
-
1. The transitions are
 $$\begin{align*}P(x, y) = Q(HyKx^{-1}), \quad x, y \in H \backslash G /K. \end{align*}$$
$$\begin{align*}P(x, y) = Q(HyKx^{-1}), \quad x, y \in H \backslash G /K. \end{align*}$$
-
2. The stationary distribution is
 $$\begin{align*}\pi(x) = \frac{|HxK|}{|G|}. \end{align*}$$
$$\begin{align*}\pi(x) = \frac{|HxK|}{|G|}. \end{align*}$$
-
3. If
 $Q(s^{-1}) = Q(s)$
, then P is reversible with respect to
$Q(s^{-1}) = Q(s)$
, then P is reversible with respect to
 $\pi $
:
$\pi $
:  $$\begin{align*}\pi(x)P(x, y) = \pi(y)P(y, x). \end{align*}$$
$$\begin{align*}\pi(x)P(x, y) = \pi(y)P(y, x). \end{align*}$$
Further, suppose Q is concentrated on a single conjugacy class
![]() $\mathcal {C}$
(that is,
$\mathcal {C}$
(that is,
![]() $Q(s) = \delta _{\mathcal {C}}(s)/|\mathcal {C}|$
). Then the Markov chain P has the following properties.
$Q(s) = \delta _{\mathcal {C}}(s)/|\mathcal {C}|$
). Then the Markov chain P has the following properties.
-
1. The eigenvalues of P are among the set
where $$\begin{align*}\left\lbrace \frac{\chi_{\lambda}(\mathcal{C})}{\chi_{\lambda}(1)} \right\rbrace_{\lambda \in \widehat{G}}, \end{align*}$$
$$\begin{align*}\left\lbrace \frac{\chi_{\lambda}(\mathcal{C})}{\chi_{\lambda}(1)} \right\rbrace_{\lambda \in \widehat{G}}, \end{align*}$$
 $\widehat {G}$
is the set of all irreducible representations of G and
$\widehat {G}$
is the set of all irreducible representations of G and
 $\chi _{\lambda }$
is the character of the irreducible representation indexed by
$\chi _{\lambda }$
is the character of the irreducible representation indexed by
 $\lambda $
.
$\lambda $
.
-
2. The multiplicity of
 $\chi _{\lambda }(\mathcal {C})/\chi _{\lambda }(1)$
is where
$\chi _{\lambda }(\mathcal {C})/\chi _{\lambda }(1)$
is where $$\begin{align*}m_{\lambda} = \left\langle \chi_{\lambda}|_H, 1 \right\rangle \cdot \left\langle \chi_{\lambda}|_K, 1 \right\rangle, \end{align*}$$
$$\begin{align*}m_{\lambda} = \left\langle \chi_{\lambda}|_H, 1 \right\rangle \cdot \left\langle \chi_{\lambda}|_K, 1 \right\rangle, \end{align*}$$
 $\left \langle \chi _{\lambda }|_H, 1 \right \rangle $
is the number of times the trivial representation appears when
$\left \langle \chi _{\lambda }|_H, 1 \right \rangle $
is the number of times the trivial representation appears when
 $\chi _{\lambda }$
is restricted to H.
$\chi _{\lambda }$
is restricted to H.
-
3. For any time
 $\ell> 0$
,
$\ell> 0$
,  $$\begin{align*}\sum_{x \in H \backslash G /K} \pi(x) \|P_x^{\ell} - \pi \|_{TV}^2 \le \frac{1}{4} \sum_{\lambda \neq 1} m_{\lambda} {\left| \frac{\chi_{\lambda}(\mathcal{C})}{\chi_{\lambda}(1)} \right|}^{2 \ell}. \end{align*}$$
$$\begin{align*}\sum_{x \in H \backslash G /K} \pi(x) \|P_x^{\ell} - \pi \|_{TV}^2 \le \frac{1}{4} \sum_{\lambda \neq 1} m_{\lambda} {\left| \frac{\chi_{\lambda}(\mathcal{C})}{\chi_{\lambda}(1)} \right|}^{2 \ell}. \end{align*}$$
This theorem shows that the properties of the induced chain are available via the character theory of G. It is proved with variations and extensions in Section 2.2. The main example is introduced next.
Example 1.3 (
 $GL_n(q)$
and Gaussian elimination).
$GL_n(q)$
and Gaussian elimination).
Fix a prime power q, and let
![]() $GL_n(q)$
be the invertible
$GL_n(q)$
be the invertible
![]() $n \times n$
matrices over
$n \times n$
matrices over
![]() $\mathbb {F}_q$
. Let
$\mathbb {F}_q$
. Let
![]() $H = K = \mathcal {B}$
be the Borel subgroup: upper-triangular matrices in
$H = K = \mathcal {B}$
be the Borel subgroup: upper-triangular matrices in
![]() $GL_n(q)$
. A classical result is the Bruhat decomposition,
$GL_n(q)$
. A classical result is the Bruhat decomposition,
where
![]() $\omega $
is the permutation matrix for the permutation
$\omega $
is the permutation matrix for the permutation
![]() $\omega \in S_n$
. This decomposition shows that the double cosets
$\omega \in S_n$
. This decomposition shows that the double cosets
![]() $\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
are indexed by permutations. As explained in Section 2.5 below, the permutation
$\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
are indexed by permutations. As explained in Section 2.5 below, the permutation
![]() $\omega $
associated to
$\omega $
associated to
![]() $M \in GL_n(q)$
is the ‘pivotal’ permutation when M is reduced to upper-triangular form by row reduction (Gaussian elimination).
$M \in GL_n(q)$
is the ‘pivotal’ permutation when M is reduced to upper-triangular form by row reduction (Gaussian elimination).
The set of transvections
![]() $\mathcal {T}_{n,q}$
is the conjugacy class containing the basic row operations
$\mathcal {T}_{n,q}$
is the conjugacy class containing the basic row operations
![]() $I + \theta E_{ij}$
; here,
$I + \theta E_{ij}$
; here,
![]() $\theta \in \mathbb {F}_q$
, and
$\theta \in \mathbb {F}_q$
, and
![]() $E_{ij}$
is the matrix with a
$E_{ij}$
is the matrix with a
![]() $1$
in position
$1$
in position
![]() $(i, j)$
and zeroes everywhere else (so
$(i, j)$
and zeroes everywhere else (so
![]() $I + \theta E_{ij}$
acts by adding
$I + \theta E_{ij}$
acts by adding
![]() $\theta $
times row i to row j). Hildebrand [Reference Hildebrand35] gave sharp convergence results for the Markov chain on
$\theta $
times row i to row j). Hildebrand [Reference Hildebrand35] gave sharp convergence results for the Markov chain on
![]() $GL_n(q)$
generated by the class function Q which gives equal probability to all transvections. He shows that n steps are necessary and sufficient for convergence to the uniform distribution for any q. Of course, convergence of the lumped chain on
$GL_n(q)$
generated by the class function Q which gives equal probability to all transvections. He shows that n steps are necessary and sufficient for convergence to the uniform distribution for any q. Of course, convergence of the lumped chain on
![]() $\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
might be faster. The results we found surprised us. Careful statements are included below. At a high level, we found:
$\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
might be faster. The results we found surprised us. Careful statements are included below. At a high level, we found:
-
• Starting from a ‘typical’ state
 $x \in S_n$
, order
$x \in S_n$
, order
 $\log n/\log q$
steps are necessary and sufficient for convergence. This is an exponential speed-up from the original chain.
$\log n/\log q$
steps are necessary and sufficient for convergence. This is an exponential speed-up from the original chain. -
• Starting from
 $id$
, order n steps are necessary and sufficient for convergence.
$id$
, order n steps are necessary and sufficient for convergence. -
• Starting from
 $\omega _0$
, the reversal permutation, order
$\omega _0$
, the reversal permutation, order
 $\log n/(2\log q)$
steps are necessary and sufficient for convergence.
$\log n/(2\log q)$
steps are necessary and sufficient for convergence.
To simplify the statement of an honest theorem, let us measure convergence in the usual chi-square or
![]() $L^2$
distance:
$L^2$
distance:
 $$\begin{align*}\chi^2_x(\ell) = \sum_y \frac{\left( P^{\ell}(x, y) - \pi_q(y) \right)^2}{\pi_q(y)}. \end{align*}$$
$$\begin{align*}\chi^2_x(\ell) = \sum_y \frac{\left( P^{\ell}(x, y) - \pi_q(y) \right)^2}{\pi_q(y)}. \end{align*}$$
In Section 3, the usual total variation distance is treated as well.
Theorem 1.4. The random transvections walk on
![]() $GL_n(q)$
induces a Markov chain
$GL_n(q)$
induces a Markov chain
![]() $P(x, y)$
on
$P(x, y)$
on
![]() $S_n \cong \mathcal {B} \backslash GL_n(q) / \mathcal {B}$
with stationary distribution.
$S_n \cong \mathcal {B} \backslash GL_n(q) / \mathcal {B}$
with stationary distribution.
for
![]() $\omega \in S_n$
, where
$\omega \in S_n$
, where
![]() $I(\omega ) = | \{ (i, j): i < j, \omega (i)> \omega (j) \}|$
is the number of inversions in
$I(\omega ) = | \{ (i, j): i < j, \omega (i)> \omega (j) \}|$
is the number of inversions in
![]() $\omega $
.
$\omega $
.
Furthermore, if
![]() $\log q> 6/n$
then the following statements are true.
$\log q> 6/n$
then the following statements are true.
-
1. (Typical start) If
 $\ell \ge (\log n + c)/(\log q - 6/n)$
for any
$\ell \ge (\log n + c)/(\log q - 6/n)$
for any
 $c> 0$
, then
$c> 0$
, then  $$\begin{align*}\sum_{x \in S_n} \pi(x) \chi_x^2(\ell) \le (e^{e^{-c}} - 1) + e^{-cn}. \end{align*}$$
$$\begin{align*}\sum_{x \in S_n} \pi(x) \chi_x^2(\ell) \le (e^{e^{-c}} - 1) + e^{-cn}. \end{align*}$$
Conversely, for any
 $\ell $
$\ell $
 $$\begin{align*}\sum_{x \in S_n} \pi(x) \chi_x^2(\ell) \ge (n-1)^2 q^{-4 \ell}. \end{align*}$$
$$\begin{align*}\sum_{x \in S_n} \pi(x) \chi_x^2(\ell) \ge (n-1)^2 q^{-4 \ell}. \end{align*}$$
These results show order
 $\log _q(n)$
steps are necessary and sufficient for convergence.
$\log _q(n)$
steps are necessary and sufficient for convergence. -
2. (Starting from
 $id$
) If
$id$
) If
 $\ell \ge (n \log q/2 + c)/(\log q - 6/n), c> 0$
, then
$\ell \ge (n \log q/2 + c)/(\log q - 6/n), c> 0$
, then  $$ \begin{align*} \chi_{id}^2(\ell) \le (e^{e^{-2c}} - 1) + e^{-cn}. \end{align*} $$
$$ \begin{align*} \chi_{id}^2(\ell) \le (e^{e^{-2c}} - 1) + e^{-cn}. \end{align*} $$
Conversely, for any
 $\ell $
,
$\ell $
,  $$\begin{align*}\chi_{id}^2(\ell) \ge (n - 1)(q^{n-1} - 1)q^{-4 \ell}. \end{align*}$$
$$\begin{align*}\chi_{id}^2(\ell) \ge (n - 1)(q^{n-1} - 1)q^{-4 \ell}. \end{align*}$$
These results show that order n steps are necessary and sufficient for convergence starting from the identity.
-
3. (Starting from
 $\omega _0$
) If
$\omega _0$
) If
 $\ell \ge (\log n/2 + c)/(\log q - 6/n)$
for
$\ell \ge (\log n/2 + c)/(\log q - 6/n)$
for
 $c \ge 2 \sqrt {2}$
, then there is a universal constant
$c \ge 2 \sqrt {2}$
, then there is a universal constant
 $K> 0$
(independent of
$K> 0$
(independent of
 $q, n$
) such that
$q, n$
) such that  $$ \begin{align*} \chi_{\omega_0}^2(\ell) \le - 2K \log(1 - e^{-c}) + K e^{-cn}. \end{align*} $$
$$ \begin{align*} \chi_{\omega_0}^2(\ell) \le - 2K \log(1 - e^{-c}) + K e^{-cn}. \end{align*} $$
Conversely, for any
 $\ell $
,
$\ell $
,  $$\begin{align*}\chi_{\omega_0}^2(\ell) \ge q^{-(n-2)}(n-1) (q^{n-1} -1) q^{-4 \ell}. \end{align*}$$
$$\begin{align*}\chi_{\omega_0}^2(\ell) \ge q^{-(n-2)}(n-1) (q^{n-1} -1) q^{-4 \ell}. \end{align*}$$
These results show that order
 $\log _q(n)/2$
steps are necessary and sufficient for convergence starting from
$\log _q(n)/2$
steps are necessary and sufficient for convergence starting from
 $\omega _0$
.
$\omega _0$
.
Remark 1.5. Note that, while Hildebrand’s result of order n convergence rate was independent of the parameter q, the rates in Theorem 1.4 depend on q.
The stationary distribution
![]() $\pi _q$
is the Mallows measure on
$\pi _q$
is the Mallows measure on
![]() $S_n$
. This measure has a large enumerative literature; see [Reference Diaconis and Simper24] Section 3 for a review or [Reference Zhong64]. It is natural to ask what the induced chain ‘looks like’ on
$S_n$
. This measure has a large enumerative literature; see [Reference Diaconis and Simper24] Section 3 for a review or [Reference Zhong64]. It is natural to ask what the induced chain ‘looks like’ on
![]() $S_n$
. After all, the chain induced by random transpositions on partitions has a simple description and is of general interest. Is there a similarly simple description of the chain in
$S_n$
. After all, the chain induced by random transpositions on partitions has a simple description and is of general interest. Is there a similarly simple description of the chain in
![]() $S_n$
? This question is treated in Section 5 using the language of Hecke algebras.
$S_n$
? This question is treated in Section 5 using the language of Hecke algebras.
Theorem 1.6. Let
![]() $H_n(q)$
be the Hecke algebra corresponding to the
$H_n(q)$
be the Hecke algebra corresponding to the
![]() $\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
double cosets and
$\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
double cosets and
![]() $D = \sum _{T \in \mathcal {T}_{n,q}} T \in H_n(q)$
be the sum of all transvections. Then,
$D = \sum _{T \in \mathcal {T}_{n,q}} T \in H_n(q)$
be the sum of all transvections. Then,
 $$\begin{align*}D = (n - 1)q^{n-1} - [n-1]_q + (q-1) \sum_{1 \le i < j \le n} q^{n - 1 - (j-i)} T_{ij}, \end{align*}$$
$$\begin{align*}D = (n - 1)q^{n-1} - [n-1]_q + (q-1) \sum_{1 \le i < j \le n} q^{n - 1 - (j-i)} T_{ij}, \end{align*}$$
with
![]() $T_{ij}$
in the Hecke algebra.
$T_{ij}$
in the Hecke algebra.
This gives a probabilistic description of the induced chain on
![]() $S_n$
. Roughly stated, from
$S_n$
. Roughly stated, from
![]() $\omega \in S_n$
pick
$\omega \in S_n$
pick
![]() $(i,j), i < j,$
with probability proportional to
$(i,j), i < j,$
with probability proportional to
![]() $q^{-(j - i)}$
and transpose i and j in
$q^{-(j - i)}$
and transpose i and j in
![]() $\omega $
using the Metropolis algorithm (reviewed in Section 2.6). This description is explained in Section 5; see also [Reference Diaconis and Ram18]. The probabilistic description is crucial in obtaining good total variation lower bounds for Theorem 1.4.
$\omega $
using the Metropolis algorithm (reviewed in Section 2.6). This description is explained in Section 5; see also [Reference Diaconis and Ram18]. The probabilistic description is crucial in obtaining good total variation lower bounds for Theorem 1.4.
Outline
Section 2 develops and surveys background material on double cosets, Markov chains (proving Theorem 1.2), transpositions and coagulation-fragmentation processes, transvections and Gaussian elimination. Theorem 1.4 is proved in Section 3. Theorem 1.6 is proved in Section 5 using a row reduction. Section 6 contains another Markov chain from a lumping of the transvections chain, and Section 7 surveys further examples—contingency tables and extensions of the
![]() $GL_n$
results to finite groups of Lie type, for which the Bruhat decomposition holds and there are natural analogs of transvections. Of course, there are an infinite variety of groups
$GL_n$
results to finite groups of Lie type, for which the Bruhat decomposition holds and there are natural analogs of transvections. Of course, there are an infinite variety of groups
![]() $G, H, K$
, and we also indicate extensions to compact Lie groups.
$G, H, K$
, and we also indicate extensions to compact Lie groups.
We have posted a more leisurely, expository version of the present paper on the arXiv [Reference Diaconis, Ram and Simper19]. This contains more examples and proof details.
Notation
Throughout, q will be a prime power. For a positive integer n, define the quantities
2 Background
This section gives the basic definitions and tools needed to prove our main results. Section 2.1 gives background on double cosets. In Section 2.2, Markov chains are reviewed and Theorem 1.2 is proved, along with extensions. Section 2.3 reviews the coagulation-fragmentation literature along with the random transpositions literature. Section 2.4 develops what we need about transvections, and Section 2.5 connects the Bruhat decomposition to Gaussian elimination. Finally, Section 2.6 reviews the Metropolis algorithm.
2.1 Double cosets
Let
![]() $H, K$
be subgroups of a finite group G. The double coset decomposition is a standard tool of elementary group theory. The original proof of Sylow’s first theorem uses double cosets, as does Mackey’s basic theorems on decomposing restrictions of induced representations. The Hecke algebra
$H, K$
be subgroups of a finite group G. The double coset decomposition is a standard tool of elementary group theory. The original proof of Sylow’s first theorem uses double cosets, as does Mackey’s basic theorems on decomposing restrictions of induced representations. The Hecke algebra
![]() $\mathrm {End}_{G}(G/H)$
—the linear maps of the right H-invariant functions that commute with the action of G—has a basis induced by H-H double cosets. Hecke algebras are basic objects of study in modern number theory. For a detailed survey, see [Reference Diaconis and Simper24] or [Reference Curtis and Reiner14]. Double cosets can have very different sizes and [Reference Diaconis and Simper24], [Reference Paguyo48] develop a probabilistic and enumerative theory. For present applications, an explicit description of the double cosets is needed.
$\mathrm {End}_{G}(G/H)$
—the linear maps of the right H-invariant functions that commute with the action of G—has a basis induced by H-H double cosets. Hecke algebras are basic objects of study in modern number theory. For a detailed survey, see [Reference Diaconis and Simper24] or [Reference Curtis and Reiner14]. Double cosets can have very different sizes and [Reference Diaconis and Simper24], [Reference Paguyo48] develop a probabilistic and enumerative theory. For present applications, an explicit description of the double cosets is needed.
Example 2.1. Let
![]() $S_{\lambda }, S_{\mu }$
be parabolic subgroups of the symmetric group
$S_{\lambda }, S_{\mu }$
be parabolic subgroups of the symmetric group
![]() $S_n$
. Here,
$S_n$
. Here,
![]() $\lambda = (\lambda _1, \dots , \lambda _I)$
and
$\lambda = (\lambda _1, \dots , \lambda _I)$
and
![]() $\mu = (\mu _1, \dots , \mu _J)$
are partitions of n. The subgroup
$\mu = (\mu _1, \dots , \mu _J)$
are partitions of n. The subgroup
![]() $S_{\lambda }$
consists of all permutations in which the first
$S_{\lambda }$
consists of all permutations in which the first
![]() $\lambda _1$
elements may only be permuted amongst each other, the next
$\lambda _1$
elements may only be permuted amongst each other, the next
![]() $\lambda _1 + 1, \dots , \lambda _1 + \lambda _2$
elements may only be permuted amongst each other and so on. It is a classical fact that the double cosets
$\lambda _1 + 1, \dots , \lambda _1 + \lambda _2$
elements may only be permuted amongst each other and so on. It is a classical fact that the double cosets
![]() $S_{\lambda } \backslash S_n / S_{\mu }$
are in bijection with ‘contingency tables’—arrays of nonnegative integers with row sums
$S_{\lambda } \backslash S_n / S_{\mu }$
are in bijection with ‘contingency tables’—arrays of nonnegative integers with row sums
![]() $\lambda $
and column sums
$\lambda $
and column sums
![]() $\mu $
. See [Reference James and Kerber38], Section 1.3. For proofs and much discussion of the connections between the group theory and applications and statistics, see [Reference Diaconis and Simper24], Section 5. Random transpositions on
$\mu $
. See [Reference James and Kerber38], Section 1.3. For proofs and much discussion of the connections between the group theory and applications and statistics, see [Reference Diaconis and Simper24], Section 5. Random transpositions on
![]() $S_n$
induces a natural Markov chain on these tables, see [Reference Simper60] and Chapter 3 of [Reference Simper59]. Contingency tables also label the double cosets of parabolic subgroups in
$S_n$
induces a natural Markov chain on these tables, see [Reference Simper60] and Chapter 3 of [Reference Simper59]. Contingency tables also label the double cosets of parabolic subgroups in
![]() $GL(n, Q)$
. See [Reference Karp and Thomas39] and Section 7.1 below.
$GL(n, Q)$
. See [Reference Karp and Thomas39] and Section 7.1 below.
Example 2.2. Let M be a finite group,
![]() $G = M \times M$
, and
$G = M \times M$
, and
![]() $H = K = M$
embedded diagonally as subgroups of G (that is,
$H = K = M$
embedded diagonally as subgroups of G (that is,
![]() $\{(m, m): m \in M \}$
). The conjugacy classes in G are products of conjugacy classes in each coordinate of M. In the double coset equivalency classes, note that
$\{(m, m): m \in M \}$
). The conjugacy classes in G are products of conjugacy classes in each coordinate of M. In the double coset equivalency classes, note that
and so double cosets can be indexed by conjugacy classes of M. If
![]() $Q_1$
is a conjugacy invariant probability on M, then
$Q_1$
is a conjugacy invariant probability on M, then
![]() $Q = Q_1 \times \delta _{id}$
is conjugacy invariant on G. The random walk on G induced by Q maps to the random walk on M induced by
$Q = Q_1 \times \delta _{id}$
is conjugacy invariant on G. The random walk on G induced by Q maps to the random walk on M induced by
![]() $Q_1$
. In this way, the double coset walks extend conjugacy invariant walks on M. Example 1.1 in the introduction is a special case.
$Q_1$
. In this way, the double coset walks extend conjugacy invariant walks on M. Example 1.1 in the introduction is a special case.
Of course, the conjugacy classes in M (and so the double cosets) can be difficult to describe. Describing the conjugacy classes of
![]() $U_n(q)$
—the unit upper-triangular matrices in
$U_n(q)$
—the unit upper-triangular matrices in
![]() $GL_n(q)$
—is a well-known ‘wild’ problem. See [Reference Aguiar, André, Benedetti, Bergeron, Chen, Diaconis, Hendrickson, Hsiao, Isaacs, Jedwab, Johnson, Karaali, Lauve, Le, Lewis, Li, Magaard, Marberg, Novelli, Pang, Saliola, Tevlin, Thibon, Thiem, Venkateswaran, Vinroot, Yan and Zabrocki2] or [Reference Diaconis and Malliaris17] for background and details. Describing the double cosets for the Sylow p-subgroup in
$GL_n(q)$
—is a well-known ‘wild’ problem. See [Reference Aguiar, André, Benedetti, Bergeron, Chen, Diaconis, Hendrickson, Hsiao, Isaacs, Jedwab, Johnson, Karaali, Lauve, Le, Lewis, Li, Magaard, Marberg, Novelli, Pang, Saliola, Tevlin, Thibon, Thiem, Venkateswaran, Vinroot, Yan and Zabrocki2] or [Reference Diaconis and Malliaris17] for background and details. Describing the double cosets for the Sylow p-subgroup in
![]() $S_n$
seems difficult.
$S_n$
seems difficult.
Example 2.3. Let G be a finite group of Lie type, defined over
![]() $\mathbb {F}_q$
, with Weyl group W. Let
$\mathbb {F}_q$
, with Weyl group W. Let
![]() $\mathcal {B}$
be the Borel subgroup (maximal solvable subgroup). Take
$\mathcal {B}$
be the Borel subgroup (maximal solvable subgroup). Take
![]() $H = K = \mathcal {B}$
. The Bruhat decomposition gives
$H = K = \mathcal {B}$
. The Bruhat decomposition gives
so the double cosets are indexed by W. See [Reference Carter11], Chapter 8, for a clear development in the language of groups with a
![]() $(\mathcal {B}, N)$
pair.
$(\mathcal {B}, N)$
pair.
Conjugacy invariant walks on G have been carefully studied in a series of papers by David Gluck, Bob Guralnick, Michael Larsen, Martin Liebeck, Aner Shalev, Pham Tiep and others. These authors develop good bounds on the character ratios needed. See [Reference Guralnick, Larsen and Tiep30] for a recent paper with careful reference to earlier work. Of course, Example 2 with
![]() $G = GL_n(q), W = S_n$
is a special case. The present paper shows what additional work is needed to transfer character ratio results from G to W.
$G = GL_n(q), W = S_n$
is a special case. The present paper shows what additional work is needed to transfer character ratio results from G to W.
The double cosets form a basis for the algebra of H-K bi-invariant functions
![]() $L(H \backslash G /K)$
with product
$L(H \backslash G /K)$
with product
This is usually developed for
![]() $H = K$
[Reference Curtis and Reiner14], [Reference Ceccherini Silberstein, Scarabotti and Tolli12], [Reference Diaconis15], but the extra flexibility is useful. We add a caveat: When
$H = K$
[Reference Curtis and Reiner14], [Reference Ceccherini Silberstein, Scarabotti and Tolli12], [Reference Diaconis15], but the extra flexibility is useful. We add a caveat: When
![]() $H = K$
, the algebra of bi-invariant functions (into
$H = K$
, the algebra of bi-invariant functions (into
![]() $\mathbb {C}$
) is semisimple and with a unit. This need not be the case for general H and K. David Craven tried many pairs of subgroups of
$\mathbb {C}$
) is semisimple and with a unit. This need not be the case for general H and K. David Craven tried many pairs of subgroups of
![]() $S_4$
and found examples which were not semisimple. For
$S_4$
and found examples which were not semisimple. For
![]() $G=S_4$
, Marty Issacs produced the example H the cyclic subgroup generated by
$G=S_4$
, Marty Issacs produced the example H the cyclic subgroup generated by
![]() $(1234)$
and K the cyclic subgroup generated by
$(1234)$
and K the cyclic subgroup generated by
![]() $(1243)$
. The algebra doesn’t have a unit and so cannot be semisimple. This occurs even for some pairs of distinct parabolic subgroups of
$(1243)$
. The algebra doesn’t have a unit and so cannot be semisimple. This occurs even for some pairs of distinct parabolic subgroups of
![]() $S_n$
. There are also distinct pairs of parabolics where the algebra is semisimple. Determining when this occurs is an open question.
$S_n$
. There are also distinct pairs of parabolics where the algebra is semisimple. Determining when this occurs is an open question.
Further examples are in Section 7. Since the theory is developed for general
![]() $H, K, G$
there is a large set of possibilities. What is needed are examples where the double cosets are indexed by familiar combinatorial objects and the walks induced on
$H, K, G$
there is a large set of possibilities. What is needed are examples where the double cosets are indexed by familiar combinatorial objects and the walks induced on
![]() $H \backslash G / K$
are of independent interest.
$H \backslash G / K$
are of independent interest.
2.2 Markov chain theory
Let
![]() $H, K$
be subgroups of a finite group G, and Q a probability on G. See [Reference Levin and Peres43] for an introduction to Markov chains; see [Reference Diaconis15] or [Reference Saloff-Coste53] for random walks on groups.
$H, K$
be subgroups of a finite group G, and Q a probability on G. See [Reference Levin and Peres43] for an introduction to Markov chains; see [Reference Diaconis15] or [Reference Saloff-Coste53] for random walks on groups.
Proposition 2.4. Let Q be a probability on G which is H-conjugacy invariant (
![]() $Q(s) = Q(h^{-1}s h) $
for
$Q(s) = Q(h^{-1}s h) $
for
![]() $h \in H, s \in G$
). The image of the random walk driven by Q on G maps to a Markov chain on
$h \in H, s \in G$
). The image of the random walk driven by Q on G maps to a Markov chain on
![]() $H \backslash G /K$
with transition kernel
$H \backslash G /K$
with transition kernel
The stationary distribution of P is
![]() $\pi (x) = |HxK|/|G|$
. If
$\pi (x) = |HxK|/|G|$
. If
![]() $Q(s) = Q(s^{-1})$
, then
$Q(s) = Q(s^{-1})$
, then
![]() $(P, \pi )$
is reversible.
$(P, \pi )$
is reversible.
Proof. The kernel P is well defined; that is, it is independent of the choice of double coset representatives for
![]() $x, y$
. Dynkin’s criteria ([Reference Kemeny and Snell40] Chapter 6, [Reference Pang49]) says that the image of a Markov chain in a partitioning of the state space is Markov if and only if for any set in the partition and any point in a second set, the chance of the original chain moving from the point to the first set is constant for points in the second set.
$x, y$
. Dynkin’s criteria ([Reference Kemeny and Snell40] Chapter 6, [Reference Pang49]) says that the image of a Markov chain in a partitioning of the state space is Markov if and only if for any set in the partition and any point in a second set, the chance of the original chain moving from the point to the first set is constant for points in the second set.
Fixing
![]() $x, y$
, observe
$x, y$
, observe
Since the uniform distribution on G is stationary for the walk generated by Q, the stationary distribution of the lumped chain is
![]() $\pi (x) = |HxK|/|G|$
. Finally, any function of a reversible chain is reversible and
$\pi (x) = |HxK|/|G|$
. Finally, any function of a reversible chain is reversible and
![]() $Q(s) = Q(s^{-1})$
gives reversibility of the walk on G.
$Q(s) = Q(s^{-1})$
gives reversibility of the walk on G.
Remark 2.5. A different sufficient condition for Proposition 2.4 is
![]() $Q(sh) = Q(s)$
for all
$Q(sh) = Q(s)$
for all
![]() $s \in G, h \in H$
.
$s \in G, h \in H$
.
Remark 2.6. Usually, a function of a Markov chain is not Markov. For relevant discussion of similar ‘orbit chains’, see [Reference Boyd, Diaconis, Parrilo and Xiao9].
In all of our examples, the measure Q is a class function (
![]() $Q(s) = Q(t^{-1}st)$
for all
$Q(s) = Q(t^{-1}st)$
for all
![]() $s, t \in G$
), which is a stronger requirement than that in Proposition 2.4. The eigenvalues of the walk on G can be given in terms of the irreducible complex characters of G. Let
$s, t \in G$
), which is a stronger requirement than that in Proposition 2.4. The eigenvalues of the walk on G can be given in terms of the irreducible complex characters of G. Let
![]() $\widehat {G}$
be an index set for these characters. We write
$\widehat {G}$
be an index set for these characters. We write
![]() $\lambda \in \widehat {G}$
and
$\lambda \in \widehat {G}$
and
![]() $\chi _{\lambda }(\mathcal {C})$
for the character value at the conjugacy class
$\chi _{\lambda }(\mathcal {C})$
for the character value at the conjugacy class
![]() $\mathcal {C}$
. Let
$\mathcal {C}$
. Let
 $$\begin{align*}\beta_{\lambda} = \frac{1}{\chi_{\lambda}(1)} \sum_{s \in G} Q(s) \chi_{\lambda}(s). \end{align*}$$
$$\begin{align*}\beta_{\lambda} = \frac{1}{\chi_{\lambda}(1)} \sum_{s \in G} Q(s) \chi_{\lambda}(s). \end{align*}$$
If Q is simply concentrated on a single conjugacy class
![]() $\mathcal {C}$
, then
$\mathcal {C}$
, then
![]() $\beta _{\lambda }$
is the character ratio
$\beta _{\lambda }$
is the character ratio
For a review of a large relevant literature on character ratios and their applications, see [Reference Guralnick, Larsen and Tiep30].
The restriction of
![]() $\chi _{\lambda }$
to H is written
$\chi _{\lambda }$
to H is written
![]() $\chi _{\lambda }|_H$
and
$\chi _{\lambda }|_H$
and
![]() $\left \langle \chi _{\lambda } |_H, 1 \right \rangle $
is the number of times the trivial representation of H appears in
$\left \langle \chi _{\lambda } |_H, 1 \right \rangle $
is the number of times the trivial representation of H appears in
![]() $\chi _{\lambda }|_H$
. By reciprocity, this is
$\chi _{\lambda }|_H$
. By reciprocity, this is
![]() $\left \langle \chi _{\lambda }, \mathrm {Ind}_H^G(1) \right \rangle $
, where
$\left \langle \chi _{\lambda }, \mathrm {Ind}_H^G(1) \right \rangle $
, where
![]() $\mathrm {Ind}_H^G$
is the induced representation from H to G.
$\mathrm {Ind}_H^G$
is the induced representation from H to G.
Proposition 2.7. Let Q be a class function on G. The induced chain
![]() $P(x, y)$
of Proposition 2.4 has eigenvalues
$P(x, y)$
of Proposition 2.4 has eigenvalues
 $$ \begin{align} \beta_{\lambda} = \frac{1}{\chi_{\lambda}(1)} \sum_{s \in G} Q(s) \chi_{\lambda}(s), \end{align} $$
$$ \begin{align} \beta_{\lambda} = \frac{1}{\chi_{\lambda}(1)} \sum_{s \in G} Q(s) \chi_{\lambda}(s), \end{align} $$
with multiplicity
The average square total variation distance to stationarity satisfies
 $$ \begin{align} \sum_x \pi(x) \|P_x^{\ell} - \pi \|_{TV}^2 \le \frac{1}{4} \sum_{\lambda \in \widehat{G}, \lambda \neq 1} m_{\lambda} \beta_{\lambda}^{2 \ell}. \end{align} $$
$$ \begin{align} \sum_x \pi(x) \|P_x^{\ell} - \pi \|_{TV}^2 \le \frac{1}{4} \sum_{\lambda \in \widehat{G}, \lambda \neq 1} m_{\lambda} \beta_{\lambda}^{2 \ell}. \end{align} $$
Proof. The eigenvalues of a lumped chain are always some subset of the eigenvalues of the original chain. To determine the multiplicity of the eigenvalue
![]() $\beta _{\lambda }$
in the lumped chain, fix
$\beta _{\lambda }$
in the lumped chain, fix
![]() $\lambda : G \to GL_{d_{\lambda }}$
an irreducible representation of G. Let
$\lambda : G \to GL_{d_{\lambda }}$
an irreducible representation of G. Let
![]() $M^{\lambda }$
be the
$M^{\lambda }$
be the
![]() $d_{\lambda } \times d_{\lambda }$
matrix representation of
$d_{\lambda } \times d_{\lambda }$
matrix representation of
![]() $\lambda $
. That is, each entry
$\lambda $
. That is, each entry
![]() $M_{ij}^{\lambda }: G \to \mathbb {C}$
is a function of G. These functions are linearly independent and can be chosen to be orthogonal with respect to
$M_{ij}^{\lambda }: G \to \mathbb {C}$
is a function of G. These functions are linearly independent and can be chosen to be orthogonal with respect to
 $$\begin{align*}\left\langle f_1, f_2 \right\rangle := \frac{1}{|G|} \sum_{g \in G} f_1(g) \overline{f_2}(g) \end{align*}$$
$$\begin{align*}\left\langle f_1, f_2 \right\rangle := \frac{1}{|G|} \sum_{g \in G} f_1(g) \overline{f_2}(g) \end{align*}$$
(see Chapter 3 of [Reference Serre58]). Let
![]() $V_{\lambda }$
be the space of all linear combinations of the functions
$V_{\lambda }$
be the space of all linear combinations of the functions
![]() $M_{ij}^{\lambda }$
. If
$M_{ij}^{\lambda }$
. If
![]() $f \in V_{\lambda }$
, then
$f \in V_{\lambda }$
, then
 $$ \begin{align*} Pf(x) = \sum_{y \in G} P(x, y)f(y) = \beta_{\lambda} f(x) \end{align*} $$
$$ \begin{align*} Pf(x) = \sum_{y \in G} P(x, y)f(y) = \beta_{\lambda} f(x) \end{align*} $$
That is,
![]() $V_{\lambda }$
is the eigenspace for the eigenvalue
$V_{\lambda }$
is the eigenspace for the eigenvalue
![]() $\beta _{\lambda }$
and it has dimension
$\beta _{\lambda }$
and it has dimension
![]() $d_{\lambda }^2 = \chi _{\lambda }(1)^2$
.
$d_{\lambda }^2 = \chi _{\lambda }(1)^2$
.
In the lumped chain on
![]() $H \backslash G / K$
, a basis for the eigenspace for eigenvalue
$H \backslash G / K$
, a basis for the eigenspace for eigenvalue
![]() $\beta _{\lambda }$
are the
$\beta _{\lambda }$
are the
![]() $H \times K$
invariant functions in
$H \times K$
invariant functions in
![]() $V_{\lambda }$
[Reference Boyd, Diaconis, Parrilo and Xiao9]. To determine the dimension of this subspace, note that
$V_{\lambda }$
[Reference Boyd, Diaconis, Parrilo and Xiao9]. To determine the dimension of this subspace, note that
![]() $G \times G$
can act on
$G \times G$
can act on
![]() $V_{\lambda }$
by
$V_{\lambda }$
by
![]() $f^{g_1, g_2}(x) = f(g_1^{-1} x g_2)$
. This gives a representation of
$f^{g_1, g_2}(x) = f(g_1^{-1} x g_2)$
. This gives a representation of
![]() $G \times G$
on
$G \times G$
on
![]() $V_{\lambda }$
. The matrix of this representation is isomorphic to
$V_{\lambda }$
. The matrix of this representation is isomorphic to
![]() $M \otimes M$
, since
$M \otimes M$
, since
![]() $M_{ij}(s^{-1} t u) = M_{ij}(s^{-1})M_{ij}(t)M_{ij}(u)$
.
$M_{ij}(s^{-1} t u) = M_{ij}(s^{-1})M_{ij}(t)M_{ij}(u)$
.
This representation restricts to a representation
![]() $M_H \otimes M_K$
of
$M_H \otimes M_K$
of
![]() $H \times K$
, and the dimension of the
$H \times K$
, and the dimension of the
![]() $H \times K$
invariant functions in
$H \times K$
invariant functions in
![]() $V_{\lambda }$
is the multiplicity of the trivial representation on
$V_{\lambda }$
is the multiplicity of the trivial representation on
![]() $M_H \otimes M_K$
. This is
$M_H \otimes M_K$
. This is
To note the total variation inequality, let
![]() $1 = \beta _1 \ge \beta _2 \ge \dots \ge \beta _n \ge \dots \ge \beta _{|S_n|} \ge -1$
be the eigenvalues with eigenfunctions
$1 = \beta _1 \ge \beta _2 \ge \dots \ge \beta _n \ge \dots \ge \beta _{|S_n|} \ge -1$
be the eigenvalues with eigenfunctions
![]() $f_j$
(chosen to be orthonormal with respect to
$f_j$
(chosen to be orthonormal with respect to
![]() $\pi $
), and we have
$\pi $
), and we have
 $$\begin{align*}\chi^2_x(\ell) := \| \frac{P_x^\ell}{\pi} - 1\|_{2, \pi}^2 = \sum_{j \neq 1} f_j(x)^2 \beta_j^{2 \ell} \end{align*}$$
$$\begin{align*}\chi^2_x(\ell) := \| \frac{P_x^\ell}{\pi} - 1\|_{2, \pi}^2 = \sum_{j \neq 1} f_j(x)^2 \beta_j^{2 \ell} \end{align*}$$
where
![]() $\| \cdot \|_{2, \pi }$
denotes the
$\| \cdot \|_{2, \pi }$
denotes the
![]() $\ell ^2$
norm with respect to the distribution
$\ell ^2$
norm with respect to the distribution
![]() $\pi $
. Multiplying by
$\pi $
. Multiplying by
![]() $\pi (x)$
and summing over all x in the state space gives
$\pi (x)$
and summing over all x in the state space gives
 $$ \begin{align} \sum_x \pi(x) \left\| \frac{P^{\ell}_x}{\pi} - 1 \right\|_{2, \pi}^2 = \sum_x \pi(x) \sum_{j \neq 1} f_j(x)^2 \beta_j^{2\ell} = \sum_{\lambda \neq 1} m_{\lambda} \beta_{\lambda}^{2 \ell}, \end{align} $$
$$ \begin{align} \sum_x \pi(x) \left\| \frac{P^{\ell}_x}{\pi} - 1 \right\|_{2, \pi}^2 = \sum_x \pi(x) \sum_{j \neq 1} f_j(x)^2 \beta_j^{2\ell} = \sum_{\lambda \neq 1} m_{\lambda} \beta_{\lambda}^{2 \ell}, \end{align} $$
using orthonormality of
![]() $f_j$
. The total variation bound arises since
$f_j$
. The total variation bound arises since
![]() $4 \|P^{\ell }_x - \pi \|_{TV}^2 \le \|P^{\ell }_x/\pi - 1 \|_{2, \pi }^2$
.
$4 \|P^{\ell }_x - \pi \|_{TV}^2 \le \|P^{\ell }_x/\pi - 1 \|_{2, \pi }^2$
.
2.3 Random transpositions and coagulation-fragmentation processes
Let
![]() $G = S_n$
be the symmetric group. The random transpositions Markov chain, studied in [Reference Diaconis and Shahshahani22], is generated by the measure
$G = S_n$
be the symmetric group. The random transpositions Markov chain, studied in [Reference Diaconis and Shahshahani22], is generated by the measure
 $$\begin{align*}Q(\omega) = \begin{cases} 1/n, & \omega = id, \\ 2/n^2, & \omega = (ij), \\ 0, & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}Q(\omega) = \begin{cases} 1/n, & \omega = id, \\ 2/n^2, & \omega = (ij), \\ 0, & \text{otherwise}. \end{cases} \end{align*}$$
This was the first Markov chain where a sharp cutoff for convergence to stationarity was observed. A sharp, explicit rate is obtained in [Reference Saloff-Coste and Zúñiga54]. They show
The asymptotic ‘profile’ (the limit of
![]() $\|Q^{\ell } - u\|_{TV}$
as a function of c for n large) is determined in [Reference Teyssier63]. Schramm [Reference Schramm56] found a sharp parallel between random transpositions and the growth of an Erdős-Rényi random graph: Given vertices
$\|Q^{\ell } - u\|_{TV}$
as a function of c for n large) is determined in [Reference Teyssier63]. Schramm [Reference Schramm56] found a sharp parallel between random transpositions and the growth of an Erdős-Rényi random graph: Given vertices
![]() $1, 2, \dots , n$
, for each transposition
$1, 2, \dots , n$
, for each transposition
![]() $(i, j)$
chosen, add an edge from vertices i to j to generate a random graph. See [Reference Berestycki, Schramm and Zeitouni6] for extensions and a comprehensive review. The results, translated by the coagulation-fragmentation description of the cycles, give a full and useful picture for the simple mean field model described in the introduction.
$(i, j)$
chosen, add an edge from vertices i to j to generate a random graph. See [Reference Berestycki, Schramm and Zeitouni6] for extensions and a comprehensive review. The results, translated by the coagulation-fragmentation description of the cycles, give a full and useful picture for the simple mean field model described in the introduction.
It must be emphasized that this mean field model is a very special case of coagulation-fragmentation models studied in the chemistry-physics-probability literature. These models study the dynamics of particles diffusing in an ambient space, and allow general collision kernels (e.g., particles close in space may be more likely to join). The books by Bertoin [Reference Bertoin7] and Pitman [Reference Pitman50] along with the survey paper of Aldous [Reference Aldous3] are recommended for a view of the richness of this subject. On the other hand, the sharp rates of convergence results available for the mean field model are not available in any generality.
There is a healthy applied mathematics literature on coagulation-fragmentation. A useful overview which treats discrete problems such as the ones treated here is [Reference Ball and Carr5]. A much more probabilistic development of the celebrated Becker–Doring version of the problem is in [Reference Hingant and Yvinec36]. This develops rates of convergence using coupling. See also [Reference Durrett, Granovsky and Gueron27] for more models with various stationary distributions on partitions.
Other lumpings of random transpositions include classical urn models—the Bernoulli–Laplace model [Reference Diaconis and Shahshahani23], [Reference Eskenazis and Nestoridi28], and random walks on phylogenetic trees [Reference Diaconis and Holmes26]. The sharp analysis of random transpositions transfers, via comparison theory, to give good rates of convergence for quite general random walks on the symmetric group [Reference Diaconis and Saloff-Coste20], [Reference Helfgott, Seress and Zuk34]. For an expository survey, see [Reference Diaconis16].
2.4 Transvections
Fix n, a prime p and
![]() $q = p^a$
for some positive integer a. A transvection is an invertible linear transformation of
$q = p^a$
for some positive integer a. A transvection is an invertible linear transformation of
![]() $\mathbb {F}_q^n$
which fixes a hyperplane, is not the identity and has all eigenvalues equal to
$\mathbb {F}_q^n$
which fixes a hyperplane, is not the identity and has all eigenvalues equal to
![]() $1$
. Transvections are convenient generators for the group
$1$
. Transvections are convenient generators for the group
![]() $SL_n(q)$
because they generalize the basic row operations of linear algebra. These properties are carefully developed in [Reference Suzuki62] Chapter 1, 9; [Reference Artin4] Chapter 4.
$SL_n(q)$
because they generalize the basic row operations of linear algebra. These properties are carefully developed in [Reference Suzuki62] Chapter 1, 9; [Reference Artin4] Chapter 4.
Using coordinates, let
![]() $\mathbf {a}, \mathbf {v} \in \mathbb {F}_q^n$
be two nonzero vectors with
$\mathbf {a}, \mathbf {v} \in \mathbb {F}_q^n$
be two nonzero vectors with
![]() $\mathbf {a}^{\top } \mathbf {v} = 0$
. A transvection, denoted
$\mathbf {a}^{\top } \mathbf {v} = 0$
. A transvection, denoted
![]() $T_{\mathbf {a}, \mathbf {v}} \in GL_n(q)$
is the linear map given by
$T_{\mathbf {a}, \mathbf {v}} \in GL_n(q)$
is the linear map given by
It adds a multiple of
![]() $\mathbf {v}$
to
$\mathbf {v}$
to
![]() $\mathbf {x}$
, the amount depending on the ‘angle’ between
$\mathbf {x}$
, the amount depending on the ‘angle’ between
![]() $\mathbf {a}$
and
$\mathbf {a}$
and
![]() $\mathbf {x}$
. As a matrix,
$\mathbf {x}$
. As a matrix,
![]() . Multiplying
. Multiplying
![]() $\mathbf {a}$
by a nonzero constant and dividing
$\mathbf {a}$
by a nonzero constant and dividing
![]() $\mathbf {v}$
by the same constant doesn’t change
$\mathbf {v}$
by the same constant doesn’t change
![]() $T_{\mathbf {a}, \mathbf {v}}$
. Let us agree to normalize
$T_{\mathbf {a}, \mathbf {v}}$
. Let us agree to normalize
![]() $\mathbf {v}$
by making its last nonzero coordinate equal to
$\mathbf {v}$
by making its last nonzero coordinate equal to
![]() $1$
. Let
$1$
. Let
![]() $\mathcal {T}_{n, q} \subset SL_n(q)$
be the set of all transvections.
$\mathcal {T}_{n, q} \subset SL_n(q)$
be the set of all transvections.
An elementary count shows
 $$ \begin{align} |\mathcal{T}_{n, q}| = \frac{(q^n - 1)(q^{n-1} - 1)}{q - 1}. \end{align} $$
$$ \begin{align} |\mathcal{T}_{n, q}| = \frac{(q^n - 1)(q^{n-1} - 1)}{q - 1}. \end{align} $$
It is easy to generate
![]() $T \in \mathcal {T}_{n, q}$
uniformly: Pick
$T \in \mathcal {T}_{n, q}$
uniformly: Pick
![]() $\mathbf {v} \in \mathbb {F}_q^n$
uniformly, discarding the zero vector. Normalize
$\mathbf {v} \in \mathbb {F}_q^n$
uniformly, discarding the zero vector. Normalize
![]() $\mathbf {v}$
so the last nonzero coordinate, say index j, is equal to
$\mathbf {v}$
so the last nonzero coordinate, say index j, is equal to
![]() $1$
. Pick
$1$
. Pick
![]() $a_1, a_2, \dots , a_{j-1}, a_{j+1}, \dots a_n$
uniformly in
$a_1, a_2, \dots , a_{j-1}, a_{j+1}, \dots a_n$
uniformly in
![]() $\mathbb {F}_q^{n-1} - \{0 \}$
, and set
$\mathbb {F}_q^{n-1} - \{0 \}$
, and set
![]() $a_j$
so that
$a_j$
so that
![]() $\mathbf {a}^{\top } \mathbf {v} = 0$
. The transvection
$\mathbf {a}^{\top } \mathbf {v} = 0$
. The transvection
![]() $T_{\mathbf {a}, \mathbf {v}}$
fixes the hyperplane
$T_{\mathbf {a}, \mathbf {v}}$
fixes the hyperplane
![]() $\{\mathbf {x}: \mathbf {a}^{\top } \mathbf {x} = 0 \}$
.
$\{\mathbf {x}: \mathbf {a}^{\top } \mathbf {x} = 0 \}$
.
Example 2.8. Taking
![]() $\mathbf {v} = \mathbf {e}_1, \mathbf {a} = \mathbf {e}_2$
gives the transvection with matrix
$\mathbf {v} = \mathbf {e}_1, \mathbf {a} = \mathbf {e}_2$
gives the transvection with matrix

This acts on
![]() $\mathbf {x}$
by adding the second coordinate to the first. Similarly, the basic row operation of adding
$\mathbf {x}$
by adding the second coordinate to the first. Similarly, the basic row operation of adding
![]() $\theta $
times the ith coordinate to the jth is given by
$\theta $
times the ith coordinate to the jth is given by
![]() $T_{\mathbf {e}_j, \theta \mathbf {e}_i}$
.
$T_{\mathbf {e}_j, \theta \mathbf {e}_i}$
.
Lemma 2.9. The set of transvections
![]() $\mathcal {T}_{n, q}$
is a conjugacy class in
$\mathcal {T}_{n, q}$
is a conjugacy class in
![]() $GL_n(q)$
.
$GL_n(q)$
.
Proof. Let
![]() $M \in GL_n(q)$
, so
$M \in GL_n(q)$
, so
![]() $M T_{\mathbf {e}_2, \mathbf {e}_1} M^{-1}$
is conjugate to
$M T_{\mathbf {e}_2, \mathbf {e}_1} M^{-1}$
is conjugate to
![]() $T_{\mathbf {e}_2, \mathbf {e}_1}$
. Then,
$T_{\mathbf {e}_2, \mathbf {e}_1}$
. Then,
Let
![]() $\mathbf {a}$
be the second column of
$\mathbf {a}$
be the second column of
![]() $(M^{-1})T_{\mathbf {e}_2, \mathbf {e}_1}$
and
$(M^{-1})T_{\mathbf {e}_2, \mathbf {e}_1}$
and
![]() $\mathbf {v}$
the first column of M, and check this last is
$\mathbf {v}$
the first column of M, and check this last is
![]() $T_{\mathbf {a}, \mathbf {v}}$
(and
$T_{\mathbf {a}, \mathbf {v}}$
(and
![]() $\mathbf {a}^{\top } \mathbf {v} = 0$
). Thus, transvections form a conjugacy class.
$\mathbf {a}^{\top } \mathbf {v} = 0$
). Thus, transvections form a conjugacy class.
2.5 Gaussian elimination and the Bruhat decomposition
The reduction of a matrix
![]() $M\in GL_n(q)$
to standard form by row operations is a classical topic in introductory linear algebra courses. It gives efficient, numerically stable ways to solve linear equations, compute inverses and calculate determinants. There are many variations.
$M\in GL_n(q)$
to standard form by row operations is a classical topic in introductory linear algebra courses. It gives efficient, numerically stable ways to solve linear equations, compute inverses and calculate determinants. There are many variations.
Example 2.10. Consider the sequence of row operations
 $$\begin{align*}M = \begin{pmatrix} 0 & 3 & 2 \cr 1 & 2 & 0 \cr 3 & 0 & 5 \end{pmatrix} \to \begin{pmatrix} 0 & 3 & 2 \cr 1 & 2 & 0 \cr 0 & -6 & 5 \end{pmatrix} \to \begin{pmatrix} 0 & 3 & 2 \cr 1 & 2 & 0 \cr 0 & 0 & 9 \end{pmatrix} \to \begin{pmatrix} 1 &2 & 0 \cr 0 & 3 & 2 \cr 0 & 0 & 9 \end{pmatrix} = U. \end{align*}$$
$$\begin{align*}M = \begin{pmatrix} 0 & 3 & 2 \cr 1 & 2 & 0 \cr 3 & 0 & 5 \end{pmatrix} \to \begin{pmatrix} 0 & 3 & 2 \cr 1 & 2 & 0 \cr 0 & -6 & 5 \end{pmatrix} \to \begin{pmatrix} 0 & 3 & 2 \cr 1 & 2 & 0 \cr 0 & 0 & 9 \end{pmatrix} \to \begin{pmatrix} 1 &2 & 0 \cr 0 & 3 & 2 \cr 0 & 0 & 9 \end{pmatrix} = U. \end{align*}$$
The first step subtracts
![]() $3$
times row
$3$
times row
![]() $2$
from row
$2$
from row
![]() $3$
, multiplication by
$3$
, multiplication by
 $$\begin{align*}L_1 = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & -3 & 1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}L_1 = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & -3 & 1 \end{pmatrix}. \end{align*}$$
The second step adds
![]() $2$
times row
$2$
times row
![]() $1$
to row
$1$
to row
![]() $3$
, multiplication by
$3$
, multiplication by
 $$\begin{align*}L_2 = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 0 \cr 2 & 0 & 1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}L_2 = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 0 \cr 2 & 0 & 1 \end{pmatrix}. \end{align*}$$
The third (pivot) step brings the matrix to upper-triangular form by switching rows
![]() $1$
and
$1$
and
![]() $2$
, which corresponds to multiplication by the matrix by
$2$
, which corresponds to multiplication by the matrix by
 $$\begin{align*}\omega_1 = \begin{pmatrix} 0 & 1 & 0 \cr 1 & 0 & 0 \cr 0 & 0 & 1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\omega_1 = \begin{pmatrix} 0 & 1 & 0 \cr 1 & 0 & 0 \cr 0 & 0 & 1 \end{pmatrix}. \end{align*}$$
This gives
![]() $\omega _1 L_2 L_1 M = U \implies M = L_2^{-1} L_1^{-1} \omega _1^{-1} U = L \omega U$
with
$\omega _1 L_2 L_1 M = U \implies M = L_2^{-1} L_1^{-1} \omega _1^{-1} U = L \omega U$
with
![]() $L = L_2^{-1} L_1^{-1}, \omega = \omega _1^{-1} = \omega _1$
.
$L = L_2^{-1} L_1^{-1}, \omega = \omega _1^{-1} = \omega _1$
.
If
![]() $\mathcal {L}, \mathcal {B}$
are the subgroups of lower and upper-triangular matrices in
$\mathcal {L}, \mathcal {B}$
are the subgroups of lower and upper-triangular matrices in
![]() $GL_n(q)$
, this gives
$GL_n(q)$
, this gives
Any linear algebra book treats these topics. A particularly clear version which uses Gaussian elimination as a gateway to Lie theory is in Howe [Reference Howe37]. Articles by Lusztig [Reference Lusztig45] and Strang [Reference Strang61] have further historical, mathematical and practical discussion.
Observe that carrying out the final pivoting step costs
![]() $d_c(\omega ,\mathrm {id})$
operations, where
$d_c(\omega ,\mathrm {id})$
operations, where
![]() $d_c(\omega ,\mathrm {id})$
, the Cayley distance of
$d_c(\omega ,\mathrm {id})$
, the Cayley distance of
![]() $\omega $
to the identity, is the minimum number of transpositions required to sort
$\omega $
to the identity, is the minimum number of transpositions required to sort
![]() $\omega $
(with arbitrary transpositions
$\omega $
(with arbitrary transpositions
![]() $(i,j)$
allowed). Cayley proved
$(i,j)$
allowed). Cayley proved
![]() $d_c(\omega ,\mathrm {id}) = n - \#\mbox {cycles in} \ \omega $
(see [Reference Diaconis16]). In the example above
$d_c(\omega ,\mathrm {id}) = n - \#\mbox {cycles in} \ \omega $
(see [Reference Diaconis16]). In the example above
![]() $n=3$
,
$n=3$
,
![]() $\omega = 213$
has two cycles and
$\omega = 213$
has two cycles and
![]() $3-2 =1$
—one transposition sorts
$3-2 =1$
—one transposition sorts
![]() $\omega $
.
$\omega $
.
How many pivot steps are needed ‘on average’? This becomes the question of the number of cycles in a pick from Mallows measure
![]() $\pi _q$
. Surprisingly, this is a difficult question. Following partial answers by Gladkich and Peled [Reference Gladkich and Peled29], this problem was recently solved by Jimmy He, Tobias Möller and Teun Verstraaten in [Reference He, Möller and Verstraaten33]. They show that, when
$\pi _q$
. Surprisingly, this is a difficult question. Following partial answers by Gladkich and Peled [Reference Gladkich and Peled29], this problem was recently solved by Jimmy He, Tobias Möller and Teun Verstraaten in [Reference He, Möller and Verstraaten33]. They show that, when
![]() $q> 1$
, the limiting behavior of the number of even cycles under
$q> 1$
, the limiting behavior of the number of even cycles under
![]() $\pi _q$
has an approximate normal distribution with mean and variance proportional to n, and that the number of odd cycles has bounded mean and variance.
$\pi _q$
has an approximate normal distribution with mean and variance proportional to n, and that the number of odd cycles has bounded mean and variance.
The Bruhat decomposition
In algebraic group theory, one uses
This holds for any semisimple group over any field with
![]() $\mathcal {B}$
replaced by the Borel group (the largest solvable subgroup) and
$\mathcal {B}$
replaced by the Borel group (the largest solvable subgroup) and
![]() $S_n$
replaced by the Weyl group.
$S_n$
replaced by the Weyl group.
Let
![]() $\omega _0 = \left (\begin {smallmatrix} 1 & 2 & \cdots & n\\ n & n-1 & \cdots & 1 \end {smallmatrix}\right )$
be the reversal permutation in
$\omega _0 = \left (\begin {smallmatrix} 1 & 2 & \cdots & n\\ n & n-1 & \cdots & 1 \end {smallmatrix}\right )$
be the reversal permutation in
![]() $S_n$
. Since
$S_n$
. Since
![]() $\mathcal {L} = \omega _0 \mathcal {B} \omega _0$
, equation (2.7) is equivalent to the LU decomposition (2.6). Given
$\mathcal {L} = \omega _0 \mathcal {B} \omega _0$
, equation (2.7) is equivalent to the LU decomposition (2.6). Given
![]() $M \in GL_n(q)$
, Gaussian elimination on
$M \in GL_n(q)$
, Gaussian elimination on
![]() $\omega _0 M$
can be used to find
$\omega _0 M$
can be used to find
![]() $\omega _0 M \in L \omega ' U$
and thus
$\omega _0 M \in L \omega ' U$
and thus
![]() $M \in B \omega B$
with
$M \in B \omega B$
with
![]() $\omega = \omega _0 \omega '$
.
$\omega = \omega _0 \omega '$
.
The subgroup
![]() $\mathcal {B}$
gives rise to the quotient
$\mathcal {B}$
gives rise to the quotient
![]() $GL_n(q)/\mathcal {B}$
. This may be pictured as the space of ‘flags’. Here, a flag F consists of an increasing sequence of subspaces
$GL_n(q)/\mathcal {B}$
. This may be pictured as the space of ‘flags’. Here, a flag F consists of an increasing sequence of subspaces
![]() with
with
![]() $\text {dim}(F_i) = i$
. Indeed,
$\text {dim}(F_i) = i$
. Indeed,
![]() $GL_n(q)$
operates transitively on flags and the subgroup fixing the standard flag
$GL_n(q)$
operates transitively on flags and the subgroup fixing the standard flag
![]() is exactly
is exactly
![]() $\mathcal {B}$
. This perspective will be further explained and used in Section 6 to study a function of the double coset Markov chain on
$\mathcal {B}$
. This perspective will be further explained and used in Section 6 to study a function of the double coset Markov chain on
![]() $\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
.
$\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
.
Remark 2.11. The double cosets of
![]() $GL_n(q)$
define equivalence classes for any subgroup of
$GL_n(q)$
define equivalence classes for any subgroup of
![]() $GL_n(q)$
. For the matrices
$GL_n(q)$
. For the matrices
![]() $SL_n(q)$
with determinant
$SL_n(q)$
with determinant
![]() $1$
, these double cosets again induce the Mallows distribution on permutations. More precisely, for
$1$
, these double cosets again induce the Mallows distribution on permutations. More precisely, for
![]() $x \in SL_n(q)$
, let
$x \in SL_n(q)$
, let
![]() $[x]_{SL_n(q)} = \{x' \in SL_n(q) : x' \in \mathcal {B} x \mathcal {B} \}$
be the equivalence class created by the double coset relation
$[x]_{SL_n(q)} = \{x' \in SL_n(q) : x' \in \mathcal {B} x \mathcal {B} \}$
be the equivalence class created by the double coset relation
![]() $\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
, within
$\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
, within
![]() $SL_n(q)$
. Note that two matrices
$SL_n(q)$
. Note that two matrices
![]() $x, x' \in SL_n(q)$
could be in the same double coset with
$x, x' \in SL_n(q)$
could be in the same double coset with
![]() $x' = b_1 x b_2$
, but
$x' = b_1 x b_2$
, but
![]() $b_1, b_2 \notin SL_n(q)$
(necessarily,
$b_1, b_2 \notin SL_n(q)$
(necessarily,
![]() $\mathrm {det}(b_1) = \mathrm {det}(b_2)^{-1}$
).
$\mathrm {det}(b_1) = \mathrm {det}(b_2)^{-1}$
).
Then,
![]() $|[\omega ]_{SL_n(q)}|/|SL_n(q)| = p_q(\omega )$
. This follows since
$|[\omega ]_{SL_n(q)}|/|SL_n(q)| = p_q(\omega )$
. This follows since
![]() $|GL_n(q)| = (q-1) \cdot |SL_n(q)|$
, and
$|GL_n(q)| = (q-1) \cdot |SL_n(q)|$
, and
![]() $|\mathcal {B} \omega \mathcal {B}| = (q - 1) \cdot |[\omega ]_{SL_n(q)}|$
. If
$|\mathcal {B} \omega \mathcal {B}| = (q - 1) \cdot |[\omega ]_{SL_n(q)}|$
. If
![]() $M \in GL_n(q)$
and
$M \in GL_n(q)$
and
![]() $M \in B \omega B$
, then
$M \in B \omega B$
, then
![]() $M/\det (M) \in [\omega ]_{SL_n(q)}$
. Conversely, for each
$M/\det (M) \in [\omega ]_{SL_n(q)}$
. Conversely, for each
![]() $M \in SL_n(q)$
there are
$M \in SL_n(q)$
there are
![]() $(q - 1)$
unique matrices in
$(q - 1)$
unique matrices in
![]() $GL_n(q)$
created by multiplying M by
$GL_n(q)$
created by multiplying M by
![]() $1, 2, \dots , q - 1$
.
$1, 2, \dots , q - 1$
.
2.6 The Metropolis algorithm
The Metropolis algorithm is a basic algorithm of scientific computing which arises in describing the random walk induced by transvections on the double cosets
![]() $\mathcal {B}_n \backslash GL_n(q) / \mathcal {B}_n$
(Section 3.2). This section gives background.
$\mathcal {B}_n \backslash GL_n(q) / \mathcal {B}_n$
(Section 3.2). This section gives background.
Given a probability distribution
![]() $\pi $
on a space
$\pi $
on a space
![]() $\mathcal {X}$
, the Metropolis algorithm gives a way of changing the output of a Markov chain with transition matrix
$\mathcal {X}$
, the Metropolis algorithm gives a way of changing the output of a Markov chain with transition matrix
![]() $K(x, y)$
to have stationary distribution
$K(x, y)$
to have stationary distribution
![]() $\pi $
on
$\pi $
on
![]() $\mathcal {X}$
. For simplicity, suppose the original chain is symmetric,
$\mathcal {X}$
. For simplicity, suppose the original chain is symmetric,
![]() $K(x, y) = K(y, x)$
(as in our examples). This implies that
$K(x, y) = K(y, x)$
(as in our examples). This implies that
![]() $K(x, y)$
has a uniform stationary distribution. Define the Metropolis Markov chain with the transition matrix:
$K(x, y)$
has a uniform stationary distribution. Define the Metropolis Markov chain with the transition matrix:
 $$\begin{align*}M(x, y) = \begin{cases} K(x, y), & \text{if} \,\,\, \pi(y) \ge \pi(x), \, x \neq y, \\ K(x, y) \cdot \frac{\pi(y)}{\pi(x)}, & \text{if} \,\,\, \pi(y) < \pi(x), \, x \neq y, \\ K(x, x) + \sum_{z: \pi(z) < \pi(x)} K(x, z) \left( 1 - \frac{\pi(z)}{\pi(x)} \right), & \text{if} \,\,\, x = y. \end{cases} \end{align*}$$
$$\begin{align*}M(x, y) = \begin{cases} K(x, y), & \text{if} \,\,\, \pi(y) \ge \pi(x), \, x \neq y, \\ K(x, y) \cdot \frac{\pi(y)}{\pi(x)}, & \text{if} \,\,\, \pi(y) < \pi(x), \, x \neq y, \\ K(x, x) + \sum_{z: \pi(z) < \pi(x)} K(x, z) \left( 1 - \frac{\pi(z)}{\pi(x)} \right), & \text{if} \,\,\, x = y. \end{cases} \end{align*}$$
These transition probabilities have a simple implementation: From x, pick y according to
![]() $K(x, y)$
. If
$K(x, y)$
. If
![]() $\pi (y) \ge \pi (x)$
, move to y. If
$\pi (y) \ge \pi (x)$
, move to y. If
![]() $\pi (y) < \pi (x)$
, flip a coin with heads probability
$\pi (y) < \pi (x)$
, flip a coin with heads probability
![]() $\pi (y)/\pi (x)$
. If the coin is heads, move to y. If the coin is tails, stay at x. Elementary calculations show that
$\pi (y)/\pi (x)$
. If the coin is heads, move to y. If the coin is tails, stay at x. Elementary calculations show that
![]() $\pi (x) M(x, y) = \pi (y) M(y, x)$
, that is, M has
$\pi (x) M(x, y) = \pi (y) M(y, x)$
, that is, M has
![]() $\pi $
as stationary distribution. Note that the normalizing constant of
$\pi $
as stationary distribution. Note that the normalizing constant of
![]() $\pi $
is not needed.
$\pi $
is not needed.
For background, applications, and theoretical properties of the Metropolis algorithm, see the textbook of Liu [Reference Liu44] or the survey [Reference Diaconis and Saloff-Coste21]. Sharp analysis of rates of convergence of the Metropolis algorithm is still an open research problem. The special cases developed in Section 3.2 show it can lead to fascinating mathematics.
3 Double coset walks on
 $\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
$\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
Throughout this section,
![]() $\mathcal {B}$
is the group of upper-triangular matrices in
$\mathcal {B}$
is the group of upper-triangular matrices in
![]() $GL_n(q)$
,
$GL_n(q)$
,
![]() $\mathcal {T}_{n,q}$
is the conjugacy class of transvections in
$\mathcal {T}_{n,q}$
is the conjugacy class of transvections in
![]() $GL_n(q)$
. This gives the probability measure on
$GL_n(q)$
. This gives the probability measure on
![]() $GL_n(q)$
defined by
$GL_n(q)$
defined by
 $$\begin{align*}Q(M) = \begin{cases} \frac{1}{|\mathcal{T}_{n,q}|}, & \text{if} \,\,\,\, M \in \mathcal{T}_{n,q}. \\ 0, & \text{else}. \end{cases} \end{align*}$$
$$\begin{align*}Q(M) = \begin{cases} \frac{1}{|\mathcal{T}_{n,q}|}, & \text{if} \,\,\,\, M \in \mathcal{T}_{n,q}. \\ 0, & \text{else}. \end{cases} \end{align*}$$
Note the random transvections measure Q is supported on
![]() $SL_n(q)$
, a subgroup of
$SL_n(q)$
, a subgroup of
![]() $GL_n(q)$
. This means that the random walk on
$GL_n(q)$
. This means that the random walk on
![]() $GL_n(q)$
driven by Q is not ergodic (there is zero probability of moving x to y if
$GL_n(q)$
driven by Q is not ergodic (there is zero probability of moving x to y if
![]() $x, y$
are matrices with different determinants). However, Q is a class function on
$x, y$
are matrices with different determinants). However, Q is a class function on
![]() $GL_n(q)$
since transvections form a conjugacy class. The image of the uniform distribution on
$GL_n(q)$
since transvections form a conjugacy class. The image of the uniform distribution on
![]() $GL_n(q)$
mapped to
$GL_n(q)$
mapped to
![]() $\mathcal {B} \backslash GL_n(q) /\mathcal {B}$
is the Mallows measure
$\mathcal {B} \backslash GL_n(q) /\mathcal {B}$
is the Mallows measure
![]() $\pi _q(\omega ) = q^{I(\omega )}/[n]_q!$
.
$\pi _q(\omega ) = q^{I(\omega )}/[n]_q!$
.
Section 3.1 introduces the definition of the Markov chain as multiplication in the Hecke algebra, which is further explained in Section 5. Section 3.3 gives the combinatorial expressions for the eigenvalues and their multiplicities, which are needed to apply Theorem 1.2 for this case. Section 4.2 shows that for the induced Markov chain on
![]() $S_n$
, starting from
$S_n$
, starting from
![]() $id \in S_n$
, order n steps are necessary and sufficient for convergence. Section 4.3 studies the chain starting from the reversal permutation, for which only order
$id \in S_n$
, order n steps are necessary and sufficient for convergence. Section 4.3 studies the chain starting from the reversal permutation, for which only order
![]() $\log n/2 \log q$
steps are required. Finally, Section 4.4 considers starting from a ‘typical’ element, according to the stationary distribution, for which
$\log n/2 \log q$
steps are required. Finally, Section 4.4 considers starting from a ‘typical’ element, according to the stationary distribution, for which
![]() $\log n/\log q$
steps are necessary and sufficient.
$\log n/\log q$
steps are necessary and sufficient.
These results can be compared to Hildebrand’s Theorem 1.1 [Reference Hildebrand35] which shows that the walk driven by Q on
![]() $GL_n(q)$
converges in
$GL_n(q)$
converges in
![]() $n + c$
steps (uniformly in q). Our results thus contribute to the program of understanding how functions of a Markov chain behave and how the mixing time depends on the starting state. In this case, changing the starting state gives an exponential speed up.
$n + c$
steps (uniformly in q). Our results thus contribute to the program of understanding how functions of a Markov chain behave and how the mixing time depends on the starting state. In this case, changing the starting state gives an exponential speed up.
3.1 Hecke algebras and the Metropolis algorithm
The set of
![]() $\mathcal {B}$
-
$\mathcal {B}$
-
![]() $\mathcal {B}$
double cosets of
$\mathcal {B}$
double cosets of
![]() $GL_n(q)$
has remarkable structure. For
$GL_n(q)$
has remarkable structure. For
![]() $\omega \in S_n$
, let
$\omega \in S_n$
, let
![]() $T_{\omega } = \mathcal {B} \omega \mathcal {B}$
. Linear combinations of double cosets form an algebra (over
$T_{\omega } = \mathcal {B} \omega \mathcal {B}$
. Linear combinations of double cosets form an algebra (over
![]() $\mathbb {C}$
, for example).
$\mathbb {C}$
, for example).
Definition 3.1. The Iwahori–Hecke algebra
![]() $H_n(q)$
is spanned by the symbols
$H_n(q)$
is spanned by the symbols
![]() $\{T_{\omega } \}_{\omega \in S_n}$
and generated by
$\{T_{\omega } \}_{\omega \in S_n}$
and generated by
![]() $T_i = T_{s_i}$
for
$T_i = T_{s_i}$
for
![]() $s_i = (i, i+1), 1 \le i \le n -1$
, with the relations
$s_i = (i, i+1), 1 \le i \le n -1$
, with the relations
 $$ \begin{align} \begin{cases} T_{s_i}T_{\omega} = T_{s_i\omega} & \text{if } I(s_i\omega) = I(\omega)+1, \\ T_{s_i}T_{\omega} = qT_{s_i \omega} +(q-1)T_{\omega} & \text{if } I(s_i\omega) = I(\omega)-1, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} T_{s_i}T_{\omega} = T_{s_i\omega} & \text{if } I(s_i\omega) = I(\omega)+1, \\ T_{s_i}T_{\omega} = qT_{s_i \omega} +(q-1)T_{\omega} & \text{if } I(s_i\omega) = I(\omega)-1, \end{cases} \end{align} $$
where
![]() $I(\omega )$
is the usual length function on
$I(\omega )$
is the usual length function on
![]() $S_n$
(
$S_n$
(
![]() $I(s_i \omega ) = I(\omega )\pm 1$
).
$I(s_i \omega ) = I(\omega )\pm 1$
).
Consider the flag space
![]() $\mathcal {F} = G/\mathcal {B}$
. The group
$\mathcal {F} = G/\mathcal {B}$
. The group
![]() $GL_n(q)$
acts on the left on
$GL_n(q)$
acts on the left on
![]() $\mathcal {F}$
. One can see
$\mathcal {F}$
. One can see
![]() $H_n(q)$
acting on the right of
$H_n(q)$
acting on the right of
![]() $\mathcal {F}$
and in fact
$\mathcal {F}$
and in fact
The Hecke algebra is the full commuting algebra of
![]() $GL_n(q)$
acting on
$GL_n(q)$
acting on
![]() $GL_n(q)/\mathcal {B}$
. Because transvections form a conjugacy class, the sum of transvections is in the center of the group algebra
$GL_n(q)/\mathcal {B}$
. Because transvections form a conjugacy class, the sum of transvections is in the center of the group algebra
![]() $\mathbb {C}[GL_n(q)]$
, and so it may be regarded as an element of
$\mathbb {C}[GL_n(q)]$
, and so it may be regarded as an element of
![]() $H_n(q)$
. This will be explicitly delineated and the character theory of
$H_n(q)$
. This will be explicitly delineated and the character theory of
![]() $H_n(q)$
used to do computations.
$H_n(q)$
used to do computations.
3.2 The Metropolis connection
The relations (3.1) can be interpreted probabilistically. Consider what equation (3.1) says as linear algebra: Left multiplication by
![]() $T_{s_i}$
can take
$T_{s_i}$
can take
![]() $\omega $
to
$\omega $
to
![]() $\omega $
or
$\omega $
or
![]() $s_i \omega $
. The matrix of this map (in the basis
$s_i \omega $
. The matrix of this map (in the basis
![]() $\{T_{\omega }\}_{\omega \in S_n}$
) has
$\{T_{\omega }\}_{\omega \in S_n}$
) has
![]() $\omega , \omega '$
entry
$\omega , \omega '$
entry
 $$ \begin{align*} \begin{cases} 1, & \text{if} \quad I(s_i \omega) = I(\omega) + 1, \,\, \text{and} \,\,\, \omega' = s_i \omega, \\ q, & \text{if} \quad I(s_i \omega) = I(\omega) - 1, \,\, \text{and} \,\,\, \omega' = \omega, \\ q - 1, & \text{if} \quad I(s_i \omega) = I(\omega) -1, \,\, \text{and} \,\,\, \omega' = s_i \omega, \\ 0, & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} 1, & \text{if} \quad I(s_i \omega) = I(\omega) + 1, \,\, \text{and} \,\,\, \omega' = s_i \omega, \\ q, & \text{if} \quad I(s_i \omega) = I(\omega) - 1, \,\, \text{and} \,\,\, \omega' = \omega, \\ q - 1, & \text{if} \quad I(s_i \omega) = I(\omega) -1, \,\, \text{and} \,\,\, \omega' = s_i \omega, \\ 0, & \text{otherwise}. \end{cases} \end{align*} $$
For example, on
![]() $GL_3(q)$
using the ordered basis
$GL_3(q)$
using the ordered basis
![]() $T_{id}, T_{s_1}, T_{s_2}, T_{s_1s_2}, T_{s_2s_1}, T_{s_1s_2s_1}$
, the matrix of left multiplication by
$T_{id}, T_{s_1}, T_{s_2}, T_{s_1s_2}, T_{s_2s_1}, T_{s_1s_2s_1}$
, the matrix of left multiplication by
![]() $s_1$
is
$s_1$
is
 $$\begin{align*}T_{s_1} = \begin{pmatrix} 0 & q & 0 & 0 & 0 & 0 \cr 1 & q-1 & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & q & 0 & 0 \cr 0 & 0 & 1 & q-1 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & q \cr 0 & 0 & 0 & 0 & 1 & q-1 \cr \end{pmatrix}. \end{align*}$$
$$\begin{align*}T_{s_1} = \begin{pmatrix} 0 & q & 0 & 0 & 0 & 0 \cr 1 & q-1 & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & q & 0 & 0 \cr 0 & 0 & 1 & q-1 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & q \cr 0 & 0 & 0 & 0 & 1 & q-1 \cr \end{pmatrix}. \end{align*}$$
The first column has a
![]() $1$
in row
$1$
in row
![]() $s_1$
because
$s_1$
because
![]() $I(s_1)> I(id)$
. The second column has entries q and
$I(s_1)> I(id)$
. The second column has entries q and
![]() $q-1$
in the first two rows because
$q-1$
in the first two rows because
![]() $I(s_1^2) = I(id) < I(s_1)$
.
$I(s_1^2) = I(id) < I(s_1)$
.
We can also write the matrices for multiplication defined by
![]() $T_{s_2}$
and
$T_{s_2}$
and
![]() $T_{s_1s_2s_1}$
as
$T_{s_1s_2s_1}$
as
 $$ \begin{align*} &T_{s_2} = \begin{pmatrix} 0 & 0 & q & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & q & 0 \cr 1 & 0 & q-1 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & q\\ 0 & 1 & 0 & 0 & q-1 & 0 \cr 0 & 0 & 0 & 1 & 0 & q-1 \cr \end{pmatrix} \\ & T_{s_1s_2s_1} = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & q^3 \cr 0 & 0 & 0 & q^2 & 0 & q^2(q - 1) \cr 0 & 0 & 0 & 0 & q^2 & q^2(q - 1) \cr 0 & q & 0 & q(q - 1) & q(q-1) & q(q-1)^2 \cr 0 & 0 & q & q(q-1) & q(q-1) & q(q-1)^2 \cr 1 & q-1 & q-1 & (q-1)^2 & (q-1)^2 & (q - 1)^3 + q(q-1)\cr \end{pmatrix}. \end{align*} $$
$$ \begin{align*} &T_{s_2} = \begin{pmatrix} 0 & 0 & q & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & q & 0 \cr 1 & 0 & q-1 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & q\\ 0 & 1 & 0 & 0 & q-1 & 0 \cr 0 & 0 & 0 & 1 & 0 & q-1 \cr \end{pmatrix} \\ & T_{s_1s_2s_1} = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & q^3 \cr 0 & 0 & 0 & q^2 & 0 & q^2(q - 1) \cr 0 & 0 & 0 & 0 & q^2 & q^2(q - 1) \cr 0 & q & 0 & q(q - 1) & q(q-1) & q(q-1)^2 \cr 0 & 0 & q & q(q-1) & q(q-1) & q(q-1)^2 \cr 1 & q-1 & q-1 & (q-1)^2 & (q-1)^2 & (q - 1)^3 + q(q-1)\cr \end{pmatrix}. \end{align*} $$
Observe that all three matrices above have constant row sums (q, q and
![]() $q^3$
, respectively). Dividing by these row sums gives three Markov transition matrices:
$q^3$
, respectively). Dividing by these row sums gives three Markov transition matrices:
![]() $M_1, M_2$
and
$M_1, M_2$
and
![]() $M_{121} = M_1M_2M_1$
.
$M_{121} = M_1M_2M_1$
.
These matrices have a simple probabilistic interpretation: Consider, for
![]() $\overline {q} = 1/q$
, the matrix defined
$\overline {q} = 1/q$
, the matrix defined
 $$\begin{align*}M_1 = \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 \cr \overline{q} & 1 - \overline{q} & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 1 & 0 & 0 \cr 0 & 0 & \overline{q} & 1 - \overline{q} & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & 1 \cr 0 & 0 & 0 & 0 & \overline{q} & 1 - \overline{q} \cr \end{pmatrix}. \end{align*}$$
$$\begin{align*}M_1 = \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 \cr \overline{q} & 1 - \overline{q} & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 1 & 0 & 0 \cr 0 & 0 & \overline{q} & 1 - \overline{q} & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & 1 \cr 0 & 0 & 0 & 0 & \overline{q} & 1 - \overline{q} \cr \end{pmatrix}. \end{align*}$$
The description of this Markov matrix is: From
![]() $\omega $
, propose
$\omega $
, propose
![]() $s_1 \omega $
:
$s_1 \omega $
:
-
• If
 $I(s_1 \omega )> I(\omega )$
, go to
$I(s_1 \omega )> I(\omega )$
, go to
 $s_1 \omega $
.
$s_1 \omega $
. -
• If
 $I(s_1 \omega ) < I(\omega )$
, go to
$I(s_1 \omega ) < I(\omega )$
, go to
 $s_1 \omega $
with probability
$s_1 \omega $
with probability
 $1/q$
, else stay at
$1/q$
, else stay at
 $\omega $
.
$\omega $
.
This is exactly the Metropolis algorithm on
![]() $S_n$
for sampling from
$S_n$
for sampling from
![]() $\pi _q(\omega )$
with the proposal given by the deterministic chain ‘multiply by
$\pi _q(\omega )$
with the proposal given by the deterministic chain ‘multiply by
![]() $s_1$
’. The matrices
$s_1$
’. The matrices
![]() $M_i, 1 \le i \le n -1$
, have a similar interpretation and satisfy
$M_i, 1 \le i \le n -1$
, have a similar interpretation and satisfy
The Metropolis algorithm always results in a reversible Markov chain. See Section 2.6 or [Reference Diaconis and Saloff-Coste21] for background. It follows that any product of
![]() $\{M_i \}$
and any convex combination of such products yields a
$\{M_i \}$
and any convex combination of such products yields a
![]() $\pi _q$
reversible chain. Note also that the Markov chain on
$\pi _q$
reversible chain. Note also that the Markov chain on
![]() $S_n$
is automatically reversible since it is induced by a reversible chain on
$S_n$
is automatically reversible since it is induced by a reversible chain on
![]() $GL_n$
.
$GL_n$
.
Corollary 3.2. The random transvections chain on
![]() $GL_n(q)$
lumped to
$GL_n(q)$
lumped to
![]() $\mathcal {B}$
-
$\mathcal {B}$
-
![]() $\mathcal {B}$
cosets gives a
$\mathcal {B}$
cosets gives a
![]() $\pi _q$
reversible Markov chain on
$\pi _q$
reversible Markov chain on
![]() $S_n$
.
$S_n$
.
Proof. Up to normalization, the matrix D in Theorem 1.6 is a positive linear combination of Markov chains corresponding to multiplication by
This yields a combination of the reversible chains
![]() .
.
Example 3.3. The transition matrix of the transvections chain on
![]() $GL_3(q)$
lumped to
$GL_3(q)$
lumped to
![]() $S_3$
is
$S_3$
is
![]() $\frac {1}{|\mathcal {T}_{n, q}|}D$
, with
$\frac {1}{|\mathcal {T}_{n, q}|}D$
, with
 $$ \begin{align*} D &= (2q^2 - q - 1) \mathbf{I} \\ & \quad + (q-1)\begin{pmatrix} 0 &q^2 &q^2 &0 &0 &q^3 \\ q &q(q-1) &0 &q^2 &q^2 &q^2(q-1) \\ q &0 &q(q-1) &q^2 &q^2 &q^2(q-1) \\ 0 &q &q &2q(q-1) &q(q-1) &q^2+q(q-1)^2 \\ 0 &q &q &q(q-1) &2q(q-1) &q^2+q(q-1)^2 \\ 1 &q-1 &q-1 &q+(q-1)^2 &q+(q-1)^2 &(q-1)^3+3q(q-1) \end{pmatrix}. \end{align*} $$
$$ \begin{align*} D &= (2q^2 - q - 1) \mathbf{I} \\ & \quad + (q-1)\begin{pmatrix} 0 &q^2 &q^2 &0 &0 &q^3 \\ q &q(q-1) &0 &q^2 &q^2 &q^2(q-1) \\ q &0 &q(q-1) &q^2 &q^2 &q^2(q-1) \\ 0 &q &q &2q(q-1) &q(q-1) &q^2+q(q-1)^2 \\ 0 &q &q &q(q-1) &2q(q-1) &q^2+q(q-1)^2 \\ 1 &q-1 &q-1 &q+(q-1)^2 &q+(q-1)^2 &(q-1)^3+3q(q-1) \end{pmatrix}. \end{align*} $$
When
![]() $q=2$
, the lumped chain has transition matrix
$q=2$
, the lumped chain has transition matrix
 $$ \begin{align*}\frac{1}{21} \begin{pmatrix} 5 &4 &4 &0 &0 &8 \\ 2 &7 &0 &4 &4 &4 \\ 2 &0 &7 &4 &4 &4 \\ 0 &2 &2 &9 &2 &6 \\ 0 &2 &2 &2 &9 &6 \\ 1 &1 &1 &3 &3 &12 \end{pmatrix}. \end{align*} $$
$$ \begin{align*}\frac{1}{21} \begin{pmatrix} 5 &4 &4 &0 &0 &8 \\ 2 &7 &0 &4 &4 &4 \\ 2 &0 &7 &4 &4 &4 \\ 0 &2 &2 &9 &2 &6 \\ 0 &2 &2 &2 &9 &6 \\ 1 &1 &1 &3 &3 &12 \end{pmatrix}. \end{align*} $$
We report that this example has been verified by several different routes including simply running the transvections chain, computing the double coset representative at each step and estimating the transition rates from a long run of the chain.
Remark 3.4. The random transvections Markov chain on
![]() $S_n$
is the ‘q-deformation’ of random transpositions on
$S_n$
is the ‘q-deformation’ of random transpositions on
![]() $S_n$
. That is, as q tends to
$S_n$
. That is, as q tends to
![]() $1$
, the transition matrix tends to the transition matrix of random transpositions. To see this, recall
$1$
, the transition matrix tends to the transition matrix of random transpositions. To see this, recall
![]() $|\mathcal {T}_{n, q}| = (q^n - 1)(q^{n-1} - 1)/(q-1)$
and use L’Hopitals rule to note, for any integer k,
$|\mathcal {T}_{n, q}| = (q^n - 1)(q^{n-1} - 1)/(q-1)$
and use L’Hopitals rule to note, for any integer k,
 $$ \begin{align*} &\lim_{q \to 1^+} \frac{(q - 1)^2 q^k(q-1)^{\ell}}{(q^n - 1)(q^{n-1} - 1)} = \begin{cases} 0, & \text{if} \,\, \ell> 0, \\ \frac{1}{n(n-1)}, & \text{if} \,\,\, \ell = 0. \end{cases} \end{align*} $$
$$ \begin{align*} &\lim_{q \to 1^+} \frac{(q - 1)^2 q^k(q-1)^{\ell}}{(q^n - 1)(q^{n-1} - 1)} = \begin{cases} 0, & \text{if} \,\, \ell> 0, \\ \frac{1}{n(n-1)}, & \text{if} \,\,\, \ell = 0. \end{cases} \end{align*} $$
The interpretation of multiplication on the Hecke algebra as various ‘systematic scan’ Markov chains is developed in [Reference Diaconis and Ram18], [Reference Bufetov and Nejjar10]. It works for other types in several variations. We are surprised to see it come up naturally in the present work.
The following corollary provides the connection to [Reference Ram52 Reference Ram, (3.16),(3.18),(3.20)] and [Reference Diaconis and Ram18, Proposition 4.9].
Corollary 3.5. Let
![]() $J_1 = 1$
, and let
$J_1 = 1$
, and let
![]() $J_k = T_{s_{k-1}}\cdots T_{s_2}T_{s_1}T_{s_1}T_{s_2}\cdots T_{s_{k-1}}$
, for
$J_k = T_{s_{k-1}}\cdots T_{s_2}T_{s_1}T_{s_1}T_{s_2}\cdots T_{s_{k-1}}$
, for
![]() $k\in \{2, \ldots , n\}$
. Then
$k\in \{2, \ldots , n\}$
. Then
 $$ \begin{align*}D = \sum_{k=1}^n q^{n-k}(J_k-1).\end{align*} $$
$$ \begin{align*}D = \sum_{k=1}^n q^{n-k}(J_k-1).\end{align*} $$
Proof. Using that
![]() $J_k = T_{s_{k-1}}J_{k-1}T_{s_{k-1}}$
, check, by induction, that
$J_k = T_{s_{k-1}}J_{k-1}T_{s_{k-1}}$
, check, by induction, that
 $$ \begin{align*}J_k = q^{k-1} + (q-1)\sum_{j=1}^{k-1} q^{j-1}T_{(j,k)}.\end{align*} $$
$$ \begin{align*}J_k = q^{k-1} + (q-1)\sum_{j=1}^{k-1} q^{j-1}T_{(j,k)}.\end{align*} $$
Thus,
 $$ \begin{align*} \sum_{k=1}^n q^{n-k}(J_k-1) &= 0+ \sum_{k=2}^n \left(q^{n-k+(k-1)} -q^{n-k} + (q-1)\sum_{j=1}^{k-1} q^{n-k+j-1}T_{(j,k)}\right) \\ &=(n-1)q^{n-1} - [n-1]_q + (q-1)D_{(21^{n-2})} = D, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^n q^{n-k}(J_k-1) &= 0+ \sum_{k=2}^n \left(q^{n-k+(k-1)} -q^{n-k} + (q-1)\sum_{j=1}^{k-1} q^{n-k+j-1}T_{(j,k)}\right) \\ &=(n-1)q^{n-1} - [n-1]_q + (q-1)D_{(21^{n-2})} = D, \end{align*} $$
where
![]() $D_{(21^{n-2})} := \sum _{i < j} q^{(n - 1) - (j-i)} T_{(i, j)}$
.
$D_{(21^{n-2})} := \sum _{i < j} q^{(n - 1) - (j-i)} T_{(i, j)}$
.
3.3 Eigenvalues and multiplicities
Hildebrand [Reference Hildebrand35] determined the eigenvalues of the random walk driven by Q on
![]() $GL_n(q)$
. His arguments use Macdonald’s version of J.A. Green’s formulas for the characters of
$GL_n(q)$
. His arguments use Macdonald’s version of J.A. Green’s formulas for the characters of
![]() $GL_n(q)$
along with sophisticated use of properties of Hall–Littlewood polynomials. Using the realization of the walk on the Hecke algebra, developed below in Section 5, and previous work of Ram and Halverson [Reference Halverson and Ram31], we can find cleaner formulas and proofs. Throughout, we have tried to keep track of how things depend on both q and n (the formulas are easier when
$GL_n(q)$
along with sophisticated use of properties of Hall–Littlewood polynomials. Using the realization of the walk on the Hecke algebra, developed below in Section 5, and previous work of Ram and Halverson [Reference Halverson and Ram31], we can find cleaner formulas and proofs. Throughout, we have tried to keep track of how things depend on both q and n (the formulas are easier when
![]() $q = 2$
).
$q = 2$
).
Theorem 3.6.
-
1. The eigenvalues
 $\beta _{\lambda }$
of the Markov chain
$\beta _{\lambda }$
of the Markov chain
 $P(x, y)$
driven by the random transvections measure Q on
$P(x, y)$
driven by the random transvections measure Q on
 $\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
are indexed by partitions
$\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
are indexed by partitions
 $\lambda \vdash n$
. These are (3.2)with b ranging over the boxes of the partition
$\lambda \vdash n$
. These are (3.2)with b ranging over the boxes of the partition $$ \begin{align} \beta_{\lambda} = \frac{1}{|\mathcal{T}_{n, q}|} \left( q^{n-1} \sum_{b \in \lambda} q^{ct(b)} - \frac{q^{n} - 1}{q - 1} \right), \end{align} $$
$$ \begin{align} \beta_{\lambda} = \frac{1}{|\mathcal{T}_{n, q}|} \left( q^{n-1} \sum_{b \in \lambda} q^{ct(b)} - \frac{q^{n} - 1}{q - 1} \right), \end{align} $$
 $\lambda $
. For the box in row i and column j, the content is defined as
$\lambda $
. For the box in row i and column j, the content is defined as
 $ct(b) = j - i$
, as in [Reference Macdonald46].
$ct(b) = j - i$
, as in [Reference Macdonald46].
-
2. The multiplicity of
 $\beta _{\lambda }$
for the induced Markov chain on
$\beta _{\lambda }$
for the induced Markov chain on
 $\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
is
$\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
is
 $f_{\lambda }^2$
, where (3.3)
$f_{\lambda }^2$
, where (3.3) $$ \begin{align} f_{\lambda} = \frac{n!}{\prod_{b \in \lambda} h(b)}. \end{align} $$
$$ \begin{align} f_{\lambda} = \frac{n!}{\prod_{b \in \lambda} h(b)}. \end{align} $$
Here,
 $h(b)$
is the hook length of box b [Reference Macdonald46].
$h(b)$
is the hook length of box b [Reference Macdonald46]. -
3. The multiplicity of
 $\beta _{\lambda }$
for the Markov chain induced by Q on
$\beta _{\lambda }$
for the Markov chain induced by Q on
 $GL_n(q)/\mathcal {B}$
is (3.4)
$GL_n(q)/\mathcal {B}$
is (3.4) $$ \begin{align} d_{\lambda} = f_{\lambda} \cdot \frac{[n]_q!}{\prod_{b \in \lambda} [h(b)]_q}. \end{align} $$
$$ \begin{align} d_{\lambda} = f_{\lambda} \cdot \frac{[n]_q!}{\prod_{b \in \lambda} [h(b)]_q}. \end{align} $$
The argument uses the representation of the Markov chain as multiplication on the Hecke algebra. This is developed further in Section 5.
Proof.
(a): Let D be the sum of transvections as in Theorem 1.6. By [Reference Halverson and Ram31] (3.20), the irreducible representation
![]() $H_n^{\lambda }$
of
$H_n^{\lambda }$
of
![]() $H_n$
indexed by
$H_n$
indexed by
![]() $\lambda $
has a ‘seminormal basis’
$\lambda $
has a ‘seminormal basis’
![]() $\{ v_T \mid \widehat {S}_n^{\lambda } \}$
such that
$\{ v_T \mid \widehat {S}_n^{\lambda } \}$
such that
![]() $J_k v_T = q^{k-1} q^{c(T(k))} v_T$
, where
$J_k v_T = q^{k-1} q^{c(T(k))} v_T$
, where
![]() $T(k)$
is the box containing k in T. Thus,
$T(k)$
is the box containing k in T. Thus,
 $$\begin{align*}Dv_T = \sum_{k = 1}^n q^{n - k} (q^{k - 1}q^{c(T(k))} - 1)v_T = \left( - \left( \frac{q^n - 1}{q - 1} \right) + \sum_{k = 1}^n q^{n-1} q^{c(T(k))} \right) v_T. \end{align*}$$
$$\begin{align*}Dv_T = \sum_{k = 1}^n q^{n - k} (q^{k - 1}q^{c(T(k))} - 1)v_T = \left( - \left( \frac{q^n - 1}{q - 1} \right) + \sum_{k = 1}^n q^{n-1} q^{c(T(k))} \right) v_T. \end{align*}$$
(b): The dimension of the irreducible representation of
![]() $H_n$
indexed by
$H_n$
indexed by
![]() $\lambda $
is the same as the dimension of the irreducible representation of
$\lambda $
is the same as the dimension of the irreducible representation of
![]() $S_n$
indexed by
$S_n$
indexed by
![]() $\lambda $
, which is well known as the hook-length formula [Reference Macdonald46, Ch. I(7.6)(ii), §6 Ex.2(a)]:
$\lambda $
, which is well known as the hook-length formula [Reference Macdonald46, Ch. I(7.6)(ii), §6 Ex.2(a)]:
(c): With
![]() $G = GL_n(q), H = H_n$
, the result follows since [Reference Macdonald46, Ch. IV(6.7)],
$G = GL_n(q), H = H_n$
, the result follows since [Reference Macdonald46, Ch. IV(6.7)],
 $$\begin{align*}\text{dim}(G^{\lambda}) = \frac{[n]_q!}{\prod_{b \in \lambda} [h(b)]_q} \quad \text{and} \quad \mathbf{1}_{\mathcal{B}}^G = \sum_{\lambda \in \widehat{S_n}} G^{\lambda} \otimes H^{\lambda}. \end{align*}$$
$$\begin{align*}\text{dim}(G^{\lambda}) = \frac{[n]_q!}{\prod_{b \in \lambda} [h(b)]_q} \quad \text{and} \quad \mathbf{1}_{\mathcal{B}}^G = \sum_{\lambda \in \widehat{S_n}} G^{\lambda} \otimes H^{\lambda}. \end{align*}$$
Example 3.7. Equation 3.2 for some specific partitions gives

The following simple lemma will be used several times in subsequent sections. It uses the usual majorization partial order (moving up boxes) on partitions of n, [Reference Macdonald46]. For example, when
![]() $n = 4$
the ordering is
$n = 4$
the ordering is
![]() $1111 \prec 211 \prec 22 \prec 31 \prec 4$
.
$1111 \prec 211 \prec 22 \prec 31 \prec 4$
.
Lemma 3.8. The eigenvalues
![]() $\beta _{\lambda }$
of Theorem 3.6 are monotone increasing in the majorization order.
$\beta _{\lambda }$
of Theorem 3.6 are monotone increasing in the majorization order.
Proof. Moving a single box (at the corner of the diagram of
![]() $\lambda $
) in position
$\lambda $
) in position
![]() $(i, j)$
to position
$(i, j)$
to position
![]() $(i', j')$
necessitates
$(i', j')$
necessitates
![]() $i' < i$
and
$i' < i$
and
![]() $j'> j$
, and so
$j'> j$
, and so
![]() $q^{j-i} < q^{j' - i'}$
. Since any
$q^{j-i} < q^{j' - i'}$
. Since any
![]() $\lambda \prec \lambda '$
can be obtained by successively moving up boxes, the proof is complete. For example,
$\lambda \prec \lambda '$
can be obtained by successively moving up boxes, the proof is complete. For example,

The partition
![]() $1^n = (1, 1, \dots , 1)$
is the minimal element in the partial order, and since
$1^n = (1, 1, \dots , 1)$
is the minimal element in the partial order, and since
![]() $\beta _{(1^n)} = 0$
, we have the following:
$\beta _{(1^n)} = 0$
, we have the following:
Corollary 3.9. If
![]() $\lambda \vdash n$
, then
$\lambda \vdash n$
, then
Corollary 3.10. If
![]() is a partition of n with
is a partition of n with
![]() $\lambda _1 = n - j$
and
$\lambda _1 = n - j$
and
![]() $j \le n/2$
, then
$j \le n/2$
, then
 $$ \begin{align*} \beta_{\lambda} \le \beta_{(n-j, j)} &= \frac{q^j(q^{n - j - 1} - 1)(q^{n - j} - 1) + (q^{n - 2} - 1)(q^j - 1)}{(q^{n-1} - 1)(q^n -1)} \\ &\le q^{-j}(1 + q^{-(n - 2j + 1)})(1 + q^{-(n - 1)})(1 + q^{-(n - 2)}). \end{align*} $$
$$ \begin{align*} \beta_{\lambda} \le \beta_{(n-j, j)} &= \frac{q^j(q^{n - j - 1} - 1)(q^{n - j} - 1) + (q^{n - 2} - 1)(q^j - 1)}{(q^{n-1} - 1)(q^n -1)} \\ &\le q^{-j}(1 + q^{-(n - 2j + 1)})(1 + q^{-(n - 1)})(1 + q^{-(n - 2)}). \end{align*} $$
Proof. The first inequality follows from Lemma 3.8. The formula for
![]() $\beta _{(n - j, j)}$
is a simple calculation from equation (3.2). Recall the elementary inequalities:
$\beta _{(n - j, j)}$
is a simple calculation from equation (3.2). Recall the elementary inequalities:
These give the inequality for
![]() $\beta _{(n - j, j)}$
:
$\beta _{(n - j, j)}$
:
 $$ \begin{align*} \beta_{(n - j, j)} &= \frac{q^j(q^{n - j - 1} - 1)(q^{n - j} - 1) + (q^{n - 2} - 1)(q^j - 1)}{(q^{n-1} - 1)(q^n -1)} \\ &\le \left( \frac{q^j q^{n - j - 1}q^{n - j} + q^{n-2}q^j}{q^{n-1} q^n} \right) \frac{1}{(1 - q^{-(n-1)})(1 - q^{-n})} \\ &\le (q^{-j} + q^{-(n - j + 1))})(1 + q^{-(n-2)})(1 + q^{-(n-1)}). \end{align*} $$
$$ \begin{align*} \beta_{(n - j, j)} &= \frac{q^j(q^{n - j - 1} - 1)(q^{n - j} - 1) + (q^{n - 2} - 1)(q^j - 1)}{(q^{n-1} - 1)(q^n -1)} \\ &\le \left( \frac{q^j q^{n - j - 1}q^{n - j} + q^{n-2}q^j}{q^{n-1} q^n} \right) \frac{1}{(1 - q^{-(n-1)})(1 - q^{-n})} \\ &\le (q^{-j} + q^{-(n - j + 1))})(1 + q^{-(n-2)})(1 + q^{-(n-1)}). \end{align*} $$
In the following sections, we will use a further bound from Corollary 3.10.
Corollary 3.11. Define
![]() $\kappa _{n, q, j} := (1 + q^{-(n - 2j + 1)})(1 + q^{-(n - 1)})(1 + q^{-(n - 2)})$
and
$\kappa _{n, q, j} := (1 + q^{-(n - 2j + 1)})(1 + q^{-(n - 1)})(1 + q^{-(n - 2)})$
and
Then for all
![]() $n, q$
,
$n, q$
,
Proof. Using
![]() $1 + x \le e^x$
, there is the initial bound
$1 + x \le e^x$
, there is the initial bound
which uses that
![]() $j \ge 1$
and so
$j \ge 1$
and so
![]() $(n - 2) \ge (n -2j)$
. Then,
$(n - 2) \ge (n -2j)$
. Then,
 $$ \begin{align*} \frac{\log(\kappa_{n, q, j})}{j} \le \frac{3 q^{-(n - 2j)}}{j}. \end{align*} $$
$$ \begin{align*} \frac{\log(\kappa_{n, q, j})}{j} \le \frac{3 q^{-(n - 2j)}}{j}. \end{align*} $$
With
![]() $f(x) = 3q^{-(n - 2x)}/x$
, we have
$f(x) = 3q^{-(n - 2x)}/x$
, we have
Since
![]() $2 \log (2)> 1$
, we see that
$2 \log (2)> 1$
, we see that
![]() $f(x)$
is increasing for
$f(x)$
is increasing for
![]() $x \ge 1$
and any
$x \ge 1$
and any
![]() $q \ge 2$
. Thus, for
$q \ge 2$
. Thus, for
![]() $1 \le j \le n/2$
,
$1 \le j \le n/2$
,
![]() $f(j)$
is maximized for
$f(j)$
is maximized for
![]() $j = n/2$
, which gives
$j = n/2$
, which gives
 $$\begin{align*}\alpha_{n, q} \le \max_{1 \le j \le n/2} \frac{3 q^{-(n - 2j)}}{j} \le \frac{6}{n}. \end{align*}$$
$$\begin{align*}\alpha_{n, q} \le \max_{1 \le j \le n/2} \frac{3 q^{-(n - 2j)}}{j} \le \frac{6}{n}. \end{align*}$$
4 Mixing time analysis
In this section, the eigenvalues from Section 3.3 are used to give bounds on the distance to stationarity for the random transvections Markov chain on
![]() $S_n$
. Section 4.1 reviews the tools which are needed for the bounds from specific starting states. Section 4.2 proves results for the chain started from the identity element, Section 4.3 proves results for the chain started from the reversal permutation, and Section 4.4 contains bounds for the average over all starting states.
$S_n$
. Section 4.1 reviews the tools which are needed for the bounds from specific starting states. Section 4.2 proves results for the chain started from the identity element, Section 4.3 proves results for the chain started from the reversal permutation, and Section 4.4 contains bounds for the average over all starting states.
4.1 Eigenvalue bounds
The following result from [Reference Diaconis and Ram18] will be the main tool for achieving bounds on the chi-square distance of the chain from different starting states.
Proposition 4.1 (Proposition 4.8 in [Reference Diaconis and Ram18]).
Let H be the Iwahori–Hecke algebra corresponding to a finite real reflection group W. Let K be a reversible Markov chain on W with stationary distribution
![]() $\pi $
determined by left multiplication by an element of H (also denoted by K). The following identities are true:
$\pi $
determined by left multiplication by an element of H (also denoted by K). The following identities are true:
-
1.
 $\chi ^2_x(\ell ) = q^{-2 I(x)}\sum _{\lambda \neq \mathbf {1}} t_{\lambda } \chi _H^{\lambda }(T_{x^{-1}} K^{2 \ell } T_x)$
,
$\chi ^2_x(\ell ) = q^{-2 I(x)}\sum _{\lambda \neq \mathbf {1}} t_{\lambda } \chi _H^{\lambda }(T_{x^{-1}} K^{2 \ell } T_x)$
,
 $x \in W$
,
$x \in W$
, -
2.
 $\sum _{x \in W} \pi (x) \chi ^2_x(\ell ) = \sum _{\lambda \neq \mathbf {1}} f_{\lambda } \chi _H^{\lambda }(K^{2 \ell })$
,
$\sum _{x \in W} \pi (x) \chi ^2_x(\ell ) = \sum _{\lambda \neq \mathbf {1}} f_{\lambda } \chi _H^{\lambda }(K^{2 \ell })$
,
where
![]() $\chi _H^{\lambda }$
are the irreducible characters,
$\chi _H^{\lambda }$
are the irreducible characters,
![]() $t_{\lambda }$
the generic degrees and
$t_{\lambda }$
the generic degrees and
![]() $f_{\lambda }$
the dimensions of the irreducible representations of W.
$f_{\lambda }$
the dimensions of the irreducible representations of W.
In general, the right-hand side of (a) could be difficult to calculate, but it simplifies for the special cases
![]() $x = id, x = \omega _0$
. These calculations, and the analysis of the sum, are contained in the following sections.
$x = id, x = \omega _0$
. These calculations, and the analysis of the sum, are contained in the following sections.
The right-hand side of the equations in Proposition 4.1 involves the following quantities, defined for
![]() $\lambda \vdash n$
:
$\lambda \vdash n$
:
-
•
 $n_{\lambda } = \sum _{i = 1}^{|\lambda |} (i - 1) \lambda _i$
,
$n_{\lambda } = \sum _{i = 1}^{|\lambda |} (i - 1) \lambda _i$
, -
•
 $c_{\lambda } = \sum _{b \in \lambda } ct(b)$
, where
$c_{\lambda } = \sum _{b \in \lambda } ct(b)$
, where
 $ct(b) = j - i$
if box b is in column j and row i,
$ct(b) = j - i$
if box b is in column j and row i, -
•
 $t_{\lambda } = q^{n_{\lambda }} \cdot r_{\lambda }$
, where
$t_{\lambda } = q^{n_{\lambda }} \cdot r_{\lambda }$
, where
 $r_{\lambda } = \frac {[n]_q!}{\prod _{b \in \lambda } [h_b]_q}$
,
$r_{\lambda } = \frac {[n]_q!}{\prod _{b \in \lambda } [h_b]_q}$
,
 $[k]_q = (q^k - 1)/(q - 1)$
and
$[k]_q = (q^k - 1)/(q - 1)$
and
 ,
, -
•
 $f_{\lambda }$
, which is the number of standard Young tableau of shape
$f_{\lambda }$
, which is the number of standard Young tableau of shape
 $\lambda $
. The formula is
$\lambda $
. The formula is  $$\begin{align*}f_{\lambda} = \frac{n!}{\prod_{b \in \lambda} h(b)}. \end{align*}$$
$$\begin{align*}f_{\lambda} = \frac{n!}{\prod_{b \in \lambda} h(b)}. \end{align*}$$
Table 1 shows these values for
![]() $n = 4$
and general q. From this example, we can observe that
$n = 4$
and general q. From this example, we can observe that
![]() $c_{\lambda }$
is increasing with respect to the partial order on partitions, while
$c_{\lambda }$
is increasing with respect to the partial order on partitions, while
![]() $n_{\lambda }$
is decreasing.
$n_{\lambda }$
is decreasing.
Table 1 The quantities involved in the eigenvalue and multiplicity calculations for
![]() $n = 4$
.
$n = 4$
.

Let us record that
 $$ \begin{align} \beta_{(n-1,1)} = \frac{q^{n-2}-1}{q^{n-1}-1}, \qquad t_{(n-1,1)} = q\cdot \frac{q^{n-1}-1}{q-1} \qquad\mbox{and}\qquad f_{(n-1,1)} = n-1. \end{align} $$
$$ \begin{align} \beta_{(n-1,1)} = \frac{q^{n-2}-1}{q^{n-1}-1}, \qquad t_{(n-1,1)} = q\cdot \frac{q^{n-1}-1}{q-1} \qquad\mbox{and}\qquad f_{(n-1,1)} = n-1. \end{align} $$
Since
![]() $n!\le n^n = e^{n\log n}$
then
$n!\le n^n = e^{n\log n}$
then
We will use the following bounds from [Reference Diaconis and Ram18, Lemma 7.2]:
 $$ \begin{align} t_{\lambda} \le q^{-\binom{\lambda_1}{2}+\binom{n}{2}}f_{\lambda}, \quad \text{and} \,\,\, \sum_{\lambda \vdash n} f_{\lambda}^2 = n!. \end{align} $$
$$ \begin{align} t_{\lambda} \le q^{-\binom{\lambda_1}{2}+\binom{n}{2}}f_{\lambda}, \quad \text{and} \,\,\, \sum_{\lambda \vdash n} f_{\lambda}^2 = n!. \end{align} $$
In addition, we need the following bounds for sums of
![]() $f_{\lambda }$
. Part (b) of the proposition below is Lemma 7.2(b) in [Reference Diaconis and Ram18]; the proof there is incomplete, so we give the simple proof below.
$f_{\lambda }$
. Part (b) of the proposition below is Lemma 7.2(b) in [Reference Diaconis and Ram18]; the proof there is incomplete, so we give the simple proof below.
Proposition 4.2.
-
1. There is a universal constant
 $K> 0$
such that, for all
$K> 0$
such that, for all
 $1 \le j \le n$
,
$1 \le j \le n$
,  $$\begin{align*}\sum_{\lambda: \lambda_1=n-j} f_{\lambda} \le \frac{n^{j}}{\sqrt{j!}} \cdot \frac{K}{j} e^{2 \sqrt{2j}}. \end{align*}$$
$$\begin{align*}\sum_{\lambda: \lambda_1=n-j} f_{\lambda} \le \frac{n^{j}}{\sqrt{j!}} \cdot \frac{K}{j} e^{2 \sqrt{2j}}. \end{align*}$$
-
2. For
 $1\le j\le n$
,
$1\le j\le n$
,  $$\begin{align*}\sum_{\lambda: \lambda_1=n-j} f^2_{\lambda} \le \frac{n^{2j}}{j!}. \end{align*}$$
$$\begin{align*}\sum_{\lambda: \lambda_1=n-j} f^2_{\lambda} \le \frac{n^{2j}}{j!}. \end{align*}$$
Proof. Recall that
![]() $f_{\lambda }$
is the number of standard tableau of shape
$f_{\lambda }$
is the number of standard tableau of shape
![]() $\lambda $
, that is, the elements
$\lambda $
, that is, the elements
![]() $1, 2, \dots , n$
are arranged in the shape
$1, 2, \dots , n$
are arranged in the shape
![]() $\lambda $
so that rows are increasing left to right and columns are increasing top to bottom. If
$\lambda $
so that rows are increasing left to right and columns are increasing top to bottom. If
![]() $\lambda _1 = n -j$
, then there are
$\lambda _1 = n -j$
, then there are
![]() $\binom {n}{j}$
ways to choose the elements not in the first row of the tableau. For a fixed partition
$\binom {n}{j}$
ways to choose the elements not in the first row of the tableau. For a fixed partition
![]() $\lambda $
, the number of ways of arranging the remaining j elements is at most the number of Young tableau corresponding to the partition of j created from the remaining rows of
$\lambda $
, the number of ways of arranging the remaining j elements is at most the number of Young tableau corresponding to the partition of j created from the remaining rows of
![]() $\lambda $
. This number is at most
$\lambda $
. This number is at most
![]() $\sqrt {j!}$
(Lemma 3 in [Reference Diaconis and Shahshahani22]). Thus,
$\sqrt {j!}$
(Lemma 3 in [Reference Diaconis and Shahshahani22]). Thus,
 $$ \begin{align*} \sum_{\lambda: \lambda_1=n-j} f_{\lambda} \le \binom{n}{j} \cdot \sqrt{j!} \cdot p(j), \end{align*} $$
$$ \begin{align*} \sum_{\lambda: \lambda_1=n-j} f_{\lambda} \le \binom{n}{j} \cdot \sqrt{j!} \cdot p(j), \end{align*} $$
where
![]() $p(j)$
is equal to the number of partitions of j. It is well known that
$p(j)$
is equal to the number of partitions of j. It is well known that
![]() $\log (p(n)) \sim B \cdot \sqrt {n}$
for a constant B. More precisely, from (2.11) in [Reference Hardy and Ramanujan32], there is a universal constant
$\log (p(n)) \sim B \cdot \sqrt {n}$
for a constant B. More precisely, from (2.11) in [Reference Hardy and Ramanujan32], there is a universal constant
![]() $K>0$
such that for all
$K>0$
such that for all
![]() $n \ge 1$
,
$n \ge 1$
,
This gives (a).
For part (b), we again use the inequality
![]() $f_{\lambda } \le \binom {n}{j} f_{\lambda ^*}$
, where
$f_{\lambda } \le \binom {n}{j} f_{\lambda ^*}$
, where
![]() $\lambda ^* = (\lambda _2, \dots , \lambda _k)$
is the partition of j determined by the rest of
$\lambda ^* = (\lambda _2, \dots , \lambda _k)$
is the partition of j determined by the rest of
![]() $\lambda $
after the first row. Then,
$\lambda $
after the first row. Then,
 $$ \begin{align*} \sum_{\lambda: \lambda_1 = n - j} f_{\lambda}^2 \le \binom{n}{j}^2 \sum_{\lambda^* \vdash j} f_{\lambda^*}^2 = \binom{n}{j}^2 \cdot j! = \left( \frac{n!}{(n - j)!j!} \right)^2 \cdot j! \le \frac{n^{2j}}{j!}. \end{align*} $$
$$ \begin{align*} \sum_{\lambda: \lambda_1 = n - j} f_{\lambda}^2 \le \binom{n}{j}^2 \sum_{\lambda^* \vdash j} f_{\lambda^*}^2 = \binom{n}{j}^2 \cdot j! = \left( \frac{n!}{(n - j)!j!} \right)^2 \cdot j! \le \frac{n^{2j}}{j!}. \end{align*} $$
Proposition 4.3. The function
![]() $s(\lambda ) := q^{c_{\lambda }} t_{\lambda }$
is monotone with respect to the partial order on partitions. For any
$s(\lambda ) := q^{c_{\lambda }} t_{\lambda }$
is monotone with respect to the partial order on partitions. For any
![]() $\lambda \vdash n$
,
$\lambda \vdash n$
,
Proof. Suppose that
![]() $\lambda \prec \widetilde {\lambda }$
and
$\lambda \prec \widetilde {\lambda }$
and
![]() $\widetilde {\lambda }$
is obtained from
$\widetilde {\lambda }$
is obtained from
![]() $\lambda $
by ‘moving up’ one box. Suppose the box at position
$\lambda $
by ‘moving up’ one box. Suppose the box at position
![]() $(i, j)$
is moved to
$(i, j)$
is moved to
![]() $(i', j')$
, with
$(i', j')$
, with
![]() $i' < i, j'> j$
.
$i' < i, j'> j$
.
Let
![]() $g(\lambda ) = c_{\lambda } + n_{\lambda }$
. Then,
$g(\lambda ) = c_{\lambda } + n_{\lambda }$
. Then,
 $$ \begin{align*} &c_{\widetilde{\lambda}} = c_{\lambda} + (j' - j) + (i - i') \\ &n_{\widetilde{\lambda}} = n_{\lambda} - (i - 1) + (i' - 1) = n_{\lambda} + (i' - i). \end{align*} $$
$$ \begin{align*} &c_{\widetilde{\lambda}} = c_{\lambda} + (j' - j) + (i - i') \\ &n_{\widetilde{\lambda}} = n_{\lambda} - (i - 1) + (i' - 1) = n_{\lambda} + (i' - i). \end{align*} $$
This implies that
Now, consider the change in
![]() $r_{\lambda }$
. The hook lengths of
$r_{\lambda }$
. The hook lengths of
![]() $\widetilde {\lambda }$
are:
$\widetilde {\lambda }$
are:
 $$ \begin{align*} &\widetilde{h}(i, j) = h(i, j) - 1 = 0, \quad \widetilde{h}(i', j') = h(i, j) + 1 = 1 \\ &\widetilde{h}(k, j) = h(k, j) - 1, \quad k < i, k \neq i' \\ &\widetilde{h}(i, l) = h(i, l) - 1, \quad l < j \\ &\widetilde{h}(k, j') = h(k, j') + 1, \quad k < i' \\ &\widetilde{h}(i', l) = h(i', l) +1, \quad l < j', l \neq j \end{align*} $$
$$ \begin{align*} &\widetilde{h}(i, j) = h(i, j) - 1 = 0, \quad \widetilde{h}(i', j') = h(i, j) + 1 = 1 \\ &\widetilde{h}(k, j) = h(k, j) - 1, \quad k < i, k \neq i' \\ &\widetilde{h}(i, l) = h(i, l) - 1, \quad l < j \\ &\widetilde{h}(k, j') = h(k, j') + 1, \quad k < i' \\ &\widetilde{h}(i', l) = h(i', l) +1, \quad l < j', l \neq j \end{align*} $$
and
![]() $\widetilde {h}(k, l) = h(k, l)$
for all other boxes
$\widetilde {h}(k, l) = h(k, l)$
for all other boxes
![]() $b = (k, l)$
. Thus,
$b = (k, l)$
. Thus,
 $$ \begin{align*} \sum_b \widetilde{h}(b) - \sum_b h(b) &= (j' - 1) + (i' - 1) - (i - 1) - (j - 1) \\ &= (j' - j) + (i' - i). \end{align*} $$
$$ \begin{align*} \sum_b \widetilde{h}(b) - \sum_b h(b) &= (j' - 1) + (i' - 1) - (i - 1) - (j - 1) \\ &= (j' - j) + (i' - i). \end{align*} $$
Using the inequalities
![]() $q^{r-1} < (q^r - 1) < q^r$
, we have
$q^{r-1} < (q^r - 1) < q^r$
, we have
 $$ \begin{align*} r(\widetilde{\lambda}) &= \frac{[n]_q!(q - 1)^n}{\prod_b (q^{h(b)} - 1)} \\ &\le \frac{[n]_q!(q - 1)^n}{q^{\sum_b \widetilde{h}(b) - n}} = \frac{1}{q^{(j' - j) + (i' - i) -n} } \frac{[n]_q!(q - 1)^n}{q^{\sum_b h(b)}} \\ &\le \frac{1}{q^{(j' - j) + (i' - i) -n} } \frac{[n]_q!(q - 1)^n}{\prod_b (q^{h(b)} - 1)} = \frac{1}{q^{(j' - j) + (i' - i) -n} } r(\lambda). \end{align*} $$
$$ \begin{align*} r(\widetilde{\lambda}) &= \frac{[n]_q!(q - 1)^n}{\prod_b (q^{h(b)} - 1)} \\ &\le \frac{[n]_q!(q - 1)^n}{q^{\sum_b \widetilde{h}(b) - n}} = \frac{1}{q^{(j' - j) + (i' - i) -n} } \frac{[n]_q!(q - 1)^n}{q^{\sum_b h(b)}} \\ &\le \frac{1}{q^{(j' - j) + (i' - i) -n} } \frac{[n]_q!(q - 1)^n}{\prod_b (q^{h(b)} - 1)} = \frac{1}{q^{(j' - j) + (i' - i) -n} } r(\lambda). \end{align*} $$
Combining this with the result for
![]() $g(\lambda )$
:
$g(\lambda )$
:
since
![]() $i> i'$
.
$i> i'$
.
Assuming the monotonicity, then if
![]() $\lambda _1 \ge n/2$
we have
$\lambda _1 \ge n/2$
we have
![]() $s(\lambda ) \le s((\lambda _1, n - \lambda _1))$
. To calculate this quantity:
$s(\lambda ) \le s((\lambda _1, n - \lambda _1))$
. To calculate this quantity:
 $$ \begin{align*} g(\lambda) &\le g((\lambda_1, n - \lambda_1)) = c_{(\lambda_1, n - \lambda_1)} + n_{(\lambda_1, n - \lambda_1)} \\ &= \left( \frac{\lambda(\lambda_1 - 1)}{2} + \frac{(n - \lambda_1 - 1)(n - \lambda_1 - 2)}{2} - 1 \right) + (n - \lambda_1) \\ &= \binom{\lambda_1}{2} + \binom{n - \lambda_1}{2} = \frac{n(n-1)}{2} - \lambda_1(n - \lambda_1). \end{align*} $$
$$ \begin{align*} g(\lambda) &\le g((\lambda_1, n - \lambda_1)) = c_{(\lambda_1, n - \lambda_1)} + n_{(\lambda_1, n - \lambda_1)} \\ &= \left( \frac{\lambda(\lambda_1 - 1)}{2} + \frac{(n - \lambda_1 - 1)(n - \lambda_1 - 2)}{2} - 1 \right) + (n - \lambda_1) \\ &= \binom{\lambda_1}{2} + \binom{n - \lambda_1}{2} = \frac{n(n-1)}{2} - \lambda_1(n - \lambda_1). \end{align*} $$
For
![]() $r_{\lambda }$
, note that the hook lengths of
$r_{\lambda }$
, note that the hook lengths of
![]() $(\lambda _1, n - \lambda _1)$
are
$(\lambda _1, n - \lambda _1)$
are

If
![]() $\lambda _1 = n - j$
, we see the terms that cancel:
$\lambda _1 = n - j$
, we see the terms that cancel:

This uses the inequality
![]() $q^{r-1} < q^r - 1 < q^r$
. Thus, if
$q^{r-1} < q^r - 1 < q^r$
. Thus, if
![]() $\lambda _1 \ge n/2$
, we have shown
$\lambda _1 \ge n/2$
, we have shown
Now, suppose
![]() $\lambda _1 \le n/2$
, so
$\lambda _1 \le n/2$
, so
![]() $s(\lambda ) \le s((n/2, n/2))$
(assume n is even). To calculate this,
$s(\lambda ) \le s((n/2, n/2))$
(assume n is even). To calculate this,
 $$ \begin{align*} g(\lambda) &\le g((n/2, n/2)) = c_{(n/2, n/2)} + n_{(n/2, n/2)} \\ &= \frac{(n/2 - 1)n/2}{2} + \frac{(n/2 - 2)(n/2 - 1)}{2} - 1 + \frac{n}{2} = \frac{n^2}{4} - \frac{n}{2}. \end{align*} $$
$$ \begin{align*} g(\lambda) &\le g((n/2, n/2)) = c_{(n/2, n/2)} + n_{(n/2, n/2)} \\ &= \frac{(n/2 - 1)n/2}{2} + \frac{(n/2 - 2)(n/2 - 1)}{2} - 1 + \frac{n}{2} = \frac{n^2}{4} - \frac{n}{2}. \end{align*} $$
To bound
![]() $r_{\lambda }$
, use the same calculation as before to get
$r_{\lambda }$
, use the same calculation as before to get
and so in total
![]() $s((n/2, n/2)) \le q^{n^2/2 - n/2} = q^{\binom {n}{2}}$
.
$s((n/2, n/2)) \le q^{n^2/2 - n/2} = q^{\binom {n}{2}}$
.
4.2 Starting from
 $\mathrm {id}$
$\mathrm {id}$
Theorem 4.4. Let P be the Markov chain on
![]() $S_n$
induced by random transvections on
$S_n$
induced by random transvections on
![]() $GL_n(q)$
.
$GL_n(q)$
.
-
1. For
 $t_{\lambda }, \beta _{\lambda }$
defined in Theorem 3.6, we have
$t_{\lambda }, \beta _{\lambda }$
defined in Theorem 3.6, we have  $$\begin{align*}4 \|P_{id}^{\ell} - \pi_q \|_{TV}^2 \le \chi_{id}^2(\ell) = \sum_{\lambda \vdash n, \lambda \neq (n)} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell}. \end{align*}$$
$$\begin{align*}4 \|P_{id}^{\ell} - \pi_q \|_{TV}^2 \le \chi_{id}^2(\ell) = \sum_{\lambda \vdash n, \lambda \neq (n)} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell}. \end{align*}$$
-
2. Let
 $\alpha _{n, q}$
be as in Corollary 3.11 and
$\alpha _{n, q}$
be as in Corollary 3.11 and
 $n, q$
such that
$n, q$
such that
 $\log q> 6/n$
. Then if
$\log q> 6/n$
. Then if
 $\ell \ge \frac {n \log q/2 + \log n + c}{(\log q - \alpha _{n, q})}, c> 0$
, we have
$\ell \ge \frac {n \log q/2 + \log n + c}{(\log q - \alpha _{n, q})}, c> 0$
, we have  $$ \begin{align*} \chi_{id}^2(\ell) &\le (e^{e^{-2c}} - 1) + e^{-cn}. \end{align*} $$
$$ \begin{align*} \chi_{id}^2(\ell) &\le (e^{e^{-2c}} - 1) + e^{-cn}. \end{align*} $$
-
3. For any
 $\ell \ge 1$
,
$\ell \ge 1$
,  $$\begin{align*}\chi_{id}^2(\ell) \ge (q^{n-1} - 1)(n - 1)q^{-4 \ell}. \end{align*}$$
$$\begin{align*}\chi_{id}^2(\ell) \ge (q^{n-1} - 1)(n - 1)q^{-4 \ell}. \end{align*}$$
-
4. If
 $\ell \le n/8$
, then for fixed q and n large, (4.4)
$\ell \le n/8$
, then for fixed q and n large, (4.4) $$ \begin{align} \|P_{id}^{\ell} - \pi_q \|_{TV} \ge 1 - o(1). \end{align} $$
$$ \begin{align} \|P_{id}^{\ell} - \pi_q \|_{TV} \ge 1 - o(1). \end{align} $$
Theorem 4.4 shows that restricting the random transvections walk from
![]() $GL_n(q)$
to the double coset space only speeds things up by a factor of
$GL_n(q)$
to the double coset space only speeds things up by a factor of
![]() $2$
when started from the identity. Hildebrand [Reference Hildebrand35] shows that the total variation distance on all of
$2$
when started from the identity. Hildebrand [Reference Hildebrand35] shows that the total variation distance on all of
![]() $GL_n(q)$
is only small after
$GL_n(q)$
is only small after
![]() $n + c$
steps. Note this is independent of q.
$n + c$
steps. Note this is independent of q.
Proof. (a): The inequality follows from Proposition 4.1 (b):
 $$ \begin{align*} \chi^2_{id}(\ell) &= q^{-2 I(id)} \sum_{\lambda \neq (n)} t_{\lambda} \chi_H^{\lambda}(T_{id} K^{2\ell}T_{id}) \\ &= \sum_{\lambda \neq (n)} t_{\lambda} \chi_H^{\lambda}(K^{2\ell}) = \sum_{\lambda \neq (n)} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell}. \end{align*} $$
$$ \begin{align*} \chi^2_{id}(\ell) &= q^{-2 I(id)} \sum_{\lambda \neq (n)} t_{\lambda} \chi_H^{\lambda}(T_{id} K^{2\ell}T_{id}) \\ &= \sum_{\lambda \neq (n)} t_{\lambda} \chi_H^{\lambda}(K^{2\ell}) = \sum_{\lambda \neq (n)} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell}. \end{align*} $$
(b): From Corollary 3.10 if
![]() $\lambda _1 = n - j$
, then
$\lambda _1 = n - j$
, then
![]() $\beta _{\lambda } \le \kappa _{n, q, j} q^{-j}$
, where
$\beta _{\lambda } \le \kappa _{n, q, j} q^{-j}$
, where
Using the bound on
![]() $t_{\lambda }$
from equation (4.3), for
$t_{\lambda }$
from equation (4.3), for
![]() $1 \le j \le \lfloor n/2 \rfloor $
, we have
$1 \le j \le \lfloor n/2 \rfloor $
, we have
 $$ \begin{align} \sum_{\lambda: \lambda_1 = n - j} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} & \le (\kappa_{n, q, j} q^{-j} )^{2\ell} \sum_{\lambda: \lambda_1 = n -j} q^{-\binom{n-j}{2} + \binom{n}{2}} f_{\lambda}^2 \notag \\ &\le (\kappa_{n, q, j} q^{-j} )^{2\ell} q^{nj - j(j+1)/2} \cdot \frac{n^{2j}}{j!} \notag \\ &\le \frac{1}{j!} \exp \left( -2 \ell j \left(\log q - \frac{\log(\kappa_{n, q, j})}{j} \right) + \log q (nj - j(j + 1)/2) + 2j \log n \right) \notag \\ &\le \frac{1}{j!} \exp \left( -2 \ell j \left(\log q - \alpha_{n, q} \right) + \log q (nj - j(j + 1)/2) + 2j \log n \right). \end{align} $$
$$ \begin{align} \sum_{\lambda: \lambda_1 = n - j} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} & \le (\kappa_{n, q, j} q^{-j} )^{2\ell} \sum_{\lambda: \lambda_1 = n -j} q^{-\binom{n-j}{2} + \binom{n}{2}} f_{\lambda}^2 \notag \\ &\le (\kappa_{n, q, j} q^{-j} )^{2\ell} q^{nj - j(j+1)/2} \cdot \frac{n^{2j}}{j!} \notag \\ &\le \frac{1}{j!} \exp \left( -2 \ell j \left(\log q - \frac{\log(\kappa_{n, q, j})}{j} \right) + \log q (nj - j(j + 1)/2) + 2j \log n \right) \notag \\ &\le \frac{1}{j!} \exp \left( -2 \ell j \left(\log q - \alpha_{n, q} \right) + \log q (nj - j(j + 1)/2) + 2j \log n \right). \end{align} $$
Recall the final inequality follows since
![]() $\alpha _{n, q} := \max _{1 \le j \le n/2} \log (\kappa _{n, q, j})/j$
. If
$\alpha _{n, q} := \max _{1 \le j \le n/2} \log (\kappa _{n, q, j})/j$
. If
![]() $\ell = \frac {n \log q/2 + \log n + c}{(\log q - \alpha _{n, q})}$
, then the exponent in equation (4.5) is
$\ell = \frac {n \log q/2 + \log n + c}{(\log q - \alpha _{n, q})}$
, then the exponent in equation (4.5) is
 $$ \begin{align*} - 2j \left( n\log q/2 + \log n + c \right) &+ \log q (nj - j(j + 1)/2) + 2j \log n \\ &= -j(2c + \log q(j+1)/2). \end{align*} $$
$$ \begin{align*} - 2j \left( n\log q/2 + \log n + c \right) &+ \log q (nj - j(j + 1)/2) + 2j \log n \\ &= -j(2c + \log q(j+1)/2). \end{align*} $$
This gives
 $$\begin{align*}\sum_{j = 1}^{\lfloor n/2 \rfloor}\sum_{\lambda: \lambda_1 = n - j} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} \le \sum_{j = 1}^{\lfloor n/2 \rfloor} \frac{e^{-2jc }}{j!} \le e^{e^{-2c}} - 1. \end{align*}$$
$$\begin{align*}\sum_{j = 1}^{\lfloor n/2 \rfloor}\sum_{\lambda: \lambda_1 = n - j} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} \le \sum_{j = 1}^{\lfloor n/2 \rfloor} \frac{e^{-2jc }}{j!} \le e^{e^{-2c}} - 1. \end{align*}$$
Next, we need to consider the partitions
![]() $\lambda $
with
$\lambda $
with
![]() $\lambda _1 \le n/2$
. For these partitions,
$\lambda _1 \le n/2$
. For these partitions,
Then we have
 $$ \begin{align*} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} t_{\lambda} f_{\lambda} \\ &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} q^{nj - j(j+1)/2} f_{\lambda}^2 \\ &\le n! \cdot \exp \left( -2 \ell (n/2) \left( \log q + \frac{\kappa_{n, q, n/2}}{n/2} \right) + n^2/2 \right) \\ &\le \exp \left( -n (n \log q/2 + \log n + c) + n^2/2 \right) \sum_{\lambda \vdash n} f_{\lambda}^2 \\ &\le n! \exp \left( -n (n \log q/2 + \log n + c) + n^2/2 \right), \end{align*} $$
$$ \begin{align*} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} t_{\lambda} f_{\lambda} \\ &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} q^{nj - j(j+1)/2} f_{\lambda}^2 \\ &\le n! \cdot \exp \left( -2 \ell (n/2) \left( \log q + \frac{\kappa_{n, q, n/2}}{n/2} \right) + n^2/2 \right) \\ &\le \exp \left( -n (n \log q/2 + \log n + c) + n^2/2 \right) \sum_{\lambda \vdash n} f_{\lambda}^2 \\ &\le n! \exp \left( -n (n \log q/2 + \log n + c) + n^2/2 \right), \end{align*} $$
using
![]() $\sum _{\lambda } f_{\lambda }^2 = n!$
and that if
$\sum _{\lambda } f_{\lambda }^2 = n!$
and that if
![]() $n/2 \le j \le n$
, then
$n/2 \le j \le n$
, then
since the function is increasing in j. Note also that if
![]() $q \ge 3$
, then
$q \ge 3$
, then
![]() $\log q> 1$
and
$\log q> 1$
and
![]() $n! \le n^n = e^{\log n}$
. To finish the bound,
$n! \le n^n = e^{\log n}$
. To finish the bound,
 $$ \begin{align*} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} &\le \exp\left( n \log n -n (n \log q/2 + \log n + c) + n^2/2 \right) \\ &= \exp\left( -(n^2/2) (\log q - 1) - cn \right) \le e^{-cn}. \end{align*} $$
$$ \begin{align*} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} &\le \exp\left( n \log n -n (n \log q/2 + \log n + c) + n^2/2 \right) \\ &= \exp\left( -(n^2/2) (\log q - 1) - cn \right) \le e^{-cn}. \end{align*} $$
(c): The lower bound comes from considering the
![]() $\lambda = (n - 1, 1)$
term from the sum in (a). Using the quantities (4.1), this gives
$\lambda = (n - 1, 1)$
term from the sum in (a). Using the quantities (4.1), this gives
 $$ \begin{align*} \chi^2_{id}(\ell) &= \sum_{\lambda \neq (n)} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2\ell} \ge t_{(n-1, 1)} f_{(n-1, 1)} \beta_{(n-1, 1)}^{2 \ell} \\ &= q \cdot \frac{q^{n-1} - 1}{q -1} (n-1) \left( \frac{q^{n-2} - 1}{q^{n-1} - 1} \right)^{2 \ell} \ge (q^{n-1} - 1)(n-1) q^{-4\ell}. \end{align*} $$
$$ \begin{align*} \chi^2_{id}(\ell) &= \sum_{\lambda \neq (n)} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2\ell} \ge t_{(n-1, 1)} f_{(n-1, 1)} \beta_{(n-1, 1)}^{2 \ell} \\ &= q \cdot \frac{q^{n-1} - 1}{q -1} (n-1) \left( \frac{q^{n-2} - 1}{q^{n-1} - 1} \right)^{2 \ell} \ge (q^{n-1} - 1)(n-1) q^{-4\ell}. \end{align*} $$
This uses that
![]() $(q^{n-2} - 1)/(q^{n-1} - 1) \ge q^{-2}$
.
$(q^{n-2} - 1)/(q^{n-1} - 1) \ge q^{-2}$
.
(d): From the alternative version of the walk on the Hecke algebra, involving
![]() $D/|\mathcal {T}_{n, q}|$
with D from 1.6, the walk proceeds by picking a transposition
$D/|\mathcal {T}_{n, q}|$
with D from 1.6, the walk proceeds by picking a transposition
![]() $(i,j), i < j$
with probability proportional to
$(i,j), i < j$
with probability proportional to
and multiplying by
![]() $T_{ij}$
. As described in Section 3.2, multiplication by
$T_{ij}$
. As described in Section 3.2, multiplication by
![]() $T_{ij}$
corresponds to proposing the transposition
$T_{ij}$
corresponds to proposing the transposition
![]() $(i, j)$
and proceeding via the Metropolis algorithm. Thus, multiplication by
$(i, j)$
and proceeding via the Metropolis algorithm. Thus, multiplication by
![]() $T_{ij}$
induces at most
$T_{ij}$
induces at most
![]() $2(j - i)$
inversions, always less than
$2(j - i)$
inversions, always less than
![]() $2n$
. From [Reference Diaconis and Shahshahani22] Theorem 5.1, under
$2n$
. From [Reference Diaconis and Shahshahani22] Theorem 5.1, under
![]() $\pi _q$
, a typical permutation has
$\pi _q$
, a typical permutation has
![]() $\binom {n}{2} - \frac {n - q}{q + 1} + O(\sqrt {n})$
inversions (and the fluctuations are Gaussian about this mean). If
$\binom {n}{2} - \frac {n - q}{q + 1} + O(\sqrt {n})$
inversions (and the fluctuations are Gaussian about this mean). If
![]() $\ell = n/8$
, the measure
$\ell = n/8$
, the measure
![]() $P_{id}^{\ell }(\cdot )$
is concentrated on permutations with at most
$P_{id}^{\ell }(\cdot )$
is concentrated on permutations with at most
![]() $n^2/4$
inversions and
$n^2/4$
inversions and
![]() $\pi _q$
is concentrated on permutations with order
$\pi _q$
is concentrated on permutations with order
![]() $n^2/2 - (n - 1)/(q + 1) + O(\sqrt {n})$
inversions.
$n^2/2 - (n - 1)/(q + 1) + O(\sqrt {n})$
inversions.
4.3 Starting from
 $\omega _0$
$\omega _0$
Theorem 4.5. Let P be the Markov chain on
![]() $S_n$
induced by random transvections on
$S_n$
induced by random transvections on
![]() $GL_n(q)$
, and let
$GL_n(q)$
, and let
![]() $\omega _0 \in S_n$
be the reversal permutation in
$\omega _0 \in S_n$
be the reversal permutation in
![]() $S_n$
.
$S_n$
.
-
1. With
 $t_{\lambda }, c_{\lambda }, \beta _{\lambda }$
defined in Section 3.3,
$t_{\lambda }, c_{\lambda }, \beta _{\lambda }$
defined in Section 3.3,  $$\begin{align*}4 \|P_{\omega_0}^{\ell} - \pi_q \|_{TV}^2 \le \chi_{\omega_0}^2(\ell) = q^{-\binom{n}{2}} \sum_{\lambda \neq (n)} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell}. \end{align*}$$
$$\begin{align*}4 \|P_{\omega_0}^{\ell} - \pi_q \|_{TV}^2 \le \chi_{\omega_0}^2(\ell) = q^{-\binom{n}{2}} \sum_{\lambda \neq (n)} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell}. \end{align*}$$
-
2. Let
 $\alpha _{n, q}$
be as in Corollary 3.11 and
$\alpha _{n, q}$
be as in Corollary 3.11 and
 $n, q$
such that
$n, q$
such that
 $\log q> 6/n$
. If
$\log q> 6/n$
. If
 $\ell \ge (\log n/2 + c)/(\log q - \alpha _{n, q})$
for
$\ell \ge (\log n/2 + c)/(\log q - \alpha _{n, q})$
for
 $c> 0$
with
$c> 0$
with
 $c \ge 2 \sqrt {2}$
then
$c \ge 2 \sqrt {2}$
then  $$\begin{align*}\chi_{\omega_0}^2(\ell) \le - 2K \log(1 - e^{-c}) + \sqrt{K} e^{- cn}, \end{align*}$$
$$\begin{align*}\chi_{\omega_0}^2(\ell) \le - 2K \log(1 - e^{-c}) + \sqrt{K} e^{- cn}, \end{align*}$$
for a universal constant
 $K> 0$
(independent of
$K> 0$
(independent of
 $q, n$
).
$q, n$
). -
3. For any
 $\ell \ge 1$
,
$\ell \ge 1$
,  $$\begin{align*}\chi^2_{\omega_0}(\ell) \ge q^{-(n-2)}(n-1) (q^{n-1} -1) q^{-4 \ell}. \end{align*}$$
$$\begin{align*}\chi^2_{\omega_0}(\ell) \ge q^{-(n-2)}(n-1) (q^{n-1} -1) q^{-4 \ell}. \end{align*}$$
Remark 4.6. Theorem 4.5 shows that the Markov chain has a cutoff in its approach to stationarity in the chi-square metric. It shows the same exponential speed up as the walk started at a typical position (Theorem 4.7 below) and indeed is faster by a factor of
![]() $2$
. This is presumably because it starts at the permutation
$2$
. This is presumably because it starts at the permutation
![]() $\omega _0$
, at which the stationary distribution
$\omega _0$
, at which the stationary distribution
![]() $\pi _q$
is concentrated, instead of ‘close to
$\pi _q$
is concentrated, instead of ‘close to
![]() $\omega _0$
’.
$\omega _0$
’.
Proof of Theorem 4.5.
(a): By Proposition 4.9 in [Reference Diaconis and Ram18], if
![]() $\omega _0$
is the longest element of W, then
$\omega _0$
is the longest element of W, then
where
![]() $\rho ^{\lambda }$
is the irreducible representation indexed by
$\rho ^{\lambda }$
is the irreducible representation indexed by
![]() $\lambda $
. Using this and 4.1 (a),
$\lambda $
. Using this and 4.1 (a),
 $$ \begin{align*} \chi^2_{\omega_0}(\ell) &= q^{-2 I(\omega_0)}\sum_{\lambda \neq \mathbf{1}} t_{\lambda} \chi_H^{\lambda}(T_{\omega_0^{-1}} K^{2 \ell} T_{\omega_0}) \\ &= q^{-2 I(\omega_0)}\sum_{\lambda \neq \mathbf{1}} t_{\lambda} \chi_H^{\lambda}( K^{2 \ell} T_{\omega_0} T_{\omega_0^{-1}}) \\ &= q^{-2 I(\omega_0)}\sum_{\lambda \neq \mathbf{1}} t_{\lambda} \chi_H^{\lambda}( K^{2 \ell} T_{\omega_0}^2) \\ &= q^{-2 I(\omega_0)}\sum_{\lambda \neq \mathbf{1}} t_{\lambda} \chi_H^{\lambda}( K^{2 \ell} q^{c_{\lambda} + I(\omega_0)}) \\ &= q^{-I(\omega_0)} \sum_{\lambda \neq \mathbf{1}} q^{c_{\lambda}} t_{\lambda} \chi_H^{\lambda}( K^{2 \ell} ) = q^{-I(\omega_0)} \sum_{\lambda \neq \mathbf{1}} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} \end{align*} $$
$$ \begin{align*} \chi^2_{\omega_0}(\ell) &= q^{-2 I(\omega_0)}\sum_{\lambda \neq \mathbf{1}} t_{\lambda} \chi_H^{\lambda}(T_{\omega_0^{-1}} K^{2 \ell} T_{\omega_0}) \\ &= q^{-2 I(\omega_0)}\sum_{\lambda \neq \mathbf{1}} t_{\lambda} \chi_H^{\lambda}( K^{2 \ell} T_{\omega_0} T_{\omega_0^{-1}}) \\ &= q^{-2 I(\omega_0)}\sum_{\lambda \neq \mathbf{1}} t_{\lambda} \chi_H^{\lambda}( K^{2 \ell} T_{\omega_0}^2) \\ &= q^{-2 I(\omega_0)}\sum_{\lambda \neq \mathbf{1}} t_{\lambda} \chi_H^{\lambda}( K^{2 \ell} q^{c_{\lambda} + I(\omega_0)}) \\ &= q^{-I(\omega_0)} \sum_{\lambda \neq \mathbf{1}} q^{c_{\lambda}} t_{\lambda} \chi_H^{\lambda}( K^{2 \ell} ) = q^{-I(\omega_0)} \sum_{\lambda \neq \mathbf{1}} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} \end{align*} $$
since
![]() $K \in Z(H)$
, that is, K commutes with all elements of the Hecke algebra.
$K \in Z(H)$
, that is, K commutes with all elements of the Hecke algebra.
(b): Suppose
![]() $\lambda _1 = n -j$
for
$\lambda _1 = n -j$
for
![]() $1 \le j \le n/2$
. Recall the definition
$1 \le j \le n/2$
. Recall the definition
![]() $s(\lambda ) = q^{c_{\lambda }}t_{\lambda }$
. From Proposition 4.3,
$s(\lambda ) = q^{c_{\lambda }}t_{\lambda }$
. From Proposition 4.3,
![]() $s(\lambda ) \le q^{\binom {n}{2}}$
. Then,
$s(\lambda ) \le q^{\binom {n}{2}}$
. Then,
 $$ \begin{align*} q^{-\binom{n}{2}} \sum_{\lambda: \lambda_1 = n - j} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} & = q^{-\binom{n}{2}} \sum_{\lambda: \lambda_1 = n - j} s(\lambda) f_{\lambda} \beta_{\lambda}^{2 \ell} \\ & \le (\kappa_{n, q, j} q^{-j} )^{2\ell} q^{-\binom{n}{2}} \sum_{\lambda: \lambda_1 = n -j} q^{ \binom{n }{2} } f_{\lambda} \\ & \le (\kappa_{n, q, j} q^{-j} )^{2\ell} \sum_{\lambda: \lambda_1 = n -j} f_{\lambda} \\ &\le (\kappa_{n, q, j} q^{-j} )^{2\ell} \cdot \frac{n^{j}}{\sqrt{j!}} \cdot \frac{K}{j}e^{2 \sqrt{2j}} \\ &\le \frac{K}{\sqrt{j!}} \exp \left( -2 \ell j \left(\log q - \frac{\log(\kappa_{n, q, j})}{j} \right) + (j-1)\log n + 2 \sqrt{2j} \right). \end{align*} $$
$$ \begin{align*} q^{-\binom{n}{2}} \sum_{\lambda: \lambda_1 = n - j} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} & = q^{-\binom{n}{2}} \sum_{\lambda: \lambda_1 = n - j} s(\lambda) f_{\lambda} \beta_{\lambda}^{2 \ell} \\ & \le (\kappa_{n, q, j} q^{-j} )^{2\ell} q^{-\binom{n}{2}} \sum_{\lambda: \lambda_1 = n -j} q^{ \binom{n }{2} } f_{\lambda} \\ & \le (\kappa_{n, q, j} q^{-j} )^{2\ell} \sum_{\lambda: \lambda_1 = n -j} f_{\lambda} \\ &\le (\kappa_{n, q, j} q^{-j} )^{2\ell} \cdot \frac{n^{j}}{\sqrt{j!}} \cdot \frac{K}{j}e^{2 \sqrt{2j}} \\ &\le \frac{K}{\sqrt{j!}} \exp \left( -2 \ell j \left(\log q - \frac{\log(\kappa_{n, q, j})}{j} \right) + (j-1)\log n + 2 \sqrt{2j} \right). \end{align*} $$
The third inequality uses Proposition 4.2 for
![]() $\sum _{\lambda : \lambda _1 = n - j} f_{\lambda }$
. Recall
$\sum _{\lambda : \lambda _1 = n - j} f_{\lambda }$
. Recall
![]() $\alpha _{n, q} := \max _{1 \le j \le n/2} \log (\kappa _{n, q, j})/j$
. If
$\alpha _{n, q} := \max _{1 \le j \le n/2} \log (\kappa _{n, q, j})/j$
. If
![]() $\ell = (\log n/2 + c)/(\log q - \alpha _{n, q})$
, then the bound becomes
$\ell = (\log n/2 + c)/(\log q - \alpha _{n, q})$
, then the bound becomes
 $$ \begin{align*} \sum_{j = 1}^{n/2} q^{-\binom{n}{2}} \sum_{\lambda: \lambda_1 = n - j} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} &\le \sum_{j = 1}^{n/2}\frac{K}{\sqrt{j!}} \exp \left( - j \log n - 2jc + (j-1)\log n + 2 \sqrt{2j} \right) \\ &\le 2 K \sum_{j = 1}^{n/2} \frac{e^{-2jc + 2 \sqrt{2j}}}{j}, \end{align*} $$
$$ \begin{align*} \sum_{j = 1}^{n/2} q^{-\binom{n}{2}} \sum_{\lambda: \lambda_1 = n - j} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} &\le \sum_{j = 1}^{n/2}\frac{K}{\sqrt{j!}} \exp \left( - j \log n - 2jc + (j-1)\log n + 2 \sqrt{2j} \right) \\ &\le 2 K \sum_{j = 1}^{n/2} \frac{e^{-2jc + 2 \sqrt{2j}}}{j}, \end{align*} $$
using the loose bound
![]() $\sqrt {j!}> j/2$
for all
$\sqrt {j!}> j/2$
for all
![]() $j \ge 1$
. With the assumption that
$j \ge 1$
. With the assumption that
![]() $c \ge 2 \sqrt {2}$
, we have
$c \ge 2 \sqrt {2}$
, we have
![]() $-2jc + 2 \sqrt {2j} \le -jc$
for all
$-2jc + 2 \sqrt {2j} \le -jc$
for all
![]() $j \ge 1$
. Finally,
$j \ge 1$
. Finally,
 $$ \begin{align*} 2 K \sum_{j = 1}^{n/2} \frac{e^{-jc}}{j} & \le 2 K \sum_{j = 1}^{\infty} \frac{e^{-jc}}{j} \\ &= - 2K \log(1 - e^{-c}). \end{align*} $$
$$ \begin{align*} 2 K \sum_{j = 1}^{n/2} \frac{e^{-jc}}{j} & \le 2 K \sum_{j = 1}^{\infty} \frac{e^{-jc}}{j} \\ &= - 2K \log(1 - e^{-c}). \end{align*} $$
Now, for the
![]() $\lambda $
with
$\lambda $
with
![]() $\lambda _1 \ge n/2$
, we have
$\lambda _1 \ge n/2$
, we have
 $$ \begin{align*} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} q^{-\binom{n}{2}} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} f_{\lambda} \\ &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{\lambda \vdash n} f_{\lambda} \\ &\le \beta_{(n/2, n/2)}^{2\ell} \left(\sum_{\lambda \vdash n} f_{\lambda}^2\right)^{1/2} \cdot p(n)^{1/2}, \end{align*} $$
$$ \begin{align*} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} q^{-\binom{n}{2}} q^{c_{\lambda}} t_{\lambda} f_{\lambda} \beta_{\lambda}^{2 \ell} &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j} f_{\lambda} \\ &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{\lambda \vdash n} f_{\lambda} \\ &\le \beta_{(n/2, n/2)}^{2\ell} \left(\sum_{\lambda \vdash n} f_{\lambda}^2\right)^{1/2} \cdot p(n)^{1/2}, \end{align*} $$
where
![]() $p(n)$
is equal to the number of partitions of n (the inequality is Cauchy–Schwarz). Since
$p(n)$
is equal to the number of partitions of n (the inequality is Cauchy–Schwarz). Since
![]() $p(n) \le \frac {K}{n} e^{2 \sqrt {2n}}$
for a constant
$p(n) \le \frac {K}{n} e^{2 \sqrt {2n}}$
for a constant
![]() $K> 0$
([Reference Hardy and Ramanujan32]) and
$K> 0$
([Reference Hardy and Ramanujan32]) and
![]() $\sum _{\lambda \vdash n} f_{\lambda }^2 = n!$
, this gives
$\sum _{\lambda \vdash n} f_{\lambda }^2 = n!$
, this gives
 $$ \begin{align*} &\le \sqrt{n!} \cdot \sqrt{\frac{K}{n}} \exp \left( \sqrt{2 n} -2 \ell (n/2) \left( \log q - \frac{\kappa_{n, q, n/2}}{n/2} \right) \right) \\ &\le \sqrt{n!} \cdot \sqrt{\frac{K}{n}} \exp \left(\sqrt{2 n} -n \log n/2 -2n c \right) \\ &\le \sqrt{K} \exp \left( -nc - n(c - \sqrt{2}n^{-1/2}) \right) \end{align*} $$
$$ \begin{align*} &\le \sqrt{n!} \cdot \sqrt{\frac{K}{n}} \exp \left( \sqrt{2 n} -2 \ell (n/2) \left( \log q - \frac{\kappa_{n, q, n/2}}{n/2} \right) \right) \\ &\le \sqrt{n!} \cdot \sqrt{\frac{K}{n}} \exp \left(\sqrt{2 n} -n \log n/2 -2n c \right) \\ &\le \sqrt{K} \exp \left( -nc - n(c - \sqrt{2}n^{-1/2}) \right) \end{align*} $$
since
![]() $\sqrt {n!} \le e^{n \log n/2}$
. Since
$\sqrt {n!} \le e^{n \log n/2}$
. Since
![]() $c> 2 \sqrt {2}$
, then the bound is
$c> 2 \sqrt {2}$
, then the bound is
![]() $\le \sqrt {K} e^{-cn}$
for any
$\le \sqrt {K} e^{-cn}$
for any
![]() $n \ge 1$
.
$n \ge 1$
.
(c): A lower bound comes from using equation (4.1) for the lead term on the right-hand side of (a):
 $$ \begin{align*} \chi_{\omega_0}^2(\ell) &\ge q^{-\binom{n}{2}} q^{c_{(n-1, 1)}} t_{(n-1, 1)} f_{(n-1, 1)} \beta_{(n-1, 1)}^{2 \ell} \\ &= q^{-\binom{n}{2}} q^{\binom{n-1}{2} + 1} \cdot q \frac{q^{n-1} - 1}{q - 1} \cdot (n-1) \left( \frac{q^{n-2} - 1}{q^{n-1} - 1} \right)^{2 \ell} \\ &\ge q^{-(n-2)}(q^{n-1} -1)(n-1) q^{-4 \ell}. \end{align*} $$
$$ \begin{align*} \chi_{\omega_0}^2(\ell) &\ge q^{-\binom{n}{2}} q^{c_{(n-1, 1)}} t_{(n-1, 1)} f_{(n-1, 1)} \beta_{(n-1, 1)}^{2 \ell} \\ &= q^{-\binom{n}{2}} q^{\binom{n-1}{2} + 1} \cdot q \frac{q^{n-1} - 1}{q - 1} \cdot (n-1) \left( \frac{q^{n-2} - 1}{q^{n-1} - 1} \right)^{2 \ell} \\ &\ge q^{-(n-2)}(q^{n-1} -1)(n-1) q^{-4 \ell}. \end{align*} $$
4.4 Starting from a typical site
In analyzing algorithms used repeatedly for simulations, as the algorithm is used, it approaches stationarity. This means the quantity
is of interest. For the problem under study,
![]() $\pi _q$
is concentrated near
$\pi _q$
is concentrated near
![]() $\omega _0$
so we expect rates similar to those in Theorem 4.5.
$\omega _0$
so we expect rates similar to those in Theorem 4.5.
Theorem 4.7. Let P be the Markov chain on
![]() $S_n$
induced by random transvections on
$S_n$
induced by random transvections on
![]() $GL_n(q)$
.
$GL_n(q)$
.
-
1. With
 $f_{\lambda }, \beta _{\lambda }$
defined in Section 3.3,
$f_{\lambda }, \beta _{\lambda }$
defined in Section 3.3,  $$\begin{align*}\left( \sum_{x \in S_n} \pi_q(x) \|P_x^{\ell} - \pi_q \|_{TV} \right)^2 \le \frac{1}{4} \sum_{x \in S_n} \pi_q(x) \chi_{x}^2(\ell) = \frac{1}{4} \sum_{\lambda \neq (n)} f_{\lambda}^2 \beta_{\lambda}^{2 \ell}. \end{align*}$$
$$\begin{align*}\left( \sum_{x \in S_n} \pi_q(x) \|P_x^{\ell} - \pi_q \|_{TV} \right)^2 \le \frac{1}{4} \sum_{x \in S_n} \pi_q(x) \chi_{x}^2(\ell) = \frac{1}{4} \sum_{\lambda \neq (n)} f_{\lambda}^2 \beta_{\lambda}^{2 \ell}. \end{align*}$$
-
2. Let
 $\alpha _{n, q}$
be as in Corollary 3.11 and
$\alpha _{n, q}$
be as in Corollary 3.11 and
 $n, q$
such that
$n, q$
such that
 $\log q> 6/n$
. If
$\log q> 6/n$
. If
 $\ell \ge (\log n + c)/(\log q - \alpha _{n, q}), c> 0$
, then
$\ell \ge (\log n + c)/(\log q - \alpha _{n, q}), c> 0$
, then  $$\begin{align*}\sum_{x \in S_n} \pi_q(x) \chi_{x}^2(\ell) \le (e^{e^{-c}} - 1) + e^{-cn}. \end{align*}$$
$$\begin{align*}\sum_{x \in S_n} \pi_q(x) \chi_{x}^2(\ell) \le (e^{e^{-c}} - 1) + e^{-cn}. \end{align*}$$
-
3. For any
 $\ell \ge 1$
,
$\ell \ge 1$
,  $$\begin{align*}\sum_{x \in S_n} \pi_q(x) \chi_{x}^2(\ell) \ge (n-1)^2 q^{-4 \ell}. \end{align*}$$
$$\begin{align*}\sum_{x \in S_n} \pi_q(x) \chi_{x}^2(\ell) \ge (n-1)^2 q^{-4 \ell}. \end{align*}$$
Proof. (a): This is simply a restatement of 4.1 part (b).
(b): We will divide the sum depending on the first entry of the partition. By Proposition 4.2, we have the bound (true for any
![]() $1 \le j \le n$
)
$1 \le j \le n$
)
 $$\begin{align*}\sum_{\lambda: \lambda_1 = n - j} f_{\lambda}^2 \le \frac{n^{2j}}{j!}. \end{align*}$$
$$\begin{align*}\sum_{\lambda: \lambda_1 = n - j} f_{\lambda}^2 \le \frac{n^{2j}}{j!}. \end{align*}$$
Combining this with Corollary 3.10, for
![]() $j \le \lfloor n/2 \rfloor $
,
$j \le \lfloor n/2 \rfloor $
,
 $$ \begin{align*} \sum_{\lambda: \lambda_1 = n - j} \beta_{\lambda}^{2 \ell} f_{\lambda}^2 &\le \sum_{\lambda: \lambda_1 = n - j} \beta_{(n - j, j)}^{2 \ell} f_{\lambda}^2 \le \beta_{(n - j, j)}^{2 \ell} \cdot \frac{n^{2j}}{j!} \\ &\le \kappa_{n, q, j}^{2\ell} q^{-2 \ell j} \cdot \frac{n^{2j}}{j!} = \frac{1}{j!} \exp \left( 2 \ell( \log(\kappa_{n, q, j}) - j\log q) + 2 j \log n \right) \\ &= \frac{1}{j!} \exp \left( 2 \ell j \left( \frac{ \log(\kappa_{n, q, j})}{j} - \log q\right) + 2 j \log n \right). \end{align*} $$
$$ \begin{align*} \sum_{\lambda: \lambda_1 = n - j} \beta_{\lambda}^{2 \ell} f_{\lambda}^2 &\le \sum_{\lambda: \lambda_1 = n - j} \beta_{(n - j, j)}^{2 \ell} f_{\lambda}^2 \le \beta_{(n - j, j)}^{2 \ell} \cdot \frac{n^{2j}}{j!} \\ &\le \kappa_{n, q, j}^{2\ell} q^{-2 \ell j} \cdot \frac{n^{2j}}{j!} = \frac{1}{j!} \exp \left( 2 \ell( \log(\kappa_{n, q, j}) - j\log q) + 2 j \log n \right) \\ &= \frac{1}{j!} \exp \left( 2 \ell j \left( \frac{ \log(\kappa_{n, q, j})}{j} - \log q\right) + 2 j \log n \right). \end{align*} $$
Define
so then if
![]() $\ell = (\log n + c)/(\log q - \alpha _{n, q})$
, the bound is
$\ell = (\log n + c)/(\log q - \alpha _{n, q})$
, the bound is
 $$ \begin{align*} &\le \frac{1}{j!} \exp \left( 2 \ell j( \alpha_{n, q} - \log q) + 2 j \log n \right) \\ & = \frac{1}{j!} \exp \left( -2 j \log n - 2j c + 2j \log n \right) = \frac{e^{-2jc}}{j!}. \end{align*} $$
$$ \begin{align*} &\le \frac{1}{j!} \exp \left( 2 \ell j( \alpha_{n, q} - \log q) + 2 j \log n \right) \\ & = \frac{1}{j!} \exp \left( -2 j \log n - 2j c + 2j \log n \right) = \frac{e^{-2jc}}{j!}. \end{align*} $$
Then summing over all possible j gives
 $$\begin{align*}\sum_{j = 1}^{\lfloor n/2 \rfloor} \sum_{\lambda: \lambda_1 = n - j} f_{\lambda}^2 \beta_{\lambda}^{2 \ell} \le \sum_{j = 1}^{\lfloor n/2 \rfloor} \frac{e^{-2jc}}{j!} \le \left( e^{e^{-c}} - 1 \right). \end{align*}$$
$$\begin{align*}\sum_{j = 1}^{\lfloor n/2 \rfloor} \sum_{\lambda: \lambda_1 = n - j} f_{\lambda}^2 \beta_{\lambda}^{2 \ell} \le \sum_{j = 1}^{\lfloor n/2 \rfloor} \frac{e^{-2jc}}{j!} \le \left( e^{e^{-c}} - 1 \right). \end{align*}$$
Now, we have to bound the contribution from partitions
![]() $\lambda $
with
$\lambda $
with
![]() $\lambda _1 \le n/2$
. Because
$\lambda _1 \le n/2$
. Because
![]() $\beta _{\lambda }$
is monotone with respect to the order on partitions, we have for all
$\beta _{\lambda }$
is monotone with respect to the order on partitions, we have for all
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda _1 \le n/2$
,
$\lambda _1 \le n/2$
,
since
![]() $\lambda \preceq (n/2, n/2)$
(assuming without essential loss that n is even). Then,
$\lambda \preceq (n/2, n/2)$
(assuming without essential loss that n is even). Then,
 $$ \begin{align*} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j}f_{\lambda}^2 \beta_{\lambda}^{2 \ell} &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{\lambda} f_{\lambda}^2 \\ &\le n! \cdot \exp \left( 2 \ell (n/2)( \log q + \frac{\kappa_{n, q, n/2}}{n/2} ) \right) \\ &\le n! \cdot \exp \left( -n (\log n + c) \right) \\ &\le e^{-cn}, \end{align*} $$
$$ \begin{align*} \sum_{j = n/2}^{n-1} \sum_{\lambda: \lambda_1 = n -j}f_{\lambda}^2 \beta_{\lambda}^{2 \ell} &\le \beta_{(n/2, n/2)}^{2\ell} \sum_{\lambda} f_{\lambda}^2 \\ &\le n! \cdot \exp \left( 2 \ell (n/2)( \log q + \frac{\kappa_{n, q, n/2}}{n/2} ) \right) \\ &\le n! \cdot \exp \left( -n (\log n + c) \right) \\ &\le e^{-cn}, \end{align*} $$
using
![]() $\sum _{\lambda } f_{\lambda }^2 = n! \le n^n$
.
$\sum _{\lambda } f_{\lambda }^2 = n! \le n^n$
.
(c): The sum is bounded below by the term for
![]() $\lambda = (n - 1, 1)$
. This is
$\lambda = (n - 1, 1)$
. This is
 $$\begin{align*}f_{(n-1, 1)}^2 \cdot \beta_{(n-1, 1)}^{2 \ell} = (n-1)^2 \left( \frac{q^{n-2} - 1}{q^{n-1} - 1} \right)^{2 \ell} \ge (n-1)^2 q^{-4 \ell}. \end{align*}$$
$$\begin{align*}f_{(n-1, 1)}^2 \cdot \beta_{(n-1, 1)}^{2 \ell} = (n-1)^2 \left( \frac{q^{n-2} - 1}{q^{n-1} - 1} \right)^{2 \ell} \ge (n-1)^2 q^{-4 \ell}. \end{align*}$$
5 Hecke algebra computations
This section proves Theorem 1.6 which describes the transvections Markov chain on
![]() $S_n$
as multiplication in the Hecke algebra from Definition 3.1. This is accomplished by careful and elementary row reduction. Our first proof used Hall–Littlewood symmetric functions. It is recorded in the expository account [Reference Diaconis, Ram and Simper19].
$S_n$
as multiplication in the Hecke algebra from Definition 3.1. This is accomplished by careful and elementary row reduction. Our first proof used Hall–Littlewood symmetric functions. It is recorded in the expository account [Reference Diaconis, Ram and Simper19].
5.1 Overview
Let
![]() $\mathbb {C}[G]$
denote the group algebra for
$\mathbb {C}[G]$
denote the group algebra for
![]() $G = GL_n(q)$
. This is the space of functions
$G = GL_n(q)$
. This is the space of functions
![]() $f: G \to \mathbb {C}$
, with addition defined
$f: G \to \mathbb {C}$
, with addition defined
![]() $(f + g)(s) = f(s) + g(s)$
and multiplication defined by
$(f + g)(s) = f(s) + g(s)$
and multiplication defined by
Equivalently,
![]() $\mathbb {C}[G] = \mathrm {span} \{g \mid g \in G \}$
and we can write an element
$\mathbb {C}[G] = \mathrm {span} \{g \mid g \in G \}$
and we can write an element
![]() $f = \sum _{g} c_g g$
for
$f = \sum _{g} c_g g$
for
![]() $c_g \in \mathbb {C}$
, so
$c_g \in \mathbb {C}$
, so
![]() $f(g) = c_g$
.
$f(g) = c_g$
.
Define elements in
![]() $\mathbb {C}[G]$
:
$\mathbb {C}[G]$
:

Note that if
![]() $b \in \mathcal {B}$
, then
$b \in \mathcal {B}$
, then
If
![]() $g \in \mathcal {B} \omega \mathcal {B}$
, so
$g \in \mathcal {B} \omega \mathcal {B}$
, so
![]() $g = b_1 \omega b_2$
with
$g = b_1 \omega b_2$
with
![]() $b_1, b_2 \in \mathcal {B}$
, then
$b_1, b_2 \in \mathcal {B}$
, then

The Hecke algebra is
![]() and has basis
and has basis
![]() $\{T_{\omega } \mid \omega \in S_n \}$
. Note that
$\{T_{\omega } \mid \omega \in S_n \}$
. Note that
![]() $H_n(q)$
are all functions in
$H_n(q)$
are all functions in
![]() $\mathbb {C}[G]$
which are
$\mathbb {C}[G]$
which are
![]() $\mathcal {B}$
-
$\mathcal {B}$
-
![]() $\mathcal {B}$
invariant, that is,
$\mathcal {B}$
invariant, that is,
![]() $f(b_1 g b_2) = f(g)$
.
$f(b_1 g b_2) = f(g)$
.
Now, let P be the transition matrix for G defined by multiplying by a random transvection. We can also write this
 $$\begin{align*}P = \frac{1}{|\mathcal{T}_{n, q}|} \sum_{T \in \mathcal{T}_{n, q}} M_T, \end{align*}$$
$$\begin{align*}P = \frac{1}{|\mathcal{T}_{n, q}|} \sum_{T \in \mathcal{T}_{n, q}} M_T, \end{align*}$$
where
![]() $M_T$
is the transition matrix ‘multiply by T’. In other words,
$M_T$
is the transition matrix ‘multiply by T’. In other words,
![]() $M_T(x, y) = \textbf {1}(y = Tx)$
.
$M_T(x, y) = \textbf {1}(y = Tx)$
.
Then P defines a linear transform on the space
![]() $\mathbb {C}[G]$
, with respect to the basis
$\mathbb {C}[G]$
, with respect to the basis
![]() $\{g \mid g \in G \}$
. The matrix
$\{g \mid g \in G \}$
. The matrix
![]() $M_T$
is just the function: Multiply by T in the group algebra. This means P is equivalent to multiplication by
$M_T$
is just the function: Multiply by T in the group algebra. This means P is equivalent to multiplication by
![]() $\frac {1}{|\mathcal {T}_{n, q}|} D$
, with
$\frac {1}{|\mathcal {T}_{n, q}|} D$
, with
![]() $D = \sum _{T \in \mathcal {T}_{n, q}} T$
as an element in
$D = \sum _{T \in \mathcal {T}_{n, q}} T$
as an element in
![]() $\mathbb {C}[G]$
. The Markov chain lumped to
$\mathbb {C}[G]$
. The Markov chain lumped to
![]() $S_n = \mathcal {B} \backslash GL_n(q) / \mathcal {B}$
is then equivalent to multiplication by D on
$S_n = \mathcal {B} \backslash GL_n(q) / \mathcal {B}$
is then equivalent to multiplication by D on
![]() $H_n(q)$
. Since D is the sum of all elements in a conjugacy class, it is in the center
$H_n(q)$
. Since D is the sum of all elements in a conjugacy class, it is in the center
![]() $Z(\mathbb {C}[G])$
. This means if
$Z(\mathbb {C}[G])$
. This means if
![]() $g \in \mathcal {B} \omega \mathcal {B}$
, then
$g \in \mathcal {B} \omega \mathcal {B}$
, then
In conclusion, to determine how D acts in
![]() $H_n(q)$
, we can compute
$H_n(q)$
, we can compute
. The remainder of the section proves the following.
Theorem 5.1. Let
![]() $D = \sum _{T \in \mathcal {T}_{n, q}} T \in \mathbb {C}[G]$
. Then,
$D = \sum _{T \in \mathcal {T}_{n, q}} T \in \mathbb {C}[G]$
. Then,

where
![]() $s_{ij}$
is the transposition switching i and j.
$s_{ij}$
is the transposition switching i and j.
5.2 Row reduction
Let
![]() $G = GL_n(q)$
and
$G = GL_n(q)$
and
![]() $\mathcal {B}$
be the upper-triangular matrices. For
$\mathcal {B}$
be the upper-triangular matrices. For
![]() $1 \le i \le n -1$
and
$1 \le i \le n -1$
and
![]() $c \in \mathbb {F}_q$
, define
$c \in \mathbb {F}_q$
, define
![]() $y_i(c) \in G$
by
$y_i(c) \in G$
by

That is, multiplication on the left by
![]() $y_i(c)$
acts by adding c times the ith row to the
$y_i(c)$
acts by adding c times the ith row to the
![]() $(i+1)$
th row, then permuting the i and
$(i+1)$
th row, then permuting the i and
![]() $i + 1$
rows.
$i + 1$
rows.
Let
![]() $\omega \in S_n$
. We can write the reduced word
$\omega \in S_n$
. We can write the reduced word
, for
![]() $s_i = (i, i+1)$
the simple reflections. Then,
$s_i = (i, i+1)$
the simple reflections. Then,
and
![]() $|\mathcal {B} \omega \mathcal {B}|/|\mathcal {B}| = q^{I(\omega )}$
and
$|\mathcal {B} \omega \mathcal {B}|/|\mathcal {B}| = q^{I(\omega )}$
and
![]() $G = \bigsqcup _{\omega \in S_n} \mathcal {B} \omega \mathcal {B}$
. This provides a very useful way for determining the double coset that a matrix M belongs to, which just amounts to performing row reduction by multiplying by different matrices
$G = \bigsqcup _{\omega \in S_n} \mathcal {B} \omega \mathcal {B}$
. This provides a very useful way for determining the double coset that a matrix M belongs to, which just amounts to performing row reduction by multiplying by different matrices
![]() $y_i(c)$
.
$y_i(c)$
.
5.3 Transvections
For every transvection
![]() $T \in \mathcal {T}_{n, q}$
, we can perform row operations, multiplying by
$T \in \mathcal {T}_{n, q}$
, we can perform row operations, multiplying by
![]() $y_i(c)$
, to determine which double coset T belongs to.
$y_i(c)$
, to determine which double coset T belongs to.
A transvection is defined by two vectors
![]() $\mathbf {a}, \mathbf {v} \in \mathbb {F}_q^n$
with
$\mathbf {a}, \mathbf {v} \in \mathbb {F}_q^n$
with
![]() $\mathbf {v}^{\top } \mathbf {a} = 0$
, with the last nonzero entry of
$\mathbf {v}^{\top } \mathbf {a} = 0$
, with the last nonzero entry of
![]() $\mathbf {v}$
normalized to be
$\mathbf {v}$
normalized to be
![]() $1$
. Assume this entry is at position j. Assume the first nonzero entry of
$1$
. Assume this entry is at position j. Assume the first nonzero entry of
![]() $\mathbf {a}$
is at position i. That is, the vectors look like:
$\mathbf {a}$
is at position i. That is, the vectors look like:
 $$ \begin{align*} &\mathbf{a} = (0, \dots, 0, a_i, a_{i+1}, \dots, a_n)^{\top}, \quad a_i \neq 0, \\ &\mathbf{v} = (v_1, \dots, v_{j-1}, 1, 0, \dots, 0)^{\top}. \end{align*} $$
$$ \begin{align*} &\mathbf{a} = (0, \dots, 0, a_i, a_{i+1}, \dots, a_n)^{\top}, \quad a_i \neq 0, \\ &\mathbf{v} = (v_1, \dots, v_{j-1}, 1, 0, \dots, 0)^{\top}. \end{align*} $$
Let
![]() $T_{\mathbf {a}, \mathbf {v}} = I + \mathbf {v} \mathbf {a}^{\top }$
. We consider the possible cases for i and j to prove the following result.
$T_{\mathbf {a}, \mathbf {v}} = I + \mathbf {v} \mathbf {a}^{\top }$
. We consider the possible cases for i and j to prove the following result.
Proposition 5.2. Let
![]() $T_{\mathbf {a}, \mathbf {v}} = I + \mathbf {v} \mathbf {a}^{\top }$
be the transvection defined by nonzero vectors
$T_{\mathbf {a}, \mathbf {v}} = I + \mathbf {v} \mathbf {a}^{\top }$
be the transvection defined by nonzero vectors
![]() $\mathbf {a}, \mathbf {v}$
with
$\mathbf {a}, \mathbf {v}$
with
![]() $\mathbf {v}^{\top } \mathbf {a} = 0$
and the last nonzero entry of
$\mathbf {v}^{\top } \mathbf {a} = 0$
and the last nonzero entry of
![]() $\mathbf {v}$
equal to
$\mathbf {v}$
equal to
![]() $1$
. Let j be the index of the last nonzero entry of
$1$
. Let j be the index of the last nonzero entry of
![]() $\mathbf {v}$
and i the index of the first nonzero entry of
$\mathbf {v}$
and i the index of the first nonzero entry of
![]() $\mathbf {a}$
. If
$\mathbf {a}$
. If
![]() $i> j$
, then
$i> j$
, then
![]() $T_{\mathbf {a}, \mathbf {v}} \in \mathcal {B}$
. If
$T_{\mathbf {a}, \mathbf {v}} \in \mathcal {B}$
. If
![]() $i < j$
, then
$i < j$
, then
The case
![]() $i = j$
does not occur.
$i = j$
does not occur.
Proof.
Case 1
![]() $i> j$
. If
$i> j$
. If
![]() $i> j$
, then
$i> j$
, then
![]() $T_{\mathbf {a}, \mathbf {v}} \in \mathcal {B}$
. To see this, suppose
$T_{\mathbf {a}, \mathbf {v}} \in \mathcal {B}$
. To see this, suppose
![]() $k> l$
. Then
$k> l$
. Then
because
![]() $v_k a_l$
can only be nonzero if
$v_k a_l$
can only be nonzero if
![]() $k \le j < i \le l$
. Now, we can count how many transvections satisfy this. There are
$k \le j < i \le l$
. Now, we can count how many transvections satisfy this. There are
![]() $(q - 1)q^{n - i}$
choices for
$(q - 1)q^{n - i}$
choices for
![]() $\mathbf {a}$
(because
$\mathbf {a}$
(because
![]() $a_i$
must be nonzero) and
$a_i$
must be nonzero) and
![]() $q^{j-1}$
choices for
$q^{j-1}$
choices for
![]() $\mathbf {v}$
(because
$\mathbf {v}$
(because
![]() $v_j$
is fixed at
$v_j$
is fixed at
![]() $1$
). In total for this case, there are
$1$
). In total for this case, there are

Case 2
![]() $i = j$
. In this case,
$i = j$
. In this case,
![]() $\mathbf {v}^{\top } \mathbf {a} = a_i \neq 0$
. This does not satisfy the condition
$\mathbf {v}^{\top } \mathbf {a} = a_i \neq 0$
. This does not satisfy the condition
![]() $\mathbf {v}^{\top } \mathbf {a} = 0$
, so this case cannot occur.
$\mathbf {v}^{\top } \mathbf {a} = 0$
, so this case cannot occur.
Case 3
![]() $i < j$
. The transvection is of the form
$i < j$
. The transvection is of the form

where
 $$\begin{align*}N_{\mathbf{a}, \mathbf{v}} = \begin{pmatrix} 1+a_iv_i &a_{i+1}v_i &a_{i+2} v_i &\cdots &a_jv_i \\ a_iv_{i+1} &1+a_{i+1}v_{i+1} & a_{i+2} v_{i+1} &\cdots &a_j v_{i+1}\\ \vdots &&&&\vdots \\ a_i &a_{i+1} &&\cdots &1+ a_j \end{pmatrix}. \end{align*}$$
$$\begin{align*}N_{\mathbf{a}, \mathbf{v}} = \begin{pmatrix} 1+a_iv_i &a_{i+1}v_i &a_{i+2} v_i &\cdots &a_jv_i \\ a_iv_{i+1} &1+a_{i+1}v_{i+1} & a_{i+2} v_{i+1} &\cdots &a_j v_{i+1}\\ \vdots &&&&\vdots \\ a_i &a_{i+1} &&\cdots &1+ a_j \end{pmatrix}. \end{align*}$$
Then,
where A is the upper-triangular matrix

See Appendix A for details of this row reduction calculation.
To count how many transvections fit Case 3: There are
-
•
 $q^{n-i}$
choices for
$q^{n-i}$
choices for
 $a_{i+1}, \dots , a_n$
.
$a_{i+1}, \dots , a_n$
. -
•
 $q - 1$
choices of
$q - 1$
choices of
 $a_i$
.
$a_i$
. -
•
 $q^{i-1}$
choices of
$q^{i-1}$
choices of
 $v_1, \dots , v_{i-1}$
.
$v_1, \dots , v_{i-1}$
. -
•
 $q^{j - 1 - i}$
choices of
$q^{j - 1 - i}$
choices of
 $v_i, \dots , v_{j-1}$
to satisfy
$v_i, \dots , v_{j-1}$
to satisfy
 .
.
The total is
 $$ \begin{align*} q^{n - i}(q - 1)q^{i - 1}q^{j - 1 - i} &= (q - 1)q^{n - i + j - 2} = (q - 1)q^{n - 1 - (j - i)}q^{2(j - 1 - i) + 1} \\ &= (q - 1)q^{n - 1 - (j - i)}q^{I(s_{ij})}. \end{align*} $$
$$ \begin{align*} q^{n - i}(q - 1)q^{i - 1}q^{j - 1 - i} &= (q - 1)q^{n - i + j - 2} = (q - 1)q^{n - 1 - (j - i)}q^{2(j - 1 - i) + 1} \\ &= (q - 1)q^{n - 1 - (j - i)}q^{I(s_{ij})}. \end{align*} $$
Proposition 5.2 now enables the proof of Theorem 5.1.
Proof of Theorem 5.1.
Let
![]() $\mathbb {C}[G]$
be the group algebra of
$\mathbb {C}[G]$
be the group algebra of
![]() $G = GL_n(q)$
, and
$G = GL_n(q)$
, and
![]() $Z(\mathbb {C}[G])$
the center. Then since transvections are a conjugacy class, the sum of transvections is in the center,
$Z(\mathbb {C}[G])$
the center. Then since transvections are a conjugacy class, the sum of transvections is in the center,
Since D commutes with every element of
![]() $\mathbb {C}[G]$
, we can compute
$\mathbb {C}[G]$
, we can compute

6 A single coset lumping
This section develops the correspondence between
![]() $\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
double cosets and flags and describes the random transpositions Markov chain in this setting. This description is useful for analyzing specific features of the Markov chain. If
$\mathcal {B} \backslash GL_n(q) / \mathcal {B}$
double cosets and flags and describes the random transpositions Markov chain in this setting. This description is useful for analyzing specific features of the Markov chain. If
![]() $\{\omega _t \}_{t \ge 0}$
is the induced chain on
$\{\omega _t \}_{t \ge 0}$
is the induced chain on
![]() $S_n$
, then
$S_n$
, then
![]() $\{\omega _t(1) \}_{t \ge 0}$
is a process on
$\{\omega _t(1) \}_{t \ge 0}$
is a process on
![]() $\{1, \dots , n \}$
. Thinking of
$\{1, \dots , n \}$
. Thinking of
![]() $\omega \in S_n$
as a deck of cards, this is the evolution of the label of the ‘top card’. It is the lumping of the chain on
$\omega \in S_n$
as a deck of cards, this is the evolution of the label of the ‘top card’. It is the lumping of the chain on
![]() $S_n$
onto cosets
$S_n$
onto cosets
![]() $S_n/S_{n-1}$
. The main result, Lemma 6.11 below, shows that the top card takes only a bounded number of steps to reach stationarity.
$S_n/S_{n-1}$
. The main result, Lemma 6.11 below, shows that the top card takes only a bounded number of steps to reach stationarity.
Remark 6.1. If Q is any probability measure which defines a random walk on G, then the process induced by multiplication on the left by Q on left cosets
![]() $G/K$
, for any subgroup
$G/K$
, for any subgroup
![]() $K \subset G$
, is always Markov. This is the special case of Proposition 2.4 with
$K \subset G$
, is always Markov. This is the special case of Proposition 2.4 with
![]() $H = \{id \}$
(similarly, if Q defines a random walk by multiplication on the right, then it always induces a Markov chain on right cosets
$H = \{id \}$
(similarly, if Q defines a random walk by multiplication on the right, then it always induces a Markov chain on right cosets
![]() $H \backslash G$
). There are many examples of random walks lumped to single cosets, for example, [Reference Diaconis and Holmes26], for which the properties of Q are used to analyze the mixing times of the lumped Markov chain.
$H \backslash G$
). There are many examples of random walks lumped to single cosets, for example, [Reference Diaconis and Holmes26], for which the properties of Q are used to analyze the mixing times of the lumped Markov chain.
6.1 Flag representation
The subgroup
![]() $\mathcal {B}$
gives rise to the quotient
$\mathcal {B}$
gives rise to the quotient
![]() $GL_n(q)/\mathcal {B}$
. This may be pictured as the space of ‘flags’.
$GL_n(q)/\mathcal {B}$
. This may be pictured as the space of ‘flags’.
Definition 6.2. Here, a flag F consists of an increasing sequence of subspaces
with
![]() $\text {dim}(F_i) = i$
. The standard flag is
$\text {dim}(F_i) = i$
. The standard flag is
Indeed,
![]() $GL_n(q)$
operates transitively on flags, and the subgroup fixing the standard flag is exactly
$GL_n(q)$
operates transitively on flags, and the subgroup fixing the standard flag is exactly
![]() $\mathcal {B}$
. There is a useful notion of ‘distance’ between two flags
$\mathcal {B}$
. There is a useful notion of ‘distance’ between two flags
![]() $F, F'$
which defines a permutation.
$F, F'$
which defines a permutation.
Definition 6.3. Let
![]() $F, F'$
be two flags. The Jordan–Holder permutation
$F, F'$
be two flags. The Jordan–Holder permutation
![]() $\omega (F, F')$
is a permutation
$\omega (F, F')$
is a permutation
![]() $\omega = \omega (F, F') \in S_n$
defined by
$\omega = \omega (F, F') \in S_n$
defined by
![]() $\omega (i) = j$
if j is the smallest index such that
$\omega (i) = j$
if j is the smallest index such that
The Jordan–Holder permutation distance satisfies
A thorough development with full proofs is in [Reference Abels1].
Lemma 6.4. For
![]() $M \in GL_n(q)$
and E the standard flag,
$M \in GL_n(q)$
and E the standard flag,
6.2 Top label chain
This representation is useful for analyzing a further projection of the chain on
![]() $S_n$
: Let
$S_n$
: Let
![]() $\{\omega _t \}_{t \ge 0}$
denote the Markov chain on
$\{\omega _t \}_{t \ge 0}$
denote the Markov chain on
![]() $S_n$
. Let
$S_n$
. Let
![]() $P_1(\cdot , \cdot )$
denote the marginal transition probabilities of the first position. That is,
$P_1(\cdot , \cdot )$
denote the marginal transition probabilities of the first position. That is,
If
![]() $\omega $
is distributed as
$\omega $
is distributed as
![]() $\pi _q$
, then the marginal distribution on
$\pi _q$
, then the marginal distribution on
![]() $\{1, \dots , n \}$
of the first card
$\{1, \dots , n \}$
of the first card
![]() $\omega (1)$
is
$\omega (1)$
is

Lemma 6.5. For
![]() $1 \le i, j \le n$
,
$1 \le i, j \le n$
,
 $$ \begin{align*} P_1(i, j) &= \begin{cases} \dfrac{(q-1)^2q^{n + j - 3}}{(q^n - 1)(q^{n-1} - 1)}, & i \neq j, \\ \dfrac{(q^{n-1} - 1)^2 + (q - 1)^2(q^{i - 1} - 1)q^{n - 2}}{(q^n - 1)(q^{n-1} - 1)}, & i = j. \end{cases} \end{align*} $$
$$ \begin{align*} P_1(i, j) &= \begin{cases} \dfrac{(q-1)^2q^{n + j - 3}}{(q^n - 1)(q^{n-1} - 1)}, & i \neq j, \\ \dfrac{(q^{n-1} - 1)^2 + (q - 1)^2(q^{i - 1} - 1)q^{n - 2}}{(q^n - 1)(q^{n-1} - 1)}, & i = j. \end{cases} \end{align*} $$
Remark 6.6. Observe that for
![]() $i \neq j$
the transition probabilities can be written
$i \neq j$
the transition probabilities can be written
 $$ \begin{align*} P_1(i, j) &= \frac{q^{j-1}}{(q^n - 1)/(q-1)} \left( \frac{(q - 1) q^{n-2}}{q^{n-1} - 1} \right) = \pi_{q, 1}(j) \cdot \left( \frac{(q - 1) q^{n-2}}{q^{n-1} - 1} \right) \\ P_1(j, j) &= \pi_{q, 1}(j) \cdot \left( \frac{(q - 1) q^{n-2}}{q^{n-1} - 1} \right) + \left(1 - \frac{(q - 1) q^{n-2}}{q^{n-1} - 1} \right). \end{align*} $$
$$ \begin{align*} P_1(i, j) &= \frac{q^{j-1}}{(q^n - 1)/(q-1)} \left( \frac{(q - 1) q^{n-2}}{q^{n-1} - 1} \right) = \pi_{q, 1}(j) \cdot \left( \frac{(q - 1) q^{n-2}}{q^{n-1} - 1} \right) \\ P_1(j, j) &= \pi_{q, 1}(j) \cdot \left( \frac{(q - 1) q^{n-2}}{q^{n-1} - 1} \right) + \left(1 - \frac{(q - 1) q^{n-2}}{q^{n-1} - 1} \right). \end{align*} $$
Write
![]() $p:= ((q - 1) q^{n-2})/(q^{n-1} - 1)$
. This provides another description of the Markov chain: At each step, flip a coin which gives heads with probability p, tails with probability
$p:= ((q - 1) q^{n-2})/(q^{n-1} - 1)$
. This provides another description of the Markov chain: At each step, flip a coin which gives heads with probability p, tails with probability
![]() $1-p$
. If heads, move to a random sample from
$1-p$
. If heads, move to a random sample from
![]() $\pi _{q, 1}$
. Otherwise, don’t move.
$\pi _{q, 1}$
. Otherwise, don’t move.
Remark 6.7. Though the Markov chain
![]() $P_1$
on
$P_1$
on
![]() $\{1, \dots , n \}$
was defined via lumping from a chain on the group
$\{1, \dots , n \}$
was defined via lumping from a chain on the group
![]() $GL_n(q)$
with
$GL_n(q)$
with
![]() $q> 1$
a prime power, note that the transitions are well defined even for
$q> 1$
a prime power, note that the transitions are well defined even for
![]() $q < 1$
. If
$q < 1$
. If
![]() $q < 1$
, then the Mallows measure
$q < 1$
, then the Mallows measure
![]() $\pi _q$
is concentrated at the identity permutation and
$\pi _q$
is concentrated at the identity permutation and
![]() $P_1(i, j)$
is largest for
$P_1(i, j)$
is largest for
![]() $j = 1$
. Note also that the description in Remark 6.6 is also valid since
$j = 1$
. Note also that the description in Remark 6.6 is also valid since
![]() $p = ((q - 1) q^{n-2})/(q^{n-1} - 1) < 1$
for all
$p = ((q - 1) q^{n-2})/(q^{n-1} - 1) < 1$
for all
![]() $q> 0$
.
$q> 0$
.
Proof. If
![]() $\omega (1) = i$
, then a flag representing the double coset has
$\omega (1) = i$
, then a flag representing the double coset has
![]() $F_1 = \mathbf {e}_i$
. Recall that a transvection T defined by vectors
$F_1 = \mathbf {e}_i$
. Recall that a transvection T defined by vectors
![]() $\mathbf {v}, \mathbf {a}$
has
$\mathbf {v}, \mathbf {a}$
has
![]() $T(\mathbf {e}_i) = \mathbf {e}_i + a_i \mathbf {v}$
. The first coordinate in the new permutation is the smallest j such that
$T(\mathbf {e}_i) = \mathbf {e}_i + a_i \mathbf {v}$
. The first coordinate in the new permutation is the smallest j such that
There are two cases when this smallest j is equal to i:
-
1.
 $a_i = 0$
, and
$a_i = 0$
, and
 $\mathbf {v}$
can be anything: There are
$\mathbf {v}$
can be anything: There are
 $(q^{n - 1} - 1)$
possibilities for
$(q^{n - 1} - 1)$
possibilities for
 $\mathbf {a}$
such that
$\mathbf {a}$
such that
 $a_i = 0$
. Then there are
$a_i = 0$
. Then there are
 $(q^{n-1} - 1)/(q - 1)$
possibilities for
$(q^{n-1} - 1)/(q - 1)$
possibilities for
 $\mathbf {v}$
.
$\mathbf {v}$
. -
2.
 $a_i \neq 0$
and
$a_i \neq 0$
and
 $\mathbf {v}$
is such that
$\mathbf {v}$
is such that
 $a_i v_i \neq - 1$
and
$a_i v_i \neq - 1$
and
 $v_k = 0$
for all
$v_k = 0$
for all
 $k> i$
. Note that if
$k> i$
. Note that if
 $i = 1$
, then this is not possible. Since the nonzero entry at the largest index in
$i = 1$
, then this is not possible. Since the nonzero entry at the largest index in
 $\mathbf {v}$
is normalized to be
$\mathbf {v}$
is normalized to be
 $1$
, there are two further possibilities:
$1$
, there are two further possibilities:-
• If
 $v_i = 1$
, then there are
$v_i = 1$
, then there are
 $(q - 2)$
possibilities for
$(q - 2)$
possibilities for
 $a_i$
,
$a_i$
,
 $(q^{i - 1} -1)$
possibilities for the rest of
$(q^{i - 1} -1)$
possibilities for the rest of
 $\mathbf {v}$
(note that it’s not allowed for the rest of
$\mathbf {v}$
(note that it’s not allowed for the rest of
 $\mathbf {v}$
to be
$\mathbf {v}$
to be
 $0$
because then we could not get
$0$
because then we could not get
 $\mathbf {a}^{\top } \mathbf {v} = 0$
), and then
$\mathbf {a}^{\top } \mathbf {v} = 0$
), and then
 $q^{n-2}$
possibilities for the rest of
$q^{n-2}$
possibilities for the rest of
 $\mathbf {a}$
.
$\mathbf {a}$
. -
• If
 $v_i = 0$
, then there are
$v_i = 0$
, then there are
 $(q^{i - 1} - 1)/(q - 1)$
possibilities for
$(q^{i - 1} - 1)/(q - 1)$
possibilities for
 $\mathbf {v}$
and then
$\mathbf {v}$
and then
 $(q - 1)q^{n-2}$
possibilities for
$(q - 1)q^{n-2}$
possibilities for
 $\mathbf {a}$
.
$\mathbf {a}$
.
-
In summary, if
![]() $i \neq 1$
, then
$i \neq 1$
, then
 $$ \begin{align*} P_1(i, i) &= \frac{1}{|\mathcal{T}_{n, q}|} \left( \frac{(q^{n-1} - 1)(q^{n - 1} -1)}{q - 1} + (q^{i - 1} -1)(q - 2)q^{n-2} + \frac{(q^{i - 1} -1)(q - 1)q^{n-2}}{q - 1} \right) \\ &= \frac{(q^{n-1} - 1)^2 + (q - 1)^2(q^{i - 1} - 1)q^{n - 2}}{(q^n - 1)(q^{n-1} - 1)}. \end{align*} $$
$$ \begin{align*} P_1(i, i) &= \frac{1}{|\mathcal{T}_{n, q}|} \left( \frac{(q^{n-1} - 1)(q^{n - 1} -1)}{q - 1} + (q^{i - 1} -1)(q - 2)q^{n-2} + \frac{(q^{i - 1} -1)(q - 1)q^{n-2}}{q - 1} \right) \\ &= \frac{(q^{n-1} - 1)^2 + (q - 1)^2(q^{i - 1} - 1)q^{n - 2}}{(q^n - 1)(q^{n-1} - 1)}. \end{align*} $$
Now, if
![]() $i \neq j$
we consider the two possibilities.
$i \neq j$
we consider the two possibilities.
-
1.
 $i> j$
: This transition will occur if
$i> j$
: This transition will occur if
 $a_i\cdot v_i = -1$
and
$a_i\cdot v_i = -1$
and
 $\mathbf {v}$
is such that
$\mathbf {v}$
is such that
 $v_j> 0$
and
$v_j> 0$
and
 $v_k = 0$
for all
$v_k = 0$
for all
 $j < k < i$
. Since the
$j < k < i$
. Since the
 $\mathbf {v}$
is normalized so that the entry at the largest index is
$\mathbf {v}$
is normalized so that the entry at the largest index is
 $1$
, this requires
$1$
, this requires
 $v_i = 1$
and
$v_i = 1$
and
 $a_i = -1$
. There are then
$a_i = -1$
. There are then
 $(q - 1)q^{j - 1}$
such
$(q - 1)q^{j - 1}$
such
 $\mathbf {v}$
, and for each
$\mathbf {v}$
, and for each
 $\mathbf {v}$
there are
$\mathbf {v}$
there are
 $q^{n-2}$
possibilities for
$q^{n-2}$
possibilities for
 $\mathbf {a}$
. This gives in total
$\mathbf {a}$
. This gives in total  $$\begin{align*}(q - 1) q^{n + j - 3}. \end{align*}$$
$$\begin{align*}(q - 1) q^{n + j - 3}. \end{align*}$$
-
2.
 $i < j$
: This transition will occur if
$i < j$
: This transition will occur if
 $a_i \neq 0$
,
$a_i \neq 0$
,
 $v_j = 1$
and
$v_j = 1$
and
 $v_k = 0$
for
$v_k = 0$
for
 $k> j$
. There are
$k> j$
. There are
 $q^{j - 1}$
possibilities for
$q^{j - 1}$
possibilities for
 $\mathbf {v}$
and then
$\mathbf {v}$
and then
 $(q - 1)q^{n-2}$
possibilities for
$(q - 1)q^{n-2}$
possibilities for
 $\mathbf {a}$
, so again in total
$\mathbf {a}$
, so again in total  $$\begin{align*}(q - 1)q^{n+ j - 3}. \end{align*}$$
$$\begin{align*}(q - 1)q^{n+ j - 3}. \end{align*}$$
In summary, for any
![]() $i \neq j$
,
$i \neq j$
,
 $$ \begin{align*} P_1(i, j) = \frac{(q-1)q^{n + j - 3}}{\vert \mathcal{T}_{n, q} \vert} = \frac{(q-1)^2q^{n + j - 3}}{(q^n - 1)(q^{n-1} - 1)}. \end{align*} $$
$$ \begin{align*} P_1(i, j) = \frac{(q-1)q^{n + j - 3}}{\vert \mathcal{T}_{n, q} \vert} = \frac{(q-1)^2q^{n + j - 3}}{(q^n - 1)(q^{n-1} - 1)}. \end{align*} $$
Lemma 6.8. Let
![]() $P_1$
be the Markov chain from Lemma 6.5 with stationary distribution
$P_1$
be the Markov chain from Lemma 6.5 with stationary distribution
![]() $\pi _{q, 1}$
. Then
$\pi _{q, 1}$
. Then
![]() $P_1$
has eigenvalues
$P_1$
has eigenvalues
![]() $\{1, \beta \}$
with
$\{1, \beta \}$
with
 $$\begin{align*}\beta = \frac{q^{n -2} -1}{q^{n-1} - 1}, \end{align*}$$
$$\begin{align*}\beta = \frac{q^{n -2} -1}{q^{n-1} - 1}, \end{align*}$$
which is equal to
![]() $\beta _{(n-1, 1)}$
from Section 3.3. The eigenvalue
$\beta _{(n-1, 1)}$
from Section 3.3. The eigenvalue
![]() $\beta $
has multiplicity
$\beta $
has multiplicity
![]() $n -1$
. If
$n -1$
. If
![]() $q> 1$
is fixed and n large, then
$q> 1$
is fixed and n large, then
![]() $\beta \sim 1/q$
.
$\beta \sim 1/q$
.
Proof. Call
![]() $P_1(i, j) = c_j$
, and remember this is constant across all
$P_1(i, j) = c_j$
, and remember this is constant across all
![]() $i \neq j$
. Then
$i \neq j$
. Then
![]() $P_1(i, i) = p_i = 1 - \sum _{j \neq i} c_j$
. Let M be the matrix with column j constant
$P_1(i, i) = p_i = 1 - \sum _{j \neq i} c_j$
. Let M be the matrix with column j constant
![]() $c_j$
, so the rows are constant
$c_j$
, so the rows are constant
![]() $[c_1, \dots , c_n]$
and let
$[c_1, \dots , c_n]$
and let
![]() $r = \sum c_j$
be the constant row sum. Note we can write our transition matrix as
$r = \sum c_j$
be the constant row sum. Note we can write our transition matrix as
Note that the diagonal entries of this matrix match what we want since
![]() $T(i, i) = (1 - r) + c_i = 1 - \sum _{j \neq i} c_j = p_i$
.
$T(i, i) = (1 - r) + c_i = 1 - \sum _{j \neq i} c_j = p_i$
.
Since M has constant columns/rows it has null space of dimension
![]() $n-1$
. That is, we can find
$n-1$
. That is, we can find
![]() $n-1$
vectors
$n-1$
vectors
![]() $v_2, v_3, \dots v_n$
such that
$v_2, v_3, \dots v_n$
such that
![]() $vM = 0$
. Then
$vM = 0$
. Then
(and remember of course the other eigenvector is the stationary distribution, with eigenvalue
![]() $1$
). This says that there is only one eigenvalue
$1$
). This says that there is only one eigenvalue
![]() $\beta = 1-r$
, with multiplicity
$\beta = 1-r$
, with multiplicity
![]() $n -1$
—eigenfunctions are basis of null space of M. The eigenvalue
$n -1$
—eigenfunctions are basis of null space of M. The eigenvalue
![]() $\beta $
is
$\beta $
is
 $$ \begin{align*} \beta = 1 - \sum_j \frac{(q - 1)^2q^{n + j -3}}{(q^n - 1)(q^{n-1} - 1)} = 1 - \frac{q^{n-2}(q - 1)}{q^{n-1} - 1} = \frac{q^{n-2} - 1}{q^{n-1} - 1}. \end{align*} $$
$$ \begin{align*} \beta = 1 - \sum_j \frac{(q - 1)^2q^{n + j -3}}{(q^n - 1)(q^{n-1} - 1)} = 1 - \frac{q^{n-2}(q - 1)}{q^{n-1} - 1} = \frac{q^{n-2} - 1}{q^{n-1} - 1}. \end{align*} $$
Note that this is the largest eigenvalue of the full chain on
![]() $S_n$
.
$S_n$
.
Remark 6.9. This lumping comes from the embedding
![]() $S_{n-1} \subset S_n$
as all permutations which fix the first coordinate. Then the coset space
$S_{n-1} \subset S_n$
as all permutations which fix the first coordinate. Then the coset space
![]() $S_n / S_{n-1}$
consists of equivalence classes of permutations which have the same label in the first element. Similarly, we could consider the embedding
$S_n / S_{n-1}$
consists of equivalence classes of permutations which have the same label in the first element. Similarly, we could consider the embedding
![]() $S_{n-2} \subset S_n$
as all permutations which fix the first two coordinates. This would induce a Markov chain on the space of
$S_{n-2} \subset S_n$
as all permutations which fix the first two coordinates. This would induce a Markov chain on the space of
![]() $\{(a, b): 1 \le a, b, \le n, a \neq b \}$
; we have not attempted to find the more complicated transitions of this chain.
$\{(a, b): 1 \le a, b, \le n, a \neq b \}$
; we have not attempted to find the more complicated transitions of this chain.
6.3 Mixing time
The mixing time of the Markov chain
![]() $P_1$
is very fast; the chain reaches stationarity within a constant number of steps (the constant depends on q but not on n). This can be proven using a strong stationary time.
$P_1$
is very fast; the chain reaches stationarity within a constant number of steps (the constant depends on q but not on n). This can be proven using a strong stationary time.
Strong stationary time
An strong stationary time for a Markov chain is a random stopping time
![]() $\tau $
at which the chain is distributed according to the stationary distribution. That is, if
$\tau $
at which the chain is distributed according to the stationary distribution. That is, if
![]() $(X_t)_{t \ge 0}$
is a Markov chain on
$(X_t)_{t \ge 0}$
is a Markov chain on
![]() $\Omega $
with stationary distribution
$\Omega $
with stationary distribution
![]() $\pi $
, then
$\pi $
, then
![]() $\tau $
satisfies
$\tau $
satisfies
In words,
![]() $X_{\tau }$
has distribution
$X_{\tau }$
has distribution
![]() $\pi $
and is independent from
$\pi $
and is independent from
![]() $\tau $
. See Section 6.4 of [Reference Levin and Peres43].
$\tau $
. See Section 6.4 of [Reference Levin and Peres43].
A strong stationary time is very powerful for bounding convergence time. Intuitively, once the strong stationary time is reached the chain has mixed, so the mixing time is bounded by the random time
![]() $\tau $
. This idea is formalized in the following.
$\tau $
. This idea is formalized in the following.
Proposition 6.10 (Proposition 6.10 from [Reference Levin and Peres43]).
If
![]() $\tau $
is a strong stationary time for a Markov chain P on state space
$\tau $
is a strong stationary time for a Markov chain P on state space
![]() $\Omega $
, then for any time t,
$\Omega $
, then for any time t,
For most Markov chains it is very difficult to find an obvious strong stationary time. A simple one exists for the chain
![]() $P_1$
, using the alternate description from Remark 6.6.
$P_1$
, using the alternate description from Remark 6.6.
To restate the alternate description, let
![]() $p := ((q - 1) q^{n-2})/(q^{n-1} - 1)$
. Let
$p := ((q - 1) q^{n-2})/(q^{n-1} - 1)$
. Let
![]() $\{R_t \}_{t \ge 1}$
be a sequence Bernoulli
$\{R_t \}_{t \ge 1}$
be a sequence Bernoulli
![]() $(p)$
random variables. The Markov chain
$(p)$
random variables. The Markov chain
![]() $\{X_t \}_{t \ge 0}$
defined by
$\{X_t \}_{t \ge 0}$
defined by
![]() $P_1$
can be coupled with the random variables
$P_1$
can be coupled with the random variables
![]() $R_t$
by: Given
$R_t$
by: Given
![]() $X_t$
,
$X_t$
,
-
1. If
 $R_{t+1} = 1$
, sample
$R_{t+1} = 1$
, sample
 $Z \sim \pi _{q, 1}$
and set
$Z \sim \pi _{q, 1}$
and set
 $X_{t+1} = Z$
.
$X_{t+1} = Z$
. -
2. If
 $R_{t+1} = 0$
, set
$R_{t+1} = 0$
, set
 $X_{t+1} = X_t$
.
$X_{t+1} = X_t$
.
Lemma 6.11. With
![]() $\{R_t \}_{t \ge 1}$
defined above, the random time
$\{R_t \}_{t \ge 1}$
defined above, the random time
![]() $ \tau = \inf \{ t> 0 : R_t = 1 \} $
is a strong stationary time for
$ \tau = \inf \{ t> 0 : R_t = 1 \} $
is a strong stationary time for
![]() $\{X_t \}_{t \ge 0}$
. If
$\{X_t \}_{t \ge 0}$
. If
 $$\begin{align*}t = c \cdot \frac{q^{n-1} - 1}{(q-1)q^{n-2}}, \quad \text{with} \,\,\, c> 0, \end{align*}$$
$$\begin{align*}t = c \cdot \frac{q^{n-1} - 1}{(q-1)q^{n-2}}, \quad \text{with} \,\,\, c> 0, \end{align*}$$
then
Proof. By the alternate description of the Markov chain
![]() $P_1$
, whenever
$P_1$
, whenever
![]() $R_t = 1$
, the next state
$R_t = 1$
, the next state
![]() $X_t$
is a sample from
$X_t$
is a sample from
![]() $\pi _{q, 1}$
. That is,
$\pi _{q, 1}$
. That is,
Then, by equation (6.2),
and
![]() $\tau $
is a strong stationary time. The time
$\tau $
is a strong stationary time. The time
![]() $\tau $
is a geometric random variable with parameter p. Note also that
$\tau $
is a geometric random variable with parameter p. Note also that
![]() $\tau $
is independent of the starting state
$\tau $
is independent of the starting state
![]() $X_0$
. Then,
$X_0$
. Then,
 $$ \begin{align*} \operatorname{\mathbb{P}}( \tau> t) &= (1-p)^{t} \le e^{-pt} = \exp \left( -t \frac{(q - 1) q^{n-2}}{(q^{n-1} - 1)} \right) \le e^{-c}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathbb{P}}( \tau> t) &= (1-p)^{t} \le e^{-pt} = \exp \left( -t \frac{(q - 1) q^{n-2}}{(q^{n-1} - 1)} \right) \le e^{-c}, \end{align*} $$
for
![]() $ t = c \cdot \frac {q^{n-1} - 1}{(q-1)q^{n-2}}$
.
$ t = c \cdot \frac {q^{n-1} - 1}{(q-1)q^{n-2}}$
.
7 Some extensions
The main example treated above has
![]() $G = GL_n(q)$
and
$G = GL_n(q)$
and
![]() $H = K$
the Borel subgroup. As explained in Theorem 1.2 for any finite group, any subgroups
$H = K$
the Borel subgroup. As explained in Theorem 1.2 for any finite group, any subgroups
![]() $H, K$
, and any H-conjugacy invariant probability measure Q on G (
$H, K$
, and any H-conjugacy invariant probability measure Q on G (
![]() $Q(hsh^{-1}) = Q(s)$
for all
$Q(hsh^{-1}) = Q(s)$
for all
![]() $s \in G, h \in H$
), the walk on G generated by Q, lumped to double cosets
$s \in G, h \in H$
), the walk on G generated by Q, lumped to double cosets
![]() $H \backslash G / K =: \mathcal {X}$
gives a Markov chain on
$H \backslash G / K =: \mathcal {X}$
gives a Markov chain on
![]() $\mathcal {X}$
with transition kernel
$\mathcal {X}$
with transition kernel
and stationary distribution the image of Haar measure on G.
There are many possible choices of
![]() $G, H, K$
and Q. This gives rise to the problem of making choices and finding interpretations that will be of interest. This section briefly describes a few examples: Gelfand pairs, contingency tables, the extension from
$G, H, K$
and Q. This gives rise to the problem of making choices and finding interpretations that will be of interest. This section briefly describes a few examples: Gelfand pairs, contingency tables, the extension from
![]() $GL_n(q)$
to finite Chevally groups and a continuous example
$GL_n(q)$
to finite Chevally groups and a continuous example
![]() $\mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
. We have high hopes that further interesting examples will emerge.
$\mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
. We have high hopes that further interesting examples will emerge.
7.1 Parabolic subgroups of
 $GL_n$
$GL_n$
In [Reference Karp and Thomas39], the authors enumerate the double cosets of
![]() $GL_n(q)$
generated by parabolic subgroups.
$GL_n(q)$
generated by parabolic subgroups.
Definition 7.1. Let
![]() $\alpha = (\alpha _1, \dots , \alpha _k)$
be a partition of n. The parabolic subgroup
$\alpha = (\alpha _1, \dots , \alpha _k)$
be a partition of n. The parabolic subgroup
![]() $P_{\alpha } \subset GL_n(q)$
consists of all invertible block upper-triangular matrices with diagonal block sizes
$P_{\alpha } \subset GL_n(q)$
consists of all invertible block upper-triangular matrices with diagonal block sizes
![]() $\alpha _1, \dots , \alpha _k$
.
$\alpha _1, \dots , \alpha _k$
.
Section 4 of [Reference Karp and Thomas39] shows that if
![]() $\alpha , \beta $
are two partitions of n, the double cosets
$\alpha , \beta $
are two partitions of n, the double cosets
![]() $P_{\alpha } \backslash GL_n(q) / P_{\beta }$
are indexed by contingency tables with row sums
$P_{\alpha } \backslash GL_n(q) / P_{\beta }$
are indexed by contingency tables with row sums
![]() $\alpha $
and column sums
$\alpha $
and column sums
![]() $\beta $
. Proposition 4.37 of [Reference Karp and Thomas39] contains a formula for the size of a double coset which corresponds to the table X, with
$\beta $
. Proposition 4.37 of [Reference Karp and Thomas39] contains a formula for the size of a double coset which corresponds to the table X, with
![]() $\theta = 1/q$
,
$\theta = 1/q$
,
 $$ \begin{align} \theta^{- n^2 + \sum_{1 \le i < i' \le I, 1 \le j < j' \le J} X_{ij} X_{i'j'}}(1 - \theta)^n \cdot \frac{\prod_{i = 1}^I[\alpha_i]_{\theta}! \prod_{j = 1}^J [\beta_j]_{\theta}!}{\prod_{i, j} [X_{ij}]_{\theta}!}, \quad I = |\alpha|, J = |\beta|. \end{align} $$
$$ \begin{align} \theta^{- n^2 + \sum_{1 \le i < i' \le I, 1 \le j < j' \le J} X_{ij} X_{i'j'}}(1 - \theta)^n \cdot \frac{\prod_{i = 1}^I[\alpha_i]_{\theta}! \prod_{j = 1}^J [\beta_j]_{\theta}!}{\prod_{i, j} [X_{ij}]_{\theta}!}, \quad I = |\alpha|, J = |\beta|. \end{align} $$
Dividing equation (7.1) by
![]() $(1-\theta )^n$
and sending
$(1-\theta )^n$
and sending
![]() $\theta \to 1$
recovers the usual Fisher–Yates distribution for partitions
$\theta \to 1$
recovers the usual Fisher–Yates distribution for partitions
![]() $\alpha , \beta $
.
$\alpha , \beta $
.
For
![]() $\alpha = (n-1, 1), \beta = (1^n)$
, the contingency tables
$\alpha = (n-1, 1), \beta = (1^n)$
, the contingency tables
![]() $P_{\alpha } \backslash GL_n(q) / P_{\beta }$
are uniquely determined by the position of the single
$P_{\alpha } \backslash GL_n(q) / P_{\beta }$
are uniquely determined by the position of the single
![]() $1$
in the second row. That is, the space is in bijection with the set
$1$
in the second row. That is, the space is in bijection with the set
![]() $\{1, 2, \dots , n \}$
. If
$\{1, 2, \dots , n \}$
. If
![]() $X^j$
denotes a table with the
$X^j$
denotes a table with the
![]() $1$
in the second row in column j, that is,
$1$
in the second row in column j, that is,
![]() $X_{2j}^j = 1, X_{2k}^j = 0$
for all
$X_{2j}^j = 1, X_{2k}^j = 0$
for all
![]() $k \neq j$
, then equation (7.1) becomes
$k \neq j$
, then equation (7.1) becomes
 $$ \begin{align*} q^{-n + n^2 - (j-1)}(q -1)^n \cdot [n-1]_{1/q}! = q^{\binom{n}{2} - (j-1)} \frac{q^n - q^{n-1}}{q^n - 1} \cdot \prod_{k = 1}^n (1 - q^k), \end{align*} $$
$$ \begin{align*} q^{-n + n^2 - (j-1)}(q -1)^n \cdot [n-1]_{1/q}! = q^{\binom{n}{2} - (j-1)} \frac{q^n - q^{n-1}}{q^n - 1} \cdot \prod_{k = 1}^n (1 - q^k), \end{align*} $$
which uses

Dividing by
![]() $|GL_n(q)| = (q - 1)^n q^{\binom {n}{2}} \cdot [n]_q$
gives
$|GL_n(q)| = (q - 1)^n q^{\binom {n}{2}} \cdot [n]_q$
gives
 $$ \begin{align*} q^{-(j-1)} \cdot \frac{(q^n - q^{n-1})(q - 1)}{(q^n - 1)^2(q - 1)^n} \prod_{k = 1}^{n} (q^k - 1). \end{align*} $$
$$ \begin{align*} q^{-(j-1)} \cdot \frac{(q^n - q^{n-1})(q - 1)}{(q^n - 1)^2(q - 1)^n} \prod_{k = 1}^{n} (q^k - 1). \end{align*} $$
Note that this distribution is equal to
![]() $\pi _{q, 1}$
from Section 6 if we map
$\pi _{q, 1}$
from Section 6 if we map
![]() $j \to n - j$
, that is, index the double cosets by
$j \to n - j$
, that is, index the double cosets by
![]() $n, n-1, \dots , 1$
instead of
$n, n-1, \dots , 1$
instead of
![]() $1, 2, \dots , n$
. The ‘follow the top card’ chain in Section 6 is then equivalent to the induced chain on double cosets
$1, 2, \dots , n$
. The ‘follow the top card’ chain in Section 6 is then equivalent to the induced chain on double cosets
![]() $P_{\alpha } \backslash GL_n(q) / P_{\beta }$
from random transvections on
$P_{\alpha } \backslash GL_n(q) / P_{\beta }$
from random transvections on
![]() $GL_n(q)$
.
$GL_n(q)$
.
It remains an open problem to further investigate probability distributions and Markov chains on the double cosets of
![]() $GL_n(q)$
from parabolic subgroups. In a reasonable sense, for finite groups of Lie type, parabolic subgroups or close cousins are the only systematic families which can occur; see [Reference Seitz57].
$GL_n(q)$
from parabolic subgroups. In a reasonable sense, for finite groups of Lie type, parabolic subgroups or close cousins are the only systematic families which can occur; see [Reference Seitz57].
7.2 Gelfand pairs
A group G with subgroup H is a Gelfand pair if the convolution of H-bi-invariant functions is commutative. Probability theory for Gelfand pairs was initiated by Letac [Reference Letac42] and Sawyer [Reference Sawyer55] who studied the induced chain on
as simple random walk on a p-ary tree. Many further examples of finite Gelfand pairs appear in [Reference Diaconis and Shahshahani23], [Reference Diaconis15], [Reference Ceccherini Silberstein, Scarabotti and Tolli12]. These allow analysis of classical problems such as the Bernoulli–Laplace model of diffusion and natural walks on phylogenetic trees. The literature cited above contains a large number of concrete examples waiting to be interpreted. For surprising examples relating Gelfand pairs, conjugacy class walks on a ‘dual group’ and ‘folding’, see [Reference Lawther41].
We also note that Gelfand pairs occur more generally for compact and noncompact groups. For example,
![]() $\mathcal {O}_n/\mathcal {O}_{n-1}$
is Gelfand and the spherical functions become the spherical harmonics of classical physics (this example is further discussed in Section 7.5 below). Gelfand pairs are even useful for large groups such as
$\mathcal {O}_n/\mathcal {O}_{n-1}$
is Gelfand and the spherical functions become the spherical harmonics of classical physics (this example is further discussed in Section 7.5 below). Gelfand pairs are even useful for large groups such as
![]() $S_{\infty }$
and
$S_{\infty }$
and
![]() $U_{\infty }$
, which are not locally compact; see [Reference Borodin and Olshanski8] and [Reference Neretin47] for research in this direction.
$U_{\infty }$
, which are not locally compact; see [Reference Borodin and Olshanski8] and [Reference Neretin47] for research in this direction.
7.3 Contingency tables
Simper [Reference Simper59] considers the symmetric group
![]() $S_n$
with parabolic subgroups
$S_n$
with parabolic subgroups
![]() $S_{\lambda }$
and
$S_{\lambda }$
and
![]() $S_{\mu }$
, for
$S_{\mu }$
, for
![]() $\lambda = (\lambda _1, \dots , \lambda _I), \mu = (\mu _1, \dots , \mu _J)$
partitions of n. Then
$\lambda = (\lambda _1, \dots , \lambda _I), \mu = (\mu _1, \dots , \mu _J)$
partitions of n. Then
![]() $S_{\lambda } \backslash S_n / S_{\mu }$
can be interpreted as
$S_{\lambda } \backslash S_n / S_{\mu }$
can be interpreted as
![]() $I \times J$
contingency tables
$I \times J$
contingency tables
![]() $\{T_{ij} \}_{1 \le i \le I, 1 \le j \le J}$
with row sums
$\{T_{ij} \}_{1 \le i \le I, 1 \le j \le J}$
with row sums
![]() $\lambda $
and column sums
$\lambda $
and column sums
![]() $\mu $
. Such tables appear in every kind of applied statistical work. See [Reference Diaconis and Simper24] Section 5 for references. The stationary distribution,
$\mu $
. Such tables appear in every kind of applied statistical work. See [Reference Diaconis and Simper24] Section 5 for references. The stationary distribution,
 $$\begin{align*}\pi(T) = \frac{1}{n!} \prod_{i, j} \frac{\lambda_i! \mu_j!}{T_{ij}!}, \end{align*}$$
$$\begin{align*}\pi(T) = \frac{1}{n!} \prod_{i, j} \frac{\lambda_i! \mu_j!}{T_{ij}!}, \end{align*}$$
is the familiar Fisher–Yates distribution underlying ‘Fisher’s exact test for independence’. Markov chains with the Fisher–Yates distribution as stationary were studied in [Reference Diaconis and Sturmfels25]. If Q is the random transposition measure on
![]() $S_n$
, [Reference Simper59] uses knowledge of the Q chain to give an eigen-analysis of the chain induced by Q on contingency tables.
$S_n$
, [Reference Simper59] uses knowledge of the Q chain to give an eigen-analysis of the chain induced by Q on contingency tables.
7.4 Chevalley groups
Let G be a finite Chevalley group (a finite simple group of Lie type). These come equipped with natural notions of Borel subgroups B and Weyl groups W. The Bruhat decomposition
is in force, and conjugacy invariant probabilities Q on G induce Markov chains on W. Let U be a minimal unipotent conjugacy class in G ([Reference Carter11], Chapter 5) and Q the uniform probability on U. Conjugacy invariance implies that convolving by Q induces an element of
![]() $\mathrm {End}_G(G/\mathcal {B})$
. This may be identified with the Hecke algebra of B-bi-invariant functions. James Parkinson has shown us that the argument of Section 2.4 (for the computation of D in the Hecke algebra) goes through for a general Chevalley groups G over a finite field
$\mathrm {End}_G(G/\mathcal {B})$
. This may be identified with the Hecke algebra of B-bi-invariant functions. James Parkinson has shown us that the argument of Section 2.4 (for the computation of D in the Hecke algebra) goes through for a general Chevalley groups G over a finite field
![]() $\mathbb {F}_q$
. Although a similar formula holds in full generality, for simplicity we will state it in the equal parameter case (nontwisted) and when G is not of type
$\mathbb {F}_q$
. Although a similar formula holds in full generality, for simplicity we will state it in the equal parameter case (nontwisted) and when G is not of type
![]() $C_n$
with character lattice equal to the root lattice. Let
$C_n$
with character lattice equal to the root lattice. Let
![]() $\theta $
be the highest root, and let
$\theta $
be the highest root, and let
![]() $\mathcal {X}_{\theta } = \{ x_{\theta }(c)\ |\ c\in \mathbb {F}_q\}$
be the corresponding root subgroup. The conjugacy class of
$\mathcal {X}_{\theta } = \{ x_{\theta }(c)\ |\ c\in \mathbb {F}_q\}$
be the corresponding root subgroup. The conjugacy class of
![]() $x_{\theta }(1)$
is an analogue, for general Chevalley groups, of the conjugacy class of transvections in
$x_{\theta }(1)$
is an analogue, for general Chevalley groups, of the conjugacy class of transvections in
![]() $GL_n(q)$
. The sum of the elements in the conjugacy class of
$GL_n(q)$
. The sum of the elements in the conjugacy class of
![]() $x_{\theta }(1)$
provides a Markov chain on
$x_{\theta }(1)$
provides a Markov chain on
![]() $\mathcal {B}\backslash G/\mathcal {B}$
which acts the same way as
$\mathcal {B}\backslash G/\mathcal {B}$
which acts the same way as
 $$ \begin{align*} D &= (q-1)\sum_{\alpha\in \Phi^+_l} q^{\frac12(I(s_{\theta})-I(s_{\alpha}))}(1+T_{s_{\alpha}}), \end{align*} $$
$$ \begin{align*} D &= (q-1)\sum_{\alpha\in \Phi^+_l} q^{\frac12(I(s_{\theta})-I(s_{\alpha}))}(1+T_{s_{\alpha}}), \end{align*} $$
where
![]() $\theta $
is the highest root,
$\theta $
is the highest root,
![]() $\Phi ^+_l$
is the set of positive long roots, and
$\Phi ^+_l$
is the set of positive long roots, and
![]() $s_{\beta }$
denotes the reflection in the root
$s_{\beta }$
denotes the reflection in the root
![]() $\beta $
and
$\beta $
and
![]() $T_w$
is the element of the Iwahori–Hecke algebra for
$T_w$
is the element of the Iwahori–Hecke algebra for
![]() $\mathcal {B}\backslash G/\mathcal {B}$
corresponding to the element w in the Weyl group.
$\mathcal {B}\backslash G/\mathcal {B}$
corresponding to the element w in the Weyl group.
Following the ideas in [Reference Diaconis and Ram18], the
![]() $T_{s_{\alpha }}$
can be interpreted via the Metropolis algorithm applied to the problem of sampling from the stationary distribution
$T_{s_{\alpha }}$
can be interpreted via the Metropolis algorithm applied to the problem of sampling from the stationary distribution
![]() $\pi (x) = Z^{-1}q^{I(x)}$
on W by choosing random generators. We have not worked out any further examples but would be pleased if someone would.
$\pi (x) = Z^{-1}q^{I(x)}$
on W by choosing random generators. We have not worked out any further examples but would be pleased if someone would.
7.5 A continuous example
Most of the generalities above extend to compact groups G and closed subgroups
![]() $H, K \neq G$
. Then,
$H, K \neq G$
. Then,
![]() $X = H \backslash G /K$
is a compact space and an H-conjugacy invariant probability Q on G induces a Markov chain on X.
$X = H \backslash G /K$
is a compact space and an H-conjugacy invariant probability Q on G induces a Markov chain on X.
To consider a simple example, let
![]() $G = \mathcal {O}_n$
, the usual orthogonal group over
$G = \mathcal {O}_n$
, the usual orthogonal group over
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $H = K = \mathcal {O}_{n-1}$
embedded as all
$H = K = \mathcal {O}_{n-1}$
embedded as all
![]() $m \in \mathcal {O}_n$
fixing the ‘north pole’
$m \in \mathcal {O}_n$
fixing the ‘north pole’
![]() $e_1 = (1, 0, 0 \dots , 0)^{\top }$
. Then,
$e_1 = (1, 0, 0 \dots , 0)^{\top }$
. Then,
![]() $\mathcal {O}_n/\mathcal {O}_{n-1}$
can be thought of as the
$\mathcal {O}_n/\mathcal {O}_{n-1}$
can be thought of as the
![]() $(n-1)$
-sphere
$(n-1)$
-sphere
![]() $\mathcal {S}_{n-1}$
. The double coset space
$\mathcal {S}_{n-1}$
. The double coset space
![]() $\mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
codes up the ‘latitude’. Consider the sphere
$\mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
codes up the ‘latitude’. Consider the sphere
![]() $\mathcal {O}_n / \mathcal {O}_{n-1}$
defined by ‘circles’ orthogonal to
$\mathcal {O}_n / \mathcal {O}_{n-1}$
defined by ‘circles’ orthogonal to
![]() $e_1$
(see Figure 1).
$e_1$
(see Figure 1).

Figure 1 The space
![]() $\mathcal {O}_n/\mathcal {O}_{n-1}$
is defined by the circles on the sphere orthogonal to
$\mathcal {O}_n/\mathcal {O}_{n-1}$
is defined by the circles on the sphere orthogonal to
![]() $e_1$
.
$e_1$
.
Then
![]() $\mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
simply codes which circle contains a given point on the sphere. Thus,
$\mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
simply codes which circle contains a given point on the sphere. Thus,
![]() $\mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
may be identified with
$\mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
may be identified with
![]() $[-1, 1]$
.
$[-1, 1]$
.
Represent a uniformly chosen point on the sphere as
![]() $x = z/\|z \|$
with
$x = z/\|z \|$
with
![]() $z = (z_1, z_2, \dots , z_n)$
independent standard normals. The latitude is
$z = (z_1, z_2, \dots , z_n)$
independent standard normals. The latitude is
![]() $z_1/\|z\|$
and so
$z_1/\|z\|$
and so
![]() $\pi (x)$
is the distribution of the square root of a
$\pi (x)$
is the distribution of the square root of a
![]() $\beta (1/2, (n-1)/2)$
distribution on
$\beta (1/2, (n-1)/2)$
distribution on
![]() $[-1, 1]$
. When
$[-1, 1]$
. When
![]() $n = 3$
,
$n = 3$
,
![]() $\pi (x)$
is uniform on
$\pi (x)$
is uniform on
![]() $[-1, 1]$
(theorem of Archimedes).
$[-1, 1]$
(theorem of Archimedes).
One simple choice for a driving measure Q on
![]() $\mathcal {O}_n$
is ‘random reflections’. In probabilistic language, this is the distribution of
$\mathcal {O}_n$
is ‘random reflections’. In probabilistic language, this is the distribution of
![]() $I - 2 U U^{\top }$
, with U uniform on
$I - 2 U U^{\top }$
, with U uniform on
![]() $\mathcal {S}_{n-1}$
. There is a nice probabilistic description of the induced walk on the sphere.
$\mathcal {S}_{n-1}$
. There is a nice probabilistic description of the induced walk on the sphere.
Lemma 7.2. The random reflections measure on
![]() $\mathcal {S}_{n-1}$
has the following equivalent description:
$\mathcal {S}_{n-1}$
has the following equivalent description:
-
• From
 $x \in \mathcal {S}_{n-1}$
, pick a line
$x \in \mathcal {S}_{n-1}$
, pick a line
 $\ell $
through x uniformly (see Figure 2). With probability
$\ell $
through x uniformly (see Figure 2). With probability
 $1$
,
$1$
,
 $\ell $
intersects the sphere in a unique point y. Move to y.
$\ell $
intersects the sphere in a unique point y. Move to y.

Figure 2 Illustration of procedure from Lemma 7.2.
Remark 7.3. As the lemma shows, there is a close connection between the walk generated from Q and the popular ‘princess and monster’ algorithm. See [Reference Comets, Popov, Schütz and Vachkovskaia13]. These algorithms proceed in general convex domains. We know all the eigenvalues of the walk on the sphere and can give sharp rates of convergence.
The induced chain on
![]() $[-1, 1] \cong \mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
is obtained by simply reporting the latitude of y. Thanks to Sourav Chatterjee for the following probabilistic description. For simplicity, it is given here for
$[-1, 1] \cong \mathcal {O}_{n-1} \backslash \mathcal {O}_n / \mathcal {O}_{n-1}$
is obtained by simply reporting the latitude of y. Thanks to Sourav Chatterjee for the following probabilistic description. For simplicity, it is given here for
![]() $n = 3$
(so
$n = 3$
(so
![]() $\pi (x)$
is uniform on
$\pi (x)$
is uniform on
![]() $[-1, 1]$
).
$[-1, 1]$
).
Lemma 7.4. For
![]() $n = 3$
, the Markov chain on
$n = 3$
, the Markov chain on
![]() $[-1, 1]$
described above is; from
$[-1, 1]$
described above is; from
![]() $x_0 \in [-1, 1]$
, the chain jumps to
$x_0 \in [-1, 1]$
, the chain jumps to
where
![]() $U_1, U_2$
are i.i.d. uniform on
$U_1, U_2$
are i.i.d. uniform on
![]() $[-1, 1]$
random variables. (We have checked that the uniform distribution is stationary using Monte Carlo.)
$[-1, 1]$
random variables. (We have checked that the uniform distribution is stationary using Monte Carlo.)
Remark 7.5. For a detailed analysis of the random reflections walk on
![]() $\mathcal {O}_n$
(including all the eigenvalues), see [Reference Porod51].
$\mathcal {O}_n$
(including all the eigenvalues), see [Reference Porod51].
A Row reduction for
 $GL_n(q)$
$GL_n(q)$
Explicit row reduction can be performed on a general transvection to determine which
![]() $\mathcal {B}$
-
$\mathcal {B}$
-
![]() $\mathcal {B}$
double coset it lies in. This allows computing transition probabilities using the combinatorics of possible transvections, which is elementary but tedious. This section proves the following result, used in Section 5.2.
$\mathcal {B}$
double coset it lies in. This allows computing transition probabilities using the combinatorics of possible transvections, which is elementary but tedious. This section proves the following result, used in Section 5.2.
Proposition A.1. Let
![]() $T_{\mathbf {a}, \mathbf {v}} = I + \mathbf {v} \mathbf {a}^{\top }$
be the transvection defined by nonzero vectors
$T_{\mathbf {a}, \mathbf {v}} = I + \mathbf {v} \mathbf {a}^{\top }$
be the transvection defined by nonzero vectors
![]() $\mathbf {a}, \mathbf {v}$
with
$\mathbf {a}, \mathbf {v}$
with
![]() $\mathbf {v}^{\top } \mathbf {a} = 0$
and the last nonzero entry of
$\mathbf {v}^{\top } \mathbf {a} = 0$
and the last nonzero entry of
![]() $\mathbf {v}$
equal to
$\mathbf {v}$
equal to
![]() $1$
. If
$1$
. If
![]() $j> i$
, then
$j> i$
, then
exactly when the last nonzero entry of
![]() $\mathbf {v}$
is
$\mathbf {v}$
is
![]() $v_j$
and the first nonzero entry of a is
$v_j$
and the first nonzero entry of a is
![]() $\mathbf {a}_i$
.
$\mathbf {a}_i$
.
The transvection corresponding to
![]() $\mathbf {a}, \mathbf {v}$
is
$\mathbf {a}, \mathbf {v}$
is
and the ith column of
![]() $T_{\mathbf {a}, \mathbf {v}}$
is
$T_{\mathbf {a}, \mathbf {v}}$
is
![]() $a_i \mathbf {v}$
except with an extra
$a_i \mathbf {v}$
except with an extra
![]() $1$
added to the ith entry. So
$1$
added to the ith entry. So
 $$ \begin{align*}T_{\mathbf{a}, \mathbf{v}} = \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &\cdots &a_nv_1 \\ a_1v_2 &1+a_2v_2 &a_3v_2 &\cdots &a_nv_2 \\ \vdots &&&&\vdots \\ a_1v_n &a_2v_n &&\cdots &1+a_nv_n \end{pmatrix} =1 + \big( a_iv_j \big)_{1\le i,j\le n}. \end{align*} $$
$$ \begin{align*}T_{\mathbf{a}, \mathbf{v}} = \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &\cdots &a_nv_1 \\ a_1v_2 &1+a_2v_2 &a_3v_2 &\cdots &a_nv_2 \\ \vdots &&&&\vdots \\ a_1v_n &a_2v_n &&\cdots &1+a_nv_n \end{pmatrix} =1 + \big( a_iv_j \big)_{1\le i,j\le n}. \end{align*} $$
As an example of the row reduction, take
![]() $n = 5$
with
$n = 5$
with
![]() $v_5 = 1, a_1 \neq 0$
. Then,
$v_5 = 1, a_1 \neq 0$
. Then,
 $$ \begin{align*} T_{\mathbf{a}, \mathbf{v}} &= \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &a_4v_1 &a_5v_1 \\ a_1v_2 &1+a_2v_2 &a_3v_2 &a_4v_2 &a_5v_2 \\ a_1v_3 &a_2v_3 &1+a_3v_3 &a_4v_3 &a_5v_3 \\ a_1v_4 &a_2v_4 &a_3v_4 &1+a_4v_4 &a_5v_4 \\ a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \end{pmatrix} \end{align*} $$
$$ \begin{align*} T_{\mathbf{a}, \mathbf{v}} &= \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &a_4v_1 &a_5v_1 \\ a_1v_2 &1+a_2v_2 &a_3v_2 &a_4v_2 &a_5v_2 \\ a_1v_3 &a_2v_3 &1+a_3v_3 &a_4v_3 &a_5v_3 \\ a_1v_4 &a_2v_4 &a_3v_4 &1+a_4v_4 &a_5v_4 \\ a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \end{pmatrix} \end{align*} $$
 $$ \begin{align*} &= y_4(v_4v_5^{-1}) \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &a_4v_1 &a_5v_1 \\ a_1v_2 &1+a_2v_2 &a_3v_2 &a_4v_2 &a_5v_2 \\ a_1v_3 &a_2v_3 &1+a_3v_3 &a_4v_3 &a_5v_3 \\ a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &a_4v_1 &a_5v_1 \\ a_1v_2 &1+a_2v_2 &a_3v_2 &a_4v_2 &a_5v_2 \\ a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &a_4v_1 &a_5v_1 \\ a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &-a_1^{-1}a_2 &-a_1^{-1}a_3 &-a_1^{-1}a_4 &z \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} &= y_4(v_4v_5^{-1}) \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &a_4v_1 &a_5v_1 \\ a_1v_2 &1+a_2v_2 &a_3v_2 &a_4v_2 &a_5v_2 \\ a_1v_3 &a_2v_3 &1+a_3v_3 &a_4v_3 &a_5v_3 \\ a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &a_4v_1 &a_5v_1 \\ a_1v_2 &1+a_2v_2 &a_3v_2 &a_4v_2 &a_5v_2 \\ a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) \begin{pmatrix} 1+a_1v_1 &a_2v_1 &a_3v_1 &a_4v_1 &a_5v_1 \\ a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &-a_1^{-1}a_2 &-a_1^{-1}a_3 &-a_1^{-1}a_4 &z \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix}, \end{align*} $$
with
![]() $(a_1^{-1}v_5^{-1}+v_1v_5^{-1})(1+a_5v_5)+z = a_5v_1$
so that
$(a_1^{-1}v_5^{-1}+v_1v_5^{-1})(1+a_5v_5)+z = a_5v_1$
so that
Thus,
 $$ \begin{align*} T_{\mathbf{a}, \mathbf{v}} &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \\ &\quad \cdot y_2(-a_2a_1^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &-a_3a_1^{-1} &-a_4a_1^{-1} &z-a_2v_2a_1^{-1}v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \\ &\quad \cdot y_2(-a_2a_1^{-1})y_3(-a_3a_1^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &-a_4a_1^{-1} &z-(a_2v_2+a_3v_3)a_1^{-1}v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \\ &\quad \cdot y_2(-a_2a_1^{-1})y_3(-a_3a_1^{-1})y_4(-a_4a_1^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \\ 0 &0 &0 &0 &z-(a_2v_2+a_3v_3+a_4v_4)a_1^{-1}v_5^{-1} \end{pmatrix} \end{align*} $$
$$ \begin{align*} T_{\mathbf{a}, \mathbf{v}} &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \\ &\quad \cdot y_2(-a_2a_1^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &-a_3a_1^{-1} &-a_4a_1^{-1} &z-a_2v_2a_1^{-1}v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \\ &\quad \cdot y_2(-a_2a_1^{-1})y_3(-a_3a_1^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &-a_4a_1^{-1} &z-(a_2v_2+a_3v_3)a_1^{-1}v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \end{pmatrix} \\ &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \\ &\quad \cdot y_2(-a_2a_1^{-1})y_3(-a_3a_1^{-1})y_4(-a_4a_1^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \\ 0 &0 &0 &0 &z-(a_2v_2+a_3v_3+a_4v_4)a_1^{-1}v_5^{-1} \end{pmatrix} \end{align*} $$
 $$ \begin{align*} &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \\ &\quad \cdot y_2(-a_2a_1^{-1})y_3(-a_3a_1^{-1})y_4(-a_4a_1^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \\ 0 &0 &0 &0 &-a_1^{-1}v_5^{-1} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} &= y_4(v_4v_5^{-1}) y_3(v_3v_5^{-1}) y_2(v_2v_5^{-1}) y_1(a_1^{-1}v_5^{-1}+v_1v_5^{-1}) \\ &\quad \cdot y_2(-a_2a_1^{-1})y_3(-a_3a_1^{-1})y_4(-a_4a_1^{-1}) \begin{pmatrix} a_1v_5 &a_2v_5 &a_3v_5 &a_4v_5 &1+a_5v_5 \\ 0 &1 &0 &0 &-v_2v_5^{-1} \\ 0 &0 &1 &0 &-v_3v_5^{-1} \\ 0 &0 &0 &1 &-v_4v_5^{-1} \\ 0 &0 &0 &0 &-a_1^{-1}v_5^{-1} \end{pmatrix}. \end{align*} $$
Acknowledgments
The authors thank Sourav Chatterjee, David Craven, Jason Fulman, Michael Geline, Bob Guralnick, Jimmy He, Marty Isaacs, Zhihan Li, Martin Liebeck, Gabriel Navarro, James Parkinson, Mehrdad Shahshahani and Nat Thiem for helpful discussions. We also thank an anonymous referee for a rapid, useful report. P.D. was partially supported by NSF grant DMS-1954042. M.S. was supported by a National Defense Science & Engineering Graduate Fellowship and a Lieberman Fellowship from Stanford University.
Conflict of Interest
The authors have no conflict of interest to declare.