Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-09T14:30:43.707Z Has data issue: false hasContentIssue false
  • English
  • Français

CONDITIONAL LARGE INITIAL DATA SCATTERING RESULTS FOR THE DIRAC–KLEIN–GORDON SYSTEM

Part of: Equations of mathematical physics and other areas of application Harmonic analysis in several variables

Published online by Cambridge University Press:  21 June 2018

TIMOTHY CANDY  and
SEBASTIAN HERR
TIMOTHY CANDY
Affiliation:
Universität Bielefeld, Fakultät für Mathematik, Postfach 100131, 33501 Bielefeld, Germany; tcandy@math.uni-bielefeld.de, herr@math.uni-bielefeld.de
SEBASTIAN HERR
Affiliation:
Universität Bielefeld, Fakultät für Mathematik, Postfach 100131, 33501 Bielefeld, Germany; tcandy@math.uni-bielefeld.de, herr@math.uni-bielefeld.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the global behaviour for large solutions of the Dirac–Klein–Gordon system in critical spaces in dimension 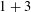$1+3$. In particular, we show that bounded solutions exist globally in time and scatter, provided that a controlling space–time Lebesgue norm is finite. A crucial step is to prove nonlinear estimates that exploit the dichotomy between transversality and null structure, and furthermore involve the controlling norm.

MSC classification

Primary: 42B37: Harmonic analysis and PDE 35Q41: Time-dependent Schrödinger equations, Dirac equations
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e9
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2018

References

Bejenaru, I. and Herr, S., ‘On global well-posedness and scattering for the massive Dirac–Klein–Gordon system’, J. Eur. Math. Soc. (JEMS) 19(8) (2017), 2445–2467. MR 3668064.CrossRefGoogle Scholar
Bjorken, J. D. and Drell, S. D., Relativistic Quantum Mechanics (McGraw-Hill Book Co., New York–Toronto–London, 1964), MR 0187641.Google Scholar
Bourgain, J., Global Solutions of Nonlinear Schrödinger Equations, American Mathematical Society Colloquium Publications, 46 (American Mathematical Society, Providence, RI, 1999). MR 1691575.Google Scholar
Candy, T., ‘Multiscale bilinear restriction estimates for general phases’, Preprint, 2017,arXiv:1707.08944 [math.CA].Google Scholar
Candy, T. and Herr, S., ‘On the Majorana condition for nonlinear Dirac systems’, Ann. Inst. H. Poincaré Anal. Non Linéaire (2018), doi:10.1016/j.anihpc.2018.02.001.Google Scholar
Candy, T. and Herr, S., ‘Transference of bilinear restriction estimates to quadratic variation norms and the Dirac–Klein–Gordon system’, Anal. PDE 11(5) (2018), 1171–1240. MR 3785603.CrossRefGoogle Scholar
Cho, Y. and Lee, S., ‘Strichartz estimates in spherical coordinates’, Indiana Univ. Math. J. 62(3) (2013), 991–1020. MR 3164853.CrossRefGoogle Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., ‘Global well-posedness and scattering for the energy-critical nonlinear Schrödinger equation in ℝ3 ’, Ann. of Math. (2) 167(3) (2008), 767–865. MR 2415387.Google Scholar
D’Ancona, P., Foschi, D. and Selberg, S., ‘Null structure and almost optimal local regularity for the Dirac–Klein–Gordon system’, J. Eur. Math. Soc. (JEMS) 9(4) (2007), 877–899. MR 2341835.Google Scholar
Dodson, B. and Smith, P., ‘A controlling norm for energy-critical Schrödinger maps’, Trans. Amer. Math. Soc. 367(10) (2015), 7193–7220. MR 3378828.CrossRefGoogle Scholar
Esteban, M. J., Georgiev, V. and Séré, E., ‘Stationary solutions of the Maxwell–Dirac and the Klein–Gordon–Dirac equations’, Calc. Var. Partial Differ. Equ. 4(3) (1996), 265–281. MR 1386737.CrossRefGoogle Scholar
Hadac, M., Herr, S. and Koch, H., ‘Well-posedness and scattering for the KP-II equation in a critical space’, Ann. Inst. H. Poincaré Anal. Non Linéaire 26(3) (2009), 917–941. MR 2526409.CrossRefGoogle Scholar
Kenig, C. E., Lectures on the Energy Critical Nonlinear Wave Equation, CBMS Regional Conference Series in Mathematics, 122 (American Mathematical Society, Providence, RI, 2015), Published for the Conference Board of the Mathematical Sciences, Washington, DC. MR 3328916.Google Scholar
Killip, R. and Vişan, M., ‘Nonlinear Schrödinger equations at critical regularity’, inEvolution Equations, Clay Math. Proc., 17 (American Mathematical Society, Providence, RI, 2013), 325–437. MR 3098643.Google Scholar
Koch, H. and Tataru, D., ‘Dispersive estimates for principally normal pseudodifferential operators’, Comm. Pure Appl. Math. 58(2) (2005), 217–284. MR 2094851.CrossRefGoogle Scholar
Koch, H., Tataru, D. and Vişan, M., Dispersive Equations and Nonlinear Waves. Generalized Korteweg-de Vries, Nonlinear Schrödinger, Wave and Schrödinger Maps, (Birkhäuser/Springer, Basel, 2014), (English).Google Scholar
Machihara, S., Nakanishi, K. and Ozawa, T., ‘Small global solutions and the nonrelativistic limit for the nonlinear Dirac equation’, Rev. Mat. Iberoam. 19(1) (2003), 179–194. MR 1993419.CrossRefGoogle Scholar
Oh, S.-J. and Tataru, D., ‘Global well-posedness and scattering of the (4 + 1)-dimensional Maxwell–Klein–Gordon equation’, Invent. Math. 205(3) (2016), 781–877. MR 3539926.Google Scholar
Oh, S.-J. and Tataru, D., ‘Local well-posedness of the (4 + 1)-dimensional Maxwell–Klein–Gordon equation at energy regularity’, Ann. PDE 2(1) (2016), 70. Art. 2, MR 3462105.CrossRefGoogle Scholar
Sterbenz, J., ‘Global regularity and scattering for general non-linear wave equations. II.(4 + 1) dimensional Yang–Mills equations in the Lorentz gauge’, Amer. J. Math. 129(3) (2007), 611–664. MR 2325100.Google Scholar
Sterbenz, J. and Tataru, D., ‘Energy dispersed large data wave maps in 2 + 1 dimensions’, Comm. Math. Phys. 298(1) (2010), 139–230. MR 2657817.CrossRefGoogle Scholar
Sterbenz, J. and Tataru, D., ‘Regularity of wave-maps in dimension 2 + 1’, Comm. Math. Phys. 298(1) (2010), 231–264.Google Scholar
Thaller, B., The Dirac Equation, Texts and Monographs in Physics (Springer, Berlin, 1992). MR 1219537.Google Scholar
Wang, X., ‘On global existence of 3D charge critical Dirac–Klein–Gordon system’, Int. Math. Res. Not. IMRN 2015(21) (2015), 10801–10846. MR 3456028.Google Scholar