Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-20T01:46:13.307Z Has data issue: false hasContentIssue false
  • English
  • Français

COLORING CURVES ON SURFACES

Part of: Graph theory Low-dimensional topology

Published online by Cambridge University Press:  04 September 2018

JONAH GASTER ,
JOSHUA EVAN GREENE  and
NICHOLAS G. VLAMIS
JONAH GASTER
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, Quebec H3A 0B9, Canada; jbgaster@gmail.com
JOSHUA EVAN GREENE
Affiliation:
Department of Mathematics, Boston College, Chestnut Hill, MA 02467, USA; joshua.greene@bc.edu
NICHOLAS G. VLAMIS
Affiliation:
Department of Mathematics, Queens College of CUNY, Flushing, NY 11367, USA; nicholas.vlamis@qc.cuny.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the chromatic number of the curve graph of a surface. We show that the chromatic number grows like 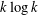$k\log k$ for the graph of separating curves on a surface of Euler characteristic 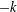$-k$. We also show that the graph of curves that represent a fixed nonzero homology class is uniquely $t$-colorable, where $t$ denotes its clique number. Together, these results lead to the best known bounds on the chromatic number of the curve graph. We also study variations for arc graphs and obtain exact results for surfaces of low complexity. Our investigation leads to connections with Kneser graphs, the Johnson homomorphism, and hyperbolic geometry.

MSC classification

Primary: 57M15: Relations with graph theory
Secondary: 05C15: Coloring of graphs and hypergraphs
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e17
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2018

References

Aougab, T., Biringer, I. and Gaster, J., ‘Packing curves on surfaces with few intersections’, Int. Math. Res. Not. IMRN (2017), rnx270.Google Scholar
Aramayona, J. and Leininger, C. J., ‘Finite rigid sets in curve complexes’, J. Topol. Anal. 5(2) (2013), 183–203.Google Scholar
Beardon, A. F., The Geometry of Discrete Groups, Graduate Texts in Mathematics, 91 (Springer, New York, 1983).Google Scholar
Bestvina, M., Bromberg, K. and Fujiwara, K., ‘Constructing group actions on quasi-trees and applications to mapping class groups’, Publ. Math. Inst. Hautes Études Sci. 122(1) (2015), 1–64.Google Scholar
Birman, J., Broaddus, N. and Menasco, W., ‘Finite rigid sets and homologically nontrivial spheres in the curve complex of a surface’, J. Topol. Anal. 7(1) (2015), 47–71.Google Scholar
Birman, J. and Menasco, W., ‘The curve complex has dead ends’, Geom. Dedicata 177 (2015), 71–74.Google Scholar
Bowditch, B. H., ‘Tight geodesics in the curve complex’, Invent. Math. 171(2) (2008), 281–300.Google Scholar
Brock, J., Canary, R. and Minsky, Y., ‘The classification of Kleinian surface groups, II: the ending lamination conjecture’, Ann. of Math. (2) 176(1) (2012), 1–149.Google Scholar
Buser, P., Geometry and Spectra of Compact Riemann Surfaces, Progress in Mathematics, 106 (Birkhäuser Boston, Inc., Boston, MA, 1992).Google Scholar
Buser, P. and Parlier, H., ‘The distribution of simple closed geodesics on a Riemann surface’, inComplex Analysis and its Applications, OCAMI Stud., 2 (Osaka Munic. Univ. Press, Osaka, 2007), 3–10.Google Scholar
Cameron, P. J. and van Lint, J. H., Designs, Graphs, Codes and their Links (Cambridge University Press, Cambridge, 1991).Google Scholar
Chillingworth, D. R. J., ‘Winding numbers on surfaces, I’, Math. Ann. 196(3) (1972), 218–249.Google Scholar
Chillingworth, D. R. J., ‘Winding numbers on surfaces. II’, Math. Ann. 199(3) (1972), 131–153.Google Scholar
Fabila-Monroy, R., Flores-Peñaloza, D., Huemer, C., Hurtado, F., Urrutia, J. and Wood, D. R., ‘On the chromatic number of some flip graphs’, Discrete Math. Theor. Comput. Sci. 11(2) (2009), 47–56.Google Scholar
Farb, B. and Margalit, D., A Primer on Mapping Class Groups (Princeton University Press, Princeton, NJ, 2011).Google Scholar
Godsil, C. and Royle, G. F., Algebraic Graph Theory, vol. 207 (Springer, New York, 2013).Google Scholar
Haas, A. and Susskind, P., ‘The geometry of the hyperelliptic involution in genus two’, Proc. Amer. Math. Soc. 105(1) (1989), 159–165.Google Scholar
Harvey, W. J., ‘Boundary structure of the modular group’, inRiemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference (State Univ. New York, Stony Brook, NY, 1978), Annals of Mathematics Studies, 97 (Princeton University Press, Princeton, NJ, 1981), 245–251.Google Scholar
Irmer, I., ‘The Chillingworth class is a signed stable length’, Algebr. Geom. Topol. 15(4) (2015), 1863–1876.Google Scholar
Ivanov, N. V., ‘Automorphisms of complexes of curves and of Teichmüller spaces’, inProgress in Knot Theory and Related Topics, Travaux en Cours, 56 (Hermann, Paris, 1997), 113–120.Google Scholar
Johnson, D., ‘An abelian quotient of the mapping class group I g ’, Math. Ann. 249(3) (1980), 225–242.Google Scholar
Johnson, D., ‘The structure of the Torelli group I: a finite set of generators for J’, Ann. of Math. (2) 118(3) (1983), 423–442.Google Scholar
Johnson, D., ‘The structure of the Torelli group II: a characterization of the group generated by twists on bounding curves’, Topology 24(2) (1985), 113–126.Google Scholar
Juvan, M., Malnič, A. and Mohar, B., ‘Systems of curves on surfaces’, J. Combin. Theory Ser. B 68(1) (1996), 7–22.Google Scholar
Kent, R. P. IV and Peifer, D., ‘A geometric and algebraic description of annular braid groups’, Internat. J. Algebra Comput. 12 (2002), 85–97.Google Scholar
Kim, S.-H. and Koberda, T., ‘Right-angled Artin groups and finite subgraphs of curve graphs’, Osaka J. Math. 53(3) (2016), 705–716.Google Scholar
Kneser, M., ‘Aufgabe 360’, Jahresber. Dtsch. Math.-Ver. 2 (1955), 27.Google Scholar
Lee, C. W., ‘The associahedron and triangulations of the n-gon’, European J. Combin. 10(6) (1989), 551–560.Google Scholar
van Lint, J. H. and Wilson, R. M., A Course in Combinatorics (Cambridge University Press, Cambridge, 2001).Google Scholar
Lovász, L., ‘Kneser’s conjecture, chromatic number, and homotopy’, J. Combin. Theory Ser. A 25(3) (1978), 319–324.Google Scholar
Malestein, J., Rivin, I. and Theran, L., ‘Topological designs’, Geom. Dedicata 168 (2014), 221–233.Google Scholar
Masur, H. A. and Minsky, Y. N., ‘Geometry of the complex of curves. I. Hyperbolicity’, Invent. Math. 138(1) (1999), 103–149.Google Scholar
Matoušek, J., ‘Using the Borsuk–Ulam Theorem’, inUniversitext, Lectures on topological methods in combinatorics and geometry, Written in cooperation with Anders Björner and Günter M. Ziegler (Springer-Verlag, Berlin, 2003), xii+196.Google Scholar
Meeks, W. H. III and Patrusky, J., ‘Representing homology classes by embedded circles on a compact surface’, Illinois J. Math. 22(2) (1978), 262–269.Google Scholar
Minsky, Y., ‘The classification of Kleinian surface groups. I. Models and bounds’, Ann. of Math. (2) 171(1) (2010), 1–107.Google Scholar
Przytycki, P., ‘Arcs intersecting at most once’, Geom. Funct. Anal. 25(2) (2015), 658–670.Google Scholar
Putman, A., ‘A note on the connectivity of certain complexes associated to surfaces’, Enseign. Math. (2) 54(34) (2008), 287–301.Google Scholar
Putman, A., ‘The Johnson homomorphism and its kernel’, J. Reine Angew. Math. 735 (2018), 109–141.Google Scholar
Sarkar, S., ‘Maslov index formulas for Whitney n-gons’, J. Symplectic Geom. 9(2) (2011), 251–270.Google Scholar
Sleator, D. D., Tarjan, R. E. and Thurston, W. P., ‘Rotation distance, triangulations, and hyperbolic geometry’, J. Amer. Math. Soc. 1(3) (1988), 647–681.Google Scholar