Article contents
A class of continuous non-associative algebras arising from algebraic groups including 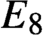 $E_8$
$E_8$
Published online by Cambridge University Press: 14 January 2021
Abstract
We give a construction that takes a simple linear algebraic group G over a field and produces a commutative, unital, and simple non-associative algebra A over that field. Two attractions of this construction are that (1) when G has type
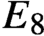 $E_8$, the algebra A is obtained by adjoining a unit to the 3875-dimensional representation; and (2) it is effective, in that the product operation on A can be implemented on a computer. A description of the algebra in the
$E_8$, the algebra A is obtained by adjoining a unit to the 3875-dimensional representation; and (2) it is effective, in that the product operation on A can be implemented on a computer. A description of the algebra in the
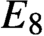 $E_8$ case has been requested for some time, and interest has been increased by the recent proof that
$E_8$ case has been requested for some time, and interest has been increased by the recent proof that
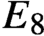 $E_8$ is the full automorphism group of that algebra. The algebras obtained by our construction have an unusual Peirce spectrum.
$E_8$ is the full automorphism group of that algebra. The algebras obtained by our construction have an unusual Peirce spectrum.
MSC classification
- Type
- Algebra
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 4
- Cited by





