Hostname: page-component-5c6d5d7d68-sv6ng Total loading time: 0 Render date: 2024-08-27T21:09:15.074Z Has data issue: false hasContentIssue false
  • English
  • Français

$A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS

Part of: Linear algebraic groups and related topics Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  24 April 2019

TIMOTHY C. BURNESS  and
DONNA M. TESTERMAN
TIMOTHY C. BURNESS
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, UK; t.burness@bristol.ac.uk
DONNA M. TESTERMAN
Affiliation:
Institute of Mathematics, Station 8, École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland; donna.testerman@epfl.ch

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 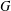$G$ be a simple exceptional algebraic group of adjoint type over an algebraically closed field of characteristic 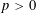$p>0$ and let 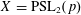$X=\text{PSL}_{2}(p)$ be a subgroup of 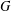$G$ containing a regular unipotent element $x$ of 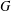$G$. By a theorem of Testerman, $x$ is contained in a connected subgroup of 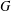$G$ of type 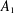$A_{1}$. In this paper we prove that with two exceptions, 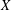$X$ itself is contained in such a subgroup (the exceptions arise when 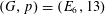$(G,p)=(E_{6},13)$ or 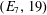$(E_{7},19)$). This extends earlier work of Seitz and Testerman, who established the containment under some additional conditions on 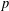$p$ and the embedding of 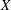$X$ in 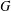$G$. We discuss applications of our main result to the study of the subgroup structure of finite groups of Lie type.

MSC classification

Primary: 20G41: Exceptional groups
Secondary: 20E32: Simple groups 20E07: Subgroup theorems; subgroup growth
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e12
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Alperin, J. L., Local Representation Theory, Cambridge Studies in Advanced Mathematics, 11 (Cambridge University Press, Cambridge, 1986).Google Scholar
Borel, A. and Tits, J., ‘Éléments unipotents et sous-groupes paraboliques de groupes réductifs. I’, Invent. Math. 12 (1971), 95–104.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: the user language’, J. Symbolic Comput. 24 (1997), 235–265.Google Scholar
Bourbaki, N., Groupes et algebrès de Lie (Chapitres 4, 5 et 6) (Hermann, Paris, 1968).Google Scholar
Carter, R. W., Simple Groups of Lie Type (Wiley, London, 1972).Google Scholar
Carter, R. W., Finite Groups of Lie Type: Conjugacy Classes and Complex Characters (Wiley, London, 1985).Google Scholar
Cohen, A. M. and Griess, R. L., ‘On finite subgroups of the complex Lie group of type E 8 ’, Proc. Sympos. Pure Math. 47 (1987), 367–405.Google Scholar
Cooperstein, B. N., ‘Maximal subgroups of G 2(2 n )’, J. Algebra 70 (1981), 23–36.Google Scholar
Craven, D. A., ‘Maximal PSL2 subgroups of exceptional groups of Lie type’, Mem. Amer. Math. Soc. to appear.Google Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups, Number 3, Mathematical Surveys and Monographs, 40 (Amererican Mathematical Society, Providence, RI, 1998).Google Scholar
Guralnick, R. and Malle, G., ‘Rational rigidity for E 8(p)’, Compos. Math. 150 (2014), 1679–1702.Google Scholar
Janusz, G. J., ‘Indecomposable representations of groups with a cyclic Sylow subgroup’, Trans. Amer. Math. Soc. 125 (1966), 288–295.Google Scholar
Kleidman, P. B., ‘The maximal subgroups of the Chevalley groups G 2(q) with q odd, the Ree groups 2 G 2(q), and their automorphism groups’, J. Algebra 117 (1988), 30–71.Google Scholar
Lawther, R., ‘Jordan block sizes of unipotent elements in exceptional algebraic groups’, Comm. Algebra 23 (1995), 4125–4156.Google Scholar
Lawther, R. and Testerman, D. M., ‘ A 1 subgroups of exceptional algebraic groups’, Mem. Amer. Math. Soc. 674 (1999), viii+131 pp.Google Scholar
Liebeck, M. W., Saxl, J. and Testerman, D. M., ‘Simple subgroups of large rank in groups of Lie type’, Proc. Lond. Math. Soc. 72 (1996), 425–457.Google Scholar
Liebeck, M. W. and Seitz, G. M., ‘Subgroups generated by root elements in groups of Lie type’, Ann. Math. 139 (1994), 293–361.Google Scholar
Liebeck, M. W. and Seitz, G. M., ‘On the subgroup structure of exceptional groups of Lie type’, Trans. Amer. Math. Soc. 350 (1998), 3409–3482.Google Scholar
Liebeck, M. W. and Seitz, G. M., ‘The maximal subgroups of positive dimension in exceptional algebraic groups’, Mem. Amer. Math. Soc. 802 (2004), vi+227 pp.Google Scholar
Liebeck, M. W. and Testerman, D. M., ‘Irreducible subgroups of algebraic groups’, Q. J. Math. 55 (2004), 47–55.Google Scholar
Litterick, A. J., ‘Finite simple subgroups of exceptional algebraic groups’, PhD Thesis, Imperial College London, 2013.Google Scholar
Litterick, A. J., ‘On non-generic finite subgroups of exceptional algebraic groups’, Mem. Amer. Math. Soc. 1207 (2018), v+156 pp.Google Scholar
Malle, G., ‘The maximal subgroups of  2 F 4(q 2)’, J. Algebra 139 (1991), 52–69.Google Scholar
Malle, G. and Testerman, D., Linear Algebraic Groups and Finite Groups of Lie Type, Cambridge Advanced Studies in Mathematics, 133 (Cambridge University Press, Cambridge, 2011).Google Scholar
Moody, R. V. and Patera, J., ‘Characters of elements of finite order in Lie groups’, SIAM J. Algebr. Discrete Methods 5 (1984), 359–383.Google Scholar
Proud, R., Saxl, J. and Testerman, D. M., ‘Subgroups of type A 1 containing a fixed unipotent element in an algebraic group’, J. Algebra 231 (2000), 53–66.Google Scholar
Saxl, J. and Seitz, G. M., ‘Subgroups of algebraic groups containing regular unipotent elements’, J. Lond. Math. Soc. 55 (1997), 370–386.Google Scholar
Seitz, G. M., ‘Unipotent elements, tilting modules, and saturation’, Invent. Math. 141 (2000), 467–502.Google Scholar
Seitz, G. M. and Testerman, D. M., ‘Extending morphisms from finite to algebraic groups’, J. Algebra 131 (1990), 559–574.Google Scholar
Seitz, G. M. and Testerman, D. M., ‘Subgroups of type A 1 containing semiregular unipotent elements’, J. Algebra 196 (1997), 595–619.Google Scholar
Serre, J.-P., ‘Exemples de plongements des groupes PSL2(F p ) dans des groupes de Lie simples’, Invent. Math. 124 (1996), 525–562.Google Scholar
Steinberg, R., ‘Representations of algebraic groups’, Nagoya Math. J. 22 (1963), 33–56.Google Scholar
Steinberg, R., ‘Endomorphisms of linear algebraic groups’, Mem. Amer. Math. Soc. 80 (1968), 108 pp.Google Scholar
Testerman, D. M., ‘The construction of the maximal A 1 ’s in the exceptional algebraic groups’, Proc. Amer. Math. Soc. 116 (1992), 635–644.Google Scholar
Testerman, D. M., ‘ A 1 -type overgroups of elements of order p in semisimple algebraic groups and the associated finite groups’, J. Algebra 177 (1995), 34–76.Google Scholar
Testerman, D. M. and Zalesski, A., ‘Irreducibility in algebraic groups and regular unipotent elements’, Proc. Amer. Math. Soc. 141 (2013), 13–28.Google Scholar
Weisfeiler, B., ‘On one class of unipotent subgroups of semisimple algebraic groups’, Preprint, 2000, arXiv:0005149.Google Scholar