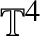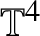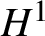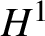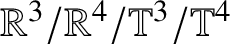1 Introduction
The cubic nonlinear Schrödinger equation (NLS) in four dimensions
 $$ \begin{align} i\partial _{t}u &= -\Delta u\pm \left\lvert u\right\rvert ^{2}u\text{ in } \mathbb{R}\times \Lambda, \\ u(0,x) &= u_{0}, \notag \end{align} $$
$$ \begin{align} i\partial _{t}u &= -\Delta u\pm \left\lvert u\right\rvert ^{2}u\text{ in } \mathbb{R}\times \Lambda, \\ u(0,x) &= u_{0}, \notag \end{align} $$where ![]() $\Lambda =\mathbb {R}^{4}$ or
$\Lambda =\mathbb {R}^{4}$ or ![]() $\mathbb {T}^{4}$, is called energy-critical, because it is invariant under the
$\mathbb {T}^{4}$, is called energy-critical, because it is invariant under the ![]() $\dot {H}^{1}$ scaling
$\dot {H}^{1}$ scaling
 $$ \begin{align*} u(t,x)\mapsto u_{\lambda }(t,x)=\frac{1}{\lambda }u\left(\frac{t}{\lambda ^{2}}, \frac{x}{\lambda }\right) \end{align*} $$
$$ \begin{align*} u(t,x)\mapsto u_{\lambda }(t,x)=\frac{1}{\lambda }u\left(\frac{t}{\lambda ^{2}}, \frac{x}{\lambda }\right) \end{align*} $$if ![]() $\Lambda =\mathbb {R}^{4}$. The large-datum global well-posedness of the defocusing case of equation (1.1) was first proved for
$\Lambda =\mathbb {R}^{4}$. The large-datum global well-posedness of the defocusing case of equation (1.1) was first proved for ![]() $\Lambda = \mathbb {R}^{4}$ in [Reference Ryckman and Vişan56], after the breakthrough on the defocusing
$\Lambda = \mathbb {R}^{4}$ in [Reference Ryckman and Vişan56], after the breakthrough on the defocusing ![]() $ \mathbb {R}^{3}$ quintic problem [Reference Bourgain3, Reference Colliander, Keel, Staffilani, Takaoka and Tao28, Reference Grillakis33]. The argument was standardised in [Reference Kenig and Merle42], in which the radial focusing
$ \mathbb {R}^{3}$ quintic problem [Reference Bourgain3, Reference Colliander, Keel, Staffilani, Takaoka and Tao28, Reference Grillakis33]. The argument was standardised in [Reference Kenig and Merle42], in which the radial focusing ![]() $\mathbb {R}^{3}$ quintic problem was addressed. After that, the global well-posedness of the energy-critical defocusing
$\mathbb {R}^{3}$ quintic problem was addressed. After that, the global well-posedness of the energy-critical defocusing ![]() $ \mathbb {T}^{3}$ quintic problem was creatively settled in [Reference Herr, Tataru and Tzvetkov36, Reference Ionescu and Pausader40], by partially invoking the
$ \mathbb {T}^{3}$ quintic problem was creatively settled in [Reference Herr, Tataru and Tzvetkov36, Reference Ionescu and Pausader40], by partially invoking the ![]() $\mathbb {R}^{3}$ result [Reference Colliander, Keel, Staffilani, Takaoka and Tao28, Reference Kenig and Merle42]. Such a problem for equation (1.1) when
$\mathbb {R}^{3}$ result [Reference Colliander, Keel, Staffilani, Takaoka and Tao28, Reference Kenig and Merle42]. Such a problem for equation (1.1) when ![]() $ \Lambda =\mathbb {T}^{4}$ was then subsequently proved in [Reference Herr, Tataru and Tzvetkov37, Reference Killip and Vişan43, Reference Yue61]. The goal of this paper is to establish
$ \Lambda =\mathbb {T}^{4}$ was then subsequently proved in [Reference Herr, Tataru and Tzvetkov37, Reference Killip and Vişan43, Reference Yue61]. The goal of this paper is to establish ![]() $H^{1}$ unconditional uniqueness for equation (1.1) on
$H^{1}$ unconditional uniqueness for equation (1.1) on ![]() $\mathbb {T}^{4}$.
$\mathbb {T}^{4}$.
Theorem 1.1. There is at most one  $C_{\left [0,T\right ]}^{0}H_{x}^{1}\cap \dot {C}_{\left [0,T\right ]}^{1}H_{x}^{-1}$ solutionFootnote 1 to equation (1.1) on
$C_{\left [0,T\right ]}^{0}H_{x}^{1}\cap \dot {C}_{\left [0,T\right ]}^{1}H_{x}^{-1}$ solutionFootnote 1 to equation (1.1) on ![]() $\mathbb {T}^{4}$.Footnote 2
$\mathbb {T}^{4}$.Footnote 2
Unconditional uniqueness is a fundamental concept raised by Kato [Reference Kato41].Footnote 3 These problems, even in the ![]() $H^{1}$-critical setting, are often overlooked, as solving them in
$H^{1}$-critical setting, are often overlooked, as solving them in ![]() $\mathbb {R}^{n}$ after proving the well-posedness is relatively simple.Footnote 4 For the NLS on
$\mathbb {R}^{n}$ after proving the well-posedness is relatively simple.Footnote 4 For the NLS on ![]() $\mathbb {T}^{n}$, such problems are delicate, as estimates on
$\mathbb {T}^{n}$, such problems are delicate, as estimates on ![]() $\mathbb {T}^{n}$, especially the
$\mathbb {T}^{n}$, especially the ![]() $ \mathbb {T}^{n}$ Strichartz estimates, are weaker than their
$ \mathbb {T}^{n}$ Strichartz estimates, are weaker than their ![]() $\mathbb {R}^{n}$ counterparts. For example, for the
$\mathbb {R}^{n}$ counterparts. For example, for the ![]() $\mathbb {R}^{n}$ case, one can easily use the existence of a better solution in Strichartz spaces to yield unconditional uniqueness. But such a technique does not work well in the
$\mathbb {R}^{n}$ case, one can easily use the existence of a better solution in Strichartz spaces to yield unconditional uniqueness. But such a technique does not work well in the ![]() $ \mathbb {T}^{n}$ case. In fact, Theorem 1.1 for the
$ \mathbb {T}^{n}$ case. In fact, Theorem 1.1 for the ![]() $ \mathbb {T}^{3}$ quintic case at
$ \mathbb {T}^{3}$ quintic case at ![]() $H^{1}$ regularity was not known until recently [Reference Chen and Holmer24].
$H^{1}$ regularity was not known until recently [Reference Chen and Holmer24].
To prove Theorem 1.1, we will use the cubic Gross–Pitaevskii (GP) hierarchy on ![]() $\mathbb {T}^{4}$, which is uncommon in the analysis of the NLS and is being explored [Reference Chen and Holmer24, Reference Herr and Sohinger35]. Let
$\mathbb {T}^{4}$, which is uncommon in the analysis of the NLS and is being explored [Reference Chen and Holmer24, Reference Herr and Sohinger35]. Let ![]() $\mathcal {L}_{k}^{1}$ denote the space of trace class operators on
$\mathcal {L}_{k}^{1}$ denote the space of trace class operators on ![]() $L^{2}\left (\mathbb {T}^{4k}\right )$. The cubic GP hierarchy on
$L^{2}\left (\mathbb {T}^{4k}\right )$. The cubic GP hierarchy on ![]() $ \mathbb {T}^{4}$ is a sequence
$ \mathbb {T}^{4}$ is a sequence  $\left \{ \gamma ^{(k)}(t)\right \} \in \oplus _{k\geq 1}C\left ( \left [ 0,T\right ] ,\mathcal {L}_{k}^{1}\right ) $ which satisfies the infinitely coupled hierarchy of equations
$\left \{ \gamma ^{(k)}(t)\right \} \in \oplus _{k\geq 1}C\left ( \left [ 0,T\right ] ,\mathcal {L}_{k}^{1}\right ) $ which satisfies the infinitely coupled hierarchy of equations
 $$ \begin{align} i\partial _{t}\gamma ^{(k)}=\sum_{j=1}^{k}\left[ -\Delta _{x_{j}},\gamma ^{(k)}\right] \pm b_{0}\sum_{j=1}^{k}{\mathop{\mathrm{Tr}}}_{k+1}\left[ \delta \left(x_{j}-x_{k+1}\right),\gamma ^{(k+1)}\right], \end{align} $$
$$ \begin{align} i\partial _{t}\gamma ^{(k)}=\sum_{j=1}^{k}\left[ -\Delta _{x_{j}},\gamma ^{(k)}\right] \pm b_{0}\sum_{j=1}^{k}{\mathop{\mathrm{Tr}}}_{k+1}\left[ \delta \left(x_{j}-x_{k+1}\right),\gamma ^{(k+1)}\right], \end{align} $$where ![]() $b_{0}>0$ is some coupling constant and
$b_{0}>0$ is some coupling constant and ![]() $\pm $ denotes defocusing/focusing. Given any solution u of equation (1.1), we generate a solution to equation (1.2) by letting
$\pm $ denotes defocusing/focusing. Given any solution u of equation (1.1), we generate a solution to equation (1.2) by letting
in operator form, or
 $$ \begin{align*} \gamma^{(k)}\left(t,\mathbf{x}_{k},\mathbf{x}_{k}^{\prime}\right)= \displaystyle\mathop{\prod}\limits_{j=1}^{k}u\left(t,x_{j}\right)\bar{u}\left(t,x_{j}^{\prime }\right), \end{align*} $$
$$ \begin{align*} \gamma^{(k)}\left(t,\mathbf{x}_{k},\mathbf{x}_{k}^{\prime}\right)= \displaystyle\mathop{\prod}\limits_{j=1}^{k}u\left(t,x_{j}\right)\bar{u}\left(t,x_{j}^{\prime }\right), \end{align*} $$in kernel form, if we write ![]() $\mathbf {x}_{k}=(x_{1},\dotsc ,x_{k})\in \mathbb {T} ^{4k}$.
$\mathbf {x}_{k}=(x_{1},\dotsc ,x_{k})\in \mathbb {T} ^{4k}$.
The hierarchy (1.2) arises in the derivation of the NLS as an ![]() $N\rightarrow \infty $ limit of quantum N-body dynamics. It was first derived in the work of Erdös, Schlein and Yau [Reference Erdős, Schlein and Yau29, Reference Erdős, Schlein and Yau30, Reference Erdős, Schlein and Yau31] for the
$N\rightarrow \infty $ limit of quantum N-body dynamics. It was first derived in the work of Erdös, Schlein and Yau [Reference Erdős, Schlein and Yau29, Reference Erdős, Schlein and Yau30, Reference Erdős, Schlein and Yau31] for the ![]() $\mathbb {R}^{3}$ defocusing cubic case around 2005.Footnote 5 They proved delicately that there is a unique solution to the
$\mathbb {R}^{3}$ defocusing cubic case around 2005.Footnote 5 They proved delicately that there is a unique solution to the ![]() $\mathbb {R} ^{3} $ cubic GP hierarchy in an
$\mathbb {R} ^{3} $ cubic GP hierarchy in an ![]() $H^{1}$-type space (unconditional uniqueness) in [Reference Erdős, Schlein and Yau29], with a sophisticated Feynman-graph analysis. This first series of groundbreaking papers motivated a large amount of work.
$H^{1}$-type space (unconditional uniqueness) in [Reference Erdős, Schlein and Yau29], with a sophisticated Feynman-graph analysis. This first series of groundbreaking papers motivated a large amount of work.
In 2007, Klainerman and Machedon [Reference Klainerman and Machedon47], inspired by [Reference Erdős, Schlein and Yau29, Reference Klainerman and Machedon46], proved the uniqueness of solutions regarding the ![]() $ \mathbb {R}^{3}$ cubic GP hierarchy in a Strichartz-type space (conditional uniqueness). They proved a collapsing-type estimate, which implies a multilinear estimate when applied to factorised solutions like equation (1.3), to estimate the inhomogeneous term and provided a different combinatorial argument, now called the Klainerman–Machedon (KM) board game, to combine the inhomogeneous terms, effectively reducing their numbers. At that time, it was unknown how to prove that the limits coming from the N-body dynamics are in Strichartz-type spaces, even though the solutions to equation (1.2) generated by the
$ \mathbb {R}^{3}$ cubic GP hierarchy in a Strichartz-type space (conditional uniqueness). They proved a collapsing-type estimate, which implies a multilinear estimate when applied to factorised solutions like equation (1.3), to estimate the inhomogeneous term and provided a different combinatorial argument, now called the Klainerman–Machedon (KM) board game, to combine the inhomogeneous terms, effectively reducing their numbers. At that time, it was unknown how to prove that the limits coming from the N-body dynamics are in Strichartz-type spaces, even though the solutions to equation (1.2) generated by the ![]() $\mathbb {R}^{3}$ cubic NLS naturally lie in both the
$\mathbb {R}^{3}$ cubic NLS naturally lie in both the ![]() $H^{1}$-type space and the Strichartz-type space. Nonetheless, [Reference Klainerman and Machedon47] has made the analysis of equation (1.2) approachable to partial-differential-equation analysts, and the KM board game has been used in every work involving the hierarchy (1.2).Footnote 6 After Kirkpatrick, Schlein and Staffilani [Reference Kirkpatrick, Schlein and Staffilani44] derived equation (1.2) in 2008 and found that the Klainerman–Machedon Strichartz-type bound can be obtained via a simple trace theorem for the defocusing case in
$H^{1}$-type space and the Strichartz-type space. Nonetheless, [Reference Klainerman and Machedon47] has made the analysis of equation (1.2) approachable to partial-differential-equation analysts, and the KM board game has been used in every work involving the hierarchy (1.2).Footnote 6 After Kirkpatrick, Schlein and Staffilani [Reference Kirkpatrick, Schlein and Staffilani44] derived equation (1.2) in 2008 and found that the Klainerman–Machedon Strichartz-type bound can be obtained via a simple trace theorem for the defocusing case in ![]() $\mathbb {R}^{2}$ and
$\mathbb {R}^{2}$ and ![]() $\mathbb {T}^{2}$, many works [Reference Chen and Pavlović8, Reference Chen14, Reference Chen16, Reference Chen and Holmer18, Reference Chen and Holmer20, Reference Chen and Holmer22, Reference Chen and Holmer23, Reference Xie60, Reference Sohinger58] then followed such a scheme for the uniqueness of GP hierarchies. However, the question of how to check the Klainerman–Machedon Strichartz-type bound in the 3D cubic case remained fully open at that time.
$\mathbb {T}^{2}$, many works [Reference Chen and Pavlović8, Reference Chen14, Reference Chen16, Reference Chen and Holmer18, Reference Chen and Holmer20, Reference Chen and Holmer22, Reference Chen and Holmer23, Reference Xie60, Reference Sohinger58] then followed such a scheme for the uniqueness of GP hierarchies. However, the question of how to check the Klainerman–Machedon Strichartz-type bound in the 3D cubic case remained fully open at that time.
T. Chen and Pavlović laid the foundation for the 3D quintic defocusing energy-critical case by studying the 1D and 2D defocusing quintic cases in [Reference Chen and Pavlović8], in which they proved that the 2D quintic case, a case usually considered equivalent to the 3D cubic case, does satisfy the Klainerman–Machedon Strichartz-type bound – although proving it for the 3D cubic case was still open.
T. Chen and Pavlović also initiated the study of the well-posedness theory of equation (1.2) with general initial datum as an independent subject away from the quantum N-body dynamics in [Reference Chen and Pavlović7, Reference Chen and Pavlović9, Reference Chen and Pavlović10] (see also [Reference Chen, Pavlović and Tzirakis12, Reference Chen and Taliaferro13, Reference Mendelson, Nahmod, Pavlović and Staffilani55, Reference Mendelson, Nahmod, Pavlović, Rosenzweig and Staffilani53, Reference Mendelson, Nahmod, Pavlović, Rosenzweig and Staffilani54, Reference Sohinger58, Reference Sohinger and Staffilani59]). On the one hand, generalising the problem could help to attack the Klainerman–Machedon Strichartz-type bound problem. On the other hand, it leads one to consider whether the hierarchy (1.2), the general equation, could hold more in store than its special solution, the NLS (equation (1.1)).Footnote 7 Then in 2011, T. Chen and Pavlović proved that the 3D cubic Klainerman–Machedon Strichartz-type bound does hold for the defocusing ![]() $\beta <1/4$ case [Reference Chen and Pavlović11]. The result was quickly improved to
$\beta <1/4$ case [Reference Chen and Pavlović11]. The result was quickly improved to ![]() $\beta \leq 2/7$ by X. Chen [Reference Chen17] and to the almost-optimal case,
$\beta \leq 2/7$ by X. Chen [Reference Chen17] and to the almost-optimal case, ![]() $\beta <1,$ by X. Chen and Holmer [Reference Chen and Holmer19, Reference Chen and Holmer21], by lifting the
$\beta <1,$ by X. Chen and Holmer [Reference Chen and Holmer19, Reference Chen and Holmer21], by lifting the ![]() $X_{1,b}$ space techniques from NLS theory into the field.
$X_{1,b}$ space techniques from NLS theory into the field.
Around the same time, Gressman, Sohinger and Staffilani [Reference Gressman, Sohinger and Staffilani32] studied the uniqueness of equation (1.2) in the ![]() $\mathbb {T} ^{3}$ setting and found that the sharp collapsing estimate on
$\mathbb {T} ^{3}$ setting and found that the sharp collapsing estimate on ![]() $\mathbb {T} ^{3} $ needs
$\mathbb {T} ^{3} $ needs ![]() $\varepsilon $ more derivatives than the
$\varepsilon $ more derivatives than the ![]() $\mathbb {R}^{3}$ case, in which one derivative is needed. Herr and Sohinger later generalised this fact to all dimensions [Reference Herr and Sohinger34] – that is, collapsing estimates on
$\mathbb {R}^{3}$ case, in which one derivative is needed. Herr and Sohinger later generalised this fact to all dimensions [Reference Herr and Sohinger34] – that is, collapsing estimates on ![]() $ \mathbb {T}^{n}$ always need
$ \mathbb {T}^{n}$ always need ![]() $\varepsilon $ more derivatives than the
$\varepsilon $ more derivatives than the ![]() $ \mathbb {R}^{n}$ case proved in [Reference Chen16].Footnote 8
$ \mathbb {R}^{n}$ case proved in [Reference Chen16].Footnote 8
In 2013, T. Chen, Hainzl, Pavlović and Seiringer introduced the quantum de Finetti theorem, from [Reference Lewin, Nam and Rougerie51], to the derivation of the time-dependent power-type NLS and provided, in [Reference Chen, Hainzl, Pavlović and Seiringer6], a simplified proof of the ![]() $ \mathbb {R}^{3}$ unconditional uniqueness theorem regarding equation (1.2) from [Reference Erdős, Schlein and Yau29]. The application of the quantum de Finetti theorem allows one to replace the collapsing estimates by the multilinear estimates. The scheme in [Reference Chen, Hainzl, Pavlović and Seiringer6], which consists of the KM board game, the quantum de Finetti theorem and the multilinear estimates, is robust. Sohinger used this scheme in [Reference Sohinger57] to address the aforementioned
$ \mathbb {R}^{3}$ unconditional uniqueness theorem regarding equation (1.2) from [Reference Erdős, Schlein and Yau29]. The application of the quantum de Finetti theorem allows one to replace the collapsing estimates by the multilinear estimates. The scheme in [Reference Chen, Hainzl, Pavlović and Seiringer6], which consists of the KM board game, the quantum de Finetti theorem and the multilinear estimates, is robust. Sohinger used this scheme in [Reference Sohinger57] to address the aforementioned ![]() $\varepsilon $-loss problem for the defocusing
$\varepsilon $-loss problem for the defocusing ![]() $ \mathbb {T}^{3}$ cubic case. Hong, Taliaferro and Xie used this scheme in [Reference Hong, Taliaferro and Xie38] to obtain unconditional uniqueness theorems for equation (1.2) in
$ \mathbb {T}^{3}$ cubic case. Hong, Taliaferro and Xie used this scheme in [Reference Hong, Taliaferro and Xie38] to obtain unconditional uniqueness theorems for equation (1.2) in ![]() $\mathbb {R}^{n}$,
$\mathbb {R}^{n}$, ![]() $n=1,2,3$, with regularities matching the NLS analysis, and in [Reference Hong, Taliaferro and Xie39] for
$n=1,2,3$, with regularities matching the NLS analysis, and in [Reference Hong, Taliaferro and Xie39] for ![]() $H^{1}$ small-solution uniqueness in the
$H^{1}$ small-solution uniqueness in the ![]() $\mathbb {R}^{3}$ quintic case (see also [Reference Chen and Holmer22, Reference Chen and Smith27]).
$\mathbb {R}^{3}$ quintic case (see also [Reference Chen and Holmer22, Reference Chen and Smith27]).
Analysis of GP hierarchy did not yield new NLS results with regularity lower than that of NLS analysis until [Reference Herr and Sohinger35, Reference Chen and Holmer24].Footnote 9, Footnote 10 In [Reference Herr and Sohinger35], using the scheme in [Reference Chen, Hainzl, Pavlović and Seiringer6], Herr and Sohinger generalised the usual Sobolev multilinear estimates to Besov spaces and obtained new unconditional-uniqueness results regarding equation (1.2) and hence the NLS (equation (1.1)) on ![]() $\mathbb {T}^{n}$. The result has pushed the regularity requirement for the uniqueness of equation (1.1) lower than the number coming from NLS analysis. Moreover, it covers the whole subcritical region for
$\mathbb {T}^{n}$. The result has pushed the regularity requirement for the uniqueness of equation (1.1) lower than the number coming from NLS analysis. Moreover, it covers the whole subcritical region for ![]() $n\geq 4$, which includes Theorem 1.1 with
$n\geq 4$, which includes Theorem 1.1 with ![]() $H^{1+\varepsilon }$ regularity.
$H^{1+\varepsilon }$ regularity.
In [Reference Chen and Holmer24], by discovering the new hierarchical uniform frequency localisation (HUFL) property for the GP hierarchy – which reduces to a new statement even for the NLS – X.C. and Holmer established a new ![]() $H^{1}$-type uniqueness theorem for the
$H^{1}$-type uniqueness theorem for the ![]() $\mathbb {T}^{3}$ quintic energy-critical GP hierarchy.Footnote 11 The new uniqueness theorem, though neither conditional nor unconditional for the GP hierarchy, implies the
$\mathbb {T}^{3}$ quintic energy-critical GP hierarchy.Footnote 11 The new uniqueness theorem, though neither conditional nor unconditional for the GP hierarchy, implies the ![]() $H^{1}$ unconditional-uniqueness result for the
$H^{1}$ unconditional-uniqueness result for the ![]() $\mathbb {T}^{3}$ quintic energy-critical NLS. It is then natural to consider the
$\mathbb {T}^{3}$ quintic energy-critical NLS. It is then natural to consider the ![]() $\mathbb {T}^{4}$ cubic energy-critical case in this paper. However, the key Sobolev multilinear estimates in [Reference Chen and Holmer24] are very difficult to prove, or may not be true, for the
$\mathbb {T}^{4}$ cubic energy-critical case in this paper. However, the key Sobolev multilinear estimates in [Reference Chen and Holmer24] are very difficult to prove, or may not be true, for the ![]() $\mathbb {T }^{4}$ cubic case here, and it turns out, surprisingly, that
$\mathbb {T }^{4}$ cubic case here, and it turns out, surprisingly, that ![]() $\mathbb {T}^{4}$ is unique or special compared to
$\mathbb {T}^{4}$ is unique or special compared to ![]() $\mathbb {R}^{3}/\mathbb {R} ^{4}/\mathbb {T}^{3}$.
$\mathbb {R}^{3}/\mathbb {R} ^{4}/\mathbb {T}^{3}$.
1.1 Outline of the proof of Theorem 1.1
We will prove Theorem 1.1 as a corollary of Theorem 3.1, a GP-hierarchy uniqueness theorem stated in Section 3. As Theorem 3.1 requires the HUFL condition, we prove that any  $C_{\left [0,T\right ]}^{0}H_{x}^{1}\cap \dot {C} _{\left [0,T\right ]}^{1}H_{x}^{-1}$ solution to equation (1.1) on
$C_{\left [0,T\right ]}^{0}H_{x}^{1}\cap \dot {C} _{\left [0,T\right ]}^{1}H_{x}^{-1}$ solution to equation (1.1) on ![]() $\mathbb {T} ^{4}$ satisfies uniform-in-time frequency localisation with Lemma 3.3 – that is, solutions to equation (1.2) generated from equation (1.1) via equation (1.3) satisfy the HUFL condition. Thus we will have established Theorem 1.1 once we have proved Theorem 3.1.
$\mathbb {T} ^{4}$ satisfies uniform-in-time frequency localisation with Lemma 3.3 – that is, solutions to equation (1.2) generated from equation (1.1) via equation (1.3) satisfy the HUFL condition. Thus we will have established Theorem 1.1 once we have proved Theorem 3.1.
As Theorem 3.1 is an energy-critical case, due to the known similarities between the ![]() $\mathbb {R}^{3}$ quintic and
$\mathbb {R}^{3}$ quintic and ![]() $\mathbb {R} ^{4}$ cubic cases, one would guess that the proof of the
$\mathbb {R} ^{4}$ cubic cases, one would guess that the proof of the ![]() $\mathbb {T}^{3}$ quintic case goes through for the
$\mathbb {T}^{3}$ quintic case goes through for the ![]() $\mathbb {T}^{4}$ cubic case as well. It does not. As mentioned before, the key Sobolev multilinear estimates in [Reference Chen and Holmer24] are very difficult to prove, or may not be true here (interested readers can see Appendix A for a discussion). In this
$\mathbb {T}^{4}$ cubic case as well. It does not. As mentioned before, the key Sobolev multilinear estimates in [Reference Chen and Holmer24] are very difficult to prove, or may not be true here (interested readers can see Appendix A for a discussion). In this ![]() $H^{1}$-critical setting, the next replacement in line would be the weaker U-V multilinear estimates. The U-V trilinear estimates do hold on
$H^{1}$-critical setting, the next replacement in line would be the weaker U-V multilinear estimates. The U-V trilinear estimates do hold on ![]() $\mathbb {T}^{4}$. This is where we start.
$\mathbb {T}^{4}$. This is where we start.
In Section 2, we first give a short introduction to the U -V space, referring the standard literature [Reference Herr, Tataru and Tzvetkov36, Reference Ionescu and Pausader40, Reference Killip and Vişan43, Reference Koch, Tataru and Vişan50], then prove the U-V version of the ![]() $\mathbb {T}^{4}$ trilinear estimates (Lemmas 2.1 and 2.2). The proof of the U-V trilinear estimates is less technical and simpler than the proof of the Sobolev multilinear estimates in [Reference Chen and Holmer24], as they are indeed weaker.Footnote 11 (As we will conclude the same unconditonal uniquness with these much weaker estimates, we can infer that our method here is indeed much stronger now.) But these U-V trilinear estimates still highly rely on the scale-invariant Stichartz estimates and the
$\mathbb {T}^{4}$ trilinear estimates (Lemmas 2.1 and 2.2). The proof of the U-V trilinear estimates is less technical and simpler than the proof of the Sobolev multilinear estimates in [Reference Chen and Holmer24], as they are indeed weaker.Footnote 11 (As we will conclude the same unconditonal uniquness with these much weaker estimates, we can infer that our method here is indeed much stronger now.) But these U-V trilinear estimates still highly rely on the scale-invariant Stichartz estimates and the ![]() $ l^{2}$-decoupling theorem in [Reference Bourgain and Demeter4, Reference Killip and Vişan43].
$ l^{2}$-decoupling theorem in [Reference Bourgain and Demeter4, Reference Killip and Vişan43].
Though the U-V trilinear estimates hold in ![]() $\mathbb {T}^{4}$, there is no method available to use them to prove uniqueness for GP hierarchies. This is why estimates in the hierarchy framework have always been about
$\mathbb {T}^{4}$, there is no method available to use them to prove uniqueness for GP hierarchies. This is why estimates in the hierarchy framework have always been about ![]() $ L_{t}^{p}H_{x}^{s}$. Even in [Reference Chen and Holmer19, Reference Chen and Holmer21], in which the
$ L_{t}^{p}H_{x}^{s}$. Even in [Reference Chen and Holmer19, Reference Chen and Holmer21], in which the ![]() $X_{s,b}$ techniques were used, they were used only once in the very end of the iteration, instead of every step of the iteration to yield smallness. Conceptually speaking, while it is easy to bound the
$X_{s,b}$ techniques were used, they were used only once in the very end of the iteration, instead of every step of the iteration to yield smallness. Conceptually speaking, while it is easy to bound the ![]() $L_{t}^{\infty }H_{x}^{s}$ norm by the U-V norms, one has to pay half a derivative in time to come back. On the one hand, we are proving an unconditional-uniqueness theorem; we have to come back to the Sobolev spaces in the end of the proof. On the other hand, we are proving a critical result; we do not have an extra half derivative in time to spare. To fix this problem, we adjust how the multilinear estimates apply to the Duhamel–Born expansion of
$L_{t}^{\infty }H_{x}^{s}$ norm by the U-V norms, one has to pay half a derivative in time to come back. On the one hand, we are proving an unconditional-uniqueness theorem; we have to come back to the Sobolev spaces in the end of the proof. On the other hand, we are proving a critical result; we do not have an extra half derivative in time to spare. To fix this problem, we adjust how the multilinear estimates apply to the Duhamel–Born expansion of ![]() $ \gamma ^{(k)}$ after the application of the KM board game, so that the U- V trilinear estimates land only on a ‘Duhamel-like’ integral.
$ \gamma ^{(k)}$ after the application of the KM board game, so that the U- V trilinear estimates land only on a ‘Duhamel-like’ integral.
The main problem now surfaces. The time-integration domain ![]() $D_{m}$ of the aforementioned ‘Duhamel-like’ integrals, coming from the KM board game, is a union of a very large number of high-dimensional simplexes under the action of a proper subset of the permutation group
$D_{m}$ of the aforementioned ‘Duhamel-like’ integrals, coming from the KM board game, is a union of a very large number of high-dimensional simplexes under the action of a proper subset of the permutation group ![]() $S_{k}$ specific to every integrand. To at least have a chance to use space-time norms like
$S_{k}$ specific to every integrand. To at least have a chance to use space-time norms like ![]() $X_{s,b}$ and U-V – which are very sensitive to the irregularity of the time domain, as they involve taking time derivatives [Reference Koch, Tataru and Vişan50, p. 68] – one would have to know what
$X_{s,b}$ and U-V – which are very sensitive to the irregularity of the time domain, as they involve taking time derivatives [Reference Koch, Tataru and Vişan50, p. 68] – one would have to know what ![]() $D_{m}$ is. It turns out that
$D_{m}$ is. It turns out that ![]() $ D_{m}$ coming from the original KM board game is not fully compatible with the U- V trilinear estimates. To this end, we establish an extended KM board game which is compatible in Section 4.
$ D_{m}$ coming from the original KM board game is not fully compatible with the U- V trilinear estimates. To this end, we establish an extended KM board game which is compatible in Section 4.
In Section 4.1, as a warm-up, we first develop – via a detailed treeFootnote 12 diagram representation – a more elaborated proof of the original KM board game, which yields, for the first time, an algorithm to directly compute ![]() $D_{m}$ and domains like it. Graphically speaking, under our tree representation the original KM board game combines all the trees with the same skeletons into an ‘upper-echelon’ class which can be represented by an upper-echelon tree.Footnote 13 The time integration domain
$D_{m}$ and domains like it. Graphically speaking, under our tree representation the original KM board game combines all the trees with the same skeletons into an ‘upper-echelon’ class which can be represented by an upper-echelon tree.Footnote 13 The time integration domain ![]() $D_{m}$ for each upper-echelon class can be directly read off from the upper-echelon tree representing the class.
$D_{m}$ for each upper-echelon class can be directly read off from the upper-echelon tree representing the class.
We then introduce, in Sections 4.2–4.5, the wild moves, which allow us to uncover more integrals in the Duhamel–Born expansion with the same integrands after permutation and combine them into ‘reference’ classes. Graphically speaking, it allows the combination of trees sharing the same reference enumeration but with different structures. However, the wild moves are not compatible with the upper-echelon classes coming from the original KM board game. We have to restart from the very beginning at the level of the ![]() $2^{k}k!$ summands.
$2^{k}k!$ summands.
Before applying the wild moves, in Sections 4.2 and 4.3 we turn the ![]() $2^{k}k!$ summands in the initial Duhamel–Born expansion into their tamed forms, which would be invariant under the wild moves, via reworked signed Klainerman-Machedon acceptable moves. We then sort the tamed forms into tamed classes via the wild moves in Section 4.4. Finally, in Section 4.5 we use the algorithm developed in Section 4.1 to calculate the time integration domain for each tamed class. In fact, we prove that given a tamed class, there is a reference form representing the tamed class, and the time integration domain for the whole tamed class can be directly read out from the reference form.
$2^{k}k!$ summands in the initial Duhamel–Born expansion into their tamed forms, which would be invariant under the wild moves, via reworked signed Klainerman-Machedon acceptable moves. We then sort the tamed forms into tamed classes via the wild moves in Section 4.4. Finally, in Section 4.5 we use the algorithm developed in Section 4.1 to calculate the time integration domain for each tamed class. In fact, we prove that given a tamed class, there is a reference form representing the tamed class, and the time integration domain for the whole tamed class can be directly read out from the reference form.
Using this extended KM board game coming from scratch, we found that the time integration domain specific for each integrand can always be ‘miraculously’ written as one single iterated integral in the integration order ready to apply the quantum de Finetti theorem, despite the fact that it was previously thought unrepresentable or even disconnected, and was expanded into ![]() $[0,T]^{k}$ in all previous work since there were no other options to use it. Moreover, once these integration limits are put together with the integrand, each distinct tamed class becomes an exact fit to apply the U-V trilinear estimates proved in Section 2. This combinatorial analysis, which is compatible with space-time norms and the method to explicitly compute the time integration domain in the general recombined Duhamel–Born expansion (which includes more than the GP hierarchies), is the main technical achievement of this paper.
$[0,T]^{k}$ in all previous work since there were no other options to use it. Moreover, once these integration limits are put together with the integrand, each distinct tamed class becomes an exact fit to apply the U-V trilinear estimates proved in Section 2. This combinatorial analysis, which is compatible with space-time norms and the method to explicitly compute the time integration domain in the general recombined Duhamel–Born expansion (which includes more than the GP hierarchies), is the main technical achievement of this paper.
With everything ready by the extended KM board game in Section 4, the quantum de Finetti theorem from [Reference Chen, Hainzl, Pavlović and Seiringer6], the U-V space techniques from [Reference Koch, Tataru and Vişan50], the trilinear estimates proved using the scale-invariant Stichartz estimates and ![]() $ l^{2}$-decoupling theorem in [Reference Bourgain and Demeter4, Reference Killip and Vişan43] and the HUFL properties from [Reference Chen and Holmer24], all work together seamlessly in Section 5 to establish Theorem 3.1 and provide a unified proof of large-solution uniqueness for the
$ l^{2}$-decoupling theorem in [Reference Bourgain and Demeter4, Reference Killip and Vişan43] and the HUFL properties from [Reference Chen and Holmer24], all work together seamlessly in Section 5 to establish Theorem 3.1 and provide a unified proof of large-solution uniqueness for the ![]() $\mathbb {R}^{3}/$
$\mathbb {R}^{3}/$![]() $\mathbb {T}^{3}$ quintic and the
$\mathbb {T}^{3}$ quintic and the ![]() $\mathbb {R}^{4}/$
$\mathbb {R}^{4}/$![]() $\mathbb {T}^{4}$ cubic energy-critical GP hierarchies, and hence the corresponding NLS. The discovery of such an unexpected close and effective collaboration of these previously independent deep theorems is the main novelty of this paper.
$\mathbb {T}^{4}$ cubic energy-critical GP hierarchies, and hence the corresponding NLS. The discovery of such an unexpected close and effective collaboration of these previously independent deep theorems is the main novelty of this paper.
We remark that putting together Theorem 3.1 and the compactness and convergence argument of [Reference Chen and Holmer24] completes a derivation of equation (1.1) from quantum many-body dynamics. We choose not to do so here, as it is not the main point of this paper. We now expect to be able to bring the full strength of dispersive estimate technology to bear on various type of hierarchies of equations and related problems, and this is our first example of it. (An immediate next step has been taken [Reference Chen, Shen and Zhang26].)
2 Trilinear estimates in the U-V spaces
As mentioned in the introduction, our proof of Theorem 1.1 requires the U-V space, whereas the ![]() $\mathbb {R}^{3}/$
$\mathbb {R}^{3}/$![]() $\mathbb {R}^{4}/\mathbb {T}^{3}$ cases do not. Here
$\mathbb {R}^{4}/\mathbb {T}^{3}$ cases do not. Here ![]() $V^{p}$ is the space of functions of bounded p-variation of Wiener, and the atomic
$V^{p}$ is the space of functions of bounded p-variation of Wiener, and the atomic ![]() $U^{p}$ space, introduced by Koch and Tataru [Reference Koch and Tataru48, Reference Koch and Tataru49], is a close relative of
$U^{p}$ space, introduced by Koch and Tataru [Reference Koch and Tataru48, Reference Koch and Tataru49], is a close relative of ![]() $V^{p}$. Referring to the now-standard text [Reference Koch, Tataru and Vişan50] for the definition of
$V^{p}$. Referring to the now-standard text [Reference Koch, Tataru and Vişan50] for the definition of ![]() $U_{t}^{p}$ and
$U_{t}^{p}$ and ![]() $V_{t}^{p}$, we define
$V_{t}^{p}$, we define
 $$ \begin{align*} \lVert u\rVert _{X^{s}\left( \left[ 0,T\right) \right) }=\left( \sum_{\xi \in \mathbb{Z}^{4}}\left\langle \xi \right\rangle ^{2s}\left\lVert \widehat{ e^{-it\Delta }u(t,\cdot )}\left( \xi \right) \right\rVert _{U_{t}^{2}}^{2}\right) ^{ \frac{1}{2}} \end{align*} $$
$$ \begin{align*} \lVert u\rVert _{X^{s}\left( \left[ 0,T\right) \right) }=\left( \sum_{\xi \in \mathbb{Z}^{4}}\left\langle \xi \right\rangle ^{2s}\left\lVert \widehat{ e^{-it\Delta }u(t,\cdot )}\left( \xi \right) \right\rVert _{U_{t}^{2}}^{2}\right) ^{ \frac{1}{2}} \end{align*} $$and
 $$ \begin{align*} \lVert u\rVert _{Y^{s}\left( \left[ 0,T\right) \right) }=\left( \sum_{\xi \in \mathbb{Z}^{4}}\left\langle \xi \right\rangle ^{2s}\left\lVert \widehat{ e^{-it\Delta }u(t,\cdot )}\left( \xi \right) \right\rVert _{V_{t}^{2}}^{2}\right) ^{ \frac{1}{2}} \end{align*} $$
$$ \begin{align*} \lVert u\rVert _{Y^{s}\left( \left[ 0,T\right) \right) }=\left( \sum_{\xi \in \mathbb{Z}^{4}}\left\langle \xi \right\rangle ^{2s}\left\lVert \widehat{ e^{-it\Delta }u(t,\cdot )}\left( \xi \right) \right\rVert _{V_{t}^{2}}^{2}\right) ^{ \frac{1}{2}} \end{align*} $$as in [Reference Herr, Tataru and Tzvetkov36, Reference Herr, Tataru and Tzvetkov37, Reference Ionescu and Pausader40, Reference Killip and Vişan43]. ![]() $X^{s}$ and
$X^{s}$ and ![]() $Y^{s}$ are endpoint replacements for the Fourier restriction spaces
$Y^{s}$ are endpoint replacements for the Fourier restriction spaces ![]() $X^{s,b}$ when
$X^{s,b}$ when  $b=\frac {1}{2}$ and
$b=\frac {1}{2}$ and ![]() $- \frac {1}{2}$. In particular, we have the usual properties
$- \frac {1}{2}$. In particular, we have the usual properties
 $$ \begin{align} \left\lVert e^{it\Delta }f\right\rVert _{Y^{s}}\lesssim \left\lVert e^{it\Delta }f\right\rVert _{X^{s}}\lesssim \lVert f\rVert _{H^{s}}, \end{align} $$
$$ \begin{align} \left\lVert e^{it\Delta }f\right\rVert _{Y^{s}}\lesssim \left\lVert e^{it\Delta }f\right\rVert _{X^{s}}\lesssim \lVert f\rVert _{H^{s}}, \end{align} $$ $$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }f(s,\cdot )ds\right\rVert _{X^{s}\left( \left[ 0,T\right) \right) }\leq \sup_{v\in Y^{-s}\left( \left[ 0,T\right) \right) :\lVert v\rVert _{Y^{-s}}=1}\int_{0}^{T}\int_{\mathbb{T}^{4}}f(t,x)\overline{v(t,x)}dtdx \quad \forall a\in \left[ 0,T\right), \end{align} $$
$$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }f(s,\cdot )ds\right\rVert _{X^{s}\left( \left[ 0,T\right) \right) }\leq \sup_{v\in Y^{-s}\left( \left[ 0,T\right) \right) :\lVert v\rVert _{Y^{-s}}=1}\int_{0}^{T}\int_{\mathbb{T}^{4}}f(t,x)\overline{v(t,x)}dtdx \quad \forall a\in \left[ 0,T\right), \end{align} $$which were proved in [Reference Koch, Tataru and Vişan50, p. 46] and in [Reference Herr, Tataru and Tzvetkov36, Propositions 2.8–2.11]. With these definitions of ![]() $X^{s}$ and
$X^{s}$ and ![]() $Y^{s}$, we have the following trilinear estimates:
$Y^{s}$, we have the following trilinear estimates:
Lemma 2.1. On ![]() $\mathbb {T}^{4}$, we have the high frequency estimate
$\mathbb {T}^{4}$, we have the high frequency estimate
 $$ \begin{align} \iint_{x,t}u_{1}(t,x)u_{2}(t,x)u_{3}(t,x)g(t,x)dxdt\lesssim \lVert u_{1}\rVert _{Y^{-1}}\lVert u_{2}\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}\lVert g\rVert _{Y^{1}} \end{align} $$
$$ \begin{align} \iint_{x,t}u_{1}(t,x)u_{2}(t,x)u_{3}(t,x)g(t,x)dxdt\lesssim \lVert u_{1}\rVert _{Y^{-1}}\lVert u_{2}\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}\lVert g\rVert _{Y^{1}} \end{align} $$and the low frequency estimate
 $$ \begin{align} \iint_{x,t}u_{1}(t,x)\left( P_{\leq M_{0}}u_{2}\right) (t,x)u_{3}(t,x)g(t,x)dxdt\lesssim T^{\frac{1}{7}}M_{0}^{ \frac{3}{5}}\lVert u_{1}\rVert _{Y^{-1}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}\lVert g\rVert _{Y^{1}} \end{align} $$
$$ \begin{align} \iint_{x,t}u_{1}(t,x)\left( P_{\leq M_{0}}u_{2}\right) (t,x)u_{3}(t,x)g(t,x)dxdt\lesssim T^{\frac{1}{7}}M_{0}^{ \frac{3}{5}}\lVert u_{1}\rVert _{Y^{-1}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}\lVert g\rVert _{Y^{1}} \end{align} $$for all ![]() $T\leq 1$ and all frequencies
$T\leq 1$ and all frequencies ![]() $M_{0}\geq 1$, or
$M_{0}\geq 1$, or
 $$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }\left( u_{1}u_{2}u_{3}\right) ds\right\rVert _{X^{-1}\left( \left[ 0,T\right) \right) }\lesssim \lVert u_{1}\rVert _{Y^{-1}}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{Y^{1}}+\left\lVert P_{>M_{0}}u_{2}\right\rVert _{Y^{1}}\right) \lVert u_{3}\rVert _{Y^{1}} \end{align} $$
$$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }\left( u_{1}u_{2}u_{3}\right) ds\right\rVert _{X^{-1}\left( \left[ 0,T\right) \right) }\lesssim \lVert u_{1}\rVert _{Y^{-1}}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{Y^{1}}+\left\lVert P_{>M_{0}}u_{2}\right\rVert _{Y^{1}}\right) \lVert u_{3}\rVert _{Y^{1}} \end{align} $$and
 $$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }\left( u_{1}u_{2}u_{3}\right) ds\right\rVert _{X^{-1}\left( \left[ 0,T\right) \right) }\lesssim \lVert u_{1}\rVert _{Y^{-1}}\lVert u_{2}\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}. \end{align} $$
$$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }\left( u_{1}u_{2}u_{3}\right) ds\right\rVert _{X^{-1}\left( \left[ 0,T\right) \right) }\lesssim \lVert u_{1}\rVert _{Y^{-1}}\lVert u_{2}\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}. \end{align} $$Moreover, if ![]() $u_{j}=e^{it\Delta }f_{j}$ for some j, then the
$u_{j}=e^{it\Delta }f_{j}$ for some j, then the ![]() $Y^{s}$ norm of
$Y^{s}$ norm of ![]() $u_{j}$ in formula (2.6) or (2.7) can be replaced by the
$u_{j}$ in formula (2.6) or (2.7) can be replaced by the ![]() $H^{s}$ norm of
$H^{s}$ norm of ![]() $f_{j}$.
$f_{j}$.
Similarly, we have ![]() $X^{1}$ estimates:
$X^{1}$ estimates:
Lemma 2.2. On ![]() $\mathbb {T}^{4}$, we have the high frequency estimate
$\mathbb {T}^{4}$, we have the high frequency estimate
 $$ \begin{align} \iint_{x,t}u_{1}(t,x)u_{2}(t,x)u_{3}(t,x)g(t,x)dxdt\lesssim \lVert u_{1}\rVert _{Y^{1}}\lVert u_{2}\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}\lVert g\rVert _{Y^{-1}} \end{align} $$
$$ \begin{align} \iint_{x,t}u_{1}(t,x)u_{2}(t,x)u_{3}(t,x)g(t,x)dxdt\lesssim \lVert u_{1}\rVert _{Y^{1}}\lVert u_{2}\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}\lVert g\rVert _{Y^{-1}} \end{align} $$and the low frequency estimate
 $$ \begin{align} \iint_{x,t}u_{1}(t,x)\left( P_{\leq M_{0}}u_{2}\right) (t,x)u_{3}(t,x)g(t,x)dxdt\lesssim T^{\frac{1}{7}}M_{0}^{ \frac{3}{5}}\lVert u_{1}\rVert _{Y^{1}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}\lVert g\rVert _{Y^{-1}}. \end{align} $$
$$ \begin{align} \iint_{x,t}u_{1}(t,x)\left( P_{\leq M_{0}}u_{2}\right) (t,x)u_{3}(t,x)g(t,x)dxdt\lesssim T^{\frac{1}{7}}M_{0}^{ \frac{3}{5}}\lVert u_{1}\rVert _{Y^{1}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}\lVert g\rVert _{Y^{-1}}. \end{align} $$In other words,
 $$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }\left( u_{1}u_{2}u_{3}\right) ds\right\rVert _{X^{1}\left( \left[ 0,T\right) \right) }\lesssim \lVert u_{1}\rVert _{Y^{1}}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{Y^{1}}+\left\lVert P_{>M_{0}}u_{2}\right\rVert _{Y^{1}}\right) \lVert u_{3}\rVert _{Y^{1}} \end{align} $$
$$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }\left( u_{1}u_{2}u_{3}\right) ds\right\rVert _{X^{1}\left( \left[ 0,T\right) \right) }\lesssim \lVert u_{1}\rVert _{Y^{1}}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{Y^{1}}+\left\lVert P_{>M_{0}}u_{2}\right\rVert _{Y^{1}}\right) \lVert u_{3}\rVert _{Y^{1}} \end{align} $$and
 $$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }\left( u_{1}u_{2}u_{3}\right) ds\right\rVert _{X^{1}\left( \left[ 0,T\right) \right) }\lesssim \lVert u_{1}\rVert _{Y^{1}}\lVert u_{2}\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}. \end{align} $$
$$ \begin{align} \left\lVert \int_{a}^{t}e^{i(t-s)\Delta }\left( u_{1}u_{2}u_{3}\right) ds\right\rVert _{X^{1}\left( \left[ 0,T\right) \right) }\lesssim \lVert u_{1}\rVert _{Y^{1}}\lVert u_{2}\rVert _{Y^{1}}\lVert u_{3}\rVert _{Y^{1}}. \end{align} $$Moreover, if ![]() $u_{j}=e^{it\Delta }f_{j}$ for some j, then the
$u_{j}=e^{it\Delta }f_{j}$ for some j, then the ![]() $Y^{s}$ norm of
$Y^{s}$ norm of ![]() $u_{j}$ in formula (2.10) or (2.11) can be replaced by the
$u_{j}$ in formula (2.10) or (2.11) can be replaced by the ![]() $H^{s}$ norm of
$H^{s}$ norm of ![]() $f_{j}$.
$f_{j}$.
We prove only Lemma 2.1. On the one hand, Lemma 2.2 follows from the proof of Lemma 2.1, with little modification. On the other hand, formula (2.8) has already been proved as [Reference Herr, Tataru and Tzvetkov37, Proposition 2.12] and [Reference Killip and Vişan43, (4.4)], and the non-scale-invariant estimate (2.9) is easy. Hence we omit the proof of Lemma 2.2. The following tools will be used to prove Lemma 2.1.
Lemma 2.3. Strichartz estimate on  $\mathbb {T}^{4}$ [Reference Bourgain and Demeter4, Reference Killip and Vişan43]
$\mathbb {T}^{4}$ [Reference Bourgain and Demeter4, Reference Killip and Vişan43]
For ![]() $p>3$,
$p>3$,
 $$ \begin{align} \left\lVert P_{\leq M}u\right\rVert _{L_{t,x}^{p}}\lesssim M^{2-\frac{6}{p}}\lVert u\rVert _{Y^{0}}. \end{align} $$
$$ \begin{align} \left\lVert P_{\leq M}u\right\rVert _{L_{t,x}^{p}}\lesssim M^{2-\frac{6}{p}}\lVert u\rVert _{Y^{0}}. \end{align} $$Corollary 2.4. Strichartz estimates on  $\mathbb {T}^{4}$ with noncentred frequency localisation
$\mathbb {T}^{4}$ with noncentred frequency localisation
Let M be a dyadic value and let Q be a (possibly) noncentred M-cube in Fourier space,
Let ![]() $P_{Q}$ be the corresponding Littlewood–Paley projection. Then by Galilean invariance, we have
$P_{Q}$ be the corresponding Littlewood–Paley projection. Then by Galilean invariance, we have
 $$ \begin{align} \left\lVert P_{Q}u\right\rVert _{L_{t,x}^{p}}\lesssim M^{2-\frac{6}{p}}\left\lVert P_{Q}u\right\rVert _{Y^{0}} \quad p>3. \end{align} $$
$$ \begin{align} \left\lVert P_{Q}u\right\rVert _{L_{t,x}^{p}}\lesssim M^{2-\frac{6}{p}}\left\lVert P_{Q}u\right\rVert _{Y^{0}} \quad p>3. \end{align} $$The net effect of this observation is that we pay a factor of only ![]() $M^{2- \frac {6}{p}}$ when applying formula (2.12).
$M^{2- \frac {6}{p}}$ when applying formula (2.12).
Proof. Such a fact is well known and widely used. Readers interested in a version of the proof can see [Reference Chen and Holmer24, Corollary 5.18].
2.1 Proof of Lemma 2.1
We first present the proof of the sharp estimate (2.4), then that of formula (2.5).
2.1.1 Proof of formula (2.4)
Let I denote the integral in formula (2.4). Decompose the four factors into Littlewood–Paley pieces so that
 $$ \begin{align*} I=\sum_{M_{1},M_{2},M_{3},M}I_{M_{1},M_{2},M_{3},M}, \end{align*} $$
$$ \begin{align*} I=\sum_{M_{1},M_{2},M_{3},M}I_{M_{1},M_{2},M_{3},M}, \end{align*} $$where
 $$ \begin{align*} I_{M_{1},M_{2},M_{3},M}=\iint_{x,t}u_{1,M_{1}}u_{2,M_{2}}u_{3,M_{3}}g_{M}dxdt, \end{align*} $$
$$ \begin{align*} I_{M_{1},M_{2},M_{3},M}=\iint_{x,t}u_{1,M_{1}}u_{2,M_{2}}u_{3,M_{3}}g_{M}dxdt, \end{align*} $$with ![]() $u_{j,M_{j}}=P_{M_{j}}u_{j}$ and
$u_{j,M_{j}}=P_{M_{j}}u_{j}$ and ![]() $g_{M}=P_{M}g$. As
$g_{M}=P_{M}g$. As ![]() $M_{2}$,
$M_{2}$, ![]() $M_{3}$ and M are symmetric, it suffices to take care of the
$M_{3}$ and M are symmetric, it suffices to take care of the ![]() $M_{1}\sim M_{2}\geq M_{3}\geq M$ case. Decompose the
$M_{1}\sim M_{2}\geq M_{3}\geq M$ case. Decompose the ![]() $M_{1}$ and
$M_{1}$ and ![]() $M_{2}$ dyadic spaces into
$M_{2}$ dyadic spaces into ![]() $ M_{3}$-size cubes; then
$ M_{3}$-size cubes; then
 $$ \begin{align*} I_{1A} &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}\sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}P_{Q_{c}}u_{2,M_{2}}u_{3,M_{3}}g_{M}\right\rVert _{L_{t,x}^{1}} \\ &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}\sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{L_{t,x}^{\frac{ 10}{3}}}\left\lVert P_{Q_{c}}u_{2,M_{2}}\right\rVert _{L_{t,x}^{\frac{10}{3} }}\left\lVert u_{3,M_{3}}\right\rVert _{L_{t,x}^{\frac{10}{3}}}\left\lVert g_{M}\right\rVert _{L_{t,x}^{10}}. \end{align*} $$
$$ \begin{align*} I_{1A} &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}\sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}P_{Q_{c}}u_{2,M_{2}}u_{3,M_{3}}g_{M}\right\rVert _{L_{t,x}^{1}} \\ &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}\sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{L_{t,x}^{\frac{ 10}{3}}}\left\lVert P_{Q_{c}}u_{2,M_{2}}\right\rVert _{L_{t,x}^{\frac{10}{3} }}\left\lVert u_{3,M_{3}}\right\rVert _{L_{t,x}^{\frac{10}{3}}}\left\lVert g_{M}\right\rVert _{L_{t,x}^{10}}. \end{align*} $$Using formulas (2.12) and (2.13),
 $$ \begin{align*} &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}\sum_{Q}M_{3}^{\frac{2}{5}}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{3,M_{3}}\right\rVert _{Y^{0}}M_{3}^{\frac{1}{5}}\left\lVert P_{Q_{c}}u_{2,M_{2}}\right\rVert _{Y^{0}}M^{\frac{7}{5}}\left\lVert g_{M}\right\rVert _{Y^{0}} \\ &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}M_{3}^{\frac{3}{5}}M^{\frac{7}{5}}\left\lVert g_{M}\right\rVert _{Y^{0}}\left\lVert u_{3,M_{3}}\right\rVert _{Y^{0}}\sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert P_{Q_{c}}u_{2,M_{2}}\right\rVert _{Y^{0}}. \end{align*} $$
$$ \begin{align*} &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}\sum_{Q}M_{3}^{\frac{2}{5}}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{3,M_{3}}\right\rVert _{Y^{0}}M_{3}^{\frac{1}{5}}\left\lVert P_{Q_{c}}u_{2,M_{2}}\right\rVert _{Y^{0}}M^{\frac{7}{5}}\left\lVert g_{M}\right\rVert _{Y^{0}} \\ &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}M_{3}^{\frac{3}{5}}M^{\frac{7}{5}}\left\lVert g_{M}\right\rVert _{Y^{0}}\left\lVert u_{3,M_{3}}\right\rVert _{Y^{0}}\sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert P_{Q_{c}}u_{2,M_{2}}\right\rVert _{Y^{0}}. \end{align*} $$Applying Cauchy–Schwarz to sum in Q, we have
 $$ \begin{align*} &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}M_{3}^{\frac{3}{5}}M^{\frac{7}{5}}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}\left\lVert u_{3,M_{3}}\right\rVert _{Y^{0}}\left\lVert g_{M}\right\rVert _{Y^{0}} \\ &\lesssim \sum_{\substack{ M_{1},M_{2} \\ M_{1}\sim M_{2}}} M_{2}M_{1}^{-1}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{-1}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{1}}\sum_{\substack{ M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}M_{3}^{-\frac{2}{5}}M^{\frac{2}{5}}\left\lVert u_{3,M_{3}}\right\rVert _{Y^{1}}\left\lVert g_{M}\right\rVert _{Y^{1}}. \end{align*} $$
$$ \begin{align*} &\lesssim \sum_{\substack{ M_{1},M_{2},M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}M_{3}^{\frac{3}{5}}M^{\frac{7}{5}}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}\left\lVert u_{3,M_{3}}\right\rVert _{Y^{0}}\left\lVert g_{M}\right\rVert _{Y^{0}} \\ &\lesssim \sum_{\substack{ M_{1},M_{2} \\ M_{1}\sim M_{2}}} M_{2}M_{1}^{-1}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{-1}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{1}}\sum_{\substack{ M_{3},M \\ M_{1}\sim M_{2}\geq M_{3}\geq M}}M_{3}^{-\frac{2}{5}}M^{\frac{2}{5}}\left\lVert u_{3,M_{3}}\right\rVert _{Y^{1}}\left\lVert g_{M}\right\rVert _{Y^{1}}. \end{align*} $$We are done, by Schur’s test.
2.1.2 Proof of formula (2.5)
We reuse the setup from the proof of formula (2.4). However, due to the symmetry assumption ![]() $M_{1}\geq M_{2}\geq M_{3}$ on the frequencies in the proof of formula (2.4), we cannot simply assume that
$M_{1}\geq M_{2}\geq M_{3}$ on the frequencies in the proof of formula (2.4), we cannot simply assume that ![]() $P_{\leq M_{0}}$ lands on
$P_{\leq M_{0}}$ lands on ![]() $u_{2}$. The worst-gain (least-gain) case here would be that
$u_{2}$. The worst-gain (least-gain) case here would be that ![]() $u_{1}$ is still put in
$u_{1}$ is still put in ![]() $Y^{-1}$ and
$Y^{-1}$ and ![]() $ P_{\leq M_{0}}$ is applied to
$ P_{\leq M_{0}}$ is applied to ![]() $u_{3}$. Thus we will prove estimate (2.5) subject to the extra localisation that
$u_{3}$. Thus we will prove estimate (2.5) subject to the extra localisation that ![]() $ P_{\leq M_{0}}$ be applied on
$ P_{\leq M_{0}}$ be applied on ![]() $u_{3}$. By symmetry in
$u_{3}$. By symmetry in ![]() $M_{2}$ and M, it suffices to take care of two cases: A,
$M_{2}$ and M, it suffices to take care of two cases: A, ![]() $M_{1}\sim M_{2}\geq M_{3}\geq M$, and B,
$M_{1}\sim M_{2}\geq M_{3}\geq M$, and B, ![]() $M_{1}\sim M_{2}\geq M\geq M_{3}$. We will get a
$M_{1}\sim M_{2}\geq M\geq M_{3}$. We will get a  $ T^{\frac {1}{4}}M_{0}^{\frac {3}{5}}$ in case A and a
$ T^{\frac {1}{4}}M_{0}^{\frac {3}{5}}$ in case A and a  $T^{\frac {1}{7}}M_{0}^{ \frac {3}{7}}$ in case B. Since formula (2.5) is nowhere near optimal, and we just need it to hold with some powers of T and
$T^{\frac {1}{7}}M_{0}^{ \frac {3}{7}}$ in case B. Since formula (2.5) is nowhere near optimal, and we just need it to hold with some powers of T and ![]() $M_{0}$, there is no need to match these powers or pursue the best power in these cases.
$M_{0}$, there is no need to match these powers or pursue the best power in these cases.
Case A:  $M_{1}\sim M_{2}\geq M_{3}\geq M$.
$M_{1}\sim M_{2}\geq M_{3}\geq M$.
Decompose the ![]() $M_{1}$ and
$M_{1}$ and ![]() $M_{2}$ dyadic spaces into
$M_{2}$ dyadic spaces into ![]() $M_{3}$-size cubes:
$M_{3}$-size cubes:
 $$ \begin{align*} I_{M_{1},M_{2},M_{3},M} &\leq \sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}P_{Q_{c}}u_{2,M_{2}}\left( P_{\leq M_{0}}u_{3,M_{3}}\right) g_{M}\right\rVert _{L_{t,x}^{1}} \\ &\leq \sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}g_{M}\right\rVert _{L_{t,x}^{2}}\left\lVert P_{Q_{C}}u_{2,M_{2}}\right\rVert _{L_{t,x}^{4}}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{L_{t,x}^{4}}, \end{align*} $$
$$ \begin{align*} I_{M_{1},M_{2},M_{3},M} &\leq \sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}P_{Q_{c}}u_{2,M_{2}}\left( P_{\leq M_{0}}u_{3,M_{3}}\right) g_{M}\right\rVert _{L_{t,x}^{1}} \\ &\leq \sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}g_{M}\right\rVert _{L_{t,x}^{2}}\left\lVert P_{Q_{C}}u_{2,M_{2}}\right\rVert _{L_{t,x}^{4}}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{L_{t,x}^{4}}, \end{align*} $$where
 $$ \begin{align*} \left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{L_{t,x}^{4}}\leq T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}M_{3}^{\frac{2}{5}}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{L_{t}^{\infty }L_{x}^{2}}\lesssim T^{\frac{1}{ 4}}M_{0}^{\frac{3}{5}}M_{3}^{\frac{2}{5}}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{0}}. \end{align*} $$
$$ \begin{align*} \left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{L_{t,x}^{4}}\leq T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}M_{3}^{\frac{2}{5}}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{L_{t}^{\infty }L_{x}^{2}}\lesssim T^{\frac{1}{ 4}}M_{0}^{\frac{3}{5}}M_{3}^{\frac{2}{5}}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{0}}. \end{align*} $$Using formulas (2.12) and (2.13),
 $$ \begin{align*} I_{M_{1},M_{2},M_{3},M}\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5} }\sum_{Q}\left( M\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert g_{M}\right\rVert _{Y^{0}}\right) M_{3}^{\frac{1}{2}}\left\lVert P_{Q_{C}}u_{2,M_{2}}\right\rVert _{Y^{0}}M_{3}^{\frac{2}{5}}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{0}}. \end{align*} $$
$$ \begin{align*} I_{M_{1},M_{2},M_{3},M}\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5} }\sum_{Q}\left( M\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert g_{M}\right\rVert _{Y^{0}}\right) M_{3}^{\frac{1}{2}}\left\lVert P_{Q_{C}}u_{2,M_{2}}\right\rVert _{Y^{0}}M_{3}^{\frac{2}{5}}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{0}}. \end{align*} $$Note that we actually used a bilinear estimate for the first factor, but did not record or use the bilinear gain factor. Using Cauchy–Schwarz to sum in Q, we have
 $$ \begin{align*} I_{M_{1},M_{2},M_{3},M}\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert g_{M}\right\rVert _{Y^{1}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}M_{3}^{\frac{9}{10} }\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{0}}. \end{align*} $$
$$ \begin{align*} I_{M_{1},M_{2},M_{3},M}\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert g_{M}\right\rVert _{Y^{1}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}M_{3}^{\frac{9}{10} }\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{0}}. \end{align*} $$Thus, summing in M nonoptimally gives
 $$ \begin{align*} I_{1A} &\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert g\right\rVert _{Y^{1}}\sum_{\substack{ M_{1},M_{2},M_{3} \\ M_{1}\sim M_{2}\geq M_{3} }}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}M_{3}^{\frac{9}{10}}\log M_{3}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{0}} \\ &\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert g\right\rVert _{Y^{1}}\sum_{\substack{ M_{1},M_{2},M_{3} \\ M_{1}\sim M_{2}\geq M_{3} }}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}\frac{M_{3}^{\frac{9}{10}}\log M_{3}}{M_{3}} \left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{1}}. \end{align*} $$
$$ \begin{align*} I_{1A} &\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert g\right\rVert _{Y^{1}}\sum_{\substack{ M_{1},M_{2},M_{3} \\ M_{1}\sim M_{2}\geq M_{3} }}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}M_{3}^{\frac{9}{10}}\log M_{3}\left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{0}} \\ &\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert g\right\rVert _{Y^{1}}\sum_{\substack{ M_{1},M_{2},M_{3} \\ M_{1}\sim M_{2}\geq M_{3} }}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}\frac{M_{3}^{\frac{9}{10}}\log M_{3}}{M_{3}} \left\lVert P_{\leq M_{0}}u_{3,M_{3}}\right\rVert _{Y^{1}}. \end{align*} $$Again, summing in ![]() $M_{3}$ nonoptimally and swapping a derivative between
$M_{3}$ nonoptimally and swapping a derivative between ![]() $ u_{1}$ and
$ u_{1}$ and ![]() $u_{2}$ give
$u_{2}$ give
 $$ \begin{align*} I_{1A} &\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert g\right\rVert _{Y^{1}}\left\lVert P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\sum _{\substack{ M_{1},M_{2} \\ M_{1}\sim M_{2}}}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{-1}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{1}} \\ &\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert u_{1}\right\rVert _{Y^{-1}}\left\lVert u_{2}\right\rVert _{Y^{1}}\left\lVert P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\left\lVert g\right\rVert _{Y^{1}}. \end{align*} $$
$$ \begin{align*} I_{1A} &\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert g\right\rVert _{Y^{1}}\left\lVert P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\sum _{\substack{ M_{1},M_{2} \\ M_{1}\sim M_{2}}}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{-1}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{1}} \\ &\lesssim T^{\frac{1}{4}}M_{0}^{\frac{3}{5}}\left\lVert u_{1}\right\rVert _{Y^{-1}}\left\lVert u_{2}\right\rVert _{Y^{1}}\left\lVert P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\left\lVert g\right\rVert _{Y^{1}}. \end{align*} $$ Case B:  $M_{1}\sim M_{2}\geq M\geq M_{3}$.
$M_{1}\sim M_{2}\geq M\geq M_{3}$.
Sum up ![]() $M_{3}$ first. We then consider
$M_{3}$ first. We then consider
 $$ \begin{align*} I_{M_{1},M_{2},M}=\iint_{x,t}u_{1,M_{1}}u_{2,M_{2}}\left( P_{\leq M}P_{\leq M_{0}}u_{3}\right) g_{M}dxdt. \end{align*} $$
$$ \begin{align*} I_{M_{1},M_{2},M}=\iint_{x,t}u_{1,M_{1}}u_{2,M_{2}}\left( P_{\leq M}P_{\leq M_{0}}u_{3}\right) g_{M}dxdt. \end{align*} $$Decompose the ![]() $M_{1}$ and
$M_{1}$ and ![]() $M_{2}$ dyadic spaces into M-size cubes:
$M_{2}$ dyadic spaces into M-size cubes:
 $$ \begin{align*} I_{M_{1},M_{2},M} &\leq \sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}P_{Q_{c}}u_{2,M_{2}}\left( P_{\leq M}P_{\leq M_{0}}u_{3}\right) g_{M}\right\rVert _{L_{t,x}^{1}} \\ &\leq \sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{L_{t,x}^{\frac{7 }{2}}}\left\lVert P_{Q_{C}}u_{2,M_{2}}\right\rVert _{L_{t,x}^{\frac{7}{2} }}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{L_{t,x}^{7}}\left\lVert g_{M}\right\rVert _{L_{t,x}^{\frac{7}{2}}}, \end{align*} $$
$$ \begin{align*} I_{M_{1},M_{2},M} &\leq \sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}P_{Q_{c}}u_{2,M_{2}}\left( P_{\leq M}P_{\leq M_{0}}u_{3}\right) g_{M}\right\rVert _{L_{t,x}^{1}} \\ &\leq \sum_{Q}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{L_{t,x}^{\frac{7 }{2}}}\left\lVert P_{Q_{C}}u_{2,M_{2}}\right\rVert _{L_{t,x}^{\frac{7}{2} }}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{L_{t,x}^{7}}\left\lVert g_{M}\right\rVert _{L_{t,x}^{\frac{7}{2}}}, \end{align*} $$where
 $$ \begin{align*} \left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{L_{t,x}^{7}} &\leq T^{\frac{1}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{L_{t}^{\infty }L_{x}^{7}} \\ &\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{L_{t}^{\infty }H_{x}^{1}} \\ &\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}. \end{align*} $$
$$ \begin{align*} \left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{L_{t,x}^{7}} &\leq T^{\frac{1}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{L_{t}^{\infty }L_{x}^{7}} \\ &\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{L_{t}^{\infty }H_{x}^{1}} \\ &\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}. \end{align*} $$Applying formulas (2.12) and (2.13),
 $$ \begin{align*} I_{M_{1},M_{2},M}\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\sum_{Q}M^{\frac{2 }{7}}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{Y^{0}}M^{\frac{2}{7} }\left\lVert P_{Q_{C}}u_{2,M_{2}}\right\rVert _{Y^{0}}M^{\frac{2}{7} }\left\lVert g_{M}\right\rVert _{Y^{0}}. \end{align*} $$
$$ \begin{align*} I_{M_{1},M_{2},M}\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\sum_{Q}M^{\frac{2 }{7}}\left\lVert P_{Q}u_{1,M_{1}}\right\rVert _{Y^{0}}M^{\frac{2}{7} }\left\lVert P_{Q_{C}}u_{2,M_{2}}\right\rVert _{Y^{0}}M^{\frac{2}{7} }\left\lVert g_{M}\right\rVert _{Y^{0}}. \end{align*} $$Applying Cauchy–Schwarz to sum in Q, we have
 $$ \begin{align*} I_{M_{1},M_{2},M}\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}M^{-\frac{1}{7} }\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}\left\lVert g_{M}\right\rVert _{Y^{1}}. \end{align*} $$
$$ \begin{align*} I_{M_{1},M_{2},M}\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M}P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}M^{-\frac{1}{7} }\left\lVert u_{1,M_{1}}\right\rVert _{Y^{0}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{0}}\left\lVert g_{M}\right\rVert _{Y^{1}}. \end{align*} $$Thus, swapping a derivative between ![]() $u_{1}$ and
$u_{1}$ and ![]() $u_{2}$ gives
$u_{2}$ gives
 $$ \begin{align*} I_{1B}\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\sum_{\substack{ M_{1},M_{2},M \\ M_{1}\sim M_{2}\geq M}}M^{-\frac{1}{7}}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{-1}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{1}}\left\lVert g_{M}\right\rVert _{Y^{1}}. \end{align*} $$
$$ \begin{align*} I_{1B}\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\sum_{\substack{ M_{1},M_{2},M \\ M_{1}\sim M_{2}\geq M}}M^{-\frac{1}{7}}\left\lVert u_{1,M_{1}}\right\rVert _{Y^{-1}}\left\lVert u_{2,M_{2}}\right\rVert _{Y^{1}}\left\lVert g_{M}\right\rVert _{Y^{1}}. \end{align*} $$Burning that ![]() $\frac {1}{7}$-derivative to sum in M and then applying Cauchy–Schwarz in
$\frac {1}{7}$-derivative to sum in M and then applying Cauchy–Schwarz in ![]() $M_{1}$, we have
$M_{1}$, we have
 $$ \begin{align*} I_{1B}\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\left\lVert u_{1}\right\rVert _{Y^{-1}}\left\lVert u_{2}\right\rVert _{Y^{1}}\left\lVert g\right\rVert _{Y^{1}}, \end{align*} $$
$$ \begin{align*} I_{1B}\lesssim T^{\frac{1}{7}}M_{0}^{\frac{3}{7}}\left\lVert P_{\leq M_{0}}u_{3}\right\rVert _{Y^{1}}\left\lVert u_{1}\right\rVert _{Y^{-1}}\left\lVert u_{2}\right\rVert _{Y^{1}}\left\lVert g\right\rVert _{Y^{1}}, \end{align*} $$as needed.
3 Uniqueness for GP hierarchy (1.2) and the proof of Theorem 1.1 – Setup
Theorem 3.1. Let  $\Gamma =\left \{ \gamma ^{(k)}\right \} \in \oplus _{k\geq 1}C\left ( \left [ 0,T_{0}\right ] ,\mathcal {L} _{k}^{1}\right ) $ be a solution to equation (1.2) in
$\Gamma =\left \{ \gamma ^{(k)}\right \} \in \oplus _{k\geq 1}C\left ( \left [ 0,T_{0}\right ] ,\mathcal {L} _{k}^{1}\right ) $ be a solution to equation (1.2) in ![]() $\left [ 0,T_{0}\right ]$, in the sense that
$\left [ 0,T_{0}\right ]$, in the sense that
(a)
 $\Gamma $ is admissible in the sense of Definition 3.4 and
$\Gamma $ is admissible in the sense of Definition 3.4 and(b)
 $\Gamma $ satisfies the kinetic energy condition that
$\Gamma $ satisfies the kinetic energy condition that  $\exists C_{0}>0$ such that
$\exists C_{0}>0$ such that  $$ \begin{align*} \sup_{t\in \left[ 0,T_{0}\right] }{\mathop{\mathrm{Tr}}}\left( \prod\limits_{j=1}^{k}\left\langle \nabla _{x_{j}}\right\rangle \right) \gamma ^{(k)}\left( t\right) \left( \prod\limits_{j=1}^{k}\left\langle \nabla _{x_{j}}\right\rangle \right) \leq C_{0}^{2k}. \end{align*} $$
$$ \begin{align*} \sup_{t\in \left[ 0,T_{0}\right] }{\mathop{\mathrm{Tr}}}\left( \prod\limits_{j=1}^{k}\left\langle \nabla _{x_{j}}\right\rangle \right) \gamma ^{(k)}\left( t\right) \left( \prod\limits_{j=1}^{k}\left\langle \nabla _{x_{j}}\right\rangle \right) \leq C_{0}^{2k}. \end{align*} $$
Then there is a threshold ![]() $\eta (C_{0})>0$ such that the solution is unique in
$\eta (C_{0})>0$ such that the solution is unique in ![]() $[0,T_{0}]$, provided
$[0,T_{0}]$, provided
 $$ \begin{align*} \sup_{t\in \lbrack 0,T_{0}]}{\mathop{\mathrm{Tr}}}\left( \prod\limits_{j=1}^{k}P_{>M}^{j}\left\langle \nabla _{x_{j}}\right\rangle \right) \gamma ^{(k)}(t)\left( \prod\limits_{j=1}^{k}P_{>M}^{j}\left\langle \nabla _{x_{j}}\right\rangle \right) \leq \eta ^{2k}, \end{align*} $$
$$ \begin{align*} \sup_{t\in \lbrack 0,T_{0}]}{\mathop{\mathrm{Tr}}}\left( \prod\limits_{j=1}^{k}P_{>M}^{j}\left\langle \nabla _{x_{j}}\right\rangle \right) \gamma ^{(k)}(t)\left( \prod\limits_{j=1}^{k}P_{>M}^{j}\left\langle \nabla _{x_{j}}\right\rangle \right) \leq \eta ^{2k}, \end{align*} $$for some frequency M. Our proof shows that ![]() $\eta (C_{0})$ can be
$\eta (C_{0})$ can be ![]() $\left ( 100CC_{0}\right ) ^{-2}$, with C being a universal constant depending on the U-V estimate constants and the Sobolev constants. The frequency threshold M is allowed to depend on
$\left ( 100CC_{0}\right ) ^{-2}$, with C being a universal constant depending on the U-V estimate constants and the Sobolev constants. The frequency threshold M is allowed to depend on ![]() $\gamma ^{(k)}$ (the particular solution under consideration) but must apply uniformly on
$\gamma ^{(k)}$ (the particular solution under consideration) but must apply uniformly on ![]() $[0,T_{0}]$.
$[0,T_{0}]$.
Here, we have intentionally stated Theorem 3.1 before writing out the definition of admissibility (Definition 3.4) to bring up readers’ attention. For the purpose of only proving Theorem 1.1, in fact, Definition 3.4 and its companion, the quantum de Finetti theorem (Theorem 3.5), are not necessary. One could just apply the proof of Theorem 3.1 to the special case
 $$ \begin{align} \gamma ^{(k)}\left( t\right) \equiv \int_{L^{2}\left(\mathbb{T}^{4}\right)}\left\lvert \phi \right\rangle \left\langle \phi \right\rvert ^{\otimes k}d\mu _{t}(\phi )\equiv \displaystyle\mathop{\prod}\limits_{j=1}^{k}u_{1}\left(t,x_{j}\right)\bar{u}_{1}\left(t,x^{\prime}_{j}\right)- \displaystyle\mathop{\prod}\limits_{j=1}^{k}u_{2}\left(t,x_{j}\right)\bar{u}_{2}\left(t,x^{\prime}_{j}\right), \end{align} $$
$$ \begin{align} \gamma ^{(k)}\left( t\right) \equiv \int_{L^{2}\left(\mathbb{T}^{4}\right)}\left\lvert \phi \right\rangle \left\langle \phi \right\rvert ^{\otimes k}d\mu _{t}(\phi )\equiv \displaystyle\mathop{\prod}\limits_{j=1}^{k}u_{1}\left(t,x_{j}\right)\bar{u}_{1}\left(t,x^{\prime}_{j}\right)- \displaystyle\mathop{\prod}\limits_{j=1}^{k}u_{2}\left(t,x_{j}\right)\bar{u}_{2}\left(t,x^{\prime}_{j}\right), \end{align} $$where ![]() $u_{1}$ and
$u_{1}$ and ![]() $u_{2}$ are two solutions to equation (1.1) and
$u_{2}$ are two solutions to equation (1.1) and ![]() $\mu _{t}$ is the signed measure
$\mu _{t}$ is the signed measure ![]() $\delta _{u_{1}}- \delta _{u_{2}}$ on
$\delta _{u_{1}}- \delta _{u_{2}}$ on ![]() $ L^{2}\left (\mathbb {T}^{4}\right )$, to get that the difference is zero for all k and to obtain a uniqueness theorem which is solely about solutions to equation (1.1). This is sufficient to conclude Theorem 1.1. Readers unfamiliar with Theorem 3.5 could first skip Definition 3.4 and Theorem 3.5, put equation (3.1) in the place of equation (3.6), get to know how the GP hierarchy is involved and then come back to Definition 3.4 and Theorem 3.5. Once one understands the role of the GP hierarchy in the proof, it is easy to see that due to Theorem 3.5, the more general theorem (Theorem 3.1) costs nothing more, and the origin of the current scheme of proving NLS uniqueness using GP hierarchies is indeed Theorem 3.5, as mentioned in the introduction. Theorem 3.1 also implies the following corollary:
$ L^{2}\left (\mathbb {T}^{4}\right )$, to get that the difference is zero for all k and to obtain a uniqueness theorem which is solely about solutions to equation (1.1). This is sufficient to conclude Theorem 1.1. Readers unfamiliar with Theorem 3.5 could first skip Definition 3.4 and Theorem 3.5, put equation (3.1) in the place of equation (3.6), get to know how the GP hierarchy is involved and then come back to Definition 3.4 and Theorem 3.5. Once one understands the role of the GP hierarchy in the proof, it is easy to see that due to Theorem 3.5, the more general theorem (Theorem 3.1) costs nothing more, and the origin of the current scheme of proving NLS uniqueness using GP hierarchies is indeed Theorem 3.5, as mentioned in the introduction. Theorem 3.1 also implies the following corollary:
Corollary 3.2. Given an intial datum ![]() $u_{0}\in H^{1}\left (\mathbb {T}^{4}\right )$, there is at most one
$u_{0}\in H^{1}\left (\mathbb {T}^{4}\right )$, there is at most one  $C\left ( \left [ 0,T_{0}\right ] ,H_{x,\text {weak}}^{1}\right ) $ solution u to equation (1.1) on
$C\left ( \left [ 0,T_{0}\right ] ,H_{x,\text {weak}}^{1}\right ) $ solution u to equation (1.1) on ![]() $\mathbb {T}^{4}$ satisfying the following two properties:
$\mathbb {T}^{4}$ satisfying the following two properties:
(1) There is a
 $C_{0}>0$ such that
$C_{0}>0$ such that  $$ \begin{align*} \sup_{t\in \lbrack 0,T_{0}]}\left\lVert u(t)\right\rVert _{H^{1}}\leq C_{0}. \end{align*} $$
$$ \begin{align*} \sup_{t\in \lbrack 0,T_{0}]}\left\lVert u(t)\right\rVert _{H^{1}}\leq C_{0}. \end{align*} $$(2) There is some frequency M such that
(3.2)for the threshold $$ \begin{align} \sup_{t\in \lbrack 0,T_{0}]}\left\lVert \nabla P_{\geq M}u(t)\right\rVert _{L_{x}^{2}}\leq \eta, \end{align} $$
$$ \begin{align} \sup_{t\in \lbrack 0,T_{0}]}\left\lVert \nabla P_{\geq M}u(t)\right\rVert _{L_{x}^{2}}\leq \eta, \end{align} $$ $\eta (C_{0})>0$ concluded in Theorem 3.1.
$\eta (C_{0})>0$ concluded in Theorem 3.1.
The known  $C\left ( \left [ 0,T_{0}\right ] ,H_{x,\text {weak}}^{1}\right ) $ blowup solutions do not satisfy formula (3.2), so Corollary 3.2 is an unclassified uniqueness theorem. It seems to be stronger than the unconditional uniqueness theorem (Theorem 1.1), as it concludes uniqueness in a larger class of solutions. We wonder if there could be a more detailed classification regarding the term ‘unconditional uniqueness’ at the critical regularity.
$C\left ( \left [ 0,T_{0}\right ] ,H_{x,\text {weak}}^{1}\right ) $ blowup solutions do not satisfy formula (3.2), so Corollary 3.2 is an unclassified uniqueness theorem. It seems to be stronger than the unconditional uniqueness theorem (Theorem 1.1), as it concludes uniqueness in a larger class of solutions. We wonder if there could be a more detailed classification regarding the term ‘unconditional uniqueness’ at the critical regularity.
Theorem 1.1 follows from Theorem 3.1 and the following lemma:
Lemma 3.3. u is a  $C_{\left [0,T_{0}\right ]}^{0}H_{x}^{1}\cap \dot {C}_{\left [0,T_{0}\right ]}^{1}H_{x}^{-1}$ solution of equation (1.1) if and only if it is a
$C_{\left [0,T_{0}\right ]}^{0}H_{x}^{1}\cap \dot {C}_{\left [0,T_{0}\right ]}^{1}H_{x}^{-1}$ solution of equation (1.1) if and only if it is a  $C_{\left [0,T_{0}\right ]}^{0}H_{x, \text {weak}}^{1}\cap \dot {C}_{\left [0,T_{0}\right ]}^{1}H_{x,\text {weak}}^{-1}$ solution and satisfies uniform-in-time frequency localisation – that is, for each
$C_{\left [0,T_{0}\right ]}^{0}H_{x, \text {weak}}^{1}\cap \dot {C}_{\left [0,T_{0}\right ]}^{1}H_{x,\text {weak}}^{-1}$ solution and satisfies uniform-in-time frequency localisation – that is, for each ![]() $\varepsilon>0$ there exists
$\varepsilon>0$ there exists ![]() $M(\varepsilon )$ such that
$M(\varepsilon )$ such that
 $$ \begin{align} \left\lVert \nabla P_{\geq M(\varepsilon )}u\right\rVert _{L_{\left[0,T_{0}\right]}^{\infty }L_{x}^{2}}\leq \varepsilon. \end{align} $$
$$ \begin{align} \left\lVert \nabla P_{\geq M(\varepsilon )}u\right\rVert _{L_{\left[0,T_{0}\right]}^{\infty }L_{x}^{2}}\leq \varepsilon. \end{align} $$Proof. This proof is postponed to Section 3.1. We remark that formula (3.3) implies formula (3.2), but the converse is not true. That is, Corollary 3.2 implies Theorem 1.1, the unconditional uniqueness theorem, but the type of uniqueness concluded in Corollary 3.2 and Theorem 3.1 is unclassified.Footnote 14
Before starting the proof of Theorem 3.1, we note that although it seems that Theorem 3.1 concludes Theorem 1.1 only up to a time-dependent ![]() $e^{i\theta (t)}$ phase,
$e^{i\theta (t)}$ phase, ![]() $\theta (t)$ is actually
$\theta (t)$ is actually ![]() $0$ (see [Reference Herr and Sohinger35, p. 12] and [Reference Chen, Shen and Zhang26, Lemma A.1]). Thus, we are left to prove Theorem 3.1.
$0$ (see [Reference Herr and Sohinger35, p. 12] and [Reference Chen, Shen and Zhang26, Lemma A.1]). Thus, we are left to prove Theorem 3.1.
We set up some notations first. We rewrite equation (1.2) in Duhamel form:
 $$ \begin{align} \gamma ^{(k)}(t_{k})=U^{(k)}(t_{k})\gamma _{0}^{(k)}\mp i\int_{0}^{t_{k}}U^{(k)}(t_{k}-t_{k+1})B^{(k+1)}\left( \gamma ^{(k+1)}(t_{k+1})\right) dt_{k+1}, \end{align} $$
$$ \begin{align} \gamma ^{(k)}(t_{k})=U^{(k)}(t_{k})\gamma _{0}^{(k)}\mp i\int_{0}^{t_{k}}U^{(k)}(t_{k}-t_{k+1})B^{(k+1)}\left( \gamma ^{(k+1)}(t_{k+1})\right) dt_{k+1}, \end{align} $$where  $U^{(k)}(t)=\prod \limits _{j=1}^{k}e^{it\left ( \Delta _{x_{j}}-\Delta _{x_{j}^{\prime }}\right ) }$ and
$U^{(k)}(t)=\prod \limits _{j=1}^{k}e^{it\left ( \Delta _{x_{j}}-\Delta _{x_{j}^{\prime }}\right ) }$ and
 $$ \begin{align*} B^{(k+1)}\left( \gamma ^{(k+1)}\right) &\equiv \sum_{j=1}^{k}B_{j,k+1}\left( \gamma ^{(k+1)}\right) \\ &\equiv \sum_{j=1}^{k}\left(B_{j,k+1}^{+}-B_{j,k+1}^{-}\right)\left( \gamma ^{(k+1)}\right) \\ &\equiv \sum_{j=1}^{k}{\mathop{\mathrm{Tr}}}_{k+1}\delta \left(x_{j}-x_{k+1}\right)\gamma ^{(k+1)}-\gamma ^{(k+1)}\delta \left(x_{j}-x_{k+1}\right). \end{align*} $$
$$ \begin{align*} B^{(k+1)}\left( \gamma ^{(k+1)}\right) &\equiv \sum_{j=1}^{k}B_{j,k+1}\left( \gamma ^{(k+1)}\right) \\ &\equiv \sum_{j=1}^{k}\left(B_{j,k+1}^{+}-B_{j,k+1}^{-}\right)\left( \gamma ^{(k+1)}\right) \\ &\equiv \sum_{j=1}^{k}{\mathop{\mathrm{Tr}}}_{k+1}\delta \left(x_{j}-x_{k+1}\right)\gamma ^{(k+1)}-\gamma ^{(k+1)}\delta \left(x_{j}-x_{k+1}\right). \end{align*} $$Here, products are interpreted as the compositions of operators. For example, in kernels,
 $$ \begin{align*} \left( {\mathop{\mathrm{Tr}}}_{k+1}\delta (x_{1}-x_{k+1})\gamma ^{(k+1)}\right) \left( \mathbf{x}_{k},\mathbf{x}^{\prime}_{k}\right) =\int \delta (x_{1}-x_{k+1})\gamma ^{(k+1)}\left(\mathbf{x}_{k},x_{k+1};\mathbf{x}^{\prime}_{k},x_{k+1}\right)dx_{k+1}. \end{align*} $$
$$ \begin{align*} \left( {\mathop{\mathrm{Tr}}}_{k+1}\delta (x_{1}-x_{k+1})\gamma ^{(k+1)}\right) \left( \mathbf{x}_{k},\mathbf{x}^{\prime}_{k}\right) =\int \delta (x_{1}-x_{k+1})\gamma ^{(k+1)}\left(\mathbf{x}_{k},x_{k+1};\mathbf{x}^{\prime}_{k},x_{k+1}\right)dx_{k+1}. \end{align*} $$ We will prove that if  $\Gamma _{1}=\left \{ \gamma _{1}^{(k)}\right \} $ and
$\Gamma _{1}=\left \{ \gamma _{1}^{(k)}\right \} $ and  $ \Gamma _{2}=\left \{ \gamma _{2}^{(k)}\right \} $ are two solutions to equation (3.4), subject to the same initial datum and Theorem 3.1(a) and (b), then
$ \Gamma _{2}=\left \{ \gamma _{2}^{(k)}\right \} $ are two solutions to equation (3.4), subject to the same initial datum and Theorem 3.1(a) and (b), then  $\Gamma =\left \{ \gamma ^{(k)}=\gamma _{1}^{(k)}-\gamma _{2}^{(k)}\right \} $ is identically zero. Note that because equation (3.4) is linear,
$\Gamma =\left \{ \gamma ^{(k)}=\gamma _{1}^{(k)}-\gamma _{2}^{(k)}\right \} $ is identically zero. Note that because equation (3.4) is linear, ![]() $\Gamma $ is a solution to equation (3.4). We will start using a representation of
$\Gamma $ is a solution to equation (3.4). We will start using a representation of ![]() $\Gamma $ given by the quantum de Finetti theorem (Theorem 3.5). To this end, we define admissibility:
$\Gamma $ given by the quantum de Finetti theorem (Theorem 3.5). To this end, we define admissibility:
Definition 3.4. [Reference Chen, Hainzl, Pavlović and Seiringer6]
A nonnegative trace class symmetric operators sequence  $\Gamma =\left \{ \gamma ^{(k)}\right \} \in \oplus _{k\geq 1}C\left ( \left [ 0,T\right ] ,\mathcal {L}_{k}^{1}\right ) $, is called admissible if for all k, one has
$\Gamma =\left \{ \gamma ^{(k)}\right \} \in \oplus _{k\geq 1}C\left ( \left [ 0,T\right ] ,\mathcal {L}_{k}^{1}\right ) $, is called admissible if for all k, one has
Here, a trace class operator is called symmetry if, written in kernel form,
 $$ \begin{align*} \gamma ^{(k)}\left(\mathbf{x}_{k};\mathbf{x}^{\prime}_{k}\right) &=\overline{\gamma ^{(k)}\left(\mathbf{x}^{\prime}_{k};\mathbf{x}_{k}\right)} \\ \gamma ^{(k)}\left(x_{1},\dotsc x_{k};x^{\prime}_{1},\dotsc,x^{\prime}_{k}\right) &=\gamma ^{(k)}\left(x_{\sigma \left( 1\right) },\dotsc,x_{\sigma \left( k\right) };x^{\prime}_{\sigma \left( 1\right)},\dotsc,x^{\prime}_{\sigma \left(k\right)}\right), \end{align*} $$
$$ \begin{align*} \gamma ^{(k)}\left(\mathbf{x}_{k};\mathbf{x}^{\prime}_{k}\right) &=\overline{\gamma ^{(k)}\left(\mathbf{x}^{\prime}_{k};\mathbf{x}_{k}\right)} \\ \gamma ^{(k)}\left(x_{1},\dotsc x_{k};x^{\prime}_{1},\dotsc,x^{\prime}_{k}\right) &=\gamma ^{(k)}\left(x_{\sigma \left( 1\right) },\dotsc,x_{\sigma \left( k\right) };x^{\prime}_{\sigma \left( 1\right)},\dotsc,x^{\prime}_{\sigma \left(k\right)}\right), \end{align*} $$for all ![]() $\sigma \in S_{k}$, the permutation group of k elements.
$\sigma \in S_{k}$, the permutation group of k elements.
Theorem 3.5. quantum de Finetti theorem [Reference Chen, Hainzl, Pavlović and Seiringer6, Reference Lewin, Nam and Rougerie51]
Under assumption (a), there exists a probability measure ![]() $ d\mu _{t}(\phi )$ supported on the unit sphere of
$ d\mu _{t}(\phi )$ supported on the unit sphere of ![]() $L^{2}\left (\mathbb {T}^{4}\right )$ such that
$L^{2}\left (\mathbb {T}^{4}\right )$ such that
 $$ \begin{align*} \gamma ^{(k)}(t)=\int \left\lvert \phi \right\rangle \left\langle \phi \right\rvert ^{\otimes k}d\mu _{t}(\phi ). \end{align*} $$
$$ \begin{align*} \gamma ^{(k)}(t)=\int \left\lvert \phi \right\rangle \left\langle \phi \right\rvert ^{\otimes k}d\mu _{t}(\phi ). \end{align*} $$ By Theorem 3.5, there exist ![]() $d\mu _{1,t}$ and
$d\mu _{1,t}$ and ![]() $d\mu _{2,t}$ representing the two solutions
$d\mu _{2,t}$ representing the two solutions ![]() $\Gamma _{1}$ and
$\Gamma _{1}$ and ![]() $\Gamma _{2}$. The same Chebyshev argument as in [Reference Chen, Hainzl, Pavlović and Seiringer6, Lemma 4.5] turns the assumptions in Theorem 3.1 into the property that
$\Gamma _{2}$. The same Chebyshev argument as in [Reference Chen, Hainzl, Pavlović and Seiringer6, Lemma 4.5] turns the assumptions in Theorem 3.1 into the property that ![]() $d\mu _{j,t}$ is supported in the set
$d\mu _{j,t}$ is supported in the set
 $$ \begin{align} S=\left\{\phi \in \mathbb{S}\left( L^{2}\left(\mathbb{T}^{4}\right)\right) :\left\lVert P_{>M}\left\langle \nabla \right\rangle \phi \right\Vert _{L^{2}}\leq \varepsilon \right\}\cap \left\{\phi \in \mathbb{S}\left( L^{2}\left(\mathbb{T}^{4}\right)\right) :\left\lVert \phi \right\rVert _{H^{1}}\leq C_{0}\right\}. \end{align} $$
$$ \begin{align} S=\left\{\phi \in \mathbb{S}\left( L^{2}\left(\mathbb{T}^{4}\right)\right) :\left\lVert P_{>M}\left\langle \nabla \right\rangle \phi \right\Vert _{L^{2}}\leq \varepsilon \right\}\cap \left\{\phi \in \mathbb{S}\left( L^{2}\left(\mathbb{T}^{4}\right)\right) :\left\lVert \phi \right\rVert _{H^{1}}\leq C_{0}\right\}. \end{align} $$That is, letting the signed measure ![]() $d\mu _{t}=d\mu _{1,t}-d\mu _{2,t}$, we have
$d\mu _{t}=d\mu _{1,t}-d\mu _{2,t}$, we have
 $$ \begin{align} \gamma ^{(k)}(t_{k})=\left( \gamma _{1}^{(k)}-\gamma _{2}^{(k)}\right)(t_{k})=\int \left\lvert \phi \right\rangle \left\langle \phi \right\rvert ^{\otimes k}d\mu _{t_{k}}(\phi ) \end{align} $$
$$ \begin{align} \gamma ^{(k)}(t_{k})=\left( \gamma _{1}^{(k)}-\gamma _{2}^{(k)}\right)(t_{k})=\int \left\lvert \phi \right\rangle \left\langle \phi \right\rvert ^{\otimes k}d\mu _{t_{k}}(\phi ) \end{align} $$and ![]() $d\mu _{t_{k}}$ is supported in the set S defined in equation (3.5).
$d\mu _{t_{k}}$ is supported in the set S defined in equation (3.5).
So our task of establishing Theorem 3.1 is now transformed into proving that the solution is zero if the solution takes the form of equation (3.6) and is subject to zero initial datum. It suffices to prove ![]() $\gamma ^{(1)}=0$, as the proof is the same for the general k case. The proof involves coupling equation (3.4) multiple times. To this end, we plug in zero initial datum, set the
$\gamma ^{(1)}=0$, as the proof is the same for the general k case. The proof involves coupling equation (3.4) multiple times. To this end, we plug in zero initial datum, set the ![]() $\mp i$ in equation (3.4) to
$\mp i$ in equation (3.4) to ![]() $1$ so that we do not need track its power (because it acts as a
$1$ so that we do not need track its power (because it acts as a ![]() $1$ in the estimates for our purpose) and rewrite equation (3.4) as
$1$ in the estimates for our purpose) and rewrite equation (3.4) as
 $$ \begin{align} \gamma ^{(k)}(t_{k})=\int_{0}^{t_{k}}U^{(k)}(t_{k}-t_{k+1})B^{(k+1)}\left( \gamma ^{(k+1)}(t_{k+1})\right) dt_{k+1}. \end{align} $$
$$ \begin{align} \gamma ^{(k)}(t_{k})=\int_{0}^{t_{k}}U^{(k)}(t_{k}-t_{k+1})B^{(k+1)}\left( \gamma ^{(k+1)}(t_{k+1})\right) dt_{k+1}. \end{align} $$Define
 $$ \begin{align*} J^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t} _{k+1}\right)=U^{(1)}(t_{1}-t_{2})B^{(2)}U^{(2)}(t_{2}-t_{3})B^{(3)}\dotsm U^{(k)}(t_{k}-t_{k+1})B^{(k+1)}f^{(k+1)}(t_{k+1}), \end{align*} $$
$$ \begin{align*} J^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t} _{k+1}\right)=U^{(1)}(t_{1}-t_{2})B^{(2)}U^{(2)}(t_{2}-t_{3})B^{(3)}\dotsm U^{(k)}(t_{k}-t_{k+1})B^{(k+1)}f^{(k+1)}(t_{k+1}), \end{align*} $$with ![]() $\underline {t}_{k+1}=\left ( t_{2},t_{3},\dotsc ,t_{k},t_{k+1}\right ) $. We can then write
$\underline {t}_{k+1}=\left ( t_{2},t_{3},\dotsc ,t_{k},t_{k+1}\right ) $. We can then write
 $$ \begin{align*} \gamma ^{(1)}(t_{1})=\int_{0}^{t_{1}}\int_{0}^{t_{2}}\dotsi\int_{0}^{t_{k}}J^{(k+1)}\left( \gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}, \end{align*} $$
$$ \begin{align*} \gamma ^{(1)}(t_{1})=\int_{0}^{t_{1}}\int_{0}^{t_{2}}\dotsi\int_{0}^{t_{k}}J^{(k+1)}\left( \gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}, \end{align*} $$after iterating equation (3.7) k times. To estimate ![]() $\gamma ^{(1)}$, we first use the KM board gameFootnote 15 to reduce the number of summands inside
$\gamma ^{(1)}$, we first use the KM board gameFootnote 15 to reduce the number of summands inside ![]() $\gamma ^{(1)},$ which is
$\gamma ^{(1)},$ which is ![]() $k!2^{k}$ at the moment, by combining them.
$k!2^{k}$ at the moment, by combining them.
Lemma 3.6. Klainerman–Machedon board game [Reference Klainerman and Machedon47]
One can express
 $$ \begin{align*} \int_{0}^{t_{1}}\int_{0}^{t_{2}}\dotsi \int_{0}^{t_{k+1}}J^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{ t}_{k+1} \end{align*} $$
$$ \begin{align*} \int_{0}^{t_{1}}\int_{0}^{t_{2}}\dotsi \int_{0}^{t_{k+1}}J^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{ t}_{k+1} \end{align*} $$as a sum of at most ![]() $4^{k}$ terms of the form
$4^{k}$ terms of the form
 $$ \begin{align*} \int_{D_{m}}J_{\mu _{m}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d \underline{t}_{k+1}, \end{align*} $$
$$ \begin{align*} \int_{D_{m}}J_{\mu _{m}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d \underline{t}_{k+1}, \end{align*} $$or in other words,
 $$ \begin{align} \int_{0}^{t_{1}}\int_{0}^{t_{2}}\dotsi \int_{0}^{t_{k+1}}J^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{ t}_{k+1}=\sum_{m}\int_{D_{m}}J_{\mu _{m}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1}, \underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align} $$
$$ \begin{align} \int_{0}^{t_{1}}\int_{0}^{t_{2}}\dotsi \int_{0}^{t_{k+1}}J^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{ t}_{k+1}=\sum_{m}\int_{D_{m}}J_{\mu _{m}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1}, \underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align} $$Here, ![]() $D_{m}$ is a subset of
$D_{m}$ is a subset of ![]() $[0,t_{1}]^{k}$, depending on
$[0,t_{1}]^{k}$, depending on ![]() $\mu _{m}$;
$\mu _{m}$; ![]() $ \left \{ \mu _{m}\right \} $ are a set of maps from
$ \left \{ \mu _{m}\right \} $ are a set of maps from ![]() $\{2,\dotsc ,k+1\}$ to
$\{2,\dotsc ,k+1\}$ to ![]() $ \{1,\dotsc ,k\}$ satisfying
$ \{1,\dotsc ,k\}$ satisfying ![]() $\mu _{m}(2)=1$ and
$\mu _{m}(2)=1$ and ![]() $\mu _{m}(l)<l$ for all
$\mu _{m}(l)<l$ for all ![]() $l,$ and
$l,$ and
 $$ \begin{align*} J_{\mu _{m}}^{(k+1)}(f^{(k+1)})(t_{1},\underline{t}_{k+1}) &=U^{(1)}(t_{1}-t_{2})B_{1,2}U^{(2)}(t_{2}-t_{3})B_{\mu _{m}(3),3}\dotsm \\ &\dotsm U^{(k)}(t_{k}-t_{k+1})B_{\mu _{m}(k+1),k+1}\left(f^{(k+1)}\right)(t_{1}). \end{align*} $$
$$ \begin{align*} J_{\mu _{m}}^{(k+1)}(f^{(k+1)})(t_{1},\underline{t}_{k+1}) &=U^{(1)}(t_{1}-t_{2})B_{1,2}U^{(2)}(t_{2}-t_{3})B_{\mu _{m}(3),3}\dotsm \\ &\dotsm U^{(k)}(t_{k}-t_{k+1})B_{\mu _{m}(k+1),k+1}\left(f^{(k+1)}\right)(t_{1}). \end{align*} $$ Using Lemma 3.6, to estimate ![]() $\gamma ^{(1)}$ it suffices to deal with a summand in the right-hand side of equation (3.8),
$\gamma ^{(1)}$ it suffices to deal with a summand in the right-hand side of equation (3.8),
 $$ \begin{align*} \int_{D_{m}}J_{\mu _{m}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d \underline{t}_{k+1}, \end{align*} $$
$$ \begin{align*} \int_{D_{m}}J_{\mu _{m}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d \underline{t}_{k+1}, \end{align*} $$at the expense of a ![]() $4^{k}$. Since
$4^{k}$. Since  $B_{j,k+1}=B_{j,k+1}^{+}-B_{j,k+1}^{-}$,
$B_{j,k+1}=B_{j,k+1}^{+}-B_{j,k+1}^{-}$,  $ J_{\mu _{m}}^{(k+1)}\left (\gamma ^{(k+1)}\right )$ is but another sum. Thus, by paying an extra
$ J_{\mu _{m}}^{(k+1)}\left (\gamma ^{(k+1)}\right )$ is but another sum. Thus, by paying an extra ![]() $2^{k}$, we can just estimate a typical term
$2^{k}$, we can just estimate a typical term
 $$ \begin{align} \int_{D_{m}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t} _{k+1}\right)d\underline{t}_{k+1}, \end{align} $$
$$ \begin{align} \int_{D_{m}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t} _{k+1}\right)d\underline{t}_{k+1}, \end{align} $$where
 $$ \begin{align} J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right) &=U^{(1)}(t_{1}-t_{2})B_{1,2}^{\operatorname{sgn}(2)}U^{(2)}(t_{2}-t_{3})B_{\mu _{m}(3),3}^{\operatorname{sgn}(3)}\dotsm \\ &\dotsm U^{(k)}(t_{k}-t_{k+1})B_{\mu _{m}(k+1),k+1}^{\operatorname{sgn}(k+1)}\left(f^{(k+1)}\right)(t_{k+1}), \notag \end{align} $$
$$ \begin{align} J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right) &=U^{(1)}(t_{1}-t_{2})B_{1,2}^{\operatorname{sgn}(2)}U^{(2)}(t_{2}-t_{3})B_{\mu _{m}(3),3}^{\operatorname{sgn}(3)}\dotsm \\ &\dotsm U^{(k)}(t_{k}-t_{k+1})B_{\mu _{m}(k+1),k+1}^{\operatorname{sgn}(k+1)}\left(f^{(k+1)}\right)(t_{k+1}), \notag \end{align} $$with ![]() $\operatorname {sgn}$ meaning the signature array
$\operatorname {sgn}$ meaning the signature array ![]() $(\operatorname {sgn}(2),\dotsc ,\operatorname {sgn}(k+1))$ and
$(\operatorname {sgn}(2),\dotsc ,\operatorname {sgn}(k+1))$ and  $ B_{j,k+1}^{\operatorname {sgn}(k+1)}$ standing for
$ B_{j,k+1}^{\operatorname {sgn}(k+1)}$ standing for  $B_{j,k+1}^{+}$ or
$B_{j,k+1}^{+}$ or ![]() $B_{j,k+1}^{-}$, depending on the sign of the
$B_{j,k+1}^{-}$, depending on the sign of the ![]() $(k+1)$-th signature element. The estimate of expression (3.9) is given by the following proposition:
$(k+1)$-th signature element. The estimate of expression (3.9) is given by the following proposition:
 $$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{D_{m}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t} _{k+1}\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}}\leq 2TC_{0}^{2}\left( CC_{0}^{3}T^{\frac{1}{7}}M_{0}^{\frac{3}{5 }}+CC_{0}^{2}\varepsilon \right) ^{\frac{2}{3}k}. \end{align*} $$
$$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{D_{m}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t} _{k+1}\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}}\leq 2TC_{0}^{2}\left( CC_{0}^{3}T^{\frac{1}{7}}M_{0}^{\frac{3}{5 }}+CC_{0}^{2}\varepsilon \right) ^{\frac{2}{3}k}. \end{align*} $$Proof. See Section 5.
Once Proposition 3.7 is proved, Theorem 3.1 then follows. In fact,
 $$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}^{-1} \right\rangle \vphantom{\left\langle\nabla_{x^{\prime}_{1}}\right\rangle^{-1}} \right. & \left. \left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\gamma ^{(1)}(t_{1})\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}} \\ &\leq 4^{k}\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{D_{m}}J_{\mu _{m}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t} _{k+1}\right)d\underline{t}_{k+1}\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}} \\ &\leq 8^{k}\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{D_{m}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t }_{k+1}\right)d\underline{t}_{k+1}\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}} \\ &\leq 2TC_{0}^{2}\left( CC_{0}^{3}T^{\frac{1}{7}}M_{0}^{\frac{3}{5} }+CC_{0}^{2}\varepsilon \right) ^{\frac{2}{3}k}. \end{align*} $$
$$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}^{-1} \right\rangle \vphantom{\left\langle\nabla_{x^{\prime}_{1}}\right\rangle^{-1}} \right. & \left. \left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\gamma ^{(1)}(t_{1})\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}} \\ &\leq 4^{k}\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{D_{m}}J_{\mu _{m}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t} _{k+1}\right)d\underline{t}_{k+1}\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}} \\ &\leq 8^{k}\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{D_{m}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t }_{k+1}\right)d\underline{t}_{k+1}\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}} \\ &\leq 2TC_{0}^{2}\left( CC_{0}^{3}T^{\frac{1}{7}}M_{0}^{\frac{3}{5} }+CC_{0}^{2}\varepsilon \right) ^{\frac{2}{3}k}. \end{align*} $$Select ![]() $\varepsilon $ small enough (the threshold
$\varepsilon $ small enough (the threshold ![]() $\eta $ is also determined here) so that
$\eta $ is also determined here) so that  $CC_{0}^{2}\varepsilon <\frac {1}{4}$ and then select T small enough so that
$CC_{0}^{2}\varepsilon <\frac {1}{4}$ and then select T small enough so that  $CC_{0}^{3}T^{\frac {1}{7}}M_{0}^{\frac {3}{5}} <\frac {1 }{4}$. We then have
$CC_{0}^{3}T^{\frac {1}{7}}M_{0}^{\frac {3}{5}} <\frac {1 }{4}$. We then have
 $$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\gamma ^{(1)}(t_{1})\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}}\leq \left( \frac{1}{ 2}\right) ^{k}\rightarrow 0\text{ as }k\rightarrow \infty. \end{align*} $$
$$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\gamma ^{(1)}(t_{1})\right\rVert _{L_{t_{1}}^{\infty }L_{x_{1},x^{\prime}_{1}}^{2}}\leq \left( \frac{1}{ 2}\right) ^{k}\rightarrow 0\text{ as }k\rightarrow \infty. \end{align*} $$We can then bootstrap to fill the whole interval ![]() $\left [ 0,T_{0}\right ]$, as M applies uniformly on
$\left [ 0,T_{0}\right ]$, as M applies uniformly on ![]() $[0,T_{0}].$
$[0,T_{0}].$
Before moving into the proof of Proposition 3.7, we remark that the extra ![]() $2T$ does not imply that the estimate is critical or subcritical; this T actually appears only once. Such a T is due to the GP-hierarchy method instead of scaling, because the
$2T$ does not imply that the estimate is critical or subcritical; this T actually appears only once. Such a T is due to the GP-hierarchy method instead of scaling, because the ![]() $dt_{k+1}$ time integral is not used for any Strichartz-type estimates. This one factor of T appears in the other energy-critical
$dt_{k+1}$ time integral is not used for any Strichartz-type estimates. This one factor of T appears in the other energy-critical ![]() $\mathbb {T}^{3}$ quintic case [Reference Chen and Holmer24] as well.
$\mathbb {T}^{3}$ quintic case [Reference Chen and Holmer24] as well.
3.1 Proof of Lemma 3.3 and uniform-in-time frequency localisation for the NLS
We provide a direct proof using the equation, even though one could look for a more abstract proof. By substituting the equation, we compute
 $$ \begin{align*} \left\lvert \partial _{t}\left\lVert \nabla P_{\leq M}u\right\rVert _{L_{x}^{2}}^{2}\right\rvert & =2\left\lvert \operatorname{Im} \int P_{\leq M}\nabla u\cdot P_{\leq M}\nabla \left(\lvert u\rvert^{2}u\right)dx\right\rvert \\ & \leq 2\left\lVert P_{\leq M}\nabla u\right\rVert _{L^{4}}\left\lVert P_{\leq M}\nabla \left(\lvert u\rvert^{2}u\right)\right\rVert _{L^{4/3}} \\ & =2M^{2}\left\lVert \tilde{P}_{\leq M}u\right\rVert _{L^{4}}\left\lVert \tilde{P}_{\leq M}\left(\lvert u\rvert^{2}u\right)\right\rVert _{L^{4/3}}, \end{align*} $$
$$ \begin{align*} \left\lvert \partial _{t}\left\lVert \nabla P_{\leq M}u\right\rVert _{L_{x}^{2}}^{2}\right\rvert & =2\left\lvert \operatorname{Im} \int P_{\leq M}\nabla u\cdot P_{\leq M}\nabla \left(\lvert u\rvert^{2}u\right)dx\right\rvert \\ & \leq 2\left\lVert P_{\leq M}\nabla u\right\rVert _{L^{4}}\left\lVert P_{\leq M}\nabla \left(\lvert u\rvert^{2}u\right)\right\rVert _{L^{4/3}} \\ & =2M^{2}\left\lVert \tilde{P}_{\leq M}u\right\rVert _{L^{4}}\left\lVert \tilde{P}_{\leq M}\left(\lvert u\rvert^{2}u\right)\right\rVert _{L^{4/3}}, \end{align*} $$where if the symbol associated to ![]() $P_{\leq M}$ is
$P_{\leq M}$ is ![]() $\chi (\xi /M)$, then the symbol associated to
$\chi (\xi /M)$, then the symbol associated to ![]() $\tilde {P}_{\leq M}$ is
$\tilde {P}_{\leq M}$ is ![]() $\tilde {\chi }(\xi /M)$, with
$\tilde {\chi }(\xi /M)$, with ![]() $ \tilde {\chi }(\xi )=\xi \chi (\xi )$. By the
$ \tilde {\chi }(\xi )=\xi \chi (\xi )$. By the ![]() $L^{p}\rightarrow L^{p}$ boundedness of the Littlewood–Paley projections (see, for example, [Reference Herr and Sohinger35, Appendix]),
$L^{p}\rightarrow L^{p}$ boundedness of the Littlewood–Paley projections (see, for example, [Reference Herr and Sohinger35, Appendix]),
 $$ \begin{align*} \left\lvert \partial _{t}\left\lVert \nabla P_{\leq M}u\right\rVert _{L_{x}^{2}}^{2}\right\rvert \lesssim M^{2}\lVert u\rVert _{L^{4}}^{4}. \end{align*} $$
$$ \begin{align*} \left\lvert \partial _{t}\left\lVert \nabla P_{\leq M}u\right\rVert _{L_{x}^{2}}^{2}\right\rvert \lesssim M^{2}\lVert u\rVert _{L^{4}}^{4}. \end{align*} $$By Sobolev embedding,
 $$ \begin{align*} \left\lvert \partial _{t}\left\lVert \nabla P_{\leq M}u\right\rVert _{L_{x}^{2}}^{2}\right\rvert \lesssim M^{2}\lVert u\rVert _{H^{1}}^{4}. \end{align*} $$
$$ \begin{align*} \left\lvert \partial _{t}\left\lVert \nabla P_{\leq M}u\right\rVert _{L_{x}^{2}}^{2}\right\rvert \lesssim M^{2}\lVert u\rVert _{H^{1}}^{4}. \end{align*} $$Hence there exists ![]() $\delta ^{\prime }>0$ – depending on M,
$\delta ^{\prime }>0$ – depending on M,  $\lVert u\rVert _{L_{\left [0,T\right ]}^{\infty }H^{1}}$ and
$\lVert u\rVert _{L_{\left [0,T\right ]}^{\infty }H^{1}}$ and ![]() $\varepsilon $ – such that for any
$\varepsilon $ – such that for any ![]() $ t_{0}\in \lbrack 0,T]$, it holds that for any
$ t_{0}\in \lbrack 0,T]$, it holds that for any ![]() $t\in (t_{0}-\delta ^{\prime },t_{0}+\delta ^{\prime })\cap \lbrack 0,T]$,
$t\in (t_{0}-\delta ^{\prime },t_{0}+\delta ^{\prime })\cap \lbrack 0,T]$,
 $$ \begin{align} \left\lvert \left\lVert \nabla P_{\leq M}u(t)\right\rVert _{L_{x}^{2}}^{2}-\left\lVert \nabla P_{\leq M}u(t_{0})\right\rVert _{L_{x}^{2}}^{2}\right\rvert \leq \tfrac{1}{16} \varepsilon ^{2}. \end{align} $$
$$ \begin{align} \left\lvert \left\lVert \nabla P_{\leq M}u(t)\right\rVert _{L_{x}^{2}}^{2}-\left\lVert \nabla P_{\leq M}u(t_{0})\right\rVert _{L_{x}^{2}}^{2}\right\rvert \leq \tfrac{1}{16} \varepsilon ^{2}. \end{align} $$On the other hand, since  $u\in C_{\left [0,T\right ]}^{0}H_{x}^{1}$, for each
$u\in C_{\left [0,T\right ]}^{0}H_{x}^{1}$, for each ![]() $t_{0}$ there exists
$t_{0}$ there exists ![]() $\delta ''>0$ such that for any
$\delta ''>0$ such that for any ![]() $t\in (t_{0}-\delta '',t_{0}+\delta '')\cap \lbrack 0,T]$,
$t\in (t_{0}-\delta '',t_{0}+\delta '')\cap \lbrack 0,T]$,
 $$ \begin{align} \left\lvert \left\lVert \nabla u(t)\right\rVert _{L_{x}^{2}}^{2}-\left\lVert \nabla u(t_{0})\right\rVert _{L_{x}^{2}}^{2}\right\rvert \leq \tfrac{1}{16}\varepsilon ^{2}. \end{align} $$
$$ \begin{align} \left\lvert \left\lVert \nabla u(t)\right\rVert _{L_{x}^{2}}^{2}-\left\lVert \nabla u(t_{0})\right\rVert _{L_{x}^{2}}^{2}\right\rvert \leq \tfrac{1}{16}\varepsilon ^{2}. \end{align} $$Note that ![]() $\delta ''$ depends on u itself (or the ‘modulus of continuity’ of u), unlike
$\delta ''$ depends on u itself (or the ‘modulus of continuity’ of u), unlike ![]() $ \delta '$, which depends only on M,
$ \delta '$, which depends only on M,  $\lVert u\rVert _{L_{\left [0,T\right ]}^{\infty }H^{1}}$ and
$\lVert u\rVert _{L_{\left [0,T\right ]}^{\infty }H^{1}}$ and ![]() $\varepsilon $. Now let
$\varepsilon $. Now let ![]() $\delta =\min (\delta ',\delta '')$. Then by formulas (3.11) and (3.12), we have that for any
$\delta =\min (\delta ',\delta '')$. Then by formulas (3.11) and (3.12), we have that for any ![]() $t\in (t_{0}-\delta ,t_{0}+\delta )\cap \lbrack 0,T]$,
$t\in (t_{0}-\delta ,t_{0}+\delta )\cap \lbrack 0,T]$,
 $$ \begin{align*} \left\lvert \left\lVert \nabla P_{>M}u(t)\right\rVert _{L_{x}^{2}}^{2}-\left\lVert \nabla P_{>M}u(t_{0})\right\rVert _{L_{x}^{2}}^{2}\right\rvert \leq \tfrac{1}{4}\varepsilon ^{2}. \end{align*} $$
$$ \begin{align*} \left\lvert \left\lVert \nabla P_{>M}u(t)\right\rVert _{L_{x}^{2}}^{2}-\left\lVert \nabla P_{>M}u(t_{0})\right\rVert _{L_{x}^{2}}^{2}\right\rvert \leq \tfrac{1}{4}\varepsilon ^{2}. \end{align*} $$For each ![]() $t\in \lbrack 0,T]$, there exists
$t\in \lbrack 0,T]$, there exists ![]() $M_{t}$ such that
$M_{t}$ such that
 $$ \begin{align*} \left\lVert \nabla P_{>M_{t}}u(t)\right\rVert _{L_{x}^{2}}\leq \tfrac{1}{2}\varepsilon. \end{align*} $$
$$ \begin{align*} \left\lVert \nabla P_{>M_{t}}u(t)\right\rVert _{L_{x}^{2}}\leq \tfrac{1}{2}\varepsilon. \end{align*} $$ By the foregoing, there exists ![]() $\delta _{t}>0$ such that on
$\delta _{t}>0$ such that on ![]() $(t-\delta _{t},t+\delta _{t})$, we have
$(t-\delta _{t},t+\delta _{t})$, we have
 $$ \begin{align*} \left\lVert \nabla P_{>M_{t}}u\right\rVert _{L_{\left(t-\delta _{t},t+\delta _{t}\right)}^{\infty }L_{x}^{2}}\leq \varepsilon. \end{align*} $$
$$ \begin{align*} \left\lVert \nabla P_{>M_{t}}u\right\rVert _{L_{\left(t-\delta _{t},t+\delta _{t}\right)}^{\infty }L_{x}^{2}}\leq \varepsilon. \end{align*} $$Here, ![]() $\delta _{t}>0$ depends on u and
$\delta _{t}>0$ depends on u and ![]() $M_{t}$. The collection of intervals
$M_{t}$. The collection of intervals ![]() $(t-\delta _{t},t+\delta _{t})$ as t ranges over
$(t-\delta _{t},t+\delta _{t})$ as t ranges over ![]() $[0,T]$ is an open cover of
$[0,T]$ is an open cover of ![]() $[0,T]$. Let
$[0,T]$. Let
be an open cover of ![]() $[0,T]$. Letting
$[0,T]$. Letting
we have established formula (3.3).
Now conversely suppose that  $u\in C_{\left [0,T\right ]}^0H_{x,\text {weak}}^1\cap C_{\left [0,T\right ]}^1H_{x,\text {weak}}^{-1}$ and satisfies formula (3.3). Then we claim that
$u\in C_{\left [0,T\right ]}^0H_{x,\text {weak}}^1\cap C_{\left [0,T\right ]}^1H_{x,\text {weak}}^{-1}$ and satisfies formula (3.3). Then we claim that  $u\in C_{\left [0,T\right ]}^0H_x^1 \cap C_{\left [0,T\right ]}^1 H_x^{-1}$. Let
$u\in C_{\left [0,T\right ]}^0H_x^1 \cap C_{\left [0,T\right ]}^1 H_x^{-1}$. Let ![]() $t_0\in [0,T]$ be arbitrary. If u is not strongly continuous at
$t_0\in [0,T]$ be arbitrary. If u is not strongly continuous at ![]() $t_0$, then there exist
$t_0$, then there exist ![]() $\epsilon>0$ and a sequence
$\epsilon>0$ and a sequence ![]() $t_k \to t_0$ such that
$t_k \to t_0$ such that ![]() $\lVert u(t_k) - u(t_0) \rVert _{H_x^1}> 2\epsilon $. Then for each k, there exists
$\lVert u(t_k) - u(t_0) \rVert _{H_x^1}> 2\epsilon $. Then for each k, there exists ![]() $\phi _k \in H_x^{-1} $ with
$\phi _k \in H_x^{-1} $ with ![]() $\lVert \phi _k \rVert _{H_x^{-1}} \leq 1$ and
$\lVert \phi _k \rVert _{H_x^{-1}} \leq 1$ and
Get M as in formula (3.3). Then
On the other hand, by the Rellich–Kondrachov compactness theorem, there exists a subsequence such that ![]() $P_{\leq M} \phi _k \to \phi $ in
$P_{\leq M} \phi _k \to \phi $ in ![]() $H_x^{-1}$. This combined with the assumption that u is weakly continuous implies that
$H_x^{-1}$. This combined with the assumption that u is weakly continuous implies that
But formulas (3.14) and (3.15) contradict formula (3.13). The proof that ![]() $\partial _t u$ is strongly continuous is similarly straightforward.
$\partial _t u$ is strongly continuous is similarly straightforward.
4 An extended KM board game
This section is divided into two main parts. First, in Section 4.1, we provide as a warm-up a more elaborated proof of the original KM board game (Lemma 3.6), which yields the previously unknown time integration limits in equation (3.8). We then prove, in Sections 4.2–4.5, an extension of Lemma 3.6 which further combines the summands inside  $J^{(k+1)}\left (f^{(k+1)}\right )\left (t_{1},\underline {t}_{k+1}\right )$ to enable the application of U-V space techniques.
$J^{(k+1)}\left (f^{(k+1)}\right )\left (t_{1},\underline {t}_{k+1}\right )$ to enable the application of U-V space techniques.
4.1 A more elaborated proof of Lemma 3.6
Let us first give a brief review of the original KM board game, which since its invention has been used in every paper involving the analysis of Gross–Pitaevskii hierarchies. Recall the notation of ![]() $ \mu $ in Lemma 3.6:
$ \mu $ in Lemma 3.6: ![]() $\left \{ \mu \right \} $ is a set of maps from
$\left \{ \mu \right \} $ is a set of maps from ![]() $\{2,\dotsc ,k+1\}$ to
$\{2,\dotsc ,k+1\}$ to ![]() $\{1,\dotsc ,k\}$ satisfying
$\{1,\dotsc ,k\}$ satisfying ![]() $\mu (2)=1$ and
$\mu (2)=1$ and ![]() $\mu (l)<l$ for all
$\mu (l)<l$ for all ![]() $l,$ and
$l,$ and
 $$ \begin{align*} J_{\mu}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right) &=U^{(1)}(t_{1}-t_{2})B_{1,2}U^{(2)}(t_{2}-t_{3})B_{\mu(3),3}\dotsm \\ &\dotsm U^{(k)}(t_{k}-t_{k+1})B_{\mu(k+1),k+1}\left(f^{(k+1)}(t_{k+1})\right). \end{align*} $$
$$ \begin{align*} J_{\mu}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right) &=U^{(1)}(t_{1}-t_{2})B_{1,2}U^{(2)}(t_{2}-t_{3})B_{\mu(3),3}\dotsm \\ &\dotsm U^{(k)}(t_{k}-t_{k+1})B_{\mu(k+1),k+1}\left(f^{(k+1)}(t_{k+1})\right). \end{align*} $$Example 1. An example of ![]() $\mu $ when
$\mu $ when ![]() $k=5$ is
$k=5$ is
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 \\ \hline \mu & 1 & 1 & 3 & 2 & 1 \\ \end{array}. \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 \\ \hline \mu & 1 & 1 & 3 & 2 & 1 \\ \end{array}. \end{align*} $$ If ![]() $\mu $ satisfies
$\mu $ satisfies ![]() $\mu (j)\leq \mu (j+1)$ for
$\mu (j)\leq \mu (j+1)$ for ![]() $2\leq j\leq k$ in addition to
$2\leq j\leq k$ in addition to ![]() $\mu (j)<j$ for all
$\mu (j)<j$ for all ![]() $2\leq j\leq k+1$, then it is in upper-echelon form Footnote 16 in the terminology of [Reference Klainerman and Machedon47].
$2\leq j\leq k+1$, then it is in upper-echelon form Footnote 16 in the terminology of [Reference Klainerman and Machedon47].
Let ![]() $\mu $ be a collapsing map as already defined and
$\mu $ be a collapsing map as already defined and ![]() $\sigma $ a permutation of
$\sigma $ a permutation of ![]() $\{2,\dotsc ,k+1\}$. A Klainerman–Machedon acceptable move, which we denote
$\{2,\dotsc ,k+1\}$. A Klainerman–Machedon acceptable move, which we denote ![]() $\text {KM}(j,j+1)$, is allowed when
$\text {KM}(j,j+1)$, is allowed when ![]() $\mu (j)\neq \mu (j+1)$ and
$\mu (j)\neq \mu (j+1)$ and ![]() $ \mu (j+1)<j$, and is the following action:
$ \mu (j+1)<j$, and is the following action: ![]() $(\mu ',\sigma ')=\text {KM}(j,j+1)(\mu ,\sigma )$:
$(\mu ',\sigma ')=\text {KM}(j,j+1)(\mu ,\sigma )$:
 $$ \begin{align*} \mu' & =(j,j+1)\circ \mu \circ (j,j+1), \\ \sigma' & =(j,j+1)\circ \sigma. \end{align*} $$
$$ \begin{align*} \mu' & =(j,j+1)\circ \mu \circ (j,j+1), \\ \sigma' & =(j,j+1)\circ \sigma. \end{align*} $$A key observation of Klainerman and Machedon [Reference Klainerman and Machedon47] is that if ![]() $(\mu ',\sigma ')=\text {KM}(j,j+1)(\mu ,\sigma )$ and
$(\mu ',\sigma ')=\text {KM}(j,j+1)(\mu ,\sigma )$ and ![]() $f^{(k+1)}$ is a symmetric density, then
$f^{(k+1)}$ is a symmetric density, then
 $$ \begin{align} J_{\mu'}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\sigma^{\prime\,-1}\left(\underline{t}_{k+1}\right)\right)=J_{\mu }^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\sigma ^{-1}\left(\underline{t}_{k+1}\right)\right), \end{align} $$
$$ \begin{align} J_{\mu'}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\sigma^{\prime\,-1}\left(\underline{t}_{k+1}\right)\right)=J_{\mu }^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\sigma ^{-1}\left(\underline{t}_{k+1}\right)\right), \end{align} $$where for ![]() $\underline {t}_{k+1}=(t_{2},\dotsc ,t_{k+1})$ we define
$\underline {t}_{k+1}=(t_{2},\dotsc ,t_{k+1})$ we define
 $$ \begin{align*} \sigma ^{-1}\left(\underline{t}_{k+1}\right)=\left(t_{\sigma ^{-1}(2)},\dotsc ,t_{\sigma ^{-1}(k+1)}\right). \end{align*} $$
$$ \begin{align*} \sigma ^{-1}\left(\underline{t}_{k+1}\right)=\left(t_{\sigma ^{-1}(2)},\dotsc ,t_{\sigma ^{-1}(k+1)}\right). \end{align*} $$Associated to each ![]() $\mu $ and
$\mu $ and ![]() $\sigma $, we define the Duhamel integrals
$\sigma $, we define the Duhamel integrals
 $$ \begin{align} I\left(\mu ,\sigma ,f^{(k+1)}\right)(t_{1})=\int_{t_{1}\geq t_{\sigma (2)}\geq \dotsb \geq t_{\sigma (k+1)}}J_{\mu }^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align} $$
$$ \begin{align} I\left(\mu ,\sigma ,f^{(k+1)}\right)(t_{1})=\int_{t_{1}\geq t_{\sigma (2)}\geq \dotsb \geq t_{\sigma (k+1)}}J_{\mu }^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align} $$It follows from equation (4.1) that
 $$ \begin{align*} I\left(\mu',\sigma',f^{(k+1)}\right)=I\left(\mu ,\sigma ,f^{(k+1)}\right). \end{align*} $$
$$ \begin{align*} I\left(\mu',\sigma',f^{(k+1)}\right)=I\left(\mu ,\sigma ,f^{(k+1)}\right). \end{align*} $$It is clear that we can combine Klainerman–Machedon acceptable moves as follows: If ![]() $\rho $ is a permutation of
$\rho $ is a permutation of ![]() $\{2,\dotsc ,k+1\}$ such that it is possible to write it as a composition of transpositions
$\{2,\dotsc ,k+1\}$ such that it is possible to write it as a composition of transpositions
for which each operator ![]() $\text {KM}\left (\tau _{j}\right )$ on the right side of
$\text {KM}\left (\tau _{j}\right )$ on the right side of
 $$ \begin{align*} \text{KM}(\rho )\overset{\text{def}}{=}\text{KM}(\tau _{1})\circ \dotsb \circ \text{KM}(\tau _{r}) \end{align*} $$
$$ \begin{align*} \text{KM}(\rho )\overset{\text{def}}{=}\text{KM}(\tau _{1})\circ \dotsb \circ \text{KM}(\tau _{r}) \end{align*} $$is an acceptable action, then ![]() $\text {KM}(\rho )$, defined by this composition, is acceptable as well. In this case,
$\text {KM}(\rho )$, defined by this composition, is acceptable as well. In this case, ![]() $(\mu ',\sigma ')=\text {KM}(\rho )(\mu ,\sigma )$ and
$(\mu ',\sigma ')=\text {KM}(\rho )(\mu ,\sigma )$ and
 $$ \begin{align*} \mu' & = \rho \circ \mu \circ \rho^{-1}, \\ \sigma' & =\rho \circ \sigma, \end{align*} $$
$$ \begin{align*} \mu' & = \rho \circ \mu \circ \rho^{-1}, \\ \sigma' & =\rho \circ \sigma, \end{align*} $$ and equations (4.1) and (4.2) hold. If ![]() $\mu $ and
$\mu $ and ![]() $\mu ^{\prime }$ are such that there exists
$\mu ^{\prime }$ are such that there exists ![]() $\rho $ for which
$\rho $ for which ![]() $(\mu ',\sigma ')=\text {KM}(\rho )(\mu ,\sigma )$, then we say that
$(\mu ',\sigma ')=\text {KM}(\rho )(\mu ,\sigma )$, then we say that ![]() $\mu '$ and
$\mu '$ and ![]() $\mu $ are KM-relatable. This is an equivalence relation that partitions the set of collapsing maps into equivalence classes.
$\mu $ are KM-relatable. This is an equivalence relation that partitions the set of collapsing maps into equivalence classes.
In short, one can describe the KM board game in [Reference Klainerman and Machedon47] which combines the ![]() $k!$ many terms in
$k!$ many terms in  $J^{(k+1)}\left (f^{(k+1)}\right )$ as follows:
$J^{(k+1)}\left (f^{(k+1)}\right )$ as follows:
Algorithm 1. [Reference Klainerman and Machedon47]
1. Convert each of the
 $k!$ many
$k!$ many  $\mu ^{\prime }_{\text {in}}$s in
$\mu ^{\prime }_{\text {in}}$s in  $J^{(k+1)}\left (f^{(k+1)}\right )$ into one of the
$J^{(k+1)}\left (f^{(k+1)}\right )$ into one of the  $\leq 4^{k}$ many upper-echelon forms
$\leq 4^{k}$ many upper-echelon forms  $\mu _{\text {out}}$ via acceptable moves, defined in the board-game argument, and at the same time produce an array
$\mu _{\text {out}}$ via acceptable moves, defined in the board-game argument, and at the same time produce an array  $\sigma $ which changes the time integration domain from the simplex into the simplex
$\sigma $ which changes the time integration domain from the simplex into the simplex $$ \begin{align*} t_{1}\geq t_{2}\geq t_{3}\geq \dotsb \geq t_{k+1} \end{align*} $$Hence, there are
$$ \begin{align*} t_{1}\geq t_{2}\geq t_{3}\geq \dotsb \geq t_{k+1} \end{align*} $$Hence, there are $$ \begin{align*} t_{1}\geq t_{\sigma (2)}\geq t_{\sigma (3)}\dotsb\geq t_{\sigma \left( k+1\right) }. \end{align*} $$
$$ \begin{align*} t_{1}\geq t_{\sigma (2)}\geq t_{\sigma (3)}\dotsb\geq t_{\sigma \left( k+1\right) }. \end{align*} $$ $\leq 4^{k}$ classes on the right-hand side of equation (3.8).
$\leq 4^{k}$ classes on the right-hand side of equation (3.8).2. For each upper-echelon form
 $\mu _{\text {out}}$, take a union of the time integration domains of its
$\mu _{\text {out}}$, take a union of the time integration domains of its  $\mu _{\text {in}}$s after the acceptable moves and use it as the time integration domain for the whole class. Thus, the integration domain
$\mu _{\text {in}}$s after the acceptable moves and use it as the time integration domain for the whole class. Thus, the integration domain  $D_{m}$ on the right-hand side of equation (3.8) depends on
$D_{m}$ on the right-hand side of equation (3.8) depends on  $\mu _{m}$, and we have successfully combined
$\mu _{m}$, and we have successfully combined  $k!$ summands into
$k!$ summands into  $\leq 4^{k}$ summands.
$\leq 4^{k}$ summands.
The key take away in Algorithm 1 is that, although it is very much not obvious, quite a few of the summands in  $J^{(k+1)}\left (f^{(k+1)}\right )$ actually have the same integrand if one switches the variable labellings in a clever way. Algorithm 1 leaves only one ambiguity – the time integration domain
$J^{(k+1)}\left (f^{(k+1)}\right )$ actually have the same integrand if one switches the variable labellings in a clever way. Algorithm 1 leaves only one ambiguity – the time integration domain ![]() $D_{m}$ – which is obviously very complicated for large
$D_{m}$ – which is obviously very complicated for large ![]() $k,$ as it is a union of a very large number of simplexes in high dimension under the action of a proper subset of the permutation group
$k,$ as it is a union of a very large number of simplexes in high dimension under the action of a proper subset of the permutation group ![]() $ S_{k} $ depending on the integrand. So far, for the analysis of GP hierarchies on
$ S_{k} $ depending on the integrand. So far, for the analysis of GP hierarchies on ![]() $\mathbb {R}^{d}/$
$\mathbb {R}^{d}/$![]() $\mathbb {T}^{d}$,
$\mathbb {T}^{d}$, ![]() $d\leq 3$, knowing
$d\leq 3$, knowing ![]() $ D_{m}\subset \left [ 0,1\right ] ^{k}$ has been enough, as the related
$ D_{m}\subset \left [ 0,1\right ] ^{k}$ has been enough, as the related ![]() $ L_{t}^{1}H^{s}$ estimates are true.
$ L_{t}^{1}H^{s}$ estimates are true. ![]() $\mathbb {T}^{4}$ appears to be the first domain on which one has to know what
$\mathbb {T}^{4}$ appears to be the first domain on which one has to know what ![]() $D_{m}$ is so that one can at least have a chance to use space-time norms like
$D_{m}$ is so that one can at least have a chance to use space-time norms like ![]() $X_{s,b}$ and U-V, as the related
$X_{s,b}$ and U-V, as the related ![]() $L_{t}^{1}H^{s}$ estimates are difficult to prove and may not even be true.
$L_{t}^{1}H^{s}$ estimates are difficult to prove and may not even be true.
It turns out that ![]() $D_{m}$ is in fact simple, as we will see. We now present a more elaborated proof of Lemma 3.6, in which
$D_{m}$ is in fact simple, as we will see. We now present a more elaborated proof of Lemma 3.6, in which ![]() $D_{m}$ is computed in a clear way. Given a
$D_{m}$ is computed in a clear way. Given a ![]() $\mu $, and hence a summand inside
$\mu $, and hence a summand inside  $J^{(k+1)}\left (f^{(k+1)}\right )$, we construct a binary tree with the following algorithm:
$J^{(k+1)}\left (f^{(k+1)}\right )$, we construct a binary tree with the following algorithm:
1. Set counter
 $j=2$.
$j=2$.2. Given j, find the next pair of indices a and b so that
 $a>j$,
$a>j$,  $b>j$, and moreover a and b are the minimal indices for which the equalities hold. It is possible that there is no such a or no such b.
$b>j$, and moreover a and b are the minimal indices for which the equalities hold. It is possible that there is no such a or no such b. $$ \begin{align*} \mu (a)=\mu (j),\qquad\mu (b)=j, \end{align*} $$
$$ \begin{align*} \mu (a)=\mu (j),\qquad\mu (b)=j, \end{align*} $$3. At the node j, put a as the left child and b as the right child (if there is no a, then the j node will be missing a left child, and if there is no b, then the j node will be missing a right child).
4. If
 $j=k+1,$ then stop; otherwise set
$j=k+1,$ then stop; otherwise set  $j=j+1$ and go to step 2.
$j=j+1$ and go to step 2.

Let us work with the following exampleFootnote 17:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 \\ \hline \mu_{\text{out}} & 1 & 1 & 1 & 2 & 3\\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 \\ \hline \mu_{\text{out}} & 1 & 1 & 1 & 2 & 3\\ \end{array} \end{align*} $$We start with ![]() $j=2$, and note that
$j=2$, and note that ![]() $\mu _{\text {out}}(2)=1$, so we need to find minimal
$\mu _{\text {out}}(2)=1$, so we need to find minimal ![]() $a>2, b>2$, such that
$a>2, b>2$, such that ![]() $\mu (a)=1$ and
$\mu (a)=1$ and ![]() $\mu (b)=2$. In this case, it is
$\mu (b)=2$. In this case, it is ![]() $a=3$ and
$a=3$ and ![]() $b=5$, so we put those as the left and right children of
$b=5$, so we put those as the left and right children of ![]() $2$, respectively, in the tree shown at left.
$2$, respectively, in the tree shown at left.

Now we move to ![]() $j=3$. Since
$j=3$. Since ![]() $\mu _{\text {out}}(3)=1$, we find minimal a and b so that
$\mu _{\text {out}}(3)=1$, we find minimal a and b so that ![]() $a>3$,
$a>3$, ![]() $b>3$,
$b>3$, ![]() $\mu (a)=1$ and
$\mu (a)=1$ and ![]() $\mu (b)=3$. We find that
$\mu (b)=3$. We find that ![]() $ a=4$ and
$ a=4$ and ![]() $b=6$, so we put these as the left and right children of
$b=6$, so we put these as the left and right children of ![]() $3$, respectively, in the tree shown at left. Since all indices appear in the tree, it is complete.
$3$, respectively, in the tree shown at left. Since all indices appear in the tree, it is complete.
Definition 4.1. A binary tree is called an admissible tree if every child node’s label is strictly larger than its parent node’s label.Footnote 18 For an admissible tree, we call the graph of the tree without any labels in its nodes the skeleton of the tree.

For example, the skeleton of the tree in Example 2 is shown at left.
By the hierarchy structure, Algorithm 2, which produces a tree from a ![]() $\mu $, produces only admissible trees. As we have made a distinction between left and right children in the algorithm, the procedure is reversible – given an admissible binary tree, we can uniquely reconstruct the
$\mu $, produces only admissible trees. As we have made a distinction between left and right children in the algorithm, the procedure is reversible – given an admissible binary tree, we can uniquely reconstruct the ![]() $\mu $ that generated it.
$\mu $ that generated it.
1. For every right child,
 $\mu $ maps the child value to the parent value (that is, if f is a right child of d, then
$\mu $ maps the child value to the parent value (that is, if f is a right child of d, then  $\mu (f)=d$). Start by filling these into the
$\mu (f)=d$). Start by filling these into the  $\mu $ table.
$\mu $ table.2. Fill in the table using the fact that for every left child,
 $\mu $ maps the child value to
$\mu $ maps the child value to  $\mu $ (the parent value).
$\mu $ (the parent value).
Example 3. Suppose we are given the following tree:

Using the fact that for every right child, ![]() $\mu $ maps the child value to the parent value, we fill in the following values in the
$\mu $ maps the child value to the parent value, we fill in the following values in the ![]() $\mu $ table:
$\mu $ table:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline \mu & 1 & & & 2 & 3 & 4 & 6 & \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline \mu & 1 & & & 2 & 3 & 4 & 6 & \\ \end{array} \end{align*} $$Now we use the left-child rule and note that since ![]() $3$ is a left child of
$3$ is a left child of ![]() $2$ and
$2$ and ![]() $\mu (2)=1$, we must have
$\mu (2)=1$, we must have ![]() $\mu (3)=1$, and so on, to recover the following table:
$\mu (3)=1$, and so on, to recover the following table:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline \mu & 1 & 1 & 1 & 2 & 3 & 4 & 6 & 6 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline \mu & 1 & 1 & 1 & 2 & 3 & 4 & 6 & 6 \\ \end{array} \end{align*} $$ One can show that in the tree representation of ![]() $\mu $, an acceptable move defined in [Reference Klainerman and Machedon47] is the operation which switches the labels of two nodes with consecutive labels on an admissible tree, provided that the outcome is still an admissible tree, by writing out the related trees on [Reference Klainerman and Machedon47, pp. 180–182]. For example, interchanging the labelling of 5 and 6 in the tree in Example 2 is an acceptable move. That is, acceptable moves in [Reference Klainerman and Machedon47] preserve the tree structures but permute the labelling under the admissibility requirement. Two collapsing maps
$\mu $, an acceptable move defined in [Reference Klainerman and Machedon47] is the operation which switches the labels of two nodes with consecutive labels on an admissible tree, provided that the outcome is still an admissible tree, by writing out the related trees on [Reference Klainerman and Machedon47, pp. 180–182]. For example, interchanging the labelling of 5 and 6 in the tree in Example 2 is an acceptable move. That is, acceptable moves in [Reference Klainerman and Machedon47] preserve the tree structures but permute the labelling under the admissibility requirement. Two collapsing maps ![]() $\mu $ and
$\mu $ and ![]() $\mu '$ are KM-relatable if and only if the trees corresponding to
$\mu '$ are KM-relatable if and only if the trees corresponding to ![]() $\mu $ and
$\mu $ and ![]() $\mu '$ have the same skeleton.
$\mu '$ have the same skeleton.
Given k, we would like to have the number of different binary tree structures of k nodes. This number is exactly defined as the Catalan number and is controlled by ![]() $4^{k}$. Hence, we have just provided a proof of the original KM board game, neglecting the trees showing the effects of acceptable moves on a tree.
$4^{k}$. Hence, we have just provided a proof of the original KM board game, neglecting the trees showing the effects of acceptable moves on a tree.
But now let us get to the main ‘elaborate’ part, namely, how to compute ![]() $D_{m}$ for a given upper-echelon class. To this end, we need to define what is an upper-echelon form. Though the requirement
$D_{m}$ for a given upper-echelon class. To this end, we need to define what is an upper-echelon form. Though the requirement ![]() $\mu (j)\leq \mu (j+1)$ for
$\mu (j)\leq \mu (j+1)$ for ![]() $2\leq j\leq k$ is good enough, we give an algorithm which produces the upper-echelon tree given the tree structure, as the tree representation of an upper-echelon form is in fact labelled in sequential order (see, for example, the tree in Example 2).
$2\leq j\leq k$ is good enough, we give an algorithm which produces the upper-echelon tree given the tree structure, as the tree representation of an upper-echelon form is in fact labelled in sequential order (see, for example, the tree in Example 2).
1. Given a tree structure with k nodes, label the top node with
 $2$ and set a counter
$2$ and set a counter  $j=2.$
$j=2.$2. If
 $j=k+1$, then stop; otherwise, continue.
$j=k+1$, then stop; otherwise, continue.3. If the node labelled j has a left child, then label that left child node with
 $j+1$, set a counter
$j+1$, set a counter  $j=j+1$ and go to step 2. If not, continue.Footnote 19
$j=j+1$ and go to step 2. If not, continue.Footnote 194. In the already-labelled nodes which have an empty right child, search for the node with the smallest label. If such a node can be found, label that node’s empty right child as
 $j+1$, set a counter
$j+1$, set a counter  $j=j+1$ and go to step 2. If none of the labelled nodes has an empty right child, then stop.
$j=j+1$ and go to step 2. If none of the labelled nodes has an empty right child, then stop.
Definition 4.2. We say ![]() $\mu $ is in upper-echelon form if
$\mu $ is in upper-echelon form if ![]() $\mu (j)\leq \mu (j+1)$ for
$\mu (j)\leq \mu (j+1)$ for ![]() $2\leq j\leq k$ or if its corresponding tree given by Algorithm 2 agrees with the tree with the same skeleton given by Algorithm 4.
$2\leq j\leq k$ or if its corresponding tree given by Algorithm 2 agrees with the tree with the same skeleton given by Algorithm 4.
We define a map ![]() $T_{D}$ which maps an upper-echelon tree to a time integration domain (a set of inequality relations) by
$T_{D}$ which maps an upper-echelon tree to a time integration domain (a set of inequality relations) by
 $$ \begin{align} T_{D}(\alpha )=\left\{ t_{j}\geq t_{k}:j,k\text{ are labels on nodes of }\alpha \text{ such that the }k\text{ node is a child of the }j\text{ node} \right\}, \end{align} $$
$$ \begin{align} T_{D}(\alpha )=\left\{ t_{j}\geq t_{k}:j,k\text{ are labels on nodes of }\alpha \text{ such that the }k\text{ node is a child of the }j\text{ node} \right\}, \end{align} $$where ![]() $\alpha $ is an upper-echelon tree. We then have the integration domain as follows:
$\alpha $ is an upper-echelon tree. We then have the integration domain as follows:
Proposition 4.3. Given a ![]() $\mu _{m}$ in upper-echelon form, we have
$\mu _{m}$ in upper-echelon form, we have
 $$ \begin{align*} \sum_{\mu \sim \mu _{m}}\int_{t_{1}\geq t_{2}\geq t_{3}\geq \dotsb\geq t_{k+1}}J_{\mu }^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d \underline{t}_{k+1}=\int_{T_{D}\left(\mu _{m}\right)}J_{\mu _{m}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align*} $$
$$ \begin{align*} \sum_{\mu \sim \mu _{m}}\int_{t_{1}\geq t_{2}\geq t_{3}\geq \dotsb\geq t_{k+1}}J_{\mu }^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d \underline{t}_{k+1}=\int_{T_{D}\left(\mu _{m}\right)}J_{\mu _{m}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align*} $$Here, ![]() $\mu \sim \mu _{m}$ means that
$\mu \sim \mu _{m}$ means that ![]() $\mu $ is equivalent to
$\mu $ is equivalent to ![]() $\mu _{m}$ under acceptable moves (the trees representing
$\mu _{m}$ under acceptable moves (the trees representing ![]() $\mu $ and
$\mu $ and ![]() $\mu _{m}$ have the same structure) and
$\mu _{m}$ have the same structure) and ![]() $T_{D}(\mu _{m})$ is the domain defined in equation (4.3).
$T_{D}(\mu _{m})$ is the domain defined in equation (4.3).
Proof. We prove by an example, as the notation is already heavy. For the general case, one merely needs to rewrite ![]() $\Sigma _{1}$ and
$\Sigma _{1}$ and ![]() $\Sigma _{2}$, to be defined in this proof. The key is the admissible condition or the simple requirement that the child must carry a larger label than the parent.
$\Sigma _{2}$, to be defined in this proof. The key is the admissible condition or the simple requirement that the child must carry a larger label than the parent.
Recall the upper-echelon tree in Example 2 and denote it with ![]() $\alpha $. Here are all the admissible trees equivalent to
$\alpha $. Here are all the admissible trees equivalent to ![]() $\alpha $:
$\alpha $:

We first read by definition that
Let ![]() $\sigma $ denote some composition of acceptable moves. We then notice the equivalence of the two sets
$\sigma $ denote some composition of acceptable moves. We then notice the equivalence of the two sets
 $$ \begin{align*} \Sigma _{1} &=\left\{ \sigma :\sigma ^{-1}(1)<\sigma ^{-1}(2)<\sigma ^{-1}(3)<\sigma ^{-1}(4),\sigma ^{-1}(2)<\sigma ^{-1}(5),\sigma ^{-1}(3)<\sigma ^{-1}(6)\right\} , \\ \Sigma _{2} &=\left\{ \sigma :\sigma \text{ takes input tree to }\alpha \text{ where the input tree is admissible}\right\}, \end{align*} $$
$$ \begin{align*} \Sigma _{1} &=\left\{ \sigma :\sigma ^{-1}(1)<\sigma ^{-1}(2)<\sigma ^{-1}(3)<\sigma ^{-1}(4),\sigma ^{-1}(2)<\sigma ^{-1}(5),\sigma ^{-1}(3)<\sigma ^{-1}(6)\right\} , \\ \Sigma _{2} &=\left\{ \sigma :\sigma \text{ takes input tree to }\alpha \text{ where the input tree is admissible}\right\}, \end{align*} $$both generated by the requirement that the child must carry a larger label than the parent. That is, both ![]() $\Sigma _{1}$ and
$\Sigma _{1}$ and ![]() $\Sigma _{2}$ classify the whole upper-echelon class represented by
$\Sigma _{2}$ classify the whole upper-echelon class represented by ![]() $\alpha $.
$\alpha $.
Hence,
 $$ \begin{align*} \bigcup _{\sigma \in \Sigma _{1}}\left\{ t_{1}\geq t_{\sigma(2)}\geq t_{\sigma (3)}\dotsb\geq t_{\sigma \left( 6\right) }\right\} =\{t_{1}\geq t_{2}\geq t_{3}\geq t_{4},t_{2}\geq t_{5},t_{3}\geq t_{6}\}=T_{D}(\alpha ), \end{align*} $$
$$ \begin{align*} \bigcup _{\sigma \in \Sigma _{1}}\left\{ t_{1}\geq t_{\sigma(2)}\geq t_{\sigma (3)}\dotsb\geq t_{\sigma \left( 6\right) }\right\} =\{t_{1}\geq t_{2}\geq t_{3}\geq t_{4},t_{2}\geq t_{5},t_{3}\geq t_{6}\}=T_{D}(\alpha ), \end{align*} $$and we are done.
4.2 Signed KM acceptable moves
While Proposition 4.3 shows that summing over an entire KM upper-echelon class yields a time integration domain with clean structure, it is not sufficient for our purposes. We prove an extended KM board game in Sections 4.2–4.5. Recall the key observation of the KM board game: Many summands in  $J^{(k+1)}\left (f^{(k+1)}\right )$ actually have the same integrand if one switches the variable labellings, and thus one can take the acceptable moves to combine them. In fact, one can combine them even more after the acceptable moves to get a larger integration domain
$J^{(k+1)}\left (f^{(k+1)}\right )$ actually have the same integrand if one switches the variable labellings, and thus one can take the acceptable moves to combine them. In fact, one can combine them even more after the acceptable moves to get a larger integration domain ![]() $D_{m}$.Footnote 20 Instead of aiming to reduce the number of summands in
$D_{m}$.Footnote 20 Instead of aiming to reduce the number of summands in  $J^{(k+1)}\left (f^{(k+1)}\right )$ even more, our goal this time is to enlarge the integration domain when estimating
$J^{(k+1)}\left (f^{(k+1)}\right )$ even more, our goal this time is to enlarge the integration domain when estimating  $J_{\mu ,\operatorname {sgn}}^{(k+1)}\left (f^{(k+1)}\right )\left (t_{1},\underline {t}_{k+1}\right )$, so that U-V techniques can actually apply. Depending on the sign combination in
$J_{\mu ,\operatorname {sgn}}^{(k+1)}\left (f^{(k+1)}\right )\left (t_{1},\underline {t}_{k+1}\right )$, so that U-V techniques can actually apply. Depending on the sign combination in  $J_{\mu _{m},\operatorname {sgn}}^{(k+1)}\left (f^{(k+1)}\right )\left (t_{1},\underline {t}_{k+1}\right )$, one could run into the problem of needing to estimate the x part and the
$J_{\mu _{m},\operatorname {sgn}}^{(k+1)}\left (f^{(k+1)}\right )\left (t_{1},\underline {t}_{k+1}\right )$, one could run into the problem of needing to estimate the x part and the ![]() $x'$ part using the same time integral. This problem is another obstacle stopping U-V space techniques from being used in the analysis of
$x'$ part using the same time integral. This problem is another obstacle stopping U-V space techniques from being used in the analysis of ![]() $GP$ hierarchies, separate from the other obstacle that
$GP$ hierarchies, separate from the other obstacle that ![]() $D_{m}$ was previously unknown.
$D_{m}$ was previously unknown.
From here on out, we denote the already unioned or combined integrals in one echelon class as a upper-echelon class integral, and we use Proposition 4.3 for its integration limits. We also put a ![]() $+$ or
$+$ or ![]() $ -$ sign at the corresponding node of a tree, as we are dealing with
$ -$ sign at the corresponding node of a tree, as we are dealing with  $J_{\mu ,\operatorname {sgn}}^{(k+1)}\left (f^{(k+1)}\right )\left (t_{1},\underline {t}_{k+1}\right )$, in which there are
$J_{\mu ,\operatorname {sgn}}^{(k+1)}\left (f^{(k+1)}\right )\left (t_{1},\underline {t}_{k+1}\right )$, in which there are ![]() $ B^{+}$ and
$ B^{+}$ and ![]() $B^{-}$ at each coupling. We start with the following example:
$B^{-}$ at each coupling. We start with the following example:
Example 4. Let us consider the two upper-echelon trees:

They have the upper-echelon class integrals
 $$ \begin{align*} I_{1} &= \int_{D_{1}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{-}U^{(2)}(t_{2}-t_{3})B_{1,3}^{+}U^{(3)}(t_{3}-t_{4})B_{2,4}^{+}\left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4}, \\ I_{2} &= \int_{D_{2}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{3}-t_{4})B_{3,4}^{+} \left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4}, \end{align*} $$
$$ \begin{align*} I_{1} &= \int_{D_{1}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{-}U^{(2)}(t_{2}-t_{3})B_{1,3}^{+}U^{(3)}(t_{3}-t_{4})B_{2,4}^{+}\left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4}, \\ I_{2} &= \int_{D_{2}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{3}-t_{4})B_{3,4}^{+} \left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4}, \end{align*} $$where ![]() $D_{1}=\{t_{2}\leq t_{1},t_{3}\leq t_{2},t_{4}\leq t_{2}\}$ and
$D_{1}=\{t_{2}\leq t_{1},t_{3}\leq t_{2},t_{4}\leq t_{2}\}$ and ![]() $D_{2}=\{t_{2}\leq t_{1},t_{3}\leq t_{2},t_{4}\leq t_{3}\}$ following from our discussions in Section 4.1.
$D_{2}=\{t_{2}\leq t_{1},t_{3}\leq t_{2},t_{4}\leq t_{3}\}$ following from our discussions in Section 4.1.
![]() $I_{1}$ and
$I_{1}$ and ![]() $I_{2}$ actually have the same integrand if one does a
$I_{2}$ actually have the same integrand if one does a ![]() $t_{2}\leftrightarrow t_{3}$ swap in
$t_{2}\leftrightarrow t_{3}$ swap in ![]() $I_{1}$, despite the fact that the trees corresponding to
$I_{1}$, despite the fact that the trees corresponding to ![]() $I_{1}$ and
$I_{1}$ and ![]() $I_{2}$ have different skeletons. In fact, shortening
$I_{2}$ have different skeletons. In fact, shortening ![]() $e^{i\left ( t_{i}-t_{j}\right ) \triangle } $ as
$e^{i\left ( t_{i}-t_{j}\right ) \triangle } $ as ![]() $U_{i,j}$, we have
$U_{i,j}$, we have
 $$ \begin{align*} I_{1} &=\int_{D_{1}}U_{1,3}\left(\left\lvert U_{3,4}\phi \right\rvert ^{2}U_{3,4}\phi \right)(x_{1})U_{1,2}\left(\overline{U_{2,4}\phi }\overline{U_{2,4}\phi }U_{2,4}\left( \left\lvert \phi \right\rvert ^{2}\phi \right) \right)\left(x^{\prime}_{1}\right)d\underline{t}_{4} \\ &=\int_{D^{\prime}_{1}}U_{1,2}\left(\left\lvert U_{2,4}\phi \right\rvert ^{2}U_{2,4}\phi \right)(x_{1})U_{1,3}\left(\overline{U_{3,4}\phi }\overline{U_{3,4}\phi }U_{3,4}\left( \left\lvert \phi \right\rvert ^{2}\phi \right) \right)\left(x^{\prime}_{1}\right)d\underline{t}_{4} \\ &=\int_{D^{\prime}_{1}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{3}-t_{4})B_{3,4}^{+}\left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4}, \end{align*} $$
$$ \begin{align*} I_{1} &=\int_{D_{1}}U_{1,3}\left(\left\lvert U_{3,4}\phi \right\rvert ^{2}U_{3,4}\phi \right)(x_{1})U_{1,2}\left(\overline{U_{2,4}\phi }\overline{U_{2,4}\phi }U_{2,4}\left( \left\lvert \phi \right\rvert ^{2}\phi \right) \right)\left(x^{\prime}_{1}\right)d\underline{t}_{4} \\ &=\int_{D^{\prime}_{1}}U_{1,2}\left(\left\lvert U_{2,4}\phi \right\rvert ^{2}U_{2,4}\phi \right)(x_{1})U_{1,3}\left(\overline{U_{3,4}\phi }\overline{U_{3,4}\phi }U_{3,4}\left( \left\lvert \phi \right\rvert ^{2}\phi \right) \right)\left(x^{\prime}_{1}\right)d\underline{t}_{4} \\ &=\int_{D^{\prime}_{1}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{3}-t_{4})B_{3,4}^{+}\left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4}, \end{align*} $$where ![]() $D^{\prime }_{1}=\{t_{3}\leq t_{1},t_{2}\leq t_{3},t_{4}\leq t_{3}\}$ and we have put in
$D^{\prime }_{1}=\{t_{3}\leq t_{1},t_{2}\leq t_{3},t_{4}\leq t_{3}\}$ and we have put in ![]() $f^{(4)}=\left ( \left \lvert \phi \right \rangle \left \langle \phi \right \rvert \right ) ^{\otimes 4}$ for simplicity.Footnote 21 Hence,
$f^{(4)}=\left ( \left \lvert \phi \right \rangle \left \langle \phi \right \rvert \right ) ^{\otimes 4}$ for simplicity.Footnote 21 Hence,
 $$ \begin{align} I_{1}+I_{2} &= \int_{D}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{2}-t_{3})B_{3,4}^{+}\left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4} \\ &= \int_{t_{4}=0}^{t_{1}}\int_{t_{2}=0}^{t_{1}} \int_{t_{3}=t_{4}}^{t_{1}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{2}-t_{3})B_{3,4}^{+}\left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4}, \notag \end{align} $$
$$ \begin{align} I_{1}+I_{2} &= \int_{D}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{2}-t_{3})B_{3,4}^{+}\left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4} \\ &= \int_{t_{4}=0}^{t_{1}}\int_{t_{2}=0}^{t_{1}} \int_{t_{3}=t_{4}}^{t_{1}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{2}-t_{3})B_{3,4}^{+}\left(f^{(4)}\right)\left(t_{1},\underline{t}_{4}\right)d\underline{t}_{4}, \notag \end{align} $$where ![]() $D=D^{\prime }_{1}\cup D_{2}=\{t_{3}\leq t_{1},t_{2}\leq t_{1},t_{4}\leq t_{3}\}$.
$D=D^{\prime }_{1}\cup D_{2}=\{t_{3}\leq t_{1},t_{2}\leq t_{1},t_{4}\leq t_{3}\}$.
Example 4 is an easy example of what we will call the wild moves, and shows that one could indeed further combine the summands in  $J^{(k+1)}\left (f^{(k+1)}\right )$ after the original KM board game has been performed. We will explain why our U-V techniques apply to
$J^{(k+1)}\left (f^{(k+1)}\right )$ after the original KM board game has been performed. We will explain why our U-V techniques apply to ![]() $I_{1}+I_{2}$ but not
$I_{1}+I_{2}$ but not ![]() $I_{1}$ and
$I_{1}$ and ![]() $I_{2}$ individually in Section 5.1. Despite the fact that Example 4 uses the already-combined upper-echelon integrals, our extended KM board game actually starts from scratch – that is, it starts from
$I_{2}$ individually in Section 5.1. Despite the fact that Example 4 uses the already-combined upper-echelon integrals, our extended KM board game actually starts from scratch – that is, it starts from ![]() $\gamma ^{(1)}(t_{1})$ instead of already-combined upper-echelon integrals – as not all upper-echelon integrals act so nicely under the wild moves. However, it is still a multistep process. We will first switch the terms in
$\gamma ^{(1)}(t_{1})$ instead of already-combined upper-echelon integrals – as not all upper-echelon integrals act so nicely under the wild moves. However, it is still a multistep process. We will first switch the terms in ![]() $\gamma ^{(1)}(t_{1})$ into their tamed form via signed KM acceptable moves in Sections 4.2 and 4.3, and then categorise the tamed forms into tamed classes via the wild moves in Sections 4.4 and 4.5.
$\gamma ^{(1)}(t_{1})$ into their tamed form via signed KM acceptable moves in Sections 4.2 and 4.3, and then categorise the tamed forms into tamed classes via the wild moves in Sections 4.4 and 4.5.
We now explain the program as follows: As before, start by expanding ![]() $\gamma ^{(1)}(t_{1})$ to coupling level k, which generates a sum expansion of
$\gamma ^{(1)}(t_{1})$ to coupling level k, which generates a sum expansion of ![]() $k!$ terms. But now for each of these
$k!$ terms. But now for each of these ![]() $k!$ terms, expand the collapsing operators
$k!$ terms, expand the collapsing operators  $B_{\mu \left (j\right ),j}^{\left (j\right )}$ into
$B_{\mu \left (j\right ),j}^{\left (j\right )}$ into ![]() $+$ and
$+$ and ![]() $-$ components, which introduces
$-$ components, which introduces ![]() $2^{k}$ terms. Thus, in all, we have
$2^{k}$ terms. Thus, in all, we have ![]() $2^{k}k!$ terms, each of which has sign-dependent collapsing operators
$2^{k}k!$ terms, each of which has sign-dependent collapsing operators
 $$ \begin{align} \gamma ^{(1)}=\sum_{\mu ,\operatorname{sgn}}I\left(\mu ,\text{id},\operatorname{sgn},\gamma ^{(k+1)}\right), \end{align} $$
$$ \begin{align} \gamma ^{(1)}=\sum_{\mu ,\operatorname{sgn}}I\left(\mu ,\text{id},\operatorname{sgn},\gamma ^{(k+1)}\right), \end{align} $$where ![]() $\text {id}$ is the identity permutation on
$\text {id}$ is the identity permutation on ![]() $\{2,\dotsc ,k+1\},$
$\{2,\dotsc ,k+1\},$
 $$ \begin{align*} I(\mu ,\sigma ,\operatorname{sgn})=\int_{t_{1}\geq t_{\sigma (2)}\geq \dotsb \geq t_{\sigma (k+1)}}J_{\mu ,\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1} \end{align*} $$
$$ \begin{align*} I(\mu ,\sigma ,\operatorname{sgn})=\int_{t_{1}\geq t_{\sigma (2)}\geq \dotsb \geq t_{\sigma (k+1)}}J_{\mu ,\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1} \end{align*} $$and  $J_{\mu ,\operatorname {sgn}}^{(k+1)}$ is defined as in equation (3.10). Equation (4.5) is a sum over all admissible
$J_{\mu ,\operatorname {sgn}}^{(k+1)}$ is defined as in equation (3.10). Equation (4.5) is a sum over all admissible ![]() $\mu $ – that is, collapsing maps that satisfy
$\mu $ – that is, collapsing maps that satisfy ![]() $\mu (j)<j$ – of which there are
$\mu (j)<j$ – of which there are ![]() $k!$. It is also a sum over all
$k!$. It is also a sum over all ![]() $\operatorname {sgn}$ maps, of which there are
$\operatorname {sgn}$ maps, of which there are ![]() $2^{k}$.
$2^{k}$.
We define a signed version of the KM acceptable moves, still denoted ![]() $\text {KM}(j,j+1)$, which is defined provided
$\text {KM}(j,j+1)$, which is defined provided ![]() $\mu (j)\neq \mu (j+1)$ and
$\mu (j)\neq \mu (j+1)$ and ![]() $\mu (j+1)<j$. It is defined as the following action on a triple
$\mu (j+1)<j$. It is defined as the following action on a triple ![]() $(\mu ,\sigma ,\operatorname {sgn})$:
$(\mu ,\sigma ,\operatorname {sgn})$:
where
 $$ \begin{align*} \mu' & = (j,j+1) \circ \mu \circ (j,j+1), \\ \sigma' & = (j,j+1) \circ \sigma, \\ \operatorname{sgn}' & = \operatorname{sgn} \circ (j,j+1). \end{align*} $$
$$ \begin{align*} \mu' & = (j,j+1) \circ \mu \circ (j,j+1), \\ \sigma' & = (j,j+1) \circ \sigma, \\ \operatorname{sgn}' & = \operatorname{sgn} \circ (j,j+1). \end{align*} $$ Graphically, this means that nodes j and ![]() $j+1$ belong to different left branches and correspond to switching nodes j and
$j+1$ belong to different left branches and correspond to switching nodes j and ![]() $j+1$, leaving the signs in place on the tree – in other words, the node previously labelled
$j+1$, leaving the signs in place on the tree – in other words, the node previously labelled ![]() $ j $ is relabelled
$ j $ is relabelled ![]() $j+1$, and the node previously labelled
$j+1$, and the node previously labelled ![]() $j+1$ is relabelled
$j+1$ is relabelled ![]() $ j $, but the signs are left in place.
$ j $, but the signs are left in place.
A slight modification of the arguments in [Reference Klainerman and Machedon47] shows that, analogous to equation (4.1), if ![]() $(\mu ',\sigma ',\operatorname {sgn}')=\text {KM}(j,j+1)(\mu ,\sigma ,\operatorname {sgn})$ and
$(\mu ',\sigma ',\operatorname {sgn}')=\text {KM}(j,j+1)(\mu ,\sigma ,\operatorname {sgn})$ and ![]() $f^{(k+1)}$ is a symmetric density, then
$f^{(k+1)}$ is a symmetric density, then
 $$ \begin{align} J_{\mu',\operatorname{sgn}'}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},{\sigma'}^{-1}\left(\underline{t}_{k+1}\right)\right)=J_{\mu ,\operatorname{sgn}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},{\sigma }^{-1}\left(\underline{t}_{k+1}\right)\right). \end{align} $$
$$ \begin{align} J_{\mu',\operatorname{sgn}'}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},{\sigma'}^{-1}\left(\underline{t}_{k+1}\right)\right)=J_{\mu ,\operatorname{sgn}}^{(k+1)}\left(f^{(k+1)}\right)\left(t_{1},{\sigma }^{-1}\left(\underline{t}_{k+1}\right)\right). \end{align} $$It follows from equation (4.6) that
 $$ \begin{align} I\left(\mu',\sigma',\operatorname{sgn}',f^{(k+1)}\right)=I\left(\mu ,\sigma ,\operatorname{sgn},f^{(k+1)}\right). \end{align} $$
$$ \begin{align} I\left(\mu',\sigma',\operatorname{sgn}',f^{(k+1)}\right)=I\left(\mu ,\sigma ,\operatorname{sgn},f^{(k+1)}\right). \end{align} $$As in the sign-independent case (or more accurately, the combined-sign case), we can combine KM acceptable moves as follows: If ![]() $\rho $ is a permutation of
$\rho $ is a permutation of ![]() $\{2,\dotsc ,k+1\}$ such that it is possible to write
$\{2,\dotsc ,k+1\}$ such that it is possible to write ![]() $\rho $ as a composition of transpositions
$\rho $ as a composition of transpositions
for which each operator ![]() $\text {KM}\left (\tau _{j}\right )$ on the right side of
$\text {KM}\left (\tau _{j}\right )$ on the right side of
 $$ \begin{align*} \text{KM}(\rho )\overset{\mathrm{def}}{=}\text{KM}(\tau _{1})\circ \dotsb \circ \text{KM}(\tau _{r}) \end{align*} $$
$$ \begin{align*} \text{KM}(\rho )\overset{\mathrm{def}}{=}\text{KM}(\tau _{1})\circ \dotsb \circ \text{KM}(\tau _{r}) \end{align*} $$is an acceptable action, then ![]() $\text {KM}(\rho )$, defined by this composition, is acceptable as well. In this case,
$\text {KM}(\rho )$, defined by this composition, is acceptable as well. In this case, ![]() $(\mu ',\sigma ',\operatorname {sgn}')=\text { KM}(\rho )(\mu ,\sigma ,\operatorname {sgn})$, and
$(\mu ',\sigma ',\operatorname {sgn}')=\text { KM}(\rho )(\mu ,\sigma ,\operatorname {sgn})$, and
 $$ \begin{align*} \mu' & =\rho \circ \mu \circ \rho ^{-1}, \\ \sigma' & =\rho \circ \sigma, \\ \operatorname{sgn}' & =\operatorname{sgn}\circ \rho ^{-1}. \end{align*} $$
$$ \begin{align*} \mu' & =\rho \circ \mu \circ \rho ^{-1}, \\ \sigma' & =\rho \circ \sigma, \\ \operatorname{sgn}' & =\operatorname{sgn}\circ \rho ^{-1}. \end{align*} $$Of course, equations (4.6) and (4.7) hold as well. If ![]() $(\mu ,\operatorname {sgn})$ and
$(\mu ,\operatorname {sgn})$ and ![]() $(\mu ',\operatorname {sgn}')$ are such that there exists
$(\mu ',\operatorname {sgn}')$ are such that there exists ![]() $\rho $ for which
$\rho $ for which ![]() $(\mu ',\sigma ',\operatorname {sgn}')=\text {KM}(\rho )(\mu ,\sigma ,\operatorname {sgn})$, then we say that
$(\mu ',\sigma ',\operatorname {sgn}')=\text {KM}(\rho )(\mu ,\sigma ,\operatorname {sgn})$, then we say that ![]() $(\mu ',\operatorname {sgn}')$ and
$(\mu ',\operatorname {sgn}')$ and ![]() $(\mu ,\operatorname {sgn})$ are KM-relatable. This is an equivalence relation that partitions the set of collapsing map/sign map pairs into equivalence classes. In the graphical representation, two such pairs are KM-relatable if and only if they have the same signed skeleton tree.
$(\mu ,\operatorname {sgn})$ are KM-relatable. This is an equivalence relation that partitions the set of collapsing map/sign map pairs into equivalence classes. In the graphical representation, two such pairs are KM-relatable if and only if they have the same signed skeleton tree.
Whereas we could use the signed KM acceptable moves to convert an arbitrary admissible ![]() $\mu $ to an upper-echelon
$\mu $ to an upper-echelon ![]() $\mu '$, this will no longer suit our purpose. Instead, our program will be to convert each pair
$\mu '$, this will no longer suit our purpose. Instead, our program will be to convert each pair ![]() $(\mu ,\operatorname {sgn})$ to a tamed form, which we define in the next section. The reason for our preference of tamed form over upper-echelon form is that it is invariant under wild moves, to be introduced in Section 4.4.
$(\mu ,\operatorname {sgn})$ to a tamed form, which we define in the next section. The reason for our preference of tamed form over upper-echelon form is that it is invariant under wild moves, to be introduced in Section 4.4.
4.3 Tamed form
In this section, we define what it means for a pair ![]() $(\mu ,\operatorname {sgn})$ and its corresponding tree representation to be tamed, in Definition 4.4. Then through an example, we present an algorithm for producing the tamed enumeration of a signed skeleton. The general algorithm is then stated in Algorithm 5. Notice that it produces a different enumeration from Algorithm 4. Compared with Algorithm 4, the tamed-form enumeration deals not just with left branches first, it also deals with
$(\mu ,\operatorname {sgn})$ and its corresponding tree representation to be tamed, in Definition 4.4. Then through an example, we present an algorithm for producing the tamed enumeration of a signed skeleton. The general algorithm is then stated in Algorithm 5. Notice that it produces a different enumeration from Algorithm 4. Compared with Algorithm 4, the tamed-form enumeration deals not just with left branches first, it also deals with ![]() $+$ first.Footnote 22 In Section 4.3.1, we exhibit how to reduce a signed tree with the same skeleton but different enumeration into the tamed form using signed KM acceptable moves.
$+$ first.Footnote 22 In Section 4.3.1, we exhibit how to reduce a signed tree with the same skeleton but different enumeration into the tamed form using signed KM acceptable moves.
We will now give a nongraphical set of conditions on ![]() $\mu $ and
$\mu $ and ![]() $\operatorname {sgn}$ that determine whether or not
$\operatorname {sgn}$ that determine whether or not ![]() $(\mu ,\operatorname {sgn})$ is tamed. First, we define the concept of a tier. We say that
$(\mu ,\operatorname {sgn})$ is tamed. First, we define the concept of a tier. We say that ![]() $j\geq 2$ is of tier q if
$j\geq 2$ is of tier q if
where ![]() $\mu ^q = \mu \circ \dotsb \circ \mu $, the composition taken q times. We write
$\mu ^q = \mu \circ \dotsb \circ \mu $, the composition taken q times. We write ![]() $t(j)$ for the tier value of j.
$t(j)$ for the tier value of j.
Definition 4.4. A pair ![]() $(\mu ,\operatorname {sgn})$ is tamed if it meets the following four requirements:
$(\mu ,\operatorname {sgn})$ is tamed if it meets the following four requirements:
1. If
 $t(\ell )<t(r)$, then
$t(\ell )<t(r)$, then  $\ell <r$.
$\ell <r$.2. If
 $t(\ell )=t(r)$,
$t(\ell )=t(r)$,  $\mu ^2(\ell ) = \mu ^2(r)$,
$\mu ^2(\ell ) = \mu ^2(r)$,  $\operatorname {sgn}(\mu (\ell ))= \operatorname {sgn}(\mu (r))$ and
$\operatorname {sgn}(\mu (\ell ))= \operatorname {sgn}(\mu (r))$ and  $\mu (\ell )<\mu (r)$, then
$\mu (\ell )<\mu (r)$, then  $\ell <r$.
$\ell <r$.3. If
 $t(\ell )=t(r)$,
$t(\ell )=t(r)$,  $\mu ^2(\ell ) = \mu ^2(r)$,
$\mu ^2(\ell ) = \mu ^2(r)$,  $\operatorname {sgn}(\mu (\ell ))=+$ and
$\operatorname {sgn}(\mu (\ell ))=+$ and  $\operatorname {sgn}(\mu (r))=-$, then
$\operatorname {sgn}(\mu (r))=-$, then  $\ell <r$.
$\ell <r$.4. If
 $t(\ell ) = t(r)$,
$t(\ell ) = t(r)$,  $\mu ^2(\ell ) \neq \mu ^2(r)$ and
$\mu ^2(\ell ) \neq \mu ^2(r)$ and  $\mu (\ell )<\mu (r)$, then
$\mu (\ell )<\mu (r)$, then  $\ell <r$.
$\ell <r$.
Note that the statement ![]() $\mu ^2(\ell ) = \mu ^2(r)$ means graphically that the parents of
$\mu ^2(\ell ) = \mu ^2(r)$ means graphically that the parents of ![]() $\ell $ and r belong to the same left branch. Conditions (2), (3) and (4) specify the ordering for
$\ell $ and r belong to the same left branch. Conditions (2), (3) and (4) specify the ordering for ![]() $\ell $ and r belonging to the same tier, and the rule depends upon whether or not the parents of
$\ell $ and r belonging to the same tier, and the rule depends upon whether or not the parents of ![]() $\ell $ and r belong to the same left branch. If they do, rule (3) says that a positive parent dominates over a negative parent, but rule (2) says that if the parents are of the same sign, then the ordering follows the parental ordering. Finally, if the parents do not belong to the same left branch, rule (4) says that the ordering follows the parental ordering regardless of the signs of the parents.
$\ell $ and r belong to the same left branch. If they do, rule (3) says that a positive parent dominates over a negative parent, but rule (2) says that if the parents are of the same sign, then the ordering follows the parental ordering. Finally, if the parents do not belong to the same left branch, rule (4) says that the ordering follows the parental ordering regardless of the signs of the parents.
Example 5. The ![]() $(\mu ,\operatorname {sgn})$ pair with tier properties indicated in the following chart is tamed:
$(\mu ,\operatorname {sgn})$ pair with tier properties indicated in the following chart is tamed:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \mu (j) & 1 & 1 & 1 & 1 & 5 & 5 & 2 & 2 & 7 & 7 & 9 &9 & 8 \\[3pt] \operatorname{sgn}(j) & - & - & + & + & - & + & - & + & - & + & + & - & + \\[3pt] t(j) & 1 & 1 & 1 & 1 & 2 & 2 & 2 & 2 & 3 & 3 & 3 & 3 & 3 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \mu (j) & 1 & 1 & 1 & 1 & 5 & 5 & 2 & 2 & 7 & 7 & 9 &9 & 8 \\[3pt] \operatorname{sgn}(j) & - & - & + & + & - & + & - & + & - & + & + & - & + \\[3pt] t(j) & 1 & 1 & 1 & 1 & 2 & 2 & 2 & 2 & 3 & 3 & 3 & 3 & 3 \\ \end{array} \end{align*} $$All four conditions in Definition 4.4 can be checked from the chart. This is in fact the ![]() $(\mu ,\operatorname {sgn})$ pair that appears in the example that follows.
$(\mu ,\operatorname {sgn})$ pair that appears in the example that follows.
In the following example, we illustrate an algorithm for determining the unique tamed enumeration of a signed skeleton tree. After the example is completed, we give the general form of the algorithm.
For the example, we start with the following skeleton, with only the signs indicated. (Recall that KM acceptable moves will leave the signs in place in the tree and change just the numbering of the nodes.) Start by considering all nodes mapping to ![]() $1$ (the universal ancestor) – this is the left branch attached to
$1$ (the universal ancestor) – this is the left branch attached to ![]() $1$ that is four nodes long in the order
$1$ that is four nodes long in the order ![]() $--++$, and we enumerate it in order as
$--++$, and we enumerate it in order as ![]() $2,3,4,5$.
$2,3,4,5$.


We then put this full left branch in the (empty) queue, listing the ![]() $+$ nodes first and then the
$+$ nodes first and then the ![]() $-$ nodes:
$-$ nodes:
Then we start working along the queue from left to right. Since ![]() $4+$ has no right child, we skip it and move to
$4+$ has no right child, we skip it and move to ![]() $5+$. Since
$5+$. Since ![]() $5+$ does have a right child, we label it with the next available number (
$5+$ does have a right child, we label it with the next available number (![]() $6$) and completely enumerate the entire left branch that starts with this
$6$) and completely enumerate the entire left branch that starts with this ![]() $6$ node (that means, in this case, labelling
$6$ node (that means, in this case, labelling ![]() $6-$ and
$6-$ and ![]() $7+$ as shown on the next graph).
$7+$ as shown on the next graph).
Then we add this entire left branch to the queue, putting the ![]() $+$ nodes before the
$+$ nodes before the ![]() $-$ nodes. We also pop
$-$ nodes. We also pop ![]() $4+$ and
$4+$ and ![]() $5+$ from the (left of the) queue, since we have already dealt with them. The queue now reads
$5+$ from the (left of the) queue, since we have already dealt with them. The queue now reads
Now we come to the next node in the queue (reading from the left), which is ![]() $2-$. The node
$2-$. The node ![]() $2$ does have a right child. We label it as
$2$ does have a right child. We label it as ![]() $8$ (the next available number) and completely enumerate the left branch that starts with
$8$ (the next available number) and completely enumerate the left branch that starts with ![]() $8$, which means labelling
$8$, which means labelling ![]() $8-$ and
$8-$ and ![]() $9+$as shown.
$9+$as shown.

From the queue, we pop ![]() $2$ and add the
$2$ and add the ![]() $8-$,
$8-$, ![]() $9+$ left branch – all
$9+$ left branch – all ![]() $+$ nodes first and then all
$+$ nodes first and then all ![]() $-$ nodes:
$-$ nodes:
Since ![]() $3-$ does not have a right child, we pop it and proceed to
$3-$ does not have a right child, we pop it and proceed to ![]() $7+$, which does have a right child, which is labelled with
$7+$, which does have a right child, which is labelled with ![]() $10$, and the left branch starting at
$10$, and the left branch starting at ![]() $10$ is enumerated as
$10$ is enumerated as ![]() $10-, 11+$, as shown.
$10-, 11+$, as shown.


The queue is updated:
By now the procedure is probably clear, so we will jump to the fully enumerated tree.
Here is the general algorithm. Recall that a queue is a data structure where elements are added on the right and removed (dequeued) on the left.
Algorithm 5. Start with a queue that at first contains only ![]() $1$, and start with a next available label
$1$, and start with a next available label ![]() $j=2$.
$j=2$.
1. Dequeue the leftmost entry
 $\ell $ of the queue. (If the queue is empty, stop.) On the tree, pass to the right child of
$\ell $ of the queue. (If the queue is empty, stop.) On the tree, pass to the right child of  $\ell $, and enumerate its left branch starting with the next available label
$\ell $, and enumerate its left branch starting with the next available label  $j, j+1, \dotsc , j+q$. If there is no right child of
$j, j+1, \dotsc , j+q$. If there is no right child of  $\ell $, return to the beginning of step 1.
$\ell $, return to the beginning of step 1.2. Take the left branch enumerated in step 1 and first list all
 $+$ nodes in the order
$+$ nodes in the order  $j, \dotsc , j+q$ and add them to the right side of the queue. Then list all
$j, \dotsc , j+q$ and add them to the right side of the queue. Then list all  $-$ nodes in the order
$-$ nodes in the order  $j, \dotsc , j+q$ and add them to the right side of the queue
$j, \dotsc , j+q$ and add them to the right side of the queue3. Set the next available label to be
 $j+q+1$, and return to step 1.
$j+q+1$, and return to step 1.
4.3.1 Reducing to tamed forms via the signed KM board game
We will now explain how to execute a sequence of signed KM acceptable moves that will bring the example tree from the previous section, with some other enumeration, into the tamed form. This tree corresponds to the following ![]() $\mu $ and
$\mu $ and ![]() $\operatorname {sgn}$ functions:
$\operatorname {sgn}$ functions:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14\\ \hline \operatorname{sgn}(j) & - & - & + & - & + & + & + & - & - & + & + & - & +\\[3pt] \mu(j) & 1 & 1 & 1 & 2 & 2 & 1 & 6 & 7 & 6 & 7 & 5 & 11 & 11 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14\\ \hline \operatorname{sgn}(j) & - & - & + & - & + & + & + & - & - & + & + & - & +\\[3pt] \mu(j) & 1 & 1 & 1 & 2 & 2 & 1 & 6 & 7 & 6 & 7 & 5 & 11 & 11 \\ \end{array} \end{align*} $$
We are going to start with the enumeration at left, which is not tamed, and explain how to execute KM acceptable moves in order to convert this tree into tamed form. Of course, this is quite similar to what Klainerman and Machedon described, with just a modification to prioritise plusses over minuses.
We will keep a queue that right now includes only the node ![]() $1$:
$1$:
Following the queue, we move all nodes (all j) for which ![]() $\mu (j)=1$ all the way to left using KM moves. Since
$\mu (j)=1$ all the way to left using KM moves. Since ![]() $\mu (7)=1$, although
$\mu (7)=1$, although ![]() $\mu (5)=2$ and
$\mu (5)=2$ and ![]() $\mu (6)=2$, we apply the KM moves
$\mu (6)=2$, we apply the KM moves ![]() $\text {KM}(6,7)$ and then
$\text {KM}(6,7)$ and then ![]() $\text {KM}(5,6)$.
$\text {KM}(5,6)$.
The ![]() $\text {KM}(6,7)$ move is
$\text {KM}(6,7)$ move is
 $$ \begin{align*} \mu & \mapsto (6,7) \circ \mu \circ (6,7), \\ \operatorname{sgn} & \mapsto \operatorname{sgn} \circ (6,7). \end{align*} $$
$$ \begin{align*} \mu & \mapsto (6,7) \circ \mu \circ (6,7), \\ \operatorname{sgn} & \mapsto \operatorname{sgn} \circ (6,7). \end{align*} $$The ![]() $\text {KM}(5,6)$ move is
$\text {KM}(5,6)$ move is
 $$ \begin{align*} \mu & \mapsto (5,6) \circ \mu \circ (5,6), \\ \operatorname{sgn} & \mapsto \operatorname{sgn} \circ (5,6), \end{align*} $$
$$ \begin{align*} \mu & \mapsto (5,6) \circ \mu \circ (5,6), \\ \operatorname{sgn} & \mapsto \operatorname{sgn} \circ (5,6), \end{align*} $$and together these result in the following:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14\\ \hline \operatorname{sgn}(j) & - & - & + & + & - & + & + & - & - & + & + & - & +\\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 2 & 2 & 7 & 5 & 7 & 5 & 6 & 11 & 11 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14\\ \hline \operatorname{sgn}(j) & - & - & + & + & - & + & + & - & - & + & + & - & +\\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 2 & 2 & 7 & 5 & 7 & 5 & 6 & 11 & 11 \\ \end{array} \end{align*} $$
These two moves have been implemented in the revised graph at left.
Inspecting the ![]() $\mu $ chart, we see that all output
$\mu $ chart, we see that all output ![]() $1$s have been moved to the left, and the complete list of j for which
$1$s have been moved to the left, and the complete list of j for which ![]() $\mu (j)=1$ is
$\mu (j)=1$ is ![]() $2-, 3-, 4+, 5+$. We add these numbers to our queue, but first add all plusses and then all minuses:
$2-, 3-, 4+, 5+$. We add these numbers to our queue, but first add all plusses and then all minuses:
Since we have completed ![]() $1$ on the queue, we next move to
$1$ on the queue, we next move to ![]() $4$, but there are no j for which
$4$, but there are no j for which ![]() $\mu (j)=4$, so we proceed to
$\mu (j)=4$, so we proceed to ![]() $5$. As we can see from the
$5$. As we can see from the ![]() $\mu $ table or from the tree,
$\mu $ table or from the tree, ![]() $\mu (9)=5$ and
$\mu (9)=5$ and ![]() $\mu (11)=5$, so we execute KM moves to bring these all the way to the left (but to the right of the
$\mu (11)=5$, so we execute KM moves to bring these all the way to the left (but to the right of the ![]() $1$s):
$1$s):
The next step is therefore to implement moves ![]() $\text {KM}(8,9)$,
$\text {KM}(8,9)$, ![]() $\text {KM} (7,8)$ and
$\text {KM} (7,8)$ and ![]() $\text {KM}(6,7)$, which brings the
$\text {KM}(6,7)$, which brings the ![]() $\mu $ table to the following:
$\mu $ table to the following:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \operatorname{sgn}(j) & - & - & + & + & - & - & + & + & - & + & + & - & + \\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 5 & 2 & 2 & 8 & 8 & 5 & 7 & 11 & 11 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \operatorname{sgn}(j) & - & - & + & + & - & - & + & + & - & + & + & - & + \\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 5 & 2 & 2 & 8 & 8 & 5 & 7 & 11 & 11 \\ \end{array} \end{align*} $$This is followed by the moves ![]() $\text {KM}(11,10)$,
$\text {KM}(11,10)$, ![]() $\text {KM}(10,9)$,
$\text {KM}(10,9)$, ![]() $\text {KM}(9,8)$ and
$\text {KM}(9,8)$ and ![]() $\text {KM}(8,7)$, which bring the
$\text {KM}(8,7)$, which bring the ![]() $\mu $ table to the following:
$\mu $ table to the following:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \operatorname{sgn}(j) & - & - & + & + & - & + & - & + & + & - & + & - & + \\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 5 & 5 & 2 & 2 & 9 & 9 & 8 & 7 & 7 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \operatorname{sgn}(j) & - & - & + & + & - & + & - & + & + & - & + & - & + \\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 5 & 5 & 2 & 2 & 9 & 9 & 8 & 7 & 7 \\ \end{array} \end{align*} $$
At this point, the tree takes the form as pictured to the left. All ![]() $5$s have been moved to their proper position in the
$5$s have been moved to their proper position in the ![]() $\mu $ table. The complete list of j for which
$\mu $ table. The complete list of j for which ![]() $\mu (j)=5$ is
$\mu (j)=5$ is ![]() $6-, 7-$, so we add these numbers to the queue, adding the plusses first and then the minuses:
$6-, 7-$, so we add these numbers to the queue, adding the plusses first and then the minuses:
Since we have addressed ![]() $5$ in the queue, we move to the next item, which is
$5$ in the queue, we move to the next item, which is ![]() $2$. This means we have to move all j for which
$2$. This means we have to move all j for which ![]() $\mu (j)=2$ all the way to the left (just to the right of
$\mu (j)=2$ all the way to the left (just to the right of ![]() $5$). Examining the
$5$). Examining the ![]() $\mu $ table, we see that these j are already in place, at positions
$\mu $ table, we see that these j are already in place, at positions ![]() $8-, 9+$. So no KM moves are needed, and we add to the queue:
$8-, 9+$. So no KM moves are needed, and we add to the queue:
Next on the queue is ![]() $3$, but there are no j for which
$3$, but there are no j for which ![]() $\mu (j)=3$, so we proceed to
$\mu (j)=3$, so we proceed to ![]() $7$ on the queue. From the
$7$ on the queue. From the ![]() $\mu $ table or the tree, we see there are two j for which
$\mu $ table or the tree, we see there are two j for which ![]() $\mu (j)=7$, namely
$\mu (j)=7$, namely ![]() $13$ and
$13$ and ![]() $14$. We therefore execute KM moves to bring these to the left in the
$14$. We therefore execute KM moves to bring these to the left in the ![]() $\mu $ table, just to the right of
$\mu $ table, just to the right of ![]() $2$.
$2$.
Specifically, we do ![]() $\text {KM}(12,13)$,
$\text {KM}(12,13)$, ![]() $\text {KM}(11,12)$ and
$\text {KM}(11,12)$ and ![]() $\text {KM}(10,11)$, which brings us to the following
$\text {KM}(10,11)$, which brings us to the following ![]() $\mu $ table:
$\mu $ table:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \operatorname{sgn}(j) & - & - & + & + & - & + & - & + & - & + & - & + & + \\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 5 & 5 & 2 & 2 & 7 & 9 & 9 & 8 & 7 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \operatorname{sgn}(j) & - & - & + & + & - & + & - & + & - & + & - & + & + \\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 5 & 5 & 2 & 2 & 7 & 9 & 9 & 8 & 7 \\ \end{array} \end{align*} $$ After that, we do ![]() $\text {KM}(13,14)$,
$\text {KM}(13,14)$, ![]() $\text {KM}(12,13)$ and
$\text {KM}(12,13)$ and ![]() $\text {KM} (11,12)$, which brings us to the following
$\text {KM} (11,12)$, which brings us to the following ![]() $\mu $ table:
$\mu $ table:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \operatorname{sgn}(j) & - & - & + & + & - & + & - & + & - & + & + & - & + \\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 5 & 5 & 2 & 2 & 7 & 7 & 9 & 9 & 8 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 \\ \hline \operatorname{sgn}(j) & - & - & + & + & - & + & - & + & - & + & + & - & + \\[3pt] \mu(j) & 1 & 1 & 1 & 1 & 5 & 5 & 2 & 2 & 7 & 7 & 9 & 9 & 8 \\ \end{array} \end{align*} $$ Now that the seven outputs are in place, we take the set of j for which ![]() $ \mu (j) = 7$, which is
$ \mu (j) = 7$, which is ![]() $10-, 11+$, and put them in the queue with plusses first, followed by minuses:
$10-, 11+$, and put them in the queue with plusses first, followed by minuses:
There are no j for which ![]() $\mu (j)=6$, so we proceed in the queue to
$\mu (j)=6$, so we proceed in the queue to ![]() $9$. However, the two
$9$. However, the two ![]() $9$s are already in place, and the next item in the queue is
$9$s are already in place, and the next item in the queue is ![]() $8$; the one
$8$; the one ![]() $8$ is already in place. So this completes the example.
$8$ is already in place. So this completes the example.
We now describe the preceding algorithm in general.
Algorithm 6. Given ![]() $(\mu ,\operatorname {sgn})$, start with a queue Q that initially contains
$(\mu ,\operatorname {sgn})$, start with a queue Q that initially contains ![]() $1$ and a marker j, which is initially set to
$1$ and a marker j, which is initially set to ![]() $j=2$. Repeat the following steps:
$j=2$. Repeat the following steps:
1. Dequeue the leftmost entry
 $\ell $ of the queue. If the queue is empty, then stop. Clear the temporary ordered list L.
$\ell $ of the queue. If the queue is empty, then stop. Clear the temporary ordered list L.2. If
 $\mu (j)=\ell $, add j to the right of L, then increment the marker j by
$\mu (j)=\ell $, add j to the right of L, then increment the marker j by  $1$ (so now j is the old
$1$ (so now j is the old  $j+1$). If (the new marker) j is out of range, jump to step 4. If
$j+1$). If (the new marker) j is out of range, jump to step 4. If  $\mu (j)\neq \ell $, then proceed to step 3; otherwise, repeat step 2.
$\mu (j)\neq \ell $, then proceed to step 3; otherwise, repeat step 2.3. Find the smallest
 $r\geq j+1$ such that
$r\geq j+1$ such that  $\mu (r) = \ell $ (if there is no such r, jump to step 4). Execute signed KM moves
$\mu (r) = \ell $ (if there is no such r, jump to step 4). Execute signed KM moves  $\text {KM}(r-1,r)$, followed by
$\text {KM}(r-1,r)$, followed by  $\text {KM}(r-2,r-1)$,
$\text {KM}(r-2,r-1)$,  $\dotsc $, until
$\dotsc $, until  $\text {KM}(j+1,j)$. Now
$\text {KM}(j+1,j)$. Now  $ \mu (j)=\ell $. Return to step 2.
$ \mu (j)=\ell $. Return to step 2.4. Take all elements of the temporary ordered list L, read all
 $+$ entries in order (from left to right) and add them to the (right end of the) queue Q; then read all
$+$ entries in order (from left to right) and add them to the (right end of the) queue Q; then read all  $-$ entries in order (from left to right) and add them to the (right end of the) queue Q. Return to step 1.
$-$ entries in order (from left to right) and add them to the (right end of the) queue Q. Return to step 1.
We have the following adaptation of Proposition 4.3, revised to include sign maps and to reference tamed forms in place of upper-echelon forms.
Proposition 4.5. Within a signed KM-relatable equivalence class of collapsing map/sign map pairs ![]() $(\mu ,\operatorname {sgn})$, there is a unique tamed
$(\mu ,\operatorname {sgn})$, there is a unique tamed ![]() $(\mu _{\ast },\operatorname {sgn}_{\ast })$. Moreover,
$(\mu _{\ast },\operatorname {sgn}_{\ast })$. Moreover,
 $$ \begin{align} \sum_{\left(\mu ,\operatorname{sgn}\right)\sim \left(\mu _{\ast },\operatorname{sgn}_{\ast }\right)}I\left(\mu ,{\mathop{\textrm{{id}}}\nolimits},\operatorname{sgn},\gamma ^{(k+1)}\right)=\int_{T_{D}\left(\mu _{\ast }\right)}J_{\mu _{\ast }, \operatorname{sgn}_{\ast }}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{ t}_{k+1}, \end{align} $$
$$ \begin{align} \sum_{\left(\mu ,\operatorname{sgn}\right)\sim \left(\mu _{\ast },\operatorname{sgn}_{\ast }\right)}I\left(\mu ,{\mathop{\textrm{{id}}}\nolimits},\operatorname{sgn},\gamma ^{(k+1)}\right)=\int_{T_{D}\left(\mu _{\ast }\right)}J_{\mu _{\ast }, \operatorname{sgn}_{\ast }}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{ t}_{k+1}, \end{align} $$where ![]() $T_{D}(\mu _{\ast })$ is defined in equation (4.3).
$T_{D}(\mu _{\ast })$ is defined in equation (4.3).
To proceed with our program, we divide the expansion (4.5) into sums over signed KM-relatable equivalence classes, and apply equation (4.8) for the sum over each equivalence class. Thus we obtain
 $$ \begin{align} \gamma ^{(1)}(t_{1})=\sum_{\left(\mu _{\ast },\operatorname{sgn}_{\ast }\right)\text{ tamed} }\int_{T_{D}\left(\mu _{\ast }\right)}J_{\mu _{\ast },\operatorname{sgn}_{\ast }}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align} $$
$$ \begin{align} \gamma ^{(1)}(t_{1})=\sum_{\left(\mu _{\ast },\operatorname{sgn}_{\ast }\right)\text{ tamed} }\int_{T_{D}\left(\mu _{\ast }\right)}J_{\mu _{\ast },\operatorname{sgn}_{\ast }}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align} $$ The next step will be to round up the tamed pairs ![]() $(\mu _{\ast },\operatorname {sgn}_{\ast })$ via wild moves, as defined and discussed in the next section. This will produce a further reduction of equation (4.9).
$(\mu _{\ast },\operatorname {sgn}_{\ast })$ via wild moves, as defined and discussed in the next section. This will produce a further reduction of equation (4.9).
4.4 Wild moves
Definition 4.6. A wild move ![]() $\text {W}(\rho )$ is defined as follows: Suppose
$\text {W}(\rho )$ is defined as follows: Suppose ![]() $(\mu ,\operatorname {sgn})$ is a collapsing operator/sign map pair in tamed form, and
$(\mu ,\operatorname {sgn})$ is a collapsing operator/sign map pair in tamed form, and ![]() $\{\ell , \dotsc , r\}$ is a full left branch – that is,
$\{\ell , \dotsc , r\}$ is a full left branch – that is,
 $$ \begin{align*} z \overset{\mathrm{def}}{=} \mu(\ell)=\mu(\ell+1)=\dotsb = \mu(r), \end{align*} $$
$$ \begin{align*} z \overset{\mathrm{def}}{=} \mu(\ell)=\mu(\ell+1)=\dotsb = \mu(r), \end{align*} $$but ![]() $\mu (\ell -1)\neq z$ (or is undefined) and
$\mu (\ell -1)\neq z$ (or is undefined) and ![]() $\mu (r+1) \neq z$ (or is undefined).
$\mu (r+1) \neq z$ (or is undefined).
Let ![]() $\rho $ be a permutation of
$\rho $ be a permutation of ![]() $\{\ell ,\ell +1, \dotsc , r \}$ that satisfies the following condition: If
$\{\ell ,\ell +1, \dotsc , r \}$ that satisfies the following condition: If ![]() $\ell \leq q<s\leq r$ and
$\ell \leq q<s\leq r$ and ![]() $\operatorname {sgn}(q)=\operatorname {sgn}(s)$, then q appears before s in the list
$\operatorname {sgn}(q)=\operatorname {sgn}(s)$, then q appears before s in the list ![]() $\left (\rho ^{-1}(\ell ), \dotsc , \rho ^{-1}(r)\right )$ – or equivalently,
$\left (\rho ^{-1}(\ell ), \dotsc , \rho ^{-1}(r)\right )$ – or equivalently, ![]() $\rho (q)<\rho (s)$.
$\rho (q)<\rho (s)$.
Then the wild move ![]() $\text {W}(\rho )$ is defined as an action on a triple
$\text {W}(\rho )$ is defined as an action on a triple ![]() $ (\mu ,\sigma , \operatorname {sgn})$, where
$ (\mu ,\sigma , \operatorname {sgn})$, where
provided
 $$ \begin{align*} \mu' & = \rho \circ \mu = \rho \circ \mu \circ \rho^{-1}, \\ \sigma' & = \rho \circ \sigma, \\ \operatorname{sgn}' & = \operatorname{sgn} \circ \rho^{-1}. \end{align*} $$
$$ \begin{align*} \mu' & = \rho \circ \mu = \rho \circ \mu \circ \rho^{-1}, \\ \sigma' & = \rho \circ \sigma, \\ \operatorname{sgn}' & = \operatorname{sgn} \circ \rho^{-1}. \end{align*} $$We note that W is an action
It is fairly straightforward to show the following, using the definition of a tamed form. It is important to note that the analogous statement for upper-echelon forms does not hold, which is the reason for introducing the tamed class.
Proposition 4.7. Suppose ![]() $(\mu ,\operatorname {sgn})$ is a collapsing operator/sign map pair in tamed form, and
$(\mu ,\operatorname {sgn})$ is a collapsing operator/sign map pair in tamed form, and ![]() $W(\rho )$ is a wild move. Letting
$W(\rho )$ is a wild move. Letting ![]() $(\mu ', \operatorname {sgn}')$ be the output,
$(\mu ', \operatorname {sgn}')$ be the output,
then ![]() $(\mu ',\operatorname {sgn}')$ is also tamed.
$(\mu ',\operatorname {sgn}')$ is also tamed.
Thus wild moves preserve the tamed class, and we can say that two tamed forms ![]() $(\mu ,\operatorname {sgn})$ and
$(\mu ,\operatorname {sgn})$ and ![]() $(\mu ',\operatorname {sgn}')$ are wildly relatable if there exists
$(\mu ',\operatorname {sgn}')$ are wildly relatable if there exists ![]() $\rho $ as in Definition 4.6 such that
$\rho $ as in Definition 4.6 such that
This is an equivalence relation, and in the sum (4.9) we can partition the class of tamed pairs ![]() $(\mu ,\operatorname {sgn})$ into equivalence classes of wildly relatable forms (we pursue this in the next section).
$(\mu ,\operatorname {sgn})$ into equivalence classes of wildly relatable forms (we pursue this in the next section).
The main result of this section is the following:
Proposition 4.8. Suppose that ![]() $\rho $ is as in Definition 4.6 and
$\rho $ is as in Definition 4.6 and
Then for any symmetric density ![]() $f^{(k+1)}$,
$f^{(k+1)}$,
 $$ \begin{align*} J_{\mu',\operatorname{sgn}'}\left( f^{(k+1)}\right)\left(t_1, {\sigma'}^{-1}\left(\underline{t}_{k+1}\right)\right) = J_{\mu,\operatorname{sgn}}\left( f^{(k+1)}\right)\left(t_1, \sigma^{-1}\left(\underline{t}_{k+1}\right)\right). \end{align*} $$
$$ \begin{align*} J_{\mu',\operatorname{sgn}'}\left( f^{(k+1)}\right)\left(t_1, {\sigma'}^{-1}\left(\underline{t}_{k+1}\right)\right) = J_{\mu,\operatorname{sgn}}\left( f^{(k+1)}\right)\left(t_1, \sigma^{-1}\left(\underline{t}_{k+1}\right)\right). \end{align*} $$Consequently, the Duhamel integrals are preserved, after adjusting for the time permutations
 $$ \begin{align*} \int_{\sigma'\left[T_D\left(\mu'\right)\right]} J_{\mu',\operatorname{sgn}'}\left( \gamma^{(k+1)}\right)\left(t_1, \underline{t}_{k+1}\right) d\underline{t} _{k+1} = \int_{\sigma\left[T_D\left(\mu\right)\right]} J_{\mu,\operatorname{sgn}}\left( \gamma^{(k+1)}\right)\left(t_1, \underline{t}_{k+1}\right) d\underline{t}_{k+1}, \end{align*} $$
$$ \begin{align*} \int_{\sigma'\left[T_D\left(\mu'\right)\right]} J_{\mu',\operatorname{sgn}'}\left( \gamma^{(k+1)}\right)\left(t_1, \underline{t}_{k+1}\right) d\underline{t} _{k+1} = \int_{\sigma\left[T_D\left(\mu\right)\right]} J_{\mu,\operatorname{sgn}}\left( \gamma^{(k+1)}\right)\left(t_1, \underline{t}_{k+1}\right) d\underline{t}_{k+1}, \end{align*} $$where ![]() $\sigma [T_D(\mu )]$ is defined by modifying equation (4.3) so that node labels are pushed forward by
$\sigma [T_D(\mu )]$ is defined by modifying equation (4.3) so that node labels are pushed forward by ![]() $\sigma $:
$\sigma $:
 $$ \begin{align*} \sigma[T_D(\mu)] = \left\{ t_{\sigma\left(j\right)}\geq t_{\sigma(k)} : \right. & j,k\text{ are labels on nodes of }\alpha \text{ such} \\ & \left. \vphantom{t_{\sigma\left(j\right)}}\text{that the }k\text{ node is a child of the }j\text{ node} \right\}. \end{align*} $$
$$ \begin{align*} \sigma[T_D(\mu)] = \left\{ t_{\sigma\left(j\right)}\geq t_{\sigma(k)} : \right. & j,k\text{ are labels on nodes of }\alpha \text{ such} \\ & \left. \vphantom{t_{\sigma\left(j\right)}}\text{that the }k\text{ node is a child of the }j\text{ node} \right\}. \end{align*} $$Proof. A permutation ![]() $\rho $ of the type described in Definition 4.6 can be written as a composition of permutations
$\rho $ of the type described in Definition 4.6 can be written as a composition of permutations
with the property that each ![]() $\tau = (i,i+1)$ for some
$\tau = (i,i+1)$ for some ![]() $i\in \{\ell , \dotsc , \ell +r\}$ and
$i\in \{\ell , \dotsc , \ell +r\}$ and ![]() $\operatorname {sgn}(i) \neq \operatorname {sgn}(i+1)$. Thus it suffices to prove
$\operatorname {sgn}(i) \neq \operatorname {sgn}(i+1)$. Thus it suffices to prove
 $$ \begin{align*} U^{(i-1)}(-t_i) B_{\mu(i),i}^- U^{(i)} (t_i -t_{i+1}) B_{\mu(i+1),i+1}^+ &U^{(i+1)}(t_{i+1}) \\ &= U^{(i-1)}(-t_{i+1}) B_{\mu(i),i}^+ U^{(i)} (t_{i+1} -t_i) B_{\mu(i+1),i+1}^- U^{(i+1)}(t_i) \end{align*} $$
$$ \begin{align*} U^{(i-1)}(-t_i) B_{\mu(i),i}^- U^{(i)} (t_i -t_{i+1}) B_{\mu(i+1),i+1}^+ &U^{(i+1)}(t_{i+1}) \\ &= U^{(i-1)}(-t_{i+1}) B_{\mu(i),i}^+ U^{(i)} (t_{i+1} -t_i) B_{\mu(i+1),i+1}^- U^{(i+1)}(t_i) \end{align*} $$when the two sides act on a symmetric density. Recall that ![]() $ z=\mu (i)=\mu (i+1) $. Without loss, we might as well take
$ z=\mu (i)=\mu (i+1) $. Without loss, we might as well take ![]() $z=1$ and
$z=1$ and ![]() $i=2$ so that this becomes
$i=2$ so that this becomes
 $$ \begin{align} U^{(1)}(-t_2) B_{1,2}^- U^{(2)} (t_2 -t_3) B_{1,3}^+ U^{(3)}(t_3)= U^{(1)}(-t_3) B_{1,2}^+ U^{(2)} (t_3 -t_2) B_{1,3}^- U^{(3)}(t_2). \end{align} $$
$$ \begin{align} U^{(1)}(-t_2) B_{1,2}^- U^{(2)} (t_2 -t_3) B_{1,3}^+ U^{(3)}(t_3)= U^{(1)}(-t_3) B_{1,2}^+ U^{(2)} (t_3 -t_2) B_{1,3}^- U^{(3)}(t_2). \end{align} $$To prove equation (4.10), on the left side we proceed as follows: First we plug in
 $$ \begin{align*} U^{(1)}(-t_2) & = U^1_{-2} U^{1'}_{2} \\ U^{(2)}(t_2-t_3) & = U_2^1 U_{-3}^1 U_{-2}^{1'} U_{3}^{1'} U_2^2 U_{-3}^2 U_{-2}^{2'} U_3^{2'} \\ U^{(3)}(t_3) & = U_3^1 U_{-3}^{1'} U_3^2 U_{-3}^{2'} U_3^3 U_{-3}^{3'}, \end{align*} $$
$$ \begin{align*} U^{(1)}(-t_2) & = U^1_{-2} U^{1'}_{2} \\ U^{(2)}(t_2-t_3) & = U_2^1 U_{-3}^1 U_{-2}^{1'} U_{3}^{1'} U_2^2 U_{-3}^2 U_{-2}^{2'} U_3^{2'} \\ U^{(3)}(t_3) & = U_3^1 U_{-3}^{1'} U_3^2 U_{-3}^{2'} U_3^3 U_{-3}^{3'}, \end{align*} $$where the subscript indicates the time variable and the superscript indicates the spatial variable. Then we note that for the two collapsing operators on the left side of equation (4.10), the following hold:
•
 $B_{1,2}^-$ acts only on the
$B_{1,2}^-$ acts only on the  $2$,
$2$,  $2'$ and
$2'$ and  $1'$ coordinates, so we can move all
$1'$ coordinates, so we can move all  $U^1$ operators in the middle to the left.
$U^1$ operators in the middle to the left.•
 $B_{1,3}^+$ acts only on the
$B_{1,3}^+$ acts only on the  $3$,
$3$,  $3'$ and
$3'$ and  $1$ coordinates, so we can move all
$1$ coordinates, so we can move all  $U^2$,
$U^2$,  $U^{2'}$ and
$U^{2'}$ and  $U^{1'}$ operators in the middle to the right.
$U^{1'}$ operators in the middle to the right.
This results in
 $$ \begin{align} \text{left side of equation~} (4.10) = U_{-3}^1 U_2^{1'} B_{1,2}^- B_{1,3}^+ U_3^1 U_{-2}^{1'} U_2^2 U_{-2}^{2'} U_3^3 U_{-3}^3. \end{align} $$
$$ \begin{align} \text{left side of equation~} (4.10) = U_{-3}^1 U_2^{1'} B_{1,2}^- B_{1,3}^+ U_3^1 U_{-2}^{1'} U_2^2 U_{-2}^{2'} U_3^3 U_{-3}^3. \end{align} $$Similarly, on the right side of equation (4.10), plug in
 $$ \begin{align*} U^{(1)}(-t_3) & = U_{-3}^1 U_3^{1'} \\ U^{(2)}(t_3-t_2) & = U_3^1 U_{-2}^1 U_{-3}^{1'} U_{2}^{1'} U_3^2 U_{-2}^2 U_{-3}^{2'} U_2^{2'} \\ U^{(3)}(t_2) & = U_2^1 U_{-2}^{1'} U_2^2 U_{-2}^{2'} U_2^3 U_{-2}^{3'}. \end{align*} $$
$$ \begin{align*} U^{(1)}(-t_3) & = U_{-3}^1 U_3^{1'} \\ U^{(2)}(t_3-t_2) & = U_3^1 U_{-2}^1 U_{-3}^{1'} U_{2}^{1'} U_3^2 U_{-2}^2 U_{-3}^{2'} U_2^{2'} \\ U^{(3)}(t_2) & = U_2^1 U_{-2}^{1'} U_2^2 U_{-2}^{2'} U_2^3 U_{-2}^{3'}. \end{align*} $$Then we note that for the two collapsing operators on the right side of equation (4.10), the following are true:
•
 $B_{1,2}^+$ acts only on the
$B_{1,2}^+$ acts only on the  $2$,
$2$,  $2'$ and
$2'$ and  $1$ coordinates, so we can move all
$1$ coordinates, so we can move all  $U^{1'}$ operators in the middle to the left.
$U^{1'}$ operators in the middle to the left.•
 $B_{1,3}^-$ acts only on the
$B_{1,3}^-$ acts only on the  $3$,
$3$,  $3'$ and
$3'$ and  $1'$ coordinates, so we can move all
$1'$ coordinates, so we can move all  $U^2$,
$U^2$,  $U^{2'}$ and
$U^{2'}$ and  $U^{1}$ operators in the middle to the right.
$U^{1}$ operators in the middle to the right.
This results in
 $$ \begin{align} \text{right side of equation~} (4.10) = U_{-3}^1 U_2^{1'} B_{1,2}^+ B_{1,3}^- U_3^1 U_{-2}^{1'} U_3^2 U_{-3}^{2'} U_2^3 U_{-2}^{3'}. \end{align} $$
$$ \begin{align} \text{right side of equation~} (4.10) = U_{-3}^1 U_2^{1'} B_{1,2}^+ B_{1,3}^- U_3^1 U_{-2}^{1'} U_3^2 U_{-3}^{2'} U_2^3 U_{-2}^{3'}. \end{align} $$Since equations (4.11) and (4.12) are equal when applied to a symmetric density, this proves equation (4.10). In particular, one just needs that to permute
Example 6. The pair ![]() $(\mu _1, \operatorname {sgn}_1)$ is defined as follows:
$(\mu _1, \operatorname {sgn}_1)$ is defined as follows:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline \mu _{1} & 1 & 1 & 1 & 2 & 4 & 4 \\[3pt] \operatorname{sgn}_{1} & + & + & - & - & + & - \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline \mu _{1} & 1 & 1 & 1 & 2 & 4 & 4 \\[3pt] \operatorname{sgn}_{1} & + & + & - & - & + & - \\ \end{array} \end{align*} $$There are five nontrivial wild moves for ![]() $j = 2, \dotsc , 6$,
$j = 2, \dotsc , 6$,
 $$ \begin{align*} \left(\mu_j,\sigma_j, \operatorname{sgn}_j\right) = W\left(\rho_j\right)(\mu_1, \text{id}, \operatorname{sgn}_1), \end{align*} $$
$$ \begin{align*} \left(\mu_j,\sigma_j, \operatorname{sgn}_j\right) = W\left(\rho_j\right)(\mu_1, \text{id}, \operatorname{sgn}_1), \end{align*} $$as indicated in the following table:
 $$ \begin{align*} \begin{array}{@{\ \ \ \ }c@{\ \ \ \ }|@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ \ \ }|@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ }|@{\ \ }|@{\ \ \ \ }c@{\ \ \ \ }|@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ \ \ }|@{\ \ \ \ }c@{\ \ \ \ }c} & 2 & 3 & 4 & 6 & 7 & & 2 & 3 & 4 & 6 & 7 \\ \hline \rho _{1} & 2 & 3 & 4 & 6 & 7 & \rho _{1}^{-1} & 2 & 3 & 4 & 6 & 7 \\[2pt] \rho _{2} & 2 & 4 & 3 & 6 & 7 & \rho _{2}^{-1} & 2 & 4 & 3 & 6 & 7 \\[2pt] \rho _{3} & 3 & 4 & 2 & 6 & 7 & \rho _{3}^{-1} & 4 & 2 & 3 & 6 &7 \\[2pt] \rho _{4} & 2 & 3 & 4 & 7 & 6 & \rho _{4}^{-1} & 2 & 3 & 4 & 7 & 6 \\[2pt] \rho _{5} & 2 & 4 & 3 & 7 & 6 & \rho _{5}^{-1} & 2 & 4 & 3 & 7 & 6 \\[2pt] \rho _{6} & 3 & 4 & 2 & 7 & 6 & \rho _{6}^{-1} & 4 & 2 & 3 & 7 & 6 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{@{\ \ \ \ }c@{\ \ \ \ }|@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ \ \ }|@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ }|@{\ \ }|@{\ \ \ \ }c@{\ \ \ \ }|@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ \ \ }c@{\ \ \ \ }|@{\ \ \ \ }c@{\ \ \ \ }c} & 2 & 3 & 4 & 6 & 7 & & 2 & 3 & 4 & 6 & 7 \\ \hline \rho _{1} & 2 & 3 & 4 & 6 & 7 & \rho _{1}^{-1} & 2 & 3 & 4 & 6 & 7 \\[2pt] \rho _{2} & 2 & 4 & 3 & 6 & 7 & \rho _{2}^{-1} & 2 & 4 & 3 & 6 & 7 \\[2pt] \rho _{3} & 3 & 4 & 2 & 6 & 7 & \rho _{3}^{-1} & 4 & 2 & 3 & 6 &7 \\[2pt] \rho _{4} & 2 & 3 & 4 & 7 & 6 & \rho _{4}^{-1} & 2 & 3 & 4 & 7 & 6 \\[2pt] \rho _{5} & 2 & 4 & 3 & 7 & 6 & \rho _{5}^{-1} & 2 & 4 & 3 & 7 & 6 \\[2pt] \rho _{6} & 3 & 4 & 2 & 7 & 6 & \rho _{6}^{-1} & 4 & 2 & 3 & 7 & 6 \\ \end{array} \end{align*} $$ Notice that each  $\rho _j^{-1}$ preserves the order of
$\rho _j^{-1}$ preserves the order of ![]() $2, 3$, as in Definition 4.6 – meaning that
$2, 3$, as in Definition 4.6 – meaning that ![]() $2$ appears before
$2$ appears before ![]() $3$ in the list
$3$ in the list  $\left (\rho _j^{-1}(2), \rho _j^{-1}(3), \rho _j^{-1}(4)\right )$; equivalently,
$\left (\rho _j^{-1}(2), \rho _j^{-1}(3), \rho _j^{-1}(4)\right )$; equivalently, ![]() $\rho (2)<\rho (3)$. Thus the action of
$\rho (2)<\rho (3)$. Thus the action of ![]() $\rho ^{-1}$ on
$\rho ^{-1}$ on ![]() $\{2,3,4\}$ is completely determined by where
$\{2,3,4\}$ is completely determined by where ![]() $4$ appears in the list
$4$ appears in the list  $\left (\rho _j^{-1}(2), \rho _j^{-1}(3), \rho _j^{-1}(4)\right )$.
$\left (\rho _j^{-1}(2), \rho _j^{-1}(3), \rho _j^{-1}(4)\right )$.
The corresponding trees and explicit mappings  $\left (\mu _{j},\operatorname {sgn}_{j}\right )$ are indicated in the following. We notice that all
$\left (\mu _{j},\operatorname {sgn}_{j}\right )$ are indicated in the following. We notice that all  $\left (\mu _{j},\operatorname {sgn}_{j}\right )$ are tamed (in accordance with Proposition 4.7) and that wild moves, unlike KM moves, do change the tree skeleton, but this change is restricted to shuffling nodes along a left branch, subject to the restrictions (indicated in Definition 4.6) that the ordering of the plus nodes and minus nodes remain intact.
$\left (\mu _{j},\operatorname {sgn}_{j}\right )$ are tamed (in accordance with Proposition 4.7) and that wild moves, unlike KM moves, do change the tree skeleton, but this change is restricted to shuffling nodes along a left branch, subject to the restrictions (indicated in Definition 4.6) that the ordering of the plus nodes and minus nodes remain intact.

4.5 Reference forms and tamed integration domains
Definition 4.9. A tamed pair ![]() $\left (\hat \mu ,\hat {\operatorname {sgn}}\right )$ will be called a reference pair provided that in every left branch, all the
$\left (\hat \mu ,\hat {\operatorname {sgn}}\right )$ will be called a reference pair provided that in every left branch, all the ![]() $+$ nodes come before all the
$+$ nodes come before all the ![]() $-$ nodes.
$-$ nodes.
Definition 4.10. Given a reference pair ![]() $\left (\hat \mu , \hat {\operatorname {sgn}}\right )$, we will call a permutation
$\left (\hat \mu , \hat {\operatorname {sgn}}\right )$, we will call a permutation ![]() $\rho $ of
$\rho $ of ![]() $\{2, \dotsc , k+1\}$ allowable if it meets the conditions in Definition 4.6 – that is, it leaves all left branches invariant and moreover, for each left branch
$\{2, \dotsc , k+1\}$ allowable if it meets the conditions in Definition 4.6 – that is, it leaves all left branches invariant and moreover, for each left branch ![]() $(\ell , \dotsc , r)$, all
$(\ell , \dotsc , r)$, all ![]() $+$ nodes appear in their original order and all
$+$ nodes appear in their original order and all ![]() $-$ nodes appear in their original order within the list
$-$ nodes appear in their original order within the list ![]() $\left (\rho ^{-1}(\ell ), \dotsc , \rho ^{-1}(r)\right )$.
$\left (\rho ^{-1}(\ell ), \dotsc , \rho ^{-1}(r)\right )$.
For example, the tree ![]() $(\mu _1,\operatorname {sgn}_1)$ in Example 6 is a reference pair. If
$(\mu _1,\operatorname {sgn}_1)$ in Example 6 is a reference pair. If ![]() $(\ell , \dotsc , r)$ is a full left branch of
$(\ell , \dotsc , r)$ is a full left branch of ![]() $\hat \mu $, then the definition of a reference pair means that there is some intermediate position m such that the
$\hat \mu $, then the definition of a reference pair means that there is some intermediate position m such that the ![]() $\operatorname {sgn}$ map looks like the following:
$\operatorname {sgn}$ map looks like the following:
 $$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & \ell & \dotsb & m-1 & m & m+1 & \dotsb & r \\ \hline \operatorname{sgn} & + & + & + & - & - & - & - \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c@{\kern10pt}c} j & \ell & \dotsb & m-1 & m & m+1 & \dotsb & r \\ \hline \operatorname{sgn} & + & + & + & - & - & - & - \\ \end{array} \end{align*} $$ However, we note that it is possible that they are all plusses ![]() $(m=r+1)$ or all minuses
$(m=r+1)$ or all minuses ![]() $(m=\ell )$. With this notation, we can say that
$(m=\ell )$. With this notation, we can say that ![]() $\rho $ is allowable if
$\rho $ is allowable if ![]() $\rho (\ell )< \dotsb < \rho (m-1)$ and
$\rho (\ell )< \dotsb < \rho (m-1)$ and ![]() $\rho (m) < \dotsb < \rho (r) $ – or equivalently, if in the list
$\rho (m) < \dotsb < \rho (r) $ – or equivalently, if in the list
 $$ \begin{align*} \left(\rho^{-1}(\ell), \dotsc, \rho^{-1}(r)\right), \end{align*} $$
$$ \begin{align*} \left(\rho^{-1}(\ell), \dotsc, \rho^{-1}(r)\right), \end{align*} $$the values ![]() $(\ell , \dotsc , m-1)$ appear in that order and the values
$(\ell , \dotsc , m-1)$ appear in that order and the values ![]() $(m, \dotsc , r)$ appear in that order.
$(m, \dotsc , r)$ appear in that order.
Proposition 4.11. An equivalence class of wildly relatable tamed pairs
contains a unique reference pair ![]() $\left (\hat \mu , \hat {\operatorname {sgn}}\right )$. By the definition of being wildly relatable, for every
$\left (\hat \mu , \hat {\operatorname {sgn}}\right )$. By the definition of being wildly relatable, for every ![]() $(\mu ,\operatorname {sgn})\in Q$ there is a unique permutation
$(\mu ,\operatorname {sgn})\in Q$ there is a unique permutation ![]() $\rho $ of
$\rho $ of ![]() $\{2, \dotsc , k+1\}$ such that
$\{2, \dotsc , k+1\}$ such that
and this ![]() $\rho $ is allowable. The collection P of all
$\rho $ is allowable. The collection P of all ![]() $\rho $ arising in this way from Q is exactly the set of all allowable
$\rho $ arising in this way from Q is exactly the set of all allowable ![]() $\rho $ with respect to the reference pair
$\rho $ with respect to the reference pair ![]() $\left (\hat \mu , \hat {\operatorname {sgn}}\right )$.
$\left (\hat \mu , \hat {\operatorname {sgn}}\right )$.
Now, recall equation (4.9):
 $$ \begin{align*} \gamma ^{(1)}(t_{1})=\sum_{\left(\mu ,\operatorname{sgn}\right)\text{ tamed}}\int_{T_{D}(\mu )}J_{\mu ,\operatorname{sgn}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d \underline{t}_{k+1}. \end{align*} $$
$$ \begin{align*} \gamma ^{(1)}(t_{1})=\sum_{\left(\mu ,\operatorname{sgn}\right)\text{ tamed}}\int_{T_{D}(\mu )}J_{\mu ,\operatorname{sgn}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d \underline{t}_{k+1}. \end{align*} $$In this sum, group together equivalence classes Q of wildly relatable ![]() $(\mu ,\operatorname {sgn})$:
$(\mu ,\operatorname {sgn})$:
 $$ \begin{align} \gamma ^{(1)}(t_{1})=\sum_{\text{classes }Q}\sum_{(\mu ,\sigma )\in Q}\int_{T_{D}(\mu )}J_{\mu ,\operatorname{sgn}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align} $$
$$ \begin{align} \gamma ^{(1)}(t_{1})=\sum_{\text{classes }Q}\sum_{(\mu ,\sigma )\in Q}\int_{T_{D}(\mu )}J_{\mu ,\operatorname{sgn}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align} $$Each class Q can be represented by a unique reference ![]() $\left (\hat {\mu },\hat {\operatorname {sgn}}\right )$, and as in Proposition 4.11, for each
$\left (\hat {\mu },\hat {\operatorname {sgn}}\right )$, and as in Proposition 4.11, for each ![]() $(\mu ,\operatorname {sgn})\in Q$, there is an allowable
$(\mu ,\operatorname {sgn})\in Q$, there is an allowable ![]() $\rho \in P$ (with respect to
$\rho \in P$ (with respect to ![]() $\left (\hat {\mu },\hat {\operatorname {sgn}}\right )$) such that
$\left (\hat {\mu },\hat {\operatorname {sgn}}\right )$) such that
Since W is an action, we can write
 $$ \begin{align*} \left(\hat{\mu},\hat{\operatorname{sgn}}\right)=W\left(\rho ^{-1}\right)(\mu ,\operatorname{sgn}). \end{align*} $$
$$ \begin{align*} \left(\hat{\mu},\hat{\operatorname{sgn}}\right)=W\left(\rho ^{-1}\right)(\mu ,\operatorname{sgn}). \end{align*} $$Into the action ![]() $W\left (\rho ^{-1}\right )$, let us input the identity time permutation and define
$W\left (\rho ^{-1}\right )$, let us input the identity time permutation and define ![]() $\sigma $ as the output time permutation:
$\sigma $ as the output time permutation:
 $$ \begin{align*} \left(\hat{\mu},\sigma ,\hat{\operatorname{sgn}}\right)=W\left(\rho ^{-1}\right)(\mu ,\text{id},\operatorname{sgn}), \end{align*} $$
$$ \begin{align*} \left(\hat{\mu},\sigma ,\hat{\operatorname{sgn}}\right)=W\left(\rho ^{-1}\right)(\mu ,\text{id},\operatorname{sgn}), \end{align*} $$where, in accordance with Definition 4.6, ![]() $\sigma =\rho ^{-1}$. Since
$\sigma =\rho ^{-1}$. Since ![]() $\rho $ is allowable, this implies that for each left brach
$\rho $ is allowable, this implies that for each left brach ![]() $(\ell ,\dotsc ,r)$ with m as already defined,
$(\ell ,\dotsc ,r)$ with m as already defined, ![]() $\sigma ^{-1}(\ell )<\dotsb <\sigma ^{-1}(m-1)$ and
$\sigma ^{-1}(\ell )<\dotsb <\sigma ^{-1}(m-1)$ and ![]() $\sigma ^{-1}(m)<\dotsb <\sigma ^{-1}(r)$. In other words,
$\sigma ^{-1}(m)<\dotsb <\sigma ^{-1}(r)$. In other words, ![]() $ (\ell ,\dotsc ,m-1)$ and
$ (\ell ,\dotsc ,m-1)$ and ![]() $(m,\dotsc ,r)$ appear in order inside the list of values
$(m,\dotsc ,r)$ appear in order inside the list of values ![]() $(\sigma (\ell ),\dotsc ,\sigma (r))$. By Proposition 4.8,
$(\sigma (\ell ),\dotsc ,\sigma (r))$. By Proposition 4.8,
 $$ \begin{align*} \int_{T_{D}(\mu )}J_{\mu ,\operatorname{sgn}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}=\int_{\sigma \left\lbrack T_{D}\left(\hat{\mu}\right)\right]}J_{\hat{\mu},\hat{\operatorname{sgn}}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align*} $$
$$ \begin{align*} \int_{T_{D}(\mu )}J_{\mu ,\operatorname{sgn}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}=\int_{\sigma \left\lbrack T_{D}\left(\hat{\mu}\right)\right]}J_{\hat{\mu},\hat{\operatorname{sgn}}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}. \end{align*} $$Now as we sum this over all ![]() $(\mu ,\operatorname {sgn})\in Q$, we are summing over all
$(\mu ,\operatorname {sgn})\in Q$, we are summing over all ![]() $\rho \in P$ and hence over all
$\rho \in P$ and hence over all ![]() $\sigma =\rho ^{-1}$ meeting the condition already mentioned. Hence the integration domains on the right side union to a set that we will denote
$\sigma =\rho ^{-1}$ meeting the condition already mentioned. Hence the integration domains on the right side union to a set that we will denote
 $$ \begin{align*} T_{R}\left(\hat{\mu},\hat{\operatorname{sgn}}\right)\overset{\text{def}}{=}\bigcup_{\rho \in P}\sigma \left(T_{D}\left(\hat{\mu}\right)\right), \end{align*} $$
$$ \begin{align*} T_{R}\left(\hat{\mu},\hat{\operatorname{sgn}}\right)\overset{\text{def}}{=}\bigcup_{\rho \in P}\sigma \left(T_{D}\left(\hat{\mu}\right)\right), \end{align*} $$which can be described as follows: For each left branch ![]() $(\ell ,\dotsc ,r)$, with
$(\ell ,\dotsc ,r)$, with
and m the division index between plus and minus nodes, ![]() $T_{R}\left (\hat {\mu },\hat {\operatorname {sgn}}\right )$ is described by the inequalities
$T_{R}\left (\hat {\mu },\hat {\operatorname {sgn}}\right )$ is described by the inequalities
Plugging into equation (4.13), we obtain the following:
Proposition 4.12. The Duhamel expansion to coupling order k can be grouped into at most ![]() $8^{k}$ terms:
$8^{k}$ terms:
 $$ \begin{align} \gamma ^{(1)}(t_{1})=\sum_{\text{reference }\left(\hat{\mu},\hat{\operatorname{sgn}}\right)}\int_{T_{R}\left(\hat{\mu},\hat{\operatorname{sgn}}\right)}J_{\mu ,\operatorname{sgn}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}, \end{align} $$
$$ \begin{align} \gamma ^{(1)}(t_{1})=\sum_{\text{reference }\left(\hat{\mu},\hat{\operatorname{sgn}}\right)}\int_{T_{R}\left(\hat{\mu},\hat{\operatorname{sgn}}\right)}J_{\mu ,\operatorname{sgn}}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}, \end{align} $$where each integration domain ![]() $T_{R}\left (\hat {\mu },\hat {\operatorname {sgn}}\right )$ is as defined in formula (4.14).
$T_{R}\left (\hat {\mu },\hat {\operatorname {sgn}}\right )$ is as defined in formula (4.14).
A quick example of formulas (4.14) and (4.15) is Example 4, in which the reference tree is the one corresponding to ![]() $I_2$. Reading from that tree, formula (4.14) becomes the set D and the combined integral is equation (4.4).
$I_2$. Reading from that tree, formula (4.14) becomes the set D and the combined integral is equation (4.4).
Returning to Example 6, ![]() $(\mu _1,\operatorname {sgn}_1)$ is the reference pair. To combine the Duhamel integrals, we convert all five other tamed forms
$(\mu _1,\operatorname {sgn}_1)$ is the reference pair. To combine the Duhamel integrals, we convert all five other tamed forms  $\left (\mu _j,\operatorname {sgn}_j\right )$ to
$\left (\mu _j,\operatorname {sgn}_j\right )$ to ![]() $(\mu _1,\operatorname {sgn}_1)$ via wild moves. The resulting combined time integration set will be read off from the
$(\mu _1,\operatorname {sgn}_1)$ via wild moves. The resulting combined time integration set will be read off from the ![]() $(\mu _1,\operatorname {sgn}_1)$ tree as
$(\mu _1,\operatorname {sgn}_1)$ tree as
Proposition 4.12 and the integration domain (4.14) are compatible with the U-V space techniques we proved in Section 2. This fact may not be so clear at the moment, as they are written with much shorthand. We will prove this fact in Section 5.2.
5 Uniqueness for the GP hierarchy (1.2) – Actual estimates
The main goal of this section is to prove Proposition 3.7 on estimating  $J_{\mu _{m},\operatorname {sgn}}^{(k+1)}$. Of course, by
$J_{\mu _{m},\operatorname {sgn}}^{(k+1)}$. Of course, by  $J_{\mu _{m},\operatorname {sgn}}^{(k+1)}$ we mean the reference form now. We first present an example in Section 5.1 to convey the basic ideas of the proof. Then in Section 5.2 we demonstrate why we need the extended KM board game and prove that Proposition 4.12 and the integration domain (4.14) are compatible with the U-V space techniques. Once that is settled, the main idea idea in Section 5.1 will work for the general case. Thus we estimate the general case in Section 5.3.
$J_{\mu _{m},\operatorname {sgn}}^{(k+1)}$ we mean the reference form now. We first present an example in Section 5.1 to convey the basic ideas of the proof. Then in Section 5.2 we demonstrate why we need the extended KM board game and prove that Proposition 4.12 and the integration domain (4.14) are compatible with the U-V space techniques. Once that is settled, the main idea idea in Section 5.1 will work for the general case. Thus we estimate the general case in Section 5.3.
The time integration limits in Section 4.5 will be put to use with Lemmas 2.1 and 2.2. With the trivial estimate ![]() $\left \lVert u\right \rVert _{Y^{s}}\lesssim \left \lVert u\right \rVert _{X^{s}}$, Lemmas 2.1 and 2.2 read as
$\left \lVert u\right \rVert _{Y^{s}}\lesssim \left \lVert u\right \rVert _{X^{s}}$, Lemmas 2.1 and 2.2 read as
 $$ \begin{align} \left\lVert \int_{a}^{t}e^{-i\left(t-t'\right)\Delta }\left(u_{1}u_{2}u_{3}\right) (\bullet ,t')dt'\right\rVert_{X^{-1}} & \leq C\lVert u_{1}\rVert _{X^{-1}}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{X^{1}}+\left\lVert P_{>M_{0}}u_{2}\right\rVert _{X^{1}}\right) \lVert u_{3}\rVert _{X^{1}}, \end{align} $$
$$ \begin{align} \left\lVert \int_{a}^{t}e^{-i\left(t-t'\right)\Delta }\left(u_{1}u_{2}u_{3}\right) (\bullet ,t')dt'\right\rVert_{X^{-1}} & \leq C\lVert u_{1}\rVert _{X^{-1}}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{X^{1}}+\left\lVert P_{>M_{0}}u_{2}\right\rVert _{X^{1}}\right) \lVert u_{3}\rVert _{X^{1}}, \end{align} $$ $$ \begin{align} \left\lVert \int_{a}^{t}e^{-i\left(t-t'\right)\Delta }\left(u_{1}u_{2}u_{3}\right) (\bullet ,t')dt'\right\rVert_{X^{1}} & \leq C\lVert u_{1}\rVert _{X^{1}}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{X^{1}}+\left\lVert P_{>M_{0}}u_{2}\right\rVert _{X^{1}}\right) \lVert u_{3}\rVert _{X^{1}}, \end{align} $$
$$ \begin{align} \left\lVert \int_{a}^{t}e^{-i\left(t-t'\right)\Delta }\left(u_{1}u_{2}u_{3}\right) (\bullet ,t')dt'\right\rVert_{X^{1}} & \leq C\lVert u_{1}\rVert _{X^{1}}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}u_{2}\right\rVert _{X^{1}}+\left\lVert P_{>M_{0}}u_{2}\right\rVert _{X^{1}}\right) \lVert u_{3}\rVert _{X^{1}}, \end{align} $$ $$ \begin{align} \left\lVert \int_{a}^{t}e^{-i\left(t-t'\right)\Delta }\left(u_{1}u_{2}u_{3}\right) (\bullet ,t')dt'\right\rVert _{X^{-1}} & \leq C\lVert u_{1}\rVert _{X^{-1}}\lVert u_{2}\rVert _{X^{1}}\lVert u_{3}\rVert _{X^{1}}, \end{align} $$
$$ \begin{align} \left\lVert \int_{a}^{t}e^{-i\left(t-t'\right)\Delta }\left(u_{1}u_{2}u_{3}\right) (\bullet ,t')dt'\right\rVert _{X^{-1}} & \leq C\lVert u_{1}\rVert _{X^{-1}}\lVert u_{2}\rVert _{X^{1}}\lVert u_{3}\rVert _{X^{1}}, \end{align} $$ $$ \begin{align} \left\lVert \int_{a}^{t}e^{-i\left(t-t'\right)\Delta }\left(u_{1}u_{2}u_{3}\right) (\bullet ,t')dt'\right\rVert_{X^{1}} & \leq C\lVert u_{1}\rVert _{X^{1}}\lVert u_{2}\rVert _{X^{1}}\lVert u_{3}\rVert _{X^{1}}. \end{align} $$
$$ \begin{align} \left\lVert \int_{a}^{t}e^{-i\left(t-t'\right)\Delta }\left(u_{1}u_{2}u_{3}\right) (\bullet ,t')dt'\right\rVert_{X^{1}} & \leq C\lVert u_{1}\rVert _{X^{1}}\lVert u_{2}\rVert _{X^{1}}\lVert u_{3}\rVert _{X^{1}}. \end{align} $$If  $u_{j}=e^{it'\Delta }f_{j}$ for some j and some
$u_{j}=e^{it'\Delta }f_{j}$ for some j and some ![]() $f_{j}$ independent of t and
$f_{j}$ independent of t and ![]() $t'$, we can replace the
$t'$, we can replace the ![]() $X^{s}$ norm of
$X^{s}$ norm of ![]() $ u_{j}$ in formulas (5.1)–(5.4) with the
$ u_{j}$ in formulas (5.1)–(5.4) with the ![]() $H^{s}$ norm of
$H^{s}$ norm of ![]() $f_{j}$. We do not use
$f_{j}$. We do not use ![]() $\lesssim $ in these equations because we are going to use them repeatedly, and the constants are going to accumulate.
$\lesssim $ in these equations because we are going to use them repeatedly, and the constants are going to accumulate.
5.1 An example of how to estimate
We estimate the integral in Example 4:
 $$ \begin{align*} I=\int_{t_{4}=0}^{t_{1}}\int_{t_{2}=0}^{t_{1}} \int_{t_{3}=t_{4}}^{t_{1}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{3}-t_{4})B_{3,4}^{+}\gamma ^{(4)}d \underline{t}_{4}, \end{align*} $$
$$ \begin{align*} I=\int_{t_{4}=0}^{t_{1}}\int_{t_{2}=0}^{t_{1}} \int_{t_{3}=t_{4}}^{t_{1}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{+}U^{(2)}(t_{2}-t_{3})B_{1,3}^{-}U^{(3)}(t_{3}-t_{4})B_{3,4}^{+}\gamma ^{(4)}d \underline{t}_{4}, \end{align*} $$where the integration limits have already been computed in Section 4.2. Its reference tree is exactly the tree corresponding to ![]() $I_{2}$ in Example 4.
$I_{2}$ in Example 4.
Plugging in equation (3.6), we find that the integrand is in fact
 $$ \begin{align*} I&=\int_{t_{4}=0}^{t_{1}}dt_{4}\int d\mu _{t_{4}}\left( \phi \right) \int_{t_{2}=0}^{t_{1}}dt_{2}\int_{t_{3}=t_{4}}^{t_{1}}U_{1,2}\left(\left\lvert U_{2,4}\phi \right\rvert ^{2}U_{2,4}\phi \right)(x_{1})\\ &\qquad {}\times U_{1,3}\left(\overline{U_{3,4}\phi }\overline{U_{3,4}\phi }U_{3,4}\left( \left\lvert \phi \right\rvert ^{2}\phi \right) \right)\left(x^{\prime}_{1}\right)dt_{3}. \end{align*} $$
$$ \begin{align*} I&=\int_{t_{4}=0}^{t_{1}}dt_{4}\int d\mu _{t_{4}}\left( \phi \right) \int_{t_{2}=0}^{t_{1}}dt_{2}\int_{t_{3}=t_{4}}^{t_{1}}U_{1,2}\left(\left\lvert U_{2,4}\phi \right\rvert ^{2}U_{2,4}\phi \right)(x_{1})\\ &\qquad {}\times U_{1,3}\left(\overline{U_{3,4}\phi }\overline{U_{3,4}\phi }U_{3,4}\left( \left\lvert \phi \right\rvert ^{2}\phi \right) \right)\left(x^{\prime}_{1}\right)dt_{3}. \end{align*} $$We denote the cubic term ![]() $\left \lvert \phi \right \rvert ^{2}\phi $ generated in the innermost coupling with
$\left \lvert \phi \right \rvert ^{2}\phi $ generated in the innermost coupling with  $\mathcal {C}_{R}^{(4)}$, where the subscript R stands for ‘rough’, as it has no propagator inside to smooth things out. That is,
$\mathcal {C}_{R}^{(4)}$, where the subscript R stands for ‘rough’, as it has no propagator inside to smooth things out. That is,
 $$ \begin{align*} I=\int_{t_{4}=0}^{t_{1}}dt_{4}\int d\mu _{t_{4}}\left( \phi \right) \int_{t_{2}=0}^{t_{1}}dt_{2}\int_{t_{3}=t_{4}}^{t_{1}}U_{1,2}\left(\left\lvert U_{2,4}\phi \right\rvert ^{2}U_{2,4}\phi \right)(x_{1})U_{1,3}\left(\overline{U_{3,4}\phi }\overline{U_{3,4}\phi }U_{3,4}\mathcal{C}_{R}^{(4)}\right)\left(x^{\prime}_{1}\right)dt_{3}. \end{align*} $$
$$ \begin{align*} I=\int_{t_{4}=0}^{t_{1}}dt_{4}\int d\mu _{t_{4}}\left( \phi \right) \int_{t_{2}=0}^{t_{1}}dt_{2}\int_{t_{3}=t_{4}}^{t_{1}}U_{1,2}\left(\left\lvert U_{2,4}\phi \right\rvert ^{2}U_{2,4}\phi \right)(x_{1})U_{1,3}\left(\overline{U_{3,4}\phi }\overline{U_{3,4}\phi }U_{3,4}\mathcal{C}_{R}^{(4)}\right)\left(x^{\prime}_{1}\right)dt_{3}. \end{align*} $$ For expression (3.9) with a general k, we will use  $\mathcal {C}_{R}^{(k+1)}$ to denote this innermost cubic term. Notice that
$\mathcal {C}_{R}^{(k+1)}$ to denote this innermost cubic term. Notice that  $\mathcal {C}_{R}^{(k+1)}$ is always independent of time and is hence qualified to be an
$\mathcal {C}_{R}^{(k+1)}$ is always independent of time and is hence qualified to be an ![]() $f_{j}$ in estimates (5.1)–(5.4).
$f_{j}$ in estimates (5.1)–(5.4).
In the second coupling, if we denote
 $$ \begin{align*} D_{\phi ,R}^{(3)}=U_{-t_{3}}\left(\overline{U_{3,4}\phi }\overline{U_{3,4}\phi } U_{3,4}\mathcal{C}_{R}^{(4)}\right)\left(x^{\prime}_{1}\right), \end{align*} $$
$$ \begin{align*} D_{\phi ,R}^{(3)}=U_{-t_{3}}\left(\overline{U_{3,4}\phi }\overline{U_{3,4}\phi } U_{3,4}\mathcal{C}_{R}^{(4)}\right)\left(x^{\prime}_{1}\right), \end{align*} $$we have
 $$ \begin{align*} \int_{t_{3}=t_{4}}^{t_{1}}U_{1,3}\left(\overline{U_{3,4}\phi }\overline{ U_{3,4}\phi }U_{3,4}\mathcal{C}_{R}^{(4)}\right)\left(x^{\prime}_{1}\right)dt_{3}=\int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}dt_{3}. \end{align*} $$
$$ \begin{align*} \int_{t_{3}=t_{4}}^{t_{1}}U_{1,3}\left(\overline{U_{3,4}\phi }\overline{ U_{3,4}\phi }U_{3,4}\mathcal{C}_{R}^{(4)}\right)\left(x^{\prime}_{1}\right)dt_{3}=\int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}dt_{3}. \end{align*} $$In general, let us use ![]() $D^{(l+1)}$, which is
$D^{(l+1)}$, which is  $D_{\phi ,R}^{(3)}$ here, to denote the cubic term together with the
$D_{\phi ,R}^{(3)}$ here, to denote the cubic term together with the ![]() $U(-t_{l+1})$ during the lth coupling where
$U(-t_{l+1})$ during the lth coupling where ![]() $l<k$. We add a
$l<k$. We add a ![]() $\phi $ subscript if the cubic term generated at the lth coupling has contracted a
$\phi $ subscript if the cubic term generated at the lth coupling has contracted a ![]() $U\phi $. We add an R subscript if the cubic term generated at the lth coupling has contracted the rough cubic term
$U\phi $. We add an R subscript if the cubic term generated at the lth coupling has contracted the rough cubic term  $\mathcal {C}_{R}^{(k+1)}$ or a
$\mathcal {C}_{R}^{(k+1)}$ or a  $ D_{R}^{\left (j+1\right )} $ for some j. The coupling process makes sure that every time integral corresponds to one and only one cubic term, and thus the notation of D is well defined. We suppress all
$ D_{R}^{\left (j+1\right )} $ for some j. The coupling process makes sure that every time integral corresponds to one and only one cubic term, and thus the notation of D is well defined. We suppress all ![]() $t_{k+1}$-dependence, which is the
$t_{k+1}$-dependence, which is the ![]() $t_{4}$-dependence here, in all the D markings, as we will not explore any smoothing given by the
$t_{4}$-dependence here, in all the D markings, as we will not explore any smoothing given by the ![]() $dt_{k+1}$ integral. Finally, notice that
$dt_{k+1}$ integral. Finally, notice that ![]() $ D^{(l+1)}$ always carries the
$ D^{(l+1)}$ always carries the ![]() $t_{l+1}$ variable and will make a Duhamel term whenever it is hit by a
$t_{l+1}$ variable and will make a Duhamel term whenever it is hit by a ![]() $U\left (t_{j}\right )$, where
$U\left (t_{j}\right )$, where ![]() $j\neq l+1$.
$j\neq l+1$.
Then, using the same marking strategy at the first coupling, we reach
 $$ \begin{align*} I=\int_{t_{4}=0}^{t_{1}}dt_{4}\int d\mu _{t_{4}}\left( \phi \right) \left( \int_{t_{2}=0}^{t_{1}}U_{1}D_{\phi }^{(2)}\left( x_{1}\right) dt_{2}\right) \left( \int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right). \end{align*} $$
$$ \begin{align*} I=\int_{t_{4}=0}^{t_{1}}dt_{4}\int d\mu _{t_{4}}\left( \phi \right) \left( \int_{t_{2}=0}^{t_{1}}U_{1}D_{\phi }^{(2)}\left( x_{1}\right) dt_{2}\right) \left( \int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right). \end{align*} $$We can now start estimating. Taking the norm inside,
 $$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ \leq &\int_{0}^{T}\int dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right) \left\lVert \left(\left\langle \nabla _{x_{1}}\right\rangle ^{-1}\int_{t_{2}=0}^{t_{1}}U_{1}D_{\phi }^{(2)}\left( x_{1}\right) dt_{2}\right)\left(\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right)\right\Vert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}}, \end{align*} $$
$$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ \leq &\int_{0}^{T}\int dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right) \left\lVert \left(\left\langle \nabla _{x_{1}}\right\rangle ^{-1}\int_{t_{2}=0}^{t_{1}}U_{1}D_{\phi }^{(2)}\left( x_{1}\right) dt_{2}\right)\left(\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right)\right\Vert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}}, \end{align*} $$the  $L_{t_{1}}^{\infty }L_{x,x'}^{2}$ norm ‘factors’ in the sense that
$L_{t_{1}}^{\infty }L_{x,x'}^{2}$ norm ‘factors’ in the sense that
 $$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ &\qquad\qquad\leq \int_{0}^{T}\int \left\lVert \int_{t_{2}=0}^{t_{1}}U_{1}D_{\phi }^{(2)}\left( x_{1}\right) dt_{2}\right\rVert _{L_{t_{1}}^{\infty }H_{x}^{-1}}\left\lVert \int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right\rVert _{L_{t_{1}}^{\infty }H_{x'}^{-1}}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right). \end{align*} $$
$$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ &\qquad\qquad\leq \int_{0}^{T}\int \left\lVert \int_{t_{2}=0}^{t_{1}}U_{1}D_{\phi }^{(2)}\left( x_{1}\right) dt_{2}\right\rVert _{L_{t_{1}}^{\infty }H_{x}^{-1}}\left\lVert \int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right\rVert _{L_{t_{1}}^{\infty }H_{x'}^{-1}}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right). \end{align*} $$The term  $D_{\phi }^{(2)}$ carries no R subscript, so we can bump it to
$D_{\phi }^{(2)}$ carries no R subscript, so we can bump it to ![]() $ H^{1} $ and then use the embedding (2.1), which gives
$ H^{1} $ and then use the embedding (2.1), which gives
 $$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ &\qquad\qquad\qquad \quad \leq \int_{0}^{T}\int \left\lVert \int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right\rVert _{X^{-1}}\left\lVert \int_{t_{2}=0}^{t_{1}}U_{1}D_{\phi }^{(2)}\left( x_{1}\right) dt_{2}\right\rVert _{X^{1}}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right). \end{align*} $$
$$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ &\qquad\qquad\qquad \quad \leq \int_{0}^{T}\int \left\lVert \int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right\rVert _{X^{-1}}\left\lVert \int_{t_{2}=0}^{t_{1}}U_{1}D_{\phi }^{(2)}\left( x_{1}\right) dt_{2}\right\rVert _{X^{1}}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right). \end{align*} $$Applying formula (5.2) to the first coupling and replacing all ![]() $\left \lVert U\phi \right \rVert _{X^{s}}$ by
$\left \lVert U\phi \right \rVert _{X^{s}}$ by ![]() $\left \lVert \phi \right \rVert _{H^{s}}$, we have
$\left \lVert \phi \right \rVert _{H^{s}}$, we have
 $$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ \leq &C\int_{0}^{T}\int \left\lVert \int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right\rVert _{X^{-1}}\left\lVert \phi \right\rVert _{H^{1}}^{2}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{1}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right). \end{align*} $$
$$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ \leq &C\int_{0}^{T}\int \left\lVert \int_{t_{3}=t_{4}}^{t_{1}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3}\right\rVert _{X^{-1}}\left\lVert \phi \right\rVert _{H^{1}}^{2}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{1}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right). \end{align*} $$Using formula (5.1) with the second coupling and replacing all ![]() $\left \lVert U\phi \right \rVert _{X^{s}}$ by
$\left \lVert U\phi \right \rVert _{X^{s}}$ by ![]() $\left \lVert \phi \right \rVert _{H^{s}}$, we have
$\left \lVert \phi \right \rVert _{H^{s}}$, we have
 $$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1} \vphantom{\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}} \right. & \left. \left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ &\leq C^{2}\int_{0}^{T}\int \left\lVert \phi \right\rVert _{H^{1}}^{3}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{2}\left\lVert \mathcal{C}_{R}^{(4)}\right\rVert _{H^{-1}}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right) \\ &= C^{2}\int_{0}^{T}\int \left\lVert \phi \right\rVert _{H^{1}}^{3}\left( T^{ \frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{2}\left\lVert \left\lvert \phi \right\rvert ^{2}\phi \right\rVert _{H^{-1}}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right). \end{align*} $$
$$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1} \vphantom{\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}} \right. & \left. \left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ &\leq C^{2}\int_{0}^{T}\int \left\lVert \phi \right\rVert _{H^{1}}^{3}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{2}\left\lVert \mathcal{C}_{R}^{(4)}\right\rVert _{H^{-1}}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right) \\ &= C^{2}\int_{0}^{T}\int \left\lVert \phi \right\rVert _{H^{1}}^{3}\left( T^{ \frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{2}\left\lVert \left\lvert \phi \right\rvert ^{2}\phi \right\rVert _{H^{-1}}dt_{4}d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right). \end{align*} $$Using the 4D Sobolev
 $$ \begin{align} \left\lVert \left\lvert \phi \right\rvert ^{2}\phi \right\rVert _{H^{-1}}\leq C\left\lVert \phi \right\rVert _{H^{1}}^{3} \end{align} $$
$$ \begin{align} \left\lVert \left\lvert \phi \right\rvert ^{2}\phi \right\rVert _{H^{-1}}\leq C\left\lVert \phi \right\rVert _{H^{1}}^{3} \end{align} $$on the rough coupling, we get to
 $$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}}\leq C^{3}\int_{0}^{T}dt_{4}\int d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right) \left\lVert \phi \right\rVert _{H^{1}}^{6}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{2}. \end{align*} $$
$$ \begin{align*} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}}\leq C^{3}\int_{0}^{T}dt_{4}\int d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right) \left\lVert \phi \right\rVert _{H^{1}}^{6}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{2}. \end{align*} $$Plugging in the support property of the measure (see equation (3.5)) yields
 $$ \begin{align} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} &\leq C^{3}C_{0}^{6}\left( T^{\frac{1}{7} }M_{0}^{\frac{3}{5}}C_{0}+\varepsilon \right) ^{2}\int_{0}^{T}dt_{4}\int d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right) \\ &\leq C^{3}C_{0}^{6}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5} }C_{0}+\varepsilon \right) ^{2}2T, \notag \end{align} $$
$$ \begin{align} \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}I\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} &\leq C^{3}C_{0}^{6}\left( T^{\frac{1}{7} }M_{0}^{\frac{3}{5}}C_{0}+\varepsilon \right) ^{2}\int_{0}^{T}dt_{4}\int d\left\lvert \mu _{t_{4}}\right\rvert \left( \phi \right) \\ &\leq C^{3}C_{0}^{6}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5} }C_{0}+\varepsilon \right) ^{2}2T, \notag \end{align} $$and we are done.
5.2 The extended KM board game is compatible
In Section 5.1, the U-V estimates worked perfectly with the integration limits obtained via the extended KM board game from Section 4. One certainly wonders whether the extended KM board game is necessary, and whether it is compatible with the estimates in the general case.
In the beginning of Section 4.2, we briefly mentioned the problem one would face without the extended KM board game. We can now explain by a concrete example. For comparison, rewrite ![]() $I_{1}$ in Example 4 with the notation
$I_{1}$ in Example 4 with the notation
 $$ \begin{align*} I_{1} &=\int_{t_{4}=0}^{t_{1}}\int_{t_{2}=t_{4}}^{t_{1}} \int_{t_{3}=0}^{t_{2}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{-}U^{(2)}(t_{2}-t_{3})B_{1,3}^{+}U^{(3)}(t_{3}-t_{4})B_{3,4}^{-}\gamma ^{(4)}d \underline{t}_{4} \\ &=\int_{t_{4}=0}^{t_{1}}dt_{4}\int d\mu _{t_{4}}\left( \phi \right) \int_{t_{2}=t_{4}}^{t_{1}}\left( U_{1}D_{\phi }^{(2)}\left( x_{1}\right) \left[ \int_{t_{3}=0}^{t_{2}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3} \right] \right) dt_{2}. \end{align*} $$
$$ \begin{align*} I_{1} &=\int_{t_{4}=0}^{t_{1}}\int_{t_{2}=t_{4}}^{t_{1}} \int_{t_{3}=0}^{t_{2}}U^{(1)}(t_{1}-t_{2})B_{1,2}^{-}U^{(2)}(t_{2}-t_{3})B_{1,3}^{+}U^{(3)}(t_{3}-t_{4})B_{3,4}^{-}\gamma ^{(4)}d \underline{t}_{4} \\ &=\int_{t_{4}=0}^{t_{1}}dt_{4}\int d\mu _{t_{4}}\left( \phi \right) \int_{t_{2}=t_{4}}^{t_{1}}\left( U_{1}D_{\phi }^{(2)}\left( x_{1}\right) \left[ \int_{t_{3}=0}^{t_{2}}U_{1}D_{\phi ,R}^{(3)}\left(x^{\prime}_{1}\right)dt_{3} \right] \right) dt_{2}. \end{align*} $$One sees that the ![]() $dt_{3}$ integral is encapsulated inside the
$dt_{3}$ integral is encapsulated inside the ![]() $dt_{2}$ integral, or the x and
$dt_{2}$ integral, or the x and ![]() $x'$ parts do not factor, even with the carefully worked-out time integration limits in the original KM board game. Hence, one cannot apply U-V estimates. To be very precise for readers who are curious about this, since there are only two integrals that got entangled,
$x'$ parts do not factor, even with the carefully worked-out time integration limits in the original KM board game. Hence, one cannot apply U-V estimates. To be very precise for readers who are curious about this, since there are only two integrals that got entangled, ![]() $I_{1}$ could in fact be estimated using [Reference Koch, Tataru and Vişan50, (4.25), p. 60], based on the idea of integration by parts. However, if one allows the coupling level to be large, it is not difficult to find, at any stage of a long coupling, multiple encapsulations which have more than three factors entangled together and cannot be estimated by the ideas of integration by parts. We are not presenting such a construction, as the formula would be unnecessarily long and does not give new ideas. Finally, we remark that such an entanglement problem, generated by the time-integral reliance of the U-V space techniques, does not show up in the couplings with only
$I_{1}$ could in fact be estimated using [Reference Koch, Tataru and Vişan50, (4.25), p. 60], based on the idea of integration by parts. However, if one allows the coupling level to be large, it is not difficult to find, at any stage of a long coupling, multiple encapsulations which have more than three factors entangled together and cannot be estimated by the ideas of integration by parts. We are not presenting such a construction, as the formula would be unnecessarily long and does not give new ideas. Finally, we remark that such an entanglement problem, generated by the time-integral reliance of the U-V space techniques, does not show up in the couplings with only ![]() $B^{+}$ or only
$B^{+}$ or only ![]() $B^{-}$, and does not have to emerge in the
$B^{-}$, and does not have to emerge in the ![]() $\mathbb {R}^{3}/\mathbb {R}^{4}/\mathbb {T}^{3}$ cases in which U-V spaces are not necessary.
$\mathbb {R}^{3}/\mathbb {R}^{4}/\mathbb {T}^{3}$ cases in which U-V spaces are not necessary.
We now prove how the extended KM board game is compatible with the U-V techniques. Given a reference tree, we will create a Duhamel tree (we write ‘D-tree’ for short) to supplement the reference tree. The D-tree supplements the given reference tree in the sense that the D-tree completely shows the arrangement of the cubic terms ![]() $D^{\left (j\right )}$, defined in Section 5.1, and one could also read off the integration limits from it as in the given reference tree. The whole point of the D-tree is to get these two pieces of information in the same picture, as the proof of compatibility then follows trivially. Of course, from now on, we assume that equation 3.6) has already been plugged in and we are doing the
$D^{\left (j\right )}$, defined in Section 5.1, and one could also read off the integration limits from it as in the given reference tree. The whole point of the D-tree is to get these two pieces of information in the same picture, as the proof of compatibility then follows trivially. Of course, from now on, we assume that equation 3.6) has already been plugged in and we are doing the ![]() $dt_{k+1}$ integral, which is from
$dt_{k+1}$ integral, which is from ![]() $0$ to
$0$ to ![]() $t_{1}$, last.
$t_{1}$, last.
Algorithm 7. In the D-tree, we will write each node prefaced by a D. Each node ![]() $D^{(j)}$ will have a left child, middle child and right child:
$D^{(j)}$ will have a left child, middle child and right child:

The labelling of ls, r+ and r![]() $-$ for the left, middle and right children, respectively, is a shorthand mnemonic for the procedure for determining the children of
$-$ for the left, middle and right children, respectively, is a shorthand mnemonic for the procedure for determining the children of ![]() $D^{\left (j\right )}$ by inspecting the reference tree. Apply the following steps for
$D^{\left (j\right )}$ by inspecting the reference tree. Apply the following steps for ![]() $j=1$ (with no left child), then repeat the steps for all
$j=1$ (with no left child), then repeat the steps for all ![]() $D^{\left (j\right )}$ that appear as children; continue to repeat the steps until all vertices without children are F:
$D^{\left (j\right )}$ that appear as children; continue to repeat the steps until all vertices without children are F:
1. To determine the left child of
 $D^{\left (j\right )}$, locate node j in the reference tree and apply the ‘left same’ rule. If node j in the reference tree is
$D^{\left (j\right )}$, locate node j in the reference tree and apply the ‘left same’ rule. If node j in the reference tree is  $+$, and
$+$, and  $j+$ has a left child
$j+$ has a left child  $\ell +$ (of the same sign
$\ell +$ (of the same sign  $+$), then place
$+$), then place  $D^{(l)}$ as the left child in the D-tree. If the j node in the reference tree is
$D^{(l)}$ as the left child in the D-tree. If the j node in the reference tree is  $-$, and
$-$, and  $j-$ has a left child
$j-$ has a left child  $\ell -$ (of the same sign
$\ell -$ (of the same sign  $-$), then place
$-$), then place  $D^{(l)}$ as the left child in the D-tree. If node j in the reference tree does not have a left child of the same sign, then place F as the left child of
$D^{(l)}$ as the left child in the D-tree. If node j in the reference tree does not have a left child of the same sign, then place F as the left child of  $D^{\left (j\right )}$ in the D-tree.
$D^{\left (j\right )}$ in the D-tree.2. To determine the middle and right children of
 $D^{\left (j\right )}$, locate node j in the reference tree. Examine the right child of j (if it exists), and consider its full left branch It is possible here that
$D^{\left (j\right )}$, locate node j in the reference tree. Examine the right child of j (if it exists), and consider its full left branch It is possible here that $$ \begin{align*} p_{1}+,\dotsc ,p_{\alpha }+,n_{1}-,\dotsc ,n_{\beta }-. \end{align*} $$
$$ \begin{align*} p_{1}+,\dotsc ,p_{\alpha }+,n_{1}-,\dotsc ,n_{\beta }-. \end{align*} $$ $\alpha =0$ (no
$\alpha =0$ (no  $+$ nodes on this left branch), and it is also possible that
$+$ nodes on this left branch), and it is also possible that  $\beta =0$ (no
$\beta =0$ (no  $-$ nodes on this left branch). In the D-tree, as the middle child of
$-$ nodes on this left branch). In the D-tree, as the middle child of  $D^{\left (j\right )}$ place
$D^{\left (j\right )}$ place  $D^{\left (p_{1}\right )}$, and as the right child of
$D^{\left (p_{1}\right )}$, and as the right child of  $D^{\left (j\right )}$ place
$D^{\left (j\right )}$ place  $D^{(n_{1})}$. If either or both is missing (
$D^{(n_{1})}$. If either or both is missing ( $\alpha =0$ or
$\alpha =0$ or  $\beta =0$, respectively), place F instead.
$\beta =0$, respectively), place F instead.
A quick and simple example is the D-tree for the integral in Section 5.1:

Here is a longer example:
Example 7. Consider the following reference tree:

Its supplemental D-tree is as follows:

Every bottom node of the form ![]() $D^{\left (j\right )}$ (as opposed to F) has implicitly three F children, except for the
$D^{\left (j\right )}$ (as opposed to F) has implicitly three F children, except for the ![]() $D^{(k+1)}$ node, which is special (in our case here, it is
$D^{(k+1)}$ node, which is special (in our case here, it is ![]() $D_{9}$). In this case, the D-tree was generated as follows. Take
$D_{9}$). In this case, the D-tree was generated as follows. Take ![]() $D^{(2)}$, for example, in the reference tree.
$D^{(2)}$, for example, in the reference tree.
• To determine the left child of
 $D^{(2)}$ in the D-tree, we look at the reference tree and follow the ‘left same’ rule. The left child of
$D^{(2)}$ in the D-tree, we look at the reference tree and follow the ‘left same’ rule. The left child of  $2+$ is
$2+$ is  $3+$, so we place
$3+$, so we place  $ D^{(3)}$ as the left child of
$ D^{(3)}$ as the left child of  $D^{(2)}$ in the D-tree. (If it were
$D^{(2)}$ in the D-tree. (If it were  $3-$ instead, we would place F in the D-tree, since the signs are different.)
$3-$ instead, we would place F in the D-tree, since the signs are different.)• To determine the middle child of
 $D^{(2)}$ in the D-tree, we look at the reference tree and follow the ‘right
$D^{(2)}$ in the D-tree, we look at the reference tree and follow the ‘right  $+$’ rule. That is, we take the right child and consider its left branch:
$+$’ rule. That is, we take the right child and consider its left branch:  $5+$,
$5+$,  $6-$,
$6-$,  $7-$. We note the first
$7-$. We note the first  $+$ node, which is
$+$ node, which is  $ 5+ $, and assign
$ 5+ $, and assign  $D^{(5)}$ as the middle child of
$D^{(5)}$ as the middle child of  $D^{(2)}$. If there were no
$D^{(2)}$. If there were no  $+$ node in the left branch, we would have assigned F.
$+$ node in the left branch, we would have assigned F.• To determine the right child of
 $D^{(2)}$ in the D-tree, we look at the reference tree and follow the ‘right
$D^{(2)}$ in the D-tree, we look at the reference tree and follow the ‘right  $-$’ rule. That is, we take the right child and consider its left branch:
$-$’ rule. That is, we take the right child and consider its left branch:  $5+$,
$5+$,  $6-$,
$6-$,  $7-$. We note the first
$7-$. We note the first  $-$ node, which is
$-$ node, which is  $6-$, and assign
$6-$, and assign  $D^{(6)}$ as the right child of
$D^{(6)}$ as the right child of  $D_{2}$. If there were no
$D_{2}$. If there were no  $-$ node in the left branch, we would have assigned F.
$-$ node in the left branch, we would have assigned F.
Proof of compatibility.
With the D-tree, we can now read formula (4.14) better. This is because the rule for assigning upper limits of time integration is actually the same rule for constructing children in the D-tree. By the construction of the D-tree, we can write the form of each ![]() $D^{\left (j\right )}$,
$D^{\left (j\right )}$, ![]() $j\neq k+1$, and the integration limit for
$j\neq k+1$, and the integration limit for ![]() $t_{j}$. If
$t_{j}$. If ![]() $D^{\left (j\right )}$ has children
$D^{\left (j\right )}$ has children ![]() $L, M, R$ (for left, middle and right) and has parent
$L, M, R$ (for left, middle and right) and has parent ![]() $D^{(l)}$ in the
$D^{(l)}$ in the ![]() $ D $-tree, then (ignoring the role of complex conjugates)
$ D $-tree, then (ignoring the role of complex conjugates)
 $$ \begin{align*} D^{\left(j\right)}\left(t_{j}\right)=U\left(-t_{j}\right)\left[\left( U_{j}L\right) \left( U_{j}M\right) \left( U_{j}R\right) \right], \end{align*} $$
$$ \begin{align*} D^{\left(j\right)}\left(t_{j}\right)=U\left(-t_{j}\right)\left[\left( U_{j}L\right) \left( U_{j}M\right) \left( U_{j}R\right) \right], \end{align*} $$and the integration of ![]() $t_{j}$ is exactly from
$t_{j}$ is exactly from ![]() $0$ to
$0$ to ![]() $t_{l}$. One can directly see from the picture in Example 7 that all Duhamel terms inside a
$t_{l}$. One can directly see from the picture in Example 7 that all Duhamel terms inside a ![]() $D^{\left (j\right )}$ must have the same integration limit, and they factor. Therefore, there is no entanglement in each stage of the coupling process. An induction then shows that there is no entanglement for any coupling of finite length or stages. Or in other words, the extended KM board game is compatible with the U-V techniques.
$D^{\left (j\right )}$ must have the same integration limit, and they factor. Therefore, there is no entanglement in each stage of the coupling process. An induction then shows that there is no entanglement for any coupling of finite length or stages. Or in other words, the extended KM board game is compatible with the U-V techniques.
For completeness, we finish Example 7 with the integration limits:
Example 8. Continuing Example 7, we have
 $$ \begin{align} D^{(2)}=U(-t_{2})\left[U_{2}D^{(3)}\cdot U_{2}D^{(5)}\cdot U_{2}D^{(6)}\right]. \end{align} $$
$$ \begin{align} D^{(2)}=U(-t_{2})\left[U_{2}D^{(3)}\cdot U_{2}D^{(5)}\cdot U_{2}D^{(6)}\right]. \end{align} $$The three terms inside this expression are
 $$ \begin{align*} D^{(3)} & =U(-t_{3})[U_{3}F(t_{9})\cdot U_{3}F(t_{9})\cdot U_{3}F(t_{9})], \\ D^{(5)} & =U(-t_{5})[U_{5}F(t_{9})\cdot U_{5}F(t_{9})\cdot U_{5}F(t_{9})], \\ D^{(6)} & =U(-t_{6})\left[U_{6}D^{(7)}\cdot U_{6}D^{(9)}\cdot U_{6}F(t_{9})\right], \end{align*} $$
$$ \begin{align*} D^{(3)} & =U(-t_{3})[U_{3}F(t_{9})\cdot U_{3}F(t_{9})\cdot U_{3}F(t_{9})], \\ D^{(5)} & =U(-t_{5})[U_{5}F(t_{9})\cdot U_{5}F(t_{9})\cdot U_{5}F(t_{9})], \\ D^{(6)} & =U(-t_{6})\left[U_{6}D^{(7)}\cdot U_{6}D^{(9)}\cdot U_{6}F(t_{9})\right], \end{align*} $$where ![]() $F(t_{i})=U(-t_{i})\phi $. On the other hand, we have
$F(t_{i})=U(-t_{i})\phi $. On the other hand, we have
 $$ \begin{align} D^{(4)}=U(-t_{4})\left[U_{4}F(t_{9})\cdot U_{4}D^{(8)}\cdot U_{4}F(t_{9})\right]. \end{align} $$
$$ \begin{align} D^{(4)}=U(-t_{4})\left[U_{4}F(t_{9})\cdot U_{4}D^{(8)}\cdot U_{4}F(t_{9})\right]. \end{align} $$Now, read the time integration limits from the reference tree or the D -tree; ![]() $t_{2}$ and
$t_{2}$ and ![]() $t_{4}$ have upper limit
$t_{4}$ have upper limit ![]() $t_{1}$, while
$t_{1}$, while ![]() $t_{3}$,
$t_{3}$, ![]() $ t_{5}$ and
$ t_{5}$ and ![]() $t_{6}$ all have upper limit
$t_{6}$ all have upper limit ![]() $t_{2}$, and so on. Start by writing
$t_{2}$, and so on. Start by writing  $ \int _{t_{9}=0}^{t_{1}}$ on the outside. Notice that this makes the inner
$ \int _{t_{9}=0}^{t_{1}}$ on the outside. Notice that this makes the inner ![]() $t_6$ integral start at
$t_6$ integral start at ![]() $t_9$ in order to retain the condition
$t_9$ in order to retain the condition ![]() $t_9\leq t_6$ from formula (4.14) and the tree reading. Take all
$t_9\leq t_6$ from formula (4.14) and the tree reading. Take all ![]() $t_{j}$ integrals for
$t_{j}$ integrals for ![]() $j=2$ or for which
$j=2$ or for which ![]() $D^{\left (j\right )}$ is a descendant of
$D^{\left (j\right )}$ is a descendant of ![]() $D^{(2)}$. This is
$D^{(2)}$. This is
 $$ \begin{align} \int_{t_{2}=0}^{t_{1}}\int_{t_{3}=0}^{t_{2}}\int_{t_{5}=0}^{t_{2}} \int_{t_{6}=t_9}^{t_{2}}\int_{t_{7}=0}^{t_{6}}. \end{align} $$
$$ \begin{align} \int_{t_{2}=0}^{t_{1}}\int_{t_{3}=0}^{t_{2}}\int_{t_{5}=0}^{t_{2}} \int_{t_{6}=t_9}^{t_{2}}\int_{t_{7}=0}^{t_{6}}. \end{align} $$Then collect all ![]() $t_{j}$ integrals for
$t_{j}$ integrals for ![]() $j=4$ or for which
$j=4$ or for which ![]() $D^{\left (j\right )}$ is a descendant of
$D^{\left (j\right )}$ is a descendant of ![]() $D^{(4)}$. This is
$D^{(4)}$. This is
 $$ \begin{align} \int_{t_{4}=0}^{t_{1}}\int_{t_{8}=0}^{t_{4}}. \end{align} $$
$$ \begin{align} \int_{t_{4}=0}^{t_{1}}\int_{t_{8}=0}^{t_{4}}. \end{align} $$Notice that expressions (5.9) and (5.10) split, by Fubini, since none of the limits of integration in expression (5.9) appear in expression (5.10), and vice versa. So we can write this piece of ![]() $\gamma ^{(1)}$ as
$\gamma ^{(1)}$ as
 $$ \begin{align} \gamma ^{(1)}(t_{1})=\int_{t_{9}=0}^{t_{1}}\left[ \int_{t_{2}=0}^{t_{1}} \int_{t_{3}=0}^{t_{2}}\int_{t_{5}=0}^{t_{2}}\int_{t_{6}=t_9}^{t_{2}} \int_{t_{7}=0}^{t_{6}}U_{1}D^{(2)}(t_{2},x_{1})\right] \left[ \int_{t_{4}=0}^{t_{1}}\int_{t_{8}=0}^{t_{4}}U_{1}D^{(4)}\left(t_{4},x^{\prime}_{1}\right)\right]. \end{align} $$
$$ \begin{align} \gamma ^{(1)}(t_{1})=\int_{t_{9}=0}^{t_{1}}\left[ \int_{t_{2}=0}^{t_{1}} \int_{t_{3}=0}^{t_{2}}\int_{t_{5}=0}^{t_{2}}\int_{t_{6}=t_9}^{t_{2}} \int_{t_{7}=0}^{t_{6}}U_{1}D^{(2)}(t_{2},x_{1})\right] \left[ \int_{t_{4}=0}^{t_{1}}\int_{t_{8}=0}^{t_{4}}U_{1}D^{(4)}\left(t_{4},x^{\prime}_{1}\right)\right]. \end{align} $$Write out ![]() $D^{(2)}$ as in equation (5.7) and
$D^{(2)}$ as in equation (5.7) and ![]() $D^{(4)}$ as in equation (5.8). Notice that we can distribute the integrals
$D^{(4)}$ as in equation (5.8). Notice that we can distribute the integrals  $\int _{t_{3}=0}^{t_{2}} \int _{t_{5}=0}^{t_{2}}\int _{t_{6}=0}^{t_{2}}$ onto the
$\int _{t_{3}=0}^{t_{2}} \int _{t_{5}=0}^{t_{2}}\int _{t_{6}=0}^{t_{2}}$ onto the ![]() $D^{(3)}$,
$D^{(3)}$, ![]() $D^{(5)}$ and
$D^{(5)}$ and ![]() $D^{(6)}$ terms, respectively:
$D^{(6)}$ terms, respectively:
 $$ \begin{align*} \int_{t_{2}=0}^{t_{1}}\int_{t_{3}=0}^{t_{2}}\int_{t_{5}=0}^{t_{2}} &\int_{t_{6}=t_9}^{t_{2}}\int_{t_{7}=0}^{t_{6}}U_{1}D^{(2)}(t_{2},x_{1}) \\ &=\int_{t_{2}=0}^{t_{1}}U_{1,2}\left[ \left( \int_{t_{3}=0}^{t_{2}}U_{2}D^{(3)}(t_{3})\right) \cdot \left( \int_{t_{5}=0}^{t_{2}}U_{2}D^{(5)}(t_{5})\right) \cdot \left( \int_{t_{6}=t_9}^{t_{2}}\int_{t_{7}=0}^{t_{6}}U_{2}D^{(6)}(t_{6})\right) \right]. \end{align*} $$
$$ \begin{align*} \int_{t_{2}=0}^{t_{1}}\int_{t_{3}=0}^{t_{2}}\int_{t_{5}=0}^{t_{2}} &\int_{t_{6}=t_9}^{t_{2}}\int_{t_{7}=0}^{t_{6}}U_{1}D^{(2)}(t_{2},x_{1}) \\ &=\int_{t_{2}=0}^{t_{1}}U_{1,2}\left[ \left( \int_{t_{3}=0}^{t_{2}}U_{2}D^{(3)}(t_{3})\right) \cdot \left( \int_{t_{5}=0}^{t_{2}}U_{2}D^{(5)}(t_{5})\right) \cdot \left( \int_{t_{6}=t_9}^{t_{2}}\int_{t_{7}=0}^{t_{6}}U_{2}D^{(6)}(t_{6})\right) \right]. \end{align*} $$We have kept the ![]() $t_{7}$ integral together with
$t_{7}$ integral together with ![]() $t_{6}$ because
$t_{6}$ because ![]() $D^{(7)}$ is a child of
$D^{(7)}$ is a child of ![]() $D^{(6)}$ in the D-tree. We can see that all the Duhamel structures are fully compatible with the U-V techniques. The rest is similar, and we omit further details.
$D^{(6)}$ in the D-tree. We can see that all the Duhamel structures are fully compatible with the U-V techniques. The rest is similar, and we omit further details.
5.3 Estimates for general k
As the compatiblity between the extended KM board game and the U-V techniques has been proved in Section 5.2, we can now apply the U-V techniques from Section 5.1 to the general case. We see from Section 5.1 that estimates (5.1) and (5.2) provide gains whenever the lth coupling contracts a ![]() $U\phi $. For large k, at least
$U\phi $. For large k, at least ![]() $\frac {2}{3}k$ of the couplings carry such a property and thus allow gains.
$\frac {2}{3}k$ of the couplings carry such a property and thus allow gains.
Definition 5.1. For ![]() $l<k$, we say that the lth coupling is an unclogged coupling if the corresponding cubic term
$l<k$, we say that the lth coupling is an unclogged coupling if the corresponding cubic term ![]() $\mathcal {C}^{(l+1)}$ or
$\mathcal {C}^{(l+1)}$ or ![]() $D^{(l+1)}$ has contracted at least one
$D^{(l+1)}$ has contracted at least one ![]() $U\phi $ factor. If the lth coupling is not unclogged, we call it a congested coupling.
$U\phi $ factor. If the lth coupling is not unclogged, we call it a congested coupling.
Lemma 5.2. For large k, there are at least ![]() $\frac {2}{3} k$ unclogged couplings in k couplings when one plugs equation (3.6) into expression (3.9).
$\frac {2}{3} k$ unclogged couplings in k couplings when one plugs equation (3.6) into expression (3.9).
Proof. Assume there are j congested couplings; then there are ![]() $(k-1-j)$ unclogged couplings. Before the
$(k-1-j)$ unclogged couplings. Before the ![]() $(k-1)$th coupling, there are
$(k-1)$th coupling, there are ![]() $2k-1$ copies of
$2k-1$ copies of ![]() $U\phi $ available. After the first coupling, all of these
$U\phi $ available. After the first coupling, all of these ![]() $2k-1$ copies of
$2k-1$ copies of ![]() $U\phi $ except one must be inside some Duhamel term. Since the j congested couplings do not consume any
$U\phi $ except one must be inside some Duhamel term. Since the j congested couplings do not consume any ![]() $U\phi $, to consume all
$U\phi $, to consume all ![]() $2k-2$ copies of
$2k-2$ copies of ![]() $ U\phi $ we have to have
$ U\phi $ we have to have
because a unclogged coupling can consume at most three copies of ![]() $U\phi $. This inequality certainly holds only if
$U\phi $. This inequality certainly holds only if  $j< \frac {k}{3}$. Hence, there are at least
$j< \frac {k}{3}$. Hence, there are at least ![]() $\frac {2k}{3}$ unclogged couplings.
$\frac {2k}{3}$ unclogged couplings.
We can now present the algorithm which proves the general case:
Step 0 Plug equation (3.6) into expression (3.9). Mark
 $\mathcal {C}_{R}^{(k+1)}$ and all
$\mathcal {C}_{R}^{(k+1)}$ and all  $ D^{(l+1)}$ for
$ D^{(l+1)}$ for  $l=1,\dotsc ,k-1$ per the general rule given in the example and Section 5.1. We obtain which ‘factors’ into
$l=1,\dotsc ,k-1$ per the general rule given in the example and Section 5.1. We obtain which ‘factors’ into $$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{I_{2}}\dotsi\int_{I_{k}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ &\qquad\leq \int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert \left( \left\langle \nabla _{x_{1}}\right\rangle ^{-1}f^{(1)}(t_{1},x_{1})\right) \left( \left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}g^{(1)}\left(t_{1},x^{\prime}_{1}\right)\right) \right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}}, \end{align*} $$for some
$$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}\int_{I_{2}}\dotsi\int_{I_{k}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}\right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ &\qquad\leq \int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert \left( \left\langle \nabla _{x_{1}}\right\rangle ^{-1}f^{(1)}(t_{1},x_{1})\right) \left( \left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}g^{(1)}\left(t_{1},x^{\prime}_{1}\right)\right) \right\rVert _{L_{t_{1}}^{\infty }L_{x,x'}^{2}}, \end{align*} $$for some $$ \begin{align*} &\leq \int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}f^{(1)}(t_{1},x_{1})\right\rVert _{L_{t_{1}}^{\infty }L_{x}^{2}}\left\lVert \left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}g^{(1)}\left(t_{1},x^{\prime}_{1}\right)\right\rVert _{L_{t_{1}}^{\infty }L_{x'}^{2}} \\ &\leq \int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert f^{(1)}\right\rVert _{X^{-1}}\left\lVert g^{(1)}\right\rVert _{X^{-1}} \end{align*} $$
$$ \begin{align*} &\leq \int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}f^{(1)}(t_{1},x_{1})\right\rVert _{L_{t_{1}}^{\infty }L_{x}^{2}}\left\lVert \left\langle \nabla _{x^{\prime}_{1}}\right\rangle ^{-1}g^{(1)}\left(t_{1},x^{\prime}_{1}\right)\right\rVert _{L_{t_{1}}^{\infty }L_{x'}^{2}} \\ &\leq \int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert f^{(1)}\right\rVert _{X^{-1}}\left\lVert g^{(1)}\right\rVert _{X^{-1}} \end{align*} $$ $f^{(1)}$ and
$f^{(1)}$ and  $g^{(1)}$. Of course, only one of
$g^{(1)}$. Of course, only one of  $f^{(1)}$ and
$f^{(1)}$ and  $ g^{(1)}$ can carry the cubic rough term
$ g^{(1)}$ can carry the cubic rough term  $\mathcal {C}_{R}^{(k+1)}$, as there is only one, so bump the other one into
$\mathcal {C}_{R}^{(k+1)}$, as there is only one, so bump the other one into  $X^{1}$. Go to step 1.
$X^{1}$. Go to step 1.Step 1 Set a counter
 $l=1$ and go to step 2.
$l=1$ and go to step 2.Step 2 If
 $D^{(l+1)}$ is a
$D^{(l+1)}$ is a  $D_{\phi ,R}^{(l+1)}$, apply estimate (5.1), put the factor carrying
$D_{\phi ,R}^{(l+1)}$, apply estimate (5.1), put the factor carrying  $\mathcal {C} _{R}^{(k+1)}$ – which will be a
$\mathcal {C} _{R}^{(k+1)}$ – which will be a  $U\mathcal {C}_{R}^{(k+1)}$ or a
$U\mathcal {C}_{R}^{(k+1)}$ or a  $ D_{R}^{\left (j+1\right )}$ for some j – in
$ D_{R}^{\left (j+1\right )}$ for some j – in  $X^{-1}$ and replace the
$X^{-1}$ and replace the  $X^{1}$ norm of
$X^{1}$ norm of  $U\phi $ by the
$U\phi $ by the  $H^{1}$ norm of
$H^{1}$ norm of  $\phi $; if the ending estimate includes
$\phi $; if the ending estimate includes  $ \left \lVert U\mathcal {C}_{R}^{(k+1)}\right \rVert _{X^{-1}}$, replace it by
$ \left \lVert U\mathcal {C}_{R}^{(k+1)}\right \rVert _{X^{-1}}$, replace it by  $ \left \lVert \mathcal {C}_{R}^{(k+1)}\right \rVert _{H^{-1}}$. Then go to step 6. If
$ \left \lVert \mathcal {C}_{R}^{(k+1)}\right \rVert _{H^{-1}}$. Then go to step 6. If  $D^{(l+1)}$ is not a
$D^{(l+1)}$ is not a  $D_{\phi ,R}^{(l+1)}$, go to step 3.
$D_{\phi ,R}^{(l+1)}$, go to step 3.Step 3 If
 $D^{(l+1)}$ is a
$D^{(l+1)}$ is a  $D_{\phi }^{(l+1)}$, apply estimate (5.2) and replace the
$D_{\phi }^{(l+1)}$, apply estimate (5.2) and replace the  $X^{1}$ norm of
$X^{1}$ norm of  $U\phi $ by the
$U\phi $ by the  $H^{1}$ norm of
$H^{1}$ norm of  $\phi $. Then go to step 6. If
$\phi $. Then go to step 6. If  $D^{(l+1)}$ is not a
$D^{(l+1)}$ is not a  $ D_{\phi }^{(l+1)}$, go to step 4.
$ D_{\phi }^{(l+1)}$, go to step 4.Step 4 If
 $D^{(l+1)}$ is a
$D^{(l+1)}$ is a  $D_{R}^{(l+1)}$, apply estimate (5.3), put the factor carrying
$D_{R}^{(l+1)}$, apply estimate (5.3), put the factor carrying  $\mathcal {C} _{R}^{(k+1)}$ – which will be a
$\mathcal {C} _{R}^{(k+1)}$ – which will be a  $U\mathcal {C}_{R}^{(k+1)}$ or a
$U\mathcal {C}_{R}^{(k+1)}$ or a  $ D_{R}^{\left (j+1\right )}$ for some j – in
$ D_{R}^{\left (j+1\right )}$ for some j – in  $X^{-1}$ and replace the
$X^{-1}$ and replace the  $X^{1}$ norm of
$X^{1}$ norm of  $U\phi $ by the
$U\phi $ by the  $H^{1}$ norm of
$H^{1}$ norm of  $\phi $; if the ending estimate includes
$\phi $; if the ending estimate includes  $ \left \lVert U\mathcal {C}_{R}^{(k+1)}\right \rVert _{X^{-1}}$, replace it by
$ \left \lVert U\mathcal {C}_{R}^{(k+1)}\right \rVert _{X^{-1}}$, replace it by  $ \left \lVert \mathcal {C}_{R}^{(k+1)}\right \rVert _{H^{-1}}$. Then go to step 6. If
$ \left \lVert \mathcal {C}_{R}^{(k+1)}\right \rVert _{H^{-1}}$. Then go to step 6. If  $D^{(l+1)}$ is not a
$D^{(l+1)}$ is not a  $D_{R}^{(l+1)}$, go to step 5.
$D_{R}^{(l+1)}$, go to step 5.Step 5 If
 $D^{(l+1)}$ is a
$D^{(l+1)}$ is a  $D^{(l+1)}$, apply estimate (5.4) and replace the
$D^{(l+1)}$, apply estimate (5.4) and replace the  $X^{1}$ norm of
$X^{1}$ norm of  $U\phi $ by the
$U\phi $ by the  $H^{1}$ norm of
$H^{1}$ norm of  $\phi $. Then go to step 6.
$\phi $. Then go to step 6.Step 6 Set the counter
 $l=l+1$. If
$l=l+1$. If  $l<k$, go to step 2; otherwise go to step 7.
$l<k$, go to step 2; otherwise go to step 7.Step 7 Replace all the leftover
 $\left \lVert U\phi \right \rVert _{X^{1}} $ by
$\left \lVert U\phi \right \rVert _{X^{1}} $ by  $\left \lVert \phi \right \rVert _{H^{1}}$. There is actually at most one leftover
$\left \lVert \phi \right \rVert _{H^{1}}$. There is actually at most one leftover  $\left \lVert U\phi \right \rVert _{X^{1}}$, which is exactly
$\left \lVert U\phi \right \rVert _{X^{1}}$, which is exactly  $ f^{(1)}$ or
$ f^{(1)}$ or  $g^{(1)}$ from the beginning and only happens when the sign
$g^{(1)}$ from the beginning and only happens when the sign  $ J_{\mu _{m},\operatorname {sgn}}^{(k+1)}$ under consideration is all
$ J_{\mu _{m},\operatorname {sgn}}^{(k+1)}$ under consideration is all  $+$ or all
$+$ or all  $-$. As it is not inside any Duhamel, it is not taken care of by steps 1–6. Go to step 8.
$-$. As it is not inside any Duhamel, it is not taken care of by steps 1–6. Go to step 8.Step 8 We are now at the kth coupling, and have applied formulas (5.1) and (5.2) at least
 $\frac {2}{3}k$ times; thus we are looking at Applying the 4D Sobolev (5.5) to the rough factor yields
$\frac {2}{3}k$ times; thus we are looking at Applying the 4D Sobolev (5.5) to the rough factor yields $$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle\nabla _{x^{\prime}_{1}}\right\rangle^{-1}\int_{I_{2}}\dotsi\int_{I_{k}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}\right\rVert_{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ \leq &C^{k-1}\int_{0}^{T}dt_{k+1}\int d\left\lvert \mu_{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert \phi \right\rVert _{H^{1}}^{\frac{4}{3}k-1}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert_{H^{1}}\right) ^{\frac{2}{3}k}\left\lVert \left\lvert \phi \right\rvert^{2}\phi \right\rVert _{H^{-1}}. \end{align*} $$Putting in the support property (3.5) gives
$$ \begin{align*} &\left\lVert \left\langle \nabla _{x_{1}}\right\rangle ^{-1}\left\langle\nabla _{x^{\prime}_{1}}\right\rangle^{-1}\int_{I_{2}}\dotsi\int_{I_{k}}J_{\mu _{m},\operatorname{sgn}}^{(k+1)}\left(\gamma ^{(k+1)}\right)\left(t_{1},\underline{t}_{k+1}\right)d\underline{t}_{k+1}\right\rVert_{L_{t_{1}}^{\infty }L_{x,x'}^{2}} \\ \leq &C^{k-1}\int_{0}^{T}dt_{k+1}\int d\left\lvert \mu_{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert \phi \right\rVert _{H^{1}}^{\frac{4}{3}k-1}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert_{H^{1}}\right) ^{\frac{2}{3}k}\left\lVert \left\lvert \phi \right\rvert^{2}\phi \right\rVert _{H^{-1}}. \end{align*} $$Putting in the support property (3.5) gives $$ \begin{align*} \leq C^{k}\int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert \phi \right\rVert _{H^{1}}^{\frac{4}{3}k+2}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{\frac{2}{3}k}. \end{align*} $$as claimed.
$$ \begin{align*} \leq C^{k}\int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) \left\lVert \phi \right\rVert _{H^{1}}^{\frac{4}{3}k+2}\left( T^{\frac{1}{7}}M_{0}^{\frac{3}{5}}\left\lVert P_{\leq M_{0}}\phi \right\rVert _{H^{1}}+\left\lVert P_{>M_{0}}\phi \right\rVert _{H^{1}}\right) ^{\frac{2}{3}k}. \end{align*} $$as claimed. $$ \begin{align*} &\leq \int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) C^{k}C_{0}^{\frac{4}{3}k+2}\left( T^{\frac{1}{7}}M_{0}^{ \frac{3}{5}}C_{0}+\varepsilon \right) ^{\frac{2}{3}k} \\ &\leq 2TC^{k}C_{0}^{\frac{4}{3}k+2}\left( T^{\frac{1}{7}}M_{0}^{\frac{3 }{5}}C_{0}+\varepsilon \right) ^{\frac{2}{3}k} \\ &\leq 2TC_{0}^{2}\left( CC_{0}^{3}T^{\frac{1}{7}}M_{0}^{\frac{3}{5} }+CC_{0}^{2}\varepsilon \right) ^{\frac{2}{3}k}, \end{align*} $$
$$ \begin{align*} &\leq \int_{0}^{T}dt_{k+1}\int d\left\lvert \mu _{t_{k+1}}\right\rvert \left( \phi \right) C^{k}C_{0}^{\frac{4}{3}k+2}\left( T^{\frac{1}{7}}M_{0}^{ \frac{3}{5}}C_{0}+\varepsilon \right) ^{\frac{2}{3}k} \\ &\leq 2TC^{k}C_{0}^{\frac{4}{3}k+2}\left( T^{\frac{1}{7}}M_{0}^{\frac{3 }{5}}C_{0}+\varepsilon \right) ^{\frac{2}{3}k} \\ &\leq 2TC_{0}^{2}\left( CC_{0}^{3}T^{\frac{1}{7}}M_{0}^{\frac{3}{5} }+CC_{0}^{2}\varepsilon \right) ^{\frac{2}{3}k}, \end{align*} $$
Thus, we have proved Proposition 3.7 and hence Theorem 3.1. As mentioned before, the main theorem (Theorem 1.1) then follows from Theorem 3.1 and Lemma 3.3, which checks Theorem 3.1(c) for solutions of equation (1.2) generated by equation (1.1) via equation (1.3).
Appendix A Some further remarks
After reading the main part of the paper, it should now be clear that the proof of Theorem 1.1 goes through if the ![]() $\mathbb {T} ^{4}$ energy-critical problem is replaced by the corresponding problems on
$\mathbb {T} ^{4}$ energy-critical problem is replaced by the corresponding problems on ![]() $ \mathbb {R}^{3}$,
$ \mathbb {R}^{3}$, ![]() $\mathbb {R}^{4}$ or
$\mathbb {R}^{4}$ or ![]() $\mathbb {T}^{3}$. (The method in this paper also provides a unified proof for the unconditional uniquness of the
$\mathbb {T}^{3}$. (The method in this paper also provides a unified proof for the unconditional uniquness of the ![]() $H^{1}$ -supercritical NLS [Reference Chen, Shen and Zhang26].) One could use the analysis in Theorem 3.1 but slightly different logic to conclude another form of Theorem 1.1, stated as Theorem A.1. It is certainly equivalent to Theorem 1.1, but its format is more closely related to well-posedness results.
$H^{1}$ -supercritical NLS [Reference Chen, Shen and Zhang26].) One could use the analysis in Theorem 3.1 but slightly different logic to conclude another form of Theorem 1.1, stated as Theorem A.1. It is certainly equivalent to Theorem 1.1, but its format is more closely related to well-posedness results.
Theorem A.1. Every  $C_{\left [0,T\right ]}^{0}H_{x}^{1}$ solution to equation (1.1) is also in
$C_{\left [0,T\right ]}^{0}H_{x}^{1}$ solution to equation (1.1) is also in ![]() $X^{1}$.
$X^{1}$.
Proof. We give only a sketch, as this route is only slightly different in the logic and is in fact messy in estimates, because it needs to run the main argument twice, one part of which is in a weaker space.
1. Plug the chosen
 $ C_{\left [0,T\right ]}^{0}H_{x}^{1}$ solution u directly (not taking a difference) into equation (3.4) and iterate.
$ C_{\left [0,T\right ]}^{0}H_{x}^{1}$ solution u directly (not taking a difference) into equation (3.4) and iterate.2. Group the terms in the Duhamel–Born expansion into free and interaction parts like in [Reference Chen17, Reference Chen and Holmer19, Reference Chen and Holmer21, Reference Chen and Holmer25].
3. Apply the analysis of Theorem 3.1 to deduce that the interaction part is zero in
 $L_{t}^{\infty }H_{x,x'}^{-1}$. That is,
$L_{t}^{\infty }H_{x,x'}^{-1}$. That is,  $\left \lvert u\right \rangle \left \langle u\right \rvert $ equals the free part.
$\left \lvert u\right \rangle \left \langle u\right \rvert $ equals the free part.4. Apply the analysis of Theorem 3.1 again, but in
 $X^{1}$, to conclude that the free part (and hence u) is in
$X^{1}$, to conclude that the free part (and hence u) is in  $X^{1}$.
$X^{1}$.
On the other hand, we remark that the ![]() $\mathbb {T}^{4}$ case is a bit ‘special’ in the aspect of multilinear estimates. The stronger
$\mathbb {T}^{4}$ case is a bit ‘special’ in the aspect of multilinear estimates. The stronger ![]() $ L_{t}^{1}H_{x}^{s}$ versions of formulas (2.7) and (2.11) can be proved easily on
$ L_{t}^{1}H_{x}^{s}$ versions of formulas (2.7) and (2.11) can be proved easily on ![]() $ \mathbb {R}^{3}$ [Reference Hong, Taliaferro and Xie39] and
$ \mathbb {R}^{3}$ [Reference Hong, Taliaferro and Xie39] and ![]() $\mathbb {R}^{4}$, and with a highly technical and careful argument on
$\mathbb {R}^{4}$, and with a highly technical and careful argument on ![]() $\mathbb {T}^{3}$ [Reference Chen and Holmer24]. In fact, here is a short proof for the
$\mathbb {T}^{3}$ [Reference Chen and Holmer24]. In fact, here is a short proof for the ![]() $\mathbb {R}^{4}$ case.
$\mathbb {R}^{4}$ case.
Lemma A.2. On ![]() $\mathbb {R}^{4},$
$\mathbb {R}^{4},$
 $$ \begin{align} \left\lVert e^{it\Delta }f_{1}e^{it\Delta }f_{2}e^{it\Delta}f_{3}\right\rVert_{L_{T}^{1}H^{-1}} &\lesssim \lVert f_{1}\rVert_{H^{-1}}\lVert f_{2}\rVert _{H^{1}}\lVert f_{3}\rVert _{H^{1}} \end{align} $$
$$ \begin{align} \left\lVert e^{it\Delta }f_{1}e^{it\Delta }f_{2}e^{it\Delta}f_{3}\right\rVert_{L_{T}^{1}H^{-1}} &\lesssim \lVert f_{1}\rVert_{H^{-1}}\lVert f_{2}\rVert _{H^{1}}\lVert f_{3}\rVert _{H^{1}} \end{align} $$ $$ \begin{align} \left\lVert e^{it\Delta }f_{1}e^{it\Delta }f_{2}e^{it\Delta }f_{3}\right\rVert_{L_{T}^{1}H^{1}} &\lesssim \lVert f_{1}\rVert _{H^{1}}\lVert f_{2}\rVert_{H^{1}}\lVert f_{3}\rVert _{H^{1}}. \end{align} $$
$$ \begin{align} \left\lVert e^{it\Delta }f_{1}e^{it\Delta }f_{2}e^{it\Delta }f_{3}\right\rVert_{L_{T}^{1}H^{1}} &\lesssim \lVert f_{1}\rVert _{H^{1}}\lVert f_{2}\rVert_{H^{1}}\lVert f_{3}\rVert _{H^{1}}. \end{align} $$In particular, these formulas imply formulas (2.7) and (2.11). That is, formulas (1) and (2) are indeed stronger than formulas (2.7) and (2.11).
Proof. We prove only formula (1), as formula (2) follows similarly. Given ![]() $g\in L_{t}^{\infty }H_{x}^{-1}$, we have
$g\in L_{t}^{\infty }H_{x}^{-1}$, we have
 $$ \begin{align*} \left\lvert \int e^{it\Delta }f_{1}e^{it\Delta }f_{2}e^{it\Delta }f_{3}gdtdx\right\rvert & \leq \left\lVert \left\lvert \nabla \right\rvert ^{-1}e^{it\Delta }f_{1}\right\rVert _{L_{t,x}^{3}}\left\lVert \left\lvert \nabla \right\rvert \left( e^{it\Delta }f_{2}e^{it\Delta }f_{3}g\right) \right\rVert _{L_{t,x}^{\frac{3}{2}}}, \end{align*} $$
$$ \begin{align*} \left\lvert \int e^{it\Delta }f_{1}e^{it\Delta }f_{2}e^{it\Delta }f_{3}gdtdx\right\rvert & \leq \left\lVert \left\lvert \nabla \right\rvert ^{-1}e^{it\Delta }f_{1}\right\rVert _{L_{t,x}^{3}}\left\lVert \left\lvert \nabla \right\rvert \left( e^{it\Delta }f_{2}e^{it\Delta }f_{3}g\right) \right\rVert _{L_{t,x}^{\frac{3}{2}}}, \end{align*} $$where
 $$ \begin{align*} \left\lVert \left\lvert \nabla \right\rvert \left( e^{it\Delta }f_{2}e^{it\Delta }f_{3}g\right) \right\rVert _{L_{t,x}^{\frac{3}{2}}} &\lesssim \left\lVert \left( \left\lvert \nabla \right\rvert e^{it\Delta }f_{2}\right) e^{it\Delta }f_{3}g\right\rVert _{L_{t,x}^{\frac{3}{2}}}+\left\lVert \left( \left\lvert \nabla \right\rvert g\right) e^{it\Delta }f_{2}e^{it\Delta }f_{3}\right\rVert _{L_{t,x}^{ \frac{3}{2}}} \\ &\lesssim \left\lVert \left\lvert \nabla \right\rvert e^{it\Delta }f_{2}\right\rVert _{L_{t,x}^{3}}\left\lVert e^{it\Delta }f_{3}\right\rVert _{L_{t}^{3}L_{x}^{12}}\lVert g\rVert _{L_{t}^{\infty }L_{x}^{4}} \\ & \quad +\left\lVert e^{it\Delta }f_{2}\right\rVert _{L_{t}^{3}L_{x}^{12}}\left\lVert e^{it\Delta }f_{3}\right\rVert _{L_{t}^{3}L_{x}^{12}}\lVert \nabla g\rVert _{L_{t}^{\infty }L_{x}^{2}} \\ &\lesssim \lVert f_{2}\rVert _{H^{1}}\lVert f_{3}\rVert _{H^{1}}\lVert g\rVert _{L_{t}^{\infty }H_{x}^{1}}. \end{align*} $$
$$ \begin{align*} \left\lVert \left\lvert \nabla \right\rvert \left( e^{it\Delta }f_{2}e^{it\Delta }f_{3}g\right) \right\rVert _{L_{t,x}^{\frac{3}{2}}} &\lesssim \left\lVert \left( \left\lvert \nabla \right\rvert e^{it\Delta }f_{2}\right) e^{it\Delta }f_{3}g\right\rVert _{L_{t,x}^{\frac{3}{2}}}+\left\lVert \left( \left\lvert \nabla \right\rvert g\right) e^{it\Delta }f_{2}e^{it\Delta }f_{3}\right\rVert _{L_{t,x}^{ \frac{3}{2}}} \\ &\lesssim \left\lVert \left\lvert \nabla \right\rvert e^{it\Delta }f_{2}\right\rVert _{L_{t,x}^{3}}\left\lVert e^{it\Delta }f_{3}\right\rVert _{L_{t}^{3}L_{x}^{12}}\lVert g\rVert _{L_{t}^{\infty }L_{x}^{4}} \\ & \quad +\left\lVert e^{it\Delta }f_{2}\right\rVert _{L_{t}^{3}L_{x}^{12}}\left\lVert e^{it\Delta }f_{3}\right\rVert _{L_{t}^{3}L_{x}^{12}}\lVert \nabla g\rVert _{L_{t}^{\infty }L_{x}^{2}} \\ &\lesssim \lVert f_{2}\rVert _{H^{1}}\lVert f_{3}\rVert _{H^{1}}\lVert g\rVert _{L_{t}^{\infty }H_{x}^{1}}. \end{align*} $$We see that formulas (1) and (2) are indeed elementary to prove if one has the  $L_{t,x}^{3}$ estimate, which is known to fail on
$L_{t,x}^{3}$ estimate, which is known to fail on ![]() $\mathbb {T}^{4}$ [Reference Bourgain2]. Scale-invariant
$\mathbb {T}^{4}$ [Reference Bourgain2]. Scale-invariant ![]() $\mathbb {T}^{4}\, L_{t}^{3}$-Strichartz estimates with derivatives are also absent in the literature. That is, proving formulas (1) and (2) on
$\mathbb {T}^{4}\, L_{t}^{3}$-Strichartz estimates with derivatives are also absent in the literature. That is, proving formulas (1) and (2) on ![]() $\mathbb {T}^{4}$ would be very difficult, and they may not even be true. In fact, if both formulas (1) and (2) hold on
$\mathbb {T}^{4}$ would be very difficult, and they may not even be true. In fact, if both formulas (1) and (2) hold on ![]() $\mathbb {T}^{4}$, we can deduce that
$\mathbb {T}^{4}$, we can deduce that  $\left \lVert e^{it\Delta }P_{\leq M}f\right \rVert _{L_{t}^{3}L_{x}^{6}}\lesssim M^{\frac {2}{3}}\left \lVert P_{\leq M}f\right \rVert _{L^{2}}$, which is a
$\left \lVert e^{it\Delta }P_{\leq M}f\right \rVert _{L_{t}^{3}L_{x}^{6}}\lesssim M^{\frac {2}{3}}\left \lVert P_{\leq M}f\right \rVert _{L^{2}}$, which is a ![]() $\mathbb {T}^{4}$ scale-invariant estimate carrying the
$\mathbb {T}^{4}$ scale-invariant estimate carrying the ![]() $ L_{t}^{3}$ exponent and may not be true. Hence, we see that the
$ L_{t}^{3}$ exponent and may not be true. Hence, we see that the ![]() $\mathbb {T} ^{4}$ case is indeed ‘special’ in the aspect of multilinear estimates, and we are forced to use the weaker U-V space estimates to be on the safe side.
$\mathbb {T} ^{4}$ case is indeed ‘special’ in the aspect of multilinear estimates, and we are forced to use the weaker U-V space estimates to be on the safe side.
On the other hand, we remark that as estimates (1) and (2) were proved using Hölder, Strichartz and so on with ![]() $\geq 2$ time exponents, using
$\geq 2$ time exponents, using  $\left \lVert \int _{0}^{t}e^{i(t-s)\Delta }f(s)ds\right \rVert _{X^{1}}\leq \left \lVert f\right \rVert _{L_{t}^{1}H_{x}^{1}}$ and the inclusion
$\left \lVert \int _{0}^{t}e^{i(t-s)\Delta }f(s)ds\right \rVert _{X^{1}}\leq \left \lVert f\right \rVert _{L_{t}^{1}H_{x}^{1}}$ and the inclusion ![]() $\left \lVert f\right \rVert _{U^{p}}\lesssim \lVert f\rVert _{U^{2}}$ for
$\left \lVert f\right \rVert _{U^{p}}\lesssim \lVert f\rVert _{U^{2}}$ for ![]() $ p\geq 2$, formulas (2.7) and (2.11) are reduced on
$ p\geq 2$, formulas (2.7) and (2.11) are reduced on ![]() $\mathbb {R}^{4}$ from formulas (1) and (2) by applying the atomic structure of
$\mathbb {R}^{4}$ from formulas (1) and (2) by applying the atomic structure of ![]() $ U^{p}$ on the nuts and bolts. We omit the details but remark that one would get a
$ U^{p}$ on the nuts and bolts. We omit the details but remark that one would get a ![]() $U^{1}$ estimate instead if one applied the atomic structure directly on the
$U^{1}$ estimate instead if one applied the atomic structure directly on the ![]() $L_{t}^{1}$ estimate. That is, one could have multiple versions of multilinear estimates yielding existence. For the moment, let us consider the
$L_{t}^{1}$ estimate. That is, one could have multiple versions of multilinear estimates yielding existence. For the moment, let us consider the ![]() $\mathbb {T}^{3}$ quintic problem as an example, since
$\mathbb {T}^{3}$ quintic problem as an example, since ![]() $\mathbb {R}^{3}/ \mathbb {R}^{4}$ are simpler and
$\mathbb {R}^{3}/ \mathbb {R}^{4}$ are simpler and ![]() $\mathbb {T}^{4}$ may not allow the ambiguity to be mentioned. Instead of using the
$\mathbb {T}^{4}$ may not allow the ambiguity to be mentioned. Instead of using the ![]() $\mathbb {T}^{3}$ versions of formulas (2.7) and (2.11), one could use the
$\mathbb {T}^{3}$ versions of formulas (2.7) and (2.11), one could use the ![]() $\mathbb {T}^{3}$ versions of formulas (1) and (2), which do not need U-V techniques, or the
$\mathbb {T}^{3}$ versions of formulas (1) and (2), which do not need U-V techniques, or the ![]() $U^{1}$ versions of their implications to show local existence for the
$U^{1}$ versions of their implications to show local existence for the ![]() $\mathbb {T}^{3}$ quintic problem in three similar but different subspaces of
$\mathbb {T}^{3}$ quintic problem in three similar but different subspaces of ![]() $H^{1}$. The only way to know if these three versions yield the same solution is an unconditional-uniqueness theorem.
$H^{1}$. The only way to know if these three versions yield the same solution is an unconditional-uniqueness theorem.
Finally, separate from answering the original mathematical problem that there could be multiple solutions coming from different spaces in which equation (1.1) is well posed, the unconditional-uniqueness problems on ![]() $\mathbb {T}^{n}$ have practical applications. An example is the control problem for the Lugiato–Lefever system, first formulated in [Reference Lugiato and Lefever52], which could be considered as an NLS with forcing:
$\mathbb {T}^{n}$ have practical applications. An example is the control problem for the Lugiato–Lefever system, first formulated in [Reference Lugiato and Lefever52], which could be considered as an NLS with forcing:
 $$ \begin{align} i\partial _{t}u_{f} &= -\Delta u_{f}\pm \left\lvert u_{f}\right\rvert ^{p-1}u_{f}+f\text{ in }\mathbb{R}\times \mathbb{T}^{n}, \\ u_{f}(0,x) &= u_{0}. \notag \end{align} $$
$$ \begin{align} i\partial _{t}u_{f} &= -\Delta u_{f}\pm \left\lvert u_{f}\right\rvert ^{p-1}u_{f}+f\text{ in }\mathbb{R}\times \mathbb{T}^{n}, \\ u_{f}(0,x) &= u_{0}. \notag \end{align} $$The problem is to find f and ![]() $u_{0}$ such that
$u_{0}$ such that ![]() $u_{f}\in X$, for some space X in which equation (3) is well posed, minimises some given functional
$u_{f}\in X$, for some space X in which equation (3) is well posed, minimises some given functional ![]() $Z(u)$. For some experimental and engineering purposes, the spatial domain has to be
$Z(u)$. For some experimental and engineering purposes, the spatial domain has to be ![]() $\mathbb {T}^{n}$. The space X in which one looks for the minimiser largely determines the difficulty. If
$\mathbb {T}^{n}$. The space X in which one looks for the minimiser largely determines the difficulty. If ![]() $X=L_{x}^{2}$ or
$X=L_{x}^{2}$ or ![]() $ H_{x}^{1}$, there are techniques readily available to hunt for minimisers. However, how to search for minimisers when X is a proper subspace of
$ H_{x}^{1}$, there are techniques readily available to hunt for minimisers. However, how to search for minimisers when X is a proper subspace of ![]() $ H_{x}^{1}$, like
$ H_{x}^{1}$, like ![]() $H_{x}^{2}$ or
$H_{x}^{2}$ or ![]() $H_{x}^{1}\cap L_{t}^{p}L_{x}^{q}$ – a common space for well-posedness – remains open. Such a dilemma can be resolved if one has unconditional-uniqueness results like Theorem 1.1.
$H_{x}^{1}\cap L_{t}^{p}L_{x}^{q}$ – a common space for well-posedness – remains open. Such a dilemma can be resolved if one has unconditional-uniqueness results like Theorem 1.1.
Acknowledgments
The first author would like to thank Manoussos Grillakis, Matei Machedon and Changxing Miao for enthusiastic discussions related to this work. Moreover, the authors would like to thank Shunlin Shen and the referees for their careful reading and checking of the paper and their insightful comments and helpful suggestions, which have made the paper better.
Funding statement
The first author was supported in part by NSF grant DMS-2005469. The second author was partially supported by NSF grant DMS-2055072.
Competing Interests
None.