Article contents
Simultaneously vanishing higher derived limits
Published online by Cambridge University Press: 14 June 2021
Abstract
In 1988, Sibe Mardešić and Andrei Prasolov isolated an inverse system
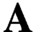 $\textbf {A}$
with the property that the additivity of strong homology on any class of spaces which includes the closed subsets of Euclidean space would entail that
$\textbf {A}$
with the property that the additivity of strong homology on any class of spaces which includes the closed subsets of Euclidean space would entail that
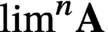 $\lim ^n\textbf {A}$
(the nth derived limit of
$\lim ^n\textbf {A}$
(the nth derived limit of
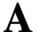 $\textbf {A}$
) vanishes for every
$\textbf {A}$
) vanishes for every
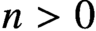 $n>0$
. Since that time, the question of whether it is consistent with the
$n>0$
. Since that time, the question of whether it is consistent with the
 $\mathsf {ZFC}$
axioms that
$\mathsf {ZFC}$
axioms that
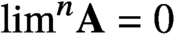 $\lim ^n \textbf {A}=0$
for every
$\lim ^n \textbf {A}=0$
for every
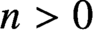 $n>0$
has remained open. It remains possible as well that this condition in fact implies that strong homology is additive on the category of metric spaces.
$n>0$
has remained open. It remains possible as well that this condition in fact implies that strong homology is additive on the category of metric spaces.
We show that assuming the existence of a weakly compact cardinal, it is indeed consistent with the
 $\mathsf {ZFC}$
axioms that
$\mathsf {ZFC}$
axioms that
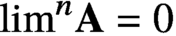 $\lim ^n \textbf {A}=0$
for all
$\lim ^n \textbf {A}=0$
for all
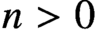 $n>0$
. We show this via a finite-support iteration of Hechler forcings which is of weakly compact length. More precisely, we show that in any forcing extension by this iteration, a condition equivalent to
$n>0$
. We show this via a finite-support iteration of Hechler forcings which is of weakly compact length. More precisely, we show that in any forcing extension by this iteration, a condition equivalent to
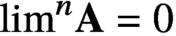 $\lim ^n\textbf {A}=0$
will hold for each
$\lim ^n\textbf {A}=0$
will hold for each
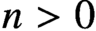 $n>0$
. This condition is of interest in its own right; namely, it is the triviality of every coherent n-dimensional family of certain specified sorts of partial functions
$n>0$
. This condition is of interest in its own right; namely, it is the triviality of every coherent n-dimensional family of certain specified sorts of partial functions
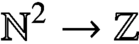 $\mathbb {N}^2\to \mathbb {Z}$
which are indexed in turn by n-tuples of functions
$\mathbb {N}^2\to \mathbb {Z}$
which are indexed in turn by n-tuples of functions
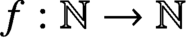 $f:\mathbb {N}\to \mathbb {N}$
. The triviality and coherence in question here generalise the classical and well-studied case of
$f:\mathbb {N}\to \mathbb {N}$
. The triviality and coherence in question here generalise the classical and well-studied case of
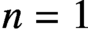 $n=1$
.
$n=1$
.
- Type
- Foundations
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press.
References
 $\underleftarrow{\lim}$
et leurs applications en théorie des modules, Lecture Notes in Mathematics, vol. 254 (
Springer-Verlag, Berlin-New York, 1972).CrossRefGoogle Scholar
$\underleftarrow{\lim}$
et leurs applications en théorie des modules, Lecture Notes in Mathematics, vol. 254 (
Springer-Verlag, Berlin-New York, 1972).CrossRefGoogle Scholar ${\underleftarrow{\lim}}^{(n)}$
’, Bull. Amer. Math. Soc. 80 (1974), 8–26.CrossRefGoogle Scholar
${\underleftarrow{\lim}}^{(n)}$
’, Bull. Amer. Math. Soc. 80 (1974), 8–26.CrossRefGoogle Scholar- 5
- Cited by





