Hostname: page-component-84b7d79bbc-x5cpj Total loading time: 0 Render date: 2024-07-29T19:41:48.599Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITELY DEPENDENT COLORING

Part of: Graph theory Stochastic processes Combinatorial probability

Published online by Cambridge University Press:  03 November 2016

ALEXANDER E. HOLROYD  and
THOMAS M. LIGGETT
ALEXANDER E. HOLROYD
Affiliation:
Microsoft Research, 1 Microsoft Way, Redmond, WA 98052, USA; holroyd@microsoft.com
THOMAS M. LIGGETT
Affiliation:
Department of Mathematics, University of California, Los Angeles, CA 90095, USA; tml@math.ucla.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that proper coloring distinguishes between block factors and finitely dependent stationary processes. A stochastic process is finitely dependent if variables at sufficiently well-separated locations are independent; it is a block factor if it can be expressed as an equivariant finite-range function of independent variables. The problem of finding non-block-factor finitely dependent processes dates back to 1965. The first published example appeared in 1993, and we provide arguably the first natural examples. Schramm proved in 2008 that no stationary 1-dependent 3-coloring of the integers exists, and asked whether a 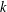$k$-dependent 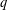$q$-coloring exists for any $k$ and 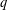$q$. We give a complete answer by constructing a 1-dependent 4-coloring and a 2-dependent 3-coloring. Our construction is canonical and natural, yet very different from all previous schemes. In its pure form it yields precisely the two finitely dependent colorings mentioned above, and no others. The processes provide unexpected connections between extremal cases of the Lovász local lemma and descent and peak sets of random permutations. Neither coloring can be expressed as a block factor, nor as a function of a finite-state Markov chain; indeed, no stationary finitely dependent coloring can be so expressed. We deduce extensions involving 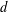$d$ dimensions and shifts of finite type; in fact, any nondegenerate shift of finite type also distinguishes between block factors and finitely dependent processes.

MSC classification

Primary: 60G10: Stationary processes 05C15: Coloring of graphs and hypergraphs 60C05: Combinatorial probability
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 4 , 2016 , e9
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Aaronson, J., Gilat, D. and Keane, M., ‘On the structure of 1-dependent Markov chains’, J. Theoret. Probab. 5(3) (1992), 545–561.Google Scholar
Aaronson, J., Gilat, D., Keane, M. and de Valk, V., ‘An algebraic construction of a class of one-dependent processes’, Ann. Probab. 17(1) (1989), 128–143.Google Scholar
Alon, N. and Feldheim, O. N., ‘A note on general sliding window processes’, Electron. Commun. Probab. 19(66) (2014), 1–7.Google Scholar
Alon, N. and Spencer, J. H., The Probabilistic Method, 3rd edn, Wiley-Interscience Series in Discrete Mathematics and Optimization , (John Wiley & Sons, Inc., Hoboken, NJ, 2008), With an appendix on the life and work of Paul Erdős.Google Scholar
Billey, S., Burdzy, K. and Sagan, B. E., ‘Permutations with given peak set’, J. Integer Seq. 16(6) (2013), Article 13.6.1, 18.Google Scholar
Borodin, A., Diaconis, P. and Fulman, J., ‘On adding a list of numbers (and other one-dependent determinantal processes)’, Bull. Amer. Math. Soc. (N.S.) 47(4) (2010), 639–670.Google Scholar
Broman, E. I., ‘One-dependent trigonometric determinantal processes are two-block-factors’, Ann. Probab. 33(2) (2005), 601–609.Google Scholar
Burton, R. M., Goulet, M. and Meester, R., ‘On 1-dependent processes and k-block factors’, Ann. Probab. 21(4) (1993), 2157–2168.Google Scholar
de Valk, V., ‘A problem on 0-1 matrices’, Compositio Math. 71(2) (1989), 139–179.Google Scholar
de Valk, V., ‘Hilbert space representations of m-dependent processes’, Ann. Probab. 21(3) (1993), 1550–1570.Google Scholar
Duminil-Copin, H. and Tassion, V., ‘A new proof of the sharpness of the phase transition for Bernoulli percolation and the Ising model’, Comm. Math. Phys. 343(2) (2016), 725–745.Google Scholar
Edelman, P., Hibi, T. and Stanley, R. P., ‘A recurrence for linear extensions’, Order 6(1) (1989), 15–18.Google Scholar
Erdős, P. and Lovász, L., ‘Problems and results on 3-chromatic hypergraphs and some related questions’, inInfinite and Finite Sets, Vol. II, Colloq. Math. Soc. János Bolyai, 10 (North-Holland, Amsterdam, 1975), 609–627.Google Scholar
Flajolet, P. and Sedgewick, R., Analytic Combinatorics (Cambridge University Press, Cambridge, 2009).Google Scholar
Gandolfi, A., Keane, M. and de Valk, V., ‘Extremal two-correlations of two-valued stationary one-dependent processes’, Probab. Theory Related Fields 80(3) (1989), 475–480.Google Scholar
Götze, F. and Hipp, C., ‘Asymptotic expansions for potential functions of i.i.d. random fields’, Probab. Theory Related Fields 82(3) (1989), 349–370.Google Scholar
Haiman, M. G., ‘Valeurs extrémales de suites stationnaires de variables aléatoires m-dépendantes’, Ann. Inst. H. Poincaré Sect. B (N.S.) 17(3) (1981), 309–330.Google Scholar
Heinrich, L., ‘Asymptotic expansions in the central limit theorem for a special class of m-dependent random fields. II. Lattice case’, Math. Nachr. 145 (1990), 309–327.Google Scholar
Hoeffding, W. and Robbins, H., ‘The central limit theorem for dependent random variables’, Duke Math. J. 15 (1948), 773–780.Google Scholar
Holroyd, A. E., One-dependent coloring by finitary factors. Ann. Inst. Henri Poincaré, arXiv:1411.1463.Google Scholar
Holroyd, A. E. and Liggett, T. M., ‘Symmetric 1-dependent colorings of the integers’, Electron. Commun. Probab. 20(31) (2015), 1–8.Google Scholar
Holroyd, A. E., Schramm, O. and Wilson, D. B., Finitary coloring. Ann. Probab., arXiv:1412.2725.Google Scholar
Ibragimov, I. A. and Linnik, Yu. V., Nezavisimye stalionarno svyazannye velichiny, Izdat , (Nauka, Moscow, 1965).Google Scholar
Ibragimov, I. A. and Linnik, Yu. V., Independent and Stationary Sequences of Random Variables (Wolters-Noordhoff Publishing, Groningen, 1971), With a supplementary chapter by I. A. Ibragimov and V. V. Petrov, Translation from the Russian edited by J. F. C. Kingman.Google Scholar
Janson, S., ‘Renewal theory for M-dependent variables’, Ann. Probab. 11(3) (1983), 558–568.Google Scholar
Janson, S., ‘Runs in m-dependent sequences’, Ann. Probab. 12(3) (1984), 805–818.Google Scholar
Janson, S., ‘On degenerate sums of m-dependent variables’, J. Appl. Probab. 52(4) (2015), 1146–1155.Google Scholar
Kallenberg, O., Foundations of Modern Probability, 2nd edn, Probability and its Applications (Springer, New York, 2002).Google Scholar
Karlin, S., Total Positivity, Vol. I (Stanford University Press, Stanford, CA, 1968).Google Scholar
Lax, P. D., Functional Analysis, Pure and Applied Mathematics (Wiley-Interscience, New York, 2002).Google Scholar
Levit, V. E. and Mandrescu, E., ‘The independence polynomial of a graph—a survey’, inProceedings of the 1st International Conference on Algebraic Informatics (Aristotle Univ. Thessaloniki, Thessaloniki, 2005), 233–254.Google Scholar
Liggett, T. M., Schonmann, R. H. and Stacey, A. M., ‘Domination by product measures’, Ann. Probab. 25(1) (1997), 71–95.Google Scholar
Linial, N., ‘Distributive graph algorithms—global solutions from local data’, in28th Annual Symposium on Foundations of Computer Science (IEEE, 1987), 331–335.Google Scholar
Mallows, C. and Shepp, L., ‘The necklace process’, J. Appl. Probab. 45(1) (2008), 271–278.Google Scholar
Matúš, F., ‘On two-block-factor sequences and one-dependence’, Proc. Amer. Math. Soc. 124(4) (1996), 1237–1242.Google Scholar
Matúš, F., ‘Combining m-dependence with Markovness’, Ann. Inst. Henri Poincaré Probab. Stat. 34(4) (1998), 407–423.Google Scholar
Nakata, T., ‘Necklace processes via Pólya urns’, J. Appl. Probab. 46(1) (2009), 284–295.Google Scholar
Naor, M., ‘A lower bound on probabilistic algorithms for distributive ring coloring’, SIAM J. Discrete Math. 4(3) (1991), 409–412.Google Scholar
Niven, I., ‘A combinatorial problem of finite sequences’, Nieuw Arch. Wiskd. (3) 16 (1968), 116–123.Google Scholar
O’Brien, G. L., ‘Scaling transformations for {0, 1}-valued sequences’, Z. Wahrsch. Verw. Gebiete 53(1) (1980), 35–49.Google Scholar
Rüschendorf, L. and de Valk, V., ‘On regression representations of stochastic processes’, Stochastic Process. Appl. 46(2) (1993), 183–198.Google Scholar
Scott, A. D. and Sokal, A. D., ‘The repulsive lattice gas, the independent-set polynomial, and the Lovász local lemma’, J. Stat. Phys. 118(5–6) (2005), 1151–1261.Google Scholar
Scott, A. D. and Sokal, A. D., ‘On dependency graphs and the lattice gas’, Combin. Probab. Comput. 15(1–2) (2006), 253–279.Google Scholar
Shearer, J. B., ‘On a problem of Spencer’, Combinatorica 5(3) (1985), 241–245.Google Scholar
Titchmarsh, E. C., The Theory of Functions (Oxford University Press, 1939).Google Scholar
Todo, S., ‘Transfer-matrix study of negative-fugacity singularity of hard-core lattice gas’, Internat. J. Modern Phys. C 10(4) (1999), 517–529.Google Scholar