Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-17T10:17:00.435Z Has data issue: false hasContentIssue false
  • English
  • Français

COCENTERS OF 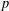$p$-ADIC GROUPS, I: NEWTON DECOMPOSITION

Part of: Representation theory of groups Lie groups

Published online by Cambridge University Press:  28 March 2018

XUHUA HE
XUHUA HE*
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, USA Institute for Advanced Study, Princeton, NJ 08540, USA; xuhuahe@math.umd.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we introduce the Newton decomposition on a connected reductive 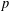$p$-adic group 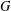$G$. Based on it we give a nice decomposition of the cocenter of its Hecke algebra. Here we consider both the ordinary cocenter associated to the usual conjugation action on 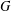$G$ and the twisted cocenter arising from the theory of twisted endoscopy. We give Iwahori–Matsumoto type generators on the Newton components of the cocenter. Based on it, we prove a generalization of Howe’s conjecture on the restriction of (both ordinary and twisted) invariant distributions. Finally we give an explicit description of the structure of the rigid cocenter.

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Secondary: 20C08: Hecke algebras and their representations
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 6 , 2018 , e2
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2018

References

Barbasch, D. and Moy, A., ‘A new proof of the Howe conjecture’, J. Amer. Math. Soc. 13(3) (2000), 639–650.Google Scholar
Bernstein, J., Deligne, P. and Kazhdan, D., ‘Trace Paley-Wiener theorem for reductive p-adic groups’, J. Anal. Math. 47 (1986), 180–192.Google Scholar
Bruhat, F. and Tits, J., ‘Groupes réductifs sur un corps local: II. Schémas en groupes. Existence d’une donnée radicielle valuée’, Publ. Math. Inst. Hautes Études Sci. 60 (1984), 197–376.CrossRefGoogle Scholar
Ciubotaru, D. and He, X., ‘Cocenters and representations of affine Hecke algebra’, J. Eur. Math. Soc. 19 (2017), 3143–3177.Google Scholar
Ciubotaru, D. and He, X., ‘Cocenters of $p$ -adic groups, III: elliptic cocenter and rigid cocenter’, Preprint, 2017, arXiv:1703.00378.Google Scholar
Clozel, L., ‘Orbital integrals on p-adic groups: a proof of the Howe conjecture’, Ann. of Math. (2) 129(2) (1989), 237–251.Google Scholar
Dat, J.-F., ‘On the K 0 of a p-adic group’, Invent. Math. 140(1) (2000), 171–226.Google Scholar
Debacker, S., ‘Lectures on harmonic analysis for reductive p-adic groups’, inRepresentations of Real and p-Adic Groups, Lecture Notes Ser. Inst. Math. Sci. Natl. Univ. Singap., 2 (Singapore University Press, Singapore, 2004), 47–94.Google Scholar
Ganapathy, R., ‘The local Langlands correspondence for GSp 4 over local function fields’, Amer. J. Math. 137 (2015), 1441–1534.Google Scholar
Haines, T. and Rapoport, M., ‘On parahoric subgroups’, Adv. Math. 219(1) (2008), 188–198; appendix to: G. Pappas and M. Rapoport, ‘Twisted loop groups and their affine flag varieties’, Adv. Math. 219(1) (2008), 118–198.Google Scholar
Harish-Chandra, ‘Admissible invariant distributions on reductive p-adic groups’, inPreface and Notes by S. DeBacker and P. Sally, University Lecture Series, 16(American Mathematical Society, Providence, RI, 1999).Google Scholar
Henniart, G. and Lemaire, B., ‘Représentations des espaces tordus sur un groupe réductif connexe p-adique’, Astérisque 386 (2017), ix+366 pp.Google Scholar
He, X., ‘Geometric and homological properties of affine Deligne–Lusztig varieties’, Ann. of Math. (2) 179 (2014), 367–404.Google Scholar
He, X., ‘Kottwitz–Rapoport conjecture on unions of affine Deligne–Lusztig varieties’, Ann. Sci. Èc. Norm. Supér. 49 (2016), 1125–1141.Google Scholar
He, X., ‘Cocenters of $p$ -adic groups, II: inclusion map’, Preprint, 2016, arXiv:1611.06825.Google Scholar
He, X. and Nie, S., ‘Minimal length elements of extended affine Weyl group’, Compos. Math. 150 (2014), 1903–1927.Google Scholar
Howe, R., ‘Two conjectures about reductive p-adic groups’, Proc. AMS Symp. Pure Math. XXVI (1973), 377–380.Google Scholar
Howe, R., ‘Harish-Chandra homomorphisms for p-adic groups’, inCBMS Regional Conference Series in Mathematics, 59 (Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1985).Google Scholar
Kazhdan, D., ‘Cuspidal geometry of p-adic groups’, J. Anal. Math. 47 (1986), 1–36.Google Scholar
Kazhdan, D., ‘Representations groups over close local fields’, J. Anal. Math. 47 (1986), 175–179.Google Scholar
Kottwitz, R., ‘Isocrystals with additional structure’, Compos. Math. 56 (1985), 201–220.Google Scholar
Kottwitz, R., ‘Isocrystals with additional structure. II’, Compos. Math. 109 (1997), 255–339.Google Scholar
Kumar, S., Kac–Moody Groups, Their Flag Varieties and Representation Theory, Progress in Mathematics, 204 (Birkhä user Boston, Inc., Boston, MA, 2002).Google Scholar
Richarz, T., ‘On the Iwahori–Weyl group’, Bull. Soc. Math. France 144 (2016), 117–124.Google Scholar
Tits, J., ‘Reductive groups over local fields’, inAutomorphic Forms, Representations and L-Functions (Oregon State University, Corvallis, OR., 1977), Part 1, Proc. Sympos. Pure Math., XXXIII (American Mathematical Society, Providence, RI, 1979), 29–69.Google Scholar
Vignéras, M.-F., Représentations l-modulaires d’un groupe réductif p-adique avec l≠p , Progr. Math., 137 (Birkhäuser, Boston, 1996).Google Scholar