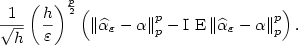Research Article
On the asymptotic properties of a simple estimate of the Mode
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 1-11
-
- Article
- Export citation
Optimisation in space of measures and optimal design
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 12-24
-
- Article
- Export citation
Linear diffusion with stationary switching regime
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 25-35
-
- Article
- Export citation
Pointwise convergence of Boltzmann solutions for grazing collisions in a Maxwell gas via a probabilitistic interpretation
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 36-55
-
- Article
- Export citation
A note on quenched moderate deviations for Sinai's random walk in random environment
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 56-65
-
- Article
- Export citation
Central limit theorem for hitting times of functionals of Markov jump processes
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 66-75
-
- Article
- Export citation
Ergodicity of a certain class of Non Feller Models: Applications to ARCH and Markov switching models
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 76-86
-
- Article
- Export citation
Functional inequalities for discrete gradients and application to the geometric distribution
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 87-101
-
- Article
- Export citation
Renormalization group of and convergence to the LISDLG process
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 102-114
-
- Article
- Export citation
Coupling a stochastic approximation version of EM with an MCMC procedure
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 115-131
-
- Article
- Export citation
Asymptotics for the Lp-deviation of the variance estimator under diffusion
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 132-149
-
- Article
- Export citation
Extreme values and kernel estimates of point processes boundaries
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 150-168
-
- Article
- Export citation
Asymptotic shape for the chemical distance and first-passage percolation on the infinite Bernoulli cluster
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 169-199
-
- Article
- Export citation
The large deviation principle for certain series
-
- Published online by Cambridge University Press:
- 15 September 2004, pp. 200-220
-
- Article
- Export citation