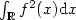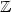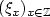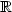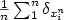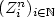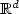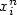Research Article
Adaptive estimation of a quadratic functional of a density by model selection
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 1-18
-
- Article
- Export citation
On the bounded laws of iterated logarithm in Banach space
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 19-37
-
- Article
- Export citation
Convergence to infinitely divisible distributions with finite variance for some weakly dependent sequences
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 38-73
-
- Article
- Export citation
Large deviations and support results for nonlinear Schrödinger equations with additive noise and applications
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 74-97
-
- Article
- Export citation
Limit theorems for U-statistics indexed by a one dimensional random walk
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 98-115
-
- Article
- Export citation
Large deviations for independent random variables – Application to Erdös-Renyi's functional law of large numbers
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 116-142
-
- Article
- Export citation
A scale-space approach with wavelets to singularity estimation
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 143-164
-
- Article
- Export citation
Asymptotic behavior of differential equations driven by periodic and random processes with slowly decaying correlations
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 165-184
-
- Article
- Export citation
On the infinite time horizon linear-quadratic regulator problem under a fractional Brownian perturbation
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 185-205
-
- Article
- Export citation
Inference on overlap coefficients under the Weibull distribution: Equal shape parameter
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 206-219
-
- Article
- Export citation
Risk bounds for mixture density estimation
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 220-229
-
- Article
- Export citation
Detecting atypical data in air pollution studies by using shorth intervals for regression
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 230-240
-
- Article
- Export citation
Estimation of parameters in a network reliability model with spatial dependence
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 241-253
-
- Article
- Export citation
On the long-time behaviour of a class of parabolic SPDE's: monotonicity methods and exchange of stability
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 254-276
-
- Article
- Export citation
A two armed bandit type problem revisited
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 277-282
-
- Article
- Export citation
Conditional principles for random weighted measures
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 283-306
-
- Article
- Export citation
On the minimizing point of the incorrectly centered empirical process and its limit distribution in nonregular experiments
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 307-322
-
- Article
- Export citation
Theory of Classification: a Survey of Some Recent Advances
-
- Published online by Cambridge University Press:
- 15 November 2005, pp. 323-375
-
- Article
- Export citation