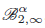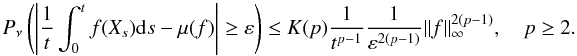Research Article
Large deviations for quasi-arithmetically self-normalized random variables
-
- Published online by Cambridge University Press:
- 06 December 2012, pp. 1-12
-
- Article
- Export citation
Local asymptotic normality for normal inverse Gaussian Lévy processes with high-frequency sampling∗
-
- Published online by Cambridge University Press:
- 06 December 2012, pp. 13-32
-
- Article
- Export citation
Nonparametric estimation of the derivatives of the stationary density for stationary processes
-
- Published online by Cambridge University Press:
- 06 December 2012, pp. 33-69
-
- Article
- Export citation
Lower large deviations for the maximal flow through tilted cylinders in two-dimensional first passage percolation
-
- Published online by Cambridge University Press:
- 06 December 2012, pp. 70-104
-
- Article
- Export citation
Asymptotic normality of randomly truncated stochastic algorithms
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 105-119
-
- Article
- Export citation
A central limit theorem for triangular arrays of weakly dependent random variables, with applications in statistics
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 120-134
-
- Article
- Export citation
Incremental moments and Hölder exponents of multifractional multistable processes
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 135-178
-
- Article
- Export citation
On the convergence of moments in the almost sure central limit theorem for stochastic approximation algorithms
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 179-194
-
- Article
- Export citation
Polynomial deviation bounds for recurrent Harris processes having general state space
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 195-218
-
- Article
- Export citation
Multifractional Brownian fields indexed by metric spaces with distances of negative type
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 219-223
-
- Article
- Export citation
Fixed-α and fixed-β efficiencies
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 224-235
-
- Article
- Export citation
Plug-in estimation of level sets in a non-compact setting with applications in multivariate risk theory
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 236-256
-
- Article
- Export citation
Meeting time of independent random walks in random environment
-
- Published online by Cambridge University Press:
- 08 February 2013, pp. 257-292
-
- Article
- Export citation
Semimartingale decomposition of convex functions of continuous semimartingales by Brownian perturbation
-
- Published online by Cambridge University Press:
- 17 May 2013, pp. 293-306
-
- Article
- Export citation
Local estimation of the Hurst index of multifractional Brownian motion by increment ratio statistic method
-
- Published online by Cambridge University Press:
- 17 May 2013, pp. 307-327
-
- Article
- Export citation
Penalization versus Goldenshluger − Lepski strategies in warped bases regression
-
- Published online by Cambridge University Press:
- 17 May 2013, pp. 328-358
-
- Article
- Export citation
Towards a universally consistent estimator of the Minkowski content∗
-
- Published online by Cambridge University Press:
- 17 May 2013, pp. 359-369
-
- Article
- Export citation
How the result of graph clustering methods depends on the construction of the graph
-
- Published online by Cambridge University Press:
- 21 May 2013, pp. 370-418
-
- Article
- Export citation
Smoothness of Metropolis-Hastings algorithm and application to entropy estimation
-
- Published online by Cambridge University Press:
- 21 May 2013, pp. 419-431
-
- Article
- Export citation
Goodness-of-fit tests in long-range dependent processes under fixed alternatives
-
- Published online by Cambridge University Press:
- 21 May 2013, pp. 432-443
-
- Article
- Export citation