Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Comte, F.
and
Rozenholc, Y.
2004.
A new algorithm for fixed design regression and denoising.
Annals of the Institute of Statistical Mathematics,
Vol. 56,
Issue. 3,
p.
449.
Boucheron, S.
and
Gassiat, E.
2006.
Error exponents for AR order testing.
IEEE Transactions on Information Theory,
Vol. 52,
Issue. 2,
p.
472.
Comte, Fabienne
Genon-Catalot, Valentine
and
Rozenholc, Yves
2007.
Penalized nonparametric mean square estimation of the coefficients of diffusion processes.
Bernoulli,
Vol. 13,
Issue. 2,
Brunel, Elodie
and
Comte, Fabienne
2008.
Adaptive Estimation of Hazard Rate with Censored Data.
Communications in Statistics - Theory and Methods,
Vol. 37,
Issue. 8,
p.
1284.
Comte, F.
Genon-Catalot, V.
and
Rozenholc, Y.
2009.
Nonparametric adaptive estimation for integrated diffusions.
Stochastic Processes and their Applications,
Vol. 119,
Issue. 3,
p.
811.
Sauvé, Marie
2009.
Histogram selection in non Gaussian regression.
ESAIM: Probability and Statistics,
Vol. 13,
Issue. ,
p.
70.
Reynaud-Bouret, Patricia
and
Schbath, Sophie
2010.
Adaptive estimation for Hawkes processes; application to genome analysis.
The Annals of Statistics,
Vol. 38,
Issue. 5,
Comte, F.
Genon-Catalot, V.
and
Rozenholc, Y.
2010.
Nonparametric estimation for a stochastic volatility model.
Finance and Stochastics,
Vol. 14,
Issue. 1,
p.
49.
Baraud, Yannick
2010.
A Bernstein-type inequality for suprema of random processes with applications to model selection in non-Gaussian regression.
Bernoulli,
Vol. 16,
Issue. 4,
Sauve, Marie
2010.
Piecewise Polynomial Estimation of a Regression Function.
IEEE Transactions on Information Theory,
Vol. 56,
Issue. 1,
p.
597.
Löcherbach, Eva
Loukianova, Dasha
and
Loukianov, Oleg
2011.
Penalized nonparametric drift estimation for a continuously observed one-dimensional diffusion process.
ESAIM: Probability and Statistics,
Vol. 15,
Issue. ,
p.
197.
Schmisser, Emeline
2011.
Non-parametric drift estimation for diffusions from noisy data.
Statistics & Decisions,
Vol. 28,
Issue. 2,
p.
119.
2012.
Statistical Methods for Stochastic Differential Equations.
p.
133.
Schmisser, Emeline
2013.
Penalized nonparametric drift estimation for a multidimensional diffusion process.
Statistics,
Vol. 47,
Issue. 1,
p.
61.
Baraud, Yannick
and
Birgé, Lucien
2014.
Estimating composite functions by model selection.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 50,
Issue. 1,
Liu, Rong
and
Yang, Lijian
2016.
SPLINE ESTIMATION OF A SEMIPARAMETRIC GARCH MODEL.
Econometric Theory,
Vol. 32,
Issue. 4,
p.
1023.
Zhou, Qifeng
Xia, Bin
Xue, Wei
Zeng, Chunqiu
Han, Ruyuan
and
Li, Tao
2017.
An Advanced Inventory Data Mining System for Business Intelligence.
p.
210.
Comte, Fabienne
and
Genon-Catalot, Valentine
2020.
Nonparametric drift estimation for i.i.d. paths of stochastic differential equations.
The Annals of Statistics,
Vol. 48,
Issue. 6,
Dion, Charlotte
and
Lemler, Sarah
2020.
Nonparametric drift estimation for diffusions with jumps driven by a Hawkes process.
Statistical Inference for Stochastic Processes,
Vol. 23,
Issue. 3,
p.
489.
Denis, Christophe
Dion-Blanc, Charlotte
and
Martinez, Miguel
2021.
A ridge estimator of the drift from discrete repeated observations of the solution of a stochastic differential equation.
Bernoulli,
Vol. 27,
Issue. 4,
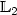 -norm and we show that it is adaptive in the minimax
sense over a large class of Besov balls of the form Bα,p,∞(R) with p ≥ 1.
-norm and we show that it is adaptive in the minimax
sense over a large class of Besov balls of the form Bα,p,∞(R) with p ≥ 1.




