Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Andreianov, Boris
Boyer, Franck
and
Hubert, Florence
2004.
Finite volume schemes for the p-Laplacian on Cartesian meshes.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 38,
Issue. 6,
p.
931.
Delcourte, Sarah
Domelevo, Komla
and
Omnes, Pascal
2007.
A Discrete Duality Finite Volume Approach to Hodge Decomposition and div‐curl Problems on Almost Arbitrary Two‐Dimensional Meshes.
SIAM Journal on Numerical Analysis,
Vol. 45,
Issue. 3,
p.
1142.
Eymard, Robert
Gallouët, Thierry
and
Herbin, Raphaèle
2007.
A new finite volume scheme for anisotropic diffusion problems on general grids: convergence analysis.
Comptes Rendus. Mathématique,
Vol. 344,
Issue. 6,
p.
403.
Andreianov, Boris
Boyer, Franck
and
Hubert, Florence
2007.
Discrete duality finite volume schemes for Leray−Lions−type elliptic problems on general 2D meshes.
Numerical Methods for Partial Differential Equations,
Vol. 23,
Issue. 1,
p.
145.
Hermeline, F.
2007.
Approximation of 2-D and 3-D diffusion operators with variable full tensor coefficients on arbitrary meshes.
Computer Methods in Applied Mechanics and Engineering,
Vol. 196,
Issue. 21-24,
p.
2497.
Manzini, Gianmarco
and
Putti, Mario
2007.
Mesh locking effects in the finite volume solution of 2-D anisotropic diffusion equations.
Journal of Computational Physics,
Vol. 220,
Issue. 2,
p.
751.
Beirão da Veiga, Lourenço
and
Manzini, Gianmarco
2008.
An a posteriori error estimator for the mimetic finite difference approximation of elliptic problems.
International Journal for Numerical Methods in Engineering,
Vol. 76,
Issue. 11,
p.
1696.
Cangiani, Andrea
and
Manzini, Gianmarco
2008.
Flux reconstruction and solution post-processing in mimetic finite difference methods.
Computer Methods in Applied Mechanics and Engineering,
Vol. 197,
Issue. 9-12,
p.
933.
Vohralík, Martin
2008.
Residual flux-based a posteriori error estimates for finite volume and related locally conservative methods.
Numerische Mathematik,
Vol. 111,
Issue. 1,
p.
121.
Hermeline, F.
Layouni, S.
and
Omnes, P.
2008.
A finite volume method for the approximation of Maxwell’s equations in two space dimensions on arbitrary meshes.
Journal of Computational Physics,
Vol. 227,
Issue. 22,
p.
9365.
Boyer, Franck
and
Hubert, Florence
2008.
Finite Volume Method for 2D Linear and Nonlinear Elliptic Problems with Discontinuities.
SIAM Journal on Numerical Analysis,
Vol. 46,
Issue. 6,
p.
3032.
Manzini, Gianmarco
and
Russo, Alessandro
2008.
A finite volume method for advection–diffusion problems in convection-dominated regimes.
Computer Methods in Applied Mechanics and Engineering,
Vol. 197,
Issue. 13-16,
p.
1242.
Djadel, K.
and
Nicaise, S.
2008.
A non-conforming finite volume element method of weighted upstream type for the two-dimensional stationary Navier–Stokes system.
Applied Numerical Mathematics,
Vol. 58,
Issue. 5,
p.
615.
Hermeline, F.
2008.
Approximating second‐order vector differential operators on distorted meshes in two space dimensions.
International Journal for Numerical Methods in Engineering,
Vol. 76,
Issue. 7,
p.
1065.
Boyer, Franck
and
Hubert, Florence
2008.
Domain Decomposition Methods in Science and Engineering XVII.
Vol. 60,
Issue. ,
p.
443.
Angot, Philippe
Boyer, Franck
and
Hubert, Florence
2009.
Asymptotic and numerical modelling of flows in fractured porous media.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 43,
Issue. 2,
p.
239.
Eymard, R.
Gallouët, T.
and
Herbin, R.
2009.
Cell centred discretisation of non linear elliptic problems on general multidimensional polyhedral grids.
Journal of Numerical Mathematics,
Vol. 17,
Issue. 3,
Hermeline, F.
2009.
A finite volume method for approximating 3D diffusion operators on general meshes.
Journal of Computational Physics,
Vol. 228,
Issue. 16,
p.
5763.
Chang, Lina
and
Yuan, Guangwei
2009.
Cell-centered finite volume methods with flexible stencils for diffusion equations on general nonconforming meshes.
Computer Methods in Applied Mechanics and Engineering,
Vol. 198,
Issue. 17-20,
p.
1638.
Traoré, Philippe
Ahipo, Yves Marcel
and
Louste, Christophe
2009.
A robust and efficient finite volume scheme for the discretization of diffusive flux on extremely skewed meshes in complex geometries.
Journal of Computational Physics,
Vol. 228,
Issue. 14,
p.
5148.
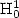 norm
and in the L² norm.
Superconvergence results are obtained on certain types of homothetically refined grids.
Finally, numerical experiments confirm these results and also show second-order convergence
in the L² norm on general grids.
They also indicate that this method performs particularly well for the approximation
of the gradient of the solution, and may be used on degenerating triangular grids.
An example of application on non-conforming locally refined grids is given.
norm
and in the L² norm.
Superconvergence results are obtained on certain types of homothetically refined grids.
Finally, numerical experiments confirm these results and also show second-order convergence
in the L² norm on general grids.
They also indicate that this method performs particularly well for the approximation
of the gradient of the solution, and may be used on degenerating triangular grids.
An example of application on non-conforming locally refined grids is given.




