In [C.W. Gear, T.J. Kaper, I.G. Kevrekidis and A. Zagaris, SIAM J. Appl. Dyn. Syst. 4 (2005) 711–732], we developed a class of iterative algorithms within the context of equation-free methods to approximate low-dimensional, attracting, slow manifolds in systems of differential equations with multiple time scales. For user-specified values of a finite number of the observables, the mth member of the class of algorithms ($m = 0, 1, \ldot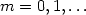s$) finds iteratively an approximation of the appropriate zero of the (m+1)st time derivative of the remaining variables and uses this root to approximate the location of the point on the slow manifold corresponding to these values of the observables. This article is the first of two articles in which the accuracy and convergence of the iterative algorithms are analyzed. Here, we work directly with fast-slow systems, in which there is an explicit small parameter, ε, measuring the separation of time scales. We show that, for each $m = 0, 1, \ldots$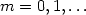, the fixed point of the iterative algorithm approximates the slow manifold up to and including terms of ${\mathcal O}(\varepsilon^m)$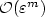. Moreover, for each m, we identify explicitly the conditions under which the mth iterative algorithm converges to this fixed point. Finally, we show that when the iteration is unstable (or converges slowly) it may be stabilized (or its convergence may be accelerated) by application of the Recursive Projection Method. Alternatively, the Newton-Krylov Generalized Minimal Residual Method may be used. In the subsequent article, we will consider the accuracy and convergence of the iterative algorithms for a broader class of systems – in which there need not be an explicit small parameter – to which the algorithms also apply.