Article contents
Un schéma d'interpolation rationnel sur un quadrilatère de classeC2
Published online by Cambridge University Press: 15 April 2002
Abstract
Let $\mathcal{Q}$ be a partition of a polygonal domain of the plan
into convexe quadrilaterals. Given a regular function f , we construct a
function πƒ
∈ C2(Ω), interpolating position values and
derivatives of f up of order 2 at vertices of $\mathcal{Q}.$
be a partition of a polygonal domain of the plan
into convexe quadrilaterals. Given a regular function f , we construct a
function πƒ
∈ C2(Ω), interpolating position values and
derivatives of f up of order 2 at vertices of $\mathcal{Q}.$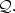 On each
quadrilateral $Q\in\mathcal{Q},$
On each
quadrilateral $Q\in\mathcal{Q},$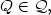 πƒ|Q is a finite element obtained
from a polynomial scheme of FVS type by adding some rational functions.
πƒ|Q is a finite element obtained
from a polynomial scheme of FVS type by adding some rational functions.
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 34 , Issue 5 , September 2000 , pp. 913 - 922
- Copyright
- © EDP Sciences, SMAI, 2000
References
- 1
- Cited by




