Article contents
Existence of a solution for a nonlinearly elastic plane membrane “under tension”
Published online by Cambridge University Press: 15 August 2002
Abstract
A justification of the two-dimensional nonlinear “membrane”
equations for a plate made of a Saint Venant-Kirchhoff material has
been given by Fox et al. [9] by means of the method of formal
asymptotic expansions applied to the three-dimensional equations of
nonlinear elasticity. This model, which retains the material-frame
indifference of the original
three dimensional problem in the sense that its energy density is
invariant under the rotations of ${\mathbb{R}}^3$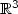 , is equivalent to finding the
critical points of a functional whose nonlinear part depends on the first
fundamental form of the unknown deformed surface. We establish here an
existence result for these equations in the case of the
membrane submitted to a boundary condition of “tension”, and we show that the
solution found in our analysis is injective and is the unique minimizer of the
nonlinear membrane functional, which is not sequentially weakly lower
semi-continuous.
We also analyze the behaviour of the membrane when the “tension” goes to
infinity
and we conclude that a “well-extended” membrane may undergo large
loadings.
, is equivalent to finding the
critical points of a functional whose nonlinear part depends on the first
fundamental form of the unknown deformed surface. We establish here an
existence result for these equations in the case of the
membrane submitted to a boundary condition of “tension”, and we show that the
solution found in our analysis is injective and is the unique minimizer of the
nonlinear membrane functional, which is not sequentially weakly lower
semi-continuous.
We also analyze the behaviour of the membrane when the “tension” goes to
infinity
and we conclude that a “well-extended” membrane may undergo large
loadings.
Keywords
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 33 , Issue 5 , September 1999 , pp. 1019 - 1032
- Copyright
- © EDP Sciences, SMAI, 1999
- 3
- Cited by




