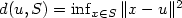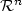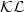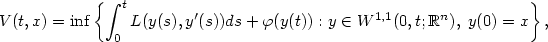Research Article
Exact boundary controllability of 3-D Euler equation
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1-44
-
- Article
- Export citation
Optimal Control of Obstacle Problems: Existence of Lagrange Multipliers
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 45-70
-
- Article
- Export citation
Relaxation of singular functionals defined on Sobolev spaces
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 71-85
-
- Article
- Export citation
Contrôle et stabilisation d'ondes électromagnétiques
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 87-137
-
- Article
- Export citation
Computation of the distance to semi-algebraic sets
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 139-156
-
- Article
- Export citation
Null controllability of nonlinear convective heat equations
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 157-173
-
- Article
- Export citation
Viability Kernels and Control Sets
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 175-185
-
- Article
- Export citation
The brachistochrone problem with frictional forces
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 187-206
-
- Article
- Export citation
Boundary control of the Maxwell dynamical system: lack of controllability by topological reasons
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 207-217
-
- Article
- Export citation
The wave equation with oscillating density: observability at low frequency
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 219-258
-
- Article
- Export citation
Optimal control approach in inverse radiative transfer problems: the problem on boundary function
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 259-278
-
- Article
- Export citation
Sufficient conditions for infinite-horizon calculus of variations problems
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 279-292
-
- Article
- Export citation
Control Lyapunov functions for homogeneous “Jurdjevic-Quinn” systems
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 293-311
-
- Article
- Export citation
A smooth Lyapunov function from a class-${\mathcal{KL}}$
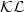 estimate
involving two positive semidefinite functions
estimate
involving two positive semidefinite functions
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 313-367
-
- Article
- Export citation
Value functions for Bolza problems with discontinuous Lagrangians and Hamilton-Jacobi inequalities
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 369-393
-
- Article
- Export citation
Absolute stability results for well-posed infinite-dimensional systems with applications to low-gain integral control
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 395-424
-
- Article
- Export citation
On some optimal control problems for the heat radiative transfer equation
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 425-444
-
- Article
- Export citation
Image deblurring, spectrum interpolation and application to satellite imaging
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 445-475
-
- Article
- Export citation
Optimal control of stationary, low Mach number, highly nonisothermal, viscous flows
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 477-500
-
- Article
- Export citation
Nonlocal variational problems arising in long wave propagatioN
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 501-528
-
- Article
- Export citation