Hostname: page-component-77c89778f8-vsgnj Total loading time: 0 Render date: 2024-07-23T09:10:39.985Z Has data issue: false hasContentIssue false
  • English
  • Français

A Haar-Rado type theorem for minimizers in Sobolev spaces

Published online by Cambridge University Press:  28 October 2010

Carlo Mariconda  and
Giulia Treu
Carlo Mariconda
Affiliation:
Dipartimento di Matematica Pura ed Applicata – Università Degli Studi di Padova, Via Trieste 63, 35121 Padova, Italy. maricond@math.unipd.it; treu@math.unipd.it
Giulia Treu
Affiliation:
Dipartimento di Matematica Pura ed Applicata – Università Degli Studi di Padova, Via Trieste 63, 35121 Padova, Italy. maricond@math.unipd.it; treu@math.unipd.it
Get access

Abstract

Let $u\in\phi+ W_0^{1,1}(\Omega)$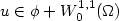 be a minimum for

$\[I(v)=\int_{\Omega}g(x,v(x))+f(\nabla v(x))\,{\rm d}x\]$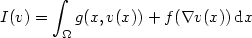

where f is convex, $v\mapsto g(x,v)$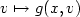 is convex for a.e. x. We prove that u shares the same modulus of continuity of ϕ whenever Ω is sufficiently regular, the right derivative of g satisfies a suitable monotonicity assumption and the following inequality holds

$\forall \gamma\in\partial\Omega\qquad |u(x)-\phi(\gamma)|\le \omega(|x-\gamma|) \quad\text{a.e. }x\in\Omega.$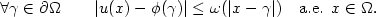

This result generalizes the classical Haar-Rado theorem for Lipschitz functions.

Keywords

HölderregularityLipschitz
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 4 , October 2011 , pp. 1133 - 1143
Copyright
© EDP Sciences, SMAI, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

H. Brezis, Analyse fonctionnelle : théorie et applications. Collection Mathématiques Appliquées pour la Maîtrise [Collection of Applied Mathematics for the Master's Degree], Masson, Paris (1983).
Brezis, H. and Sibony, M., Équivalence de deux inéquations variationnelles et applications. Arch. Rational Mech. Anal. 41 (1971) 254–265. CrossRef
Cellina, A., On the bounded slope condition and the validity of the Euler Lagrange equation. SIAM J. Control Optim. 40 (2002) 1270–1279. CrossRef
Cellina, A., Comparison results and estimates on the gradient without strict convexity. SIAM J. Control Optim. 46 (2007) 738–749. CrossRef
Clarke, F., Continuity of solutions to a basic problem in the calculus of variations. Ann. Sc. Norm. Super. Pisa Cl. Sci. 4 (2005) 511–530.
L.C. Evans and R.F. Gariepy, Measure theory and fine properties of functions. Studies in Advanced Mathematics, CRC Press, Boca Raton (1992).
M. Giaquinta and L. Martinazzi, An introduction to the regularity theory for elliptic systems, harmonic maps and minimal graphs, Scuola Normale Superiore di Pisa (Nuova Serie) [Lecture Notes. Scuola Normale Superiore di Pisa (New Series)] 2. Edizioni della Normale, Pisa (2005).
Hartman, P., On the bounded slope condition. Pacific J. Math. 18 (1966) 495–511. CrossRef
Hartman, P. and Stampacchia, G., On some non-linear elliptic differential-functional equations. Acta Math. 115 (1966) 271–310. CrossRef
Mariconda, C. and Treu, G., Lipschitz regularity for minima without strict convexity of the Lagrangian. J. Differ. Equ. 243 (2007) 388–413. CrossRef
Mariconda, C. and Treu, G., Local Lipschitz regularity of minima for a scalar problem of the calculus of variations. Commun. Contemp. Math. 10 (2008) 1129–1149. CrossRef
Mariconda, C. and Treu, G., Hölder regularity for a classical problem of the calculus of variations. Adv. Calc. Var. 2 (2009) 311–320. CrossRef
Miranda, M., Un teorema di esistenza e unicità per il problema dell'area minima in n variabili. Ann. Scuola Norm. Sup. Pisa 19 (1965) 233–249.
Treu, G. and Vornicescu, M., On the equivalence of two variational problems. Calc. Var. Partial Differential Equations 11 (2000) 307–319. CrossRef