Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-16T00:28:45.298Z Has data issue: false hasContentIssue false
  • English
  • Français

An optimal matching problem

Published online by Cambridge University Press:  15 December 2004

Ivar Ekeland
Ivar Ekeland*
Affiliation:
University of British Columbia, Vancouver BC, V6T 1Z2  Canada. ekeland@math.ubc.ca
Get access

Abstract

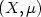Given two measured spaces $(X,\mu)$ and $(Y,\nu)$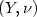, and a third space Z, given two functions u(x,z) and v(x,z), we study the problem of finding two maps $s:X\rightarrow Z$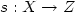 and $t:Y\rightarrow Z$ 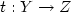such that the images $s(\mu)$ 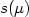and $t(\nu)$ 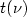coincide, and the integral $\int_{X}u(x,s(x))d\mu-\int _{Y}v(y,t(y))d\nu$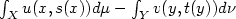 is maximal. We give condition on u and v for which there is a unique solution.

Keywords

optimal transportationmeasure-preserving maps.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 11 , Issue 1 , January 2005 , pp. 57 - 71
Copyright
© EDP Sciences, SMAI, 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brenier, Y., Polar factorization and monotone rearrangements of vector-valued functions. Comm. Pure App. Math. 44 (1991) 375–417. CrossRef
G. Carlier, Duality and existence for a class of mass transportation problems and economic applications, Adv. Math. Economics 5 (2003) 1–21.
I. Ekeland and R. Temam, Convex analysis and variational problems. North-Holland Elsevier (1974) new edition, SIAM Classics in Appl. Math. (1999).
Gangbo, W. and McCann, R., The geometry of optimal transportation. Acta Math. 177 (1996) 113–161. CrossRef
Ekeland, I., Heckman, J. and Nesheim, L., Identification and estimation of hedonic models. J. Political Economy 112 (2004) 60–109. CrossRef
L. Kantorovitch, On the transfer of masses, Dokl. Ak. Nauk USSR 37 (1942) 7–8.
S. Rachev and A. Ruschendorf, Mass transportation problems. Springer-Verlag (1998).
C. Villani, Topics in mass transportation. Grad. Stud. Math. 58 (2003)