Article contents
Relaxation in BV of integrals with superlinear growth
Published online by Cambridge University Press: 13 August 2014
Abstract
We study properties of the functional 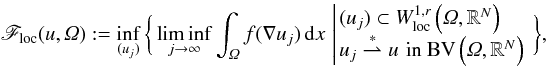 Floc(u,Ω):=inf(uj)liminfj→∞∫Ωf(∇uj)dx,
Floc(u,Ω):=inf(uj)liminfj→∞∫Ωf(∇uj)dx,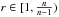 r∈[1,nn−1), we prove that
Floc satisfies
the lower bound
r∈[1,nn−1), we prove that
Floc satisfies
the lower bound 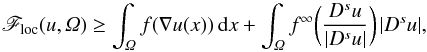 Floc(u,Ω)≥∫Ωf(∇u(x))dx+∫Ωf∞Dsu|Dsu||Dsu|,
Floc(u,Ω)≥∫Ωf(∇u(x))dx+∫Ωf∞Dsu|Dsu||Dsu|,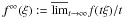 f∞(ξ):=limt→∞f(tξ)/t) is assumed to be finite in
certain rank-one directions. The proof of this result involves adapting work by
[Kristensen, Calc. Var. Partial Differ. Eqs. 7 (1998)
249–261], and [Ambrosio and Dal Maso, J. Funct. Anal. 109
(1992) 76–97], and applying a non-standard blow-up technique that exploits fine
properties of BV maps. It also makes use of the fact that Floc has a measure
representation, which is proved in the appendix using a method of [Fonseca and Malý,
Annal. Inst. Henri Poincaré Anal. Non Linéaire 14 (1997)
309–338].
f∞(ξ):=limt→∞f(tξ)/t) is assumed to be finite in
certain rank-one directions. The proof of this result involves adapting work by
[Kristensen, Calc. Var. Partial Differ. Eqs. 7 (1998)
249–261], and [Ambrosio and Dal Maso, J. Funct. Anal. 109
(1992) 76–97], and applying a non-standard blow-up technique that exploits fine
properties of BV maps. It also makes use of the fact that Floc has a measure
representation, which is proved in the appendix using a method of [Fonseca and Malý,
Annal. Inst. Henri Poincaré Anal. Non Linéaire 14 (1997)
309–338].
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 20 , Issue 4 , October 2014 , pp. 1078 - 1122
- Copyright
- © EDP Sciences, SMAI, 2014
References
- 2
- Cited by




