Article contents
Homogenization and localization in locally periodic transport
Published online by Cambridge University Press: 15 August 2002
Abstract
In this paper, we study the homogenization and localization of a
spectral transport equation posed in a locally periodic
heterogeneous domain. This equation models the equilibrium of
particles interacting with an underlying medium in the presence of a
creation mechanism such as, for instance, neutrons in nuclear
reactors. The physical coefficients of the domain are
ε-periodic functions modulated by a macroscopic variable, where
ε is a small parameter. The mean free path of the particles is
also of order ε. We assume that the leading eigenvalue of the
periodicity cell problem admits a unique minimum in the domain at a
point x0 where its Hessian matrix is positive definite. This
assumption yields a concentration phenomenon around x0, as ε
goes to 0, at a new scale of the order of $\sqrt{\varepsilon}$ which is
superimposed with the usual ε oscillations of the homogenized
limit. More precisely, we prove that the particle density is
asymptotically the product of two terms. The first one is the
leading eigenvector of a cell transport equation with periodic
boundary conditions. The second term is the first eigenvector of a
homogenized diffusion equation in the whole space with quadratic
potential, rescaled by a factor $\sqrt{\varepsilon}$
which is
superimposed with the usual ε oscillations of the homogenized
limit. More precisely, we prove that the particle density is
asymptotically the product of two terms. The first one is the
leading eigenvector of a cell transport equation with periodic
boundary conditions. The second term is the first eigenvector of a
homogenized diffusion equation in the whole space with quadratic
potential, rescaled by a factor $\sqrt{\varepsilon}$ , i.e., of the form
$\exp \left (- \frac {1} {2 \varepsilon} M (x-x_0)\cdot (x-x_0) \right )$
, i.e., of the form
$\exp \left (- \frac {1} {2 \varepsilon} M (x-x_0)\cdot (x-x_0) \right )$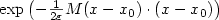 ,
where M is a positive definite matrix. Furthermore, the
eigenvalue corresponding to this second term gives a first-order
correction to the eigenvalue of the heterogeneous spectral transport
problem.
,
where M is a positive definite matrix. Furthermore, the
eigenvalue corresponding to this second term gives a first-order
correction to the eigenvalue of the heterogeneous spectral transport
problem.
Keywords
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 8: A tribute to JL Lions , 2002 , pp. 1 - 30
- Copyright
- © EDP Sciences, SMAI, 2002
References
- 6
- Cited by




