Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-04-30T18:53:23.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly aperiodic SFTs on generalized Baumslag–Solitar groups

Part of: Structure and classification of infinite or finite groups Topological dynamics Designs and configurations

Published online by Cambridge University Press:  20 June 2023

NATHALIE AUBRUN Open the ORCID record for NATHALIE AUBRUN [Opens in a new window] ,
NICOLÁS BITAR Open the ORCID record for NICOLÁS BITAR [Opens in a new window]  and
SACHA HURIOT-TATTEGRAIN
NATHALIE AUBRUN
Affiliation:
CNRS, Université Paris-Saclay, LISN, Orsay 91400, France (e-mail: nathalie.aubrun@lisn.fr)
NICOLÁS BITAR*
Affiliation:
CNRS, Université Paris-Saclay, LISN, Orsay 91400, France (e-mail: nathalie.aubrun@lisn.fr)
SACHA HURIOT-TATTEGRAIN
Affiliation:
École Normale Supérieure Paris-Saclay, Gif-sur-Yvette 91190, France (e-mail: sachahuriot@gmail.com)
*
e-mail: nicolas.bitar@lisn.upsaclay.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We look at constructions of aperiodic subshifts of finite type (SFTs) on fundamental groups of graph of groups. In particular, we prove that all generalized Baumslag-Solitar groups (GBS) admit a strongly aperiodic SFT. Our proof is based on a structural theorem by Whyte and on two constructions of strongly aperiodic SFTs on 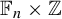$\mathbb {F}_n\times \mathbb {Z}$ and 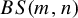$BS(m,n)$ of our own. Our two constructions rely on a path-folding technique that lifts an SFT on 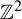$\mathbb {Z}^2$ inside an SFT on 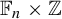$\mathbb {F}_n\times \mathbb {Z}$ or an SFT on the hyperbolic plane inside an SFT on 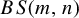$BS(m,n)$. In the case of 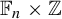$\mathbb {F}_n\times \mathbb {Z}$, the path folding technique also preserves minimality, so that we get minimal strongly aperiodic SFTs on unimodular GBS groups.

Keywords

symbolic dynamicsgeneralized Baumslag–Solitar groupsaperiodicitysubshift of finite type

MSC classification

Primary: 20E06: Free products, free products with amalgamation, Higman-Neumann-Neumann extensions, and generalizations
Secondary: 37B10: Symbolic dynamics 05B45: Tessellation and tiling problems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 5 , May 2024 , pp. 1209 - 1238
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubrun, N., Barbieri, S. and Jeandel, E.. About the domino problem for subshifts on groups. Sequences, Groups, and Number Theory (Trends in Mathematics). Eds. Berthé, V. and Rigo, M.. Springer International Publishing, Cham, 2018, pp. 331–389.10.1007/978-3-319-69152-7_9CrossRefGoogle Scholar
Aubrun, N., Barbieri, S. and Moutot, E.. The domino problem is undecidable on surface groups. Proc. 44th International Symposium on Mathematical Foundations of Computer Science, MFCS 2019, Aachen, Germany, August 26–30, 2019 (LIPIcs, 138). Eds. Rossmanith, P., Heggernes, P. and Katoen, J.. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, Aachen, Germany, 2019, pp. 46:1–46:14.Google Scholar
Aubrun, N., Barbieri, S. and Thomassé, S.. Realization of aperiodic subshifts and uniform densities in groups. Groups Geom. Dyn. 13(1) (2018), 107–129.CrossRefGoogle Scholar
Aubrun, N. and Kari, J.. Tiling problems on Baumslag–Solitar groups. Proceedings Machines, Computations and Universality 2013, Zürich, Switzerland, 9/09/2013–11/09/2013 (Electronic Proceedings in Theoretical Computer Science, 128). Eds. T. Neary and M. Cook. Open Publishing Association, Waterloo, Australia, 2013, pp. 35–46.Google Scholar
Aubrun, N. and Kari, J.. Addendum to “Tilings problems on Baumslag–Solitar groups”. Preprint, 2021, arXiv:2101.12470.10.1016/j.tcs.2021.09.002CrossRefGoogle Scholar
Aubrun, N. and Kari, J.. On the domino problem of the Baumslag–Solitar groups. Theoret. Comput. Sci. 894 (2021), 12–22; Building Bridges – Honoring Nataša Jonoska on the Occasion of Her 60th Birthday.10.1016/j.tcs.2021.09.002CrossRefGoogle Scholar
Aubrun, N. and Schraudner, M.. Tilings of the hyperbolic plane of substitutive origin as subshifts of finite type on Baumslag–Solitar groups $\mathrm{BS}(1,n)$ . Preprint, 2020, arXiv:2012.11037.Google Scholar
Barbieri, S.. A geometric simulation theorem on direct products of finitely generated groups. Discrete Anal. 9 (2019), 25pp.Google Scholar
Barbieri, S. and Sablik, M.. A generalization of the simulation theorem for semidirect products. Ergod. Th. & Dynam. Sys. 39(12) (2019), 3185–3206.10.1017/etds.2018.21CrossRefGoogle Scholar
Barbieri, S., Sablik, M. and Salo, V.. Groups with self-simulable zero-dimensional dynamics. Preprint, 2022, arXiv:2104.05141.Google Scholar
Bartholdi, L. and Salo, V.. Simulations and the lamplighter group. Groups Geom. Dyn. 16(4) (2022), 1461–1514.10.4171/ggd/692CrossRefGoogle Scholar
Baumslag, G. and Solitar, D.. Some two-generator one-relator non-Hopfian groups. Bull. Amer. Math. Soc. (N.S.) 68(3) (1962), 199–201.10.1090/S0002-9904-1962-10745-9CrossRefGoogle Scholar
Boyle, M. and Lind, D.. Expansive subdynamics. Trans. Amer. Math. Soc. 349(1) (1997), 55–102.CrossRefGoogle Scholar
Carroll, D. and Penland, A.. Periodic points on shifts of finite type and commensurability invariants of groups. New York J. Math. 21 (2015), 811–822.Google Scholar
Casals-Ruiz, M., Kazachkov, I. and Zakharov, A.. Commensurability of Baumslag–Solitar groups. Preprint, 2019, arXiv:1910.02117.Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. Cellular Automata and Groups (Springer Monographs in Mathematics), 2010 edition. Springer, Berlin, 2010.10.1007/978-3-642-14034-1CrossRefGoogle Scholar
Cohen, D. B.. The large scale geometry of strongly aperiodic subshifts of finite type. Adv. Math. 308 (2017), 599–626.CrossRefGoogle Scholar
Cohen, D. B. and Goodman-Strauss, C.. Strongly aperiodic subshifts on surface groups. Groups Geom. Dyn. 11(3) (2017), 1041–1059.CrossRefGoogle Scholar
Cohen, D. B., Goodman-Strauss, C. and Rieck, Y.. Strongly aperiodic subshifts of finite type on hyperbolic groups. Ergod. Th. & Dynam. Sys. 42 (2017), 2740–2783.CrossRefGoogle Scholar
Crisp, J.. Automorphisms and abstract commensurators of 2–dimensional Artin groups. Geom. Topol. 9(3) (2005), 1381–1441.CrossRefGoogle Scholar
Culik, K. and Kari, J.. An aperiodic set of Wang cubes. J.UCS The Journal of Universal Computer Science. Eds. Maurer, H., Calude, C. and Salomaa, A.. Springer, Berlin, 1996, pp. 675–686.CrossRefGoogle Scholar
Delgado, A. L., Robinson, D. J. S. and Timm, M.. Cyclic normal subgroups of generalized Baumslag–Solitar groups. Comm. Algebra 45(4) (2017), 1808–1818.10.1080/00927872.2016.1226859CrossRefGoogle Scholar
Dunwoody, M. J.. The accessibility of finitely presented groups. Invent. Math. 81(3) (1985), 449–457.CrossRefGoogle Scholar
Esnay, S. J. and Moutot, E.. Aperiodic SFTs on Baumslag–Solitar groups . Theoret. Comput. Sci. 917 (2022), 31–50.CrossRefGoogle Scholar
Farb, B. and Mosher, L.. A rigidity theorem for the solvable Baumslag–Solitar groups. Invent. Math. 131 (1998), 419–451.10.1007/s002220050210CrossRefGoogle Scholar
Forester, M.. On uniqueness of JSJ decompositions of finitely generated groups. Comment. Math. Helv. 78(4) (2003), 740–751.CrossRefGoogle Scholar
Forester, M.. Splittings of generalized Baumslag–Solitar groups. Geom. Dedicata 121(1) (2006), 43–59.10.1007/s10711-006-9085-9CrossRefGoogle Scholar
Gao, S., Jackson, S. and Seward, B.. A coloring property for countable groups. Math. Proc. Cambridge Philos. Soc. 147 (2009), 579–592.10.1017/S0305004109002655CrossRefGoogle Scholar
Gentimis, T.. Asymptotic dimension of finitely presented groups. Proc. Amer. Math. Soc. 136(12) (2008), 4103–4110.10.1090/S0002-9939-08-08973-9CrossRefGoogle Scholar
Gromov, M.. Hyperbolic groups. Essays in Group Theory. Ed. Gersten, S. M.. Springer, New York, NY, 1987, pp. 75–263.CrossRefGoogle Scholar
Higman, G.. A finitely related group with an isomorphic proper factor group. J. Lond. Math. Soc. (2) 1(1) (1951), 59–61.CrossRefGoogle Scholar
Jeandel, E.. Aperiodic subshifts of finite type on groups. Preprint, 2015, arXiv:1501.06831.Google Scholar
Jeandel, E. and Vanier, P.. The undecidability of the domino problem. Substitution and Tiling Dynamics: Introduction to Self-inducing Structures. Eds. Akiyama, S. and Arnoux, P.. Springer, Cham, 2020, pp. 293–357.CrossRefGoogle Scholar
Kari, J.. A small aperiodic set of Wang tiles. Discrete Math. 160(1–3) (1996, 259–264.CrossRefGoogle Scholar
Kari, J.. The tiling problem revisited. Machines, Computations, and Universality (Lecture Notes in Computer Science, 4664). Eds. Durand-Lose, J. O. and Margenstern, M.. Springer, Berlin, 2007, pp. 72–79.10.1007/978-3-540-74593-8_6CrossRefGoogle Scholar
Khukhro, A.. A characterisation of virtually free groups via minor exclusion. Int. Math. Res. Not. 2022 (2022), rnac184.Google Scholar
Labbé, S.. Markov partitions for toral ${\mathbb{Z}}^2$ -rotations featuring Jeandel–Rao Wang shift and model sets. Ann. H. Lebesgue 4 (2021), 283–324.10.5802/ahl.73CrossRefGoogle Scholar
Labbé, S.. Rauzy induction of polygon partitions and toral ${\mathbb{Z}}^2$ -rotations. J. Mod. Dyn. 17 (2021), 481.CrossRefGoogle Scholar
Labbé, S., Mann, C. and McLoud-Mann, J.. Nonexpansive directions in the Jeandel–Rao Wang shift. Discrete Contin. Dyn. Syst. doi: https://doi.org/10.3934/dcds.2023046.CrossRefGoogle Scholar
Levitt, G.. On the automorphism group of generalized Baumslag–Solitar groups. Geom. Topol. 11(1) (2007), 473–515.10.2140/gt.2007.11.473CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.10.1017/CBO9780511626302CrossRefGoogle Scholar
Lyman, R. A.. Train tracks on graphs of groups and outer automorphisms of hyperbolic groups. Preprint, 2020, arXiv:2005.00164 [math].Google Scholar
Mosher, L., Sageev, M. and Whyte, K.. Quasi-actions on trees. I. Bounded valence. Ann. of Math. (2) 158 (2003), 115–164.CrossRefGoogle Scholar
Piantadosi, S. T.. Symbolic dynamics on free groups. Discrete Contin. Dyn. Syst. 20(3) (2008), 725.CrossRefGoogle Scholar
Rieck, Y.. Strongly aperiodic SFTs on hyperbolic groups: where to find them and why we love them. Rev. Union Mat. Argent. 64(2) (2023), 355–373.CrossRefGoogle Scholar
Robinson, R.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.10.1007/BF01418780CrossRefGoogle Scholar
Rolfsen, D.. Knots and Links (AMS Chelsea Publishing, 346). American Mathematical Society, Providence, RI, 2003.Google Scholar
Şahin, A. A., Schraudner, M. and Ugarcovici, I.. A strongly aperiodic shift of finite type on the discrete Heisenberg group using Robinson tilings. Illinois J. Math. 65(3) (2021), 655–686.10.1215/00192082-9446050CrossRefGoogle Scholar
Serre, J.-P.. Trees. Springer, Berlin, 1980.CrossRefGoogle Scholar
Whyte, K.. The large scale geometry of the higher Baumslag–Solitar groups. Geom. Funct. Anal. 11 (2004), 1327–1343.CrossRefGoogle Scholar