Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-24T14:43:08.663Z Has data issue: false hasContentIssue false
  • English
  • Français

Return- and hitting-time distributions of small sets in infinite measure preserving systems

Part of: Ergodic theory Low-dimensional dynamical systems Measure-theoretic ergodic theory Limit theorems

Published online by Cambridge University Press:  02 January 2019

SIMON RECHBERGER  and
ROLAND ZWEIMÜLLER Open the ORCID record for ROLAND ZWEIMÜLLER [Opens in a new window]
SIMON RECHBERGER
Affiliation:
Fakultät für Mathematik, Universität Wien, Oskar-Morgenstern-Platz 1, 1090 Vienna, Austria email rechberger_simon@gmx.at, roland.zweimueller@univie.ac.at
ROLAND ZWEIMÜLLER
Affiliation:
Fakultät für Mathematik, Universität Wien, Oskar-Morgenstern-Platz 1, 1090 Vienna, Austria email rechberger_simon@gmx.at, roland.zweimueller@univie.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

We study convergence of return- and hitting-time distributions of small sets 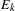$E_{k}$ with 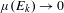$\unicode[STIX]{x1D707}(E_{k})\rightarrow 0$ in recurrent ergodic dynamical systems preserving an infinite measure $\unicode[STIX]{x1D707}$. Some properties which are easy in finite measure situations break down in this null-recurrent set-up. However, in the presence of a uniform set $Y$ with wandering rate regularly varying of index $1-\unicode[STIX]{x1D6FC}$ with 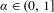$\unicode[STIX]{x1D6FC}\in (0,1]$, there is a scaling function suitable for all subsets of $Y$. In this case, we show that return distributions for the 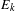$E_{k}$ converge if and only if the corresponding hitting-time distributions do, and we derive an explicit relation between the two limit laws. Some consequences of this result are discussed. In particular, this leads to improved sufficient conditions for convergence to 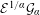${\mathcal{E}}^{1/\unicode[STIX]{x1D6FC}}{\mathcal{G}}_{\unicode[STIX]{x1D6FC}}$, where 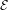${\mathcal{E}}$ and 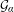${\mathcal{G}}_{\unicode[STIX]{x1D6FC}}$ are independent random variables, with 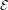${\mathcal{E}}$ exponentially distributed and 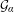${\mathcal{G}}_{\unicode[STIX]{x1D6FC}}$ following the one-sided stable law of order $\unicode[STIX]{x1D6FC}$ (and 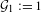${\mathcal{G}}_{1}:=1$). The same principle also reveals the limit laws (different from the above) which occur at hyperbolic periodic points of prototypical null-recurrent interval maps. We also derive similar results for the barely recurrent 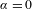$\unicode[STIX]{x1D6FC}=0$ case.

Keywords

infinite invariant measurerare eventsindifferent fixed pointsreturn-time statisticshitting-time statistics

MSC classification

Primary: 28D05: Measure-preserving transformations 37A50: Relations with probability theory and stochastic processes
Secondary: 37A40: Nonsingular (and infinite-measure preserving) transformations 37E05: Maps of the interval (piecewise continuous, continuous, smooth) 60F05: Central limit and other weak theorems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 8 , August 2020 , pp. 2239 - 2273
Check for updates
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory. American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
Aaronson, J.. The asymptotic distributional behaviour of transformations preserving infinite measures. J. Anal. Math. 39 (1981), 203–234.CrossRefGoogle Scholar
Aaronson, J.. Random f-expansions. Ann. Probab. 14 (1986), 1037–1057.CrossRefGoogle Scholar
Aaronson, J. and Zweimüller, R.. Limit theory for some positive stationary processes with infinite mean. Ann. Inst. H. Poincaré 50 (2014), 256–284.CrossRefGoogle Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L.. Regular Variation. Cambridge University Press, Cambridge, 1989.Google Scholar
Bressaud, X. and Zweimüller, R.. Non-exponential law of entrance times in asymptotically rare events for intermittent maps with infinite invariant measure. Ann. Inst. H. Poincaré 2 (2001), 501–512.CrossRefGoogle Scholar
Dvoretzky, A. and Erdős, P.. Some problems on random walk in space. Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability. Ed. Neyman, J.. University of California Press, Berkeley, CA, 1951, pp. 353–367.Google Scholar
Freitas, J. M.. Extremal behaviour of chaotic dynamics. Dyn. Syst. 28 (2013), 302–332.CrossRefGoogle Scholar
Haydn, N., Lacroix, Y. and Vaienti, S.. Hitting and return times in ergodic dynamical systems. Ann. Probab. 33 (2005), 2043–2050.CrossRefGoogle Scholar
Hirata, M., Saussol, B. and Vaienti, S.. Statistics of return times: a general framework and new applications. Comm. Math. Phys. 206 (1999), 33–55.CrossRefGoogle Scholar
Keller, G.. Rare events, exponential hitting times and extremal indices via spectral perturbation. Dyn. Syst. 27 (2012), 11–27.CrossRefGoogle Scholar
Kupsa, M. and Lacroix, Y.. Asymptotics for hitting times. Ann. Probab. 33 (2005), 610–619.CrossRefGoogle Scholar
Pène, F. and Saussol, B.. Quantitative recurrence in two-dimensional extended processes. Ann. Inst. H. Poincaré 45 (2009), 1065–1084.CrossRefGoogle Scholar
Pène, F. and Saussol, B.. Back to balls in billiards. Comm. Math. Phys. 293 (2010), 837–866.CrossRefGoogle Scholar
Pène, F., Saussol, B. and Zweimüller, R.. Recurrence rates and hitting-time distributions for random walks on the line. Ann. Probab. 41 (2013), 619–635.CrossRefGoogle Scholar
Pène, F., Saussol, B. and Zweimüller, R.. Return- and hitting-time limits for rare events of null-recurrent Markov maps. Ergod. Th. & Dynam. Sys. 37 (2017), 244–276.CrossRefGoogle Scholar
Thaler, M.. Transformations on [0,1] with infinite invariant measures. Israel J. Math. 46 (1983), 67–96.CrossRefGoogle Scholar
Thaler, M.. A limit theorem for the Perron–Frobenius operator of transformations on [0, 1] with indifferent fixed points. Israel J. Math. 91 (1995), 111–127.CrossRefGoogle Scholar
Thaler, M.. The Dynkin–Lamperti arc-sine laws for measure preserving transformations. Trans. Amer. Math. Soc. 350 (1998), 4593–4607.CrossRefGoogle Scholar
Yassine, N.. Quantitative recurrence of some dynamical systems with an infinite measure in dimension one. Discrete Contin. Dyn. Syst. A 38 (2018), 343–361.CrossRefGoogle Scholar
Zweimüller, R.. Ergodic structure and invariant densities of non-Markovian interval maps with indifferent fixed points. Nonlinearity 11 (1998), 1263–1276.CrossRefGoogle Scholar
Zweimüller, R.. Ergodic properties of infinite measure preserving interval maps with indifferent fixed points. Ergod. Th. & Dynam. Sys. 20 (2000), 1519–1549.CrossRefGoogle Scholar
Zweimüller, R.. S-unimodal Misiurewicz maps with flat critical points. Fund. Math. 181 (2004), 1–25.CrossRefGoogle Scholar
Zweimüller, R.. Mixing limit theorems for ergodic transformations. J. Theoret. Probab. 20 (2007), 1059–1071.CrossRefGoogle Scholar
Zweimüller, R.. Infinite measure preserving transformations with compact first regeneration. J. Anal. Math. 103 (2007), 93–131.CrossRefGoogle Scholar
Zweimüller, R.. Waiting for long excursions and close visits to neutral fixed points of null-recurrent ergodic maps. Fund. Math. 198 (2008), 125–138.CrossRefGoogle Scholar
Zweimüller, R.. Hitting-time limits for some exceptional rare events of ergodic maps. Stochastic Process. Appl. (2018), in press, doi:10.1016/j.spa.2018.05.011.CrossRefGoogle Scholar