Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-07-05T03:27:52.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Random products of automorphisms of Heisenberg nilmanifolds and Weil’s representation

Published online by Cambridge University Press:  17 November 2010

BACHIR BEKKA  and
JEAN-ROMAIN HEU
BACHIR BEKKA
Affiliation:
UFR Mathématiques, Université de Rennes 1, Campus Beaulieu, F-35042 Rennes Cedex, France (email: bachir.bekka@univ-rennes1.fr, jean-romain.heu@univ-rennes1.fr)
JEAN-ROMAIN HEU
Affiliation:
UFR Mathématiques, Université de Rennes 1, Campus Beaulieu, F-35042 Rennes Cedex, France (email: bachir.bekka@univ-rennes1.fr, jean-romain.heu@univ-rennes1.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

For n≥1, let H be the (2n+1)-dimensional real Heisenberg group, and let Λ be a lattice in H. Let Γ be the group of automorphisms of the corresponding nilmanifold Λ∖H and U the associated unitary representation of Γ on L2 (Λ∖H) . Denote by T the maximal torus factor associated to Λ∖H. Using Weil’s representation (also known as the metaplectic representation), we show that a dense set of matrix coefficients of the restriction of U to the orthogonal complement of L2 (T) in L2 (Λ∖H) belong to ℓ4n+2+ε (Γ) for every ε>0 . We give the following application to random walks on Λ∖H defined by a probability measure μ on Aut (Λ∖H) . Denoting by Γ(μ) the subgroup of Aut (Λ∖H) generated by the support of μ and by U0 and V0 the restrictions of U to, respectively, the subspaces of L2 (Λ∖H) and L2 (T) with zero mean, we prove the following inequality: 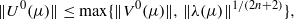where λ is the left regular representation of Γ(μ) on ℓ2 (Γ(μ)) . In particular, the action of Γ(μ) on Λ∖H has a spectral gap if and only if the corresponding action of Γ(μ) on T has a spectral gap.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 31 , Issue 5 , October 2011 , pp. 1277 - 1286
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[Ausl77]Auslander, L.. Lecture Notes on Nil-Theta Functions (CBMS Regional Conference Series in Mathematics, 34). American Mathematical Society, Providence, RI, 1977.CrossRefGoogle Scholar
[BeHV08]Bekka, B., de la Harpe, P. and Valette, A.. Kazhdan’s Property (T). Cambridge University Press, Cambridge, 2008.Google Scholar
[BeMa00]Bekka, B. and Mayer, M.. Ergodic Theory and Topological Dynamics of Group Actions on Homogeneous Spaces (London Mathematical Society Lecture Note Series, 269). Cambridge University Press, Cambridge, 2000.CrossRefGoogle Scholar
[Conz09]Conze, J.-P.. Action d’un groupe d’applications affines sur une nilvariété compacte. Preprint, 2009.Google Scholar
[Foll89]Folland, G. B.. Harmonic Analysis in Phase Space (Annals of Mathematics Studies, 122). Princeton University Press, Princeton, NJ, 1989.CrossRefGoogle Scholar
[FuSh99]Furman, A. and Shalom, Y.. Sharp ergodic theorems for group actions and strong ergodicity. Ergod. Th. & Dynam. Sys. 19 (1999), 1037–1061.CrossRefGoogle Scholar
[Guiv05]Guivarc’h, Y.. Limit theorems for random walks and products of random matrices. Probability Measures on Groups: Recent Directions and Trends. Tata Institute of Fundamental Research, Mumbai, 2006, pp. 255–330.Google Scholar
[Heu09]Heu, J.-R.. Dynamical properties of groups of automorphisms on Heisenberg nilmanifolds. Geom. Dedicata 145 (2010), 89–101.CrossRefGoogle Scholar
[Howe82]Howe, R.. On a notion of rank for unitary representations of the classical groups. Harmonic Analysis and Group Representations. Liguori, Haples, 1982, pp. 223–331.Google Scholar
[HoMo79]Howe, R. and Moore, C. C.. Asymptotic properties of unitary representations. J. Funct. Anal. 32 (1979), 72–96.Google Scholar
[HoTa92]Howe, R. and Tan, E. C.. Non-Abelian Harmonic Analysis. Springer, Berlin, 1992.CrossRefGoogle Scholar
[JuRo79]del Junco, A. and Rosenblatt, J.. Counterexamples in ergodic theory and number theory. Math. Ann. 245 (1979), 185–197.CrossRefGoogle Scholar
[Lubo94]Lubotzky, A.. Discrete Groups, Expanding Graphs and Invariant Measures. Birkhäuser, Basel, 1994.Google Scholar
[Moor65]Moore, C. C.. Decomposition of unitary representations defined by discrete subgroups of nilpotent Lie groups. Ann. Math. 82 (1965), 146–182.Google Scholar
[Nevo98]Nevo, A.. Spectral transfer and pointwise ergodic theorems for semisimple Kazhdan groups. Math. Res. Lett. 5 (1998), 305–325.CrossRefGoogle Scholar
[Parr69]Parry, W.. Ergodic properties of affine transformations and flows on nilmanifolds. Amer. J. Math. 9 (1969), 757–771.Google Scholar
[Parr70]Parry, W.. Dynamical systems on nilmanifolds. Bull. London Math. Soc. 2 (1970), 37–40.CrossRefGoogle Scholar
[Sarn90]Sarnak, P.. Some Applications of Modular Forms. Cambridge University Press, Cambridge, 1990.CrossRefGoogle Scholar
[Schmi80]Schmidt, K.. Asymptotically invariant sequences and an action of SL(2,Z) on the 2-sphere. Israel J. Math. 37 (1980), 193–208.Google Scholar
[Shal62]Shale, D.. Linear symmetries of free boson fields. Trans. Amer. Math. Soc. 103 (1962), 149–167.CrossRefGoogle Scholar
[Toli78]Tolimieri, R.. Heisenberg manifolds and theta functions. Trans. Amer. Math. Soc. 239 (1978), 293–319.CrossRefGoogle Scholar
[Weil64]Weil, A.. Sur certains groupes d’opérateurs unitaires. Acta Math. 111 (1964), 143–211.Google Scholar