Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-20T02:05:09.965Z Has data issue: false hasContentIssue false
  • English
  • Français

Physical measures of discretizations of generic diffeomorphisms

Published online by Cambridge University Press:  19 September 2016

PIERRE-ANTOINE GUIHÉNEUF
PIERRE-ANTOINE GUIHÉNEUF*
Affiliation:
Université Paris-Sud, Universidade Federal Fluminense, Niterói, Brazil email pierre-antoine.guiheneuf@math.u-psud.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

What is the ergodic behaviour of numerically computed segments of orbits of a diffeomorphism? In this paper, we try to answer this question for a generic conservative 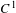$C^{1}$-diffeomorphism and segments of orbits of Baire-generic points. The numerical truncation is modelled by a spatial discretization. Our main result states that the uniform measures on the computed segments of orbits, starting from a generic point, accumulate on the whole set of measures that are invariant under the diffeomorphism. In particular, unlike what could be expected naively, such numerical experiments do not see the physical measures (or, more precisely, cannot distinguish physical measures from the other invariant measures).

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 4 , June 2018 , pp. 1422 - 1458
Copyright
© Cambridge University Press, 2016 

References

Abdenur, F., Bonatti, C. and Crovisier, S.. Nonuniform hyperbolicity for C 1 -generic diffeomorphisms. Israel J. Math. 183 (2011), 1–60.CrossRefGoogle Scholar
Avila, A., Crovisier, S. and Wilkinson, A.. Diffeomorphisms with positive metric entropy. Preprint, 2014, arXiv:1408.4252 [math.DS].Google Scholar
Arnaud, M.-C.. Le ‘closing lemma’ en topologie C 1 . Mém. Soc. Math. Fr. (N.S.) 74 (1998), pp. vi+120.Google Scholar
Anosov, D. V. and Sinaĭ, J. G.. Certain smooth ergodic systems. Uspekhi Mat. Nauk 22(5(137)) (1967), 107–172.Google Scholar
Avila, A.. On the regularization of conservative maps. Acta Math. 205(1) (2010), 5–18.CrossRefGoogle Scholar
Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158(1) (2004), 33–104.CrossRefGoogle Scholar
Boyarsky, A.. Computer orbits. Comput. Math. Appl. Ser. A 12(10) (1986), 1057–1064.Google Scholar
Franks, J.. Necessary conditions for stability of diffeomorphisms. Trans. Amer. Math. Soc. 158 (1971), 301–308.CrossRefGoogle Scholar
Góra, P. and Boyarsky, A.. Why computers like Lebesgue measure. Comput. Math. Appl. 16(4) (1988), 321–329.CrossRefGoogle Scholar
Guihéneuf, P.-A.. Degree of recurrence of generic diffeomorphisms. Preprint, 2015, arXiv:1510.00723.Google Scholar
Guihéneuf, P.-A.. Discrétisations spatiales de systèmes dynamiques génériques. PhD Thesis, Université Paris-Sud, 2015.Google Scholar
Guihéneuf, P.-A.. Dynamical properties of spatial discretizations of a generic homeomorphism. Ergod. Th. & Dynam. Sys. 35(5) (2015), 1474–1523.CrossRefGoogle Scholar
Guihéneuf, P.-A.. Model sets, almost periodic patterns, uniform density and linear maps. Preprint, 2015, arXiv:1512.00650.Google Scholar
Guihéneuf, P.-A.. Discretizations of isometries. Discrete Geometry for Computer Imagery: Proc. 19th IAPR Int. Conf., DGCI 2016 (Nantes, France, 18–20 April 2016). Eds. Normand, N., Guédon, J. and Autrusseau, F.. Springer International, Switzerland, 2016, pp. 71–92.CrossRefGoogle Scholar
Keller, G.. Stochastic stability in some chaotic dynamical systems. Monatsh. Math. 94(4) (1982), 313–333.CrossRefGoogle Scholar
Kifer, Y.. Progress in Probability and Statistics, 10. Birkhäuser, Boston, MA, 1986.Google Scholar
Kifer, Y.. General random perturbations of hyperbolic and expanding transformations. J. Anal. Math. 47 (1986), 111–150.CrossRefGoogle Scholar
Mañé, R.. An ergodic closing lemma. Ann. of Math. (2) 116(3) (1982), 503–540.CrossRefGoogle Scholar
Meyer, Y.. Quasicrystals, almost periodic patterns, mean-periodic functions and irregular sampling. Afr. Diaspora J. Math. 13(1) (2012), 1–45.Google Scholar
Moody, R.. Model sets: a survey. From Quasicrystals to More Complex Systems (Centre de Physique des Houches, 13) . Springer, Berlin, 2000, pp. 145–166.CrossRefGoogle Scholar
Moser, J.. On the volume elements on a manifold. Trans. Amer. Math. Soc. 120 (1965), 286–294.CrossRefGoogle Scholar
Viana, M.. Stochastic Dynamics of Deterministic Systems (Brazilian Mathematics Colloquium) . IMPA, Rio de Janeiro, Brazil, 1997.Google Scholar
Young, L.-S.. What are SRB measures, and which dynamical systems have them? J. Stat. Phys. 108(5–6) (2002), 733–754, dedicated to David Ruelle and Yasha Sinai on the occasion of their 65th birthdays.CrossRefGoogle Scholar
Young, L.-S.. Stochastic stability of hyperbolic attractors. Ergod. Th. & Dynam. Sys. 6(2) (1986), 311–319.CrossRefGoogle Scholar