Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-26T11:30:05.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic point free homeomorphisms and irrational rotation factors

Part of: Low-dimensional dynamical systems

Published online by Cambridge University Press:  03 November 2020

ALEJANDRO KOCSARD
ALEJANDRO KOCSARD*
Affiliation:
IME – Universidade Federal Fluminense, Rua Prof. Marcos Waldemar de Freitas Reis, S/N Bloco H, 4∘ andar. 24.210-201, Gragoatá, Niterói, RJ, Brasil (e-mail: akocsard@id.uff.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide a complete characterization of periodic point free homeomorphisms 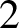of the $2$ -torus admitting irrational circle rotations as topological factors. Given a homeomorphism of the 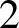$2$ -torus without periodic points and exhibiting uniformly bounded rotational deviations with respect to a rational direction, we show that annularity and the geometry of its non-wandering set are the only possible obstructions for the existence of an irrational circle rotation as topological factor. Through a very precise study of the dynamics of the induced $\rho $ -centralized skew-product, we extend and generalize considerably previous results of Jäger.

Keywords

low-dimensional dynamicstopological dynamicsrotation theorytopological factors

MSC classification

Primary: 37E45: Rotation numbers and vectors 37E10: Maps of the circle
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 10 , October 2021 , pp. 2946 - 2982
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Addas-Zanata, S.. On properties of the vertical rotation interval for twist mappings. Ergod. Th. & Dynam. Sys. 25(3) (2005), 641–660.CrossRefGoogle Scholar
Doeff, E. and Misiurewicz, M.. Shear rotation numbers. Nonlinearity 10(6) (1997), 1755–1762.10.1088/0951-7715/10/6/017CrossRefGoogle Scholar
Doeff, E.. Rotation measures for homeomorphisms of the torus homotopic to a Dehn twist. Ergod. Th. & Dynam. Sys. 17 (3) (1997), 575–591.CrossRefGoogle Scholar
Edeko, N.. On equicontinuous factors of flows on locally path-connected compact spaces. Preprint, 2019, arXiv:1904.12203.CrossRefGoogle Scholar
Fathi, A.. An orbit closing proof of Brouwer’s lemma on translation arcs. Enseign. Math. (2) 33 (3–4) (1987), 315–322.Google Scholar
Franks, J. and Misiurewicz, M.. Rotation sets of toral flows. Proc. Amer. Math. Soc. 109(1) (1990), 243–249.CrossRefGoogle Scholar
Gottschalk, W. and Hedlund, G.. Topological Dynamics. American Mathematical Society, Providence, RI, 1955.CrossRefGoogle Scholar
Hauser, T. and Jäger, T.. Monotonicity of maximal equicontinuous factors and an application to toral flows. Proc. Amer. Math. Soc. 147(10) (2019), 4539–4554.CrossRefGoogle Scholar
Jäger, T.. Linearization of conservative toral homeomorphisms. Invent. Math. 176(3) (2009), 601–616.CrossRefGoogle Scholar
Jäger, T. and Passeggi, A.. On torus homeomorphisms semiconjugate to irrational rotations. Ergod. Th. & Dynam. Sys. 35(7) (2015), 2114–2137.CrossRefGoogle Scholar
Jäger, T. and Tal, F.. Irrational rotation factors for conservative torus homeomorphisms. Ergod. Th. & Dynam. Sys. 37(5) (2017), 1537–1546.10.1017/etds.2015.112CrossRefGoogle Scholar
Kocsard, A. and Koropecki, A.. A mixing-like property and inexistence of invariant foliations for minimal diffeomorphisms of the 2-torus. Proc. Amer. Math. Soc. 137(10) (2009), 3379–3386.CrossRefGoogle Scholar
Kocsard, A.. On the dynamics of minimal homeomorphisms of ${T}^2$ which are not pseudo-rotations. Preprint, 2016, arXiv:1611.03784, Ann. Sci. Ec. Norm. Supér., to appear.Google Scholar
Kocsard, A. and Pereira-Rodrigues, F.. Rotational deviations and invariant pseudo-foliations for periodic point free torus homeomorphisms. Math. Z. 290(3–4) (2018), 1223–1247.CrossRefGoogle Scholar
Koropecki, A., Passeggi, A. and Sambarino, M.. The Franks–Misiurewicz conjecture for extensions of irrational rotations. Preprint, 2016, arXiv:1611.05498. Ann. Sci. Ec. Norm. Supér., to appear.Google Scholar
Koropecki, A. and Tal, F.. Strictly toral dynamics. Invent. Math. 196(2) (2014), 339–381.CrossRefGoogle Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets for maps of tori. J. Lond. Math. Soc. 2(3) (1989), 490–506.CrossRefGoogle Scholar
Poincaré, H.. Mémoire sur les courbes définies par les équations différentielles I–VI, oeuvre I . Gauthier-Villar, Paris, 1880, pp. 375–422.Google Scholar
Passeggi, A. and Sambarino, M.. Deviations in the Franks–Misiurewicz conjecture. Ergod. Th. & Dynam. Sys. 40(9) (2020), 2533–2540.10.1017/etds.2019.8CrossRefGoogle Scholar
Tao, T.. Poincaré’s Legacies: Pages from Year Two of a Mathematical Blog. American Mathematical Society, Providence, RI, 2009.Google Scholar
Wang, J. and Zhang, Z.. The rigidity of pseudo-rotations on the two-torus and a question of Norton-Sullivan. Geom. Funct. Anal. 28(5) (2018), 1487–1516.CrossRefGoogle Scholar