Hostname: page-component-5c6d5d7d68-txr5j Total loading time: 0 Render date: 2024-08-07T07:10:03.819Z Has data issue: false hasContentIssue false
  • English
  • Français

On the ergodicity of hyperbolic Sinaĭ–Ruelle–Bowen measures: the constant unstable dimension case

Published online by Cambridge University Press:  11 February 2015

MICHIHIRO HIRAYAMA  and
NAOYA SUMI
MICHIHIRO HIRAYAMA
Affiliation:
Faculty of Engineering, Kyushu Institute of Technology, Tobata, Fukuoka 804-8550, Japan email hirayama@math.tsukuba.ac.jp
NAOYA SUMI
Affiliation:
Department of Mathematics, Kumamoto University, Kurokami, Kumamoto 860-8555, Japan email sumi@sci.kumamoto-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider diffeomorphisms preserving hyperbolic Sinaĭ–Ruelle–Bowen (SRB) probability measures 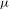${\it\mu}$ having intersections for almost every pair of the stable and unstable manifolds. In this context, when the dimension of the unstable manifold is constant almost everywhere, we show the ergodicity of 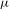${\it\mu}$. As an application we obtain another proof of the ergodicity of a hyperbolic SRB measure for transitive surface diffeomorphisms, which is shown by Rodriguez Hertz, Rodriguez Hertz, Tahzibi and Ures [Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Comm. Math. Phys.306(1) (2011), 35–49].

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 5 , August 2016 , pp. 1494 - 1515
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, J., Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140 (2000), 351–398.Google Scholar
Anosov, D. V.. Geodesic flows on closed Riemann manifolds with negative curvature. Tr. Mat. Inst. Steklova 90 (1967).Google Scholar
Anosov, D. V. and Sinaĭ, Ya. G.. Certain smooth ergodic systems. Uspekhi Mat. Nauk 22(5) (1967), 107–172.Google Scholar
Barreira, L. and Pesin, Ya. B.. Nonuniform Hyperbolicity: Dynamics of Systems with Nonzero Lyapunov Exponents (Encyclopedia of Mathematics and its Applications, 115) . Cambridge University Press, Cambridge, 2007.Google Scholar
Bonatti, C., Díaz, L. and Pujals, E.. A C 1 -generic dichotomy for diffeomorphisms: weak form of hyperbolicity or infinitely many sinks or sources. Ann. of Math. (2) 158 (2003), 355–418.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.Google Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29 (1975), 181–202.Google Scholar
Burns, K., Dolgopyat, D. and Pesin, Ya. B.. Partial hyperbolicity, Lyapunov exponents and Stable ergodicity. J. Stat. Phys. 108 (2002), 927–942.CrossRefGoogle Scholar
Burns, K., Dolgopyat, D., Pesin, Ya. B. and Pollicott, M.. Stable ergodicity for partially hyperbolic attractors with negative central exponents. J. Mod. Dyn. 2 (2008), 63–81.Google Scholar
Burns, K. and Wilkinson, A.. On the ergodicity of partially hyperbolic diffeomorphisms. Ann. of Math. (2) 171 (2010), 451–489.Google Scholar
Buzzi, J., Fisher, T., Sambarino, M. and Vásquez, C.. Maximal entropy measures for certain partially hyperbolic, derived from Anosov systems. Ergod. Th. & Dynam. Sys. 32 (2011), 63–79.CrossRefGoogle Scholar
Dolgopyat, D. and Wilkinson, A.. Stable accessibility is C 1 dense. Astérisque 287 (2003), 33–60.Google Scholar
Hasselblatt, B. and Pesin, Ya. B.. Partially Hyperbolic Dynamical Systems (Handbook of Dynamical Systems, 1B) . Eds. Hasselblatt, B. and Katok, A.. Elsevier, Amsterdam, 2005.Google Scholar
Hedlund, G.. On the metrical transitivity of the geodesics on closed surfaces of constant negative curvature. Ann. of Math. (2) 35 (1934), 787–808.Google Scholar
Hirayama, M. and Sumi, N.. Hyperbolic measures with transverse intersections of stable and unstable manifolds. Discrete Contin. Dyn. Syst. 33(4) (2013), 1451–1476.Google Scholar
Hopf, E.. Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krümmung. Ber. Verh. Sächs. Akad. Wiss. Leipzig 91 (1939), 261–304.Google Scholar
Katok, A. B.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Inst. Hautes Ètudes Sci. Publ. Math. 51 (1980), 137–173.Google Scholar
Ledrappier, F.. Propriétés ergodiques des mesures de Sinaï. Inst. Hautes Ètudes Sci. Publ. Math. 59 (1984), 163–188.Google Scholar
Ledrappier, F. and Strelcyn, J. M.. A proof of estimation from below in Pesin’s entropy formula. Ergod. Th. & Dynam. Sys. 2 (1982), 203–219.Google Scholar
Pesin, Ya. B.. Families of invariant manifolds corresponding to nonzero characteristic exponents. Izv. Ross. Akad. Nauk Ser. Mat. 40(6) (1976), 1332–1379.Google Scholar
Pugh, C. and Shub, M.. Stable ergodicity and partial hyperbolicity. International Conference on Dynamical Systems (Montevideo, 1995) (Pitman Research Notes in Mathematics Series, 362) . Longman, Harlow, 1996, pp. 182–187.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M., Tahzibi, A. and Ures, R.. New criteria for ergodicity and nonuniform hyperbolicity. Duke Math. J. 160(3) (2011), 599–629.CrossRefGoogle Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M., Tahzibi, A. and Ures, R.. Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Comm. Math. Phys. 306(1) (2011), 35–49.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. and Ures, R.. A survey of partially hyperbolic dynamics. Fields Inst. Commun. 51 (2007), 35–87.Google Scholar
Rokhlin, V. A.. Lectures on the theory of entropy of transformation with invariant measure. Russian Math. Surveys 22(5) (1967), 1–52.Google Scholar
Ruelle, D.. A measure associated with Axiom A attractors. Amer. J. Math. 98 (1976), 619–654.Google Scholar
Sinaĭ, Ya. G.. Gibbs measure in ergodic theory. Uspekhi Mat. Nauk 27(4) (1972), 21–64.Google Scholar
Tahzibi, A.. Stably ergodic diffeomorphisms which are not partially hyperbolic. Israel J. Math. 142 (2004), 315–344.CrossRefGoogle Scholar