Hostname: page-component-7479d7b7d-68ccn Total loading time: 0 Render date: 2024-07-11T12:15:54.081Z Has data issue: false hasContentIssue false
  • English
  • Français

On the ergodicity of hyperbolic Sinaĭ–Ruelle–Bowen measures II: the low-dimensional case

Published online by Cambridge University Press:  02 May 2017

MICHIHIRO HIRAYAMA  and
NAOYA SUMI
MICHIHIRO HIRAYAMA
Affiliation:
Division of Mathematics, University of Tsukuba, Tennodai, Ibaraki 305-8571, Japan email hirayama@math.tsukuba.ac.jp
NAOYA SUMI
Affiliation:
Department of Mathematics, Kumamoto University, Kurokami, Kumamoto 860-8555, Japan email sumi@sci.kumamoto-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider diffeomorphisms on a closed manifold 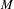$M$ preserving a hyperbolic Sinaĭ–Ruelle–Bowen probability measure $\unicode[STIX]{x1D707}$ having intersections for almost every pair of stable and unstable manifolds. In this context, we show the ergodicity of $\unicode[STIX]{x1D707}$ when the dimension of 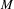$M$ is at most three. If $\unicode[STIX]{x1D707}$ is smooth, then it is ergodic when the dimension of 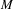$M$ is at most four. As a byproduct of our arguments, we obtain sufficient (topological) conditions which guarantee that there exists at most one hyperbolic ergodic Sinaĭ–Ruelle–Bowen probability measure. Even in higher dimensional cases, we show that every transitive topological Anosov diffeomorphism admits at most one hyperbolic Sinaĭ–Ruelle–Bowen probability measure.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 8 , December 2018 , pp. 3042 - 3061
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, J., Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140(2) (2000), 351–398.Google Scholar
Anosov, D. V.. Geodesic flows on closed Riemann manifolds with negative curvature. Tr. Mat. Inst. Steklova 90 (1967), 3–210; Engl. Transl. Proc. Steklov. Inst. Math. 90 (1967), 1–235.Google Scholar
Anosov, D. V. and Sinaĭ, Ja. G.. Certain smooth ergodic systems. Uspekhi Mat. Nauk 22(5) (1967), 107–172; Engl. Transl. Russian Math. Surveys 22(5) (1967), 103–167.Google Scholar
Barreira, L. and Pesin, Ya. B.. Nonuniform Hyperbolicity: Dynamics of Systems with Nonzero Lyapunov Exponents (Encyclopedia of Mathematics and its Applications, 115) . Cambridge University Press, Cambridge, 2007.Google Scholar
Benedicks, M. and Young, L.-S.. Sinai–Bowen–Ruelle measures for certain Hénon map. Invent. Math. 112(3) (1993), 541–576.Google Scholar
Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics Beyond Uniform hyperbolicity: A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102) . Mathematical Physics, III. Springer, Berlin, 2005.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.Google Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29 (1975), 181–202.Google Scholar
Brin, M. I. and Pesin, Ja. B.. Partially hyperbolic dynamical systems. Izv. Akad. Nauk SSSR Ser. Mat. 38(1) (1974), 170–212; Engl. Transl. Math. USSR-Isv. 8(1) (1974), 177–218.Google Scholar
Burns, K. and Wilkinson, A.. On the ergodicity of partially hyperbolic diffeomorphisms. Ann. of Math. (2) 171 (2010), 451–489.Google Scholar
Enrich, H.. A heteroclinic bifurcation of Anosov diffeomorphisms. Ergod. Th. & Dynam. Sys. 18 (1998), 567–608.Google Scholar
Hasselblatt, B. and Pesin, Ya. B.. Partially hyperbolic dynamical systems. Handbook of Dynamical Systems, Vol. 1B. Eds. Hasselblatt, B. and Katok, A.. Elsevier, Amsterdam, 2006, pp. 1–55.Google Scholar
Hirayama, M. and Sumi, N.. On the ergodicity of hyperbolic Sinaĭ–Ruelle–Bowen measures: the constant unstable dimension case. Ergod. Th. & Dynam. Sys. 36 (2016), 1494–1515.Google Scholar
Hirsh, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583) . Springer, Berlin, 1977.Google Scholar
Hopf, E.. Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krümmung. Ber. Verh. Sächs. Akad. Wiss. Leipzig 91 (1939), 261–304.Google Scholar
Hu, H. and Young, L.-S.. Nonexistence of SBR measures for some diffeomorphisms that are ‘almost Anosov’. Ergod. Th. & Dynam. Sys. 15 (1995), 67–76.Google Scholar
Kan, I.. Open sets of diffeomorphisms having two attractors, each with an everywhere dense basin. Bull. Amer. Math. Soc. 31 (1994), 68–74.Google Scholar
Katok, A. B.. Bernoulli diffeomorphisms on surfaces. Ann. of Math. (2) 110 (1979), 529–547.Google Scholar
Katok, A. B.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Ètudes Sci. 51 (1980), 137–173.Google Scholar
Ledrappier, F.. Propriétés ergodiques des mesures de Sinaï. Publ. Math. Inst. Hautes Ètudes Sci. 59 (1984), 163–188.Google Scholar
Ledrappier, F. and Strelcyn, J. M.. A proof of estimation from below in Pesin’s entropy formula. Ergod. Th. & Dynam. Sys. 2 (1982), 203–219.Google Scholar
Pesin, Ja. B.. Families of invariant manifolds corresponding to nonzero characteristic exponents. Izv. Akad. Nauk SSSR Ser. Mat. 40(6) (1976), 1332–1379; Engl. Transl. Math. USSR-Isv. 40(6) (1976), 1261–1305.Google Scholar
Pesin, Ya. B. and Sinaĭ, Ya. G.. Gibbs measures for partially hyperbolic attractors. Ergod. Th. & Dynam. Sys. 2 (1982), 417–438.Google Scholar
Pugh, C. and Shub, M.. Stable ergodicity and partially hyperbolicity. International Conference on Dynamical Systems (Montevideo, 1995) (Pitman Res. Notes. Math. Ser., 362) . Longman, Harlow, 1996, pp. 182–187.Google Scholar
Robinson, C.. Dynamical Systems: Stability, Symbolic Dynamics, and Chaos (Studies in Advanced Mathematics) . CRC Press, Boca Raton, FL, 1995.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A., Tahzibi, A. and Ures, R.. Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Commun. Math. Phys. 306(1) (2011), 35–49.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A. and Ures, R.. A survey of partially hyperbolic dynamics. Fields Inst. Commun. 51 (2007), 35–87.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A. and Ures, R.. Accessibility and stable ergodicity for partially hyperbolic diffeomorphisms with 1D-center bundle. Invent. Math. 172 (2008), 353–381.Google Scholar
Rokhlin, V. A.. Lectures on the theory of entropy of transformation with invariant measure. Uspekhi Mat. Nauk 22(5) (1967), 3–56; Engl. Transl. Russian Math. Surveys 22(5) (1967), 1–52.Google Scholar
Sinaĭ, Ja. G.. Gibbs measure in ergodic theory. Uspekhi Mat. Nauk 27(4) (1972), 21–64; Engl. Transl. Russian Math. Surveys 27(4) (1972), 21–69.Google Scholar