Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-16T09:31:30.320Z Has data issue: false hasContentIssue false
  • English
  • Français

On the entropy of actions of nilpotent Lie groups and their lattice subgroups

Published online by Cambridge University Press:  21 October 2011

A. H. DOOLEY  and
V. YA. GOLODETS
A. H. DOOLEY
Affiliation:
School of Mathematics, University of N.S.W. Sydney, NSW 2052, Australia (email: a.dooley@unsw.edu.au, v.golodets@unsw.edu.au)
V. YA. GOLODETS
Affiliation:
School of Mathematics, University of N.S.W. Sydney, NSW 2052, Australia (email: a.dooley@unsw.edu.au, v.golodets@unsw.edu.au)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a natural class 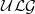of connected, simply connected nilpotent Lie groups which contains ℝn, the group 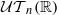of all triangular unipotent matrices over ℝ and many of its subgroups, and is closed under direct products. If 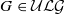, then 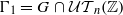is a lattice subgroup of G. We prove that if 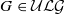and Γ is a lattice subgroup of G, then a free ergodic measure-preserving action T of G on a probability space (X,ℬ,μ) has completely positive entropy (CPE) if and only if the restriction TΓ of T to Γ has CPE. We can deduce from this the following version of a well-known conjecture in this case: the action T has CPE if and only if T is uniformly mixing. Moreover, such T has a Lebesgue spectrum with infinite multiplicity. We further consider an ergodic free action T with positive entropy and suppose TΓ is ergodic for any lattice subgroup Γ of G. This holds, in particular, if the spectrum of T does not contain a discrete component. Then we show the Pinsker algebra Π(T) of T exists and coincides with the Pinsker algebras Π(TΓ) of TΓ for any lattice subgroup Γ of G. In this case, T always has Lebesgue spectrum with infinite multiplicity on the space ℒ20(X,μ)⊖ℒ20(Π(T)) , where ℒ20(Π(T)) contains all Π(T) -measurable functions from ℒ20(X,μ) . To prove these results, we use the following formula: h(T)=∣G(Γ)∣−1hK (TΓ) , where h(T) is the Ornstein–Weiss entropy of T, hK (TΓ) is a Kolmogorov–Sinai entropy of TΓ, and the number ∣G(TΓ)∣ is the Haar measure of the compact subset G(Γ) of G. In particular, h(T)=hK (TΓ1) , and hK (TΓ1)=∣G(Γ)∣−1hK (TΓ) . The last relation is an analogue of the Abramov formula for flows.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 32 , Issue 2: Daniel J. Rudolph – in Memoriam , April 2012 , pp. 535 - 573
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abramov, L. M.. On the entropy of a flow. Trans. Amer. Math. Soc. 49(2) (1965), 167–170.Google Scholar
[2]Avni, N.. Entropy theory of cross sections. GAFA Geom. Funct. Anal. 19 (2010), 1515–1538.CrossRefGoogle Scholar
[3]Blanchard, F.. Partitions extremals de flots d’entropie infini. Z. Wahrsch. Verw. Gebiete 36 (1976), 129–136.CrossRefGoogle Scholar
[4]Connes, A., Feldman, J. and Weiss, B.. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys. 1 (1981), 431–450.CrossRefGoogle Scholar
[5]Conze, J. P.. Entropie d’un groupe abelien de transformations. Z. Wahrsch. Verw. Gebiete 25 (1972), 11–30.CrossRefGoogle Scholar
[6]Cornfeld, I. P., Fomin, S. V. and Sinai, Ya. G.. Ergodic Theory. Springer, 1982.CrossRefGoogle Scholar
[7]Danilenko, A. I.. Entropy theory from the orbital point of view. Monatsh. Math. 134 (2001), 121–141.CrossRefGoogle Scholar
[8]Danilenko, A. I. and Park, K. K.. Generators and Bernoulli factors for amenable actions and cocycles on their orbits. Ergod. Th. & Dynam. Sys. 22 (2002), 1715–1745.CrossRefGoogle Scholar
[9]Dixmier, J.. Les Algèbres d’Operateurs dans l’Espace Hilbertien, 2nd edn. Gauthier-Villars, Paris, 1969.Google Scholar
[10]Dixmier, J.. Les C *-Algebres et Leurs Représentations. Gauthier-Villars, Paris, 1969.Google Scholar
[11]Dooley, A. H. and Golodets, V. Ya.. The spectrum of completely positive entropy actions of countable amenable groups. J. Funct. Anal. 196 (2002), 1–18.CrossRefGoogle Scholar
[12]Dooley, A. H., Golodets, V. Ya., Rudolph, D. J. and Sinel’shchikov, S. D.. Non-Bernoulli systems with completely positive entropy. Ergod. Th. & Dynam. Sys. 28 (2008), 87–124.CrossRefGoogle Scholar
[13]Feldman, J.. r-entropy, equipartition and Ornstein’s isomorphism theorem in ℝn. Israel J. Math. 36 (1980), 321–345.CrossRefGoogle Scholar
[14]Feldman, J., Hahn, P. and Moore, C. C.. Orbit structure and countable sections for actions of continuous groups. Adv. Math. 28 (1978), 186–230.CrossRefGoogle Scholar
[15]Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
[16]Glasner, E., Thouvenot, J.-P. and Weiss, B.. Entropy theory without past. Ergod. Th. & Dynam. Sys. 20 (2000), 1355–1370.CrossRefGoogle Scholar
[17]Golodets, V. and Sinel’shchikov, S.. On the entropy theory of finitely generated nilpotent group actions. Ergod. Th. & Dynam. Sys. 22 (2002), 1747–1771.CrossRefGoogle Scholar
[18]Golodets, V. and Sinel’shchikov, S.. Complete positivity of entropy and non-Bernoullicity for transformation groups. Colloq. Math. 84/85 (2000), 421–429.CrossRefGoogle Scholar
[19]Gurevich, B. M.. Some existence conditions for K-decompositions for special flows. Trans. Moscow Math. Soc. 17 (1967), 99–128.Google Scholar
[20]Gurevich, B. M.. Perfect partitions for ergodic flows. Funktsional. Anal. i Prilozhen. 11 (1977), 20–23 (in Russian).Google Scholar
[21]Kamiński, B.. The theory of invariant partitions for ℤd-actions. Bull. Acad. Polon. Sci., Ser. Sci. Math. 29 (1981), 349–362.Google Scholar
[22]Katok, A.. Fifty years of entropy in dynamics 1958–2007. J. Mod. Dyn. 1 (2007), 545–596.CrossRefGoogle Scholar
[23]Katznelson, I. and Weiss, B.. Commuting measure preserving transformations. Israel J. Math. 12 (1972), 161–173.CrossRefGoogle Scholar
[24]Kechris, A. S. and Miller, B. D.. Topics in Orbit Equivalence Theory (Lecture Notes in Mathematics, 1852). Springer, New York, 2004.CrossRefGoogle Scholar
[25]Kieffer, J. C.. A generalized Shannon–McMillan theorem for the actions of amenable groups on a probability space. Ann. Probab. 3 (1975), 1031–1037.CrossRefGoogle Scholar
[26]Kolmogorov, A. N.. A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces. Dokl. Acad. Nauk SSSR 119 (1958), 861–864 (in Russian).Google Scholar
[27]Mackey, G.. Ergodic theory and virtual groups. Math. Ann. 166 (1966), 187–207.CrossRefGoogle Scholar
[28]Mackey, G. W.. Borel structure in groups and their duals. Trans. Amer. Math. Soc. 85 (1957), 134–169.CrossRefGoogle Scholar
[29]Ornstein, D.. Ergodic Theory, Randomness and Dynamical Systems. Yale University Press, New Haven, 1974.Google Scholar
[30]Ornstein, D. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.CrossRefGoogle Scholar
[31]Pinsker, M. S.. Dynamical systems with completely positive and zero entropy. Dokl. Acad. Nauk SSSR 133 (1960), 1025–1026 (in Russian).Google Scholar
[32]Pitzkel, B. S.. On information futures of amenable groups. Dokl. Acad. Sci. USSR 223 (1975), 1067–1070 (in Russian).Google Scholar
[33]Raghunathan, M. S.. Discrete Subgroups of Lie Groups. Springer, Berlin–Heidelberg–Ney York, 1972.CrossRefGoogle Scholar
[34]Reed, M. and Simon, B.. Methods of Modern Mathematical Physics I: Functional Analysis, Revised and Enlarged Edition. Academic Press, Inc., Boston–San Diego–New York–Sydney–Tokyo–Toronto, 1980.Google Scholar
[35]Riesz, F. and Sz-Nagy, B.. Leçons d’Analyse Fonctionnelle. Academiai Kiado, Budapest, 1972.Google Scholar
[36]Rokhlin, V. A.. Lectures on the entropy theory of transformations with invariant measure. Uspekhi Mat. Nauk. 22 (1967), 4–54 (in Russian).Google Scholar
[37]Rokhlin, V. A. and Sinai, Ya. G.. Construction and properties of invariant measurable partitions. Dokl. Akad. Nauk. SSSR 141 (1961), 1038–1041 (in Russian).Google Scholar
[38]Rosenthal, A.. Finite uniform generators for ergodic, finite entropy free actions of amenable groups. Probab. Theory Related Fields 77 (1988), 147–166.CrossRefGoogle Scholar
[39]Rudolph, D. J.. Fundamentals of Measurable Dynamics. Oxford University Press, Oxford, 1990.Google Scholar
[40]Rudolph, D. J.. A two-valued stepcoding for ergodic flows. Proceedings Mathematical Physics. Rennes, Sept, 1975, pp. 14–21.Google Scholar
[41]Rudolph, D. J. and Weiss, B.. Entropy and mixing for amenable group actions. Ann. of Math. (2) 151 (2000), 1119–1150.CrossRefGoogle Scholar
[42]Safonov, A. V.. Information pasts in groups. Izv. Acad. Sci. USSR 47 (1983), 421–426 (in Russian).Google Scholar
[43]Sinai, J. G.. A weak isomorphism of transfomations with invariant measure. Amer. Math. Soc. Transl. Ser. 2 57 (1966), 123–143.Google Scholar
[44]Thouvenot, J.-P.. Quelques propriétés des systèmes dynamiques qui se décomposent en un produit de deux systèms dont l’un schéma de Bernolli. Israel J. Math. 21 (1975), 177–207.CrossRefGoogle Scholar
[45]Thouvenot, J.-P.. Entropy, Isomorphism and Equivalence in Ergodic Theory (Handbook of Dynamical Systems, 1A). North-Holland, Amsterdam, 2002, pp. 205–237.Google Scholar
[46]Ward, T. and Zhang, Q.. The Abramov–Rokhlin entropy addition formula for amenable group actions. Monatsh. Math. 114 (1992), 317–329.CrossRefGoogle Scholar
[47]Weiss, B.. Actions of amenable groups. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Notes Series, 310). Eds. Bezuglyi, S. and Kolyada, S.. Cambridge University Press, Cambridge, 2003, pp. 226–262.CrossRefGoogle Scholar
[48]Weiss, B.. Monotileable amenable groups. Topology, Ergodic Theory, Real Algebraic Geometry (American Mathematical Society Translations, 202). Eds. Turaev, V. and Vershik, A.. American Mathematical Society, Providence, RI, 2001, pp. 257–262.Google Scholar