Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-26T10:53:13.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Bernoulli systems with completely positive entropy

Published online by Cambridge University Press:  01 February 2008

A. H. DOOLEY ,
V. YA. GOLODETS ,
D. J. RUDOLPH  and
S. D. SINEL’SHCHIKOV
A. H. DOOLEY
Affiliation:
School of Mathematics, University of New South Wales, Sydney 2052, Australia (email: a.dooley@unsw.edu.au, golodets@maths.unsw.edu.au)
V. YA. GOLODETS
Affiliation:
School of Mathematics, University of New South Wales, Sydney 2052, Australia (email: a.dooley@unsw.edu.au, golodets@maths.unsw.edu.au)
D. J. RUDOLPH
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, USA (email: djr@math.umd.edu)
S. D. SINEL’SHCHIKOV
Affiliation:
Institute for Low Temperature Physics & Engineering, Ukrainian National Academy of Sciences, 47 Lenin Avenue, 61103 Kharkov, Ukraine (email: sinelshchikov@ilt.kharkov.ua)
Get access Rights & Permissions [Opens in a new window]

Abstract

A new approach to actions of countable amenable groups with completely positive entropy (cpe), allowing one to answer some basic questions in this field, was recently developed. The question of the existence of cpe actions which are not Bernoulli was raised. In this paper, we prove that every countable amenable group G, which contains an element of infinite order, has non-Bernoulli cpe actions. In fact we can produce, for any 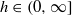, an uncountable family of cpe actions of entropy h, which are pairwise automorphically non-isomorphic. These actions are given by a construction which we call co-induction. This construction is related to, but different from the standard induced action. We study the entropic properties of co-induction, proving that if αG is co-induced from an action αΓ of a subgroup Γ, then h(αG)=h(αΓ). We also prove that if αΓ is a non-Bernoulli cpe action of Γ, then αG is also non-Bernoulli and cpe. Hence the problem of finding an uncountable family of pairwise non-isomorphic cpe actions of the same entropy is reduced to one of finding an uncountable family of non-Bernoulli cpe actions of 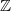, which pairwise satisfy a property we call ‘uniform somewhat disjointness’. We construct such a family using refinements of the classical cutting and stacking methods.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 1 , February 2008 , pp. 87 - 124
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Avni, N.. Spectral and mixing property of actions of amenable groups. Electron. Res. Announc. Amer. Math. Soc. 11 (2005), 57–63.CrossRefGoogle Scholar
[2]Connes, A., Feldman, J. and Weiss, B.. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys. 1 (1981), 431–450.CrossRefGoogle Scholar
[3]Cornfeld, I. P., Fomin, S. V. and Sinai, Ya. G.. Ergodic Theory. Springer, Berlin, 1982.CrossRefGoogle Scholar
[4]Danilenko, A. I.. Entropy theory from the orbital point of view. Monatsh. Math. 134 (2001), 121–141.CrossRefGoogle Scholar
[5]Danilenko, A. I.. Explicit solution of Rokhlin’s problem on homogeneous spectrum and applications. Ergod. Th. & Dynam. Sys. 26 (2006), 1467–1490.CrossRefGoogle Scholar
[6]Dooley, A. H. and Golodets, V. Ya.. The spectrum of completely positive entropy actions of countable amenable groups. J. Funct. Anal. 196 (2002), 1–18.CrossRefGoogle Scholar
[7]Feldman, J.. New K-automorphisms and a problem of Kakutani. Israel J. Math. 24 (1976), 16–38.CrossRefGoogle Scholar
[8]Fieldsteel, A.. Stability of a weak Pinsker property for flows. Ergod. Th. & Dynam. Sys. 4 (1984), 381–390.CrossRefGoogle Scholar
[9]Gaboriau, D.. Examples of groups that are measure equivalent to the free group. Ark. Mat. 1 (2005) DS/0503181.CrossRefGoogle Scholar
[10]Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs). American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
[11]Glasner, E., Thouvenot, J.-P. and Weiss, B.. Entropy theory without past. Ergod. Th. & Dynam. Sys. 20 (2000), 1355–1370.CrossRefGoogle Scholar
[12]Golodets, V. and Sinel’shchikov, S.. On the entropy theory of finitely generated nilpotent group actions. Ergod. Th. & Dynam. Sys. 22 (2002), 1747–1771.CrossRefGoogle Scholar
[13]Golodets, V. and Sinel’shchikov, S.. Complete positivity of entropy and non-Bernoullicity for transformation groups. Colloq. Math. 84/85 (2000), 421–429.CrossRefGoogle Scholar
[14]Grigorchuk, R. I.. The growth degrees of finitely generated groups and the theory of invariant means. Izv. Akad. Nauk SSSR 48 (1984), 939–985.Google Scholar
[15]Hoffman, C.. A K-counterexample machine. Trans. Amer. Math. Soc. 351 (1999), 4263–4280.CrossRefGoogle Scholar
[16]Kalikow, S.. The T,T −1-transformation is not loosely Bernoulli. Ann. of Math. 115 (1982), 393–409.CrossRefGoogle Scholar
[17]Kamiński, B.. The theory of invariant partitions for -actions. Bull. Acad. Sci., Sér. Sci. Math. 29 (1981), 349–362.Google Scholar
[18]Kamiński, B. and Liardet, P.. Spectrum of multi-dimensional dynamical systems with positive entropy. Studia Math. 108 (1994), 77–85.CrossRefGoogle Scholar
[19]Katok, A.. Change of time, monotone equivalence and standard dynamical systems. Dokl. Akad. Nauk SSR 223 (1975), 789–792.Google Scholar
[20]Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1998.Google Scholar
[21]Lindenstrauss, E. and Weiss, B.. Mean topological dimension. Israel J. Math. 115 (2000), 1–24.CrossRefGoogle Scholar
[22]Mackey, G.. Ergodic theory and virtual groups. Math. Ann. 166 (1966), 187–207.CrossRefGoogle Scholar
[23]Ollagnier, J. M.. Ergodic Theory and Statistical Mechanics (Springer Lecture Notes in Mathematics, 1115). Springer, Berlin, 1985.CrossRefGoogle Scholar
[24]Ornstein, D.. Ergodic Theory, Randomness and Dynamical Systems. Yale University Press, New Haven, 1974.Google Scholar
[25]Ornstein, D., Rudolph, D. J. and Weiss, B.. Equivalence of measure preserving transformations. Mem. Amer. Math. Soc. 37 (1982), 1–166.Google Scholar
[26]Ornstein, D. and Shields, P. C.. An uncountable family of K-automorphisms. Adv. Math. 10 (1973), 63–88.CrossRefGoogle Scholar
[27]Ornstein, D. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.CrossRefGoogle Scholar
[28]Rokhlin, V. A.. Lectures on the entropy theory of transformations with invariant measure. Uspekhi Mat. Nauk. 22 (1967), 4–54 (in Russian).Google Scholar
[29]Rokhlin, V. A. and Sinai, Ya. G.. Construction and properties of invariant measurable partitions. Dokl. Akad. Nauk. SSSR 141 (1961), 1038–1041 (in Russian).Google Scholar
[30]Rosenthal, A.. Finite uniform generators for ergodic, finite entropy, free actions of amenable groups. Probab. Theory Related Fields 77 (1988), 147–166.CrossRefGoogle Scholar
[31]Rudolph, D. J.. Fundamentals of Measurable Dynamics. Oxford University Press, Oxford, 1990.Google Scholar
[32]Rudolph, D. J.. An isomorphism theory for Bernoulli free Z skew-compact group actions. Adv. Math. 47 (1983), 241–257.CrossRefGoogle Scholar
[33]Rudolph, D. J.. An example of a measure-preserving map with a minimal self-joinings, and applications. J. Anal. Math. 35 (1979), 97–122.CrossRefGoogle Scholar
[34]Rudolph, D. J.. If a finite extension of a Bernoulli shift has no finite rotation factor it is Bernoulli. Israel J. Math. 30 (1979), 193–206.CrossRefGoogle Scholar
[35]Rudolph, D. J.. Two non-isomorphic K-automorphisms all of whose powers beyond one are isomorphic. Israel J. Math. 27 (1977), 277–298.CrossRefGoogle Scholar
[36]Rudolph, D. J.. Two non-isomorphic K-automorphisms with isomorphic squares. Israel J. Math. 23 (1976), 274–287.CrossRefGoogle Scholar
[37]Rudolph, D. J. and Weiss, B.. Entropy and mixing for amenable group actions. Ann. of Math. 151 (2000), 1119–1150.CrossRefGoogle Scholar
[38]Thouvenot, J.-P.. Quelques propriétés des systèmes dynamiques qui se décomposent en un produit de deux systèmes dont l’un est un schéma de Bernoulli. Israel J. Math. 21 (1975), 177–207.CrossRefGoogle Scholar
[39]Thouvenot, J.-P.. On stability of the weak Pinsker property. Israel J. Math. 27 (1977), 150–162.CrossRefGoogle Scholar
[40]Weiss, B.. Actions of amenable groups. Topics in Dynamics and Ergodic Theory (LMS Lecture Notes Series, 310). Cambridge University Press, Cambridge, 2003, pp. 226–262.CrossRefGoogle Scholar
[41]Weiss, B.. Monotileable amenable groups. Topology, Ergodic Theory, Real Algebraic Geometry (AMS Translations, II-202). Eds. V. Turaev and A. Vershik. American Mathematical Society, Providence, RI, pp. 257–262.CrossRefGoogle Scholar
[42]Zimmer, R. J.. Induced and amenable ergodic actions of Lie groups. Ann. Sci. École. Norm. Sup. 11 (1978), 407–428.CrossRefGoogle Scholar
[43]Zimmer, R. J.. Ergodic Theory and Semisimple Groups. Birkhäuser, Boston, 1984.CrossRefGoogle Scholar