Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T04:20:16.150Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-scale geometry of homeomorphism groups

Published online by Cambridge University Press:  03 April 2017

KATHRYN MANN  and
CHRISTIAN ROSENDAL
KATHRYN MANN
Affiliation:
Department of Mathematics, UC Berkeley, 970 Evans Hall, Berkeley, CA 94720, USA email kpmann@math.berkeley.edu
CHRISTIAN ROSENDAL
Affiliation:
Department of Mathematics, Statistics, and Computer Science (M/C 249), University of Illinois at Chicago, 851 S. Morgan Street, Chicago, IL 60607-7045, USA email rosendal.math@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 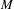$M$ be a compact manifold. We show that the identity component 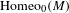$\operatorname{Homeo}_{0}(M)$ of the group of self-homeomorphisms of 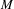$M$ has a well-defined quasi-isometry type, and study its large-scale geometry. Through examples, we relate this large-scale geometry to both the topology of 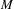$M$ and the dynamics of group actions on 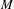$M$. This gives a rich family of examples of non-locally compact groups to which one can apply the large-scale methods developed in previous work of the second author.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 7 , October 2018 , pp. 2748 - 2779
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albiac, F. and Kalton, N.. Topics in Banach Space Theory. Springer, New York, 2006.Google Scholar
Arens, R.. Topologies for homeomorphism groups. Amer. J. Math. 68 (1946), 593–610.Google Scholar
Bing, R. H.. Partitionable sets. Bull. Amer. Math. Soc. 55(12) (1949), 1101–1110.Google Scholar
Burago, D., Burago, Y. and Ivanov, S.. A Course in Metric Geometry (Graduate Studies in Mathematics, 33) . American Mathematical Society, Providence, RI, 2001.Google Scholar
Burago, D., Ivanov, S. and Polterovich, L.. Conjugation-invariant norms on groups of geometric origin. Groups of Diffeomorphisms (Advanced Studies in Pure Mathematics, 52) . Eds. Penner, R., Kotschick, D., Tsuboi, T., Kawazumi, N., Kitano, T. and Mitsumatsu, Y.. Mathematical Society of Japan, Tokyo, 2008, pp. 221–250.Google Scholar
Calegari, D. and Freedman, M. H.. Distortion in transformation groups. Geom. Topol. 10 (2006), 267–293; with an appendix by Yves de Cornulier.Google Scholar
Edwards, R. D. and Kirby, R. C.. Deformations of spaces of imbeddings. Ann. of Math. (2) 93 (1971), 63–88.Google Scholar
Eisenbud, D., Hirsch, U. and Neumann, W.. Transverse foliations of Seifert bundles and self homeomorphisms of the circle. Comment. Math. Helv. 56 (1981), 638–660.Google Scholar
Fabian, M., Habala, P., Hájek, P., Montesinos, V. and Zizler, V.. Banach space theory. The basis for linear and nonlinear analysis. CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC. Springer, NewYork, 2011.Google Scholar
Fisher, D.. Groups acting on manifolds: around the Zimmer program. Geometry, Rigidity, and Group Actions (Chicago Lectures in Mathematics, 57) . University of Chicago Press, Chicago, 2011.Google Scholar
Fisher, D. and Silberman, L.. Groups not acting on manifolds. Int. Math. Res. Not. IMRN 11 (2008), rnn060.Google Scholar
Franks, J.. Recurrence and fixed points of surface homeomorphisms. Ergod. Th. & Dynam. Sys. 8 (1988), 99–107.Google Scholar
Franks, J. and Handel, M.. Distortion elements in group actions on surfaces. Duke Math. J. 131(3) (2006), 441–468.Google Scholar
Gersten, A. M.. Bounded cocycles and combings of groups. Internat. J. Algebra Comput. 2 (1992), 307–326.Google Scholar
Hurtado, S.. Continuity of discrete homomorphisms of diffeomorphism groups. Geom. Topol. 19 (2015), 2117–2154.Google Scholar
Kalton, N. J.. Coarse and uniform embeddings into reflexive spaces. Q. J. Math. 58 (2007), 393–414.Google Scholar
Kleiner, B. and Leeb, B.. Groups quasi-isometric to symmetric spaces. Comm. Anal. Geom. 9 (2001), 239–260.Google Scholar
Militon, E.. Éléments de distorsion de Diff0 ∞ (M). Bull. Soc. Math. France 141.1 (2013), 35–46.Google Scholar
Militon, E.. Distortion elements for surface homeomorphisms. Geom. Topol. 18 (2014), 521–614.Google Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets for maps of tori. J. Lond. Math. Soc. (2) 40 (1989), 490–506.Google Scholar
Polterovich, L.. Growth of maps, distortion in groups and symplectic geometry. Invent. Math. 150 (2002), 655–686.Google Scholar
Roe, J.. Lectures on Coarse Geometry (University Lecture Series, 31) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Rosendal, C.. A topological version of the Bergman property. Forum Math. 21(2) (2009), 299–332.Google Scholar
Rosendal, C.. Coarse geometry of topological groups. Preprint, 2014. Available at http://homepages.math.uic.edu/∼rosendal/PapersWebsite/CoarseGeometry20.pdf.Google Scholar
Struble, R. A.. Metrics in locally compact groups. Compos. Math. 28 (1974), 217–222.Google Scholar
Uspenskiĭ, V. V.. A universal topological group with a countable basis. Russ. Funktsional. Anal. i Prilozhen. 20(2) (1986), 86–87.Google Scholar