Hostname: page-component-84b7d79bbc-4hvwz Total loading time: 0 Render date: 2024-07-30T17:55:31.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Inner amenability, property Gamma, McDuff 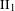$\text{II}_{1}$ factors and stable equivalence relations

Published online by Cambridge University Press:  14 March 2017

TOBE DEPREZ  and
STEFAAN VAES
TOBE DEPREZ
Affiliation:
KU Leuven, Department of Mathematics, Leuven, Belgium email tobe.deprez@kuleuven.be, stefaan.vaes@kuleuven.be
STEFAAN VAES
Affiliation:
KU Leuven, Department of Mathematics, Leuven, Belgium email tobe.deprez@kuleuven.be, stefaan.vaes@kuleuven.be
Get access Rights & Permissions [Opens in a new window]

Abstract

We say that a countable group 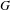$G$ is McDuff if it admits a free ergodic probability measure preserving action such that the crossed product is a McDuff 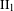$\text{II}_{1}$ factor. Similarly, 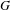$G$ is said to be stable if it admits such an action with the orbit equivalence relation being stable. The McDuff property, stability, inner amenability and property Gamma are subtly related and several implications and non-implications were obtained in Effros [Property $\unicode[STIX]{x1D6E4}$ and inner amenability. Proc. Amer. Math. Soc.47 (1975), 483–486], Jones and Schmidt [Asymptotically invariant sequences and approximate finiteness. Amer. J. Math.109 (1987), 91–114], Vaes [An inner amenable group whose von Neumann algebra does not have property Gamma. Acta Math.208 (2012), 389–394], Kida [Inner amenable groups having no stable action. Geom. Dedicata173 (2014), 185–192] and Kida [Stability in orbit equivalence for Baumslag–Solitar groups and Vaes groups. Groups Geom. Dyn.9 (2015), 203–235]. We complete the picture with the remaining implications and counterexamples.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 7 , October 2018 , pp. 2618 - 2624
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

de Cornulier, Y.. Finitely presentable, non-Hopfian groups with Kazhdan’s property (T) and infinite outer automorphism group. Proc. Amer. Math. Soc. 135 (2007), 951–959.Google Scholar
Choda, M.. Inner amenability and fullness. Proc. Amer. Math. Soc. 86 (1982), 663–666.Google Scholar
Connes, A., Feldman, J. and Weiss, B.. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys. 1 (1981), 431–450.Google Scholar
Ershov, M.. Kazhdan groups whose FC-radical is not virtually abelian. Preprint, 2010, available at http://people.virginia.edu/∼mve2x/Research/Kazhdan_infFC0706.pdf.Google Scholar
Effros, E. G.. Property 𝛤 and inner amenability. Proc. Amer. Math. Soc. 47 (1975), 483–486.Google Scholar
Jolissaint, P.. On property (T) for pairs of topological groups. Enseign. Math. 51 (2005), 31–45.Google Scholar
Jones, V. F. R. and Schmidt, K.. Asymptotically invariant sequences and approximate finiteness. Amer. J. Math. 109 (1987), 91–114.Google Scholar
Kida, Y.. Inner amenable groups having no stable action. Geom. Dedicata 173 (2014), 185–192.Google Scholar
Kida, Y.. Stability in orbit equivalence for Baumslag–Solitar groups and Vaes groups. Groups Geom. Dyn. 9 (2015), 203–235.Google Scholar
McDuff, D.. Central sequences and the hyperfinite factor. Proc. Lond. Math. Soc. (3) 21 (1970), 443–461.Google Scholar
Murray, F. J. and von Neumann, J.. Rings of operators IV. Ann. of Math. (2) 44 (1943), 716–808.Google Scholar
Popa, S. and Vaes, S.. On the fundamental group of II1 factors and equivalence relations arising from group actions. Quanta of Maths, Proc. Conf. in Honor of A. Connes’ 60th Birthday (Clay Mathematics Institute Proceedings 11) . American Mathematical Society, Providence, RI, 2011, pp. 519–541.Google Scholar
Stalder, Y.. Moyennabilité intérieure et extensions HNN. Ann. Inst. Fourier (Grenoble) 56 (2006), 309–323.Google Scholar
Vaes, S.. An inner amenable group whose von Neumann algebra does not have property Gamma. Acta Math. 208 (2012), 389–394.Google Scholar