Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-15T21:14:23.756Z Has data issue: false hasContentIssue false
  • English
  • Français

Ideal structure and pure infiniteness of ample groupoid $C^{\ast }$-algebras

Published online by Cambridge University Press:  14 June 2018

CHRISTIAN BÖNICKE  and
KANG LI
CHRISTIAN BÖNICKE
Affiliation:
Mathematisches Institut der WWU Münster, Einsteinstrasse 62, 48149 Münster, Germany email c.boenicke@wwu.de, lik@uni-muenster.de
KANG LI
Affiliation:
Mathematisches Institut der WWU Münster, Einsteinstrasse 62, 48149 Münster, Germany email c.boenicke@wwu.de, lik@uni-muenster.de
Get access Rights & Permissions [Opens in a new window]

Abstract

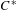In this paper, we study the ideal structure of reduced 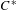$C^{\ast }$-algebras 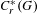$C_{r}^{\ast }(G)$ associated to étale groupoids 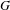$G$. In particular, we characterize when there is a one-to-one correspondence between the closed, two-sided ideals in 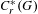$C_{r}^{\ast }(G)$ and the open invariant subsets of the unit space 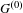$G^{(0)}$ of 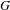$G$. As a consequence, we show that if 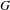$G$ is an inner exact, essentially principal, ample groupoid, then 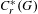$C_{r}^{\ast }(G)$ is (strongly) purely infinite if and only if every non-zero projection in 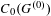$C_{0}(G^{(0)})$ is properly infinite in 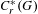$C_{r}^{\ast }(G)$. We also establish a sufficient condition on the ample groupoid 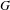$G$ that ensures pure infiniteness of 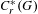$C_{r}^{\ast }(G)$ in terms of paradoxicality of compact open subsets of the unit space 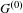$G^{(0)}$. Finally, we introduce the type semigroup for ample groupoids and also obtain a dichotomy result: let 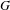$G$ be an ample groupoid with compact unit space which is minimal and topologically principal. If the type semigroup is almost unperforated, then 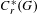$C_{r}^{\ast }(G)$ is a simple 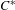$C^{\ast }$-algebra which is either stably finite or strongly purely infinite.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 1 , January 2020 , pp. 34 - 63
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C. and Renault, J.. Amenable Groupoids (Monographies de L’Enseignement Mathématique [Monographs of L’Enseignement Mathématique], 36) . L’Enseignement Mathématique, Geneva, 2000.Google Scholar
Anantharaman-Delaroche, C.. Some remarks about the weak containment property for groupoids and semigroups. Preprint, 2016, arXiv:1604.01724.Google Scholar
Ara, P. and Exel, R.. Dynamical systems associated to separated graphs, graph algebras, and paradoxical decompositions. Adv. Math. 252 (2014), 748–804.Google Scholar
Ara, P., Li, K., Lledó, F. and Wu, J.. Amenability of coarse spaces and K-algebras. Bull. Math. Sci. (2017), https://doi.org/10.1007/s13373-017-0109-6.Google Scholar
Ara, P., Li, K., Lledó, F. and Wu, J.. Amenability and uniform Roe algebras. J. Math. Anal. Appl. 459(2) (2018), 686–716.Google Scholar
Blackadar, B. and Rørdam, M.. Extending states on preordered semigroups and the existence of quasitraces on C ∗ -algebras. J. Algebra 152(1) (1992), 240–247.10.1016/0021-8693(92)90098-7Google Scholar
Blanchard, E. and Kirchberg, E.. Non-simple purely infinite C ∗ -algebras: the Hausdorff case. J. Funct. Anal. 207(2) (2004), 461–513.Google Scholar
Brown, J., Clark, L. O., Farthing, C. and Sims, A.. Simplicity of algebras associated to étale groupoids. Semigroup Forum 88(2) (2014), 433–452.Google Scholar
Brown, J., Clark, L. O. and Sierakowski, A.. Purely infinite C ∗ -algebras associated to étale groupoids. Ergod. Th. & Dynam. Sys. 35(8) (2015), 2397–2411.10.1017/etds.2014.47Google Scholar
Brown, N. P. and Ozawa, N.. C ∗ -Algebras and Finite-Dimensional Approximations (Graduate Studies in Mathematics, 88) . American Mathematical Society, Providence, RI, 2008.Google Scholar
Chen, X. and Wang, Q.. Ideal structure of uniform Roe algebras of coarse spaces. J. Funct. Anal. 216(1) (2004), 191–211.Google Scholar
Cuntz, J.. K-theory for certain C ∗ -algebras. Ann. of Math. (2) 113(1) (1981), 181–197.10.2307/1971137Google Scholar
de la Harpe, P., Grigorchuk, R. I. and Ceccherini-Silberstein, T.. Amenability and paradoxical decompositions for pseudogroups and discrete metric spaces. Tr. Mat. Inst. Steklova 224 (1999), 68–111.Google Scholar
Exel, R.. Reconstructing a totally disconnected groupoid from its ample semigroup. Proc. Amer. Math. Soc. 138(8) (2010), 2991–3001.Google Scholar
Giordano, T. and Sierakowski, A.. Purely infinite partial crossed products. J. Funct. Anal. 266(9) (2014), 5733–5764.Google Scholar
Green, P.. The local structure of twisted covariance algebras. Acta Math. 140(3–4) (1978), 191–250.10.1007/BF02392308Google Scholar
Gromov, M.. Random walk in random groups. Geom. Funct. Anal. 13(1) (2003), 73–146.Google Scholar
Guentner, E., Willett, R. and Yu, G.. Dynamic asymptotic dimension: relation to dynamics, topology, coarse geometry, and C ∗ -algebras. Math. Ann. 367(1–2) (2017), 785–829.Google Scholar
Higson, N. and Roe, J.. Amenable group actions and the Novikov conjecture. J. Reine Angew. Math. 519 (2000), 143–153.Google Scholar
Hong, J. H. and Szymański, W.. Purely infinite Cuntz–Krieger algebras of directed graphs. Bull. Lond. Math. Soc. 35(5) (2003), 689–696.10.1112/S0024609303002364Google Scholar
Jolissaint, P. and Robertson, G.. Simple purely infinite C ∗ -algebras and n-filling actions. J. Funct. Anal. 175(1) (2000), 197–213.Google Scholar
Kang, S. and Pask, D.. Aperiodicity and primitive ideals of row-finite k-graphs. Internat. J. Math. 25(3) (2014),1450022 25.Google Scholar
Kellerhals, J., Monod, N. and Rørdam, M.. Non-supramenable groups acting on locally compact spaces. Doc. Math. 18 (2013), 1597–1626.Google Scholar
Kerr, D. and Nowak, P. W.. Residually finite actions and crossed products. Ergod. Th. & Dynam. Sys. 32(5) (2012), 1585–1614.Google Scholar
Kirchberg, E.. The classification of purely infinite $C^{\ast }$ -algebras using Kasparov’s theory. Preprint, 1994.Google Scholar
Kirchberg, E.. Das nicht-kommutative Michael–Auswahlprinzip und die Klassifikation nicht-einfacher Algebren (C ∗ -algebras (Münster, 1999)) . Springer, Berlin, 2000, pp. 92–141.Google Scholar
Kirchberg, E. and Rørdam, M.. Non-simple purely infinite C ∗ -algebras. Amer. J. Math. 122(3) (2000), 637–666.Google Scholar
Kirchberg, E. and M., Rørdam. Infinite non-simple C ∗ -algebras: absorbing the Cuntz algebras 𝓞∞ . Adv. Math. 167(2) (2002), 195–264.Google Scholar
Kirchberg, E. and Sierakowski, A.. Filling families and strong pure infiniteness. Preprint, 2016, arXiv: 1503.08519.Google Scholar
Kumjian, A. and Pask, D.. Higher rank graph C ∗ -algebras. New York J. Math. 6 (2000), 1–20.Google Scholar
Kwaśniewski, B. K. and Szymański, W.. Pure infiniteness and ideal structure of C ∗ -algebras associated to Fell bundles. J. Math. Anal. Appl. 445(1) (2017), 898–943.10.1016/j.jmaa.2016.07.044Google Scholar
Laca, M. and Spielberg, J.. Purely infinite C ∗ -algebras from boundary actions of discrete groups. J. Reine Angew. Math. 480 (1996), 125–139.Google Scholar
Li, X. and Renault, J.. Cartan subalgebras in $C^{\ast }$ -algebras. existence and uniqueness. Preprint, 2017, arXiv:1703.10505.Google Scholar
Osajda, D.. Small cancellation labellings of some infinite graphs and applications. Preprint, 2014, arXiv: 1406.5015v2.Google Scholar
Pask, D., Sierakowski, A. and Sims, A.. Real rank and topological dimension of higher-rank graph algebras. Indiana Univ. Math. J. 66(6) (2017), 2137–2168.Google Scholar
Pask, D., Sierakowski, A. and Sims, A.. Unbounded quasitraces, stable finiteness and pure infiniteness. Preprint, 2017, arXiv:1705.01268.Google Scholar
Pasnicu, C. and Rørdam, M.. Purely infinite C ∗ -algebras of real rank zero. J. Reine Angew. Math. 613 (2007), 51–73.Google Scholar
Paterson, A. L. T.. Groupoids, Inverse Semigroups, and their Operator Algebras (Progress in Mathematics, 170) . Birkhäuser Boston, Boston, MA, 1999.Google Scholar
Phillips, N. C.. A classification theorem for nuclear purely infinite simple C ∗ -algebras. Doc. Math. 5 (2000), 49–114.Google Scholar
Rainone, T.. Finiteness and paradoxical decompositions in C*-dynamical systems. J. Noncommut. Geom. 11(2) (2017), 791–822.10.4171/JNCG/11-2-11Google Scholar
Rainone, T. and Sims, A.. A dichotomy for groupoid $C^{\ast }$ -algebras. Preprint, 2017, arXiv:1707.04516.Google Scholar
Renault, J.. A Groupoid Approach to C ∗ -Algebras (Lecture Notes in Mathematics, 793) . Springer, Berlin, 1980.Google Scholar
Renault, J.. The ideal structure of groupoid crossed product C ∗ -algebras. J. Operator Theory 25(1) (1991), 3–36.Google Scholar
Renault, J.. Cartan subalgebras in C ∗ -algebras. Irish Math. Soc. Bull. 61 (2008), 29–63.Google Scholar
Roe, J.. Lectures on Coarse Geometry (University Lecture Series, 31) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Roe, J. and Willett, R.. Ghostbusting and property A. J. Funct. Anal. 266(3) (2014), 1674–1684.Google Scholar
Rørdam, M. and Sierakowski, A.. Purely infinite C ∗ -algebras arising from crossed products. Ergod. Th. & Dynam. Sys. 32(1) (2012), 273–293.Google Scholar
Sierakowski, A.. The ideal structure of reduced crossed products. Münster J. Math. 3 (2010), 237–261.Google Scholar
Skandalis, G., Tu, J. L. and Yu, G.. The coarse Baum–Connes conjecture and groupoids. Topology 41(4) (2002), 807–834.Google Scholar
Spielberg, J.. Graph-based models for Kirchberg algebras. J. Operator Theory 57(2) (2007), 347–374.Google Scholar
Tikuisis, A., White, S. and Winter, W.. Quasidiagonality of nuclear C ∗ -algebras. Ann. of Math. (2) 185(1) (2017), 229–284.10.4007/annals.2017.185.1.4Google Scholar
Tu, J.-L.. La conjecture de Baum–Connes pour les feuilletages moyennables. K-Theory 17(3) (1999), 215–264.Google Scholar
Wagon, S.. The Banach–Tarski Paradox. Cambridge University Press, Cambridge, 1993, corrected reprint of the 1985 original.Google Scholar
Williams, D. P.. Crossed Products of C ∗ -Algebras (Mathematical Surveys and Monographs, 134) . American Mathematical Society, Providence, RI, 2007.Google Scholar
Winter, W. and Zacharias, J.. The nuclear dimension of C ∗ -algebras. Adv. Math. 224(2) (2010), 461–498.Google Scholar