Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-06-05T06:16:35.662Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow equivalence of sofic beta-shifts

Published online by Cambridge University Press:  28 January 2016

RUNE JOHANSEN
RUNE JOHANSEN*
Affiliation:
Department of Mathematics, University of Copenhagen, Universitetsparken 5, 2100 København Ø, Denmark email rune@math.ku.dk
Get access Rights & Permissions [Opens in a new window]

Abstract

The Fischer, Krieger, and fiber product covers of sofic beta-shifts are constructed and used to show that every strictly sofic beta-shift is 2-sofic. Flow invariants based on the covers are computed, and shown to depend only on a single integer that can easily be determined from the 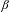$\unicode[STIX]{x1D6FD}$-expansion of 1. It is shown that any beta-shift is flow equivalent to a beta-shift given by some 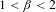$1<\unicode[STIX]{x1D6FD}<2$, and concrete constructions lead to further reductions of the flow classification problem. For each sofic beta-shift, there is an action of 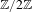$\mathbb{Z}/2\mathbb{Z}$ on the edge shift given by the fiber product, and it is shown precisely when there exists a flow equivalence respecting these 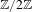$\mathbb{Z}/2\mathbb{Z}$-actions. This opens a connection to ongoing efforts to classify general irreducible 2-sofic shifts via flow equivalences of reducible shifts of finite type (SFTs) equipped with 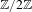$\mathbb{Z}/2\mathbb{Z}$-actions.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 3 , May 2017 , pp. 786 - 801
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boyle, M., Carlsen, T. M. and Eilers, S.. Flow equivalence and isotopy for subshifts. In preparation.Google Scholar
Boyle, M., Carlsen, T. M. and Eilers, S.. Flow equivalence of sofic shifts. In preparation.Google Scholar
Boyle, M. and Huang, D.. Poset block equivalence of integral matrices. Trans. Amer. Math. Soc. 355(10) (2003), 3861–3886 (electronic).CrossRefGoogle Scholar
Blanchard, F.. 𝛽-expansions and symbolic dynamics. Theoret. Comput. Sci. 65(2) (1989), 131–141.CrossRefGoogle Scholar
Bertrand-Mathis, A.. Questions diverses relatives aux systèmes codés: applications au $\unicode[STIX]{x1D703}$ -shift. Preprint.Google Scholar
Bertrand-Mathis, A.. Développement en base 𝜃; répartition modulo un de la suite (x𝜃 n ) n≥0 ; langages codés et 𝜃-shift. Bull. Soc. Math. France 114(3) (1986), 271–323.CrossRefGoogle Scholar
Boyle, M.. Flow equivalence of shifts of finite type via positive factorizations. Pacific J. Math. 204(2) (2002), 273–317.CrossRefGoogle Scholar
Boyle, M. and Sullivan, M. C.. Equivariant flow equivalence for shifts of finite type, by matrix equivalence over group rings. Proc. Lond. Math. Soc. (3) 91(1) (2005), 184–214.CrossRefGoogle Scholar
Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527) . Springer, Berlin, 1976.CrossRefGoogle Scholar
Fischer, R.. Sofic systems and graphs. Monatsh. Math. 80(3) (1975), 179–186.CrossRefGoogle Scholar
Franks, J.. Flow equivalence of subshifts of finite type. Ergod. Th. & Dynam. Sys. 4(1) (1984), 53–66.CrossRefGoogle Scholar
Huang, D.. Flow equivalence of reducible shifts of finite type. Ergod. Th. & Dynam. Sys. 14(4) (1994), 695–720.CrossRefGoogle Scholar
Johnson, K. C.. Beta-shift dynamical systems and their associated languages. PhD Thesis, The University of North Carolina at Chapel Hill, 1999.Google Scholar
Johansen, R.. On flow equivalence of sofic shifts. PhD Thesis, University of Copenhagen, 2011.Google Scholar
Johansen, R.. On the structure of covers of sofic shifts. Doc. Math. 16 (2011), 111–131.CrossRefGoogle Scholar
Katayama, Y., Matsumoto, K. and Watatani, Y.. Simple C ∗ -algebras arising from 𝛽-expansion of real numbers. Ergod. Th. & Dynam. Sys. 18(4) (1998), 937–962.CrossRefGoogle Scholar
Krieger, W.. On sofic systems. I. Israel J. Math. 48(4) (1984), 305–330.CrossRefGoogle Scholar
Lind, D.. The entropies of topological Markov shifts and a related class of algebraic integers. Ergod. Th. & Dynam. Sys. 4(2) (1984), 283–300.CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
Parry, W. and Sullivan, D.. A topological invariant of flows on 1-dimensional spaces. Topology 14(4) (1975), 297–299.CrossRefGoogle Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.CrossRefGoogle Scholar
Schmidt, K.. On periodic expansions of Pisot numbers and Salem numbers. Bull. Lond. Math. Soc. 12(4) (1980), 269–278.CrossRefGoogle Scholar
Weiss, B.. Subshifts of finite type and sofic systems. Monatsh. Math. 77 (1973), 462–474.CrossRefGoogle Scholar