Hostname: page-component-7479d7b7d-q6k6v Total loading time: 0 Render date: 2024-07-11T23:57:56.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite group extensions of shifts of finite type: 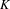$K$-theory, Parry and Livšic

Published online by Cambridge University Press:  11 February 2016

MIKE BOYLE  and
SCOTT SCHMIEDING
MIKE BOYLE
Affiliation:
University of Maryland, Department of Mathematics, College Park, MD20742-4015, USA email mmb@math.umd.edu, scott@math.umd.edu
SCOTT SCHMIEDING
Affiliation:
University of Maryland, Department of Mathematics, College Park, MD20742-4015, USA email mmb@math.umd.edu, scott@math.umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper extends and applies algebraic invariants and constructions for mixing finite group extensions of shifts of finite type. For a finite abelian group 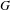$G$, Parry showed how to define a 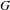$G$-extension 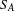$S_{A}$ from a square matrix over 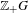$\mathbb{Z}_{+}G$, and classified the extensions up to topological conjugacy by the strong shift equivalence class of $A$ over 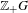$\mathbb{Z}_{+}G$. Parry asked, in this case, if the dynamical zeta function 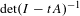$\det (I-tA)^{-1}$ (which captures the ‘periodic data’ of the extension) would classify the extensions by 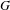$G$ of a fixed mixing shift of finite type up to a finite number of topological conjugacy classes. When the algebraic 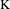$\text{K}$-theory group 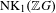$\text{NK}_{1}(\mathbb{Z}G)$ is non-trivial (e.g. for 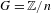$G=\mathbb{Z}/n$ with $n$ not square-free) and the mixing shift of finite type is not just a fixed point, we show that the dynamical zeta function for any such extension is consistent with an infinite number of topological conjugacy classes. Independent of 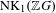$\text{NK}_{1}(\mathbb{Z}G)$, for every non-trivial abelian 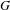$G$ we show that there exists a shift of finite type with an infinite family of mixing non-conjugate 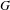$G$ extensions with the same dynamical zeta function. We define computable complete invariants for the periodic data of the extension for 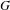$G$ (not necessarily abelian), and extend all the above results to the non-abelian case. There is other work on basic invariants. The constructions require the ‘positive 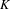$K$-theory’ setting for positive equivalence of matrices over 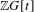$\mathbb{Z}G[t]$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 4 , June 2017 , pp. 1026 - 1059
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R., Kitchens, B. and Marcus, B.. Almost topological classification of finite-to-one factor maps between shifts of finite type. Ergod. Th. & Dynam. Sys. 5(4) (1985), 485–500.CrossRefGoogle Scholar
Adler, R. L., Kitchens, B. and Marcus, B. H.. Finite group actions on shifts of finite type. Ergod. Th. & Dynam. Sys. 5(1) (1985), 1–25.CrossRefGoogle Scholar
Araújo, P. V.. A stochastic analogue of a theorem of Boyle’s on almost flow equivalence. Ergod. Th. & Dynam. Sys. 13(3) (1993), 417–444.Google Scholar
Boyle, M.. Positive K-theory and symbolic dynamics. Dynamics and Randomness (Santiago, 2000) (Nonlinear Phenom. Complex Systems, 7) . Kluwer Academic Publishers, Dordrecht, 2002, pp. 31–52.Google Scholar
Boyle, M.. Open problems in symbolic dynamics. Geometric and Probabilistic Structures in Dynamics (Contemporary Mathematics, 469) . American Mathematical Society, Providence, RI, 2008, pp. 69–118.Google Scholar
Boyle, M., Carlsen, T. and Eilers, S.. Flow equivalence of G shifts of finite type. Preliminary manuscript, 2015, 36 pages.Google Scholar
Boyle, M. and Handelman, D.. The spectra of nonnegative matrices via symbolic dynamics (including Appendix 4 joint with Kim and Roush). Ann. of Math. (2) 133(2) (1991), 249–316.Google Scholar
Boyle, M. and Schmieding, S.. The generalized spectral conjecture for nonnegative matrices. Linear Algebra Appl. to appear. Preprint, 2015, arXiv:1501.04697.CrossRefGoogle Scholar
Boyle, M. and Schmieding, S.. Strong shift equivalence and algebraic $K$ -theory. J. Reine Angew. Math. to appear. Preprint, 2015, arXiv:1501.04695.Google Scholar
Boyle, M. and Sullivan, M. C.. Equivariant flow equivalence for shifts of finite type, by matrix equivalence over group rings. Proc. Lond. Math. Soc. (3) 91(1) (2005), 184–214.Google Scholar
Boyle, M. and Wagoner, J. B.. Positive algebraic K-theory and shifts of finite type. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 45–66.Google Scholar
Brooksbank, P. A. and Mizuhara, M. S.. On groups with a class-preserving outer automorphism. Involve 7(2) (2014), 171–179.CrossRefGoogle Scholar
Farrell, F. T.. The nonfiniteness of Nil. Proc. Amer. Math. Soc. 65(2) (1977), 215–216.CrossRefGoogle Scholar
Fitting, H.. Über den Zusammenhang zwischen dem Begriff der Gleichartigkeit zweier Ideale und dem Äquivalenzbegriff der Elementarteilertheorie. Math. Ann. 112(1) (1936), 572–582.Google Scholar
Hambleton, I. and Lück, W.. Induction and computation of Bass Nil groups for finite groups. Pure Appl. Math. Q. 8(1) (2012), 199–219.CrossRefGoogle Scholar
Handelman, D.. Matrices of positive polynomials. Electron. J. Linear Algebra 19 (2009), 2–89.Google Scholar
Harmon, D. R.. NK 1 of finite groups. Proc. Amer. Math. Soc. 100(2) (1987), 229–232.Google Scholar
Kalinin, B.. Livšic theorem for matrix cocycles. Ann. of Math. (2) 173(2) (2011), 1025–1042.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54) . Cambridge University Press, Cambridge, 1995; With a supplementary chapter by Katok and Leonardo Mendoza.Google Scholar
Kim, K. H., Ormes, N. S. and Roush, F. W.. The spectra of nonnegative integer matrices via formal power series. J. Amer. Math. Soc. 13(4) (2000), 773–806 (electronic).CrossRefGoogle Scholar
Kim, K. H. and Roush, F. W.. Some results on decidability of shift equivalence. J. Comb. Inf. Syst. Sci. 4(2) (1979), 123–146.Google Scholar
Kim, K. H. and Roush, F. W.. Free Z p actions on subshifts. Pure Math. Appl. 8(2–4) (1997), 293–322.Google Scholar
Kim, K. H., Roush, F. W. and Wagoner, J. B.. Characterization of inert actions on periodic points. I. Forum Math. 12(5) (2000), 565–602.Google Scholar
Kim, K. H., Roush, F. W. and Wagoner, J. B.. Characterization of inert actions on periodic points. II. Forum Math. 12(6) (2000), 671–712.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Livšic, A. N.. Certain properties of the homology of Y-systems. Mat. Zametki 10 (1971), 555–564.Google Scholar
Long, N.. Fixed point shifts of inert involutions. Discrete Contin. Dyn. Syst. 25(4) (2009), 1297–1317.Google Scholar
Marcus, B. and Tuncel, S.. The weight-per-symbol polytope and scaffolds of invariants associated with Markov chains. Ergod. Th. & Dynam. Sys. 11(1) (1991), 129–180.Google Scholar
Martin, R. D.. Nilgroups of finite abelian groups. PhD Thesis, Columbia University, ProQuest LLC, Ann Arbor, MI, 1976.Google Scholar
Pajitnov, A. V.. Closed orbits of gradient flows and logarithms of non-abelian Witt vectors. K-Theory 21(4) (2000), 301–324; Special issues dedicated to Daniel Quillen on the occasion of his sixtieth birthday, Part V.Google Scholar
Pajitnov, A. V. and Ranicki, A. A.. The Whitehead group of the Novikov ring. K-Theory 21(4) (2000), 325–365; Special issues dedicated to Daniel Quillen on the occasion of his sixtieth birthday, Part V.Google Scholar
Parry, W.. The Livšic periodic point theorem for non-abelian cocycles. Ergod. Th. & Dynam. Sys. 19(3) (1999), 687–701.CrossRefGoogle Scholar
Parry, W. and Tuncel, S.. On the stochastic and topological structure of Markov chains. Bull. Lond. Math. Soc. 14(1) (1982), 16–27.Google Scholar
Pollicott, M., Sharp, R., Tuncel, S. and Walters, P.. The mathematical research of William Parry FRS. Ergod. Th. & Dynam. Sys. 28(2) (2008), 321–337.Google Scholar
Pollicott, M.. Dynamical zeta functions. Integers 11B (2011), Paper No. A11, 50.Google Scholar
Pollicott, M. and Weiss, H.. Free energy as a dynamical invariant (or Can you hear the shape of a potential?). Commun. Math. Phys. 240(3) (2003), 457–482.CrossRefGoogle Scholar
Rosenberg, J.. Algebraic K-theory and its Applications (Graduate Texts in Mathematics, 147) . Springer, New York, 1994.Google Scholar
Sadovskaya, V.. Cohomology of GL (2, ℝ)-valued cocycles over hyperbolic systems. Discrete Contin. Dyn. Syst. 33(5) (2013), 2085–2104.CrossRefGoogle Scholar
Schmidt, K.. Remarks on Livšic’ theory for nonabelian cocycles. Ergod. Th. & Dynam. Sys. 19(3) (1999), 703–721.Google Scholar
Schmieding, S.. Explicit examples in $\text{NK}_{1}$ . Preprint, 2015, arXiv:1506.07418.Google Scholar
Schmieding, S.. The Nil group of the group ring of a finitely generated abelian group. In preparation, 2015.Google Scholar
Sehgal, S. K.. Topics in Group Rings (Monographs and Textbooks in Pure and Applied Mathematics, 50) . Marcel Dekker, Inc., New York, 1978.Google Scholar
Sheiham, D.. Non-commutative characteristic polynomials and Cohn localization. J. Lond. Math. Soc. (2) 64(1) (2001), 13–28.Google Scholar
Sheiham, D.. Whitehead groups of localizations and the endomorphism class group. J. Algebra 270(1) (2003), 261–280.Google Scholar
Weibel, C. A.. Mayer–Vietoris sequences and module structures on NK ∗ . Algebraic K-Theory, Evanston 1980 (Proc. Conf., Northwestern Univ., Evanston, IL, 1980) (Lecture Notes in Mathematics, 854) . Springer, Berlin, 1981, pp. 466–493.Google Scholar
Weibel, C.. NK 0 and NK 1 of the groups C 4 and D 4 . Addendum to ‘Lower algebraic K-theory of hyperbolic 3-simplex reflection groups’ by J.-F. Lafont and I. J. Ortiz [mr2495796]. Comment. Math. Helv. 84(2) (2009), 339–349.Google Scholar
Weibel, C. A.. The K-book: An Introduction to Algebraic K-theory (Graduate Studies in Mathematics, 145) . American Mathematical Society, Providence, RI, 2013.Google Scholar
Williams, R. F.. Classification of subshifts of finite type. Ann. of Math. (2) 98 (1973), 120–153; erratum, ibid. 99 (1974), 380–381.Google Scholar