Article contents
Exact Hausdorff and packing measures of Cantor sets with overlaps
Published online by Cambridge University Press: 11 August 2014
Abstract
Let 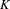 $K$ be the attractor of a linear iterated function system (IFS)
$K$ be the attractor of a linear iterated function system (IFS) 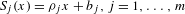 $S_{j}(x)={\it\rho}_{j}x+b_{j},j=1,\ldots ,m$, on the real line
$S_{j}(x)={\it\rho}_{j}x+b_{j},j=1,\ldots ,m$, on the real line 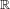 $\mathbb{R}$ satisfying the generalized finite type condition (whose invariant open set
$\mathbb{R}$ satisfying the generalized finite type condition (whose invariant open set 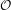 ${\mathcal{O}}$ is an interval) with an irreducible weighted incidence matrix. This condition was recently introduced by Lau and Ngai [A generalized finite type condition for iterated function systems. Adv. Math.208 (2007), 647–671] as a natural generalization of the open set condition, allowing us to include many important overlapping cases. They showed that the Hausdorff and packing dimensions of
${\mathcal{O}}$ is an interval) with an irreducible weighted incidence matrix. This condition was recently introduced by Lau and Ngai [A generalized finite type condition for iterated function systems. Adv. Math.208 (2007), 647–671] as a natural generalization of the open set condition, allowing us to include many important overlapping cases. They showed that the Hausdorff and packing dimensions of 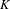 $K$ coincide and can be calculated in terms of the spectral radius of the weighted incidence matrix. Let
$K$ coincide and can be calculated in terms of the spectral radius of the weighted incidence matrix. Let  ${\it\alpha}$ be the dimension of
${\it\alpha}$ be the dimension of 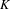 $K$. In this paper, we state that
$K$. In this paper, we state that 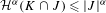 $$\begin{eqnarray}{\mathcal{H}}^{{\it\alpha}}(K\cap J)\leq |J|^{{\it\alpha}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}^{{\it\alpha}}(K\cap J)\leq |J|^{{\it\alpha}}\end{eqnarray}$$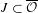 $J\subset \overline{{\mathcal{O}}}$, and
$J\subset \overline{{\mathcal{O}}}$, and 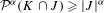 $$\begin{eqnarray}{\mathcal{P}}^{{\it\alpha}}(K\cap J)\geq |J|^{{\it\alpha}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}^{{\it\alpha}}(K\cap J)\geq |J|^{{\it\alpha}}\end{eqnarray}$$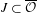 $J\subset \overline{{\mathcal{O}}}$ centered in
$J\subset \overline{{\mathcal{O}}}$ centered in 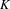 $K$, where
$K$, where 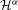 ${\mathcal{H}}^{{\it\alpha}}$ denotes the
${\mathcal{H}}^{{\it\alpha}}$ denotes the  ${\it\alpha}$-dimensional Hausdorff measure and
${\it\alpha}$-dimensional Hausdorff measure and 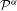 ${\mathcal{P}}^{{\it\alpha}}$ denotes the
${\mathcal{P}}^{{\it\alpha}}$ denotes the  ${\it\alpha}$-dimensional packing measure. This result extends a recent work of Olsen [Density theorems for Hausdorff and packing measures of self-similar sets. Aequationes Math.75 (2008), 208–225] where the open set condition is required. We use these inequalities to obtain some precise density theorems for the Hausdorff and packing measures of
${\it\alpha}$-dimensional packing measure. This result extends a recent work of Olsen [Density theorems for Hausdorff and packing measures of self-similar sets. Aequationes Math.75 (2008), 208–225] where the open set condition is required. We use these inequalities to obtain some precise density theorems for the Hausdorff and packing measures of 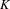 $K$. Moreover, using these density theorems, we describe a scheme for computing
$K$. Moreover, using these density theorems, we describe a scheme for computing 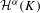 ${\mathcal{H}}^{{\it\alpha}}(K)$ exactly as the minimum of a finite set of elementary functions of the parameters of the IFS. We also obtain an exact algorithm for computing
${\mathcal{H}}^{{\it\alpha}}(K)$ exactly as the minimum of a finite set of elementary functions of the parameters of the IFS. We also obtain an exact algorithm for computing 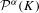 ${\mathcal{P}}^{{\it\alpha}}(K)$ as the maximum of another finite set of elementary functions of the parameters of the IFS. These results extend previous ones by Ayer and Strichartz [Exact Hausdorff measure and intervals of maximum density for Cantor sets. Trans. Amer. Math. Soc.351 (1999), 3725–3741] and by Feng [Exact packing measure of Cantor sets. Math. Natchr.248–249 (2003), 102–109], respectively, and apply to some new classes allowing us to include Cantor sets in
${\mathcal{P}}^{{\it\alpha}}(K)$ as the maximum of another finite set of elementary functions of the parameters of the IFS. These results extend previous ones by Ayer and Strichartz [Exact Hausdorff measure and intervals of maximum density for Cantor sets. Trans. Amer. Math. Soc.351 (1999), 3725–3741] and by Feng [Exact packing measure of Cantor sets. Math. Natchr.248–249 (2003), 102–109], respectively, and apply to some new classes allowing us to include Cantor sets in 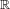 $\mathbb{R}$ with overlaps.
$\mathbb{R}$ with overlaps.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 2
- Cited by




