Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-21T15:36:48.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivariant spectral decomposition for flows with a ℤ-action

Published online by Cambridge University Press:  19 September 2008

Lee Mosher
Lee Mosher
Affiliation:
Institute for Advanced Studies†, and CUNY Graduate School‡, New York, 10036, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

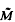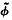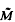Given a manifold equipped with a free, properly discontinuous, cocompact ℤ-action, and a flow on which is ℤ-equivariant, we study the qualitative dynamics of 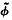. Under certain hypotheses on 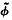, we show that the chain recurrent set of 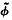has a decomposition which is the analogue, in the category of ℤ-equivariant flows, of Smale's spectral decomposition for recurrent sets of Axiom A flows.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 9 , Issue 2 , June 1989 , pp. 329 - 378
Copyright
Copyright © Cambridge University Press 1989

References

REFERENCES

[B1]Bowen, R.. One dimensional hyperbolic sets for flows. J. Differential Equations 12 (1972), 173–179.CrossRefGoogle Scholar
[B2]Bowen, R.. Symbolic dynamics for hyperbolic flows. Amer. J. Math. 95 (1973), 429–460.CrossRefGoogle Scholar
[C]Conley, C.. Isolated invariant sets and the Morse index. CBMS Regional Conference Series in Math. 38 (1978).CrossRefGoogle Scholar
[CE]Conley, C. & Easton, B.. Isolated invariant sets and isolating blocks. Trans. AMS 158 (1) (1971), 35–61.CrossRefGoogle Scholar
[FLP]Poenaru, Fathi Laudenbach et al. Travaux de Thurston sur les Surfaces. Astérisque 66–67 (1979).Google Scholar
[F1]Fried, D.. Fibrations over S1 with pseudo-Anosov monodromy, exposé 14 of Travaux de Thurston sur les surfaces. Astérisque 66–67 (1979).Google Scholar
[F2]Fried, D.. The geometry of cross sections to flows. Topology 21 (4) (1982), 353–371.CrossRefGoogle Scholar
[G]Gabai, D.. Foliations and the topology of 3-manifolds. J. Diff. Geom. 18 (1983), 445–503.Google Scholar
[H1]Handel, M.. Global shadowing of pseudo-Anosovs. Ergod. Th. & Dynam. Sys. 5 (1985), 373–377.CrossRefGoogle Scholar
[H2]Handel, M.. Entropy and semi-conjugacy in dimension two. Ergod. Th. & Dynam. Sys. 8 (1988) 585–596.CrossRefGoogle Scholar
[HW]Hardy, G. H. & Wright, E. M.. An Introduction to the Theory of Numbers 5th ed. (Oxford University Press, 1979).Google Scholar
[M]Mosher, L.. Surfaces and branched surfaces transverse to pseudo-Anosov flows on 3-manifolds. J. Diff. Geom., to appear.Google Scholar
[O]Oertel, U.. Homology branched surfaces: Thurston's norm on H2 (M3). In: Epstein, D. B. A., ed., Low-dimensional Topology and Kleinian Groups. London Math. Soc. Lecture Notes Series 112 (1984), 253–272.Google Scholar
[Sch]Schwartzman, S.. Asymptotic cycles. Ann. Math. 66 (1957), 270–284.CrossRefGoogle Scholar
[Sh]Shub, M.. Global stability of dynamical systems. (Springer Verlag: New York, 1987).CrossRefGoogle Scholar
[Sm]Smale, S.. Differentiate dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.CrossRefGoogle Scholar
[T]Thurston, W.. A norm on the homology of 3-manifolds. Memoirs of the AMS 339 (1986).Google Scholar