Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T03:18:11.890Z Has data issue: false hasContentIssue false
  • English
  • Français

Equilibrium states for a class of skew products

Part of: Ergodic theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  14 May 2019

MARIA CARVALHO Open the ORCID record for MARIA CARVALHO [Opens in a new window]  and
SEBASTIÁN A. PÉREZ Open the ORCID record for SEBASTIÁN A. PÉREZ [Opens in a new window]
MARIA CARVALHO
Affiliation:
Centro de Matemática da Universidade do Porto, Rua do Campo Alegre 687, 4169-007Porto, Portugal email mpcarval@fc.up.pt, sebastian.opazo@fc.up.pt
SEBASTIÁN A. PÉREZ
Affiliation:
Centro de Matemática da Universidade do Porto, Rua do Campo Alegre 687, 4169-007Porto, Portugal email mpcarval@fc.up.pt, sebastian.opazo@fc.up.pt
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider skew products on 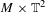$M\times \mathbb{T}^{2}$, where 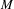$M$ is the two-sphere or the two-torus, which are partially hyperbolic and semi-conjugate to an Axiom A diffeomorphism. This class of dynamics includes the open sets of $\unicode[STIX]{x1D6FA}$-non-stable systems introduced by Abraham and Smale [Non-genericity of Ł-stability. Global Analysis (Proceedings of Symposia in Pure Mathematics, XIV (Berkeley 1968)). American Mathematical Society, Providence, RI, 1970, pp. 5–8.] and Shub [Topological Transitive Diffeomorphisms in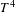$T^{4}$ (Lecture Notes in Mathematics, 206). Springer, Berlin, 1971, pp. 39–40]. We present sufficient conditions, both on the skew products and the potentials, for the existence and uniqueness of equilibrium states, and discuss their statistical stability.

Keywords

skew productpartial hyperbolicitystatistical stabilityequilibrium state

MSC classification

Primary: 37D35: Thermodynamic formalism, variational principles, equilibrium states 37A35: Entropy and other invariants, isomorphism, classification 37D30: Partially hyperbolic systems and dominated splittings
Secondary: 37A05: Measure-preserving transformations 37A30: Ergodic theorems, spectral theory, Markov operators
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 11 , November 2020 , pp. 3030 - 3050
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, R. and Smale, S.. Non-genericity of 𝛺-stability. Global Analysis (Proceedings of Symposia in Pure Mathematics, XIV (Berkeley 1968)) . American Mathematical Society, Providence, RI, 1970, pp. 5–8.CrossRefGoogle Scholar
Barrientos, P. G., Ki, Y. and Raibekas, A.. Symbolic blender-horseshoes and applications. Nonlinearity 27 (2014), 2805–2839.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity (Encyclopaedia of Mathematical Sciences, 102) . Springer, Berlin, 2005.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.CrossRefGoogle Scholar
Bowen, R.. Entropy-expansive maps. Trans. Amer. Math. Soc. 164 (1972), 323–331.CrossRefGoogle Scholar
Bowen, R.. Some systems with unique equilibrium states. Math. Sys. Theory 8(3) (1974), 193–202.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . Springer, Berlin, 1975.CrossRefGoogle Scholar
Buzzi, J. and Fisher, T.. Entropic stability beyond partial hyperbolicity. J. Mod. Dyn. 7(4) (2013), 527–552.Google Scholar
Buzzi, J., Fisher, T., Sambarino, M. and Vásquez, C.. Maximal entropy measures for certain partially hyperbolic, derived from Anosov systems. Ergod. Th. & Dynam. Sys. 32(1) (2012), 63–79.CrossRefGoogle Scholar
Climenhaga, V., Fisher, T. and Thompson, D. J.. Unique equilibrium states for Bonatti–Viana diffeomorphisms. Nonlinearity 31(6) (2018), 2532–2570.CrossRefGoogle Scholar
Climenhaga, V., Fisher, T. and Thompson, D. J.. Unique equilibrium states for Mañé diffeomorphisms. Ergod. Th. & Dynam. Sys. (2018), https://doi.org/10.1017/etds.2017.125, Published online 18 January 2018.Google Scholar
Climenhaga, V. and Thompson, D. J.. Unique equilibrium states for flows and homeomorphisms with non-uniform structure. Adv. Math. 303 (2016), 745–799.CrossRefGoogle Scholar
Cowieson, W. and Young, L.-S.. SRB measures as zero-noise limits. Ergod. Th. & Dynam. Sys. 25(4) (2005), 1115–1138.CrossRefGoogle Scholar
Crisostomo, J. and Tahzibi, A.. Equilibrium states for partially hyperbolic diffeomorphisms with hyperbolic linear part. Nonlinearity 32(2) (2019), 584–602.CrossRefGoogle Scholar
Díaz, L. and Fisher, T.. Symbolic extensions and partially hyperbolic diffeomorphisms. Discrete Contin. Dyn. Syst. 29 (2011), 1419–1441.CrossRefGoogle Scholar
Díaz, L., Fisher, T., Pacífico, M. J. and Vieitez, J.. Entropy-expansiveness for partially hyperbolic diffeomorphisms. Discrete Contin. Dyn. Syst. 32(12) (2012), 4195–4207.Google Scholar
Fisher, T., Potrie, R. and Sambarino, M.. Dynamical coherence for partially hyperbolic diffeomorphisms of tori isotopic to Anosov. Math. Z. 278(1–2) (2014), 149–168.CrossRefGoogle Scholar
Franks, J.. Anosov diffeomorphisms on tori. Trans. Amer. Math. Soc. 145 (1969), 117–124.CrossRefGoogle Scholar
Gorodetski, A. S.. Regularity of central leaves of partially hyperbolic sets and applications. Izv. Ross. Akad. Nauk Ser. Mat. 70 (2006), 19–44 (translation in Izv. Math. 70, 1093–116).Google Scholar
Hasselblatt, B. and Pesin, Y.. Partially Hyperbolic Dynamical Systems (Handbook of Dynamical Systems, 1B) . Elsevier, Amsterdam, 2006, pp. 1–55.Google Scholar
Hertz, F. R., Hertz, M. A., Tahzibi, A. and Ures, R.. Maximizing measures for partially hyperbolic systems with compact center leaves. Ergod. Th. & Dynam. Sys. 32(2) (2012), 825–839.CrossRefGoogle Scholar
Hertz, F. R., Hertz, M. A. and Ures, R.. A non-dynamically coherent example on T 3 . Ann. Inst. Henri Poincaré C 33 (2012), 1023–1032.CrossRefGoogle Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583) . Springer, 1977.CrossRefGoogle Scholar
Ilyashenko, Y. and Negut, A.. Hölder properties of perturbed skew products and Fubini regained. Nonlinearity 25 (2012), 2377–2399.CrossRefGoogle Scholar
Ledrappier, F. and Walters, P.. A relativized variational principle for continuous transformations. J. Lond. Math. Soc. 16 (1977), 568–576.CrossRefGoogle Scholar
Mañé, R.. Contributions to the stability conjecture. Topology 17(4) (1978), 383–396.CrossRefGoogle Scholar
Misiurewicz, M.. Diffeomorphisms without any measure with maximal entropy. Bull. Acad. Pol. Sci. 21 (1973), 903–910.Google Scholar
Misiurewicz, M.. Topological conditional entropy. Stud. Math. 55(2) (1976), 175–200.CrossRefGoogle Scholar
Newhouse, S. and Young, L.-S.. Dynamics of Certain Skew Products (Lecture Notes in Mathematics, 1007) . Springer, Berlin, 1983, pp. 611–629.Google Scholar
Pavlov, R.. On intrinsic ergodicity and weakenings of the specification property. Adv. Math. 295 (2016), 250–270.CrossRefGoogle Scholar
Pujals, E. and Sambarino, M.. A sufficient condition for robustly minimal foliations. Ergod. Th. & Dynam. Sys. 26(1) (2006), 281–289.CrossRefGoogle Scholar
Shub, M.. Topological Transitive Diffeomorphisms in T 4 (Lecture Notes in Mathematics, 206) . Springer, Berlin, 1971, pp. 39–40.Google Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.CrossRefGoogle Scholar
Ures, R.. Intrinsic ergodicity of partially hyperbolic diffeomorphisms with a hyperbolic linear part. Proc. Amer. Math. Soc. 140(6) (2012), 1973–1985.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1981.Google Scholar
Young, L.-S.. On the prevalence of horseshoes. Trans. Amer. Math. Soc. 263(1) (1981), 75–88.CrossRefGoogle Scholar