Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-11T11:51:13.278Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity of packing measure functions of self-similar iterated function systems

Published online by Cambridge University Press:  24 May 2011

HUA QIU
HUA QIU*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing, China (email: huatony@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we focus on the packing measures of self-similar sets. Let K be a self-similar set whose Hausdorff dimension and packing dimension equal s. We state that if K satisfies the strong open set condition with an open set 𝒪, then 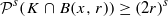for each open ball B(x,r)⊂𝒪 centred in K, where 𝒫s denotes the s-dimensional packing measure. We use this inequality to obtain some precise density theorems for the packing measures of self-similar sets. These theorems can be used to compute the exact value of the s-dimensional packing measure 𝒫s (K) of K. Moreover, by using the above results, we show the continuity of the packing measure function of the attractors on the space of self-similar iterated function systems satisfying the strong separation condition. This result gives a complete answer to a question posed by Olsen in [15].

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 32 , Issue 3 , June 2012 , pp. 1101 - 1115
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ayer, E. and Strichartz, R.. Exact Hausdorff measure and intervals of maximum density for Cantor sets. Trans. Amer. Math. Soc. 351 (1999), 3725–3741.CrossRefGoogle Scholar
[2]Centore, P. M. and Vrscay, E. R.. Continuity of attractors and invariant measures for iterated function systems. Canad. Math. Bull. 37 (1994), 315–329.CrossRefGoogle Scholar
[3]Falconer, K. J.. Fractal Geometry – Mathematical Foundations and Applications. John Wiley & Sons, New York, NY, 1990.CrossRefGoogle Scholar
[4]Feng, D., Hua, S. and Wen, Z.. Some relations between packing premeasure and packing measure. Bull. Lond. Math. Soc. 31 (1999), 665–670.CrossRefGoogle Scholar
[5]Feng, D.. Exact packing measure of Cantor sets. Math. Nachr. 248–149 (2003), 102–109.CrossRefGoogle Scholar
[6]Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981), 713–747.CrossRefGoogle Scholar
[7]Marion, J.. Measure de Hausdorff d’un fractal à similitude interne. Ann. Sci. Math. Québec 10 (1986), 51–84.Google Scholar
[8]Marion, J.. Measures de Hausdorff d’ensembles fractals. Ann. Sci. Math. Québec 11 (1987), 111–132.Google Scholar
[9]Mattila, P.. Geometry of sets and measures in Euclidean spaces. Fractals and Rectifiability. Cambridge University Press, Cambridge, 1995.Google Scholar
[10]Mattila, P.. On the structure of self-similar fractals. Ann. Acad. Sci. Fenn. Ser. A I Math. 7 (1982), 189–195.CrossRefGoogle Scholar
[11]Mattila, P. and Mauldin, R. D.. Measure and dimension function: measurability and densities. Math. Proc. Cambridge Philos. Soc. 121 (1997), 81–100.CrossRefGoogle Scholar
[12]Moran, P. A. P.. Additive functions of intervals and Hausdorff measure. Proc. Cambridge Philos. Soc. 42 (1946), 15–23.CrossRefGoogle Scholar
[13]Morán, M.. Computability of the Hausdorff and packing measures on self-similar sets and the self-similar tiling principle. Nonlinearity 18 (2005), 559–570.CrossRefGoogle Scholar
[14]Olsen, L.. Density theorems for Hausdorff and packing measures of self-similar sets. Aequationes Math. 75 (2008), 208–225.CrossRefGoogle Scholar
[15]Olsen, L.. Hausdorff and packing measure functions of self-similar sets: continuity and measurability. Ergod. Th. & Dynam. Sys. 28 (2008), 1635–1655.CrossRefGoogle Scholar
[16]Schief, A.. Separation properties for self-similar sets. Proc. Amer. Math. Soc. 122 (1994), 111–115.CrossRefGoogle Scholar
[17]Taylor, S. J. and Tricot, C.. Packing measure, and its evaluation for a Brownian path. Trans. Amer. Math. Soc. 288 (1985), 679–699.CrossRefGoogle Scholar
[18]Tricot, C.. Two definitions of fractional dimension. Math. Proc. Cambridge Philos. Soc. 91 (1982), 54–74.CrossRefGoogle Scholar
[19]Zhou, Z. and Feng, L.. Twelve open questions on the exact value of the Hausdorff measure and on the topological entropy: a brief review of recent results. Nonlinearity 17 (2004), 493–502.CrossRefGoogle Scholar