Hostname: page-component-77c89778f8-gq7q9 Total loading time: 0 Render date: 2024-07-25T01:45:30.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Compound Poisson statistics for multiple returns in shrinking cylinders for mixing processes

Published online by Cambridge University Press:  11 February 2015

ARIEL RAPAPORT
ARIEL RAPAPORT*
Affiliation:
Department of Mathematics, The Hebrew University of Jerusalem, Jerusalem, Israel email ariel.rapaport@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

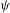Given a periodic point ${\it\omega}$ in a ${\it\psi}$-mixing shift with countable alphabet, the sequence 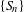$\{S_{n}\}$ of random variables counting the number of multiple returns in shrinking cylindrical neighborhoods of ${\it\omega}$ is considered. Necessary and sufficient conditions for the convergence in distribution of 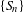$\{S_{n}\}$ are obtained, and it is shown that the limit is a Pólya–Aeppli distribution. A global condition on the shift system which guarantees the convergence in distribution of 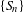$\{S_{n}\}$ for every periodic point is introduced. This condition is used to derive results for 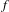$f$-expansions and Gibbs measures. Results are also obtained concerning the possible limit distribution of sub-sequences 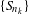$\{S_{n_{k}}\}$. A family of examples in which there is no convergence is presented. We also exhibit an example for which the limit distribution is pure Poissonian.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 5 , August 2016 , pp. 1616 - 1643
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abadi, M. and Vergne, N.. Poisson approximation for search of rare words in DNA sequences. ALEA Lat. Am. J. Probab. Math. Stat. 4 (2008), 223–244.Google Scholar
Abadi, M. and Vergne, N.. Sharp errors for point-wise Poisson approximations in mixing processes. Nonlinearity 21 (2008), 2871–2885.Google Scholar
Billingsley, P.. Probability and Measure (Wiley Series in Probability and Mathematical Statistics) . Wiley, New York, 1995.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms. Ed. Chazottes, J.-R.. Springer, Berlin, 2008.Google Scholar
Barbour, A. D., Holst, L. and Janson, S.. Poisson Approximation. Oxford University Press, Oxford, 1992.Google Scholar
Freitas, A. C. M., Freitas, J. M. and Todd, M.. The compound Poisson limit ruling periodic extreme behavior of non-uniformly hyperbolic dynamic. Comm. Math. Phys. 321 (2013), 483–527.CrossRefGoogle Scholar
Heinrich, L.. Mixing properties and central limit theorem for a class of non-identical piecewise monotonic C 2 -transformations. Math. Nachr. 181 (1996), 185–214.Google Scholar
Hirata, M.. Poisson law for Axiom A diffeomorphisms. Ergod. Th. & Dynam. Sys. 13 (1993), 533–556.Google Scholar
Haydn, N. and Vaienti, S.. The compound Poisson distribution and return times in dynamical systems. Probab. Theory Related Fields 144 (2009), 517–542.Google Scholar
Kifer, Y.. Nonconventional Poisson limit theorems. Israel J. Math. 195 (2013), 373–392.Google Scholar
Kifer, Y. and Rapaport, A.. Poisson and compound Poisson approximations in conventional and nonconventional setups. Probab. Theory Related Fields 160 (2014), 797–831.Google Scholar
Pitskel, B.. Poisson limit law for Markov chains. Ergod. Th. & Dynam. Sys. 11 (1991), 501–513.Google Scholar
Sarig, O.. Lecture Notes on Thermodynamic Formalism for Topological Markov Shifts. Pennsylvania State University, Pennsylvania, 2009.Google Scholar
Walters, P.. Some Results on the Classification of Non-invertible Measure Preserving Transformations (Lecture Notes in Mathematics, 318) . Springer, Berlin, 1973, pp. 266–276.Google Scholar