Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kirchberg, Eberhard
and
Vaillant, Ghislain
1992.
OnC *-algebras having linear, polynomial and subexponential growth.
Inventiones Mathematicae,
Vol. 108,
Issue. 1,
p.
635.
Voiculescu, Dan
1992.
Mathematical Physics X.
p.
303.
Jorgensen, Palle E.T
and
Price, Geoffrey L
1992.
Index theory and second quantization of boundary value problems.
Journal of Functional Analysis,
Vol. 104,
Issue. 2,
p.
243.
Várilly, Joseph C.
and
Gracia-Bondía, JoséM.
1993.
Connes' noncommutative differential geometry and the standard model.
Journal of Geometry and Physics,
Vol. 12,
Issue. 4,
p.
223.
Applebaum, David
1993.
Fermionic stochastic differential equations and the index of Fredholm operators.
Letters in Mathematical Physics,
Vol. 28,
Issue. 3,
p.
231.
Voiculescu, Dan
1994.
First European Congress of Mathematics Paris, July 6–10, 1992.
p.
475.
Park, Efton
1995.
Isometries of unbounded Fredholm modules over reduced group 𝐶*-algebras.
Proceedings of the American Mathematical Society,
Vol. 123,
Issue. 6,
p.
1839.
Park, Efton
1995.
Isometries of noncommutative metric spaces.
Proceedings of the American Mathematical Society,
Vol. 123,
Issue. 1,
p.
97.
Popa, Sorin
1997.
On local finite dimensional approximation of C∗-algebras.
Pacific Journal of Mathematics,
Vol. 181,
Issue. 1,
p.
141.
Pavlović, Branka
1998.
Defining metric spaces via operators from unital C∗-algebras.
Pacific Journal of Mathematics,
Vol. 186,
Issue. 2,
p.
285.
Schrohe, Elmar
Walze, Markus
and
Warzecha, Jan-Martin
1998.
Construction de triplets spectraux à partir de modules de Fredholm.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 326,
Issue. 10,
p.
1195.
Samet-Vaillant, A.Y.
2000.
Free *-subalgebras of C*-algebras.
Journal of Functional Analysis,
Vol. 171,
Issue. 2,
p.
432.
Samet-Vaillant, A.Y.
2000.
C*-Algebras, Gelfand–Kirillov Dimension, and Følner Sets.
Journal of Functional Analysis,
Vol. 171,
Issue. 2,
p.
346.
RENNIE, A.
2001.
COMMUTATIVE GEOMETRIES ARE SPIN MANIFOLDS.
Reviews in Mathematical Physics,
Vol. 13,
Issue. 04,
p.
409.
Carey, Alan
Phillips, John
and
Sukochev, Fyodor
2003.
Spectral flow and Dixmier traces.
Advances in Mathematics,
Vol. 173,
Issue. 1,
p.
68.
Antonescu, Cristina
and
Christensen, Erik
2004.
Metrics on group C∗-algebras and a non-commutative Arzelà–Ascoli theorem.
Journal of Functional Analysis,
Vol. 214,
Issue. 2,
p.
247.
Latrémolière, Frédéric
2005.
Approximation of quantum tori by finite quantum tori for the quantum Gromov–Hausdorff distance.
Journal of Functional Analysis,
Vol. 223,
Issue. 2,
p.
365.
Wu, Wei
2005.
Non-commutative metric topology on matrix state space.
Proceedings of the American Mathematical Society,
Vol. 134,
Issue. 2,
p.
443.
Li, Hanfeng
2005.
?-Deformations as Compact Quantum Metric Spaces.
Communications in Mathematical Physics,
Vol. 256,
Issue. 1,
p.
213.
Wu, Wei
2006.
Quantized Gromov–Hausdorff distance.
Journal of Functional Analysis,
Vol. 238,
Issue. 1,
p.
58.
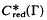 of a non amenable discrete group. Both for the needs of non commutative differential geometry and of analysis in infinite dimension we are led to the better notion of the θ-summable Fredholm module.
of a non amenable discrete group. Both for the needs of non commutative differential geometry and of analysis in infinite dimension we are led to the better notion of the θ-summable Fredholm module.



