No CrossRef data available.
Article contents
Automorphisms of 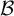 ${\mathcal B}$-free and other Toeplitz shifts
${\mathcal B}$-free and other Toeplitz shifts
Published online by Cambridge University Press: 13 June 2023
Abstract
We present sufficient conditions for the triviality of the automorphism group of regular Toeplitz subshifts and give a broad class of examples from the class of 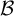 ${\mathcal B}$-free subshifts satisfying them, extending the work of Dymek [Automorphisms of Toeplitz
${\mathcal B}$-free subshifts satisfying them, extending the work of Dymek [Automorphisms of Toeplitz 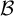 ${\mathcal B}$-free systems. Bull. Pol. Acad. Sci. Math. 65(2) (2017), 139–152]. Additionally, we provide an example of a
${\mathcal B}$-free systems. Bull. Pol. Acad. Sci. Math. 65(2) (2017), 139–152]. Additionally, we provide an example of a 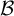 ${\mathcal B}$-free Toeplitz subshift whose automorphism group has elements of arbitrarily large finite order, answering Question 11 of S. Ferenczi et al [Sarnak’s conjecture: what’s new. Ergodic Theory and Dynamical Systems in their Interactions with Arithmetics and Combinatorics (Lecture Notes in Mathematics, 2213). Eds. S. Ferenczi, J. Kułaga-Przymus and M. Lemańczyk. Springer, Cham, 2018, pp. 163–235].
${\mathcal B}$-free Toeplitz subshift whose automorphism group has elements of arbitrarily large finite order, answering Question 11 of S. Ferenczi et al [Sarnak’s conjecture: what’s new. Ergodic Theory and Dynamical Systems in their Interactions with Arithmetics and Combinatorics (Lecture Notes in Mathematics, 2213). Eds. S. Ferenczi, J. Kułaga-Przymus and M. Lemańczyk. Springer, Cham, 2018, pp. 163–235].
Keywords
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press





