No CrossRef data available.
Article contents
Asymptotically holomorphic methods for infinitely renormalizable 
$C^r$ unimodal maps
Published online by Cambridge University Press: 29 November 2022
Abstract
The purpose of this paper is to initiate a theory concerning the dynamics of asymptotically holomorphic polynomial-like maps. Our maps arise naturally as deep renormalizations of asymptotically holomorphic extensions of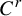 
$C^r$ (
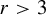$r>3$) unimodal maps that are infinitely renormalizable of bounded type. Here we prove a version of the Fatou–Julia–Sullivan theorem and a topological straightening theorem in this setting. In particular, these maps do not have wandering domains and their Julia sets are locally connected.
MSC classification
Primary:
37F10: Polynomials; rational maps; entire and meromorphic functions
37E20: Universality, renormalization
Secondary:
30C62: Quasiconformal mappings in the plane
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Anderson, J. M. and Hinkkanen, A.. Quasiconformal self-mappings with smooth boundary values. Bull. Lond. Math. Soc. 26(6) (1994), 549–556.10.1112/blms/26.6.549CrossRefGoogle Scholar
Astala, K., Iwaniec, T. and Martin, G.. Elliptic Partial Differential Equations and Quasiconformal Mappings in the Plane (Princeton Mathematical Series, 48). Princeton University Press, Princeton, NJ and Oxford, 2009.Google Scholar
Avila, A. and Krikorian, R.. Monotonic cocycles. Invent. Math 202(1) (2015), 271–331.10.1007/s00222-014-0572-6CrossRefGoogle Scholar
Avila, A. and Lyubich, M.. The full renormalization horseshoe for unimodal maps of higher degree: exponential contraction along hybrid classes. Publ. Math. Inst. Hautes Études Sci. 114(1) (2011), 171–223.10.1007/s10240-011-0034-2CrossRefGoogle Scholar
Benini, A. M. and Lyubich, M.. Repelling periodic points and landing of rays for post-singularly bounded exponential maps. Ann. Inst. Fourier (Grenoble) 64(4) (2014), 1493–1520.10.5802/aif.2888CrossRefGoogle Scholar
Blokh, A. M. and Lyubich, M. Y.. Nonexistence of wandering intervals and structure of topological attractors of one-dimensional dynamical systems. II. The smooth case. Ergod. Th. & Dynam. Sys. 9 (1989), 751–758.10.1017/S0143385700005319CrossRefGoogle Scholar
Bonk, M. and Heinonen, J.. Quasiregular mappings and cohomology. Acta Math. 186(2) (2001), 219–238.CrossRefGoogle Scholar
Carleson, L.. On mappings, conformal at the boundary. J. Anal. Math. 19 (1967), 1–13.10.1007/BF02788706CrossRefGoogle Scholar
Cheraghi, D. and Shishikura, M.. Satellite renormalization of quadratic polynomials. Preprint, 2015, arXiv:1509.07843.Google Scholar
Clark, T. and van Strien, S.. Quasisymmetric rigidity in dimension one. Preprint, 2018, arXiv:1805.09284.Google Scholar
Clark, T., van Strien, S. and Trejo, S.. Complex bounds for real maps. Comm. Math. Phys. 355(3) (2017), 1001–1119.10.1007/s00220-017-2958-yCrossRefGoogle Scholar
de Faria, E. and de Melo, W.. Rigidity of critical circle mappings I. J. Eur. Math. Soc. (JEMS) 1 (1999), 339–392.10.1007/s100970050011CrossRefGoogle Scholar
de Faria, E. and de Melo, W.. Rigidity of critical circle mappings II. J. Amer. Math. Soc. 13 (2000), 343–370.10.1090/S0894-0347-99-00324-0CrossRefGoogle Scholar
de Faria, E. and de Melo, W.. Mathematical Tools for One-dimensional Dynamics (Cambridge Studies in Advanced Mathematics, 115). Cambridge University Press, Cambridge, 2008.10.1017/CBO9780511755231CrossRefGoogle Scholar
de Faria, E., de Melo, W. and Pinto, A.. Global hyperbolicity of renormalization for
${C}^r$
unimodal mappings. Ann. of Math. (2) 164 (2006), 731–824.CrossRefGoogle Scholar
${C}^r$
unimodal mappings. Ann. of Math. (2) 164 (2006), 731–824.CrossRefGoogle Scholarde Faria, E. and Guarino, P.. Real bounds and Lyapunov exponents. Discrete Contin. Dyn. Syst. Ser. A 36 (2016), 1957–1982.Google Scholar
de Melo, W. and van Strien, S.. A structure theorem in one-dimensional dynamics. Ann. of Math. (2)
129(3) (1989), 519–546.10.2307/1971516CrossRefGoogle Scholar
de Melo, W. and van Strien, S.. One-Dimensional Dynamics. Springer-Verlag, New York, 1993.10.1007/978-3-642-78043-1CrossRefGoogle Scholar
Douady, A. and Hubbard, J. H.. On the dynamics of polynomial-like mappings. Ann. Sci. Éc. Norm. Supér. (4) 18(2) (1985), 287–343.10.24033/asens.1491CrossRefGoogle Scholar
Dyn’kin, E.. Estimates for asymptotically conformal mappings. Ann. Acad. Sci. Fenn. Math. 22(2) (1997), 275–304.Google Scholar
Gardiner, F. and Sullivan, D.. Symmetric structures on a closed curve. Amer. J. Math. 114 (1992), 683–736.CrossRefGoogle Scholar
Gardiner, F. and Sullivan, D.. Lacunary series as quadratic differentials in conformal dynamics. Contemp. Math. 169 (1994), 307–330.CrossRefGoogle Scholar
Graczyk, J., Sands, D. and Swiatek, G.. Decay of geometry for unimodal maps: negative Schwarzian case. Ann. of Math. (2) 161(2) (2005), 613–677.10.4007/annals.2005.161.613CrossRefGoogle Scholar
Graczyk, J. and Swiatek, G.. Polynomial-like property for real quadratic polynomials. Topology Proc. 21 (1996), 33–112.Google Scholar
Graczyk, J. and Swiatek, G.. Generic hyperbolicity in the logistic family. Ann. of Math. (2) 146 (1997), 1–52.10.2307/2951831CrossRefGoogle Scholar
Guarino, P. and de Melo, W.. Rigidity of smooth critical circle maps. J. Eur. Math. Soc. (JEMS) 19(6) (2017), 1729–1783.10.4171/JEMS/704CrossRefGoogle Scholar
Guarino, P., Martens, M. and de Melo, W.. Rigidity of critical circle maps. Duke Math. J. 167 (2018), 2125–2188.10.1215/00127094-2018-0017CrossRefGoogle Scholar
Guckenheimer, J.. Sensitive dependence to initial conditions for one-dimensional maps. Comm. Math. Phys. 70(2) (1979), 133–160.10.1007/BF01982351CrossRefGoogle Scholar
Hubbard, J. H.. Local connectivity of Julia sets and bifurcation loci: three theorems of J.-C. Yoccoz. Topological Methods in Modern Mathematics (Stony Brook, NY, 1991). Eds. Goldberg, L. R. and Phillips, A. V.. Publish or Perish, Houston, TX, 1993, pp. 467–511.Google Scholar
Inou, H. and Shishikura, M., The renormalization for parabolic fixed points and their perturbation. Preprint, 2006, available at https://www.math.kyoto-u.ac.jp/mitsu/pararenorm/ParabolicRenormalization.pdf.Google Scholar
Kahn, J.. A priori bounds for some infinitely renormalizable maps: I. Bounded primitive combinatorics. Preprint, IMS at Stony Brook, 2006/05.Google Scholar
Kahn, J. and Lyubich, M.. A priori bounds for some infinitely renormalizable quadratics. II. Decorations. Ann. Sci. Éc. Norm. Supér. (4)
41(1) (2008), 57–84.CrossRefGoogle Scholar
Kahn, J. and Lyubich, M.. A priori bounds for some infinitely renormalizable quadratics. III. Molecules. Complex Dynamics. Families and Friends. Ed. Schleicher, D.. A K Peters, Wellesley, MA, 2009, pp. 229–254.CrossRefGoogle Scholar
Kangasniemi, I., Okuyama, Y., Pankka, P. and Sahlsten, T.. Entropy in uniformly quasiregular dynamics. Ergod. Th. & Dynam. Sys. 41(8), 2397–2427.CrossRefGoogle Scholar
Khanin, K. and Teplinsky, A.. Robust rigidity for circle diffeomorphisms with singularities. Invent. Math. 169(1) (2007), 193–218.10.1007/s00222-007-0047-0CrossRefGoogle Scholar
Kozlovski, O., Shen, W. and van Strien, S., Rigidity for real polynomials. Ann. of Math. (2)
165(3) (2007), 749–841.CrossRefGoogle Scholar
Kozlovski, O., Shen, W. and van Strien, S.. Density of hyperbolicity. Ann. of Math. (2)
166(1) (2007), 145–182.10.4007/annals.2007.166.145CrossRefGoogle Scholar
Kozlovski, O. and van Strien, S.. Local connectivity and quasi-conformal rigidity of non-renormalizable polynomials. Proc. Lond. Math. Soc. (3)
99(2) (2009), 275–296.10.1112/plms/pdn055CrossRefGoogle Scholar
Lanford, O. E.. A computer assisted proof of the Feigenbaum conjectures. Bull. Amer. Math. Soc. (N.S.) 6 (1982), 427–434.CrossRefGoogle Scholar
Levin, G. and Przytycki, F.. External rays to periodic points. Israel J. Math. 94 (1995), 29–57.10.1007/BF02762696CrossRefGoogle Scholar
Levin, G. and van Strien, S.. Local connectivity of the Julia set of real polynomials. Ann. of Math. (2)
147(3) (1998), 471–541.CrossRefGoogle Scholar
Lyubich, M.. Teichmüller space of Fibonacci maps. New Trends in One-Dimensional Dynamics (Springer Proceedings in Mathematics & Statistics, 285). Eds. Pacifico, M. and Guarino, P.. Springer, Cham, 2019, pp. 221–237.10.1007/978-3-030-16833-9_12CrossRefGoogle Scholar
Lyubich, M.. Dynamics of quadratic polynomials. I, II, Acta Math. 178 (1997), 185–247, 247–297.CrossRefGoogle Scholar
Lyubich, M.. Feigenbaum–Coullet–Tresser universality and Milnor’s hairiness conjecture. Ann. of Math. (2)
149(2) (1999), 319–420.10.2307/120968CrossRefGoogle Scholar
Lyubich, M. and Yampolsky, M.. Dynamics of quadratic polynomials: complex bounds for real maps. Ann. Inst. Fourier (Grenoble) 47 (1997), 1219–1255.CrossRefGoogle Scholar
Lyubich, M. Y.. Non-existence of wandering intervals and structure of topological attractors of one dimensional dynamical systems: 1. The case of negative Schwarzian derivative. Ergod. Th. & Dynam. Sys. 9 (1989), 737–749.10.1017/S0143385700005307CrossRefGoogle Scholar
Manton, J.. Differential calculus, tensor products and the importance of notation. Preprint, 2013, arXiv:1208.0197.Google Scholar
Martens, M.. The periodic points of renormalization. Ann. of Math. (2)
147(3) (1998), 543–584.10.2307/120959CrossRefGoogle Scholar
Martens, M., de Melo, W. and van Strien, S.. Julia–Fatou–Sullivan theory for real one-dimensional dynamics. Acta Math. 168(3–4) (1992), 273–318.CrossRefGoogle Scholar
McMullen, C.. Renormalization and 3-Manifolds Which Fiber Over the Circle (Annals of Mathematics Studies, 142). Princeton University Press, Princeton, NJ, 1996.CrossRefGoogle Scholar
Milnor, J.. Local connectivity of Julia sets: expository lectures. The Mandelbrot Set, Theme and Variations (London Mathematical Society Lecture Note Series, 274. Ed. Lei, T.. Cambridge University Press, Cambridge, 2000, pp. 67–116.10.1017/CBO9780511569159.006CrossRefGoogle Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematics Studies, 160). Princeton University Press, Princeton, NJ and Oxford, 2006.Google Scholar
Shen, W.. On the metric properties of multimodal interval maps and
${C}^2$
density of Axiom A. Invent. Math. 156(2) (2004), 301–403.CrossRefGoogle Scholar
${C}^2$
density of Axiom A. Invent. Math. 156(2) (2004), 301–403.CrossRefGoogle ScholarSmania, D.. Complex bounds for multimodal maps: bounded combinatorics. Nonlinearity 14(5) (2001), 1311–1330.10.1088/0951-7715/14/5/320CrossRefGoogle Scholar
Smania, D.. Phase space universality for multimodal maps. Bull. Braz. Math. Soc. (N.S.) 36(2) (2005), 225–274.CrossRefGoogle Scholar
Smania, D.. On the hyperbolicity of the period-doubling fixed point. Trans. Amer. Math. Soc. 358(4) (2006), 1827–1846.CrossRefGoogle Scholar
Smania, D.. Solenoidal attractors with bounded combinatorics are shy. Ann. of Math. (2) 191(1) (2020), 1–79.CrossRefGoogle Scholar
Sörensen, D.. Infinitely renormalizable quadratic polynomials, with non-locally connected Julia set. J. Geom. Anal. 10(1) (2000), 169–206.CrossRefGoogle Scholar
Sullivan, D.. Quasiconformal homeomorphisms and dynamics. I. Solution of the Fatou–Julia problem on wandering domains. Ann. of Math. (2)
122(3) (1985), 401–418.CrossRefGoogle Scholar
Sullivan, D.. Bounds, quadratic differentials, and renormalization conjectures. AMS Centennial Publications, 2. Mathematics into the Twenty-first Century, 1988.Google Scholar
van Strien, S. and Vargas, E.. Real bounds, ergodicity and negative Schwarzian for multimodal maps. J. Amer. Math. Soc. 17(4) (2004), 749–782.10.1090/S0894-0347-04-00463-1CrossRefGoogle Scholar
Yampolsky, M.. Hyperbolicity of renormalization of critical circle maps. Publ. Math. Inst. Hautes Etudes Sci. 96 (2002), 1–41.10.1007/s10240-003-0007-1CrossRefGoogle Scholar
Yoccoz, J.-C.. On the local connectivity of the Mandelbrot set. Unpublished, 1990.Google Scholar