Hostname: page-component-68945f75b7-77sjt Total loading time: 0 Render date: 2024-09-03T12:59:19.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular perturbation of symbolic dynamics via thermodynamic formalism

Published online by Cambridge University Press:  01 August 2008

TAKEHIKO MORITA  and
HARUYOSHI TANAKA
TAKEHIKO MORITA
Affiliation:
Department of Mathematics, Graduate School of Science, Hiroshima University, Higashi-Hiroshima 739–8526, Japan (email: take@math.sci.hiroshima-u.ac.jp, hoxy-hd052710@hiroshima-u.ac.jp)
HARUYOSHI TANAKA
Affiliation:
Department of Mathematics, Graduate School of Science, Hiroshima University, Higashi-Hiroshima 739–8526, Japan (email: take@math.sci.hiroshima-u.ac.jp, hoxy-hd052710@hiroshima-u.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider singular perturbation of a mixing subshift of finite type by means of thermodynamic formalism. In our formulation, the perturbed systems are described by a family of potentials {Φ(α,⋅)} with large parameter α on a fixed subshift of finite type, and the original (unperturbed) system is characterized as the system at infinity obtained by collapsing the perturbed system upon taking 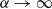. We apply our formulation to the collapse of cookie-cutter systems and dispersing open billiards.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 4 , August 2008 , pp. 1261 - 1289
Copyright
Copyright © 2008 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 1975.CrossRefGoogle Scholar
[2]Bowen, R.. Hausdorff dimension of quasi-circles. Publ. Math. IHES 50 (1979), 259–273.CrossRefGoogle Scholar
[3]Ikawa, M.. Singular perturbation of symbolic flows and poles of the zeta functions. Osaka J. Math. 27 (1990), 281–300.Google Scholar
[4]Ikawa, M.. Singular perturbation of symbolic flows and poles of the zeta functions. Addendum. Osaka J. Math. 29 (1992), 161–174.Google Scholar
[5]Dunford, N. and Schwartz, J. T.. Linear Operators Part I. Wiley, New York, 1988.Google Scholar
[6]Ionescu Tulcea, C. T. and Marinescu, G.. Théorie ergodique pour des classes d’opérateurs non comètement continues. Ann. of Math. 52 (1950), 140–147.CrossRefGoogle Scholar
[7]Kato, T.. Perturbation Theory for Linear Operators. Springer, Berlin, 1976.Google Scholar
[8]Morita, T.. The symbolic representation of billiards without boundary condition. Trans. Amer. Math. Soc. 325 (1991), 819–828.Google Scholar
[9]Morita, T.. Construction of K-stable foliations for two-dimensional dispersing billiards without eclipse. J. Math. Soc. Japan 56 (2004), 803–831.Google Scholar
[10]Morita, T.. Meromorphic extensions of a class of dynamical zeta functions and their special values at the origin. Ergod. Th. & Dynam. Sys. 26 (2006), 1127–1158.Google Scholar
[11]Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamical systems. Astérisque (1990), 187–188.Google Scholar
[12]Pesin, Ya. B.. Dimension Theory in Dynamical Systems: Comtemporary Views and Applications. The University of Chicago Press, Chicago, 1997.Google Scholar
[13]Ruelle, D.. Thermodynamic Formalism. Addison-Wesley, Reading, MA, 1978.Google Scholar
[14]Stoyanov, L.. Exponential instability and entropy of a class of dispersing billiards. Ergod. Th. & Dynam. Sys. 19 (1999), 201–226.Google Scholar
[15]Walters, P.. Introduction to Ergodic Theory. Springer, Berlin, 1982.Google Scholar